디멘의 블로그
Dimen's Blog
이데아를 여행하는 히치하이커
Alice in Logicland
Modal Logic
01 Apr 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
Types
| Name | Entailment | Axioms |
|---|---|---|
| K | Kripke model for possible worlds | $\Box(p \to q) \to (\Box p \to \Box q)$ |
| T | Reflexivity | K + $\Box p \to p$ |
| S4 | Reflexivity + Transitivity | T + $\Box p \to \Box \Box p$ |
| S4.2 | Reflexivity + Transitivity + R-convergence | S4 + $\Diamond \Box p \to \Box \Diamond p$ |
| S4.3 | Reflexivity + Transitivity + R-linearity | S4 + $(\Diamond p \land \Diamond q) \to$ $(\Diamond (p \land \Diamond q) \lor \Diamond(\Diamond p \land q))$ |
| S5 | Reflexivity + Transitivity + Symmetry | S4 + $(p \to \Box \Diamond p)$ |
The logics become strictly stronger as one moves down the table.
Modal Reduction
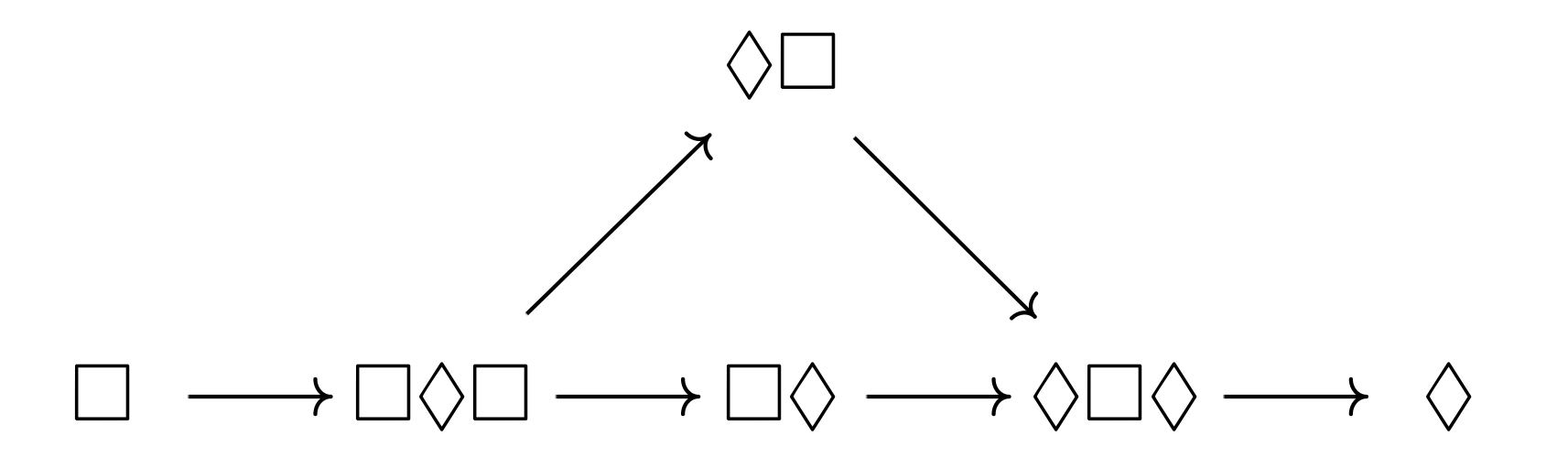
Theorem. In S4, any sequence of modal operators is equivalent to one of six combinations, and the entailment relations amongst these combinations are as follows:
Theorem. In S5, any sequence of modal operators is equivalent to either $\Box$ or $\Diamond$. Furthermore, every formula is equivalent to a flat formula—that is, a formula containing no modal operators within the scope of other modal operators.
Completeness Theorem
Theorem. K is complete.
Proof.
Lindenbaum’s Lemma. Any consistent theory can be extended to a maximally consistent theory.
The completeness statement is equivalent to “every consistent theory is satisfiable”, and applying Lindenbaum’s lemma, this is equivalent to “every maximally consistent theory is satisfiable”.
Let $u, v$ be maximally consistent theories. We write $u \lhd v$ when $\Box p \in u \implies p \in v$. The following can be shown without difficulty:
- When $u \lhd v$, we have $p \in v \implies \Diamond p \in u$
- For any maximally consistent theory $u$, if $p \in u$ and $\Box p \notin u$, then there exist maximally consistent theories $v, v’$ such that $p \in v, \lnot p \in v’$ and $u \lhd v, v’$.
From this, for a maximally consistent theory $u$, we can define the canonical Kripke model $\mathfrak{K} = (U, \prec, V)$ as follows:
- The collection of possible worlds $U$ is the collection of $v$ satisfying $u \lhd v$.
- The accessibility relation $\prec$ is $\lhd$.
- The valuation function $V(p, v)$ is true if and only if $p \in v$.
It can be shown without difficulty that $\mathfrak{K}$ satisfies $u$. ■
요네다 보조정리
21 Mar 2025Notation.
- $-$는 매개변수의 자릿값이다. $-$가 두 개 쓰였으면 매개변수가 두 개라는 뜻이다. 어느 매개변수가 어느 자리에 해당하는지는 맥락으로 파악한다.
- $\bullet$은 $-$를 우선하는 매개변수이다. 따라서 $\hom(-, \bullet)$은 $A$를 함자 $\hom(-, A)$에 대응시키는 함자이다.
- 함자 $F, G$에 대해 $[F, G]$를 $F$에서 $G$로 가는 자연적 변환natural transformation들의 모임으로 정의한다.
- 모든 범주는 국소적으로 작은locally small 범주라고 가정한다.
요네다 보조정리Yoneda lemma는 표현가능함자representable가 다른 함자를 바라볼 때 보이는 것이 무엇인지를 알려주는 정리이다.
예를 들어 $A \in \mathcal{A}$에 대해, 표현가능함자 $\hom_{\mathcal{A}}(-, A)$를 생각하자. 이 함자가 속하는 범주는 $[\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$이다. 따라서 $\hom_{\mathcal{A}}(-, A)$가 함자 $F : \mathcal{A}^{\mathrm{op}} \to \mathbf{Set}$를 바라볼 때 보이는 것은 다음 자연적 변환들의 집합이다.
\[[\hom_{\mathcal{A}}(-, A), F]\]위 집합은 $A \in \mathcal{A}$와 $F \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$으로부터 정의된 집합이다. 그런데 $A, F$로부터 집합을 정의할 수 있는 또다른 자연스러운 방식이 있다. 단순히 $F$에 $A$를 취하는 것이다.
\[F(A)\]요네다 보조정리에 따르면 두 집합은 동형isomorphic이다. 게다가 그냥 동형인 것이 아니라, $A \in \mathcal{A}$와 $F \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$에서 자연스럽게 동형naturally isomorphic이다. 요컨대 다음 두 함자가 $[\mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}], \mathbf{Set}]$에서 동형이다.
\[\begin{aligned} \text{(i)} \quad \mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] &\xrightarrow{\hspace{0.15cm} \hom_{\mathcal{A}}(-, \cdot)^{\mathrm{op}} \times 1 \hspace{0.15cm}} [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] \\ &\xrightarrow{\hom_{[\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]}(-, -)} \mathbf{Set} \\\\ \text{(ii)} \quad \mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] &\xrightarrow{-(-)} \mathbf{Set} \end{aligned}\]Remark. $\hom_{\mathcal{A}}(-, \cdot)^{\mathrm{op}}$에 붙은 $\mathrm{op}$는 함자의 정의역을 $\mathcal{A}^\mathrm{op}$로 맞춰주기 위함이고, 실질적으로는 $\hom_{\mathcal{A}}(-, \cdot)$와 같다.
증명. 증명의 개요만 적자면, $\hat{(\;\;)} : [\hom_\mathcal{A}(-, A), F] \to F(A)$와 $\tilde{(\;\;)}: F(A) \to [\hom_\mathcal{A}(-, A), F]$를 다음과 같이 정의한다.
\[\hat{\alpha} = \alpha_A(1_A), \quad \tilde{x} = \theta\]여기서 $\theta$는 $f : A’ \to A$를 다음과 같이 사상하는 자연적 변환이다.
\[\theta_{A'}: f \mapsto F(f^{\mathrm{op}})(x)\]$\theta$를 위와 같이 정의하는 이유는 다음 가환 도식을 만족하게끔 만들기 위함이다. ($(-)$에 $1_A$를 대입해 확인해 보라.)
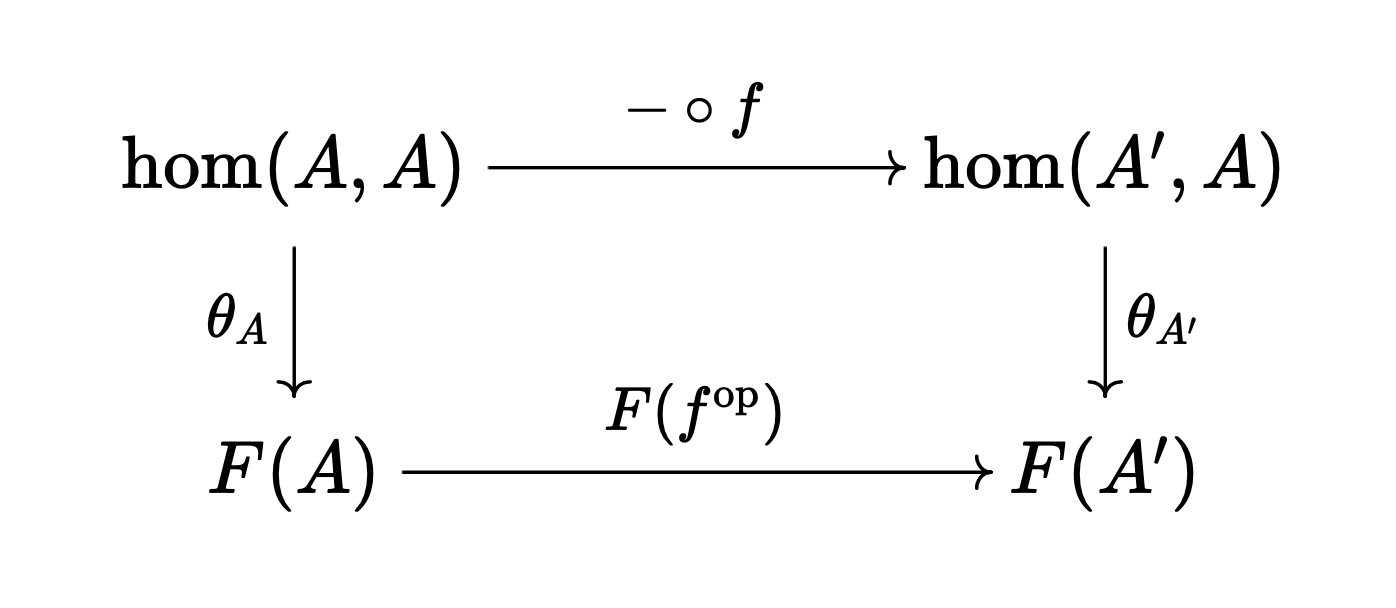
이제 임의의 $A \in \mathcal{A}, F : \mathcal{A}^\mathrm{op} \to \mathbf{Set}$에 대해 다음이 성립함을 보여아 한다.
- 임의의 $\alpha \in [\hom_\mathcal{A}(-, A), F]$에 대해 $\tilde{\hat{\alpha}} = \alpha$이다.
- 임의의 $x \in F(A)$에 대해 $\hat{\tilde{x}} = x$이다.
이것은 $[\hom_\mathcal{A}(-, A), F] \cong F(A)$임을 보인다. 여기에 더해, 해당 동형이 자연적임을 보여아 한다. 자아아알 생각해 보면 이것은 임의의 $A, A’ \in \mathcal{A}$와 $F, G \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$와 $f: A’ \to A$와 $\alpha: F \Rightarrow G$에 대해 다음 도식이 가환임을 보이는 것과 같다.
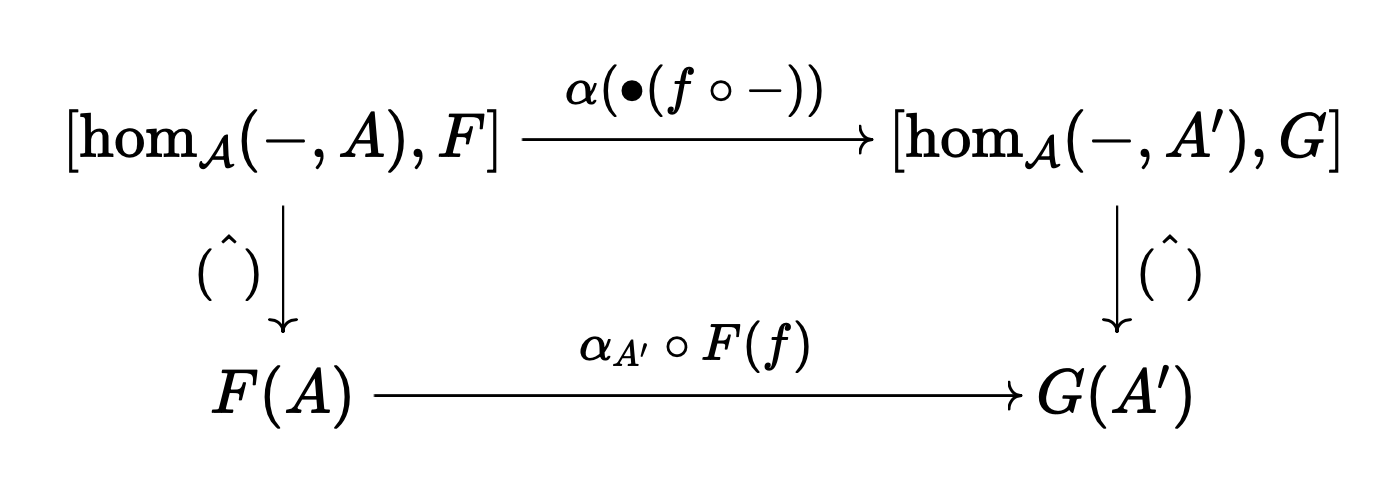
원소 단위로 적으면,
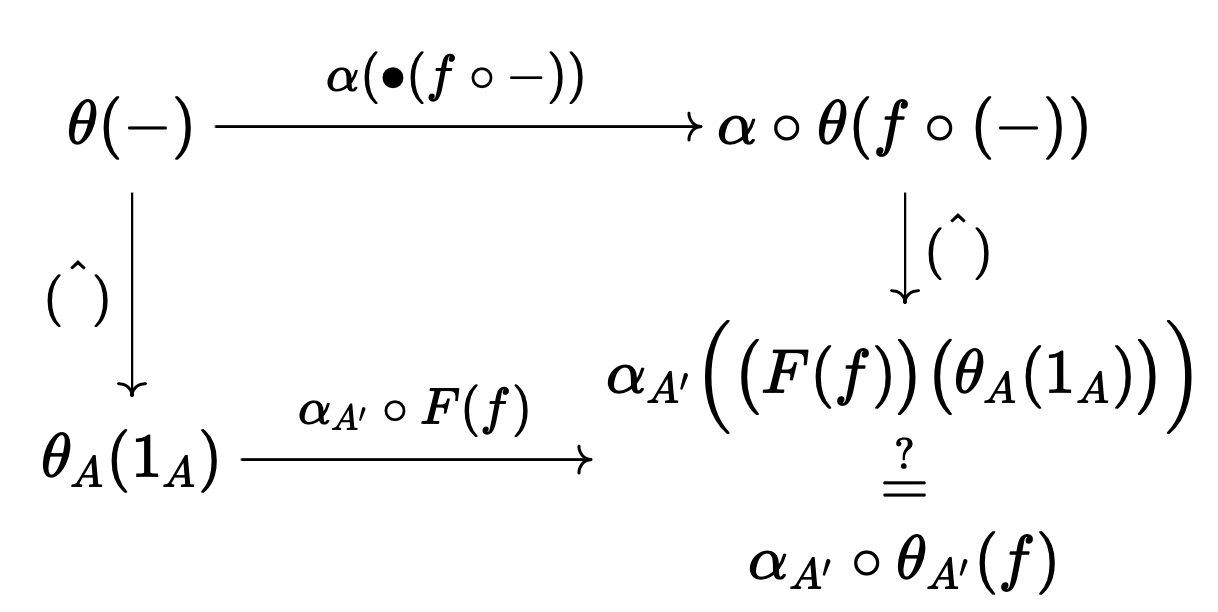
위가 성립함은 $\theta$의 자연성으로부터 따라 나온다. ■
요네다 따름정리와 관계론적 존재론
요네다 보조정리가 함의하는 결과 중 다음은 아주 중요하다. 필자는 이를 그냥 요네다 따름정리라고 부른다.
요네다 따름정리. $X, Y \in \mathcal{A}$라고 하자.
- $[\hom(-, X), \hom(-, Y)] \cong \hom(X, Y)$
- $X \cong Y \iff \hom(-, X) \cong \hom(-, Y)$
증명. $F = \hom(-, Y)$로 둔다. ■
요컨대 범주론에서 대상은, 그것이 받는 사상들의 집합과 다름없다. 일례로 정수 순서 범주에서 $0$은 초기 대상으로 정의할 수 있고, 더 일반적으로 $n$은 받는 사상들의 수가 $n$개인 대상으로 정의할 수 있다. 요네다 따름정리는 이처럼 대상을 그것이 다른 대상과 맺는 사상들로서 정의하는 접근이 모든(엄밀히는 국소적으로 작은) 범주에서 유효함을 보장한다. 필자는 이 접근을 관계론적 존재론이라고 부른다.
Yoneda Lemma
21 Mar 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
Notation.
- $-$ denotes a parameter placeholder. If two $-$ are used, it means there are two parameters. Which parameter corresponds to which position is determined by context.
- $\bullet$ is a parameter that takes precedence over $-$. Therefore, $\hom(-, \bullet)$ is a functor that maps $A$ to the functor $\hom(-, A)$.
- For functors $F, G$, we define $[F, G]$ as the collection of natural transformations from $F$ to $G$.
- We assume all categories are locally small categories.
The Yoneda lemma is a theorem that tells us what a representable functor sees when it looks at another functor.
For example, for $A \in \mathcal{A}$, consider the representable functor $\hom_{\mathcal{A}}(-, A)$. This functor belongs to the category $[\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$. Therefore, what $\hom_{\mathcal{A}}(-, A)$ sees when it looks at a functor $F : \mathcal{A}^{\mathrm{op}} \to \mathbf{Set}$ is the following set of natural transformations:
\[[\hom_{\mathcal{A}}(-, A), F]\]The above set is a set defined from $A \in \mathcal{A}$ and $F \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$. However, there is another natural way to define a set from $A, F$. Simply applying $F$ to $A$:
\[F(A)\]According to the Yoneda lemma, the two sets are isomorphic. Moreover, they are not just isomorphic, but naturally isomorphic in $A \in \mathcal{A}$ and $F \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$. In short, the following two functors are isomorphic in $[\mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}], \mathbf{Set}]$:
\[\begin{aligned} \text{(i)} \quad \mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] &\xrightarrow{\hspace{0.15cm} \hom_{\mathcal{A}}(-, \cdot)^{\mathrm{op}} \times 1 \hspace{0.15cm}} [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] \\ &\xrightarrow{\hom_{[\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]}(-, -)} \mathbf{Set} \\\\ \text{(ii)} \quad \mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] &\xrightarrow{-(-)} \mathbf{Set} \end{aligned}\]Remark. The $\mathrm{op}$ attached to $\hom_{\mathcal{A}}(-, \cdot)^{\mathrm{op}}$ is to adjust the domain of the functor to $\mathcal{A}^\mathrm{op}$, and is essentially the same as $\hom_{\mathcal{A}}(-, \cdot)$.
Proof. To outline the proof, we define $\hat{(\;\;)} : [\hom_\mathcal{A}(-, A), F] \to F(A)$ and $\tilde{(\;\;)}: F(A) \to [\hom_\mathcal{A}(-, A), F]$ as follows:
\[\hat{\alpha} = \alpha_A(1_A), \quad \tilde{x} = \theta\]where $\theta$ is a natural transformation that maps $f : A’ \to A$ as follows:
\[\theta_{A'}: f \mapsto F(f^{\mathrm{op}})(x)\]The reason for defining $\theta$ as above is to satisfy the following commutative diagram. (Verify by substituting $1_A$ for $(-)$.)
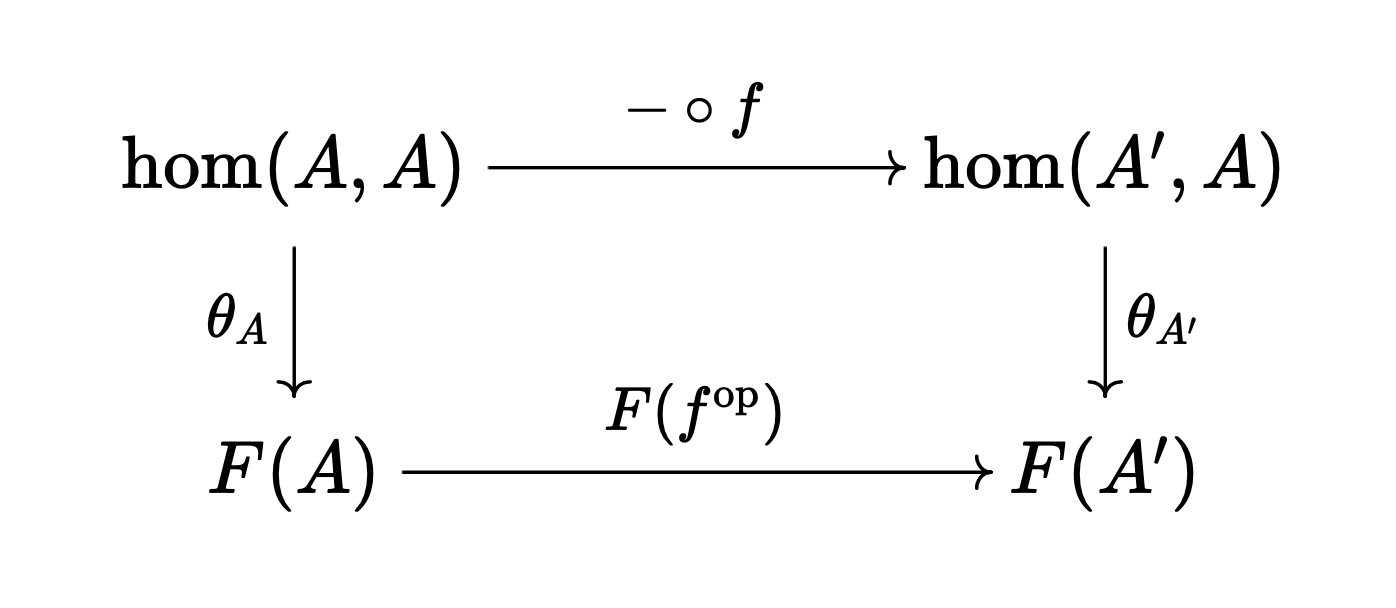
Now we must show that for any $A \in \mathcal{A}, F : \mathcal{A}^\mathrm{op} \to \mathbf{Set}$, the following holds:
- For any $\alpha \in [\hom_\mathcal{A}(-, A), F]$, we have $\tilde{\hat{\alpha}} = \alpha$.
- For any $x \in F(A)$, we have $\hat{\tilde{x}} = x$.
This shows that $[\hom_\mathcal{A}(-, A), F] \cong F(A)$. In addition, we must show that this isomorphism is natural. Upon careful consideration, this is equivalent to showing that for any $A, A’ \in \mathcal{A}$ and $F, G \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$ and $f: A’ \to A$ and $\alpha: F \Rightarrow G$, the following diagram commutes:
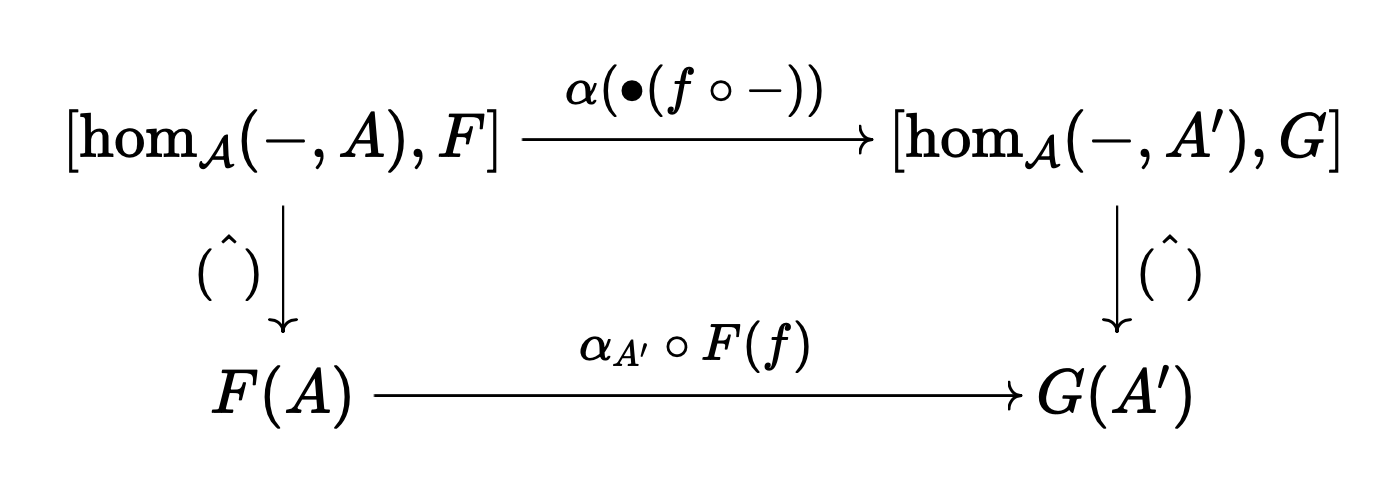
In terms of elements:
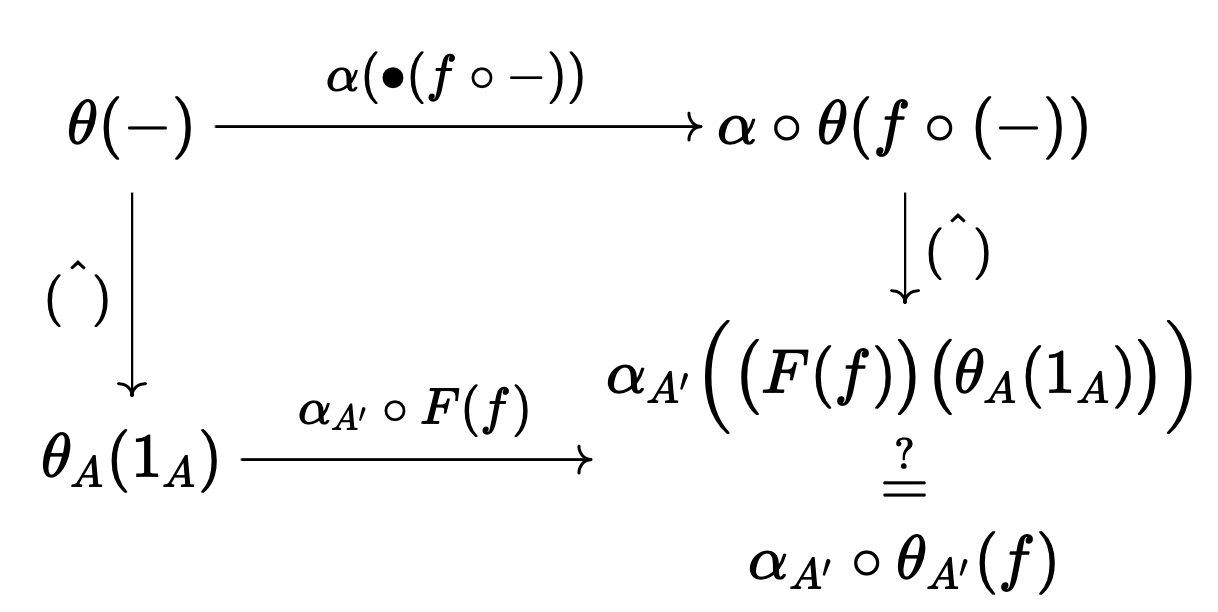
That the above holds follows from the naturality of $\theta$. ■
The Yoneda Corollary and Relational Ontology
Among the results implied by the Yoneda lemma, the following is particularly important. I shall simply call this the Yoneda corollary.
Yoneda Corollary. Let $X, Y \in \mathcal{A}$.
- $[\hom(-, X), \hom(-, Y)] \cong \hom(X, Y)$
- $X \cong Y \iff \hom(-, X) \cong \hom(-, Y)$
Proof. Let $F = \hom(-, Y)$. ■
In essence, in category theory, an object is nothing more than the collection of morphisms it receives. For instance, in the integer order category, $0$ can be defined as the initial object, and more generally, $n$ can be defined as the object that receives $n$ morphisms. The Yoneda corollary guarantees that this approach of defining objects through the morphisms they form with other objects is valid in all (strictly speaking, locally small) categories. I call this approach relational ontology.
양상 문맥 내 존재 양화에 관하여 — 콰인과 프레게
18 Mar 2025이 글은 David Kaplan, Quantifying In (1968)을 정리한 것이다.
1. 평범한 발생, 우연적 발생, 모호한 발생
다음 두 문장을 보자.
(1)과 (2)에서 모두 ‘둘’이 나타나지만, 매우 다른 방식으로 나타난다. (1)에서 ‘둘’이 나타나는 방식을 평범한 발생vulgar occurence이라고 하고, (2)에서 ‘둘’이 나타나는 방식을 우연적 발생accidental occurence이라고 하자.
단어가 평범하게 발생할 경우 해당 단어는 지시하며, 동일성에 대한 라이프니츠 원리를 만족한다(예컨데 ‘둘’을 ‘화성의 위성 개수’로 대치해도 문장의 진릿값이 보존된다). 단어가 우연적으로 발생할 경우 해당 단어는 지시하지 않으며, 라이프니츠 원리를 만족하지 않는다.
이제 다음의 문장들을 보자.
(3), (4), (5)에서 ‘둘’은 지시를 하는 것으로 보인다. 그러나 ‘둘’을 ‘화성의 위성 개수’로 바꾸면 문장의 진릿값이 보존되지 않는 것으로 보인다. 이것을 모호한 발생intermediate occurence이라고 하자.
언어철학에서 모호한 발생은 크게 두 가지 방식으로 설명된다. 첫째는 모호한 발생을 우연적 발생에 동화하는 것이고, 둘째는 모호한 발생을 평범한 발생에 동화하는 것이다.
2. 콰인: 모호한 발생은 우연적 발생이다
콰인은 모호한 발생을 우연적 발생에 동화한다. 그는 (3)에서 따옴표로 감싸진 문장은 하나의 단어이고, (5)에서 둘이 하나보다 크다고 믿었다 는 원자 술어라고 주장한다. 특히 (3), (4), (5)에서 ‘둘’이 나타나는 문맥을 불투명 문맥opaque context이라고 명명한 것은 그가 모호한 발생과 우연적 발생의 동일시를 염두에 뒀음을 시사한다.
콰인은 (3), (4), (5)와, 다음의 (6), (7), (8)을 대조한다.
(3), (4), (5)와 달리 (6), (7), (8)의 문형에서 ‘둘’은 평범하게 발생하는 것으로 보인다 (콰인이라면 ‘하나’는 여전히 우연적으로 발생한다고 주장할 것이다). 그러나 (6), (7), (8)은 고전 논리로 표현할 수 있는 문장이 아니다. 고전 논리는 ‘There exists $x$ such that…‘이라는 문형은 허용하지만 ‘$n$ is such that…‘이라는 표현은 결여하기 때문이다. 따라서 (6), (7), (8)의 의미론을 정당화하는 것이 과제로 남는다.
우선 (6)부터 보자. 최소한의 논리적 분석으로도 (6)이 적형식well-formed formula이 아님을 알 수 있다. 주어의 둘 은 이름의 사용use에 해당하지만, 뒤에 ‘하나보다 크다’를 적기 는 이름의 언급mention에 해당하기 때문이다. 따라서 (6)은 의미론적으로 정당하지 않다.
(7)의 의미는 아리스토텔레스적 본질주의Aristotelian essentialism로써 설명할 수 있다. 이 설명은 임의의 대상에 대해, 그에게 본질적인 속성과 우연적인 속성이 무엇인지를 규정한다. 콰인은 이같은 방식으로 (7)의 정당성을 설명한 바 있다.
(8)이 의미론적으로 정당함을 시사하는 예시는 많이 있다. 러셀의 다음 유명한 문장을 보자.
- 네 요트의 길이에 대해, 내가 생각한 네 요트의 길이는 그것보다 길다. The length of your yacht is such that I thought that your yacht was longer than that.
위 문장은 직관적으로 이해가 되며, 참인 듯하다. 이것은 (8)의 의미론적 정당성을 지지한다. 또한 콰인은 다음의 유명한 문장의 쌍을 거론한다.
a. 랄프는 누군가가 스파이라고 믿는다. Ralph believes that someone is a spy.
b. 누군가에 대해, 랄프는 그가 스파이라고 믿는다. Someone is such that Ralph believes they are a spy.
a에서는 존재 양화가 믿음 문맥 안에서, b에서는 밖에서 이루어진다. 한편 콰인은 믿음 문맥 속의 단어들을 우연적 발생과 동일시하기 때문에, 그에 따르면
- 랄프는 올트커트가 스파이라고 믿는다.
로부터 $\exists$-첨가를 적용하여 b를 유도할 수 없음에 유의하라. 그러나,
- 올트커트 씨에 대해, 랄프는 그가 스파이라고 믿는다.
로부터 b를 유도하는 것은 가능하다.
결론적으로 애매한 발생에 대한 콰인의 입장은 두 가지이다. 첫째, 애매한 발생은 우연적 발생과 동일시할 수 있다. 둘째, 불투명 문맥 안과 밖에서 단어가 등장하는 경우를 구분해야 할 필요가 있을 때는 ‘…에 대해such that’ 구문을 사용할 수 있다. 콰인은 이 구문을 관계론적 의미에서의 믿음relational sense of belief이라고 부른다. 마찬가지로 우리는 관계론적 의미에서의 양상, 주장, 생각 등의 구문을 도입할 수 있겠으나, 각 구문의 도입은 별도의 정당화를 요구한다.
3. 프레게: 모호한 발생은 평범한 발생이다
프레게는 모호한 발생을 평범한 발생에 동화한다. 프레게는 모호한 발생에서 라이프니츠 원리가 어긋나는 것으로 보이는 이유는, 해당 문맥에서 단어들의 실제 지시체를 우리가 혼동하기 때문이라고 주장한다. 이 혼동에는 두 가지 원인이 있다. 첫째는 지시 표현이 언제나 동일한 대상을 지시한다는 믿음이다. 이로부터 도출되는 둘째 믿음은, 대부분의 맥락에서 같은 대상을 지시하는 지시 표현은 언제나 같은 대상을 지시한다는 믿음이다.
그러나 지시 표현이 언제나 같은 대상을 지시한다는 믿음에 반하는 사례는 많다. 일례로 다음과 같이 중의적이거나 모호한ambiguous 단어의 사례가 있다.
(11)에 대한 자연스러운 분석은, 전자의 ‘F.D.R.’은 정치인을 지칭하는 한편 후자의 ‘F.D.R.’은 텔레비전 방송을 지칭한다고 보는 것이다. 이 경우 두 ‘F.D.R.’은 모두 평범한 발생이다. 그러나 극단적인 이름-지시체-일대일-대응-주의자라면 (11)이 ‘텔레비전에 딱 한 번 방영되었다’가 불투명 문맥임을 드러내며, 후자의 ‘F.D.R.’은 우연적 발생이라고 주장할지 모른다. 이 입장을 조금 더 그럴듯하게 포장하면, (11)은 올바르지 않은 문장이며 후자의 ‘F.D.R.’은 ‘‘F.D.R’이라는 이름의 텔레비전 방송’으로 수정되어야 한다고 주장할 수 있다.
이 사례가 보여주는 것은, 누군가 불투명 문맥으로 이해할 문장을 누군가는 모호함의 발생으로 이해할 수 있다는 것이다. 프레게는 지시 표현은 보통 그 일상적인 지시체를 지시하지만, 뜻sense 따위의 중간 대상을 지시할 수도 있으며, 이같은 모호함이 철학자들을 애매한 발생의 문제로 빠뜨린 원인이라고 주장한다. 프레게는 전자를 직접 지시direct reference, 후자를 간접 지시indirect reference라고 부른다.
| 콰인 | 프레게 | |
|---|---|---|
| 둘은 하나보다 크다 | 지시 문맥 | 직접 지시 |
| 필연적으로, 둘은 하나보다 크다 | 불투명 문맥 | 간접 지시 |
그렇다면 애매한 발생에서 표현의 지시체가 무엇인지 어떻게 알아낼 수 있을까? 저자는 합성의 원리principle of compositionality가 핵심이라고 말한다. 문장을 이루는 개별 요소의 지칭체가 불분명하다면, 문장 전체의 지칭체를 먼저 확인하고, 문장의 지칭체가 어떻게 분석 가능한지를 파악함으로써 개별 요소의 지칭체를 역추적할 수 있다는 것이다.
이 방법론에 따라 프레게는 인용구 안의 표현expression들은 자기 자신을 지시한다는 입장에 도달했다. 예를 들어 $\ulcorner 1 + 2 = 3 \urcorner$에서 $\ulcorner 1 \urcorner$의 지시체는 $\ulcorner 1 \urcorner$이다. 이같은 프레게의 입장은 인용 문맥 내의 양화사 사용을 가능하게 만든다. 로마 문자의 정의역이 대상이고, 그리스 문자의 정의역이 표현이라고 하면 프레게의 이론 하에서 우리는 다음과 같은 참을 표현할 수 있다.
표현에 비해 뜻sense 또는 의미meaning의 존재론적 위상은 불분명하지만, 비슷한 접근을 시도해 볼 수 있다. 먼저 다음의 사례로 예증되는 의미 따옴표를 도입하자.
고딕 문자의 정의역이 의미라고 하면 프레게주의는 다음과 같은 참을 표현할 수 있다.
Remark. 작은따옴표는 표현을 나타내는 반면, $\ulcorner$…$\urcorner$은 표현들의 합성을 의미한다. 마찬가지로 m…m은 의미를 나타내는 반면, M…M은 의미들의 합성을 의미한다. 물론 표현들의 합성도 표현이고, 의미들의 합성도 의미이기 때문에, 등식 1, 2가 성립한다. 저자가 등식 1, 2를 등식 3에 빗대어 설명했다는 사실을 떠올리면 도움이 된다.
- ‘The cat is on the mat’ $=$ $\ulcorner$The cat is on the mat$\urcorner$
- mThe cat is on the matm $=$ MThe cat is on the matM
- $237 = 2 \times 10^2 + 3 \times 10 + 7$
그러나 작은따옴표와 $\ulcorner$…$\urcorner$가 완전히 같고, 그리고 m…m과 M…M이 완전히 같은 것은 결코 아니다. 각 경우 전자는 불투명하지만 후자는 투명하기 때문이다. 따라서 1은 불가능하지만 2는 가능하다. 이것은 3은 말이 안 되지만 4는 올바른 것과 같은 이치이다.
- $\exists \alpha\; \big($ ‘$\alpha$ is on the mat’ is true$\big)$
- $\exists \alpha\; \big(\ulcorner \alpha$ is on the mat$\urcorner$ is true$\big)$
- $\exists n\; (237 < 2n7)$
- $\exists n\; (237 < 2 \times 10^2 + n \times 10 + 7)$
4. 지시 술어를 통한 프레게주의의 보강
이제 프레게주의가 (6), (7), (8)을 어떻게 설명하는지 보자.
그에 앞서, (4), (5), (7), (8)에서 믿음의 대상이 되는 것이 정확히 무엇인지를 명료화하는 것이 도움이 된다. S가 문장일 때, 누군가가 S를 믿는다는 것, 또는 S가 필연적이라는 것은 어떻게 형식화할 수 있는가? 본 논문에서는 간단한 길을 택하여, 문장은 자기 자신을 지시하는 것으로 간주하고, 필연을 문장에 대한 단항 술어로, 믿음을 주체와 문장 사이의 이항 술어로 간주한다. 따라서 (4), (5)는 다음과 같이 적을 수 있다.
(7), (8)을 콰인식으로 형식화하기 위해, 콰인의 관계론적 믿음과 관계론적 필연을 나타낼 술어 $\mathbf{Nec}$와 $\mathbf{Bel}$를 도입하자.
여기서 볼드체 문자 $\mathbf{x}$는 $\mathbf{x}$가 지시적으로서가 아닌, 오직 자리값placeholder으로서 사용되었음을 의미한다. 콰인에 따르면 $\mathbf{x}$는 불투명 문맥에 있으므로, 지시할 수 없기 때문이다.
프레게주의는 (15)와 (16)을 다음과 같이 형식한다.
상술한 Remark로 인해 동일한 술어 $\mathbf{N}, \mathbf{B}$를 사용할 수 있다.
하지만 (19)와 (20)만으로는 부족한 점이 있다. (19)와 (20)의 ‘둘’이 지시적이긴 하지만, (7)과 (8)의 ‘둘’과는 다른 대상을 지시한다. 전자는 표현을, 후자는 수를 지시하기 때문이다. 따라서 (7)과 (8), 또는 (17)과 (18)로부터 가능했을 논리적 추론이 (19)와 (20)만으로는 얻어지지 않는다. 예를 들어 (17)과 다음이 주어졌을 때,
다음을 도출할 수 있다.
그러나 (19)와 (21)은 다음을 도출하는 데 그친다.
- $\exists y \big(y =$ 화성의 위성 수 $\land$ $\mathbf{N}\ulcorner$둘은 하나보다 크다$\urcorner\big)$
한편 다음은 올바르지 않다. $\alpha$는 수가 아니라 표현이기 때문이다.
- $\exists \alpha \big(\alpha =$ 화성의 위성 수 $\land$ $\mathbf{N}\ulcorner \alpha$는 하나보다 크다$\urcorner\big)$
그러나 이 문제는 처치가 도입한 바 있는 지시 술어 $\Delta$를 도입함으로써 해결할 수 있다. $\alpha$가 $c$를 지칭할 때, 그리고 오직 그럴 때만 $\Delta(\alpha, c)$라고 하자. 그러면 프레게식으로 (22), (17), 그리고 (18)은 각각 다음과 같이 적을 수 있다.
논문의 저자는 (23), (24), (25)가 원 문장의 직관적인 의미를 포착할 뿐 아니라, 콰인과 달리 $\mathbf{Bel}, \mathbf{Nec}$ 등의 추가적인 술어를 소개하고 정의할 필요가 없다는 점을 강조한다.
5. 올트커트 역설
콰인은 다음의 사고실험을 제시한 바 있다. 랄프는 골목에서 갈색 모자를 쓴 수상한 인물이 벤치 밑의 서류가방을 가져가는 것을 보고는 그가 스파이일 것이라고 믿는다. 한편 랄프는 그가 속한 도시의 시장을 존경하며, 그가 스파이일 리가 없다고 믿는다. 그런데 사실 수상한 사람과 시장은 동일한 인물, 올트커트 씨이다.
콰인은 이를 다음과 같이 형식화한다.
(26), (27)을 관계론적 믿음으로 표현하면,
(28)에 의해 (29), (30)은 각각 다음을 시사한다.
따라서 랄프는 다음을 믿는 것으로 보인다.
그러나 (34)는 문제적이다. 콰인은 문제의 원인이 (32), (33)으로부터 (34)를 도출하는 데 있다고 주장한다. 프레게적 형식화는 콰인의 직관이 올바름을 증명한다. 자세한 과정은 생략하지만, (26), (27), (28)은 오직 다음을 도출한다.
여기까지는 좋다. 문제는 두 번째 역설이다. (9)가 참이라고 하자. 즉, 랄프는 스파이의 존재를 믿는다. 또한 랄프는 세상에 키가 정확히 똑같은 두 사람은 존재하지 않는다고 믿으므로 (매우 합당한 믿음이다) 키가 가장 짧은 스파이가 존재하리라 믿는다. 따라서 (39)가 성립한다.
콰인식으로 ‘키가 가장 작은 스파이’를 추출exportation하면,
$\exists$-첨가에 의해,
그리고 (41)은 (10)과 내용이 같다. 따라서 (9)와 (10)이 서로를 시사하게 되는 모순이 발생한다. 논문의 저자는 이 문제가 너무 까다로운 나머지 한때 양상 및 믿음 문맥에서 양화하는 것은 불가능하다는 입장으로 기울었으나, 이를 공략할 방안이 떠올랐다는 일화를 이야기한다. 이에 대해서는 다음 글에서 소개하도록 하겠다.
On Existential Quantification in Modal Contexts — Quine and Frege
18 Mar 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
This article is a summary of David Kaplan, Quantifying In (1968).
1. Vulgar Occurrence, Accidental Occurrence, and Intermediate Occurrence
Consider the following two sentences:
Although ‘two’ appears in both (1) and (2), it occurs in very different ways. Let us call the way ‘two’ appears in (1) a vulgar occurrence, and the way ‘two’ appears in (2) an accidental occurrence.
When a word occurs vulgarly, it refers and satisfies Leibniz’s principle of identity (for instance, substituting ‘two’ with ‘the number of moons of Mars’ preserves the truth value of the sentence). When a word occurs accidentally, it does not refer and fails to satisfy Leibniz’s principle.
Now consider the following sentences:
In (3), (4), and (5), ‘two’ appears to refer. However, substituting ‘two’ with ‘the number of moons of Mars’ does not appear to preserve the truth value of the sentences. This is called an intermediate occurrence.
In philosophy of language, intermediate occurrences are explained in two main ways. The first is to assimilate intermediate occurrences to accidental occurrences, and the second is to assimilate intermediate occurrences to vulgar occurrences.
2. Quine: Intermediate Occurrence is Accidental Occurrence
Quine assimilates intermediate occurrences to accidental occurrences. He argues that the sentence enclosed in quotation marks in (3) is a single word, and that believed that two is greater than one in (5) is an atomic predicate. In particular, Quine’s designation of the contexts in which ‘two’ appears in (3), (4), and (5) as opaque contexts suggests that he had in mind the identification of intermediate and accidental occurrences.
Quine contrasts (3), (4), and (5) with the following (6), (7), and (8):
Unlike (3), (4), and (5), in the sentence forms (6), (7), and (8), ‘two’ appears to occur vulgarly (though Quine would argue that ‘one’ still occurs accidentally). However, (6), (7), and (8) are not sentences that can be expressed in classical logic. Classical logic permits the form ‘There exists $x$ such that…’, but lacks the expression ‘$n$ is such that…’. Therefore, the task remains to justify the semantics of (6), (7), and (8).
Let us first consider (6). Even with minimal logical analysis, we can see that (6) is not a well-formed formula. The subject two corresponds to the use of a name, while writing it after ‘is greater than one’ corresponds to the mention of a name. Therefore, (6) is not semantically justified.
The meaning of (7) can be explained by Aristotelian essentialism. This explanation specifies, for any object, what properties are essential and what properties are accidental to it. Quine has explained the justification of (7) in this manner.
There are many examples suggesting that (8) is semantically justified. Consider Russell’s famous sentence:
- The length of your yacht is such that I thought that your yacht was longer than that.
This sentence is intuitively comprehensible and appears to be true. This supports the semantic justification of (8). Quine also mentions the following famous pair of sentences:
a. Ralph believes that someone is a spy.
b. Someone is such that Ralph believes they are a spy.
In (a), existential quantification occurs within the belief context, while in (b) it occurs outside. Since Quine identifies words in belief contexts with accidental occurrences, according to him, note that (b) cannot be derived from
- Ralph believes that Ortcutt is a spy
by applying $\exists$-addition. However, it is possible to derive (b) from
- Ortcutt is such that Ralph believes he is a spy.
In conclusion, Quine’s position on intermediate occurrences is twofold. First, intermediate occurrences can be identified with accidental occurrences. Second, when it is necessary to distinguish between cases where words appear inside and outside opaque contexts, the ‘such that’ construction can be used. Quine calls this construction belief in the relational sense. Similarly, we could introduce constructions of modality, assertion, thought, etc., in the relational sense, but the introduction of each construction requires separate justification.
3. Frege: Intermediate Occurrence is Vulgar Occurrence
Frege assimilates intermediate occurrences to vulgar occurrences. Frege argues that the reason Leibniz’s principle appears to fail in intermediate occurrences is that we confuse the actual referents of words in those contexts. This confusion has two causes. The first is the belief that referring expressions always refer to the same object. The second belief, derived from this, is that referring expressions that refer to the same object in most contexts always refer to the same object.
However, there are many cases that contradict the belief that referring expressions always refer to the same object. For instance, there are cases of ambiguous words:
A natural analysis of (11) is that the former ‘F.D.R.’ refers to the politician while the latter ‘F.D.R.’ refers to the television programme. In this case, both instances of ‘F.D.R.’ are vulgar occurrences. However, an extreme name-referent-one-to-one-correspondence theorist might argue that (11) reveals that ‘was broadcast on television only once’ is an opaque context, and that the latter ‘F.D.R.’ is an accidental occurrence. This position could be made slightly more plausible by arguing that (11) is an incorrect sentence and that the latter ‘F.D.R.’ should be corrected to ‘the television programme named “F.D.R.”’.
What this case shows is that what someone understands as an opaque context, someone else can understand as the occurrence of ambiguity. Frege argues that referring expressions usually refer to their ordinary referents, but can also refer to intermediate objects such as senses, and that such ambiguity is what led philosophers into the problem of intermediate occurrences. Frege calls the former direct reference and the latter indirect reference.
| Quine | Frege | |
|---|---|---|
| Two is greater than one | Referential context | Direct reference |
| Necessarily, two is greater than one | Opaque context | Indirect reference |
How then can we determine what the referent of an expression is in intermediate occurrences? The author states that the principle of compositionality is key. If the referents of the individual elements that make up a sentence are unclear, we can first identify the referent of the entire sentence and then trace back the referents of the individual elements by understanding how the referent of the sentence can be analysed.
Following this methodology, Frege arrived at the position that expressions within quotations refer to themselves. For example, in $\ulcorner 1 + 2 = 3 \urcorner$, the referent of $\ulcorner 1 \urcorner$ is $\ulcorner 1 \urcorner$. This position of Frege makes it possible to use quantifiers within quotational contexts. If the domain of Roman letters is objects and the domain of Greek letters is expressions, then under Frege’s theory we can express the following truth:
Although the ontological status of senses or meanings is unclear compared to expressions, we can attempt a similar approach. First, let us introduce meaning quotation marks exemplified by the following case:
If the domain of Gothic letters is meanings, then Fregeanism can express the following truth:
Remark. Single quotation marks denote expressions, while $\ulcorner$…$\urcorner$ signifies the composition of expressions. Similarly, m…m denotes meanings, while M…M signifies the composition of meanings. Of course, the composition of expressions is also an expression, and the composition of meanings is also a meaning, so equations 1 and 2 hold. It is helpful to recall that the author explained equations 1 and 2 by analogy with equation 3.
- ‘The cat is on the mat’ $=$ $\ulcorner$The cat is on the mat$\urcorner$
- mThe cat is on the matm $=$ MThe cat is on the matM
- $237 = 2 \times 10^2 + 3 \times 10 + 7$
However, single quotation marks and $\ulcorner$…$\urcorner$ are not completely identical, nor are m…m and M…M completely identical. In each case, the former is opaque while the latter is transparent. Therefore, 1 is impossible but 2 is possible. This is analogous to how 3 is nonsensical but 4 is correct.
- $\exists \alpha\; \big($ ‘$\alpha$ is on the mat’ is true$\big)$
- $\exists \alpha\; \big(\ulcorner \alpha$ is on the mat$\urcorner$ is true$\big)$
- $\exists n\; (237 < 2n7)$
- $\exists n\; (237 < 2 \times 10^2 + n \times 10 + 7)$
4. Strengthening Fregeanism through Denotation Predicates
Let us now see how Fregeanism explains (6), (7), and (8).
Before this, it is helpful to clarify precisely what is the object of belief in (4), (5), (7), and (8). When S is a sentence, how can we formalise that someone believes S, or that S is necessary? In this paper, we take the simple path of considering that sentences refer to themselves, and regard necessity as a unary predicate on sentences and belief as a binary predicate between subjects and sentences. Therefore, (4) and (5) can be written as follows:
To formalise (7) and (8) in Quine’s manner, let us introduce predicates $\mathbf{Nec}$ and $\mathbf{Bel}$ to represent Quine’s relational belief and relational necessity.
Here, the bold letter $\mathbf{x}$ signifies that $\mathbf{x}$ is used not referentially but solely as a placeholder. According to Quine, $\mathbf{x}$ is in an opaque context and therefore cannot refer.
Fregeanism formalises (15) and (16) as follows:
Due to the aforementioned Remark, we can use the same predicates $\mathbf{N}, \mathbf{B}$.
However, (19) and (20) alone are insufficient. Although ‘two’ in (19) and (20) is referential, it refers to a different object from ‘two’ in (7) and (8). The former refers to an expression, while the latter refers to a number. Therefore, logical inferences that were possible from (7) and (8), or (17) and (18), cannot be obtained from (19) and (20) alone. For example, when (17) and the following are given:
we can derive the following:
However, (19) and (21) only derive the following:
- $\exists y \big(y =$ the number of moons of Mars $\land$ $\mathbf{N}\ulcorner$two is greater than one$\urcorner\big)$
Moreover, the following is incorrect because $\alpha$ is an expression, not a number:
- $\exists \alpha \big(\alpha =$ the number of moons of Mars $\land$ $\mathbf{N}\ulcorner \alpha$ is greater than one$\urcorner\big)$
However, this problem can be solved by introducing the denotation predicate $\Delta$ that Church introduced. Let $\Delta(\alpha, c)$ when and only when $\alpha$ denotes $c$. Then under Frege’s theory, (22), (17), and (18) can be written as follows respectively:
The author of the paper emphasises that (23), (24), and (25) not only capture the intuitive meaning of the original sentences but also, unlike Quine, do not require the introduction and definition of additional predicates such as $\mathbf{Bel}$ and $\mathbf{Nec}$.
5. The Ortcutt Paradox
Quine presented the following thought experiment. Ralph sees a suspicious figure in a brown hat taking a briefcase from under a bench in an alley and believes that he is a spy. Meanwhile, Ralph respects the mayor of his city and believes that he could not possibly be a spy. However, the suspicious person and the mayor are actually the same individual, Mr Ortcutt.
Quine formalises this as follows:
Expressing (26) and (27) as relational beliefs:
By (28), (29) and (30) respectively suggest the following:
Therefore, Ralph appears to believe the following:
However, (34) is problematic. Quine argues that the problem lies in deriving (34) from (32) and (33). Fregean formalisation proves that Quine’s intuition is correct. Although the detailed process is omitted, (26), (27), and (28) only derive the following:
This is fine so far. The problem is the second paradox. Suppose (9) is true, i.e., Ralph believes in the existence of spies. Also, since Ralph believes that there are no two people in the world with exactly the same height (a very reasonable belief), he believes that there exists a shortest spy. Therefore, (39) holds:
Exporting ‘the shortest spy’ in Quine’s manner:
By $\exists$-addition:
And (41) has the same content as (10). Therefore, a contradiction arises where (9) and (10) imply each other. The author of the paper relates that this problem was so intractable that he once leaned towards the position that quantifying in modal and belief contexts is impossible, but that a way to tackle this occurred to him. This will be introduced in the next article.
참에 대한 이론이란 무엇인가?
12 Mar 2025이 글은 Scott Soames, What is a Theory of Truth? (1984)을 정리한 것이다.
초록
필드는 양상 반박을 통해 타르스키의 참 정의가 참의 의미를 해명하지 못한다고 주장했다. 이에 필드는 인과 이론으로부터 참을 정의하려는 기획을 세웠다. 그러나 본 논문에서는 필드의 기획 또한 양상 반박에 직면하기 때문에 실패한다고 주장한다. 대신 논문의 저자는 타르스키의 참 정의가 각 언어별로 참이 무엇인지를 해명할 수 있도록 하는 언어의 재정의를 제안한다.
1. 타르스키의 이론은 무엇을 시도하는가?
참 이론의 세 가지 목적
타르스키의 참 이론의 철학적 의의는, 의심의 여지가 없는 그 수학적 의의와는 다르게, 꾸준한 논쟁의 대상이다. 논쟁이 지속되는 이유 중 하나는 참에 대한 이론theory of truth의 목적이 무엇인지에 관해 학자마다 의견이 다르기 때문이다. 주요 의견은 다음과 같다.
- ‘참’이 무슨 의미인지를 설명한다.
- ‘참’을 다른 술어 및 논리 관계로 환원한다.
- ‘참’을 선험적인 개념으로 인정한 후 이로부터 철학적 입장을 발전시킨다.
1을 시도하는 이론은 ‘처치의 정리는 참이다’, ‘요한복음 1장 14절은 참이다’와 같이 참 술어가 문장이 아닌 명제에 적용되는 경우를 고려해야 한다. 타르스키의 참 이론은 오로지 형식적 문장에만 적용되므로, 1에 해당하지 않는다.
또한 그의 이론은 3에도 해당하지 않는다. 타르스키는 자신의 참 이론이 인식론과는 완전히 무관하다는 입장을 다음과 같이 밝혔다.
참에 대한 의미론적 정의는 “눈은 희다”라는 문장이 어떤 조건에서 승인되는지에 관해서는 아무 제약도 가하지 않는다. 그것은 오직, “눈은 희다”라는 문장을 승인하거나 거부할 때, 마찬가지로 “‘눈은 희다’는 참이다”를 승인하거나 거부해야 한다는 제약만을 가한다. 따라서 우리는 참에 대한 의미론적 정의를, 기존의 인식론적 태도에 어떠한 수정 없이 받아들일 수 있다. 우리는 소박한 실재론자로 남을 수도 있고, 비판적 실재론자, 관념론자, 경험론자, 형이상학자로도 남아 있을 수 있다.
의미론적 상승
그럼에도 타르스키의 참 술어는, 콰인이 의미론적 상승semantic ascent이라고 부른 기작을 통해 철학적 입장의 명제화에 도움을 줄 수 있다. 예를 들어 다음 형태의 추론들을 일반화하고 싶다고 하자.
- 눈의 희다 $\to$ (하늘은 푸르다 $\to$ 눈은 희다)
- 지구는 돈다 $\to$ (태양은 차갑다 $\to$ 지구는 돈다)
- …
자연스러운 일반화는 다음과 같다.
- 임의의 문장 $p, q$에 대해 ($p$가 참이다 $\to$ ($q$가 참이다 $\to$ $p$가 참이다))
이 형식화에서 참 술어는 나열한 각 사례를 일반화하는 데 불가피하다. 이에 대해 혹자는 다음과 같이 참 술어에 대한 의존을 없앨 수 있다고 반문할 수 있다.
- 임의의 문장 $p, q$에 대해 $p \to (q \to p)$
그러나 위 문장은 형태론적으로 올바르지 않다. 철학적 문제가 산재해 있는 2차 논리에 의존할 것이 아니라면, $p, q$는 명제가 아니라 문장이어야 하기 때문이다. 여기서 말하는 문장이란 수리논리적인 의미에서의 문장, 즉 자유변수가 없는 명제가 아니라, 철학적인 의미에서의 문장, 즉 기호들의 나열이다. 굳이 수리논리학의 언어를 쓰자면 $p, q$는 문장의 괴델 수이다. 요컨대 1이 아니라 2라는 것이다.
- $p =$ 눈은 희다, $q = $ 하늘은 푸르다
- $p =$ “눈은 희다”, $q = $ “하늘은 푸르다”
그런데 $\to$는 논리 연산자이므로, 양항에 문장이 아닌 명제가 와야 한다(수리논리학의 언어로는, 괴델 수가 아닌 문장이 와야 한다). 따라서 $p$를, $p$는 참이다 라는 명제로 만들어 줘야 한다. 형식적으로 쓰자면 다음과 같다.
- $\forall p, q \in \mathbb{N} \;\; T(\ulcorner p \;\dot{\to}\; (q \;\dot{\to}\; p) \urcorner)$
이같은 의미론적 상승 덕분에 몇몇 철학적 입장을 명제화할 수 있다. 예를 들어 실재론은 다음과 같이 정리할 수 있다.
어떤 문장 $s$가 존재하여 $s$는 참이지만, 인간의 인식으로는 $s$에 대한 충분한 근거를 찾는 것이 불가능하다.
이처럼 참 술어가 철학적 입장의 명제화에 자주 등장하기 때문에 일부 철학자는 ‘참’이 철학적으로 심오한 개념이라고 믿었지만, 이미 타르스키와 콰인이 지적했듯이 이것은 순전히 표현의 편의를 위한 사용에 지나지 않으며, 참에 대한 정의 자체는 여타 철학적 입장과 무관하다.
물리주의와 환원
타르스키의 참 이론은 2에 해당하며, 여기에는 그의 철학적 배경이 작용했다. 타르스키는 검소한 물리주의자moderate physicalist였다. ‘검소한’의 의미는 그가 환원의 종착지를 물리학뿐 아니라 논리학과 집합론까지 포함하는 것으로 이해했다는 것이다. 그는 자신의 물리주의와 호환 가능한 참의 정의를 원했으며, 때문에 참을 선험적 개념으로 인정하고 그 특징에 관한 공리를 나열하는 방식을 거부했다. 대신 그는 어떤 집합을 귀납적으로 정의한 다음에, ① 해당 집합을 진리집합으로 가지는 술어가 T-스키마를 모두 함의한다는 사실과, ② 해당 귀납적 정의를 만족하는 집합이 유일함을 보임으로써 참을 집합론으로 환원했다.
현대에 이르러 타르스키의 참 이론은 철학적 비판의 대상이 되었다. 본 논문의 저자는 이것이 부당한 비판이라고 주장한다. 비판의 주된 골자는 그의 이론이 참에 대한 이론이 응당 갖춰야 할 조건을 갖추지 못했다는 것인데, 이 조건들이 사실은 부당하거나 비정합적이기 때문이다.
2. 필드Hartry Field의 비판
타르스키식 정의의 두 단계
필드는 타르스키의 참 정의를 두 단계로 구분한다. 첫째는 원시적 지칭primitive denotation이다. 이 단계에서는 언어 $L$에서 이름 $n$이 대상 $o$를 지칭한다는 것과, 술어 $P$가 대상 $o$에 대해 성립한다는 것이 무엇인지 정의한다. 이 정의는 다음과 같이 이루어져 있다.
- 이름 $n$은 $L$에서 대상 $o$를 지칭한다 $\iff$ 다음 중 하나가 성립:
- $n = \text{‘apple’}, o = $ 사과
- $n = \text{‘banana’}, o = $ 바나나
- $n = \text{‘coconut’}, o = $ 코코넛
- …
- 술어 $P$는 $L$에서 대상 $o$에 대해 성립한다 $\iff$ 다음 중 하나가 성립:
- $P = \text{‘Round’}, o = $ 사과, 코코넛, …
- $P = \text{‘Long’}, o = $ 바나나, …
- …
두 번째 단계는 참에 대한 재귀적 정의이다. 이 정의는 다음과 같다.
- 문장 $S$는 $L$에서 참이다 $\iff$ $S \in K$
여기서 $K$는 다음을 만족하는 유일한 집합이다.
- 어떤 대상 $o$가 존재하여 $n$이 $o$를 지칭하고 $P$가 $o$에 대해 성립할 때, $\ulcorner Pn \urcorner \in K$
- $A \in K$이거나 $B \in K$일 때, $\ulcorner A \lor B \urcorner \in K$
- $A \notin K$일 때, $\ulcorner \lnot K \urcorner \in K$
양상 반박과 필드의 기획
필드는 원시적 지칭은 ‘$n$이 $o$를 지칭한다’의 의미를 해명하지 못한다고 주장한다. 필드에 따르면 지칭 관계는 언어 사용자들의 심리에 의존적이다. 따라서 ‘apple’이 사과가 아닌 바나나를 지칭하는 경우가 가능했다. 그러나 타르스키의 원시적 지칭에서는 $n$이 $o$를 지칭하는 필요충분조건 안에 ‘apple’이 사과와 결부되어 있으므로 ‘apple’이 사과를 지칭하는 것은 필연적이다. 요컨대 지칭의 정의가 하드코딩되어 있다는 점이 문제이다.
따라서 필드는 지칭에 대한 물리주의적 환원을 제시함으로써 타르스키의 한계를 극복하고자 한다. 필드의 기획은 크립키의 이론을 토대로 지칭에 대한 물리-인과적 이론을 제시함으로써, 임의의 화자의 언어 $L$에 대해 올바른 참의 정의를 도출하는 이론을 제시하는 것이다.
필드의 기획의 문제
그러나 필드의 기획에는 문제가 있다. 첫 번째 문제는 인과적 효력을 지니지 않는 것으로 보이는 추상적 대상의 지칭이 제기하는 문제이다.
그러나 그보다 심각한 두 번째 문제는, 필드의 반박대로라면 원시적 지칭이 지칭에 대한 의미를 해명하지 않을 뿐 아니라, 참에 대한 재귀적 정의 또한 참에 대한 의미를 해명하지 않는다는 점이다. 왜냐하면 참에 대한 재귀적 정의에는 논리 연산자와 관련된 규칙이 하드코딩되어 있기 때문이다. 따라서 양상 반박이 동일하게 유효하다. 일례로 $\lor$이 논리합을 의미하는 것은 분명 우연적이지만, 재귀적 정의에 따르면 “$T(\ulcorner A \lor B \urcorner) \Leftrightarrow T(\ulcorner A \urcorner)$ 또는 $T(\ulcorner B \urcorner)$”는 필연적이다.
따라서 필드는 1과 2뿐 아니라 3, 4, 5, …에 대한 물리주의적 환원 또한 제시해야 한다.
- 이름 $n$이 대상 $o$를 지칭한다.
- 술어 $P$가 대상 $o$에 대해 성립한다.
- 문장 $A$가 문장 $B$의 부정이다.
- 문장 $A$가 문장 $B, C$의 논리합이다.
- 문장 $A$가 문장 $B$에서 변수 $u$의 존재를 양화한다. (…)
그러나 어떻게 3, 4, 5, …를 참에 대한 순환적 의존 없이 환원할 수 있는가는 불분명하다. 논문의 저자는 지금까지 이루어진 이 작업에 대한 시도가 성공적이지 못했다고 주장한다. 그 예시로 콰인이 진릿값 연산자를 언어 공동체의 집단적 승인 또는 거부로 환원하려고 했던 시도를 거론하는데, 이것이 문제적인 이유는 Alan Berger, Quine on ‘Alternative Logics’ and Verdict Tables (1980)을 참고하라고 한다. (난 아직 안 읽어봤는데 아마 양상 문제일듯)
덤. Burgess는 Truth에서 필드의 기획이 크립키의 이론에 의존하는 것 또한 문제적이라고 지적한다. 크립키의 이론은 지시에 대한 이론이 아니기 때문이다. 크립키의 이론은 이름 $n$을 사용하여 대상 $o$를 지시하는 최초의 행위가 어떻게 이어짐으로써 이름의 의미론을 형성하는지에 대한 이론으로, 그의 이론에서 지시는 선험적 개념이다. 크립키 본인도 자신의 이론이 지시에 대한 환원주의라는 세간의 의견에 강하게 반발했다.
3. 의미와 참의 관계
대부분의 언어철학자는 의미와 참이 상호 시사적인 관계에 있음을 인정한다. 일례로 다음을 인정한다.
- 문장 $S$가 언어 $L$에서 $p$를 의미한다면, $S$가 $L$에서 참일 필요충분조건은 $p$이다.
따라서 일부 철학자들은 타르스키의 참 이론이 의미에 대한 이론으로 확장될 수 있으리라 기대했다. 그러나 양상 반박은 타르스키의 참 이론이 의미에 대한 이론으로 연결될 수 없음 또한 보여준다. 예컨데 페아노 산술에 대해 정의한 타르스키의 참 술어는 1을 시사하지만 2를 시사하지는 않기 때문이다. 오히려 타르스키의 정의는 3을 시사한다.
- $T(\ulcorner 1 \;\dot{+}\; 1 = 2 \urcorner) \Leftrightarrow 1 + 1 = 2$
- $\dot{+}$의 의미가 곱셈이었다면, $T(\ulcorner 1 \;\dot{+}\; 1 = 2 \urcorner) \Leftrightarrow 1 \times 1 = 2$
- $\dot{+}$의 의미가 곱셈이었다면, $T(\ulcorner 1 \;\dot{+}\; 1 = 2 \urcorner) \Leftrightarrow 1 + 1 = 2$
물론 타르스키는 참에 대한 정의가 실질적으로 적합materially adequate할 것을 요구하기 때문에, $\dot{+}$의 의미가 실제로 곱셈이었다면 $T(\ulcorner 1 \;\dot{+}\; 1 = 2 \urcorner) \Leftrightarrow 1 + 1 = 2$를 시사하는 $T$는 올바른 참의 정의가 아니라고 주장할 것이다. 즉, 타르스키는 다음을 주장한다. ($\square p$는 $p$가 필연적이라는 의미이다)
a. $\square($ $T$가 참 술어이다 $\to$ ( 문장 $S$의 의미가 $\phi$이다 $\to$ $\;T(S) \Leftrightarrow \phi$이다 ) $)$
그러나 참에 대한 이론으로부터 의미에 대한 이론을 유도하려는 접근은 다음의 명제에 의존한다.
b. $T$가 참 술어이다 $\to$ $\square($ 문장 $S$의 의미가 $\phi$이다 $\to$ $\;T(S) \Leftrightarrow \phi$이다 $)$
a와 b는 다른 명제이다. 타르스키의 이론은 a를 보장하지만 b는 보장하지 않는다.
4. 새롭게 정의하는 ‘참에 대한 이론’
언어의 본질적 성질로서의 의미
지금까지 살펴 본 타르스키의 참에 대한 비판은, 언어 $L$에서 이름이 지칭하는 대상들이 우연적이어야 함을, 즉 의미론이 $L$의 화자에 의존적임을 전제했다. 그러나 논문의 저자는 이같은 방식으로 언어를 바라보는 대신, 이름이 무엇을 지칭하는가에 대한 정보 또한 언어의 일부로 볼 것을 제안한다.
일례로 1차 논리에서 언어 $L$은 삼중쌍 $\langle S_L, D_L, F_L \rangle$로 간주할 수 있다(여기서 말하는 언어는 모델론의 언어와 사뭇 다르다. 여기서의 언어는 형태론뿐 아니라 의미론도 가지고 있다). 각각의 의미는 다음과 같다.
- $S_L$: 적형식well-formed formula의 집합
- $D_L$: 지칭 가능한 대상들의 집합
- $F_L$: 각각의 이름을 대상에 대응시키는 해석interpretation 함수
이와 같이 언어를 정의할 경우, 타르스키의 참 정의는 임의의 언어 $L$에 대해 실질적으로 적합한 참 술어 $T_L$을 내놓는다. 또한 $F_L$은 튜플의 집합에 불과하므로, 타르스키의 물리주의적 노선에서 벗어나지 않는다. 요컨대 논문의 저자는 언어의 의미론을 그 언어의 본질적 성질essential property로 간주함으로써 타르스키의 참 정의를 일반적인 참의 정의로 승격시킬 수 있다고 주장한다. 따라서 언어 $L$에서 이름 $n$이 그것이 지칭하는 대상 $o$가 아닌 다른 대상을 지시했을 경우는 없다. 언어 사용자 집단은 언어에 의미론을 부여하는 주체가 아니라, 어떤 언어를 사용할지 선택하는 주체이다. 그리고 집단이 사용하는 언어를 판단하는 문제는 의미론의 문제가 아닌 화용론의 문제이다.
유형type과 토큰token
필드의 물리주의적 배경은 그가 문장보다 발화utterance에 주목하게끔 만들었다. 필드는 타르스키가 문장에 대한 참의 정의만 제시했을 뿐, 발화에 대한 참의 정의는 제시하지 못했다고 주장한다. 만약 타르스키가 이 반박을 들었다면, 그는 이 작업이 다음과 같이 두 단계로 구분되어야 한다고 말했을 것이다.
- 언어 $L$에서 발화 $u$가 문장 $s$의 발화가 되는 것은 어떤 원리를 통해서인가?
- 언어 $L$에서 문장 $s$가 참이라는 것은 무슨 의미인가?
따라서 타르스키의 정의는 유형 정의이다. 반면 필드는 다음 질문에 답하고자 한다.
- 언어 $L$에서 토큰 $t$가 참이 되는 것은 무슨 의미인가?
여기서 토큰은 종이에 적힌 흑연 자국일 수도 있고, 칠판의 백묵 자국일 수도 있고, 음성일 수도 있다. 즉 필드가 모색하는 것은 토큰 정의이다. 그러나 참에 대한 토큰 정의가 가능하지는 의문스럽다. 필드 본인은 다음과 같이 타르스키의 정의를 변형함으로써 토큰 정의에 도달하고자 시도했다.
- $\ulcorner \lnot e \urcorner$의 토큰이 참이다 $\Leftrightarrow$ 해당 토큰이 포함하는 $e$의 토큰이 참이 아니다.
그러나 앞서 말했듯이 위 정의는 $\lnot$의 의미를 부정으로 하드코딩하므로, 똑같이 양상 반론에 직면한다는 문제가 있다. 따라서 위의 정의는 다음과 같이 수정되어야 한다.
- 명제 $B$의 부정인 명제 $A$의 토큰이 참이다 $\Leftrightarrow$ 어떤 $B$의 토큰이 거짓이다
하지만 설령 ‘…의 부정이다’가 물리주의적으로 환원될 수 있다고 하더라도, 주어진 맥락에서 유관한 $B$의 토큰을 어떻게 특정할 수 있는지가 불분명하다. 예를 들어 다음 예문을 보자.
기후 위기와 관련된 트럼프의 그 주장은 틀렸다.
트럼프가 기후 위기와 관련하여 한 수많은 발언 토큰들 중 무엇이 위 문장에서 부정의 대상이 되어야 하는지는 불분명하다. 심지어 $B$의 토큰은 아예 존재하지 않을 수도 있다. 예를 들어 다음 예문을 보자.
트럼프가 윤리학 강의를 진행한다면 대부분의 내용이 틀릴 것이다.
필자가 아는 한에서 트럼프는 윤리학 강의를 진행한 적이 없으므로, 위 문장에서 부정의 대상이 되는 토큰은 존재하지 않는다. 그러나 위 문장이 참이라고 주장하는 것은 충분히 합당해 보인다. 이것은 참에 대한 토큰 정의이 봉착하는 난관을 드러낸다. 이로부터 논문의 저자는 참에 대한 타르스키의 유형 정의를 일단 받아들이고, 언어, 표현, 화자, 그리고 발화 사이의 화용론적 관계가 물리주의로 환원될 수 있는지는 별개의 문제로 봐야 한다고 주장한다.
화용론의 문제
비록 논문의 저자는 언어와 화자의 관계를 화용론에 영역에 귀속시켰지만, 그렇다고 해서 이 문제가 중요하지 않은 것은 아니라고 강조한다. 언어와 화자의 관계에 대해서도 여러 철학적 고찰점이 있기 때문이다. 일례로 콰인은 “화자 $A$가 언어 $L$을 사용한다”라는 진술이 물리주의적으로 환원될 수 없다고 주장한다(가바가이 논증). 논문의 저자에 따르면 콰인의 입장은, 타르스키의 참 정의를 받아들이되 언어와 화자의 관계를 물리주의적으로 환원하는 것을 거부하는 입장으로 볼 수 있다.
참 선제론의 문제
마지막으로 논문의 저자는 참의 개념으로부터 의미에 대한 이론을 유도하려는 시도, 특히 참 개념의 습득이 의미론적 능력semantic competence의 전제 조건이라는 이론 일반은 모두 성공할 수 없다고 주장한다. 자세히 설명하지는 않지만, 아마 다음과 같은 문제이지 않을까 싶다. 참의 개념으로부터 의미에 대한 이론을 유도하려는 시도는 1로부터 2를 주장하고자 한다.
- 문장 $S$의 의미가 $p$이다 $\implies$ $S$가 참이다 $\leftrightarrow p$
- $S$가 참이다 $\leftrightarrow p$ $\implies$ 문장 $S$의 의미가 $p$이다.
하지만 $\leftrightarrow$를 고전 논리의 동치 관계로 이해하든, 양상 논리의 필연적 동치 관계로 이해하든 간에 2는 성립하지 않는다. 예를 들어 다음은 필연적으로 성립한다.
- $1 + 1 = 2 \leftrightarrow $ 페르마의 마지막 정리
그러나 $1 + 1 = 2$의 의미가 페르마의 마지막 정리인 것은 아니다.
5. 결론
결론적으로 논문의 저자는 참에 대한 이론이 의미에 대한 이론과 직결되어 있어야 한다는 요구는 부당하다고 주장함으로써 타르스키의 참 정의와, 그것이 함의하는 참에 대한 축소주의deflationism를 옹호한다. 이것이 참에 대한 이론이 불필요함을 의미하지는 않는다. 크립키의 참 이론은 타르스키의 참 이론을 실질적으로 발전시켰다. 그러나 그 발전은 이미 우리에게 익숙한 참의 성질들을 T-스키마로써 정확히 해명하고, 올바르게 설계된 형태론으로 거짓말쟁이 역설과 같은 모순을 회피하는 데 있다. 참에 대한 이론으로부터 이 이상을 기대하는 것은 바람직하지 않다.
What is a Theory of Truth?
12 Mar 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
This article is a summary of Scott Soames, What is a Theory of Truth? (1984).
Abstract
Field argued through modal objections that Tarski’s definition of truth fails to elucidate the meaning of truth. In response, Field proposed a project to define truth from causal theory. However, this paper argues that Field’s project also fails because it faces the same modal objections. Instead, the author proposes a redefinition of language that enables Tarski’s definition of truth to elucidate what truth is for each language.
1. What Does Tarski’s Theory Attempt?
Three Purposes of Theories of Truth
The philosophical significance of Tarski’s theory of truth, unlike its indubitable mathematical significance, has been the subject of ongoing debate. One reason for the continuing controversy is that scholars disagree about what the purpose of a theory of truth should be. The main positions are as follows:
- To explain what ‘truth’ means.
- To reduce ‘truth’ to other predicates and logical relations.
- To accept ‘truth’ as a primitive concept and develop philosophical positions from it.
A theory attempting 1 must consider cases where the truth predicate applies to propositions rather than sentences, such as ‘Church’s theorem is true’ or ‘John 1:14 is true’. Since Tarski’s theory of truth applies only to formal sentences, it does not correspond to 1.
Moreover, his theory does not correspond to 3 either. Tarski expressed his position that his theory of truth is completely unrelated to epistemology as follows:
The semantic definition of truth does not impose any constraints on the conditions under which the sentence “snow is white” is accepted. It only imposes the constraint that when accepting or rejecting the sentence “snow is white”, one must likewise accept or reject “‘snow is white’ is true”. Therefore, we can accept the semantic definition of truth without any modification to existing epistemological attitudes. We can remain naive realists, or remain critical realists, idealists, empiricists, or metaphysicians.
Semantic Ascent
Nevertheless, Tarski’s truth predicate can assist in the articulation of philosophical positions through what Quine called semantic ascent. For example, suppose we wish to generalise inferences of the following form:
- Snow is white $\to$ (The sky is blue $\to$ Snow is white)
- The Earth rotates $\to$ (The sun is cold $\to$ The Earth rotates)
- …
The natural generalisation is as follows:
- For any sentences $p, q$: ($p$ is true $\to$ ($q$ is true $\to$ $p$ is true))
In this formalisation, the truth predicate is indispensable for generalising each enumerated case. One might object that the dependence on the truth predicate can be eliminated as follows:
- For any sentences $p, q$: $p \to (q \to p)$
However, the above sentence is not syntactically correct. Unless we rely on second-order logic, which is fraught with philosophical problems, $p, q$ must be sentences rather than propositions. The sentences here are sentences in the mathematical logical sense, i.e., not propositions without free variables, but sentences in the philosophical sense, i.e., strings of symbols. To use the language of mathematical logic precisely, $p, q$ are Gödel numbers of sentences. In short, it is 2 rather than 1.
- $p =$ Snow is white, $q = $ The sky is blue
- $p =$ “Snow is white”, $q = $ “The sky is blue”
However, since $\to$ is a logical operator, propositions rather than sentences must appear on both sides(in the language of mathematical logic, sentences rather than Gödel numbers must appear). Therefore, $p$ must be made into the proposition $p$ is true. Formally, this is written as follows:
- $\forall p, q \in \mathbb{N} \;\; T(\ulcorner p \;\dot{\to}\; (q \;\dot{\to}\; p) \urcorner)$
Thanks to such semantic ascent, several philosophical positions can be articulated. For example, realism can be formulated as follows:
There exists some sentence $s$ such that $s$ is true, but it is impossible for human cognition to find sufficient grounds for $s$.
Because the truth predicate frequently appears in the articulation of philosophical positions, some philosophers believed that ‘truth’ is a philosophically profound concept. However, as Tarski and Quine already pointed out, this is merely for expressive convenience, and the definition of truth itself is unrelated to other philosophical positions.
Physicalism and Reduction
Tarski’s theory of truth corresponds to 2, and his philosophical background played a role here. Tarski was a moderate physicalist. The meaning of ‘moderate’ is that he understood the terminus of reduction to include not only physics but also logic and set theory. He wanted a definition of truth compatible with his physicalism, and therefore rejected the approach of accepting truth as a primitive concept and listing axioms about its characteristics. Instead, he reduced truth to set theory by inductively defining a certain set, then showing both ① that a predicate having that set as its truth set entails all T-schemas, and ② that the set satisfying that inductive definition is unique.
In modern times, Tarski’s theory of truth has become the subject of philosophical criticism. The author of this paper argues that this is unjust criticism. The main thrust of the criticism is that his theory lacks the conditions that a theory of truth should properly possess, but these conditions are in fact unjust or incoherent.
2. Field’s Criticism
Two Stages of Tarskian Definition
Field distinguishes Tarski’s definition of truth into two stages. The first is primitive denotation. In this stage, one defines what it means for a name $n$ to denote an object $o$ in language $L$, and for a predicate $P$ to hold of an object $o$. This definition consists of the following:
- Name $n$ denotes object $o$ in $L$ $\iff$ one of the following holds:
- $n = \text{‘apple’}, o = $ apple
- $n = \text{‘banana’}, o = $ banana
- $n = \text{‘coconut’}, o = $ coconut
- …
- Predicate $P$ holds of object $o$ in $L$ $\iff$ one of the following holds:
- $P = \text{‘Round’}, o = $ apple, coconut, …
- $P = \text{‘Long’}, o = $ banana, …
- …
The second stage is the recursive definition of truth. This definition is as follows:
- Sentence $S$ is true in $L$ $\iff$ $S \in K$
where $K$ is the unique set satisfying the following:
- When there exists an object $o$ such that $n$ denotes $o$ and $P$ holds of $o$, then $\ulcorner Pn \urcorner \in K$
- When $A \in K$ or $B \in K$, then $\ulcorner A \lor B \urcorner \in K$
- When $A \notin K$, then $\ulcorner \lnot A \urcorner \in K$
Modal Objections and Field’s Project
Field argues that primitive denotation fails to elucidate the meaning of ‘$n$ denotes $o$’. According to Field, the denotation relation depends on the psychology of language users. Therefore, it was possible for ‘apple’ to denote banana rather than apple. However, in Tarski’s primitive denotation, since ‘apple’ is coupled with apple within the necessary and sufficient condition for $n$ to denote $o$, it is necessary that ‘apple’ denotes apple. In short, the problem is that the definition of denotation is hardcoded.
Therefore, Field seeks to overcome Tarski’s limitations by presenting a physicalist reduction of denotation. Field’s project is to present a physico-causal theory of denotation based on Kripke’s theory, thereby providing a theory that derives the correct definition of truth for any speaker’s language $L$.
Problems with Field’s Project
However, Field’s project has problems. The first problem is the issue raised by the denotation of abstract objects that appear to lack causal efficacy.
However, a more serious second problem is that, following Field’s objection, not only does primitive denotation fail to elucidate the meaning of denotation, but the recursive definition of truth also fails to elucidate the meaning of truth. This is because rules related to logical operators are hardcoded in the recursive definition of truth. Therefore, the modal objection is equally valid. For instance, while it is clearly contingent that $\lor$ means disjunction, according to the recursive definition, “$T(\ulcorner A \lor B \urcorner) \Leftrightarrow T(\ulcorner A \urcorner)$ or $T(\ulcorner B \urcorner)$” is necessary.
Therefore, Field must also present physicalist reductions of 3, 4, 5, … as well as 1 and 2.
- Name $n$ denotes object $o$.
- Predicate $P$ holds of object $o$.
- Sentence $A$ is the negation of sentence $B$.
- Sentence $A$ is the disjunction of sentences $B, C$.
- Sentence $A$ existentially quantifies variable $u$ in sentence $B$. (…)
However, it is unclear how 3, 4, 5, … can be reduced without circular dependence on truth. The author argues that attempts at this work so far have not been successful. As an example, he mentions Quine’s attempt to reduce truth-functional operators to collective acceptance or rejection by the linguistic community, which is problematic for reasons given in Alan Berger, Quine on ‘Alternative Logics’ and Verdict Tables (1980). (I haven’t read this yet, but it’s probably a modal problem.)
Addition. Burgess points out in Truth that Field’s project’s dependence on Kripke’s theory is also problematic. This is because Kripke’s theory is not a theory of reference. Kripke’s theory is about how the initial act of using name $n$ to refer to object $o$ continues to form the semantics of names; in his theory, reference is a primitive concept. Kripke himself strongly objected to the popular opinion that his theory is reductionist about reference.
3. The Relationship Between Meaning and Truth
Most philosophers of language acknowledge that meaning and truth are in a mutually suggestive relationship. For instance, they acknowledge the following:
- If sentence $S$ means $p$ in language $L$, then the necessary and sufficient condition for $S$ to be true in $L$ is $p$.
Therefore, some philosophers expected that Tarski’s theory of truth could be extended to a theory of meaning. However, the modal objection also shows that Tarski’s theory of truth cannot be connected to a theory of meaning. For example, Tarski’s truth predicate defined for Peano arithmetic suggests 1 but not 2. Rather, Tarski’s definition suggests 3.
- $T(\ulcorner 1 \;\dot{+}\; 1 = 2 \urcorner) \Leftrightarrow 1 + 1 = 2$
- If the meaning of $\dot{+}$ were multiplication, then $T(\ulcorner 1 \;\dot{+}\; 1 = 2 \urcorner) \Leftrightarrow 1 \times 1 = 2$
- If the meaning of $\dot{+}$ were multiplication, then $T(\ulcorner 1 \;\dot{+}\; 1 = 2 \urcorner) \Leftrightarrow 1 + 1 = 2$
Of course, since Tarski requires that the definition of truth be materially adequate, he would argue that if the meaning of $\dot{+}$ were actually multiplication, then $T$ suggesting $T(\ulcorner 1 \;\dot{+}\; 1 = 2 \urcorner) \Leftrightarrow 1 + 1 = 2$ would not be a correct definition of truth. That is, Tarski claims the following: ($\square p$ means that $p$ is necessary.)
a. $\square($ $T$ is a truth predicate $\to$ ( sentence $S$ means $\phi$ $\to$ $\;T(S) \Leftrightarrow \phi$ ) $)$
However, the approach of deriving a theory of meaning from a theory of truth depends on the following proposition:
b. $T$ is a truth predicate $\to$ $\square($ sentence $S$ means $\phi$ $\to$ $\;T(S) \Leftrightarrow \phi$ $)$
a and b are different propositions. Tarski’s theory guarantees a but not b.
4. Newly Defining ‘Theory of Truth’
Meaning as an Essential Property of Language
The criticism of Tarski’s definition of truth examined so far presupposes that the objects denoted by names in language $L$ must be contingent, i.e., that semantics is dependent on the speakers of $L$. However, instead of viewing language in this way, the author proposes to view information about what names denote as also part of the language.
For instance, in first-order logic, language $L$ can be regarded as a triple $\langle S_L, D_L, F_L \rangle$(the language spoken of here is quite different from the language of model theory. The language here has not only syntax but also semantics). The meaning of each is as follows:
- $S_L$: The set of well-formed formulae
- $D_L$: The set of denotable objects
- $F_L$: An interpretation function that maps each name to an object
When language is defined in this way, Tarski’s definition of truth produces a materially adequate truth predicate $T_L$ for any language $L$. Moreover, since $F_L$ is merely a set of tuples, it does not depart from Tarski’s physicalist line. In short, the author argues that by regarding the semantics of a language as an essential property of that language, Tarski’s definition of truth can be elevated to a general definition of truth. Therefore, there is no case where name $n$ in language $L$ denoted an object other than the object $o$ it denotes. The community of language users is not the agent that gives semantics to language, but the agent that chooses which language to use. And the problem of determining the language used by a community is a matter of pragmatics, not semantics.
Type and Token
Field’s physicalist background led him to focus on utterances rather than sentences. Field argues that Tarski only provided a definition of truth for sentences, but failed to provide a definition of truth for utterances. If Tarski had heard this objection, he would have said that this work should be divided into two stages as follows:
- Through what principle does utterance $u$ in language $L$ become an utterance of sentence $s$?
- What does it mean for sentence $s$ to be true in language $L$?
Therefore, Tarski’s definition is a type definition. In contrast, Field seeks to answer the following question:
- What does it mean for token $t$ to be true in language $L$?
Here, a token might be graphite marks on paper, chalk marks on a blackboard, or speech sounds. That is, what Field seeks is a token definition. However, it is questionable whether a token definition of truth is possible. Field himself attempted to reach a token definition by modifying Tarski’s definition as follows:
- A token of $\ulcorner \lnot e \urcorner$ is true $\Leftrightarrow$ the token of $e$ contained in that token is not true.
However, as mentioned earlier, the above definition hardcodes the meaning of $\lnot$ as negation, so it faces the same modal objection. Therefore, the above definition should be modified as follows:
- A token of proposition $A$ that is the negation of proposition $B$ is true $\Leftrightarrow$ some token of $B$ is false
But even if ‘…is the negation of’ can be reduced physicalistically, it is unclear how to specify the relevant token of $B$ in a given context. For example, consider the following sentence:
Trump’s claim about climate crisis is wrong.
It is unclear which of the numerous utterance tokens Trump has made regarding climate crisis should be the object of negation in the above sentence. The token of $B$ might not even exist. For example, consider the following sentence:
If Trump were to give a lecture on ethics, most of the content would be wrong.
To my knowledge, Trump has never given a lecture on ethics, so the token that is the object of negation in the above sentence does not exist. However, it seems perfectly reasonable to claim that the above sentence is true. This reveals the difficulties faced by a token definition of truth. From this, the author argues that we should accept Tarski’s type definition of truth for now, and regard whether the pragmatic relationship between language, expression, speaker, and utterance can be reduced to physicalism as a separate issue.
The Problem of Pragmatics
Although the author has attributed the relationship between language and speaker to the realm of pragmatics, this does not mean that this problem is unimportant. This is because there are various philosophical considerations regarding the relationship between language and speaker. For instance, Quine argues that the statement “speaker $A$ uses language $L$” cannot be reduced physicalistically(the gavagai argument). According to the author, Quine’s position can be seen as accepting Tarski’s definition of truth while rejecting the physicalist reduction of the relationship between language and speaker.
The Problem of Truth-Conditional Semantics
Finally, the author argues that attempts to derive a theory of meaning from the concept of truth, particularly theories that the acquisition of the concept of truth is a prerequisite for semantic competence, cannot all succeed. Although not explained in detail, it is probably the following problem. Attempts to derive a theory of meaning from the concept of
하지만 $\leftrightarrow$를 고전 논리의 동치 관계로 이해하든, 양상 논리의 필연적 동치 관계로 이해하든 간에 2는 성립하지 않는다. 예를 들어 다음은 필연적으로 성립한다.
- $1 + 1 = 2 \leftrightarrow $ 페르마의 마지막 정리
그러나 $1 + 1 = 2$의 의미가 페르마의 마지막 정리인 것은 아니다.
5. 결론
결론적으로 논문의 저자는 참에 대한 이론이 의미에 대한 이론과 직결되어 있어야 한다는 요구는 부당하다고 주장함으로써 타르스키의 참 정의와, 그것이 함의하는 참에 대한 축소주의deflationism를 옹호한다. 이것이 참에 대한 이론이 불필요함을 의미하지는 않는다. 크립키의 참 이론은 타르스키의 참 이론을 실질적으로 발전시켰다. 그러나 그 발전은 이미 우리에게 익숙한 참의 성질들을 T-스키마로써 정확히 해명하고, 올바르게 설계된 형태론으로 거짓말쟁이 역설과 같은 모순을 회피하는 데 있다. 참에 대한 이론으로부터 이 이상을 기대하는 것은 바람직하지 않다.
시제 논리
10 Mar 2025도입
다음의 세 문장을 보자.
- 가영이는 언젠가 등교할 것이다.
- 나영이는 언젠가 등교할 것이다.
- 나영이는 가영이가 등교하기 전에 등교하지 않는다.
위로부터 다음을 추론할 수 있다.
4. 가영이가 먼저 등교하고 나영이가 등교할 것이다.
그러나 고전 논리는 — 적어도 표면적으로는 — 위의 추론 관계를 함의하지 않는다. 따라서 우리에게 필요한 것은 시간에 대해 추론할 수 있는 논리학, 즉 시제 논리temporal logic이다.
1. 고전적 시제 논리
1.1. 의미론
시제 논리를 정의하는 길은 두 가지가 있다. 첫째는 고전 논리에 특정 구조를 부과함으로써 시제 논리를 얻는 것이다. 이 방법을 먼저 알아보자.
시제 논리의 부호수signature는 하나의 이항 관계 $\prec$와, 0개 이상의 일항 술어 $P, Q, \dots$로 이루어져 있다. 시제 논리의 모델은 다음과 같다. (이 모델을 크립키Kripke 모델이라고 한다)
\[\mathcal{T} = (T, \prec^\mathcal{T}, P^\mathcal{T}, Q^\mathcal{T}, \dots)\]- 전체universe $T$: 상정하는 모든 순간을 의미한다.
- $t_1 \prec^\mathcal{T} t_2$: $t_1$이 $t_2$보다 과거라는 의미이다.
- $P^\mathcal{T}(t)$: $P$가 시점 $t$에서 참이라는 의미이다.
예를 들어 어제, 오늘, 그리고 내일만을 고려하는 시제 논리의 경우 $T = \lbrace -1, 0, 1 \rbrace $로 둘 수 있다. 고전 역학은 $T = \mathbb{R}$을 간주한다.
가영이가 등교하는 사건을 $A$, 나영이가 등교하는 사건을 $B$라고 하면 도입의 3은 다음과 같이 쓸 수 있다.
\[\forall t_1 \forall t_2 \; \big( A(t_1) \land B(t_2) \rightarrow t_1 \prec t_2 \big)\]$\phi$가 하나의 자유변수 $x$를 가지는 문장이라고 하자. $t \in T$를 현재로 뒀을 때 $\phi$가 참이라는 것을, $\mathcal{T} \vDash \phi[t]$와 같이 적는다.
1.2. 프레임
집합과, 그 위에 정의된 이항 관계의 쌍 $(T, \prec)$를 프레임frame이라고 부른다. $\mathbf{F}$가 프레임의 모임class이라고 하자. $(T, \prec) \in \mathbf{F}$인 임의의 모델 $\mathcal{T} = (T, \prec, \lbrace P^\mathcal{T} \rbrace )$와 임의의 $t \in T$에 대해 $\mathcal{T} \vDash \phi[t]$일 때, $\phi$가 $\mathbf{F}$에 대해 참이라고 한다.
$\mathbf{F}$가 특정 성질을 가질 것을 요구함으로써 시간의 특징을 포착할 수 있다. 다음과 같은 성질을 요구할 수 있다.
- 추이성transitivity: 임의의 서로 다른 $t_1, t_2, t_3 \in T$에 대해 $t_1 \prec t_2, t_2 \prec t_3$라면 $t_1 \prec t_3$이다.
- 선형성linearity: 임의의 서로 다른 $t_1, t_2 \in T$에 대해 $t_1 \prec t_2$이거나 $t_2 \prec t_1$이다.
- 조밀성denseness: 임의의 서로 다른 $t_1, t_2 \in T$에 대해 어떤 $t_3 \in T$가 존재하여 $t_1 \prec t_3 \prec t_2$이다.
- 우 연장성R-extendability: 임의의 $t \in T$에 대해 어떤 $t’ \in T$가 존재하여 $t \prec t’$이다.
- 좌 연장성L-extendability: 임의의 $t \in T$에 대해 어떤 $t’ \in T$가 존재하여 $t’ \prec t$이다.
도입의 논증은 선형 프레임에 대해 참임을 보일 수 있다.
2. 독립적 시제 논리
시제 논리를 정의하는 두 번째 방식은 시제 논리에 특수한 논리 기호를 도입하는 것이다. 각각 다음과 같이 읽는다.
- $\mathsf{F}p$: 언젠가 $p$일 것이다Future p
- $\mathsf{P}p$: 언젠가 $p$였다Past p
- $\mathsf{G}p$: 언제나 $p$일 것이다Going to always be p
- $\mathsf{H}p$: 언제나 $p$였다Has always been p
$\mathsf{F}, \mathsf{P}, \mathsf{G}, \mathsf{H}$의 관계는 다음과 같다.
- $\mathsf{F}p \equiv \lnot\mathsf{G}\lnot p$
- $\mathsf{P}p \equiv \lnot\mathsf{H}\lnot p$
독립적 시제 논리의 명제는 메레디스 번역Meredith translation을 통해 언제나 고전적 시제 논리의 명제로 변환할 수 있다. 예를 들어 $\mathsf{G}p$는 $\forall x \succ t \; p(x)$로 번역된다. 그러나 역은 성립하지 않는다. 따라서 독립적 시제 논리는 고전적 시제 논리보다 표현력이 약하다. 그럼에도 독립적 시제 논리가 연구할 만한 주제인 이유는, 표현력을 일부 포기하는대가로 결정 가능성, 완전성 등의 좋은 성질을 얻을 수 있을 뿐더러, 양상 논리와의 연결 고리를 제공하는 등 철학적 의의 또한 크기 때문이다.
독립적 시제 논리의 모델은 종속적 시제 논리와 마찬가지로 $\mathcal{T} = (T, \prec, \lbrace P^\mathcal{T} \rbrace )$이다. 만족 관계는 자연스럽게 정의한다. 예를 들어,
- $\mathcal{T} \vDash \mathsf{F}p[t] \iff$ 어떤 $t \prec t’$에 대해, $\mathcal{T} \vDash p[t’]$
3. 시제 공리
지금까지 시제 논리의 의미론을 살펴 보았다. 이제 시제 논리의 증명을 살펴본다.
3.1. 최소 시제 논리
최소 시제 논리 $L_0$는 다음의 공리로 이루어져 있다.
- $\tau$가 명제 논리의 항진명제일 때, $\tau$
- $\mathsf{G}(\phi \to \psi) \to (\mathsf{G}\phi \to \mathsf{G}\psi)$
- $\mathsf{H}(\phi \to \psi) \to (\mathsf{H}\phi \to \mathsf{H}\psi)$
- $\phi \to \mathsf{GP}\phi$
- $\phi \to \mathsf{HF}\phi$
그리고 다음의 추론 규칙으로 이루어져 있다.
- MP $\vdash \phi, \phi \to \psi \implies \vdash \psi$
- TG1: $\vdash \phi \implies \vdash \mathsf{G}\phi$
- TG2: $\vdash \phi \implies \vdash \mathsf{H}\phi$
MP는 Modus Ponens, TG는 Temporal Generalisation의 약어이다.
TG가 $\vdash \phi \to \mathsf{G}\phi$를 의미하지 않는다는 사실에 유의하라. TG는 논리적으로 증명된 명제 $\phi$에 한해, $\mathsf{G}\phi$ 또는 $\mathsf{H}\phi$를 도출할 수 있다는 의미이다. 즉, TG는 논리적 명제가 시간과 무관하다는 의미이다.
정리. $L_0$는 건전하다.
증명. 명제 논리의 건전성 정리와 거의 동일하게, 논리식의 형태에 대한 귀납법으로 증명한다.
정리. $L_0$에서 증명 가능성은 다음 규칙에 대해 닫혀 있다.
- 거울 규칙mirror rule: 명제 $\phi$에 등장하는 $\mathsf{G}$와 $\mathsf{H}$, $\mathsf{F}$와 $\mathsf{P}$를 서로 바꾼 명제를 거울 명제 $\bar{\phi}$라고 하자. $\vdash \phi$라면 $\vdash \bar{\phi}$이다.
- 베커 규칙Becker’s rule: $\mathsf{T}$가 $\mathsf{G, H, F, P}$ 중 하나라고 하자. $\vdash \phi \to \psi$라면 $\vdash \mathsf{T}\phi \to \mathsf{T}\psi$이다.
- 쌍대 규칙dual rule: 명제 $\phi$에 등장하는 $\land$와 $\lor$, $\mathsf{G}$와 $\mathsf{F}$, $\mathsf{H}$와 $\mathsf{P}$를 서로 바꾼 명제를 쌍대 명제 $\phi^\ast$라고 하자. $\vdash \phi$라면 $\vdash \phi^\ast$이다.
증명. 연습문제 (^^)
정리. $L_0$는 모든 프레임의 모임 $\mathbf{F}_0$에 대해 완전하다.
증명. TODO
3.2. 고전역학의 시제 논리
추이성, 선형성, 조밀성, 좌우 연장성을 가지는 프레임들의 모임 $\mathbf{F}_1$을 고려하자. $\mathbf{F}_1$은 고전역학에서 상정하는 시간이다. $\mathbf{F}_1$에서 건전하고 완전한 공리계를 찾아 보자.
고전역학의 시제 논리 $L_1$은 $L_0$에 다음 공리를 추가한 것이다.
- $\mathsf{G} p \to \mathsf{GG}p$ (추이성)
- $(\mathsf{P}p \land \mathsf{P}q) \to (\mathsf{P}(p \land \mathsf{P}q) \lor \mathsf{P}(p \land q) \lor \mathsf{P}(\mathsf{P}p \land q))$ (좌 선형성)
- $(\mathsf{F}p \land \mathsf{F}q) \to (\mathsf{F}(p \land \mathsf{F}q) \lor \mathsf{F}(p \land q) \lor \mathsf{F}(\mathsf{F}p \land q))$ (우 선형성)
- $\mathsf{H}p \to \mathsf{P}p$ (좌 연장성)
- $\mathsf{G}p \to \mathsf{F}p$ (우 연장성)
- $\mathsf{GG}p \to \mathsf{G}p$ (조밀성)
햄린Hamblin의 정리. $L_1$에서 시제 기호의 조합은 14가지 시제 중 하나와 동치이다. 14가지 시제는 $\mathsf{FH, H, PH, HP, P, GP}$와 $\mathsf{PG, G, FG, GF, F, HF}$, 그리고 $\mathsf{GH} = \mathsf{HG}$와 $\mathsf{FP} = \mathsf{PF}$이다.
증명. 추이적 프레임에서 $\mathsf{PP}$와 같이 중첩된 시제는 단일 시제 $\mathsf{P}$와 동치임을 쉽게 보일 수 있다. 따라서 $\mathsf{X} \neq \mathsf{Y}$, $\mathsf{Y} \neq \mathsf{Z}$인 시제들의 조합 $\mathsf{XYZ}$은 어떤 두 시제 조합과 동치임을 보이면 된다. 거울 규칙과 쌍대 규칙에 의해 $\mathsf{Z} = \mathsf{G}$인 경우만 고려하면 된다. 한편 $\mathsf{XY}$와 $\mathsf{X’Y’}$가 서로 동치가 아니라는 것을 보이기 위해서는 함의 관계가 성립하지 않는 크립키 모델을 찾으면 된다.
정리. $L_1$은 $\mathbf{F}_1$에 대해 완전하다.
4. 시제 술어 논리
고전 논리학에서 술어 논리는 명제 논리에 다음 공리를 추가한 것이다.
- $\forall x \phi \to \phi[y/x]$ (단, $y$는 $\phi$에서 $x$에 대해 자유)
- $\forall x (\phi \to \psi) \to (\phi \to \forall x \psi)$ (단, $x$는 $\phi$의 자유변수가 아님)
- $x = x$
- $x = y \to (\phi[x/z] \to \phi[y / z]$) (단, $x, y$는 $\phi$에서 $z$에 대해 자유)
그리고 다음의 추론 규칙을 추가한다.
- UGUniversal Generalisation: $\vdash \phi \implies \vdash \forall x \phi$
시제 논리 $L_0$에 상술한 공리들과 추론 규칙을 추가한 논리 체계를 시제 술어 논리 $L_P$라고 하자.
정리. $L_P$는 다음을 증명한다.
- 정 바르칸direct Barcan: $\forall x \mathsf{G}\phi \to \mathsf{G}\forall x \phi$
- 역 바르칸converse Barcan: $\mathsf{G}\forall x \phi \to \forall x \mathsf{G} \phi$
- 동일성의 영속성permanence of identity: $x = y \to \mathsf{G}(x = y)$
증명. 역 바르칸 명제만 증명해 보자.
\[\begin{aligned} &1. &&\forall x \phi \to \phi &&&\text{Axiom} \\ &2. &&\mathsf{G}\forall x \phi \to \mathsf{G} \phi &&&\text{Becker}\\ &3. &&\forall x (\mathsf{G}\forall x \phi \to \mathsf{G}\phi) &&&\text{2, UG}\\ &4. &&\forall x (\mathsf{G}\forall x \phi \to \mathsf{G}\phi) \to (\mathsf{G}\forall x \phi \to \forall x \mathsf{G}\phi) &&&\text{Axiom}\\ &5. &&\mathsf{G}\forall x \phi \to \forall x \mathsf{G} \phi \quad &&&\text{3, 4, MP} \\ & \blacksquare \end{aligned}\]자연 언어로 풀어 쓰자면,
- 정 바르칸: 현재 존재하는 모든 대상이 언제나 ____라고 하자. 그러면 임의의 미래 시점에 대해, 그때 존재하는 모든 대상은 ____이다.
- 역 바르칸: 임의의 미래 시점에서 대해, 그때 존재하는 모든 대상은 ____라고 하자. 그러면 현재 존재하는 모든 대상이 언제나 ____이다.
- 동일성의 영속성: 동일한 두 대상은 언제나 동일하다.
동일성의 영속성은 시제 논리에서 상수가 고정 지시어rigid designator처럼 행동한다고 직관적으로 올바르다. 그러나 바르칸 명제는 직관적으로 틀렸다. 일례로 $\phi(x)$를 “$x$가 존재한다”로 치환해 보자.
- 역 바르칸: ① 임의의 미래 시점에서 대해, 그때 존재하는 모든 대상은 존재한다고 하자. ② 그러면 현재 존재하는 모든 대상이 언제나 존재한다.
하지만 이 명제는 틀렸다. ①은 자명하게 성립하지만, 현재 존재하는 모든 대상이 영원히 존재할 것은 아니므로 ②는 성립하지 않기 때문이다. 따라서 역 바르칸 명제는 문제적이다.
$L_P$가 바르칸 명제 같은 병리적 명제를 도출하는 이유는 TG가 열린 명제에 대해 유효하지 않기 때문이다(TG는 베커 규칙의 증명에 필요하다. 즉, 증명의 문제는 2단계에 있다). 앞서 말했듯이 TG는 논리적으로 참인 명제는 시간에 상관 없이 참이라는 의미이다. 그러나 열린 명제는 참도 아니고 거짓도 아니다. 열린 명제는 특정 대상에 의해 만족되거나, 만족되지 않기 때문이다.
이 문제를 극복하기 위해 TG를 닫힌 명제에 대해서만 적용 가능하도록 제안하는 방안을 강구할 수 있으나, 제한된 시제 술어 논리는 일부 바람직한 명제를 증명하지 못함이 알려져 있다. 건전하면서도 완전한 시제 술어 논리를 만드는 작업은 아직도 해결되지 않은 문제이다.
Temporal Logic
10 Mar 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
Introduction
Consider the following three statements.
- Gayeong will go to school at some point.
- Nayeong will go to school at some point.
- Nayeong will not go to school before Gayeong goes to school.
From these, we can infer the following.
4. Gayeong will go to school first, and then Nayeong will go to school.
However, classical logic—at least superficially—does not entail the above inference relation. Therefore, what we need is a logic that can reason about time, namely temporal logic.
1. Classical Temporal Logic
1.1. Semantics
There are two ways to define temporal logic. The first is to obtain temporal logic by imposing a particular structure on classical logic. Let us examine this method first.
The signature of temporal logic consists of one binary relation $\prec$ and zero or more unary predicates $P, Q, \dots$. A model of temporal logic is as follows. (This model is called a Kripke model.)
\[\mathcal{T} = (T, \prec^\mathcal{T}, P^\mathcal{T}, Q^\mathcal{T}, \dots)\]- Universe $T$: represents all the moments under consideration.
- $t_1 \prec^\mathcal{T} t_2$: means that $t_1$ is earlier than $t_2$.
- $P^\mathcal{T}(t)$: means that $P$ is true at time $t$.
For example, in temporal logic considering only yesterday, today, and tomorrow, we can set $T = \lbrace -1, 0, 1 \rbrace $. Classical mechanics considers $T = \mathbb{R}$.
If we let $A$ denote the event of Gayeong going to school and $B$ denote the event of Nayeong going to school, then statement 3 from the introduction can be written as follows.
\[\forall t_1 \forall t_2 \; \big( A(t_1) \land B(t_2) \rightarrow t_1 \prec t_2 \big)\]Let $\phi$ be a formula with one free variable $x$. When $\phi$ is true with $t \in T$ taken as the present, we write this as $\mathcal{T} \vDash \phi[t]$.
1.2. Frames
A pair $(T, \prec)$ consisting of a set and a binary relation defined on it is called a frame. Let $\mathbf{F}$ be a class of frames. When $\mathcal{T} \vDash \phi[t]$ for any model $\mathcal{T} = (T, \prec, \lbrace P^\mathcal{T} \rbrace )$ with $(T, \prec) \in \mathbf{F}$ and any $t \in T$, we say that $\phi$ is true with respect to $\mathbf{F}$.
By requiring $\mathbf{F}$ to have certain properties, we can capture characteristics of time. The following properties can be required:
- Transitivity: for any distinct $t_1, t_2, t_3 \in T$, if $t_1 \prec t_2$ and $t_2 \prec t_3$, then $t_1 \prec t_3$.
- Linearity: for any distinct $t_1, t_2 \in T$, either $t_1 \prec t_2$ or $t_2 \prec t_1$.
- Density: for any distinct $t_1, t_2 \in T$, there exists some $t_3 \in T$ such that $t_1 \prec t_3 \prec t_2$.
- Right-extendability: for any $t \in T$, there exists some $t’ \in T$ such that $t \prec t’$.
- Left-extendability: for any $t \in T$, there exists some $t’ \in T$ such that $t’ \prec t$.
The argument from the introduction can be shown to be valid with respect to linear frames.
2. Independent Temporal Logic
The second way to define temporal logic is to introduce logical symbols specific to temporal logic. Each is read as follows:
- $\mathsf{F}p$: Future $p$ (at some point $p$ will be the case)
- $\mathsf{P}p$: Past $p$ (at some point $p$ was the case)
- $\mathsf{G}p$: Going to always be $p$ (always $p$ will be the case)
- $\mathsf{H}p$: Has always been $p$ (always $p$ was the case)
The relationships between $\mathsf{F}, \mathsf{P}, \mathsf{G}, \mathsf{H}$ are as follows:
- $\mathsf{F}p \equiv \lnot\mathsf{G}\lnot p$
- $\mathsf{P}p \equiv \lnot\mathsf{H}\lnot p$
Propositions of independent temporal logic can always be translated into propositions of classical temporal logic through the Meredith translation. For example, $\mathsf{G}p$ is translated as $\forall x \succ t \; p(x)$. However, the converse does not hold. Therefore, independent temporal logic has weaker expressive power than classical temporal logic. Nevertheless, independent temporal logic is a subject worth studying because, in exchange for sacrificing some expressive power, one can obtain good properties such as decidability and completeness, and it also provides connections to modal logic, amongst other significant philosophical merits.
The model of independent temporal logic is $\mathcal{T} = (T, \prec, \lbrace P^\mathcal{T} \rbrace )$, the same as dependent temporal logic. The satisfaction relation is defined naturally. For example,
- $\mathcal{T} \vDash \mathsf{F}p[t] \iff$ for some $t \prec t’$, $\mathcal{T} \vDash p[t’]$
3. Temporal Axioms
So far we have examined the semantics of temporal logic. Now let us examine proofs in temporal logic.
3.1. Minimal Temporal Logic
The minimal temporal logic $L_0$ consists of the following axioms:
- When $\tau$ is a tautology of propositional logic, $\tau$
- $\mathsf{G}(\phi \to \psi) \to (\mathsf{G}\phi \to \mathsf{G}\psi)$
- $\mathsf{H}(\phi \to \psi) \to (\mathsf{H}\phi \to \mathsf{H}\psi)$
- $\phi \to \mathsf{GP}\phi$
- $\phi \to \mathsf{HF}\phi$
And it consists of the following inference rules:
- MP $\vdash \phi, \phi \to \psi \implies \vdash \psi$
- TG1: $\vdash \phi \implies \vdash \mathsf{G}\phi$
- TG2: $\vdash \phi \implies \vdash \mathsf{H}\phi$
MP is an abbreviation for Modus Ponens, and TG is an abbreviation for Temporal Generalisation.
Note that TG does not mean $\vdash \phi \to \mathsf{G}\phi$. TG means that only for logically proven propositions $\phi$, one can derive $\mathsf{G}\phi$ or $\mathsf{H}\phi$. That is, TG means that logical propositions are independent of time.
Theorem. $L_0$ is sound.
Proof. The proof is by induction on the form of logical formulae, almost identical to the soundness theorem for propositional logic.
Theorem. Provability in $L_0$ is closed under the following rules:
- Mirror rule: Let the mirror proposition $\bar{\phi}$ be the proposition obtained by swapping $\mathsf{G}$ with $\mathsf{H}$ and $\mathsf{F}$ with $\mathsf{P}$ in proposition $\phi$. If $\vdash \phi$, then $\vdash \bar{\phi}$.
- Becker’s rule: Let $\mathsf{T}$ be one of $\mathsf{G, H, F, P}$. If $\vdash \phi \to \psi$, then $\vdash \mathsf{T}\phi \to \mathsf{T}\psi$.
- Dual rule: Let the dual proposition $\phi^\ast$ be the proposition obtained by swapping $\land$ with $\lor$, $\mathsf{G}$ with $\mathsf{F}$, and $\mathsf{H}$ with $\mathsf{P}$ in proposition $\phi$. If $\vdash \phi$, then $\vdash \phi^\ast$.
Proof. Exercise (^^)
Theorem. $L_0$ is complete with respect to the class of all frames $\mathbf{F}_0$.
Proof. TODO
3.2. Temporal Logic of Classical Mechanics
Consider the class $\mathbf{F}_1$ of frames that have transitivity, linearity, density, and left and right extendability. $\mathbf{F}_1$ represents time as postulated in classical mechanics. Let us find an axiom system that is sound and complete for $\mathbf{F}_1$.
The temporal logic of classical mechanics $L_1$ is obtained by adding the following axioms to $L_0$:
- $\mathsf{G} p \to \mathsf{GG}p$ (transitivity)
- $(\mathsf{P}p \land \mathsf{P}q) \to (\mathsf{P}(p \land \mathsf{P}q) \lor \mathsf{P}(p \land q) \lor \mathsf{P}(\mathsf{P}p \land q))$ (left linearity)
- $(\mathsf{F}p \land \mathsf{F}q) \to (\mathsf{F}(p \land \mathsf{F}q) \lor \mathsf{F}(p \land q) \lor \mathsf{F}(\mathsf{F}p \land q))$ (right linearity)
- $\mathsf{H}p \to \mathsf{P}p$ (left extendability)
- $\mathsf{G}p \to \mathsf{F}p$ (right extendability)
- $\mathsf{GG}p \to \mathsf{G}p$ (density)
Hamblin’s theorem. In $L_1$, combinations of temporal symbols are equivalent to one of 14 tenses. The 14 tenses are $\mathsf{FH, H, PH, HP, P, GP}$ and $\mathsf{PG, G, FG, GF, F, HF}$, together with $\mathsf{GH} = \mathsf{HG}$ and $\mathsf{FP} = \mathsf{PF}$.
Proof. In transitive frames, nested tenses such as $\mathsf{PP}$ can easily be shown to be equivalent to the single tense $\mathsf{P}$. Therefore, it suffices to show that combinations $\mathsf{XYZ}$ of tenses where $\mathsf{X} \neq \mathsf{Y}$ and $\mathsf{Y} \neq \mathsf{Z}$ are equivalent to some combination of two tenses. By the mirror rule and dual rule, we need only consider the case where $\mathsf{Z} = \mathsf{G}$. Meanwhile, to show that $\mathsf{XY}$ and $\mathsf{X’Y’}$ are not equivalent to each other, one can find a Kripke model where the implication relation does not hold.
Theorem. $L_1$ is complete with respect to $\mathbf{F}_1$.
4. Temporal Predicate Logic
In classical logic, predicate logic is obtained by adding the following axioms to propositional logic:
- $\forall x \phi \to \phi[y/x]$ (provided $y$ is free for $x$ in $\phi$)
- $\forall x (\phi \to \psi) \to (\phi \to \forall x \psi)$ (provided $x$ is not a free variable of $\phi$)
- $x = x$
- $x = y \to (\phi[x/z] \to \phi[y / z]$) (provided $x, y$ are free for $z$ in $\phi$)
And the following inference rule is added:
- UG (Universal Generalisation): $\vdash \phi \implies \vdash \forall x \phi$
The logical system obtained by adding the aforementioned axioms and inference rule to temporal logic $L_0$ is called temporal predicate logic $L_P$.
Theorem. $L_P$ proves the following:
- Direct Barcan: $\forall x \mathsf{G}\phi \to \mathsf{G}\forall x \phi$
- Converse Barcan: $\mathsf{G}\forall x \phi \to \forall x \mathsf{G} \phi$
- Permanence of identity: $x = y \to \mathsf{G}(x = y)$
Proof. Let us prove only the converse Barcan formula.
\[\begin{aligned} &1. &&\forall x \phi \to \phi &&&\text{Axiom} \\ &2. &&\mathsf{G}\forall x \phi \to \mathsf{G} \phi &&&\text{Becker}\\ &3. &&\forall x (\mathsf{G}\forall x \phi \to \mathsf{G}\phi) &&&\text{2, UG}\\ &4. &&\forall x (\mathsf{G}\forall x \phi \to \mathsf{G}\phi) \to (\mathsf{G}\forall x \phi \to \forall x \mathsf{G}\phi) &&&\text{Axiom}\\ &5. &&\mathsf{G}\forall x \phi \to \forall x \mathsf{G} \phi \quad &&&\text{3, 4, MP} \\ & \blacksquare \end{aligned}\]In natural language terms:
- Direct Barcan: suppose that all objects currently existing will always be ____. Then for any future time point, all objects existing at that time will be ____.
- Converse Barcan: suppose that for any future time point, all objects existing at that time will be ____. Then all objects currently existing will always be ____.
- Permanence of identity: two identical objects are always identical.
The permanence of identity is intuitively correct, as constants behave like rigid designators in temporal logic. However, the Barcan formulae are intuitively false. As an example, let us substitute “$x$ exists” for $\phi(x)$.
- Converse Barcan: ① suppose that for any future time point, all objects existing at that time exist. ② Then all objects currently existing will always exist.
But this proposition is false. ① holds trivially, but ② does not hold since not all objects currently existing will exist forever. Therefore, the converse Barcan formula is problematic.
The reason $L_P$ derives pathological propositions like the Barcan formulae is that TG is not valid for open formulae (TG is needed for the proof of Becker’s rule. That is, the problem in the proof is at step 2). As mentioned earlier, TG means that logically true propositions are true regardless of time. However, open formulae are neither true nor false. Open formulae are satisfied or not satisfied by particular objects.
To overcome this problem, one might propose restricting TG to apply only to closed formulae, but it is known that restricted temporal predicate logic fails to prove some desirable propositions. The task of creating a temporal predicate logic that is both sound and complete remains an unsolved problem.
텐서곱에 관한 노트
04 Mar 2025TL;DR. 벡터 공간의 텐서곱은 다음의 의미를 가진다.
- 다중 선형 사상의 선형화를 위한 정의역
- 다중 선형 사상의 공간
엄밀히 말해 1이 $U \otimes V$에 해당하고, 2는 $U^\ast \otimes V^\ast$이다. 하지만 혼용되는 경향이 있는 듯하다.
1. 도입
정의. $U, V, W$가 체 $\mathbb{F}$ 위에서 정의된 벡터 공간이라고 하자. $b: U \times V \to W$가 쌍선형 사상bilinear map이라는 것은 각 항에 대해서 $B$가 선형이라는 것이다. 즉, 임의의 $\mathbf{u}_1, \mathbf{u}_2 \in U, \mathbf{v}_1, \mathbf{v}_2 \in V$와 스칼라 $\alpha \in \mathbb{F}$에 대해 다음이 성립한다.
\[b(\alpha \mathbf{u}_1 + \mathbf{u}_2, \mathbf{v}_1) = \alpha b(\mathbf{u}_1, \mathbf{v}_1) + b(\mathbf{u}_2, \mathbf{v}_1)\] \[b(\mathbf{u}_1, \alpha \mathbf{v}_1 + \mathbf{v}_2) = \alpha b(\mathbf{u}_1, \mathbf{v}_1) + b(\mathbf{u}_1, \mathbf{v}_2)\]
예를 들어 실수 벡터 공간에서의 내적 $\cdot : V \times V \to \mathbb{R}$은, $\mathbb{R}$을 1차원 벡터 공간으로 간주했을 때 쌍선형 사상이다. 비슷한 방식으로 다중 선형 사상multilinear form을 정의할 수 있다. $V$가 $n$차원 벡터 공간일 때, $\mathrm{det}: V \times \dots \times V \to \mathbb{R}$은 $n$중 선형 사상이다.
$b: U \times V \to W$가 쌍선형 사상이라고 하자. 당연하게도 $b$는 선형 사상이 아니다. $b$는 서로 다른 두 공간의 벡터를 매개변수로 받는 사상이지, 한 공간의 벡터를 매개변수로 받는 사상이 아니기 때문이다. 설령 $b$를 직합 $U \oplus V$에서 $W$로 가는 사상으로 생각하더라도, $b(\alpha(u, v)) = b((\alpha u, \alpha v)) = \alpha^2 b(u, v)$이므로 선형성을 만족하지 않는다.
그러나 텐서곱을 이용하면 $b$를 선형 사상과 동일시할 수 있다.
2. 텐서곱의 정의
정의. 벡터 공간 $U, V$에 대해, 텐서곱tensor product $U \otimes V$를 다음 보편 성질universal property를 만족하는 벡터 공간으로 정의한다.
또한 $U \otimes V$의 원소를 텐서라고 한다.
정리. 임의의 벡터 공간의 텐서곱은 언제나 존재하며, 동형 사상에 대해 유일하다.
증명. 유한 차원 벡터 공간에 대해서만 증명한다. $U$와 $V$의 차원이 각각 $n, m$이고, 기저가 $\lbrace e_1, \dots, e_n\rbrace , \lbrace f_1, \dots, f_m\rbrace$이라고 하자. $T$가 차원이 $nm$인 벡터 공간이라고 하자. 차원이 같은 벡터 공간은 모두 동형이므로, 그러한 $T$는 동형 사상에 대해 유일하다. $T$의 형식적 기저를 다음과 같이 두자.
\[\mathcal{B} = \{ e_1f_1, \dots, e_1f_m, \dots, e_nf_1, \dots, e_nf_m \}\]$T$가 $U$와 $V$의 텐서곱임을 보이기 위해서 임의의 쌍선형 사상 $b: U \times V \to W$를 상정한다. $b$로부터 다음의 행벡터를 정의한다.
\[\tilde {b} = \big[ b(e_1, f_1), \dots, b(e_1, f_m), \dots, b(e_n, f_1), \dots, b(e_n, f_m) \big]_\mathcal{B}\]또한 $\otimes: V \times W \to T$를 다음과 같이 정의한다.
\[\otimes: (u, v) = (u_1e_1 + \dots + u_ne_n, v_1f_1 + \dots + v_mf_m) \mapsto \begin{bmatrix} u_1v_1 \\ \vdots \\ u_1v_m \\ \vdots \\ u_nv_1 \\ \vdots \\ u_nf_m \end{bmatrix}_{\mathcal{B}}\]이때 다음이 성립한다.
\[\begin{align} \tilde {b}(\otimes(u, v)) &= \sum_i \sum_j (u_i v_j)b(e_i, f_j) \\ &= b\left( \sum_i u_i e_i, \sum_j v_j f_j \right) && (\text{by bilinearity})\\ &= b(u, v) && \blacksquare \end{align}\]3. 텐서와 다중 선형 사상의 동일시
지금까지의 논의를 한 줄로 요약하면 다음과 같다.
\[\mathrm{Hom}^2(U \times V, W) \cong \mathrm{Hom}(U \otimes V, W)\]여기서 $\mathrm{Hom}^2$은 쌍선형 사상의 공간을 의미한다. 특히 $W = \mathbb{F}$일 때, 쌍대 공간의 정의에 의해 다음이 성립한다.
\[\mathrm{Hom}^2(U \times V, \mathbb{F}) \cong \mathrm{Hom}(U \otimes V, \mathbb{F}) \cong (U \otimes V)^*\]이 관계를 이용하면 텐서곱을 쌍선형 사상의 선형화를 위한 정의역으로 보는 시각을 넘어, 쌍선형 사상의 공간 그 자체로 볼 수도 있다. 먼저 다음의 보조정리를 증명한다.
보조정리. $(U \otimes V)^\ast = U^\ast \otimes V^\ast$
증명. 앞선 관계식과 쌍대 공간의 정의로 인해 다음을 보이면 충분하다.
\[\mathrm{Hom}^2(U \times V, \mathbb{F}) \cong \mathrm{Hom}(U, \mathbb{F}) \otimes \mathrm{Hom}(V, \mathbb{F})\]즉, $\mathrm{Hom}^2(U \times V, \mathbb{F})$가 보편 성질을 만족함을 보이면 된다. 이는 앞선 증명과 거의 동일하므로 생략한다. ■
보조정리로부터 다음이 성립한다.
정리. $\mathrm{Hom}^2(U \times V, \mathbb{F}) \cong U^\ast \otimes V^\ast$
증명.
\[\begin{align} U^* \otimes V^* &\cong U^{***} \otimes V^{***} \\ &\cong (U^{**} \otimes V^{**})^* \\ &\cong (U \otimes V)^* \\ &\cong \mathrm{Hom}^2(U \times V, \mathbb{F}) \end{align}\]두 번째 식에서 세 번째 식으로 넘어갈 때 $V \cong V^{\ast\ast}$ 표준canonical 동일시를 사용했다. ■
따라서 쌍대 공간의 텐서는 쌍선형 사상과 표준적으로 동일시할 수 있다.