The Łoś-Tarski Preservation Theorem

17 Apr 2025

This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.

For subgroups $H, K$ of a group $G$, the intersection $H \cap K$ is always a group. The same holds for rings and fields. This can be explained as a consequence of the Łoś-Tarski theorem.

Notation. In this article, $T$ is a first-order theory in language $\mathcal{L}$, and Fraktur letters $\mathfrak{M}, \mathfrak{N}, \dots$ denote $\mathcal{L}$-structures. Furthermore, we write the domains of $\mathfrak{M}, \mathfrak{N}, \dots$ as $M, N, \dots$ respectively.

Basic Concepts

Definition. When $N \subseteq M$ and the interpretation in $\mathfrak{N}$ is the restriction of the interpretation in $\mathfrak{M}$ to $N$, we call $\mathfrak{N}$ a submodel of $\mathfrak{M}$, and write $\mathfrak{N} \subseteq \mathfrak{M}$. Furthermore, $\mathfrak{M}$ is called an extension of $\mathfrak{N}$.

For example, $(2\mathbb{Z}, +)$ is a submodel of $(\mathbb{Z}, +)$, and $(\mathbb{Q}, +, \cdot)$ is a submodel of $(\mathbb{R}, +, \cdot)$.

Definition. When $\mathfrak{M} \vDash \phi \iff \mathfrak{N} \vDash \phi$ for any $\mathcal{L}$-sentence $\phi$, we say that $\mathfrak{M}$ and $\mathfrak{N}$ are elementarily equivalent, and write $\mathfrak{M} \equiv \mathfrak{N}$.

By the Löwenheim-Skolem theorem, if $\kappa$ is an infinite cardinal at least $|\mathcal{L}|$, then for any infinite structure $\mathfrak{M}$, there exists a model $\mathfrak{N}$ of cardinality $\kappa$ that is elementarily equivalent to $\mathfrak{M}$. (cf. Łoś-Vaught test)

Definition. When $\mathfrak{M}$ and $\mathfrak{N}$ are structurally identical, they are called isomorphic, written $\mathfrak{M} \cong \mathfrak{N}$. Specifically, $\mathfrak{M} \cong \mathfrak{N}$ when there exists a bijection $\phi: M \to N$ such that for any function $f$ and relation $R$ in $\mathcal{L}$, the following holds for any $a_1, \dots, a_n \in M$:

\[\begin{gather} \phi(f_\mathfrak{M}(a_1, \dots, a_n)) = f_\mathfrak{N}(\phi(a_1), \dots, \phi(a_n)), \\\\ R_\mathfrak{M}(a_1, \dots, a_n) \iff R_\mathfrak{N}(\phi(a_1), \dots, \phi(a_n)) \end{gather}\]

$(\mathbb{Z}, +)$ and $(2\mathbb{Z}, +)$ are isomorphic via $\phi: x \mapsto 2x$, but $(\mathbb{Q}, +, \cdot)$ and $(\mathbb{R}, +, \cdot)$ are not isomorphic.

The proof of the following theorem is almost trivial.

Theorem. Two isomorphic structures are elementarily equivalent.

Definition. Let $\mathfrak{N} \subseteq \mathfrak{M}$. When $\mathfrak{N} \vDash \phi[g] \iff \mathfrak{M} \vDash \phi[g]$ for any $\mathcal{L}$-formula $\phi$ and any assignment $g$ of free variables in $\mathfrak{N}$, we call $\mathfrak{N}$ an elementary submodel of $\mathfrak{M}$, and write $\mathfrak{N} \preceq \mathfrak{M}$.

Conditions 2 and 3 are stronger than 1, but 2 and 3 do not imply each other.

1. $\mathfrak{N} \subseteq \mathfrak{M}$, $\mathfrak{N} \equiv \mathfrak{M}$
2. $\mathfrak{N} \subseteq \mathfrak{M}$, $\mathfrak{N} \cong \mathfrak{M}$
3. $\mathfrak{N} \preceq \mathfrak{M}$

The reason why 2 and 3 do not imply each other is that 2 requires structural equivalence, making it no weaker than 3, while 3 requires equivalence for arbitrary assignments, making it no weaker than 2. For instance, for $\mathfrak{M} = (\mathbb{R}, +, \cdot)$, for $\mathfrak{N}$ to be an isomorphic submodel of $\mathfrak{M}$, it must be structurally identical with respect to constructible real numbers, whereas for $\mathfrak{N}$ to be an elementary submodel of $\mathfrak{M}$, the two models must be elementarily equivalent with respect to all real numbers.

	2	3
2 is no weaker than 3	Structural identity	Elementary identity
3 is no weaker than 2	Constructible objects	Arbitrary objects

For example, as we saw earlier, $(2\mathbb{Z}, +)$ is an isomorphic submodel of $(\mathbb{Z}, +)$, but considering the assignment $x \mapsto 2$ for $\exists y \; (y + y = x)$, we can see that it is not an elementary submodel.

The Łoś-Tarski Theorem

Let $\mathfrak{M}$ be a model of $T$. What kind of theory must $T$ be for any submodel of $\mathfrak{M}$ to also be a model of $T$? The answer is given by the following theorem.

The Łoś-Tarski Preservation Theorem. A necessary and sufficient condition for submodels of models of $T$ to also be models of $T$ is that $T$ is equivalent to a theory consisting of $\Pi_1$ sentences.

What $\Pi_1$ sentences are has been covered in the arithmetic hierarchy article. To explain briefly, these are theories having only $\forall$ as quantifiers. Intuitively, $\Pi_1$ sentences become easier to satisfy as the domain is restricted, so if $T$ is a $\Pi_1$ theory, then $T$ will be preserved under submodels. The necessity is somewhat more challenging to prove.

Proof. The sufficiency is almost trivial, so we prove only the necessity. We prove the following lemma.

Lemma. Let $T$ be a consistent theory in language $\mathcal{L}$. When a set $\Delta$ of $\mathcal{L}$-sentences satisfies the following two conditions, $\Delta$ contains an axiomatisation of $T$.

1. $\Delta$ is closed under disjunction. That is, if $\phi, \psi \in \Delta$, then $\phi \lor \psi \in \Delta$.
2. For a model $\mathfrak{A}$ of $T$, if $\mathfrak{B}$ satisfies all sentences in $\Delta$ that are satisfied in $\mathfrak{A}$, then $\mathfrak{B}$ is also a model of $T$.

Proof of the lemma. Let $\Gamma = \lbrace \delta \in \Delta : T \vDash \delta \rbrace $. To show that $\Delta$ contains an axiomatisation of $T$, it suffices to show the following:

\[\mathfrak{B} \vDash \Gamma \implies \mathfrak{B} \vDash T\]

Suppose $\mathfrak{B}$ is a model of $\Gamma$. Define:

\[\Sigma = \{ \lnot \delta : \delta \in \Delta, \mathfrak{B} \not\vDash \delta \}\]

We show that $T \cup \Sigma$ is a consistent theory. If $T \cup \Sigma$ were inconsistent, then for some $\lnot\delta_1, \dots, \lnot\delta_n \in \Sigma$, we would have $T \vdash \lnot(\lnot\delta_1 \land \cdots \land \lnot\delta_n)$, so $T \vdash \delta_1 \lor \cdots \lor \delta_n$. Since $\Delta$ is closed under disjunction, $\delta_1 \lor \cdots \lor \delta_n \in \Delta$. By the definition of $\Gamma$, $\delta_1 \lor \cdots \lor \delta_n \in \Gamma$, so $\mathfrak{B} \vDash \delta_1 \lor \cdots \lor \delta_n$. This contradicts $\lnot\delta_1, \dots, \lnot\delta_n \in \Sigma$.

Since $T \cup \Sigma$ is consistent, by the completeness theorem it has a model. Let this model be $\mathfrak{A}$. Since $\mathfrak{B}$ satisfies all sentences in $\Delta$ that $\mathfrak{A}$ satisfies, by assumption $\mathfrak{B}$ is a model of $T$. □

Now we proceed to the proof of the main theorem. Let $\Delta$ be the set of all $\Pi_1$ sentences in $\mathcal{L}$. Our goal is to show that $\Delta$ contains an axiomatisation of $T$. Since $\Pi_1$ sentences are closed under disjunction, by the lemma it suffices to show the following:

Let $T$ be a theory that is preserved under submodels. For a model $\mathfrak{A}$ of $T$, if $\mathfrak{B}$ satisfies all $\Pi_1$ sentences satisfied in $\mathfrak{A}$, then $\mathfrak{B}$ is also a model of $T$.

Following the notation from this article, let us define $E(\mathfrak{B})$. That is, $\mathfrak{M}$ satisfies $E(\mathfrak{B})$ when $\mathfrak{B} \preceq \mathfrak{M}$.

We show that $T \cup E(\mathfrak{B})$ is consistent. If $T \cup E(\mathfrak{B})$ were inconsistent, then there would exist some sentence $\phi(b_1, \dots, b_n)$ from $E(\mathfrak{B})$ such that $T \cup \lbrace \phi \rbrace $ has no model. Therefore, $\mathfrak{A}$, being a model of $T$, cannot be extended to an $\mathcal{L} \cup \lbrace b_1, \dots, b_n \rbrace $ model that satisfies $\phi$. That is, the following holds:

\[\mathfrak{A} \vDash \forall x_1 \cdots \forall x_n \lnot \phi(x_1, \dots, x_n)\]

The right-hand side is a $\Pi_1$ sentence, so by assumption $\mathfrak{B} \vDash \forall x_1 \cdots \forall x_n \lnot \phi(x_1, \dots, x_n)$. However, since $\phi(b_1, \dots, b_n) \in E(\mathfrak{B})$, this is a contradiction. Therefore, $T \cup E(\mathfrak{B})$ is consistent and by the completeness theorem has a model $\mathfrak{C}$. Since $\mathfrak{C}$ satisfies $E(\mathfrak{B})$, we have $\mathfrak{B} \preceq \mathfrak{C}$. Meanwhile, since $\mathfrak{C}$ is a model of $T$, which is preserved under submodels, $\mathfrak{B}$ is a model of $T$. ■

Applications

The first-order logical axiomatisation of groups differs depending on whether the identity element and inverse are represented as separate constant $e$ and function $(-)^{-1}$.

Without representation

Define theory $T_1$ in language $\mathcal{L}_1 = \lbrace G, \cdot \rbrace $ as follows:

• $\forall x, y, z : (x \cdot y) \cdot z = x \cdot (y \cdot z)$
• $\exists x \forall y : x \cdot y = y \cdot x = y$
• $\forall x \exists y \forall z : (x \cdot y) \cdot z = (y \cdot x) \cdot z = z$

With representation

Define theory $T_2$ in language $\mathcal{L}_2 = \lbrace G, \cdot, e, (-)^{-1} \rbrace $ as follows:

• $\forall x, y, z : (x \cdot y) \cdot z = x \cdot (y \cdot z)$
• $\forall x : x \cdot e = e \cdot x = x$
• $\forall x : x \cdot x^{-1} = x^{-1} \cdot x = e$

$T_1$ is not a $\Pi_1$ theory, but $T_2$ is a $\Pi_1$ theory. Therefore, by the Łoś-Tarski theorem, $T_1$ is not submodel-preserving while $T_2$ is preserving. That $T_1$ is not submodel-preserving means that a subset of a group being closed under the operation does not always make it a subgroup(for instance, the subset $\mathbb{Z}_{> 0}$ of $\mathbb{Z}$ is closed under the operation but is not a group as it lacks inverses). Conversely, that $T_2$ is submodel-preserving means the following holds:

For a group $G$, if a subset $H$ of $G$ satisfies the following, then $H$ is a subgroup of $G$:

1. Closed under the operation.
2. Closed under inverses.
3. Contains the identity element of $G$.

However, the following stronger result generally holds:

For a group $G$, if a subset $H$ of $G$ satisfies the following, then $H$ is a subgroup of $G$:

1. Closed under the operation.
2. Closed under inverses.

That is, even in language $\mathcal{L}_3 = \lbrace G, \cdot, (-)^{-1} \rbrace$ lacking a constant to denote the identity element, the theory of groups is submodel-preserving, which means there exists a $\Pi_1$ theory formalising groups in $\mathcal{L}_3$. With some clever thinking, one can indeed discover that the following theory $T_3$ exists:

• $\forall x, y, z : (x \cdot y) \cdot z = x \cdot (y \cdot z)$
• $\forall x, y : (x \cdot x^{-1}) \cdot y = y \cdot (x \cdot x^{-1}) = y$

완전성 정리와 뢰벤하임-스콜렘 정리

10 Apr 2025

괴델의 완전성 정리와 뢰벤하임-스콜렘 정리는 수리논리학의 가장 기본적인 정리들이다. 그래도 기본기를 다져보는 김에, 이 정리들의 증명을 복습해 보았다. 이 글에서 $T$는 언어 $\mathcal{L}$의 1차 논리 이론으로 간주한다.

괴델의 완전성 정리

괴델의 완전성 정리. $T \vDash \phi$라면 $T \vdash \phi$이다.

증명

다음의 동치인 진술을 증명한다. (연습문제: 왜 동치인가?)

$T$가 무모순적인_consistent 이론이라면, $T$는 모델을 가진다.

1. $\mathcal{L}$을 스콜렘 언어 $\mathcal{L}_S$로 확장하기

$\kappa = \mathrm{max}(\aleph_0, |\mathcal{L}|)$라고 하자. $T$에 상수 $\lbrace c_\alpha \rbrace _{\alpha \in \kappa}$ ($\alpha$는 서수)를 추가한 언어를 $\mathcal{L}_S$라고 하자. 여기서 첨자 $S$는 각 상수가 스콜렘 상수_{Skolem constant}의 역할을 담당할 것임을 의미한다.

2. $T$를 헨킨 이론 $T_H$로 확장하기

$\mathcal{L}_S$의 명제 중 하나의 자유변수를 가지는 명제들의 집합의 크기는 $\kappa$와 같으므로, 정렬 원리로부터 $\lbrace P_\alpha \rbrace _{\alpha \in \kappa}$와 같이 나타낼 수 있다. 이로부터 다음의 문장 집합을 정의한다.

\[\Sigma = \{ Q_\alpha := \exists x P_\alpha \rightarrow P_\alpha(c_\lambda) \mid \alpha \in \kappa \}\]

여기서 $c_\lambda$는 $P_\alpha$와 $Q_\beta \; (\beta < \alpha)$에 등장하지 않는 상수 중 첨자가 최소인 상수이다(그러한 상수가 존재함은 서수가 정렬이라는 사실로부터 보장된다). 이제 $T_H = T \cup \Sigma$로 정의한다. $T_H$를 헨킨 이론_{Henkin theory}이라고 하고, $Q_\alpha$를 헨킨 공리라고 한다.

3. $T_H$를 극대적으로 무모순적인 이론 $\overline{T_H}$로 확장하기

린덴바움 보조정리. $T$가 무모순적인 이론일 때, $T$를 확장하는 극대적으로 무모순적인_{maximally consistent} 이론 $\overline{T}$가 존재한다. 즉, $T \subseteq T’$이고 임의의 $\mathcal{L}$ 문장 $\phi$에 대해 $\phi \in \overline{T}$거나 $\lnot\phi \in \overline{T}$이다.

증명. $T$를 확장하는 무모순적인 이론들의 모임에 $\subseteq$로 순서 관계를 준 뒤, 초른의 보조정리를 적용한다.

$T$가 무모순적인 이론일 때 $T_H$ 또한 무모순적임을 쉽게 보일 수 있다. 따라서 린덴바움 보조정리에 의해 $T_H$를 확장하는 극대적으로 무모순적인 이론 $\overline{T_H}$가 존재한다.

4. $\overline{T_H}$의 표준적_canonical 모델 정의하기

$c_\alpha \sim c_\beta$를 $(c_\alpha = c_\beta) \in \overline{T_H}$일 때 성립하는 관계로 정의하자. $\overline{T_H}$가 무모순적인 이론이라는 사실로부터 $\sim$이 동치 관계임을 보일 수 있다. 따라서 상수들의 동치류 $[c_\alpha]$가 잘 정의된다. 이제 다음과 같이 $\mathcal{L}_S$의 구조 $\mathfrak{M}$을 정의한다.

1. 상수: $c_\alpha^{\mathfrak{M}} = [c_\alpha]$
2. 술어: $R^{\mathfrak{M}}(c_{\alpha_1}^\mathfrak{M}, \dots, c_{\alpha_n}^{\mathfrak{M}}) \iff \overline{T_H} \vdash R(c_{\alpha_1}, \dots, c_{\alpha_n}) $
3. 함수: $f(c_\alpha^\mathfrak{M}) = c_\beta^\mathfrak{M} \iff T_H \vdash \exists x (f(c_\alpha) = x) \rightarrow f(c_\alpha) = c_\beta$

$\overline{T_H}$가 극대적으로 무모순적이므로 2가 잘 정의되고, 헨킨 이론이므로 3이 잘 정의된다. 따라서 $\mathfrak{M}$이 잘 정의되며, $\mathfrak{M}$이 $\overline{T_H}$의 모델임을 쉽게 확인할 수 있다. 그리고 $\mathfrak{M}$은 $T$의 모델이기도 하므로, $T$는 모델을 가진다. ■

Remark 1. 완전성 정리의 증명은 정렬 원리와 초른의 보조정리를 사용한다는 점에서 선택 공리에 의존적이다. 쾨니히 보조정리나 의존적 선택 공리와 같이 더 약한 유형의 선택 공리로도 증명할 수 있긴 하다.

Remark 2. 콤팩트성 정리가 완전성 정리의 따름정리로서 얻어진다. (연습문제)

Remark 3. 완전성 정리의 증명에서 구축하는 모델의 크기는 $\kappa = \mathrm{max}(\aleph_0, |\mathcal{L}|)$를 넘지 않는다. 마지막 단계에서 동치류를 취하므로 $\kappa$와 같다는 보장은 없다.

뢰벤하임-스콜렘 정리

뢰벤하임-스콜렘 정리. $T$가 무한 모델을 가진다고 하자. 임의의 $\kappa \geq \mathrm{max}(\aleph_0, |\mathcal{L}|)$에 대해, 크기가 $\kappa$인 $T$의 모델이 존재한다.

증명

하향 뢰벤하임-스콜렘 정리

하향 뢰벤하임-스콜렘 정리. $T$는 크기가 $\mathrm{max}(\aleph_0, |\mathcal{L}|)$을 넘지 않는 모델을 가진다.

증명. Remark 2에서 즉시 얻어진다. □

상향 뢰벤하임-스콜렘 정리

상향 뢰벤하임-스콜렘 정리. $T$가 무한 모델을 가진다고 하자. 임의의 무한 기수 $\kappa$에 대해, 크기가 $\kappa$ 이상인 $T$의 모델이 존재한다.

증명. $\mathcal{L}’$을 $\mathcal{L}$에 상수 $\lbrace c_\alpha \rbrace _{\alpha \in \kappa}$를 추가한 언어로 정의하자. 다음의 $\mathcal{L}’$-문장 집합을 정의하자.

\[\Sigma = \{ c_\alpha \neq c_\beta : \alpha, \beta \in \kappa, \alpha \neq \beta \}\]

$T’ = T \cup \Sigma$라고 하자. $T$가 무한 모델 $\mathfrak{M}$을 가지므로, 임의의 $T’$의 유한 부분이론은 $\mathfrak{M}$에 의해 만족된다. 따라서 콤팩트성 정리에 의해 $T’$은 무모순적이며, 완전성 정리에 의해 모델을 가진다. $\Sigma$는 $T’$의 모델이 적어도 $\kappa$개의 원소를 가질 것을 요구하므로, $T’$은 크기가 $\kappa$ 이상인 모델을 가지며, 이에 따라 $T$ 또한 크기가 $\kappa$ 이상인 모델을 가진다. □

뢰벤하임-스콜렘 정리

$\kappa \geq \mathrm{max}(\aleph_0, |\mathcal{L}|)$라고 하자. $\mathcal{L}’$과 $T’$을 앞선 바와 같이 정의한다.

$\mathrm{max}(\aleph_0, |\mathcal{L}’|) = \kappa$이므로 하향 뢰벤하임-스콜렘 정리에 의해 $T’$은 크기가 $\kappa$를 넘지 않는 모델을 가진다. 그런데 상향 뢰벤하임-스콜렘 정리의 증명에서 지적했듯이 $T’$의 모든 모델은 크기가 $\kappa$ 이상이다. 따라서 $T’$은 크기가 정확히 $\kappa$인 모델을 가지며, 이에 따라 $T$ 또한 크기가 정확히 $\kappa$인 모델을 가진다. ■

Completeness Theorem and Löwenheim-Skolem Theorem

10 Apr 2025

This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.

Gödel’s completeness theorem and the Löwenheim-Skolem theorem are amongst the most fundamental theorems in mathematical logic. To consolidate the fundamentals, I have revisited the proofs of these theorems. In this article, $T$ is considered as a first-order logical theory in language $\mathcal{L}$.

Gödel’s Completeness Theorem

Gödel’s Completeness Theorem. If $T \vDash \phi$, then $T \vdash \phi$.

Proof

We prove the following equivalent statement. (Exercise: Why is this equivalent?)

If $T$ is a consistent theory, then $T$ has a model.

1. Extending $\mathcal{L}$ to the Skolem language $\mathcal{L}_S$

Let $\kappa = \mathrm{max}(\aleph_0, |\mathcal{L}|)$. Let $\mathcal{L}_S$ be the language obtained by adding constants $\lbrace c_\alpha \rbrace _{\alpha \in \kappa}$ (where $\alpha$ is an ordinal) to $T$. Here, the subscript $S$ indicates that each constant will serve as a Skolem constant.

2. Extending $T$ to the Henkin theory $T_H$

Since the size of the set of formulae in $\mathcal{L}_S$ with one free variable is equal to $\kappa$, by the well-ordering principle, we can represent them as $\lbrace P_\alpha \rbrace _{\alpha \in \kappa}$. From this, we define the following set of sentences:

\[\Sigma = \{ Q_\alpha := \exists x P_\alpha \rightarrow P_\alpha(c_\lambda) \mid \alpha \in \kappa \}\]

where $c_\lambda$ is the constant with the smallest index amongst the constants that do not appear in $P_\alpha$ and $Q_\beta \; (\beta < \alpha)$ (the existence of such a constant is guaranteed by the fact that ordinals are well-ordered). Now we define $T_H = T \cup \Sigma$. We call $T_H$ the Henkin theory and $Q_\alpha$ the Henkin axioms.

3. Extending $T_H$ to a maximally consistent theory $\overline{T_H}$

Lindenbaum’s Lemma. When $T$ is a consistent theory, there exists a maximally consistent theory $\overline{T}$ that extends $T$. That is, $T \subseteq T’$ and for any $\mathcal{L}$ sentence $\phi$, either $\phi \in \overline{T}$ or $\lnot\phi \in \overline{T}$.

Proof. We order the collection of consistent theories that extend $T$ by $\subseteq$ and apply Zorn’s lemma.

When $T$ is a consistent theory, we can easily show that $T_H$ is also consistent. Therefore, by Lindenbaum’s lemma, there exists a maximally consistent theory $\overline{T_H}$ that extends $T_H$.

4. Defining the canonical model of $\overline{T_H}$

Let $c_\alpha \sim c_\beta$ be the relation that holds when $(c_\alpha = c_\beta) \in \overline{T_H}$. From the fact that $\overline{T_H}$ is a consistent theory, we can show that $\sim$ is an equivalence relation. Therefore, the equivalence classes $[c_\alpha]$ of constants are well-defined. We now define a structure $\mathfrak{M}$ for $\mathcal{L}_S$ as follows:

1. Constants: $c_\alpha^{\mathfrak{M}} = [c_\alpha]$
2. Predicates: $R^{\mathfrak{M}}(c_{\alpha_1}^\mathfrak{M}, \dots, c_{\alpha_n}^{\mathfrak{M}}) \iff \overline{T_H} \vdash R(c_{\alpha_1}, \dots, c_{\alpha_n}) $
3. Functions: $f(c_\alpha^\mathfrak{M}) = c_\beta^\mathfrak{M} \iff T_H \vdash \exists x (f(c_\alpha) = x) \rightarrow f(c_\alpha) = c_\beta$

Since $\overline{T_H}$ is maximally consistent, (2) is well-defined, and since it is a Henkin theory, (3) is well-defined. Therefore, $\mathfrak{M}$ is well-defined, and we can easily verify that $\mathfrak{M}$ is a model of $\overline{T_H}$. Since $\mathfrak{M}$ is also a model of $T$, $T$ has a model. ■

Remark 1. The proof of the completeness theorem depends on the axiom of choice in that it uses the well-ordering principle and Zorn’s lemma. It can also be proved using weaker forms of the axiom of choice such as König’s lemma or the axiom of dependent choice.

Remark 2. The compactness theorem is obtained as a corollary of the completeness theorem. (Exercise)

Remark 3. The size of the model constructed in the proof of the completeness theorem does not exceed $\kappa = \mathrm{max}(\aleph_0, |\mathcal{L}|)$. Since we take equivalence classes in the final step, there is no guarantee that it equals $\kappa$.

Löwenheim-Skolem Theorem

Löwenheim-Skolem Theorem. Suppose $T$ has an infinite model. For any $\kappa \geq \mathrm{max}(\aleph_0, |\mathcal{L}|)$, there exists a model of $T$ of size $\kappa$.

Proof

Downward Löwenheim-Skolem Theorem

Downward Löwenheim-Skolem Theorem. $T$ has a model of size not exceeding $\mathrm{max}(\aleph_0, |\mathcal{L}|)$.

Proof. This follows immediately from Remark 2. □

Upward Löwenheim-Skolem Theorem

Upward Löwenheim-Skolem Theorem. Suppose $T$ has an infinite model. For any infinite cardinal $\kappa$, there exists a model of $T$ of size at least $\kappa$.

Proof. Let $\mathcal{L}’$ be the language obtained by adding constants $\lbrace c_\alpha \rbrace _{\alpha \in \kappa}$ to $\mathcal{L}$. Define the following set of $\mathcal{L}’$-sentences:

\[\Sigma = \{ c_\alpha \neq c_\beta : \alpha, \beta \in \kappa, \alpha \neq \beta \}\]

Let $T’ = T \cup \Sigma$. Since $T$ has an infinite model $\mathfrak{M}$, any finite subtheory of $T’$ is satisfied by $\mathfrak{M}$. Therefore, by the compactness theorem, $T’$ is consistent, and by the completeness theorem, it has a model. Since $\Sigma$ requires that any model of $T’$ has at least $\kappa$ elements, $T’$ has a model of size at least $\kappa$, and thus $T$ also has a model of size at least $\kappa$. □

Löwenheim-Skolem Theorem

Let $\kappa \geq \mathrm{max}(\aleph_0, |\mathcal{L}|)$. Define $\mathcal{L}’$ and $T’$ as above.

Since $\mathrm{max}(\aleph_0, |\mathcal{L}’|) = \kappa$, by the downward Löwenheim-Skolem theorem, $T’$ has a model of size not exceeding $\kappa$. However, as pointed out in the proof of the upward Löwenheim-Skolem theorem, every model of $T’$ has size at least $\kappa$. Therefore, $T’$ has a model of size exactly $\kappa$, and thus $T$ also has a model of size exactly $\kappa$. ■

자이페르트-판 캄펀 정리에 대한 노트

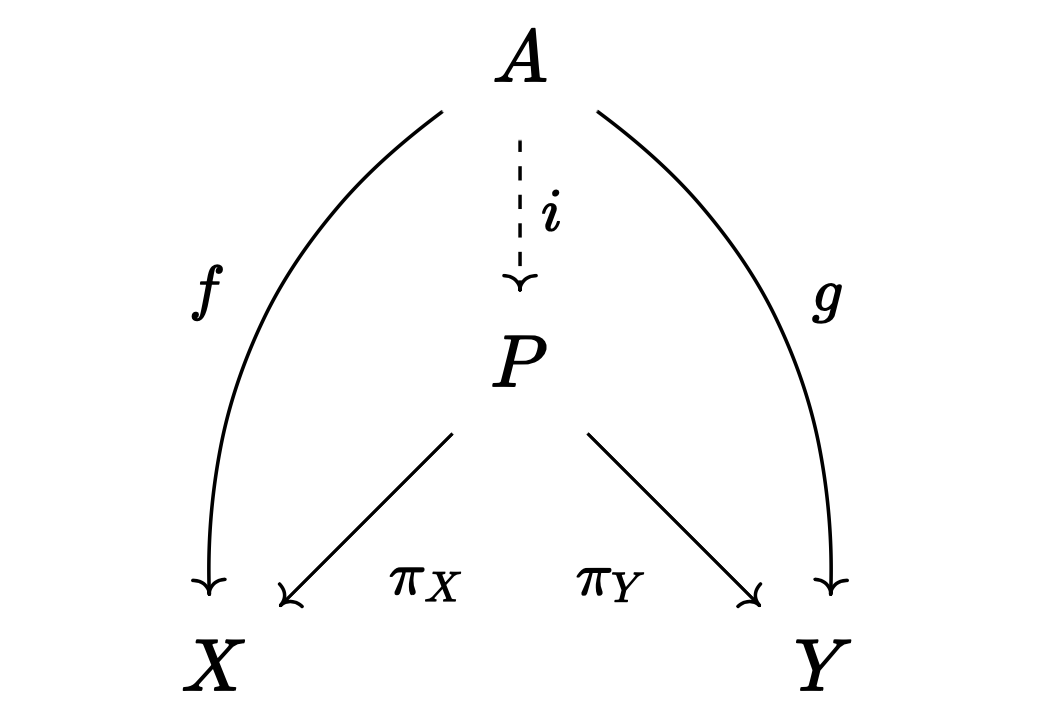
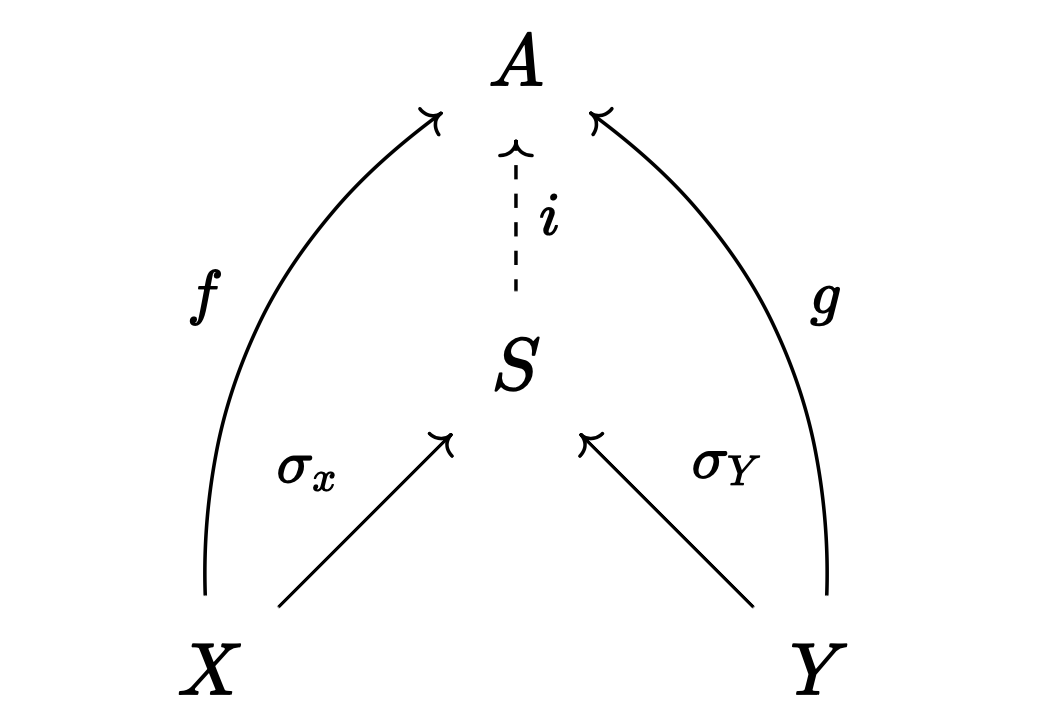
04 Apr 2025

위상공간 $X$의 열린 덮개 $U, V$를 생각하자. 위상공간들의 범주 $\mathbf{Top}$에서 다음 푸시아웃_pushout 도식의 극한은 $X$이다.

자이페르트-판 캄펀 정리는, $U, V$가 경로 연결_{path connected}이고 $x_0 \in U \cap V$일 때, 위 극한이 함자 $\pi_1(-, x_0): \mathbf{Top} \to \mathbf{Grp}$에 대해 보존된다는 내용이다.

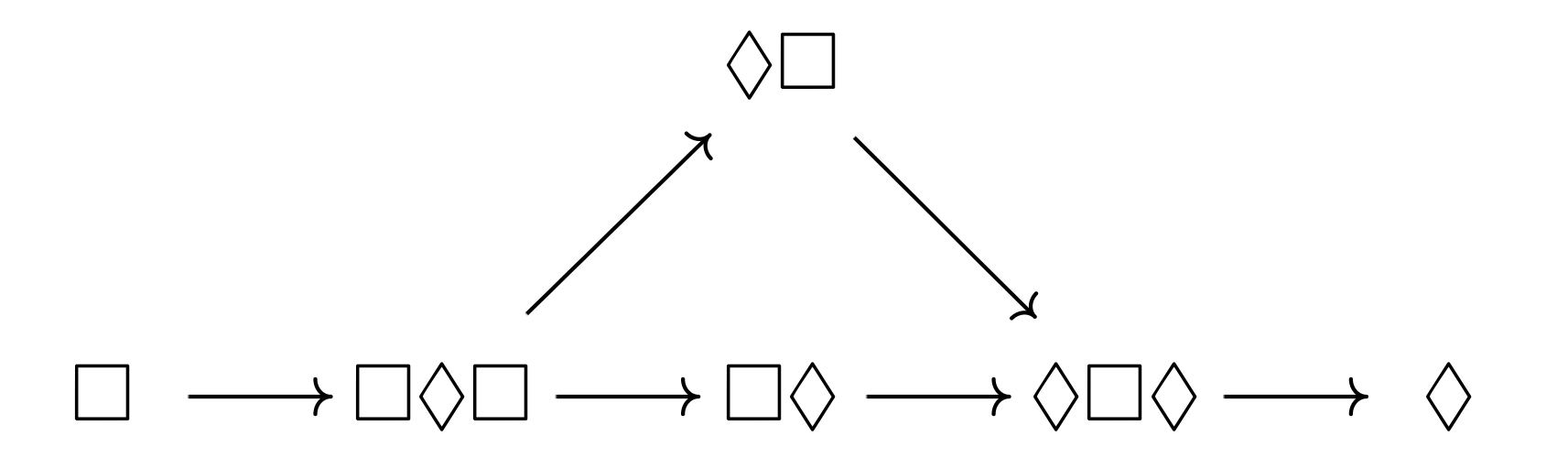
그런데 푸시아웃의 극한은 왼쪽 도식의 쌍대 극한_colimit이다. 만약 $I$에 대응되는 대상이 초기 대상_{initial object}이라면, 사상 $I \to J, J \to K$는 유일하게 결정되므로 사실상 왼쪽 도식의 쌍대 극한은 오른쪽 도식의 쌍대 극한과 같으며, 이는 범주론적 합에 해당한다.

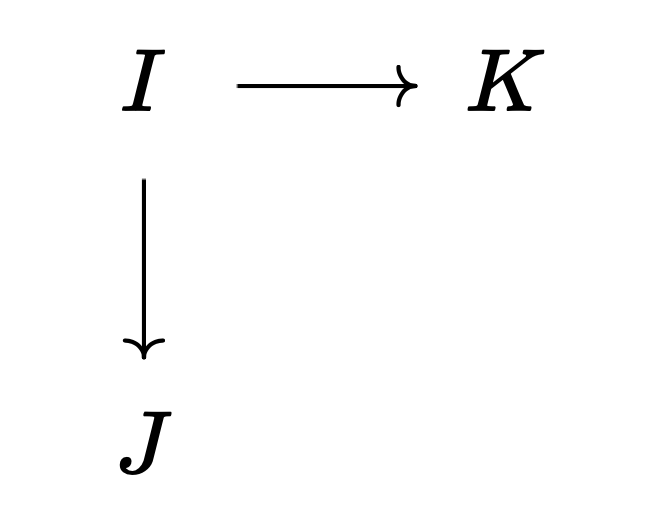
$\mathbf{Grp}$의 초기 대상은 자명군_{trivial group}이며, 범주론적 합은 자유곱이다. 이에 따라 $U \cap V$가 단순 연결 공간일 때, $\pi_1(X)$는 $\pi_1(U)$와 $\pi_1(V)$의 자유곱이라는 결론을 얻는다.

Notes on the Seifert-van Kampen Theorem

04 Apr 2025

This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.

Consider an open cover $U, V$ of a topological space $X$. In the category of topological spaces $\mathbf{Top}$, the limit of the following pushout diagram is $X$.

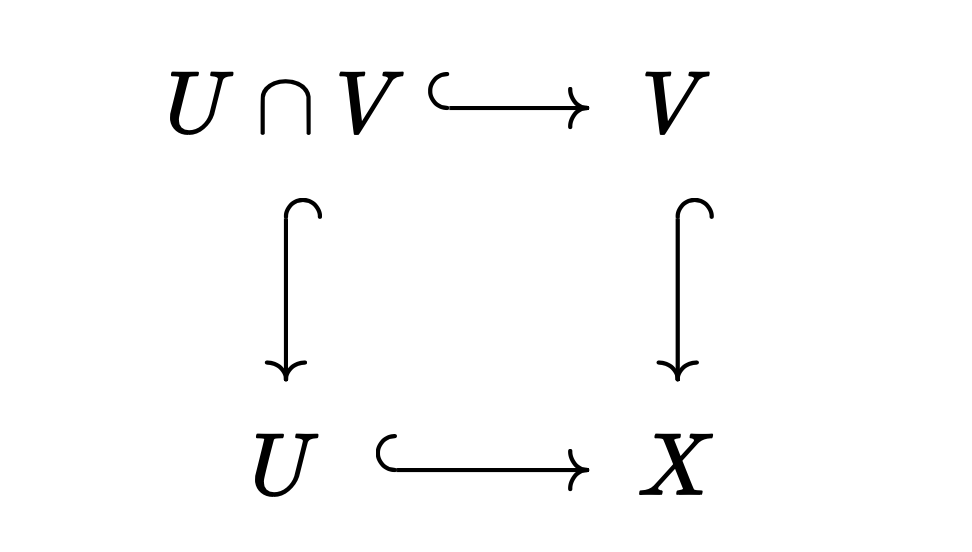
The Seifert-van Kampen theorem states that when $U, V$ are path connected and $x_0 \in U \cap V$, the above limit is preserved under the functor $\pi_1(-, x_0): \mathbf{Top} \to \mathbf{Grp}$.

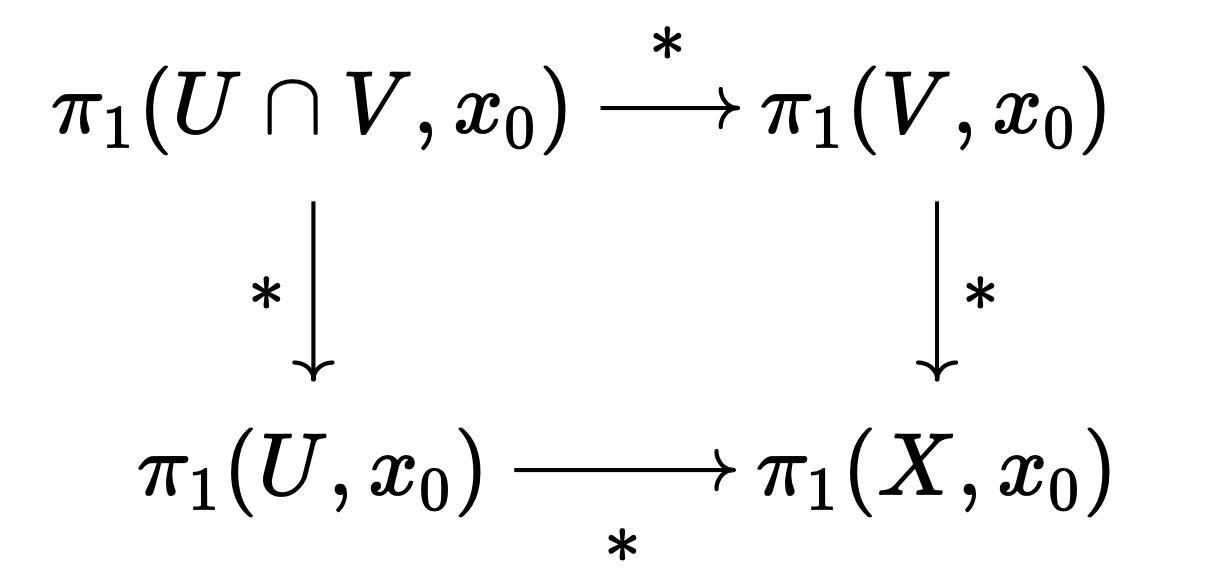
However, the limit of a pushout is the colimit of the left diagram. If the object corresponding to $I$ is an initial object, then the morphisms $I \to J, J \to K$ are uniquely determined, so the colimit of the left diagram is essentially the same as the colimit of the right diagram, which corresponds to the categorical sum.

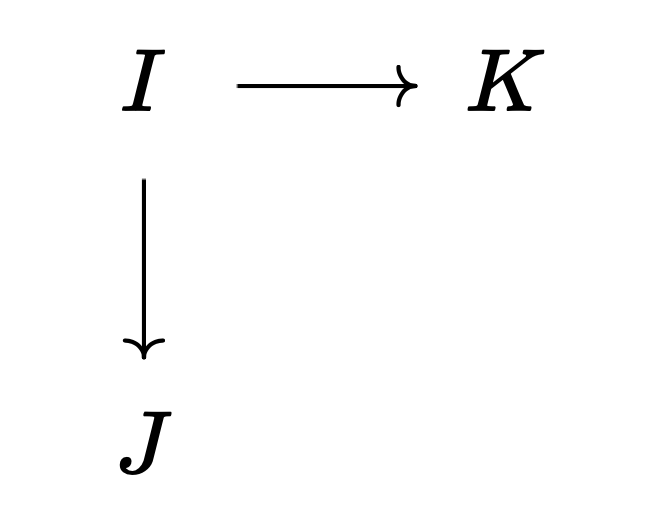
The initial object in $\mathbf{Grp}$ is the trivial group, and the categorical sum is the free product. Accordingly, when $U \cap V$ is a simply connected space, we obtain the conclusion that $\pi_1(X)$ is the free product of $\pi_1(U)$ and $\pi_1(V)$.

범주론적 관점에서의 곱 위상·상자 위상과 직곱·직합의 차이

02 Apr 2025

곱 위상과 상자 위상

학부 위상에서 곱 위상_{product topology}과 상자 위상_{box topology}을 다루는 부분은 많은 학생에게 난관으로 다가오는 대목이다. 겉보기에는 상자 위상이 훨씬 직관적인데, 교재에서는 상자 위상보다 곱 위상이 다루기에 자연스러운 개념이라고 가르치기 때문이다.

정의. 위상공간의 모임 $\lbrace X_i \rbrace _{i \in I}$에 대해, 상자 위상공간 $\prod X_i$는 다음의 기저로 생성되는 위상공간이다.

\[\left\{ \prod U_i : U_i \text{ is open in } X_i \right\}\]

정의. 위상공간의 모임 $\lbrace X_i \rbrace _{i \in I}$에 대해, 곱 위상공간 $\prod X_i$는 다음의 기저로 생성되는 위상공간이다.

\[\left\{ \prod U_i : U_i \text{ is open in } X_i,\; U_i \neq X_i \text{ for only finitely many } i\right\}\]

일례로 $\mathbb{R}^\omega$에서 $(1, 1, 1, \dots)$의 근방은 각각 다음과 같다.

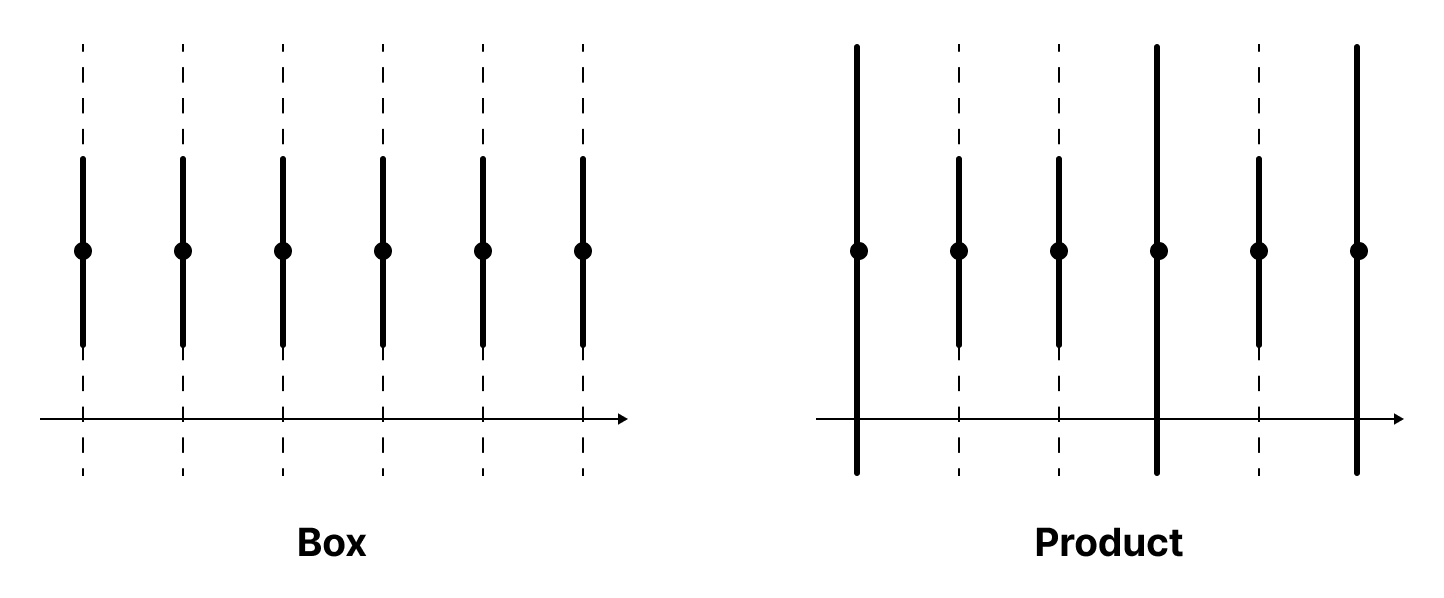
왜 곱 위상은 상자 위상보다 자연스러운 위상으로 간주될까? 그 이유는 범주론에서 대상의 곱을 정의하는 방법과 관련이 있다.

정의. $X, Y$가 범주 $\mathcal{A}$의 대상이라고 하자. $P \in \mathcal{A}$와 사상 $\pi_X : P \to X$, $\pi_Y : P \to Y$에 대해, 다음 조건이 만족될 때 $P$를 $X, Y$의 곱_product이라고 하며, $P = X \times Y$와 같이 적는다.

• 임의의 $A \in \mathcal{A}$와 $f: A \to X$, $g: A \to Y$에 대해 다음 도식이 가환이 되도록 하는 사상 $i: A \to P$가 언제나 유일하게 존재한다.

위의 정의는 자연스러운 방식으로 3개 이상, 또는 무한한 대상들의 곱으로 일반화된다. 극한_limit의 개념이 익숙한 독자라면, 곱은 이산 범주의 극한으로 이해할 수 있다. 또는, 곱은 주어진 대상들의 정보를 온전히 인코딩하는 가장 작은 범주로 이해할 수 있다.

집합들의 범주에서 곱은 곱집합과 같다. 특히 $\pi_X, \pi_Y$는 각각 $(x, y) \mapsto x$, $(x, y) \mapsto y$로 주어진다.

위상공간들의 범주에서 곱은 상자 위상이 아닌 곱 위상이다. 이는 다음의 정리로 보증된다.

정리. 사영함수 $\pi_k : \prod_{i \in I}X_i \to X_k$가 각 $k \in I$에 대해 연속이 되도록 하는 가장 작은 $\prod_{i \in I}X_i$의 위상은 곱 위상이다.

상자 위상도 각 사영함수가 연속이라는 특징을 가지지만, 상자 위상은 곱 위상보다 큰 토폴로지이다. 따라서 상자 위상은 범주론적 곱이 아니다.

상자 위상이 곱이 아님을 보이는 반례를 살펴보자. $\mathbb{R}^\omega$에 상자 위상을 부여하자. 만약 상자 위상이 범주론적 곱이라면, 임의의 연속인 $f_k: \mathbb{R} \to \mathbb{R}$에 대해 $\pi_k \circ i = f_k$가 되도록 하는 연속함수 $i : \mathbb{R} \to \mathbb{R}^\omega$가 존재해야 한다. $f_k: x \mapsto kx$라면 $i$는 $x \mapsto (x, 2x, 3x, \dots)$이다. 상자 위상에서는 $U = (0, 1)^\omega$가 열린 집합이므로, $i$가 연속이면 $i^{-1}(U)$가 열린집합이다. 그런데 $i^{-1}(U) = \lbrace 0 \rbrace $이므로, 상자 위상은 곱의 성질을 만족하지 않는다.

직곱과 직합

상자 위상과 곱 위상의 차이는 전체 공간이 아닌 인덱스가 유한한지의 여부에 있다. 이와 유사한 차이를 대수학에서도 발견할 수 있다.

정의. 벡터 공간들의 모임 $\lbrace V_i \rbrace _{i \in I}$에 대해, 직곱_{direct product} $\prod V_i$를 다음과 같이 정의한다.

\[\prod V_i = \left\{ (v_i)_{i \in I} : v_i \in V_i \right\}\]

정의. 벡터 공간들의 모임 $\lbrace V_i \rbrace _{i \in I}$에 대해, 직합_{direct sum} $\bigoplus V_i$를 다음과 같이 정의한다.

\[\bigoplus V_i = \left\{ (v_i)_{i \in I} : v_i \in V_i,\; v_i \neq 0 \text{ for only finitely many }i \right\}\]

벡터의 연산은 항별_term-wise로 정의한다. 또한 벡터 공간이 아닌 군에 대해서도 같은 방식으로 직곱과 직합을 정의할 수 있다.

직곱과 상자 위상, 직합과 곱 위상의 정의가 비슷하다는 점으로부터 직합이 범주론적 곱에 대응된다고 생각할 수 있지만 그렇지 않다. 대수의 경우 범주론적 곱에 대응되는 것은 직곱이다. 직합은 범주론적 곱의 조건을 일반적으로 만족하지 않는다.

일례로 다음의 경우를 보자. 일차원 실수 공간 $\mathbb{R}$의 직합 $\mathbb{R}^\omega$를 고려하자. 만약 직합이 범주론적 곱이라면, 임의의 선형인 $f_k: \mathbb{R} \to \mathbb{R}$에 대해 $\pi_k \circ i = f_k$가 되도록 하는 연속함수 $i : \mathbb{R} \to \mathbb{R}^\omega$가 존재해야 한다. $f_k: x \mapsto x$라면 $i$는 $x \mapsto (x, x, x, \dots)$이다. 그런데 $i(1) = (1, 1, 1, \dots) \notin \mathbb{R}^\omega$이므로, 직합은 곱의 성질을 만족하지 않는다.

대신 직합은 범주론적 합_sum에 대응된다. 범주론적 합은 곱의 켤레_dual이기 때문에 쌍곱_coproduct이라고도 한다.

정의. $X, Y$가 범주 $\mathcal{A}$의 대상이라고 하자. $S \in \mathcal{A}$와 사상 $\sigma_X : X \to S$, $\sigma_Y : Y \to S$에 대해, 다음 조건이 만족될 때 $S$를 $X, Y$의 합_sum이라고 하며, $S = X + Y$와 같이 적는다.

• 임의의 $A \in \mathcal{A}$와 $f: X \to A$, $g: Y \to X$에 대해 다음 도식이 가환이 되도록 하는 사상 $i: S \to A$가 언제나 유일하게 존재한다.

앞서 들었던 예시를 다시 보자. 직합 $\bigoplus_\omega \mathbb{R}$를 고려하자. $\sigma_k: \mathbb{R} \to \bigoplus_\omega \mathbb{R}$은 다음과 같이 주어진다.

\[x \mapsto (0, \dots, 0, x, 0, \dots) \quad \text{($x$ is at the $k$th index)}\]

$A = \mathbb{R}$이라고 하고, 항등사상 $f_k : \mathbb{R} \to \mathbb{R}$을 고려하자. $\bigoplus_\omega \mathbb{R}$가 범주론적 합이라면 $i \circ \sigma_k = f_k$가 되도록 하는 연속함수 $i : \bigoplus_\omega \mathbb{R} \to \mathbb{R}$가 존재해야 한다. 실제로 이는 다음과 같이 존재한다.

\[i: (x_i)_{i \in \omega} \mapsto \sum_{i \in \omega} x_i\]

$\bigoplus_\omega \mathbb{R}$의 원소는 오직 유한한 비자명 항을 가지므로 $i$는 잘 정의됨에 주목하라. 반면, 이 예시는 직곱 $\mathbb{R}^\omega$가 범주론적 합이 아님을 보여준다. 직곱의 경우 $i$가 잘 정의되지 않기 때문이다. 이는 $i$에 $(1, 1, 1, \dots)$를 대입해 보면 알 수 있다.

군의 경우 범주론적 곱과 범주론적 합에 대응되는 연산은 일반적인 군의 범주를 따지냐, 아벨군의 범주를 따지냐에 따라 조금 다르다. 이 부분은 간단한 노트 정도로 남겨둔다.

	대수적 정의	범주론적 정의
자유곱	형식적 단어의 집합 + 병치 연산	$\mathbf{Grp}$의 합
직합	유한한 비자명 항을 가지는 튜플의 집합 + 항별 연산	$\mathbf{Ab}$의 합
직곱	튜플의 집합 + 항별 연산	$\mathbf{Grp}$의 곱

The Difference Between Product and Box Topologies, and Direct Product and Direct Sum from a Categorical Perspective

02 Apr 2025

Product Topology and Box Topology

Product topology and box topology often stir confusion among many undergraduate students. For, although the box topology appears more intuitive at first glance, textbooks teach that the product topology is the more “natural” concept to work with.

Definition. For a collection of topological spaces $\lbrace X_i \rbrace _{i \in I}$, the box topological space $\prod X_i$ is the topological space generated by the following basis:

\[\left\{ \prod U_i : U_i \text{ is open in } X_i \right\}\]

Definition. For a collection of topological spaces $\lbrace X_i \rbrace _{i \in I}$, the product topological space $\prod X_i$ is the topological space generated by the following basis:

\[\left\{ \prod U_i : U_i \text{ is open in } X_i,\; U_i \neq X_i \text{ for only finitely many } i\right\}\]

For instance, the neighbourhoods of $(1, 1, 1, \dots)$ in $\mathbb{R}^\omega$ are as follows:

Why is the product topology considered more natural than the box topology? The reason is related to how products of objects are defined in category theory.

Definition. Let $X, Y$ be objects in category $\mathcal{A}$. For $P \in \mathcal{A}$ and morphisms $\pi_X : P \to X$, $\pi_Y : P \to Y$, we call $P$ the product of $X, Y$ and write $P = X \times Y$ when the following condition is satisfied:

• For any $A \in \mathcal{A}$ and morphisms $f: A \to X$, $g: A \to Y$, there exists a unique morphism $i: A \to P$ such that the following diagram commutes:

The above definition naturally generalises to products of three or more, or infinitely many objects. Readers familiar with the concept of limits will recognise that the product can be understood as the limit of a discrete category. Alternatively, the product can be understood as the smallest category that fully encodes the information of the given objects.

In the category of sets, the product coincides with the Cartesian product. In particular, $\pi_X, \pi_Y$ are given by $(x, y) \mapsto x$ and $(x, y) \mapsto y$ respectively.

In the category of topological spaces, the product is the product topology, not the box topology. This is seen by the following theorem:

Theorem. The smallest topology on $\prod_{i \in I}X_i$ such that the projection functions $\pi_k : \prod_{i \in I}X_i \to X_k$ are continuous for each $k \in I$ is the product topology.

while the box topology also has the property that each projection function is continuous, the box topology is a larger topology than the product topology. Therefore, the box topology is not the categorical product.

Let us examine a counterexample showing that the box topology is not the categorical product. Consider $\mathbb{R}^\omega$ with the box topology. If the box topology were the categorical product, then for any continuous functions $f_k: \mathbb{R} \to \mathbb{R}$, there would exist a continuous function $i : \mathbb{R} \to \mathbb{R}^\omega$ such that $\pi_k \circ i = f_k$. If $f_k: x \mapsto kx$, then $i$ would be $x \mapsto (x, 2x, 3x, \dots)$. In the box topology, $U = (0, 1)^\omega$ is an open set, so if $i$ were continuous, then $i^{-1}(U)$ would be an open set. However, $i^{-1}(U) = \lbrace 0 \rbrace $, so the box topology does not satisfy the property of a product. (Note that in the case of product topology, $U$ is not an open set.)

Direct Product and Direct Sum

The difference between the box topology and product topology lies in whether only finitely many indices are allowed to be non-trivial. A similar difference can be found in algebra.

Definition. For a collection of vector spaces $\lbrace V_i \rbrace _{i \in I}$, the direct product $\prod V_i$ is defined as follows:

\[\prod V_i = \left\{ (v_i)_{i \in I} : v_i \in V_i \right\}\]

Definition. For a collection of vector spaces $\lbrace V_i \rbrace _{i \in I}$, the direct sum $\bigoplus V_i$ is defined as follows:

\[\bigoplus V_i = \left\{ (v_i)_{i \in I} : v_i \in V_i,\; v_i \neq 0 \text{ for only finitely many }i \right\}\]

Vector operations are defined term-wise. The same definitions of direct product and direct sum can be applied to groups as well.

From the similarity between the definitions of direct product and box topology, and direct sum and product topology, one might think that the direct sum corresponds to the categorical product, but this is not the case. In algebra, the direct product corresponds to the categorical product. The direct sum does not generally satisfy the conditions of a categorical product.

Consider the following example: Let us examine the direct sum $\mathbb{R}^\omega$ of one-dimensional real spaces $\mathbb{R}$. If the direct sum were the categorical product, then for any linear maps $f_k: \mathbb{R} \to \mathbb{R}$, there would exist a continuous function $i : \mathbb{R} \to \mathbb{R}^\omega$ such that $\pi_k \circ i = f_k$. If $f_k: x \mapsto x$, then $i$ would be $x \mapsto (x, x, x, \dots)$. However, $i(1) = (1, 1, 1, \dots) \notin \mathbb{R}^\omega$, so the direct sum does not satisfy the property of a product.

Instead, the direct sum corresponds to the categorical sum. The categorical sum is also called a coproduct because it is the dual of the categorical product.

Definition. Let $X, Y$ be objects in category $\mathcal{A}$. For $S \in \mathcal{A}$ and morphisms $\sigma_X : X \to S$, $\sigma_Y : Y \to S$, we call $S$ the sum of $X, Y$ and write $S = X + Y$ when the following condition is satisfied:

• For any $A \in \mathcal{A}$ and morphisms $f: X \to A$, $g: Y \to A$, there exists a unique morphism $i: S \to A$ such that the following diagram commutes:

Let us revisit the earlier example. Consider the direct sum $\bigoplus_\omega \mathbb{R}$. The morphism $\sigma_k: \mathbb{R} \to \bigoplus_\omega \mathbb{R}$ is given by:

\[x \mapsto (0, \dots, 0, x, 0, \dots) \quad \text{($x$ is at the $k$th index)}\]

Let $A = \mathbb{R}$ and consider the identity morphism $f_k : \mathbb{R} \to \mathbb{R}$. If $\bigoplus_\omega \mathbb{R}$ is the categorical sum, then there must exist a continuous function $i : \bigoplus_\omega \mathbb{R} \to \mathbb{R}$ such that $i \circ \sigma_k = f_k$. Indeed, this exists as follows:

\[i: (x_i)_{i \in \omega} \mapsto \sum_{i \in \omega} x_i\]

Note that $i$ is well-defined because elements of $\bigoplus_\omega \mathbb{R}$ have only finitely many non-trivial terms. Conversely, this example shows that the direct product $\mathbb{R}^\omega$ is not the categorical sum. In the case of the direct product, $i$ is not well-defined. This can be seen by substituting $(1, 1, 1, \dots)$ into $i$.

For groups, the operations corresponding to categorical products and categorical sums differ slightly depending on whether we consider the general category of groups or the category of abelian groups. I shall leave this as a brief note.

	Algebraic Definition	Categorical Definition
Free Product	Set of formal words + concatenation operation	Sum in $\mathbf{Grp}$
Direct Sum	Set of tuples with finitely many non-trivial terms + term-wise operation	Sum in $\mathbf{Ab}$
Direct Product	Set of tuples + term-wise operation	Product in $\mathbf{Grp}$

양상 논리

01 Apr 2025

종류

이름	함의	공리
K	가능세계에 대한 크립키 모델	$\Box(p \to q) \to (\Box p \to \Box q)$
T	반사성	K + $\Box p \to p$
S4	반사성 + 추이성	T + $\Box p \to \Box \Box p$
S4.2	반사성 + 추이성 + R-수렴성	S4 + $\Diamond \Box p \to \Box \Diamond p$
S4.3	반사성 + 추이성 + R-선형성	S4 + $(\Diamond p \land \Diamond q) \to$ $(\Diamond (p \land \Diamond q) \lor \Diamond(\Diamond p \land q))$
S5	반사성 + 추이성 + 대칭성	S4 + $(p \to \Box \Diamond p)$

표의 밑으로 갈수록 논리는 엄격히 강해진다.

양상의 축약

정리. S4에서 양상 연산자의 나열은 6개의 조합 중 하나와 동등하며, 각 조합의 함의 관계는 다음과 같다.

정리. S5에서 양상 연산자의 나열은 $\Box$ 또는 $\Diamond$와 동등하다. 나아가 모든 논리식은 평평한_flat 논리식 — 즉, 양상 연산자 안에 양상 연산자가 있는 경우가 없는 논리식과 동치이다.

완전성 정리

정리. K는 완전하다.

증명.

린덴바움 보조정리. 임의의 무모순적인 이론은 극대적으로 무모순적인_{maximally consistent} 이론으로 확장될 수 있다.

완전성 진술은 “무모순적인 이론은 만족 가능하다”와 동치이며, 여기에 린덴바움 보조정리를 적용하면 이는 “극대적으로 무모순적인 이론은 만족 가능하다”와 동치이다.

$u, v$가 극대적으로 무모순적인 이론이라고 하자. $\Box p \in u \implies p \in v$일 때 $u \lhd v$라고 적자. 다음을 어렵지 않게 보일 수 있다.

• $u \lhd v$일 때, $p \in v \implies \Diamond p \in u$
• 임의의 극대적으로 무모순적인 이론 $u$에 대해, $p \in u$이고 $\Box p \notin u$라면, 어떤 극대적으로 무모순적인 이론 $v, v’$가 존재하여 $p \in v, \lnot p \in v’$이고 $u \lhd v, v’$이다.

이로부터 극대적으로 무모순적인 이론 $u$에 대해, 표준적_canonical 크립키 모델 $\mathfrak{K} = (U, \prec, V)$를 다음과 같이 정의할 수 있다.

• 가능세계들의 모임 $U$는 $u \lhd v$를 만족하는 $v$의 모임이다.
• 접근 관계 $\prec$은 $\lhd$이다.
• 평가 함수_{valuation function} $V(p, v)$는 $p \in v$일 때, 그리고 오직 그 경우에만 참이다.

$\mathfrak{K}$가 $u$를 만족함을 어렵지 않게 보일 수 있다. ■

Modal Logic

01 Apr 2025

This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.

Types

Name	Entailment	Axioms
K	Kripke model for possible worlds	$\Box(p \to q) \to (\Box p \to \Box q)$
T	Reflexivity	K + $\Box p \to p$
S4	Reflexivity + Transitivity	T + $\Box p \to \Box \Box p$
S4.2	Reflexivity + Transitivity + R-convergence	S4 + $\Diamond \Box p \to \Box \Diamond p$
S4.3	Reflexivity + Transitivity + R-linearity	S4 + $(\Diamond p \land \Diamond q) \to$ $(\Diamond (p \land \Diamond q) \lor \Diamond(\Diamond p \land q))$
S5	Reflexivity + Transitivity + Symmetry	S4 + $(p \to \Box \Diamond p)$

The logics become strictly stronger as one moves down the table.

Modal Reduction

Theorem. In S4, any sequence of modal operators is equivalent to one of six combinations, and the entailment relations amongst these combinations are as follows:

Theorem. In S5, any sequence of modal operators is equivalent to either $\Box$ or $\Diamond$. Furthermore, every formula is equivalent to a flat formula—that is, a formula containing no modal operators within the scope of other modal operators.

Completeness Theorem

Theorem. K is complete.

Proof.

Lindenbaum’s Lemma. Any consistent theory can be extended to a maximally consistent theory.

The completeness statement is equivalent to “every consistent theory is satisfiable”, and applying Lindenbaum’s lemma, this is equivalent to “every maximally consistent theory is satisfiable”.

Let $u, v$ be maximally consistent theories. We write $u \lhd v$ when $\Box p \in u \implies p \in v$. The following can be shown without difficulty:

• When $u \lhd v$, we have $p \in v \implies \Diamond p \in u$
• For any maximally consistent theory $u$, if $p \in u$ and $\Box p \notin u$, then there exist maximally consistent theories $v, v’$ such that $p \in v, \lnot p \in v’$ and $u \lhd v, v’$.

From this, for a maximally consistent theory $u$, we can define the canonical Kripke model $\mathfrak{K} = (U, \prec, V)$ as follows:

• The collection of possible worlds $U$ is the collection of $v$ satisfying $u \lhd v$.
• The accessibility relation $\prec$ is $\lhd$.
• The valuation function $V(p, v)$ is true if and only if $p \in v$.

It can be shown without difficulty that $\mathfrak{K}$ satisfies $u$. ■

요네다 보조정리

21 Mar 2025

Notation.

1. $-$는 매개변수의 자릿값이다. $-$가 두 개 쓰였으면 매개변수가 두 개라는 뜻이다. 어느 매개변수가 어느 자리에 해당하는지는 맥락으로 파악한다.
2. $\bullet$은 $-$를 우선하는 매개변수이다. 따라서 $\hom(-, \bullet)$은 $A$를 함자 $\hom(-, A)$에 대응시키는 함자이다.
3. 함자 $F, G$에 대해 $[F, G]$를 $F$에서 $G$로 가는 자연적 변환_{natural transformation}들의 모임으로 정의한다.
4. 모든 범주는 국소적으로 작은_{locally small} 범주라고 가정한다.

요네다 보조정리_{Yoneda lemma}는 표현가능함자_{representable}가 다른 함자를 바라볼 때 보이는 것이 무엇인지를 알려주는 정리이다.

예를 들어 $A \in \mathcal{A}$에 대해, 표현가능함자 $\hom_{\mathcal{A}}(-, A)$를 생각하자. 이 함자가 속하는 범주는 $[\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$이다. 따라서 $\hom_{\mathcal{A}}(-, A)$가 함자 $F : \mathcal{A}^{\mathrm{op}} \to \mathbf{Set}$를 바라볼 때 보이는 것은 다음 자연적 변환들의 집합이다.

\[[\hom_{\mathcal{A}}(-, A), F]\]

위 집합은 $A \in \mathcal{A}$와 $F \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$으로부터 정의된 집합이다. 그런데 $A, F$로부터 집합을 정의할 수 있는 또다른 자연스러운 방식이 있다. 단순히 $F$에 $A$를 취하는 것이다.

\[F(A)\]

요네다 보조정리에 따르면 두 집합은 동형_isomorphic이다. 게다가 그냥 동형인 것이 아니라, $A \in \mathcal{A}$와 $F \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$에서 자연스럽게 동형_{naturally isomorphic}이다. 요컨대 다음 두 함자가 $[\mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}], \mathbf{Set}]$에서 동형이다.

\[\begin{aligned} \text{(i)} \quad \mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] &\xrightarrow{\hspace{0.15cm} \hom_{\mathcal{A}}(-, \cdot)^{\mathrm{op}} \times 1 \hspace{0.15cm}} [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] \\ &\xrightarrow{\hom_{[\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]}(-, -)} \mathbf{Set} \\\\ \text{(ii)} \quad \mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] &\xrightarrow{-(-)} \mathbf{Set} \end{aligned}\]

Remark. $\hom_{\mathcal{A}}(-, \cdot)^{\mathrm{op}}$에 붙은 $\mathrm{op}$는 함자의 정의역을 $\mathcal{A}^\mathrm{op}$로 맞춰주기 위함이고, 실질적으로는 $\hom_{\mathcal{A}}(-, \cdot)$와 같다.

증명. 증명의 개요만 적자면, $\hat{(\;\;)} : [\hom_\mathcal{A}(-, A), F] \to F(A)$와 $\tilde{(\;\;)}: F(A) \to [\hom_\mathcal{A}(-, A), F]$를 다음과 같이 정의한다.

\[\hat{\alpha} = \alpha_A(1_A), \quad \tilde{x} = \theta\]

여기서 $\theta$는 $f : A’ \to A$를 다음과 같이 사상하는 자연적 변환이다.

\[\theta_{A'}: f \mapsto F(f^{\mathrm{op}})(x)\]

$\theta$를 위와 같이 정의하는 이유는 다음 가환 도식을 만족하게끔 만들기 위함이다. ($(-)$에 $1_A$를 대입해 확인해 보라.)

이제 임의의 $A \in \mathcal{A}, F : \mathcal{A}^\mathrm{op} \to \mathbf{Set}$에 대해 다음이 성립함을 보여아 한다.

• 임의의 $\alpha \in [\hom_\mathcal{A}(-, A), F]$에 대해 $\tilde{\hat{\alpha}} = \alpha$이다.
• 임의의 $x \in F(A)$에 대해 $\hat{\tilde{x}} = x$이다.

이것은 $[\hom_\mathcal{A}(-, A), F] \cong F(A)$임을 보인다. 여기에 더해, 해당 동형이 자연적임을 보여아 한다. 자아아알 생각해 보면 이것은 임의의 $A, A’ \in \mathcal{A}$와 $F, G \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$와 $f: A’ \to A$와 $\alpha: F \Rightarrow G$에 대해 다음 도식이 가환임을 보이는 것과 같다.

원소 단위로 적으면,

위가 성립함은 $\theta$의 자연성으로부터 따라 나온다. ■

요네다 따름정리와 관계론적 존재론

요네다 보조정리가 함의하는 결과 중 다음은 아주 중요하다. 필자는 이를 그냥 요네다 따름정리라고 부른다.

요네다 따름정리. $X, Y \in \mathcal{A}$라고 하자.

1. $[\hom(-, X), \hom(-, Y)] \cong \hom(X, Y)$
2. $X \cong Y \iff \hom(-, X) \cong \hom(-, Y)$

증명. $F = \hom(-, Y)$로 둔다. ■

요컨대 범주론에서 대상은, 그것이 받는 사상들의 집합과 다름없다. 일례로 정수 순서 범주에서 $0$은 초기 대상으로 정의할 수 있고, 더 일반적으로 $n$은 받는 사상들의 수가 $n$개인 대상으로 정의할 수 있다. 요네다 따름정리는 이처럼 대상을 그것이 다른 대상과 맺는 사상들로서 정의하는 접근이 모든(엄밀히는 국소적으로 작은) 범주에서 유효함을 보장한다. 필자는 이 접근을 관계론적 존재론이라고 부른다.