오일러-라그랑주 방정식과 라그랑주 역학

27 Feb 2025

1. 도입

1차원 위에서 운동하는 입자의 운동 경로는 $x(t)$와 같이 표현할 수 있다. 입자의 위치와 속도에 의존적인 함수 $f(x, x’)$를 생각하자. 이 입자가 시간 $t_1$일 때 $x_1$에서 출발하여 시간 $t_2$일 때 $x_2$에 도착하는데, 그 과정에서 다음 값을 극화_extremise하는 경로, 즉 다음 값이 극대 또는 극소가 되도록 하는 경로 $x(t)$를 찾는 것이 목표이다.

\[A[x] = \int^{t_2}_{t_1} f(x, \dot{x}) dt\]

대괄호는 $A$의 매개변수가 실수가 아닌 함수임을 의미한다. 따라서 직관적으로 생각했을 때 $A[x]$를 최소화하는 $x(t)$를 찾기 위해서는 함수에 대한 미분식을 세워야 한다.

\[\frac{dA[x]}{dx(t)} = 0?\]

2. 오일러-라그랑주 방정식

물론 함수에 대한 미분을 우리는 정의한 적이 없다. 하지만 간단한 트릭을 통해 함수에 대한 미분을 일반적인 미분으로 환원할 수 있다. 먼저 $x_0(t)$가 우리가 찾고자 하는 경로, 즉 $A[x]$를 극화시키는 경로라고 하자. $x_0(t)$의 ‘주변’에 있는 경로는 다음과 같은 꼴이다.

\[x(\alpha, t) = x_0(t) + \alpha h(t)\]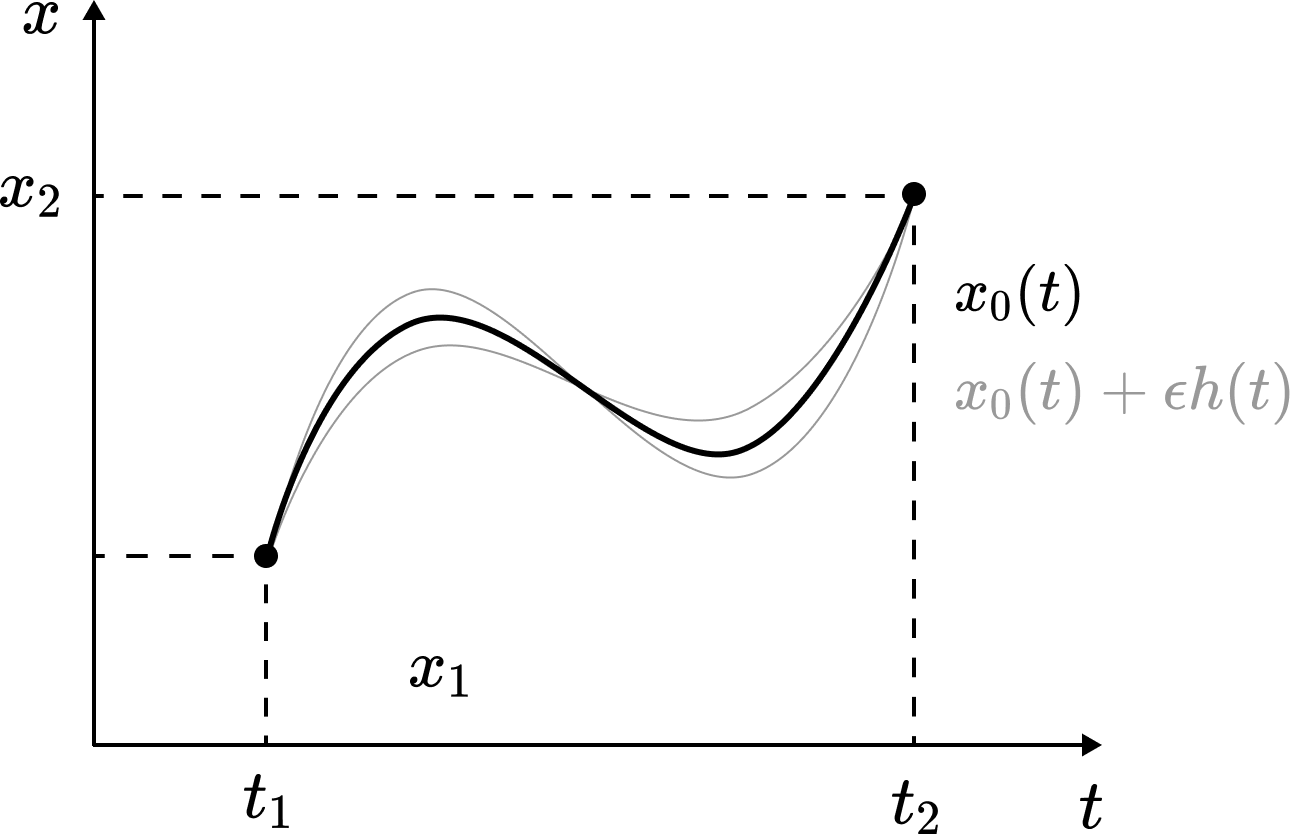

경계 조건은 $h(t_1) = h(t_2) = 0$이다. $x_0(t)$가 $A[x]$를 극화시키므로, 충분히 작은 $\epsilon$에 대해 $A[x_0] = A[x(0, t)] \leq A[x(\epsilon, t)]$이다. 따라서,

\[\left. \frac{dA[x(\alpha, t)]}{d\alpha} \right\vert_{\alpha = 0} = 0\]

위 식을 전개하면 다음과 같다.

\[\begin{aligned} \frac{dA}{d\alpha} &= \int^{t_2}_{t_1} \frac{d}{d\alpha} \Big[ f \big( x(\alpha, t), \dot{x}(\alpha, t) \big) \Big] dt \\ &= \int^{t_2}_{t_1} \left( \frac{\partial f}{\partial x}\frac{\partial x}{\partial \alpha} + \frac{\partial f}{\partial \dot{x}}\frac{\partial \dot{x}}{\partial \alpha} \right) dt \\ &= \int^{t_2}_{t_1} \frac{\partial f}{\partial x}\frac{\partial x}{\partial \alpha} dt + \int^{t_2}_{t_1} \frac{\partial f}{\partial \dot{x}} \cdot \frac{d}{dt} \left( \frac{\partial x}{\partial \alpha} \right) dt \\ &= \int^{t_2}_{t_1} \frac{\partial f}{\partial x}\frac{\partial x}{\partial \alpha} dt + \left[ \frac{\partial f}{\partial \dot{x}} \frac{\partial x}{\partial \alpha} \right]^{t_2}_{t_1} - \int^{t_2}_{t_1} \frac{d}{dt} \left( \frac{\partial f}{\partial \dot{x}} \right) \frac{\partial x}{\partial \alpha} dt \end{aligned}\]

3번 식에서 4번 식으로 넘어가는 데 부분적분이 쓰였다. ${\partial x}/{\partial \alpha} = h(t)$이므로, 경계 조건에 의해 4번 식의 두 번째 항은 소거된다. 따라서,

\[\frac{dA}{d\alpha} = \int^{t_2}_{t_1} \left( \frac{\partial f}{\partial x} - \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{x}} \right) \right) \frac{\partial x}{\partial \alpha} dt = 0\]

임의의 $h \in C^1$에 대해 위 식이 만족되어야 하므로, $x(t)$가 $A$를 극화할 다음의 필요조건을 얻는다.

\[\frac{\partial f}{\partial x} = \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{x}} \right)\]

이것이 오일러-라그랑주 방정식_{Euler-Lagrange equation}이다. 값 $A$를 극화한다는 것을 $\delta A = 0$과 같이 표현하므로, 오일러-라그랑주 방정식의 결론은 다음과 같이 적을 수 있다.

\[\delta A = 0 \implies \frac{\partial f}{\partial x} = \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{x}} \right)\]

방금 우리는 일변수 함수에 대해 증명했지만, 다변수 함수에 대해서도 마찬가지 식이 성립한다. 즉, 어떤 입자(들)의 운동을 나타내는 좌표가 $\lbrace q_i \rbrace _{i \leq n}$라고 하자. 예를 들어 2개의 입자가 3차원에서 운동하는 경우 $n = 6$이다. 이들의 운동이 $\int f(q_1, \dot{q_1}, \dots, q_n, \dot{q_n}) dt$를 극화할 필요조건은 각 $i$에 대해 다음이 성립하는 것이다.

\[\frac{\partial f}{\partial q_i} = \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{q_i}} \right)\]

3. 라그랑주 역학

정의. 계 $S$의 입자(들)의 운동을 나타내는 좌표가 $\lbrace q_i \rbrace _{1 \leq i \leq n}$라고 하자. $S$의 라그랑지안_Lagrangian $\mathcal{L}(\lbrace q , \dot{q} \rbrace, t)$를, 다음의 값을 극화시키는 조건에 대한 방정식이 입자들의 운동 방정식과 같아지도록 하는 함수로 정의한다.

\[\mathcal{S} = \int^{t_2}_{t_1} \mathcal{L}(\{ q, \dot{q} \}, t) dt\]

$\mathcal{S}$를 작용_action이라고 부른다.

예를 들어 1차원 퍼텐셜 장 $V(x)$에 속하는 입자의 라그랑지안은 다음과 같다.

\[\begin{aligned} \mathcal{L}(x, \dot{x}) &= T - V \\ &= \frac{1}{2}m\dot{x}^2 - V(x) \end{aligned}\]

위 함수가 라그랑지안이라는 것을 확인해 보자. 오일러-라그랑주 방정식을 사용하면 해당 라그랑지안에 따른 작용이 극화될 조건은 다음과 같다.

\[\begin{aligned} \delta \mathcal{S} = 0 &\implies \frac{\partial \mathcal{L}}{\partial x} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{x}} \\ &\iff -\frac{dV}{dx} = \frac{d}{dt}(m\dot{x}) \\ &\iff -\frac{dV}{dx} = m\ddot{x} \end{aligned}\]

마지막 식은 뉴턴의 운동 방정식이다. 따라서 $\mathcal{L}$은 이 계의 라그랑지안이 맞다. 일반적으로 다음이 성립한다.

정리. 다음 두 조건을 만족하는 고전역학적 계의 라그랑지안은 $\mathcal{L} = T - V$로 주어진다.

1. 계의 경계 조건이 홀로노믹_holonomic하다. 즉, 경계 조건이 입자들의 위치에만 의존하고 속도에 의존하지 않는다.
2. 계에 작용하는 힘 $\mathbf{F}_i$가 퍼텐셜 함수 $U_i(\lbrace q, \dot{q} \rbrace, t)$를 가진다.

증명. 링크된 SE 포스트를 참조.

그러나 일반적으로 계의 라그랑지안이 $T - V$로 주어지는 것은 아니다. 예를 들어 상대론적 입자의 운동 에너지는 $(\gamma - 1)m_0c^2$이지만, 올바른 라그랑지안은 $-m_0c^2/\gamma$이다.

뉴턴 역학과 달리 라그랑주 역학은 매우 자유로운 좌표계 변환을 허용한다는 점에서 강점을 가진다. 뉴턴 역학과 달리 라그랑주 역학은 일반 공변성을 가지기 때문이다. 이에 대한 자세한 설명은 다음 글에 있다.