텐서곱에 관한 노트

04 Mar 2025

TL;DR. 벡터 공간의 텐서곱은 다음의 의미를 가진다.

1. 다중 선형 사상의 선형화를 위한 정의역
2. 다중 선형 사상의 공간

엄밀히 말해 1이 $U \otimes V$에 해당하고, 2는 $U^\ast \otimes V^\ast$이다. 하지만 혼용되는 경향이 있는 듯하다.

1. 도입

정의. $U, V, W$가 체 $\mathbb{F}$ 위에서 정의된 벡터 공간이라고 하자. $b: U \times V \to W$가 쌍선형 사상_{bilinear map}이라는 것은 각 항에 대해서 $B$가 선형이라는 것이다. 즉, 임의의 $\mathbf{u}_1, \mathbf{u}_2 \in U, \mathbf{v}_1, \mathbf{v}_2 \in V$와 스칼라 $\alpha \in \mathbb{F}$에 대해 다음이 성립한다.

\[b(\alpha \mathbf{u}_1 + \mathbf{u}_2, \mathbf{v}_1) = \alpha b(\mathbf{u}_1, \mathbf{v}_1) + b(\mathbf{u}_2, \mathbf{v}_1)\] \[b(\mathbf{u}_1, \alpha \mathbf{v}_1 + \mathbf{v}_2) = \alpha b(\mathbf{u}_1, \mathbf{v}_1) + b(\mathbf{u}_1, \mathbf{v}_2)\]

예를 들어 실수 벡터 공간에서의 내적 $\cdot : V \times V \to \mathbb{R}$은, $\mathbb{R}$을 1차원 벡터 공간으로 간주했을 때 쌍선형 사상이다. 비슷한 방식으로 다중 선형 사상_{multilinear form}을 정의할 수 있다. $V$가 $n$차원 벡터 공간일 때, $\mathrm{det}: V \times \dots \times V \to \mathbb{R}$은 $n$중 선형 사상이다.

$b: U \times V \to W$가 쌍선형 사상이라고 하자. 당연하게도 $b$는 선형 사상이 아니다. $b$는 서로 다른 두 공간의 벡터를 매개변수로 받는 사상이지, 한 공간의 벡터를 매개변수로 받는 사상이 아니기 때문이다. 설령 $b$를 직합 $U \oplus V$에서 $W$로 가는 사상으로 생각하더라도, $b(\alpha(u, v)) = b((\alpha u, \alpha v)) = \alpha^2 b(u, v)$이므로 선형성을 만족하지 않는다.

그러나 텐서곱을 이용하면 $b$를 선형 사상과 동일시할 수 있다.

2. 텐서곱의 정의

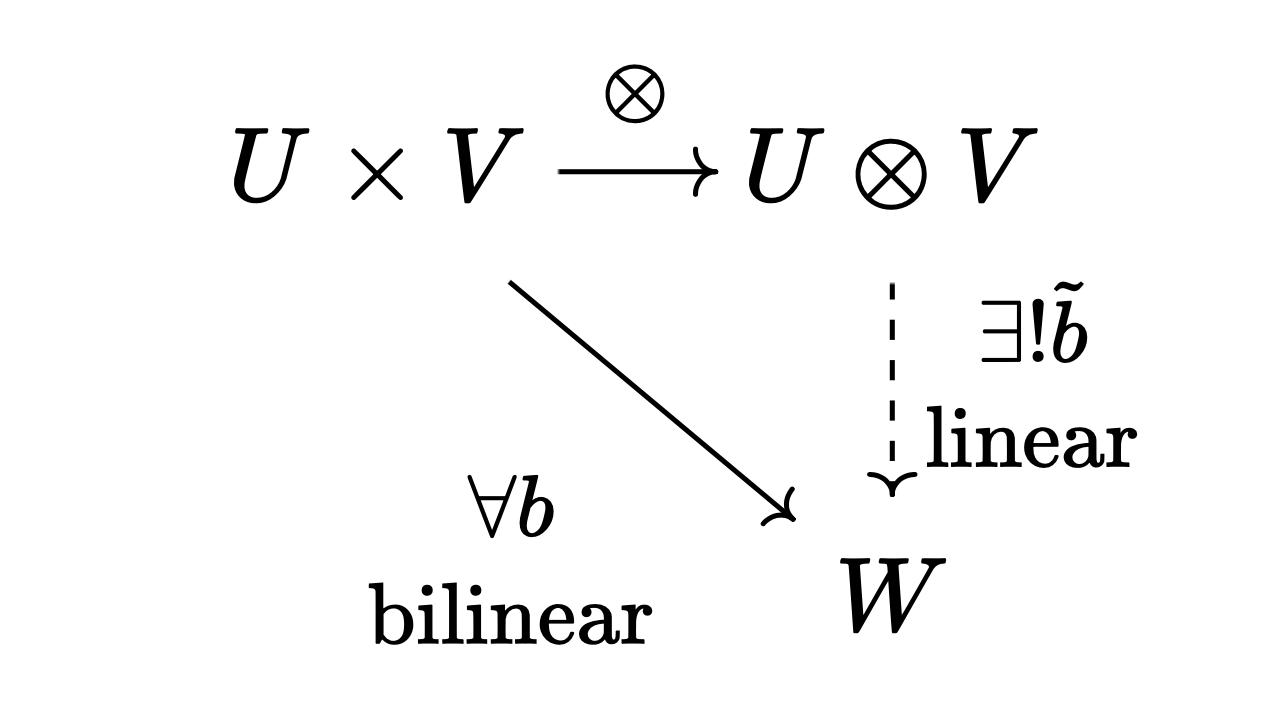
정의. 벡터 공간 $U, V$에 대해, 텐서곱_{tensor product} $U \otimes V$를 다음 보편 성질_{universal property}를 만족하는 벡터 공간으로 정의한다.

또한 $U \otimes V$의 원소를 텐서라고 한다.

정리. 임의의 벡터 공간의 텐서곱은 언제나 존재하며, 동형 사상에 대해 유일하다.

증명. 유한 차원 벡터 공간에 대해서만 증명한다. $U$와 $V$의 차원이 각각 $n, m$이고, 기저가 $\lbrace e_1, \dots, e_n\rbrace , \lbrace f_1, \dots, f_m\rbrace$이라고 하자. $T$가 차원이 $nm$인 벡터 공간이라고 하자. 차원이 같은 벡터 공간은 모두 동형이므로, 그러한 $T$는 동형 사상에 대해 유일하다. $T$의 형식적 기저를 다음과 같이 두자.

\[\mathcal{B} = \{ e_1f_1, \dots, e_1f_m, \dots, e_nf_1, \dots, e_nf_m \}\]

$T$가 $U$와 $V$의 텐서곱임을 보이기 위해서 임의의 쌍선형 사상 $b: U \times V \to W$를 상정한다. $b$로부터 다음의 행벡터를 정의한다.

\[\tilde {b} = \big[ b(e_1, f_1), \dots, b(e_1, f_m), \dots, b(e_n, f_1), \dots, b(e_n, f_m) \big]_\mathcal{B}\]

또한 $\otimes: V \times W \to T$를 다음과 같이 정의한다.

\[\otimes: (u, v) = (u_1e_1 + \dots + u_ne_n, v_1f_1 + \dots + v_mf_m) \mapsto \begin{bmatrix} u_1v_1 \\ \vdots \\ u_1v_m \\ \vdots \\ u_nv_1 \\ \vdots \\ u_nf_m \end{bmatrix}_{\mathcal{B}}\]

이 때 다음이 성립한다.

\[\begin{align} \tilde {b}(\otimes(u, v)) &= \sum_i \sum_j (u_i v_j)b(e_i, f_j) \\ &= b\left( \sum_i u_i e_i, \sum_j v_j f_j \right) && (\text{by bilinearity})\\ &= b(u, v) && \blacksquare \end{align}\]

3. 텐서와 다중 선형 사상의 동일시

지금까지의 논의를 한 줄로 요약하면 다음과 같다.

\[\mathrm{Hom}^2(U \times V, W) \cong \mathrm{Hom}(U \otimes V, W)\]

여기서 $\mathrm{Hom}^2$은 쌍선형 사상의 공간을 의미한다. 특히 $W = \mathbb{F}$일 때, 쌍대 공간의 정의에 의해 다음이 성립한다.

\[\mathrm{Hom}^2(U \times V, \mathbb{F}) \cong \mathrm{Hom}(U \otimes V, \mathbb{F}) \cong (U \otimes V)^*\]

이 관계를 이용하면 텐서곱을 쌍선형 사상의 선형화를 위한 정의역으로 보는 시각을 넘어, 쌍선형 사상의 공간 그 자체로 볼 수도 있다. 먼저 다음의 보조정리를 증명한다.

보조정리. $(U \otimes V)^\ast = U^\ast \otimes V^\ast$

증명. 앞선 관계식과 쌍대 공간의 정의로 인해 다음을 보이면 충분하다.

\[\mathrm{Hom}^2(U \times V, \mathbb{F}) \cong \mathrm{Hom}(U, \mathbb{F}) \otimes \mathrm{Hom}(V, \mathbb{F})\]

즉, $\mathrm{Hom}^2(U \times V, \mathbb{F})$가 보편 성질을 만족함을 보이면 된다. 이는 앞선 증명과 거의 동일하므로 생략한다. ■

보조정리로부터 다음이 성립한다.

정리. $\mathrm{Hom}^2(U \times V, \mathbb{F}) \cong U^\ast \otimes V^\ast$

증명.

\[\begin{align} U^* \otimes V^* &\cong U^{***} \otimes V^{***} \\ &\cong (U^{**} \otimes V^{**})^* \\ &\cong (U \otimes V)^* \\ &\cong \mathrm{Hom}^2(U \times V, \mathbb{F}) \end{align}\]

두 번째 식에서 세 번째 식으로 넘어갈 때 $V \cong V^{\ast\ast}$ 표준_canonical 동일시를 사용했다. ■

따라서 쌍대 공간의 텐서는 쌍선형 사상과 표준적으로 동일시할 수 있다.