디멘의 블로그
Dimen's Blog
이데아를 여행하는 히치하이커
Alice in Logicland
Notes on Tensor Products
04 Mar 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
TL;DR. The tensor product of vector spaces has the following significance:
- A domain for the linearisation of multilinear maps
- A space of multilinear maps
Strictly speaking, 1 corresponds to $U \otimes V$, while 2 corresponds to $U^\ast \otimes V^\ast$. However, these appear to be used interchangeably.
1. Introduction
Definition. Let $U, V, W$ be vector spaces defined over a field $\mathbb{F}$. A map $b: U \times V \to W$ is called a bilinear map if $B$ is linear in each argument. That is, for any $\mathbf{u}_1, \mathbf{u}_2 \in U, \mathbf{v}_1, \mathbf{v}_2 \in V$ and scalar $\alpha \in \mathbb{F}$, the following hold:
\[b(\alpha \mathbf{u}_1 + \mathbf{u}_2, \mathbf{v}_1) = \alpha b(\mathbf{u}_1, \mathbf{v}_1) + b(\mathbf{u}_2, \mathbf{v}_1)\] \[b(\mathbf{u}_1, \alpha \mathbf{v}_1 + \mathbf{v}_2) = \alpha b(\mathbf{u}_1, \mathbf{v}_1) + b(\mathbf{u}_1, \mathbf{v}_2)\]
For example, the inner product $\cdot : V \times V \to \mathbb{R}$ in real vector spaces is a bilinear map when $\mathbb{R}$ is regarded as a one-dimensional vector space. Similarly, one can define multilinear forms. When $V$ is an $n$-dimensional vector space, $\mathrm{det}: V \times \dots \times V \to \mathbb{R}$ is an $n$-multilinear map.
Let $b: U \times V \to W$ be a bilinear map. Naturally, $b$ is not a linear map. This is because $b$ takes vectors from two different spaces as arguments, rather than vectors from a single space. Even if we consider $b$ as a map from the direct sum $U \oplus V$ to $W$, we have $b(\alpha(u, v)) = b((\alpha u, \alpha v)) = \alpha^2 b(u, v)$, which does not satisfy linearity.
However, using tensor products, we can identify $b$ with a linear map.
2. Definition of Tensor Products
Definition. For vector spaces $U, V$, the tensor product $U \otimes V$ is defined as the vector space satisfying the following universal property:
Elements of $U \otimes V$ are called tensors.
Theorem. The tensor product of any vector spaces always exists and is unique up to isomorphism.
Proof. We prove this only for finite-dimensional vector spaces. Suppose $U$ and $V$ have dimensions $n$ and $m$ respectively, with bases $\lbrace e_1, \dots, e_n\rbrace$ and $\lbrace f_1, \dots, f_m\rbrace$. Let $T$ be a vector space of dimension $nm$. Since vector spaces of the same dimension are isomorphic, such a $T$ is unique up to isomorphism. Let the formal basis of $T$ be:
\[\mathcal{B} = \{ e_1f_1, \dots, e_1f_m, \dots, e_nf_1, \dots, e_nf_m \}\]To show that $T$ is the tensor product of $U$ and $V$, consider an arbitrary bilinear map $b: U \times V \to W$. From $b$, define the following row vector:
\[\tilde {b} = \big[ b(e_1, f_1), \dots, b(e_1, f_m), \dots, b(e_n, f_1), \dots, b(e_n, f_m) \big]_\mathcal{B}\]Also define $\otimes: V \times W \to T$ as follows:
\[\otimes: (u, v) = (u_1e_1 + \dots + u_ne_n, v_1f_1 + \dots + v_mf_m) \mapsto \begin{bmatrix} u_1v_1 \\ \vdots \\ u_1v_m \\ \vdots \\ u_nv_1 \\ \vdots \\ u_nf_m \end{bmatrix}_{\mathcal{B}}\]Then the following holds:
\[\begin{align} \tilde {b}(\otimes(u, v)) &= \sum_i \sum_j (u_i v_j)b(e_i, f_j) \\ &= b\left( \sum_i u_i e_i, \sum_j v_j f_j \right) && (\text{by bilinearity})\\ &= b(u, v) && \blacksquare \end{align}\]3. Identification of Tensors with Multilinear Maps
The discussion thus far can be summarised in one line:
\[\mathrm{Hom}^2(U \times V, W) \cong \mathrm{Hom}(U \otimes V, W)\]Here $\mathrm{Hom}^2$ denotes the space of bilinear maps. In particular, when $W = \mathbb{F}$, by the definition of dual spaces, the following holds:
\[\mathrm{Hom}^2(U \times V, \mathbb{F}) \cong \mathrm{Hom}(U \otimes V, \mathbb{F}) \cong (U \otimes V)^*\]Using this relationship, we can view tensor products not merely as domains for the linearisation of bilinear maps, but as spaces of bilinear maps themselves. First, we prove the following lemma.
Lemma. $(U \otimes V)^\ast = U^\ast \otimes V^\ast$
Proof. By the previous relationship and the definition of dual spaces, it suffices to show:
\[\mathrm{Hom}^2(U \times V, \mathbb{F}) \cong \mathrm{Hom}(U, \mathbb{F}) \otimes \mathrm{Hom}(V, \mathbb{F})\]That is, we need to show that $\mathrm{Hom}^2(U \times V, \mathbb{F})$ satisfies the universal property. This is almost identical to the previous proof, so we omit it. ■
From the lemma, the following holds:
Theorem. $\mathrm{Hom}^2(U \times V, \mathbb{F}) \cong U^\ast \otimes V^\ast$
Proof.
\[\begin{align} U^* \otimes V^* &\cong U^{***} \otimes V^{***} \\ &\cong (U^{**} \otimes V^{**})^* \\ &\cong (U \otimes V)^* \\ &\cong \mathrm{Hom}^2(U \times V, \mathbb{F}) \end{align}\]In going from the second to the third expression, we used the canonical identification $V \cong V^{\ast\ast}$. ■
Therefore, tensors in dual spaces can be canonically identified with bilinear maps.
일반 공변성에 대한 노트
27 Feb 2025어떤 이론이 일반 공변적general covariant이라는 것은, 물리 법칙의 형태form가 미분가능한 좌표계 변환에 대해 보존된다는 것이다. 구체적으로, 좌표계 $\lbrace q_i \rbrace $와 좌표계 $\lbrace q’_i \rbrace $가 다음 관계에 있다고 하자.
\[q_i' = f_i(\{ q \})\]각 $i$에 대해 $f_i$가 미분 가능하다고 하자. 일반 공변적 이론이라면 좌표계 $\lbrace q_i \rbrace $를 사용했을 때와 좌표계 $\lbrace q_i’ \rbrace $를 사용했을 때의 물리 법칙이 형태가 같아야 한다.
예시를 보자. 퍼텐셜이 0인 계 안의 입자의 위치를 극좌표계 $(r, \theta)$ 또는 직교 좌표계 $(x, y)$를 사용하여 표현하는 경우를 생각해 보자. 두 좌표계는 다음 관계에 있다.
\[\begin{gather} x = f_1(r, \theta) = r \cos \theta\\ y = f_2(r, \theta) = r \sin \theta \end{gather}\]$f_1$과 $f_2$가 미분 가능하므로 일반 공변적 이론은 두 좌표계로 표현했을 때의 형태가 같아야 한다.
먼저 뉴턴 역학의 경우를 보자. 뉴턴 역학의 물리 법칙은 다음과 같다.
\[\begin{gather} -\frac{dV(x, y)}{dx} = m\ddot{x} \\ -\frac{dV(x, y)}{dy} = m\ddot{y} \end{gather}\]$V(x, y) = 0$이므로 $\ddot{x} = \ddot{y} = 0$이다. 즉 입자는 등속 선형 운동을 한다. 만약 뉴턴 역학이 일반 공변적이라면 위 법칙을 $(x, y)$에서 $(r, \theta)$로 바꿔 표현해도 결과가 같아야 한다.
\[\begin{gather} -\frac{dV(r, \theta)}{dr} = m\ddot{r} \\ -\frac{dV(r, \theta)}{d\theta} = m\ddot{\theta} \end{gather}\]$V(r, \theta) = 0$이므로 $\ddot{r} = \ddot{\theta} = 0$이다. 이번에는 입자가 등속 원운동을 한다. 결과가 달라졌으므로 뉴턴 역학은 일반 공변적이지 않다.
이제 라그랑주 역학의 경우를 보자. 라그랑주 역학의 물리 법칙은 다음과 같다.
\[\begin{gather} \frac{\partial \mathcal{L}}{\partial x} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{x}} \\ \frac{\partial \mathcal{L}}{\partial y} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{y}} \end{gather}\]$\mathcal{L}(x, y) = T - V = \frac{m}{2}(\dot{x}^2 + \dot{y}^2)$를 대입하면 $\ddot{x} = \ddot{y} = 0$, 즉 등속 선형 운동을 얻는다. 여기까지는 뉴턴 역학과 같다.
이제 오일러-라그랑주 방정식의 $(x, y)$를 $(r, \theta)$로 치환해 보자.
\[\begin{gather} \frac{\partial \mathcal{L}}{\partial r} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{r}} \\ \frac{\partial \mathcal{L}}{\partial \theta} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \end{gather}\]$x = r\cos\theta, y = r\sin\theta$를 대입하여 정리하면 $\mathcal{L}(r, \theta)$는 다음과 같다.
\[\mathcal{L}(r, \theta) = \frac{m}{2}(\dot{r}^2 + r^2 \dot{\theta}^2)\]Remark. 오일러-라그랑주 방정식에서는 단순히 $(x, y)$를 $(r, \theta)$로 치환했지만, 라그랑지안에서는 $x = r \cos \theta, y = r \sin \theta$ 관계식을 대입하는 이유는 라그랑지안이 실수쌍에 대한 함수가 아니라 시공간의 점에 대한 함수이기 때문이다. 일반 공변성은 무지성, 일편단률적인 좌표 변환에 대해서 식의 형태가 유지된다는 의미가 아니라, 물리계를 표현하는 함수들은 유지된 채 그것을 표현하는 좌표가 바뀌었을 때 식의 형태가 유지된다는 의미이다.
대입하여 계산하면 다음과 같다.
\[\begin{gather} \ddot{r} = r\dot{\theta}^2 \\ 2\dot{r}\dot{\theta} + r\ddot{\theta} = 0 \end{gather}\]미분방정식이 복잡해서 알아보기 힘들지만, 위 두 미분방정식은 $\ddot{x} = \ddot{y} = 0$과 동치이다. 일례로 $\theta = \tan^{-1}t, r = \sqrt{1 + t^2}$가 방정식의 해인 것을 확인할 수 있다.
일반적으로 다음이 성립한다.
정리. 라그랑주 역학은 일반 공변성을 가진다.
뉴턴 역학은 일반 공변성이 없지만 라그랑주 역학은 있다는 것이 신기하게 느껴질 수 있지만, 잘 생각해 보면 이것은 당연하다. 뉴턴의 제1법칙은 보통 $F = 0 \implies \ddot{x} = 0$이라는 수식으로 표현되지만 정확한 진술은 다음과 같다.
외력을 받지 않는 입자의 시공간 다이어그램은 선형이다.
‘선형’이라는 표현에 주목하라. 선형성은 특정한 기하학에 의존적인 표현이다. 예를 들어 유클리드 기하학에서 ‘선형’이란 우리가 흔히 말하는 직선이지만, 구면 기하학에서 ‘선형’은 대원으로 주어진다. 그러므로 위 진술은 다음과 같이 밝혀 쓰는 것이 가장 정확하다.
뉴턴 역학. 외력을 받지 않는 입자의 시공간 다이어그램은 유클리드 기하학의 선형이다.
그리고 유클리드 기하학의 선형은 직교 좌표계에서 $\ddot{x} = \ddot{y} = 0$ 꼴로 주어진다. 따라서 $F = 0 \implies \ddot{x} = 0$은, 유클리드 기하학과 직교 좌표계를 전제했을 때에만 올바른 수식인 것이다.
거꾸로 말해, 이론이 특정한 기하학에 의존하지 않는다면 그 이론은 일반 공변적이다. 라그랑주 역학은 그러한 이론의 사례이다. 라그랑주 역학의 진술은 다음과 같이 표현할 수 있다.
라그랑주 역학. 라그랑지안의 적분을 극화시키는 경로가 입자의 운동 경로이다.
그리고 라그랑지안은 특정 기하학에 의존적인 함수가 아닌, 그저 시공간의 점들에 대해 실숫값을 출력하는 함수이다. 따라서 위 진술은 어떠한 기하학에 대해서도 의존적이지 않으며, 라그랑주 역학은 일반 공변적이다.
구멍 논증hole argument에 따르면 일반 공변적인 이론들은 형이상학적인 의미에서 비결정론적이다. 이에 대한 설명은 나중에 하도록 하겠다.
Notes on General Covariance
27 Feb 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
A theory is said to be general covariant when the form of physical laws is preserved under differentiable coordinate transformations. Specifically, suppose coordinate systems $\lbrace q_i \rbrace$ and $\lbrace q’_i \rbrace$ are related by:
\[q_i' = f_i(\{ q \})\]Let each $f_i$ be differentiable for all $i$. If a theory is generally covariant, then the physical laws must have the same form when using coordinate system $\lbrace q_i \rbrace$ as when using coordinate system $\lbrace q_i’ \rbrace$.
Consider an example. Suppose we describe the position of a particle in a system with zero potential using either polar coordinates $(r, \theta)$ or Cartesian coordinates $(x, y)$. The two coordinate systems are related by:
\[\begin{gather} x = f_1(r, \theta) = r \cos \theta\\ y = f_2(r, \theta) = r \sin \theta \end{gather}\]Since $f_1$ and $f_2$ are differentiable, a generally covariant theory must have the same form when expressed in both coordinate systems.
First, consider the case of Newtonian mechanics. The physical laws of Newtonian mechanics are:
\[\begin{gather} -\frac{dV(x, y)}{dx} = m\ddot{x} \\ -\frac{dV(x, y)}{dy} = m\ddot{y} \end{gather}\]Since $V(x, y) = 0$, we have $\ddot{x} = \ddot{y} = 0$. That is, the particle undergoes uniform linear motion. If Newtonian mechanics were generally covariant, then expressing the above laws in terms of $(r, \theta)$ instead of $(x, y)$ should yield the same result.
\[\begin{gather} -\frac{dV(r, \theta)}{dr} = m\ddot{r} \\ -\frac{dV(r, \theta)}{d\theta} = m\ddot{\theta} \end{gather}\]Since $V(r, \theta) = 0$, we have $\ddot{r} = \ddot{\theta} = 0$. This time, the particle undergoes uniform circular motion. Since the results differ, Newtonian mechanics is not generally covariant.
Now consider the case of Lagrangian mechanics. The physical laws of Lagrangian mechanics are:
\[\begin{gather} \frac{\partial \mathcal{L}}{\partial x} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{x}} \\ \frac{\partial \mathcal{L}}{\partial y} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{y}} \end{gather}\]Substituting $\mathcal{L}(x, y) = T - V = \frac{m}{2}(\dot{x}^2 + \dot{y}^2)$ yields $\ddot{x} = \ddot{y} = 0$, i.e., uniform linear motion. This is the same as in Newtonian mechanics thus far.
Now let us substitute $(r, \theta)$ for $(x, y)$ in the Euler-Lagrange equations:
\[\begin{gather} \frac{\partial \mathcal{L}}{\partial r} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{r}} \\ \frac{\partial \mathcal{L}}{\partial \theta} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{\theta}} \end{gather}\]Substituting $x = r\cos\theta, y = r\sin\theta$ and simplifying, $\mathcal{L}(r, \theta)$ becomes:
\[\mathcal{L}(r, \theta) = \frac{m}{2}(\dot{r}^2 + r^2 \dot{\theta}^2)\]Remark. while in the Euler-Lagrange equations we simply substitute $(r, \theta)$ for $(x, y)$, in the Lagrangian we substitute the relation $x = r \cos \theta, y = r \sin \theta$ because the Lagrangian is not a function of pairs of real numbers but rather a function of points in spacetime. General covariance does not mean that the form of equations is preserved under mindless, uniform coordinate transformations, but rather that when the functions describing a physical system are maintained while the coordinates expressing them are changed, the form of equations is preserved.
Substituting and calculating yields:
\[\begin{gather} \ddot{r} = r\dot{\theta}^2 \\ 2\dot{r}\dot{\theta} + r\ddot{\theta} = 0 \end{gather}\]Although the differential equations are complex and difficult to interpret, the above two differential equations are equivalent to $\ddot{x} = \ddot{y} = 0$. For instance, one can verify that $\theta = \tan^{-1}t, r = \sqrt{1 + t^2}$ is a solution to the equations.
In general, the following holds:
Theorem. Lagrangian mechanics possesses general covariance.
It may seem surprising that Newtonian mechanics lacks general covariance while Lagrangian mechanics possesses it, but upon reflection, this is quite natural. Newton’s first law is commonly expressed mathematically as $F = 0 \implies \ddot{x} = 0$, but the precise statement is:
The spacetime diagram of a particle not subject to external forces is linear.
Note the expression ‘linear’. Linearity is a concept dependent upon specific geometry. For example, in Euclidean geometry, ‘linear’ refers to what we commonly call a straight line, but in spherical geometry, ‘linear’ is given by great circles. Therefore, the above statement is most accurately written as:
Newtonian mechanics. The spacetime diagram of a particle not subject to external forces is linear in Euclidean geometry.
Linear motion in Euclidean geometry is given by $\ddot{x} = \ddot{y} = 0$ in Cartesian coordinates. Therefore, $F = 0 \implies \ddot{x} = 0$ is a correct equation only when Euclidean geometry and Cartesian coordinates are presupposed.
Conversely, if a theory does not depend upon specific geometry, then that theory is generally covariant. Lagrangian mechanics is an example of such a theory. The statement of Lagrangian mechanics can be expressed as:
Lagrangian mechanics. The path that extremises the integral of the Lagrangian is the particle’s trajectory.
The Lagrangian is not a function dependent upon specific geometry, but merely a function that outputs real values for points in spacetime. Therefore, the above statement is not dependent upon any particular geometry, and Lagrangian mechanics is generally covariant.
According to the hole argument, generally covariant theories are indeterministic in a metaphysical sense. An explanation of this will be provided later.
오일러-라그랑주 방정식과 라그랑주 역학
27 Feb 20251. 도입
1차원 위에서 운동하는 입자의 운동 경로는 $x(t)$와 같이 표현할 수 있다. 입자의 위치와 속도에 의존적인 함수 $f(x, x’)$를 생각하자. 이 입자가 시간 $t_1$일 때 $x_1$에서 출발하여 시간 $t_2$일 때 $x_2$에 도착하는데, 그 과정에서 다음 값을 극화extremise하는 경로, 즉 다음 값이 극대 또는 극소가 되도록 하는 경로 $x(t)$를 찾는 것이 목표이다.
\[A[x] = \int^{t_2}_{t_1} f(x, \dot{x}) dt\]대괄호는 $A$의 매개변수가 실수가 아닌 함수임을 의미한다. 따라서 직관적으로 생각했을 때 $A[x]$를 최소화하는 $x(t)$를 찾기 위해서는 함수에 대한 미분식을 세워야 한다.
\[\frac{dA[x]}{dx(t)} = 0?\]2. 오일러-라그랑주 방정식
물론 함수에 대한 미분을 우리는 정의한 적이 없다. 하지만 간단한 트릭을 통해 함수에 대한 미분을 일반적인 미분으로 환원할 수 있다. 먼저 $x_0(t)$가 우리가 찾고자 하는 경로, 즉 $A[x]$를 극화시키는 경로라고 하자. $x_0(t)$의 ‘주변’에 있는 경로는 다음과 같은 꼴이다.
\[x(\alpha, t) = x_0(t) + \alpha h(t)\]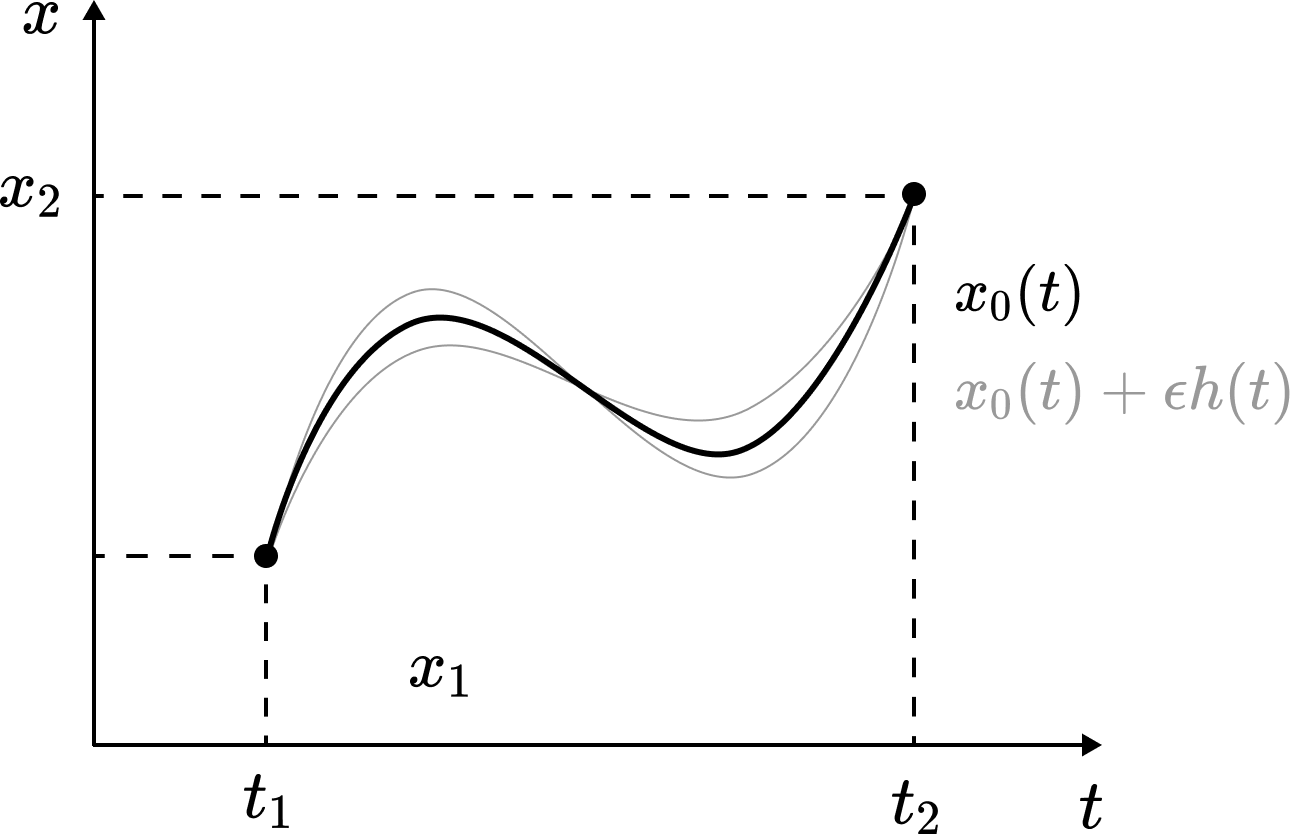
경계 조건은 $h(t_1) = h(t_2) = 0$이다. $x_0(t)$가 $A[x]$를 극화시키므로, 충분히 작은 $\epsilon$에 대해 $A[x_0] = A[x(0, t)] \leq A[x(\epsilon, t)]$이다. 따라서,
\[\left. \frac{dA[x(\alpha, t)]}{d\alpha} \right\vert_{\alpha = 0} = 0\]위 식을 전개하면 다음과 같다.
\[\begin{aligned} \frac{dA}{d\alpha} &= \int^{t_2}_{t_1} \frac{d}{d\alpha} \Big[ f \big( x(\alpha, t), \dot{x}(\alpha, t) \big) \Big] dt \\ &= \int^{t_2}_{t_1} \left( \frac{\partial f}{\partial x}\frac{\partial x}{\partial \alpha} + \frac{\partial f}{\partial \dot{x}}\frac{\partial \dot{x}}{\partial \alpha} \right) dt \\ &= \int^{t_2}_{t_1} \frac{\partial f}{\partial x}\frac{\partial x}{\partial \alpha} dt + \int^{t_2}_{t_1} \frac{\partial f}{\partial \dot{x}} \cdot \frac{d}{dt} \left( \frac{\partial x}{\partial \alpha} \right) dt \\ &= \int^{t_2}_{t_1} \frac{\partial f}{\partial x}\frac{\partial x}{\partial \alpha} dt + \left[ \frac{\partial f}{\partial \dot{x}} \frac{\partial x}{\partial \alpha} \right]^{t_2}_{t_1} - \int^{t_2}_{t_1} \frac{d}{dt} \left( \frac{\partial f}{\partial \dot{x}} \right) \frac{\partial x}{\partial \alpha} dt \end{aligned}\]3번 식에서 4번 식으로 넘어가는 데 부분적분이 쓰였다. ${\partial x}/{\partial \alpha} = h(t)$이므로, 경계 조건에 의해 4번 식의 두 번째 항은 소거된다. 따라서,
\[\frac{dA}{d\alpha} = \int^{t_2}_{t_1} \left( \frac{\partial f}{\partial x} - \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{x}} \right) \right) \frac{\partial x}{\partial \alpha} dt = 0\]임의의 $h \in C^1$에 대해 위 식이 만족되어야 하므로, $x(t)$가 $A$를 극화할 다음의 필요조건을 얻는다.
\[\frac{\partial f}{\partial x} = \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{x}} \right)\]이것이 오일러-라그랑주 방정식Euler-Lagrange equation이다. 값 $A$를 극화한다는 것을 $\delta A = 0$과 같이 표현하므로, 오일러-라그랑주 방정식의 결론은 다음과 같이 적을 수 있다.
\[\delta A = 0 \implies \frac{\partial f}{\partial x} = \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{x}} \right)\]방금 우리는 일변수 함수에 대해 증명했지만, 다변수 함수에 대해서도 마찬가지 식이 성립한다. 즉, 어떤 입자(들)의 운동을 나타내는 좌표가 $\lbrace q_i \rbrace _{i \leq n}$라고 하자. 예를 들어 2개의 입자가 3차원에서 운동하는 경우 $n = 6$이다. 이들의 운동이 $\int f(q_1, \dot{q_1}, \dots, q_n, \dot{q_n}) dt$를 극화할 필요조건은 각 $i$에 대해 다음이 성립하는 것이다.
\[\frac{\partial f}{\partial q_i} = \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{q_i}} \right)\]3. 라그랑주 역학
정의. 계 $S$의 입자(들)의 운동을 나타내는 좌표가 $\lbrace q_i \rbrace _{1 \leq i \leq n}$라고 하자. $S$의 라그랑지안Lagrangian $\mathcal{L}(\lbrace q , \dot{q} \rbrace, t)$를, 다음의 값을 극화시키는 조건에 대한 방정식이 입자들의 운동 방정식과 같아지도록 하는 함수로 정의한다.
\[\mathcal{S} = \int^{t_2}_{t_1} \mathcal{L}(\{ q, \dot{q} \}, t) dt\]$\mathcal{S}$를 작용action이라고 부른다.
예를 들어 1차원 퍼텐셜 장 $V(x)$에 속하는 입자의 라그랑지안은 다음과 같다.
\[\begin{aligned} \mathcal{L}(x, \dot{x}) &= T - V \\ &= \frac{1}{2}m\dot{x}^2 - V(x) \end{aligned}\]위 함수가 라그랑지안이라는 것을 확인해 보자. 오일러-라그랑주 방정식을 사용하면 해당 라그랑지안에 따른 작용이 극화될 조건은 다음과 같다.
\[\begin{aligned} \delta \mathcal{S} = 0 &\implies \frac{\partial \mathcal{L}}{\partial x} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{x}} \\ &\iff -\frac{dV}{dx} = \frac{d}{dt}(m\dot{x}) \\ &\iff -\frac{dV}{dx} = m\ddot{x} \end{aligned}\]마지막 식은 뉴턴의 운동 방정식이다. 따라서 $\mathcal{L}$은 이 계의 라그랑지안이 맞다. 일반적으로 다음이 성립한다.
정리. 다음 두 조건을 만족하는 고전역학적 계의 라그랑지안은 $\mathcal{L} = T - V$로 주어진다.
- 계의 경계 조건이 홀로노믹holonomic하다. 즉, 경계 조건이 입자들의 위치에만 의존하고 속도에 의존하지 않는다.
- 계에 작용하는 힘 $\mathbf{F}_i$가 퍼텐셜 함수 $U_i(\lbrace q, \dot{q} \rbrace, t)$를 가진다.
증명. 링크된 SE 포스트를 참조.
그러나 일반적으로 계의 라그랑지안이 $T - V$로 주어지는 것은 아니다. 예를 들어 상대론적 입자의 운동 에너지는 $(\gamma - 1)m_0c^2$이지만, 올바른 라그랑지안은 $-m_0c^2/\gamma$이다.
뉴턴 역학과 달리 라그랑주 역학은 매우 자유로운 좌표계 변환을 허용한다는 점에서 강점을 가진다. 뉴턴 역학과 달리 라그랑주 역학은 일반 공변성을 가지기 때문이다. 이에 대한 자세한 설명은 다음 글에 있다.
The Euler-Lagrange Equation and Lagrangian Mechanics
27 Feb 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
1. Introduction
The trajectory of a particle moving in one dimension can be expressed as $x(t)$. Consider a function $f(x, x’)$ that depends on the particle’s position and velocity. Our objective is to find the path $x(t)$ along which the particle travels from position $x_1$ at time $t_1$ to position $x_2$ at time $t_2$, such that the following quantity is extremised—that is, the path that renders this quantity either maximum or minimum:
\[A[x] = \int^{t_2}_{t_1} f(x, \dot{x}) dt\]The square brackets indicate that the parameter of $A$ is a function rather than a real number. Therefore, intuitively, to find $x(t)$ that minimises $A[x]$, we should establish a differential equation for functions.
\[\frac{dA[x]}{dx(t)} = 0?\]2. The Euler-Lagrange Equation
Of course, we have never defined differentiation with respect to functions. However, through a simple trick, we can reduce differentiation with respect to functions to ordinary differentiation. First, let $x_0(t)$ be the path we seek—that is, the path that extremises $A[x]$. A path in the ‘neighbourhood’ of $x_0(t)$ takes the following form:
\[x(\alpha, t) = x_0(t) + \alpha h(t)\]
The boundary conditions are $h(t_1) = h(t_2) = 0$. Since $x_0(t)$ extremises $A[x]$, for sufficiently small $\epsilon$, we have $A[x_0] = A[x(0, t)] \leq A[x(\epsilon, t)]$. Therefore,
\[\left. \frac{dA[x(\alpha, t)]}{d\alpha} \right\vert_{\alpha = 0} = 0\]Expanding the above equation yields:
\[\begin{aligned} \frac{dA}{d\alpha} &= \int^{t_2}_{t_1} \frac{d}{d\alpha} \Big[ f \big( x(\alpha, t), \dot{x}(\alpha, t) \big) \Big] dt \\ &= \int^{t_2}_{t_1} \left( \frac{\partial f}{\partial x}\frac{\partial x}{\partial \alpha} + \frac{\partial f}{\partial \dot{x}}\frac{\partial \dot{x}}{\partial \alpha} \right) dt \\ &= \int^{t_2}_{t_1} \frac{\partial f}{\partial x}\frac{\partial x}{\partial \alpha} dt + \int^{t_2}_{t_1} \frac{\partial f}{\partial \dot{x}} \cdot \frac{d}{dt} \left( \frac{\partial x}{\partial \alpha} \right) dt \\ &= \int^{t_2}_{t_1} \frac{\partial f}{\partial x}\frac{\partial x}{\partial \alpha} dt + \left[ \frac{\partial f}{\partial \dot{x}} \frac{\partial x}{\partial \alpha} \right]^{t_2}_{t_1} - \int^{t_2}_{t_1} \frac{d}{dt} \left( \frac{\partial f}{\partial \dot{x}} \right) \frac{\partial x}{\partial \alpha} dt \end{aligned}\]Integration by parts is employed in the transition from the third to the fourth equation. Since ${\partial x}/{\partial \alpha} = h(t)$, the second term in the fourth equation vanishes due to the boundary conditions. Therefore,
\[\frac{dA}{d\alpha} = \int^{t_2}_{t_1} \left( \frac{\partial f}{\partial x} - \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{x}} \right) \right) \frac{\partial x}{\partial \alpha} dt = 0\]Since the above equation must be satisfied for arbitrary $h \in C^1$, we obtain the following necessary condition for $x(t)$ to extremise $A$:
\[\frac{\partial f}{\partial x} = \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{x}} \right)\]This is the Euler-Lagrange equation. Since extremising the value $A$ is expressed as $\delta A = 0$, the conclusion of the Euler-Lagrange equation can be written as follows:
\[\delta A = 0 \implies \frac{\partial f}{\partial x} = \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{x}} \right)\]We have just proved this for functions of one variable, but the same equation holds for functions of multiple variables. That is, let the coordinates representing the motion of some particle(s) be $\lbrace q_i \rbrace _{i \leq n}$. For example, if two particles move in three dimensions, then $n = 6$. The necessary condition for their motion to extremise $\int f(q_1, \dot{q_1}, \dots, q_n, \dot{q_n}) dt$ is that the following holds for each $i$:
\[\frac{\partial f}{\partial q_i} = \frac{d}{dt}\left( \frac{\partial f}{\partial \dot{q_i}} \right)\]3. Lagrangian Mechanics
Definition. Let the coordinates representing the motion of the particles in system $S$ be $\lbrace q_i \rbrace _{1 \leq i \leq n}$. The Lagrangian $\mathcal{L}(\lbrace q , \dot{q} \rbrace, t)$ of $S$ is defined as a function such that the equation for the condition that extremises the following quantity becomes identical to the equations of motion of the particles:
\[\mathcal{S} = \int^{t_2}_{t_1} \mathcal{L}(\{ q, \dot{q} \}, t) dt\]$\mathcal{S}$ is called the action.
For example, the Lagrangian of a particle in a one-dimensional potential field $V(x)$ is as follows:
\[\begin{aligned} \mathcal{L}(x, \dot{x}) &= T - V \\ &= \frac{1}{2}m\dot{x}^2 - V(x) \end{aligned}\]Let us verify that the above function is indeed the Lagrangian. Using the Euler-Lagrange equation, the condition for the action corresponding to this Lagrangian to be extremised is as follows:
\[\begin{aligned} \delta \mathcal{S} = 0 &\implies \frac{\partial \mathcal{L}}{\partial x} = \frac{d}{dt} \frac{\partial \mathcal{L}}{\partial \dot{x}} \\ &\iff -\frac{dV}{dx} = \frac{d}{dt}(m\dot{x}) \\ &\iff -\frac{dV}{dx} = m\ddot{x} \end{aligned}\]The final equation is Newton’s equation of motion. Therefore, $\mathcal{L}$ is indeed the Lagrangian of this system. In general, the following holds:
Theorem. The Lagrangian of a classical mechanical system satisfying the following two conditions is given by $\mathcal{L} = T - V$:
- The constraints of the system are holonomic. That is, the constraints depend only on the positions of the particles and not on their velocities.
- The forces $\mathbf{F}_i$ acting on the system have potential functions $U_i(\lbrace q, \dot{q} \rbrace, t)$.
Proof. See the linked SE post.
However, in general, the Lagrangian of a system is not necessarily given by $T - V$. For instance, while the kinetic energy of a relativistic particle is $(\gamma - 1)m_0c^2$, the correct Lagrangian is $-m_0c^2/\gamma$.
Unlike Newtonian mechanics, Lagrangian mechanics has the advantage of permitting very flexible coordinate transformations. This is because, unlike Newtonian mechanics, Lagrangian mechanics possesses general covariance. A detailed explanation of this can be found in the following article.
르베그 가측 집합과 보렐 가측 집합
25 Feb 20251. 르베그 측도
카라테오도리 정리로부터 다음과 같이 측도 $m$을 정의할 수 있다.
-
$\mathcal{A}_0 = \lbrace \cup^n_{k=1} (a_k, b_k] : a_k, b_k \in \mathbb{R}^\infty \rbrace $는 대수임을 보인다.
-
$A \in \mathcal{A}_0$에 대해, $A = \sqcup^n_{k=1} (a_k, b_k]$로 표현하는 방법이 유일함을 보인다.
-
함수 $\rho: \mathcal{A}_0 \to [0, \infty]$를
\[\rho(\sqcup^n_{k=1} (a_k, b_k]) = \sum^n_{k=1}(b_k - a_k)\]와 같이 정의했을 때 $\rho$가 예비측도임을 보인다.
-
$\mathcal{A}_0, \rho$에 대해 카라테오도리 구축 정리를 적용하여 외측도 $m^\ast$을 얻는다.
-
$m^\ast$의 정의역을 $m^\ast$-가측집합으로 제한하여 측도 $m$을 얻는다.
대수는 유한 합집합에만 닫혀 있기 때문에 1, 2, 3은 거의 자명하다. 4, 5의 증명은 관련 글을 참조하라.
정의. 상술한 $m$을 르베그 측도Lebesgue measure라고 부른다. 또한, $m$의 정의역에 속하는 집합을 르베그 가측Lebesgue measurable이라고 부른다.
카라테오도리 정리들로부터 다음 사실들이 어렵지 않게 따라 나온다.
정리.
- $m([a, b]) = m((a, b)) = m((a, b]) = m([a, b)) = b - a$
- $A \subset \mathbb{R}$이 가산일 때, $m(A) = 0$
그리고 카라테오도리 확장 정리로 얻어지는 측도는 완비 측도complete measure이므로 다음이 성립한다.
정리. $m$은 완비 측도이다.
또한 $\sigma(\mathcal{A}_0)$는 보렐 $\sigma$-대수 $\mathcal{B}$이므로, 다음이 따라 나온다.
정리. 보렐 가측 집합은 르베그 가측이다.
2. 르베그 가측이지만 보렐 가측이 아닌 집합
정의. 집합열 $\lbrace C_n \rbrace$을 다음과 같이 정의한다.
\[\begin{gather} C_0 = [0, 1]\\ C_1 = I_0 \setminus (1/3, 2/3) \\ C_2 = I_1 \setminus \{ (1/9, 2/9) \cup (7/9, 8/9) \} \\ \vdots \end{gather}\]칸토어 집합Cantor set $C$를 $\cap^\infty_{n = 0}C_n$으로 정의한다.
정리.
- 칸토어 집합은 비가산이다.
- 칸토어 집합은 르베그 측도 0이다.
증명.
-
칸토어 집합에 속하는 원소들은 삼진법으로 소숫점 전개했을 때 어느 자리에도 2가 등장하지 않는 수들이다. 그러한 수는 $2^\aleph_0$개 있으므로 비가산이다.
-
$m(C_n) = (2/3)^n$이므로 $m(C) = \lim_{n \to infty} (2/3)^n = 0$. ■
정의. 칸토어 집합을 정의할 때 각 단계에서 빠지는 집합을 $J_n$이라고 하자. 즉,
\[\begin{gather} J_1 = (1/3, 2/3) \\ J_2 = (1/9, 2/9) \cup (7/9, 8/9) \\ \vdots \end{gather}\]다음과 같이 함수열을 정의한다.
\[\begin{gather} \operatorname{dom} f_1 = J_1,\; f_1(x) = \frac{1}{2} \\\\ \operatorname{dom} f_2 = J_1 \cup J_2, \; f_2(x) = \begin{cases} 1/4 & x \in (1/9, 2/9) \\ 1/2 & x \in (1/3, 2/3) \\ 3/4 & x \in (7/9, 8/9) \end{cases} \\\\ \vdots \end{gather}\]$f: I \to I$를 다음과 같이 정의한다.
\[f(x) = \inf \{ f_n(y) : y \geq x, y \in \mathrm{dom} f \}\]$f$를 칸토어 함수Cantor function라고 한다.
정리. 칸토어 함수는 연속이다.
증명. $f$를 칸토어 함수라고 하자. $f$는 증가함수이므로 $f$가 불연속점을 가진다면 해당 불연속은 틈 불연속gap discontinuity이며, 따라서 어떤 $\epsilon > 0$와 $y_0 \in I$에 대해 $(y_0 - \epsilon, y_0 + \epsilon)$이 $\operatorname{im} f$ 밖에 속한다. 그런데 $(y_0 - \epsilon, y_0 + \epsilon)$의 원소 중에는 이진법으로 소숫점 전개했을 때 자릿수가 유한한 수가 존재한다. 해당 수는 $\operatorname{im}f$에 속하므로 모순이다. ■
정리. 르베그 가측이지만 보렐 가측이 아닌 함수가 존재한다.
증명.
보조정리. $f$가 증가함수라면 $f^{-1}$은 보렐 집합을 보렐 집합에 사상한다.
보조정리의 증명. $\mathcal{A} = \lbrace S \subset I : f^{-1}(S) \in \mathcal{B} \rbrace $라고 하자. 열린 집합들의 모음 $\mathcal{G}$에 대해 $\mathcal{G} \subset \mathcal{A}$임이 자명하다. 또한 $\mathcal{A}$가 $\sigma$-대수임이 역함수의 성질로부터 자명하다. 따라서 $\mathcal{A} = \sigma(\mathcal{G}) = \mathcal{B}$이다.
$f$가 칸토어 함수라고 하고, $F$를 다음과 같이 정의하자.
\[F(x) =\inf \{y : f(y) \geq x \}\]$F$는 엄격히 증가하는 함수이고, $\operatorname{im} F = C$이다($C$는 칸토어 집합). $V$를 비탈리 집합이라고 하자. $F[V]$는 $C$에 포함되므로 르베그 측도 0이며, 르베그 측도의 완비성에 따라 르베그 가측이다. 그러나 $F[V]$는 보렐 가측이 아니다. 만약 보렐 가측이었다면 $F$가 증가함수이므로 $F^{-1}(F[V]) = V$가 가측이어야 하기 때문이다. ■
Lebesgue Measurable Sets and Borel Measurable Sets
25 Feb 20251. Lebesgue Measure
From Carathéodory’s theorem, we can define a measure $m$ on $\mathbb{R}$ as follows.
-
Show that $\mathcal{A}_0 = \lbrace \cup^n_{k=1} (a_k, b_k] : a_k, b_k \in \mathbb{R}^\infty \rbrace $ is an algebra.
-
For $A \in \mathcal{A}_0$, show that the representation $A = \sqcup^n_{k=1} (a_k, b_k]$ is unique.
-
Define $\rho: \mathcal{A}_0 \to [0, \infty]$ as:
\[\rho(\sqcup^n_{k=1} (a_k, b_k]) = \sum^n_{k=1}(b_k - a_k)\]Show that $\rho$ is a premeasure.
-
Apply Carathéodory’s extension theorem to $\mathcal{A}_0, \rho$ to obtain the outer measure $m^\ast$.
-
Restrict the domain of $m^\ast$ to $m^\ast$-measurable sets to obtain $m$.
Since algebras are only closed under finite unions, steps 1, 2, and 3 are almost trivial. For the proofs of steps 4 and 5, see the related post.
Definition. The aforementioned $m$ is called the Lebesgue measure. Moreover, sets belonging to the domain of $m$ are called Lebesgue measurable.
The following facts follow readily from Carathéodory’s theorems.
Theorem.
- $m([a, b]) = m((a, b)) = m((a, b]) = m([a, b)) = b - a$
- When $A \subset \mathbb{R}$ is countable, $m(A) = 0$
Since the measure obtained by Carathéodory’s extension theorem is a complete measure, the following holds.
Theorem. $m$ is a complete measure.
Furthermore, since $\sigma(\mathcal{A}_0)$ is the Borel $\sigma$-algebra $\mathcal{B}$, it follows that:
Theorem. Borel measurable sets are Lebesgue measurable.
2. Sets That Are Lebesgue Measurable but Not Borel Measurable
Definition. Define the sequence of sets $\lbrace C_n \rbrace$ as follows:
\[\begin{gather} C_0 = [0, 1]\\ C_1 = I_0 \setminus (1/3, 2/3) \\ C_2 = I_1 \setminus \{ (1/9, 2/9) \cup (7/9, 8/9) \} \\ \vdots \end{gather}\]The Cantor set $C$ is defined as $\cap^\infty_{n = 0}C_n$.
Theorem.
- The Cantor set is uncountable.
- The Cantor set has Lebesgue measure 0.
Proof.
-
Elements belonging to the Cantor set are numbers whose ternary decimal expansion contains no digit 2 in any position. There are $2^\aleph_0$ such numbers, hence uncountable.
-
Since $m(C_n) = (2/3)^n$, we have $m(C) = \lim_{n \to infty} (2/3)^n = 0$. ■
Definition. Let $J_n$ denote the sets removed at each stage in defining the Cantor set. That is,
\[\begin{gather} J_1 = (1/3, 2/3) \\ J_2 = (1/9, 2/9) \cup (7/9, 8/9) \\ \vdots \end{gather}\]Define the sequence of functions as follows:
\[\begin{gather} \operatorname{dom} f_1 = J_1,\; f_1(x) = \frac{1}{2} \\\\ \operatorname{dom} f_2 = J_1 \cup J_2, \; f_2(x) = \begin{cases} 1/4 & x \in (1/9, 2/9) \\ 1/2 & x \in (1/3, 2/3) \\ 3/4 & x \in (7/9, 8/9) \end{cases} \\\\ \vdots \end{gather}\]Define $f: I \to I$ as follows:
\[f(x) = \inf \{ f_n(y) : y \geq x, y \in \mathrm{dom} f \}\]$f$ is called the Cantor function.
Theorem. The Cantor function is continuous.
Proof. Let $f$ be the Cantor function. Since $f$ is an increasing function, if $f$ has discontinuities, they would be jump discontinuities. Therefore, for some $\epsilon > 0$ and $y_0 \in I$, the interval $(y_0 - \epsilon, y_0 + \epsilon)$ would lie outside $\operatorname{im} f$. However, among the elements of $(y_0 - \epsilon, y_0 + \epsilon)$, there exists a number whose binary decimal expansion has finitely many digits. Such a number belongs to $\operatorname{im}f$, which is a contradiction. ■
Theorem. There exist sets that are Lebesgue measurable but not Borel measurable.
Proof.
Lemma. If $f: I \to I$ is an increasing function, then $f^{-1}$ maps Borel sets to Borel sets.
Proof of lemma. Let $\mathcal{A} = \lbrace S \subset I : f^{-1}(S) \in \mathcal{B} \rbrace $. It is trivial that $\mathcal{G} \subset \mathcal{A}$, where $\mathcal{G}$ is the collection of open sets of $I$. Moreover, it is trivial from properties of inverse functions that $\mathcal{A}$ is a $\sigma$-algebra. Therefore, $\mathcal{A} \supseteq \sigma(\mathcal{G}) = \mathcal{B}$.
Let $f$ be the Cantor function and define $F$ as follows:
\[F(x) =\inf \{y : f(y) \geq x \}\]$F$ is a strictly increasing function with $\operatorname{im} F = C$ (where $C$ is the Cantor set). Let $V$ be the Vitali set. Since $F[V]$ is contained in $C$, it is a null set and thus, is Lebesgue measurable by the completeness of Lebesgue measure. However, $F[V]$ is not Borel measurable. If it were Borel measurable, then since $F$ is strictly increasing (hence injective), $F^{-1}(F[V]) = V$ would have to be measurable. ■
카라테오도리 정리를 이용한 측도의 구성
25 Feb 2025필자는 카라테오도리 정리Carathéodory theorem를 3가지로 구분해서 이해하는 방식을 선호하기 때문에, 이 글에서도 해당 방식을 따른다. 각각 다음과 같다.
- 카라테오도리 구축 정리: 임의의 집합족과 양함수로부터 외측도outer measure 를 정의할 수 있다.
- 카라테오도리 제한 정리: 외측도의 정의역을 가측 집합으로 제한한 함수는 측도가 된다.
- 카라테오도리 확장 정리: 대수 $\mathcal{A}_0$ 위의 예비측도premeasure $\mu_0$를 확장하는 $\sigma(\mathcal{A}_0)$ 위의 측도는, 집합족을 $\mathcal{A}_0$, 양함수를 $\mu_0$로 잡은 뒤 구축 정리를 적용하여 얻은 외측도 $\mu^\ast$에, 제한 정리를 적용하여 얻은 측도가 유일하다.
도식적으로, 다음과 같이 이해할 수 있다.
| (1) | (2) | (3) | |
|---|---|---|---|
| 정의역 | 대수 $\mathcal{A}_0$ | $\sigma$-대수 $\mathcal{A}$ | 멱집합 $\mathcal{P}(X)$ |
| 함수 | 예비측도 $\mu_0$ | 측도 $\mu$ | 외측도 $\mu^\ast$ |
구축 정리는 (1) → (3), 제한 정리는 (3) → (2), 확장 정리는 (1) → (2)의 방향을 가진다. 하나하나 살펴 보자.
정의. $X$ 위의 외측도 $\mu^\ast: \mathcal{P}(X) \to [0, \infty]$는 다음을 만족하는 함수이다.
- $\mu^\ast(\varnothing) = 0$
- $A \subset B \implies \mu^\ast(A) \leq \mu^\ast(B)$
- $\mu^\ast\left( \bigcup_{n \in \mathbb{N}} A_n \right) \leq \sum_{n \in \mathbb{N}} \mu^\ast(A_n)$
카라테오도리 구축 정리. $X$의 부분집합으로 이루어진 임의의 집합족 $\mathcal{S}$와, $l(\varnothing) = 0$을 만족하는 임의의 함수 $l: \mathcal{S} \to [0, \infty]$가 주어졌을 때, 다음과 같이 정의된 $\mu^\ast$은 외측도이다.
\[\mu^*(E) = \inf \left\{ \sum_{n \in \mathbb{N}} l(A_n) : \{ A_n \} \subset \mathcal{S} \text{ covers }E \right\}\]
즉, $\mu^\ast$은 덮개의 극한으로서 $E$의 ‘측도’ 비스무리한 것을 정의하는 함수이며, 구분구적법에서 상합upper sum과 개념적으로 비슷하다.
증명. 1과 2는 자명하다. 3을 보인다.
$A = \bigcup A_n$이라고 하고, 임의의 $\epsilon > 0$이 주어졌다고 하자. $\mu^\ast$의 정의에 의해, 각 $n$에 대해 다음을 만족하는 $A_n$의 덮개 $\mathcal{C}_n = \lbrace A_{nm} \rbrace_{m \in \mathbb{N}} \subset \mathcal{S}$가 존재한다.
\[\sum l(A_{nm}) \leq \mu^*(A_n) + \epsilon/2^n\]따라서,
\[\sum_{n, m \in \mathbb{N}} l(A_{nm}) \leq \sum \mu^*(A_n) + \epsilon.\]그리고 $\bigcup \mathcal{C}_n$이 $A$를 덮으므로, $\mu^\ast$의 정의에 의해 $\mu^\ast(A) \leq \sum_{n, m \in \mathbb{N}} l(A_{nm})$이다. ■
정의. $\mu^\ast$가 외측도라고 하자. 임의의 $E$에 대해 다음을 만족하는 집합 $A$를 $\mu^\ast$에 대해 가측measurable이라고 한다.
\[\mu^*(E) = \mu^*(E \cap A) + \mu^*(E \cap A^c)\]
정의. $\mu^\ast$가 외측도라고 하자. $\mu^\ast(N) = 0$인 $N$을 영집합null set이라고 한다.
즉, 가측 집합은 $\mu^\ast$에 대해 임의의 집합을 ‘깔끔하게’ 분할하는 집합이다. 따라서 가측 집합으로만 이루어진 모임 위에서 $\mu^\ast$은 일반적인 측도와 같이 행동할 것으로 예측할 수 있다. 이 예측을 입증하는 것이 다음의 제한 정리이다.
카라테오도리 제한 정리. $\mu^\ast$가 외측도라고 하자. $\mu^\ast$에 대해 가측인 집합들의 모임을 $\mathcal{A}$라고 할 때, 다음이 성립한다.
- $\mathcal{A}$는 $\sigma$-대수이다.
- $\mu^\ast |_\mathcal{A}$는 측도이다.
- $\mathcal{A}$는 $\mu^\ast$의 모든 영집합을 포함한다.
증명.
1. $\mathcal{A}$는 대수이다.
여집합 닫힘은 자명하다. 유한 교집합 닫힘임을 보인다.
$A, B$가 가측이라고 하자. $A \cap B$가 가측임을 보이기 위해 다음을 보이면 충분하다.
\[\mu^*(E \cap (A \cap B)) + \mu^*(E \cap (A \cap B)^c) \leq \mu^*(E) \quad \cdots \quad (*)\]$A, B$가 가측이므로 다음이 성립한다.
\[\begin{aligned} \mu^*(E) &= \mu^*(E \cap A) + \mu^*(E \cap A^c) \\ &= \mu^*(E \cap A \cap B) + \mu^*(E \cap A \cap B^c) \\ &+ \mu^*(E \cap A^c \cap B) + \mu^*(E \cap A^c \cap B^c) \end{aligned}\]따라서 $(\ast)$은 다음과 동치이다.
\[\begin{aligned} \mu^*(E \cap (A^c \cup B^c)) &\leq \mu^*(E \cap A \cap B^c) \\ &+ \mu^*(E \cap A^c \cap B) \quad \cdots \quad (**) \\ &+ \mu^*(E \cap A^c \cap B^c) \end{aligned}\]간단한 집합론으로부터 다음을 알 수 있다.
\[A^c \cup B^c = (A \cap B^c) \cup (A^c \cap B) \cup (A^c \cap B^c)\]따라서 $(\ast\ast)$가 성립한다. □
2. $\mathcal{A}$는 $\sigma$-대수이다.
$A_n \uparrow A$인 $\lbrace A_n \rbrace \subset \mathcal{A}$에 대해 $A \in \mathcal{A}$임을 보이면 충분하다. (why?)
외측도의 정의에 의해 $\mu^\ast(E \cap A_n) \leq \mu^\ast(E \cap A)$이다. $C_1 = A_1, C_n = A_n \setminus A_{n - 1}$이라고 하자. $\bigsqcup C_n = A$이다. 또한,
\[\begin{aligned} \mu^*(E \cap A_n) &= \mu^*(E \cap A_n \cap C_n) + \mu^*(E \cap A_n \cap C_n^c) \\ &= \mu^*(E \cap C_n) + \mu^*(E \cap A_{n - 1}) \\ &= \cdots \\ &= \sum^n_{k = 1} \mu^*(E \cap C_k) \end{aligned}\]이다. 따라서 $\sum^\infty \mu^\ast(E \cap C_n) \leq \mu^\ast(E \cap A)$이다. 그런데 $\lbrace E \cap C_n \rbrace $이 $E \cap A$를 덮으므로, $\sum^\infty \mu^\ast(E \cap C_n) \geq \mu^\ast(E \cap A)$이다. 따라서 $\sum^\infty \mu^\ast(E \cap C_n) = \mu^\ast(E \cap A)$이다.
따라서 임의의 $\epsilon > 0$에 대해, 충분히 큰 $N$이 존재하여 $\mu^\ast(E \cap A) - \epsilon \leq \mu^\ast(E \cap A_n)$이다. 따라서,
\[\begin{aligned} \mu^*(E \cap A_n^c) &= \mu^*(E) - \mu^*(E \cap A_n) \\ &\leq \mu^*(E) - \mu^*(E \cap A) + \epsilon \end{aligned}\]이므로 다음을 얻는다.
\[\mu^*(E) \leq \mu^*(E \cap A_n) + \mu^*(E \cap A_n^c) \leq \mu^*(E) + \epsilon\]$n \to \infty$로 보내면 $\mu^\ast(E \cap A) + \mu^\ast(E \cap A^c) = \mu^\ast(E)$이다. □
3. $\mu^\ast|_\mathcal{A}$는 측도이다, 4. $\mathcal{A}$는 모든 영집합을 포함한다.
Left as an exercise to the readers. (어렵지 않음) ■
정의. $\mathcal{A}_0$가 대수라고 하자. $\rho: \mathcal{A}_0 \to [0, \infty]$가 예비측도라는 것은 다음을 만족한다는 것이다.
- $\rho(\varnothing) = 0$
- 쌍으로 서로소인 가산 집합족 $\lbrace A_n \rbrace $에 대해, $\bigcup A_n \in \mathcal{A}_0$라면 $\rho\left( \bigcup A_n \right) = \sum \rho(A_n)$
카라테오도리 확장 정리. 대수 $\mathcal{A}_0$ 위의 예비측도 $\rho$에 대해, 다음과 같이 정의하자.
\[\mu^*(E) = \inf \left\{ \sum_{n \in \mathbb{N}} \mu_0(A_n) : \{ A_n \} \subset \mathcal{A}_0 \text{ covers }E \right\}\]이때, 다음이 성립한다.
- $A \in \mathcal{A}_0$라면 $\mu^\ast(A) = \rho(A)$이다.
- $\sigma(\mathcal{A}_0)$는 $\mu^\ast$에 대해 가측이다.
- $\rho$가 $\sigma$-유한이라면, $\rho$의 정의역을 $\sigma(\mathcal{A}_0)$로 확장하는 측도는 $\mu^\ast|_{\sigma(\mathcal{A}_0)}$가 유일하다.
증명.
1. $A \in \mathcal{A}_0$라면 $\mu^\ast(A) = \rho(A)$이다.
$A$가 $A$의 덮개이므로 $\mu^\ast(A) \leq \rho(A)$이다. 만약 $\mu^\ast(A) < \rho(A)$라면 어떤 $A$의 덮개 $\lbrace A_n \rbrace $이 존재하여 $\sum \rho(A_n) < \rho(A)$이다. 그런데 $\rho$가 예비측도이므로 이는 모순이다. □
2. $\sigma(\mathcal{A}_0)$는 $\mu^\ast$에 대해 가측이다.
먼저 $\mathcal{A}_0$가 가측임을 보인다. 임의의 $A \in \mathcal{A}_0$에 대해 $\mu^\ast(E \cap A) + \mu^\ast(E \cap A^c) \leq \mu^\ast(E)$임을 보이면 충분하다. $\mu^\ast$의 정의에 의해, 임의의 $\epsilon > 0$에 대해 어떤 $E$의 덮개 $\mathcal{C}$가 존재하여 다음이 성립한다.
\[\sum^\infty_{n = 1} \rho(C_n) \leq \mu^*(E) + \epsilon\]$\mathcal{A}_0$가 대수이므로, $A \cap C_n, A^c \cap C_n \in \mathcal{A}_0$이다. 따라서,
\[\begin{aligned} \mu^*(E \cap A) + \mu^*(E \cap A^c) &\leq \sum^\infty_{n = 1} \mu^*(A \cap C_n) + \sum^\infty_{n = 1} \mu^*(A^c \cap C_n) \\ &= \sum^\infty_{n = 1} \rho(A \cap C_n) + \sum^\infty_{n = 1} \rho(A^c \cap C_n) \\ &= \sum^\infty_{n = 1} \rho(C_n) \leq \mu^*(E) + \epsilon \end{aligned}\](엄밀히 따지자면 $\sum^n_{k=1}$을 고려한 다음에 $n \to \infty$ 극한을 취해야 한다) 따라서 $\mu^\ast(E \cap A) + \mu^\ast(E \cap A^c) \leq \mu^\ast(E)$이며, $\mathcal{A}_0$는 가측이다. 카라테오도리 제한 정리에 의해 가측 집합은 $\sigma$-대수를 이루므로, $\sigma(\mathcal{A}_0)$ 또한 가측이다. □
3. $\rho$가 $\sigma$-유한이라면, $\rho$의 정의역을 $\sigma(\mathcal{A}_0)$로 확장하는 측도는 $\mu^\ast|_{\sigma(\mathcal{A}_0)}$가 유일하다.
먼저 $\rho < \infty$를 가정하자. $\sigma(\mathcal{A}_0)$ 위에서 정의된 측도 $\nu$가 $\mathcal{A}_0$에서 $\rho$와 일치한다고 하자. 또한 $\mu = \mu^\ast|_{\sigma(\mathcal{A}_0)}$라고 하자. $\nu = \mu$임을 보인다.
$E \in \sigma(\mathcal{A}_0)$라고 하자. 어떤 $E$의 덮개 $\lbrace A_n \rbrace \subset \mathcal{A}_0$가 존재하여,
\[\sum \rho(A_n) \leq \mu(E) + \epsilon\]이다. $\nu$가 $\mathcal{A}_0$에서 $\rho$와 일치하므로, $\sum \rho(A_n) = \sum \nu(A_n) \geq \nu(E)$이다. 따라서 $\nu \leq \mu$이다.
이제 $B_n = \bigcup^n_{k=1}A_k$로 정의하고, $A = \bigcup^\infty_{n = 1} A_n = \lim_{n \to \infty} B_n$이라고 하자. $\mu(B) = \sum \rho(A_n) \leq \mu(E) + \epsilon$이므로 $\mu(B \setminus E) \leq \epsilon$이다. $\nu$가 측도이므로,
\[\mu(A) = \lim \rho(B_n) = \lim \nu(B_n) = \nu(A)\]따라서,
\[\begin{aligned} \mu(E) \leq \mu(B) &= \mu(B \setminus E) + \mu(E) \\ &\leq \epsilon + \nu(E) \end{aligned}\]즉 $\mu \leq \nu$이다. 따라서 $\mu = \nu$이다.
이제 $\rho$가 $\sigma$-유한하다고 가정하자. 어떤 집합족 $\lbrace C_n \rbrace $이 존재하여 $C_n \uparrow X$이고, $\rho(C_n) < \infty$이다. 앞선 논의에 의해 $C_n$에서 $\mu$와 $\nu$는 일치한다. 따라서,
\[\mu(A) = \lim \mu(A \cap C_i) = \lim \nu (A \cap C_i) = \nu(A)\]이므로 $\mu$와 $\nu$는 전체 공간에서 일치한다. ■
다음 글에서는 카라테오도리 정리를 이용하여 르베그 측도를 구성한 뒤, 모든 보렐 가측 집합은 르베그 가측 집합이지만 그 역은 성립하지 않음을 보인다.
Construction of Measures via Carathéodory's Theorem
25 Feb 2025I prefer to approach Carathéodory’s theorem by dividing it into three subtheorems. They are as follows:
- Carathéodory Construction Theorem: Any collection of sets and a positive function define an outer measure.
- Carathéodory Restriction Theorem: Restricting the domain of an outer measure to measurable sets yields a measure.
- Carathéodory Extension Theorem: There exists a unique extension of premeasure $\mu_0$ on an algebra $\mathcal{A}_0$ to a measure $\mu$ on the $\sigma$-algebra $\sigma(\mathcal{A}_0)$. Furthermore, $\mu$ is the measure obtained by applying the construction theorem with the collection of sets as $\mathcal{A}_0$ and the positive function as $\mu_0$, and then applying the restriction theorem.
Schematically, this can be understood as follows:
| (1) | (2) | (3) | |
|---|---|---|---|
| Domain | Algebra $\mathcal{A}_0$ | $\sigma$-algebra $\mathcal{A}$ | Power set $\mathcal{P}(X)$ |
| Function | Premeasure $\mu_0$ | Measure $\mu$ | Outer measure $\mu^\ast$ |
The construction theorem goes in the direction (1) → (3), the restriction theorem goes (3) → (2), and the extension theorem goes (1) → (2). Let us examine each one by one.
Definition. An outer measure $\mu^\ast: \mathcal{P}(X) \to [0, \infty]$ on $X$ is a function satisfying the following:
- $\mu^\ast(\varnothing) = 0$
- $A \subset B \implies \mu^\ast(A) \leq \mu^\ast(B)$
- $\mu^\ast\left( \bigcup_{n \in \mathbb{N}} A_n \right) \leq \sum_{n \in \mathbb{N}} \mu^\ast(A_n)$
Carathéodory Construction Theorem. Given any collection $\mathcal{S}$ of subsets of $X$ and any function $l: \mathcal{S} \to [0, \infty]$ satisfying $l(\varnothing) = 0$, the function $\mu^\ast$ defined as follows is an outer measure:
\[\mu^*(E) = \inf \left\{ \sum_{n \in \mathbb{N}} l(A_n) : \{ A_n \} \subset \mathcal{S} \text{ covers }E \right\}\]
That is, $\mu^\ast$ is a function that defines something akin to a ‘measure’ of $E$ as an infimum over covers, and is conceptually similar to the upper sumupper sum in Riemann integration.
Proof. Properties 1 and 2 are trivial. We prove property 3.
Let $A = \bigcup A_n$ and suppose an arbitrary $\epsilon > 0$ is given. By the definition of $\mu^\ast$, for each $n$, there exists a cover $\mathcal{C}_n = \lbrace A_{nm} \rbrace_{m \in \mathbb{N}} \subset \mathcal{S}$ of $A_n$ satisfying:
\[\sum l(A_{nm}) \leq \mu^*(A_n) + \epsilon/2^n\]Therefore,
\[\sum_{n, m \in \mathbb{N}} l(A_{nm}) \leq \sum \mu^*(A_n) + \epsilon.\]Since $\bigcup \mathcal{C}_n$ covers $A$, by the definition of $\mu^\ast$, we have $\mu^\ast(A) \leq \sum_{n, m \in \mathbb{N}} l(A_{nm})$. ■
Definition. Let $\mu^\ast$ be an outer measure. A set $A$ is said to be measurable with respect to $\mu^\ast$ if it satisfies the following for any $E$:
\[\mu^*(E) = \mu^*(E \cap A) + \mu^*(E \cap A^c)\]
Definition. Let $\mu^\ast$ be an outer measure. A set $N$ with $\mu^\ast(N) = 0$ is called a null set.
That is, a measurable set is one that ‘cleanly’ partitions any set with respect to $\mu^\ast$. Therefore, we can expect that $\mu^\ast$ will behave like an ordinary measure on the collection consisting only of measurable sets. The following restriction theorem validates this expectation.
Carathéodory Restriction Theorem. Let $\mu^\ast$ be an outer measure. Let $\mathcal{A}$ be the collection of sets that are measurable with respect to $\mu^\ast$. Then the following hold:
- $\mathcal{A}$ is a $\sigma$-algebra.
- $\mu^\ast |_\mathcal{A}$ is a measure.
- $\mathcal{A}$ contains all null sets of $\mu^\ast$.
Proof.
1. $\mathcal{A}$ is an algebra.
Closure under complements is trivial. We show closure under finite intersections.
Suppose $A, B$ are measurable. To show that $A \cap B$ is measurable, it suffices to prove:
\[\mu^*(E \cap (A \cap B)) + \mu^*(E \cap (A \cap B)^c) \leq \mu^*(E) \quad \cdots \quad (*)\]Since $A, B$ are measurable, the following holds:
\[\begin{aligned} \mu^*(E) &= \mu^*(E \cap A) + \mu^*(E \cap A^c) \\ &= \mu^*(E \cap A \cap B) + \mu^*(E \cap A \cap B^c) \\ &+ \mu^*(E \cap A^c \cap B) + \mu^*(E \cap A^c \cap B^c) \end{aligned}\]Therefore, $(\ast)$ is equivalent to:
\[\begin{aligned} \mu^*(E \cap (A^c \cup B^c)) &\leq \mu^*(E \cap A \cap B^c) \\ &+ \mu^*(E \cap A^c \cap B) \quad \cdots \quad (**) \\ &+ \mu^*(E \cap A^c \cap B^c) \end{aligned}\]From elementary set theory, we have:
\[A^c \cup B^c = (A \cap B^c) \cup (A^c \cap B) \cup (A^c \cap B^c)\]Therefore, $(\ast\ast)$ holds. □
2. $\mathcal{A}$ is a $\sigma$-algebra.
It suffices to show that for $\lbrace A_n \rbrace \subset \mathcal{A}$ with $A_n \uparrow A$, we have $A \in \mathcal{A}$. (Why?)
By the definition of outer measure, $\mu^\ast(E \cap A_n) \leq \mu^\ast(E \cap A)$. Let $C_1 = A_1, C_n = A_n \setminus A_{n - 1}$. Then $\bigsqcup C_n = A$. Moreover,
\[\begin{aligned} \mu^*(E \cap A_n) &= \mu^*(E \cap A_n \cap C_n) + \mu^*(E \cap A_n \cap C_n^c) \\ &= \mu^*(E \cap C_n) + \mu^*(E \cap A_{n - 1}) \\ &= \cdots \\ &= \sum^n_{k = 1} \mu^*(E \cap C_k) \end{aligned}\]Therefore, $\sum^\infty \mu^\ast(E \cap C_n) \leq \mu^\ast(E \cap A)$. Since $\lbrace E \cap C_n \rbrace $ covers $E \cap A$, we have $\sum^\infty \mu^\ast(E \cap C_n) \geq \mu^\ast(E \cap A)$. Therefore, $\sum^\infty \mu^\ast(E \cap C_n) = \mu^\ast(E \cap A)$.
Thus, for any $\epsilon > 0$, there exists a sufficiently large $N$ such that $\mu^\ast(E \cap A) - \epsilon \leq \mu^\ast(E \cap A_n)$. Therefore,
\[\begin{aligned} \mu^*(E \cap A_n^c) &= \mu^*(E) - \mu^*(E \cap A_n) \\ &\leq \mu^*(E) - \mu^*(E \cap A) + \epsilon \end{aligned}\]whence we obtain:
\[\mu^*(E) \leq \mu^*(E \cap A_n) + \mu^*(E \cap A_n^c) \leq \mu^*(E) + \epsilon\]Letting $n \to \infty$, we get $\mu^\ast(E \cap A) + \mu^\ast(E \cap A^c) = \mu^\ast(E)$. □
3. $\mu^\ast|_\mathcal{A}$ is a measure, 4. $\mathcal{A}$ contains all null sets.
Left as an exercise to the readers. (Not difficult) ■
Definition. Let $\mathcal{A}_0$ be an algebra. A function $\rho: \mathcal{A}_0 \to [0, \infty]$ is called a premeasure if it satisfies the following:
- $\rho(\varnothing) = 0$
- For any pairwise disjoint countable collection $\lbrace A_n \rbrace $, if $\bigcup A_n \in \mathcal{A}_0$, then $\rho\left( \bigcup A_n \right) = \sum \rho(A_n)$
Carathéodory Extension Theorem. For a premeasure $\rho$ on an algebra $\mathcal{A}_0$, define:
\[\mu^*(E) = \inf \left\{ \sum_{n \in \mathbb{N}} \mu_0(A_n) : \{ A_n \} \subset \mathcal{A}_0 \text{ covers }E \right\}\]Then the following hold:
- If $A \in \mathcal{A}_0$, then $\mu^\ast(A) = \rho(A)$.
- $\sigma(\mathcal{A}_0)$ is measurable with respect to $\mu^\ast$.
- If $\rho$ is $\sigma$-finite, then $\mu^\ast|_{\sigma(\mathcal{A}_0)}$ is the unique measure that extends $\rho$ to $\sigma(\mathcal{A}_0)$.
Proof.
1. If $A \in \mathcal{A}_0$, then $\mu^\ast(A) = \rho(A)$.
Since $A$ is a cover of $A$, we have $\mu^\ast(A) \leq \rho(A)$. If $\mu^\ast(A) < \rho(A)$, then there exists some cover $\lbrace A_n \rbrace $ of $A$ such that $\sum \rho(A_n) < \rho(A)$. However, since $\rho$ is a premeasure, this is a contradiction. □
2. $\sigma(\mathcal{A}_0)$ is measurable with respect to $\mu^\ast$.
First, we show that $\mathcal{A}_0$ is measurable. For any $A \in \mathcal{A}_0$, it suffices to show $\mu^\ast(E \cap A) + \mu^\ast(E \cap A^c) \leq \mu^\ast(E)$. By the definition of $\mu^\ast$, for any $\epsilon > 0$, there exists some cover $\mathcal{C}$ of $E$ such that:
\[\sum^\infty_{n = 1} \rho(C_n) \leq \mu^*(E) + \epsilon\]Since $\mathcal{A}_0$ is an algebra, $A \cap C_n, A^c \cap C_n \in \mathcal{A}_0$. Therefore,
\[\begin{aligned} \mu^*(E \cap A) + \mu^*(E \cap A^c) &\leq \sum^\infty_{n = 1} \mu^*(A \cap C_n) + \sum^\infty_{n = 1} \mu^*(A^c \cap C_n) \\ &= \sum^\infty_{n = 1} \rho(A \cap C_n) + \sum^\infty_{n = 1} \rho(A^c \cap C_n) \\ &= \sum^\infty_{n = 1} \rho(C_n) \leq \mu^*(E) + \epsilon \end{aligned}\](Strictly speaking, one should consider $\sum^n_{k=1}$ and then take the limit $n \to \infty$) Therefore, $\mu^\ast(E \cap A) + \mu^\ast(E \cap A^c) \leq \mu^\ast(E)$, and $\mathcal{A}_0$ is measurable. By the Carathéodory restriction theorem, measurable sets form a $\sigma$-algebra, so $\sigma(\mathcal{A}_0)$ is also measurable. □
3. If $\rho$ is $\sigma$-finite, then $\mu^\ast|_{\sigma(\mathcal{A}_0)}$ is the unique measure that extends $\rho$ to $\sigma(\mathcal{A}_0)$.
First, assume $\rho < \infty$. Suppose a measure $\nu$ defined on $\sigma(\mathcal{A}_0)$ agrees with $\rho$ on $\mathcal{A}_0$. Let $\mu = \mu^\ast|_{\sigma(\mathcal{A}_0)}$. We show $\nu = \mu$.
Let $E \in \sigma(\mathcal{A}_0)$. There exists some cover $\lbrace A_n \rbrace \subset \mathcal{A}_0$ of $E$ such that:
\[\sum \rho(A_n) \leq \mu(E) + \epsilon\]Since $\nu$ agrees with $\rho$ on $\mathcal{A}_0$, we have $\sum \rho(A_n) = \sum \nu(A_n) \geq \nu(E)$. Therefore, $\nu \leq \mu$.
Now define $B_n = \bigcup^n_{k=1}A_k$ and let $A = \bigcup^\infty_{n = 1} A_n = \lim_{n \to \infty} B_n$. Since $\mu(B) = \sum \rho(A_n) \leq \mu(E) + \epsilon$, we have $\mu(B \setminus E) \leq \epsilon$. Since $\nu$ is a measure,
\[\mu(A) = \lim \rho(B_n) = \lim \nu(B_n) = \nu(A)\]Therefore,
\[\begin{aligned} \mu(E) \leq \mu(B) &= \mu(B \setminus E) + \mu(E) \\ &\leq \epsilon + \nu(E) \end{aligned}\]That is, $\mu \leq \nu$. Therefore, $\mu = \nu$.
Now assume $\rho$ is $\sigma$-finite. There exists a collection $\lbrace C_n \rbrace $ such that $C_n \uparrow X$ and $\rho(C_n) < \infty$. By the preceding argument, $\mu$ and $\nu$ agree on $C_n$. Therefore,
\[\mu(A) = \lim \mu(A \cap C_i) = \lim \nu (A \cap C_i) = \nu(A)\]so $\mu$ and $\nu$ agree on the entire space. ■
In the next article, we shall construct Lebesgue measure using Carathéodory’s theorem, and then show that while every Borel measurable set is Lebesgue measurable, the converse does not hold.
대수와 측도의 정의
24 Feb 20251. 비탈리 정리
정의. $\mu$가 집합 $X$ 위의 측도measure라는 것은 다음을 만족한다는 것이다.
- $\mu(\varnothing) = 0$
- 쌍으로 서로소pairwise disjoint인 가산 집합족 $\lbrace A_n \rbrace$에 대해, $\mu\left( \bigcup A_n \right) = \sum \mu(A_n)$
유감스럽게도 $X = \mathbb{R}$일 때, 측도 $\mu$는 실수의 모든 부분집합에 대해서 정의될 수 없다.
비탈리 정리. 다음을 모두 만족하는 $\mathbb{R}$의 측도 $\mu$는 존재하지 않는다.
- 항등적으로 0이 아니다.
- 평행이동에 대해 보존적이다. 즉, 임의의 $r \in \mathbb{R}$에 대해 $\mu(A + r) = \mu(A)$.
- $\operatorname{dom} \mu = \mathcal{P}(\mathbb{R})$
증명. 그러한 측도 $\mu$가 존재한다고 가정하자. $\mathbb{R}$ 위에서 다음의 동치 관계를 정의하자.
\[x \sim y \iff x - y \in \mathbb{Q}\]선택 공리에 의해 $[0, 1]/{\sim}$의 선택 함수 $\iota$가 존재한다. $V = \operatorname{im} \iota$라고 하자. $V$를 비탈리 집합Vitali set이라고 부른다. 예를 들어 $V = \lbrace 0.1, \pi - 3, \sqrt{2} - 1, \dots \rbrace$이다. $\mu$는 $V$에서 정의될 수 없음을 보인다.
$V$의 정의에 의해, $q \in \mathbb{Q}$에 대해 $V$와 $V + q$는 서로소이다. 또한 $[0, 1] \subset \bigcup_{q \in \mathbb{Q}} (V + q) \subset [-1, 3]$이다. 따라서,
\[1 \leq \sum_{q \in \mathbb{Q}}\mu(V + q) \leq 4.\]그런데 $\mu(V + q) = \mu(V)$이므로, $\mu(V) = 0$이면 왼쪽 부등식이 성립하지 않고 $\mu(V) > 0$이면 오른쪽 부등식이 성립하지 않는다. 따라서 모순이다. ■
2. $\sigma$-대수
따라서 올바른 측도를 구축하기 위해서는 측도의 정의역을 적절히 제한할 필요가 있다. 이에 대수의 개념을 도입한다.
정의. 집합 $X$의 대수algebra $\mathcal{A}_0$는 다음을 만족하는 집합족이다.
- $\varnothing, X \in \mathcal{A}_0$
- $A \in \mathcal{A}_0 \implies A^c \in \mathcal{A}_0$
- $A, B \in \mathcal{A}_0 \implies A \cup B \in \mathcal{A}_0$
Remark. 2번 공리와 드모르간의 법칙에 의해, 3번 공리는 $A \cap B \in \mathcal{A}_0$ 또한 시사한다.
대수의 3번 정의를 가산 합집합으로 강화하면 $\sigma$-대수의 정의를 얻는다. 즉,
정의. 집합 $X$의 $\sigma$-대수 $\mathcal{A}$는 다음을 만족하는 대수이다.
- $\lbrace A_n \rbrace _{n \in \mathbb{N}} \subset \mathcal{A}_0 \implies \bigcup_{n \in \mathbb{N}} A_n \in \mathcal{A}$
정리. $\lbrace \mathcal{A}_i \rbrace_{i \in I}$가 $X$의 $\sigma$-대수들의 모임이라면 $\bigcap_{i \in I}\mathcal{A}_i$ 또한 $X$의 $\sigma$-대수이다.
증명. $\sigma$-대수의 정의로부터 쉽게 증명할 수 있다. 그런데 이렇게만 적으면 재미 없으니까, 조금 독특한 증명을 남긴다. 워시-타르스키 정리Łoś-Tarski theorem에 따르면 1차 이론이 교집합에 대해 보존적일 필요충분조건은 1차 이론의 모든 문장이 $\Pi_1$ 문장인 것이다. 그리고 $\sigma$-대수의 세 공리는 모두 $\Pi_1$ 문장이므로, $\sigma$-대수는 교집합에 대해 보존적이다. ■
따름정리. $\mathcal{C}$가 $X$의 부분집합으로 이루어진 집합족일 때, $\mathcal{C}$를 포함하는 가장 작은 $\sigma$-대수가 존재한다. 그러한 $\sigma$-대수를 $\sigma(\mathcal{C})$와 같이 적는다.
증명. $\mathcal{S} = \lbrace \mathcal{A} : \mathcal{A} \text{ is an algebra containing } \mathcal{C} \rbrace$라고 하자. $\mathcal{P}(X) \in \mathcal{S}$이므로 $\mathcal{S}$는 공집합이 아니다. $\sigma(\mathcal{C}) = \bigcap_{\mathcal{A} \in \mathcal{S}} \mathcal{A}$이다.
대표적인 $\sigma$-대수의 예시로, 보렐 $\sigma$-대수를 살펴보자.
정의. $\mathcal{G}$가 $\mathbb{R}$의 열린 집합들의 집합족이라고 하자. $\sigma(\mathcal{G})$를 보렐 $\sigma$-대수Borel $\sigma$-algebra라고 하며, $\mathcal{B}$와 같이 적는다.
보렐 $\sigma$-대수는 보렐 위계Borel hierarchy를 통해서 이해할 수도 있다. $\Sigma_1$을 열린 집합들의 모임, $\Pi_1$을 닫힌 집합들의 모임이라고 하자. 다음과 같이 정의한다.
- $\Delta_n = \Sigma_n \cap \Pi_n$
- $\Sigma_{n + 1} = \lbrace S : \exists \lbrace P_n \rbrace _{n \in \mathbb{N}} \subset \Pi_n \; S = \bigcup_{n \in \mathbb{N}} P_n \rbrace$
- $\Pi_n = \lbrace P : \exists S \in \Sigma_n \; P = S^c \rbrace$
즉 $\Sigma_2 = F_\sigma$, $\Pi_2 = G_\delta$이다. 합집합을 $\exists$, 교집합을 $\forall$로 생각했을 때 산술 위계와 정의의 형태가 유사함에 주목하라.
정리. $\mathcal{B} = \Sigma_{\omega_1} = \Pi_{\omega_1} = \Delta_{\omega_1}$
증명. 생략. 하지만 직관적으로 이해할 수 있다. $\mathcal{B}$는 가산 교집합과 가산 합집합, 그리고 여집합에 대해 닫혀 있어야 하므로 모든 가산 서수 $\alpha$에 대해 $\Sigma_\alpha, \Pi_\alpha, \Delta_\alpha \subset \mathcal{B}$이다. 이 사실로부터 초한 귀납을 취해 정리를 얻는다. ■
어떤 집합 위의 대수와 예비측도라는 것이 주어졌을 때, 이로부터 측도를 정의하는 방법이 알려져 있다. 이 방법을 카라테오도리 방법Carathéodory method이라고 부른다. 예비측도는 구성하기가 매우 쉽기 때문에, 이 방법을 이용하면 측도를 아주 쉽게 구성할 수 있다. 카라테오도리 방법에 대해서는 다음 글에서 알아본다.