디멘의 블로그
Dimen's Blog
이데아를 여행하는 히치하이커
Alice in Logicland
An Intuitive Understanding of Adjoints
16 Dec 2024One of the central concepts in category theory is that of an adjoint.
Definition. Let $\mathcal{A}, \mathcal{B}$ be categories, and let $F: \mathcal{A} \to \mathcal{B}, G: \mathcal{B} \to \mathcal{A}$ be functors. We say that $F$ is a left adjoint to $G$, written as $F \dashv G$, if for any $A \in \mathcal{A}, B \in \mathcal{B}$, there exists a natural correspondence between $\hom_\mathcal{B}(F(A), B)$ and $\hom_\mathcal{A}(A, G(B))$. That is,
\[\begin{gather} (F(A) \xrightarrow{g} B) \quad \mapsto \quad (A \xrightarrow{\bar{g}} G(B))\\ (A \xrightarrow{f} G(B)) \quad \mapsto \quad (F(A) \xrightarrow{\bar{f}} B) \end{gather}\]We also call $G$ the right adjoint to $F$.
This may feel very abstract, but there is a couple of examples that could be of assist in grasping the definition.
1. Adjoints as Approximations
When $F \dashv G$, the functors $F$ and $G$ can be thought of as approximating objects in $\mathcal{A}$ and $\mathcal{B}$ with respect to each other. In particular, the left adjoint represents approximation ‘from left to right’, while the right adjoint represents approximation ‘from right to left’.
For example, let $\mathbf{Z}$ be a category whose objects are integers, with a unique morphism $x \to y$ existing if and only if $x \leq y$. Similarly, let $\mathbf{R}$ be a category whose objects are real numbers, with a unique morphism $x \to y$ existing if and only if $x \leq y$. We may think of $\lceil \cdot \rceil, \lfloor \cdot \rfloor$ as functors $\mathbf{R} → \mathbf{Z}$, and the inclusion map $\iota$ as a functor $\mathbf{Z} → \mathbf{R}$. It then follows that $\lceil \cdot \rceil \dashv \iota \dashv \lfloor \cdot \rfloor$.
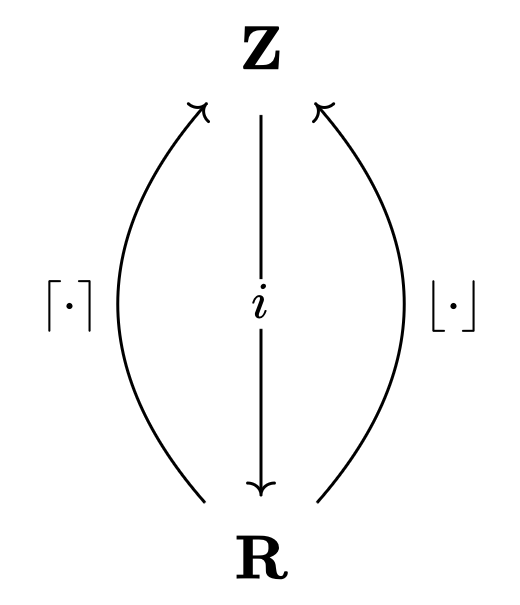
That is, $\lceil \cdot \rceil$ is a transformation that ‘lifts [a number] from left to right’ by mapping $r$ to $\lceil r \rceil$ with $r \leq \lceil r \rceil$, while $\lfloor \cdot \rfloor$ is a transformation that ‘pulls [a number] from right to left’ by mapping $r$ to $\lfloor r \rfloor$ with $\lfloor r \rfloor \leq r$.
Furthermore, let $I$ and $T$ be the initial object and terminal object of $\mathcal{A}$ respectively. That is, for any $A \in \mathcal{A}$:
- There exists a unique morphism $I \to A$.
- There exists a unique morphism $A \to T$.
For instance, in $\mathbf{Set}$, the empty set is the initial object and any singleton set is a terminal object.
For the singleton category $\mathcal{S}$, there exists a unique functor $F: \mathcal{A} \to \mathcal{S}$ that maps every object of $\mathcal{A}$ to the single object of $\mathcal{S}$. Let $G_I, G_T: \mathcal{S} \to \mathcal{A}$ be functors that maps the single object of $\mathcal{S}$ to $I$ and $T$, respectively. It then follows that $G_T \dashv F \dashv G_I$. (Since the terminal object is the ‘rightmost’ object, $G_T$ represents approximation ‘from left to right’, while since the initial object is the ‘leftmost’ object, $G_I$ represents approximation ‘from right to left’.)
2. Adjoints as Construction and Destruction
Left adjoints are associated with construction, while right adjoints are associated with destruction. Therefore, free functors are generally left adjoints, while forgetful functors are right adjoints.
For instance, let $\mathbf{Grp}$ be the category of groups and $\mathbf{Mon}$ be the category of monoids. Let $F$ be the free functor and $U$ be the forgetful functor. Define $R: \mathbf{Mon} → \mathbf{Grp}$ as follows:
- $R(M) = \lbrace m \in M : \exists m^{-1} \in M \rbrace$
- $R(f): m \mapsto f(m)$
Then the following diagram holds, yielding $F \dashv U \dashv R$.
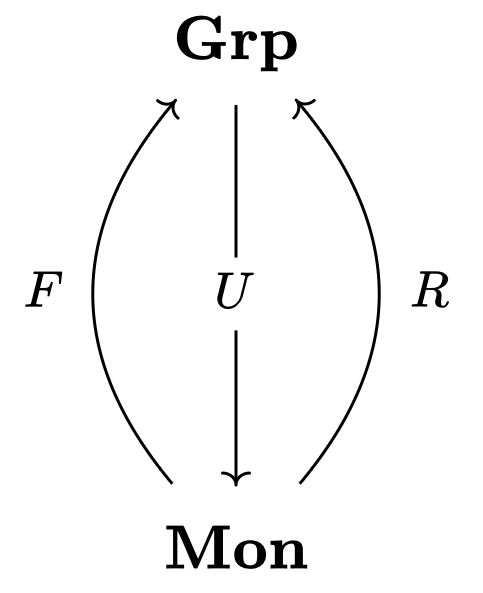
One can understand $U \dashv R$ as expressing that $R$ is more destructive than $U$.
굴림에 대한 두 가지 삽화
11 Dec 2024학부 시절 고전역학 수강 때 개인 공부용으로 만든 삽화인데, 잘 정리한 듯하여 이곳에도 공유한다.
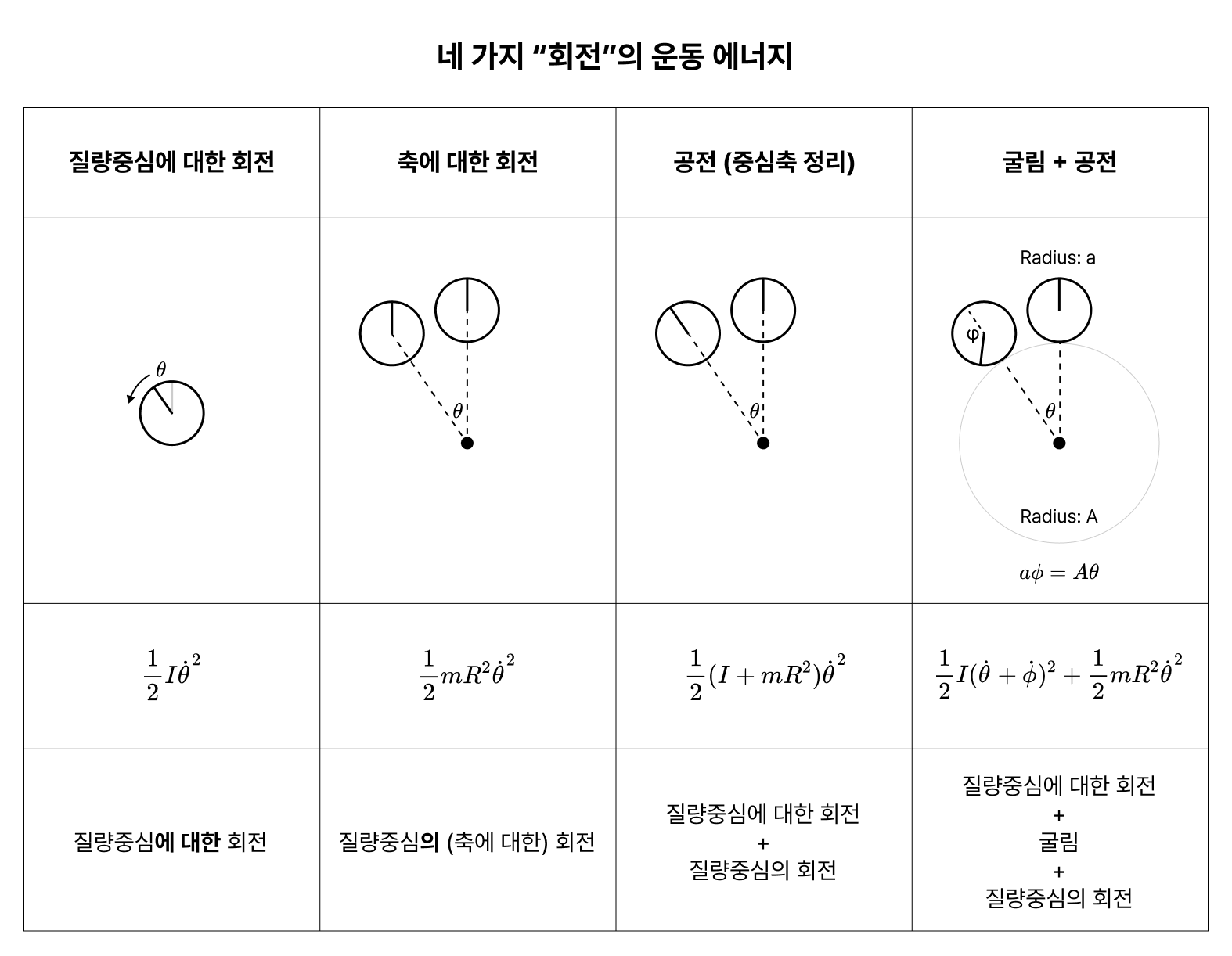

굴림을 바퀴의 CM 기준으로 분석할 때 땅 또한 움직인다는 사실에 유의하자.
Two Illustrations on Rolling
11 Dec 2024These are illustrations I made when I studied classical mechanics in my BA. They seem to be well-made, so I decided to share them here, too.
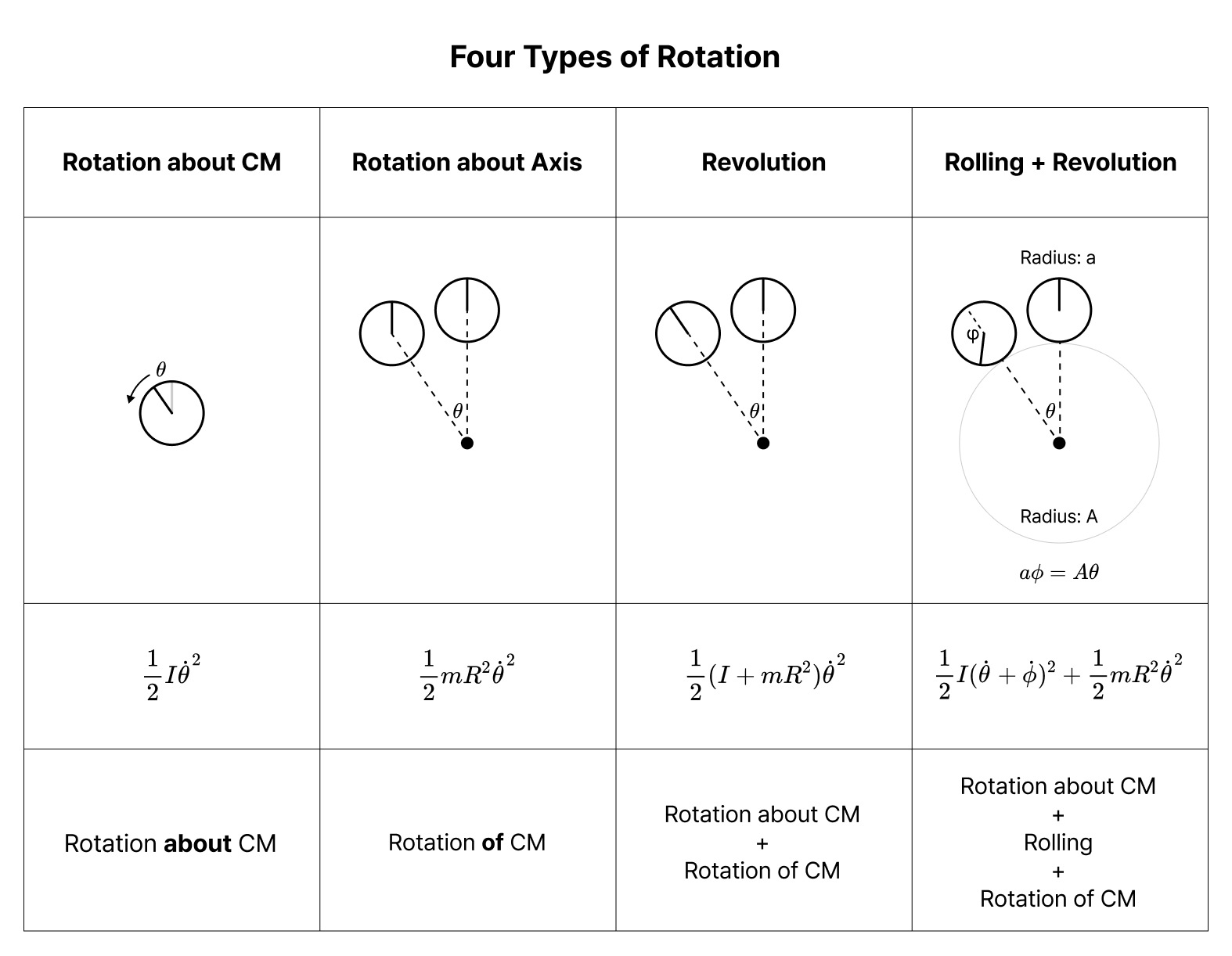
Note that decomposing Revolution as the sum of Rotation about CM and Rotation about Axis is a specific case of the central axis theorem.

Note that when analysing Rolling from CM’s frame, the ground also moves at $v = -r\omega$.
V = L 공리의 무모순성
11 Dec 2024영문 버전의 글이 더 정확하고 설명이 풍부하니 참고하시길 바랍니다.
1. 전체
1.1. 폰 노이만 전체
초한귀납적으로 $\lbrace V_\alpha \rbrace$를 정의하자.
- $V_0 = \varnothing$
- $V_{\alpha + 1} = V_\alpha \cup \mathcal{P}(V_\alpha)$
- $\lambda$가 극한 서수일 때, $V_\lambda = \bigcup_{\alpha < \lambda} V_\alpha$
처음 몇 개의 $V_\alpha$는 다음과 같다.
- $V_1 = \lbrace \varnothing \rbrace$
- $V_2 = \lbrace \varnothing, \lbrace \varnothing \rbrace \rbrace$
- $V_3 = \lbrace \varnothing, \lbrace \varnothing \rbrace, \lbrace \lbrace \varnothing \rbrace \rbrace, \lbrace \varnothing, \lbrace \lbrace \varnothing\rbrace \rbrace \rbrace$
- $V_\omega = \mathsf{HF}$
모든 서수 $\alpha$에 대해 $V_\alpha$를 모아둔 모임을 폰 노이만 전체라고 한다.
\[V = \bigcup_{\alpha \in \mathrm{Ord}} V_\alpha\]$x \in y \in z$가 $x \in z$를 시사할 때 $z$를 추이적 집합transitive set이라고 한다. 이것은 $V$의 중요한 특징이다.
정리.
- $\alpha \in \mathrm{Ord}$에 대해 $V_\alpha$는 추이적이다.
- $V$는 추이적이다.
증명은 초한귀납법을 이용한다. 이에 따라 $V$를 다음과 같이 정의해도 무방하다.
- $V_0 = \varnothing$
- $V_{\alpha + 1} = \mathcal{P}(V_\alpha)$
- $\lambda$가 극한 서수일 때, $V_\lambda = \bigcup_{\alpha < \lambda}V_\alpha$
직관적으로 생각했을 때 $V$는 모든 집합을 포함하는 듯하다. 실제로 다음을 증명할 수 있다.
정리. $x$가 집합이라면 $x \in V$이다.
증명. 집합 $x$에 대해 $x$의 추이적 폐포 $\bar{x}$를, $x$를 원소로 가지는 가장 작은 추이적 집합으로 정의한다(추이적 집합들의 교집합은 추이적이기 때문에 이 정의는 정당하다).
$x \notin V$라고 가정하자. 분류 공리에 의해 $y = \lbrace u \in \bar{x} : u \notin V \rbrace$가 집합이며, 정초 공리에 의해 $y$의 $\in$-극소 원소 $z$가 존재한다. 만약 $w \notin V$인 $w \in z$가 존재한다면, 추이성에 의해 $w \in y$가 되어 $z$의 $\in$-극소성과 모순된다. 따라서 $z$의 모든 원소는 $V$에 있으며, 치환 공리로부터 $\Omega = \lbrace \alpha \in \mathrm{Ord} \mid \exists w \in z : w \in V_\alpha\rbrace$가 집합이다. $\beta = \bigcup_{\alpha \in \Omega}\alpha$라고 하자. $\beta$는 서수이며, $z \in V_{\beta + 1}$이다. (이 부분에서 $V_{\beta + 1} = \mathcal{P}(V_\beta)$임이 필요하다) 따라서 모순이다. ■
이에 따라 $V$는 집합이 아니다. 따라서 $V$는 모든 집합을 포함한다는 점에서 ZFC의 모델이지만, 많은 수학자들은 모델이 집합일 것을 요구하기 때문에 엄격한 의미에서의 모델은 아니다. 하지만 이 글에서는 편의를 위해 $V$를 집합론의 모델이라고 부르도록 한다. 또한 $x \in V$를 “$x$는 집합이다“의 형식적 표현으로 이해하도록 한다.
1.2. 괴델 구성 가능 전체
먼저 다음과 같이 구성 가능성을 정의한다.
정의. $u$가 집합 $S$로부터 구성 가능하다는 것은, 어떤 1차 논리 명제 $\phi(y, x_1, \dots, x_n)$와 $c_1, \dots, c_n \in S$가 존재하여 다음이 성립하는 것이다.
\[y \in u \iff y \in S \land \phi(y, c_1, \dots, c_n)\]단, $\phi$의 양화사의 정의역은 $S$이다.
예를 들어 $S = \lbrace 0, 1, 2\rbrace$일 때 다음은 $u = \lbrace 1, 2 \rbrace$를 구성한다.
- $\phi(y, x_1, x_2) := (y = x_1) \lor (y = x_2)$
- $c_1 = 1, c_2 = 2$
또한 $S = \mathbb{N}$일 때 다음은 $u = \lbrace 0, 3, 6, 9, \dots \rbrace$를 구성한다.
- $\phi(y, x_1) := x_1 \mid y$
- $c_1 = 3$
괴델의 구성가능성은 일반적인 의미에서의 구성가능성, 즉 언어로서의 표현가능성과 다르다. 일례로 언어로 표현가능한 실수의 집합은 가산이므로, 어떤 실수는 언어로 표현이 불가능하다. 그러한 실수를 $r$이라고 하자. 이제 $S = \mathbb{R}$일 때, 다음은 $u = \lbrace r \rbrace$을 구성한다.
- $\phi(y, x_1) := x_1 = y$
- $c_1 = r$
즉, 괴델의 구성가능성은 자유변수의 초기화를 임의의 원소에 대해 허용한다는 점에서 강력하다. 그러나 자유변수의 수가 유한하다는 점에서 한계를 가진다. 이제 초한귀납적으로 $\lbrace L_\alpha \rbrace$를 정의하자.
- $L_0 = \varnothing$
- $L_{\alpha + 1} = \lbrace x : x \text{ is constructible from } L_\alpha \rbrace$
- $\lambda$가 극한 서수일 때, $L_\lambda = \bigcup_{\alpha < \lambda} L_\alpha$
- $L = \bigcup_{\alpha < \lambda} L_\alpha$
$\alpha < \omega$일 때 $L_\alpha = V_\alpha$임을 쉽게 보일 수 있다. $\alpha = n$일 때, 최대 $n$개의 $\lor$ 연언으로 $x \in V_\alpha$를 구성할 수 있기 때문이다. 따라서,
- $L_1 = \lbrace \varnothing \rbrace$
- $L_2 = \lbrace \varnothing, \lbrace \varnothing \rbrace \rbrace$
- $L_3 = \lbrace \varnothing, \lbrace \varnothing \rbrace, \lbrace \lbrace \varnothing \rbrace \rbrace, \lbrace \varnothing, \lbrace \lbrace \varnothing\rbrace \rbrace \rbrace$
- $L_\omega = \mathsf{HF}$
하지만 $L_{\omega + 1} \subsetneq V_{\omega + 1}$이다. $\mathcal{P}(\mathbb{N}) \subset V_{\omega + 1}$이므로 $V_{\omega + 1}$은 비가산인 반면, 1차 논리 문장들의 집합과 $L_\omega$는 모두 가산이므로 $L_{\omega + 1}$ 또한 가산이기 때문이다. 일반적으로 $\alpha$가 가산일 때 $L_\alpha$는 가산이다.
그럼에도 $L$은 $V$와 많은 특징을 공유한다. 일례로,
정리. $\alpha \in \mathrm{Ord}$에 대해 다음이 성립한다.
- $L_\alpha$는 추이적이다. (따라서 $L$이 추이적이다)
- $\alpha \in L_{\alpha + 1} \setminus L_{\alpha}$
증명은 초한귀납법을 사용한다.
$L$은 모든 서수를 포함하므로 부랄리포르티 정리에 의해 집합이 아님에 유의하라. 대신 $x \in L_\alpha$에 대응되는 1차 논리식 $\mathsf{IsInL}_\alpha(x)$가 존재한다. 증명은 조금 까다로운데, 괴델 수를 이용하여 명제를 산술화하면 된다. (링크 참조) 따라서 $x \in L$을 $\exists \alpha \in \mathrm{Ord} :\mathsf{IsInL}_\alpha(x)$를 대체하는 형식적 표현으로 이해하여 사용하도록 한다. (물론 $\alpha \in \mathrm{Ord}$ 또한 1차 논리식을 대체하는 형식적 표현으로 이해되어야 한다)
2. 상대화
2.1. 명제의 상대화
1차 논리 명제는 양화사를 포함할 수 있다. 때문에 양화사의 정의역을 어떻게 설정하느냐의 따라 명제의 의미가 달라진다.
명제 $\phi$와 집합 (또는 모임) $A$에 대해, $\phi$의 상대화 $\phi^A$를 $\phi$의 모든 양화사를 $A$로 제한한 명제로 정의한다. 약간의 서사적 표현을 곁들이자면, $\phi^A$는 $A$의 “내부”에서 이해한 $\phi$라고 할 수 있겠다. 예를 들어, $\phi : \forall x \; \exists y : y < x$일 때
- $\phi^\mathbb{N} : \forall x \in \mathbb{N} \; \exists y \in \mathbb{N} : y < x$
- $\phi^\mathbb{Z} : \forall x \in \mathbb{Z} \; \exists y \in \mathbb{Z} : y < x$
$T_\mathbb{Q}$가 자연수 및 정수를 특정할 수 있는 정도의 표현력을 지니는 유리수 이론이라고 하면,
- $T_\mathbb{Q} \vdash \phi$
- $T_\mathbb{Q} \not\vdash \phi^\mathbb{N}$
- $T_\mathbb{Q} \vdash \phi^{\mathbb{Z}}$
이다. 따라서 $\phi$는 자연수와 유리수를 성공적으로 구분해 내지만, 정수와 유리수는 구분해 내지 못한다. 이 관찰을 일반화하면, 이론 $T$와 집합 $A$에 대해 $T \vdash \phi \leftrightarrow \phi^A$인 $\phi$가 많으면 많을수록 $A$는 $T$의 기술에 잘 “부합한다“고 말할 수 있다.
위 논의를 조금 일반화하여, 다음과 같이 정의한다.
정의. 이론 $T$와 집합 $A$에 대해서
\[T \vdash \forall x_1, \dots, x_n \in A (\phi(x_1, \dots, x_n) \leftrightarrow \phi^A(x_1, \dots, x_n))\]일 때, $\phi$는 $A$에 대해 절대적absolute이라고 한다.
일례로 $T_\mathbb{Q}$에 대해 $\phi(x) : \exists y (y < x)$는 정수에 대해 절대적이지만 자연수에 대해 절대적이지는 않다.
2.2. $L$-상대화
이제 우리의 목표는 $L$이 $\mathsf{ZF}$와 극대적으로 부합함을 보이는 것이다. 즉,
정리 1. $\phi$가 ZF의 공리라면 $\mathsf{ZF} \vdash \phi^L$이다.
정리 1의 의미를 말로 풀어 보자면,
“$L$의 내부에서 보았을 때 $L$은 ZF의 모델이다”를 ZF로 증명할 수 있다.
물론 우리는 $L \subset V$만 알고 $V = L$인지는 알지 못하기 때문에, 어떤 집합 $x$는 $L$에 속하지 않을 수도 있다. 그러나 설령 $x \in V \setminus L$인 집합 $x$가 있더라도, 그러한 $x$의 결여는 $L$의 내적 정합성을 깨뜨리지 않는다는 것이 정리 1의 내용이다.
예를 들어 어떤 집합 $y, z$에 대해 $x = \lbrace y, z \rbrace$가 $L$에 결여되어 있다고 하자. 일면 $x$의 결여는 $L$이 짝 공리 $\mathsf{Pair}$을 만족하지 않음을 시사하는 듯하다.
\[\mathsf{Pair} := \forall y, z \; \exists x \; \forall w: w \in x \leftrightarrow (w = y \lor w = z)\]하지만 $L$의 내부에서 본 짝 공리는 다음과 같다.
\[\mathsf{Pair}^L := \forall y, z \in L \; \exists x \in L \; \forall w \in L: w \in x \leftrightarrow (w = y \lor w = z)\]$\forall y, z$의 양화 또한 $L$로 한정됨에 주목하라. 즉, $x = \lbrace y, z \rbrace$의 결여가 $L$에게 문제를 일으키는 경우는 $y, z \in L$일 때이다. 거꾸로 말해, $x = \lbrace y, z \rbrace \notin L$이 $y, z \notin L$을 시사한다면 $L$은 $\mathsf{Pair}^L$을 만족한다. 이것이 “$L$이 내적 정합성을 유지하는 방식으로 집합을 결여한다”의 의미이다.
정리 1이 성립하는 핵심 이유는 $L$과 $V$가 추이성이라는 성질을 공유하기 때문이다.
보조정리. 다음 술어는 ZF에서 $L$에 대해 절대적이다.
- $x \in y$
- $x \subset y$
- $x = \bigcup y$
- $x = \lbrace y, z \rbrace$
- $\alpha \in \mathrm{Ord}$
- $x$는 추이적이다.
- $\Delta_0$ 논리식
또한 다음을 증명할 수 있다.
정리 2. $\mathsf{ZF} \vdash (V = L)^L$
여기서 $V = L$은, “모든 집합이 $L$에 속한다”를 의미한다. 따라서 일면 보기에 $(V = L)^L$은 “$L$에 속하는 모든 집합이 $L$에 속한다”라는 자명한 명제인 듯하다. 하지만 실제로 $V = L$을 논리식으로 적으면
\[\forall x \; \exists \alpha : \alpha \in \mathrm{Ord} \land x \in L_\alpha\]이므로 $(V = L)^L$은
\[\forall x \in L \; \exists \alpha \in L : (\alpha \in \mathrm{Ord})^L \land (x \in L_\alpha)^L\]이다. 특히, $\alpha \in \mathrm{Ord}$와 $x \in L_\alpha$가 진정한 의미에서의 $\in$-술어가 아닌 1차 논리식의 형식적 표현이기 때문에 마찬가지로 $L$로 상대화해야 함에 유의하라. 이에 따라 $(V = L)^L$을 ZF에서 증명하기 위해서는 $\alpha \in \mathsf{Ord}$와 $x \in L_\alpha$가 절대적임을 증명해야 한다. 두 증명 모두 초한귀납법을 사용하면 가능하다.
정리 1과 정리 2로부터 다음을 증명할 수 있다.
정리 3. $\mathsf{ZFL} \vdash \phi \implies \mathsf{ZF} \vdash \phi^L$
증명. $\mathsf{ZFL} \vdash \phi$의 증명 길이에 대한 귀납법으로 증명한다. 증명 길이가 0일 때 $\phi$는 ZFL의 공리이다. $\phi$가 ZF의 공리일 때 정리 1로부터 증명되고, $\phi$가 $V = L$일 때 정리 2로부터 증명된다.
이제 $\phi$가 $\lbrace \psi_1, \dots, \psi_n \rbrace$에 추론 규칙을 적용하는 것으로 증명된다고 가정하자. $\psi_k$의 증명 길이는 $\phi$보다 작으므로 귀납 가정에 의해 $\mathsf{ZF} \vdash \psi_k^L$이며, 논리 공리와 추론 규칙은 $L$에 대해 절대적임을 쉽게 보일 수 있다. 따라서 $(\psi_1 \land \dots \land \psi_n) \rightarrow \phi$가 논리적 참이라면 $(\psi_1^L \land \dots \land \psi_n^L) → \phi^L$ 또한 논리적 참이며, 이에 따라 $\mathsf{ZF} \vdash \phi^L$이다. ■
정리 3의 따름정리로서 정리 4를 얻는다.
정리 4. ZF가 무모순적이라면 ZFL 또한 무모순적이다.
증명. ZFL이 모순적이라면 $\mathsf{ZFL} \vdash \varnothing \neq \varnothing$이며, 정리 3에 의해 $\mathsf{ZF} \vdash (\varnothing \neq \varnothing)^L \iff \mathsf{ZF} \vdash \varnothing \neq \varnothing$이다.
따라서 V = L은 ZF와 일관적이다.
Consistency of the V = L Axiom
11 Dec 20241. Universe
1.1. Von Neumann Universe
We define $\lbrace V_\alpha \rbrace$ using transfinite recursion.
- $V_0 = \varnothing$
- $V_{\alpha + 1} = V_\alpha \cup \mathcal{P}(V_\alpha)$
- When $\lambda$ is a limit ordinal, $V_\lambda = \bigcup_{\alpha < \lambda} V_\alpha$
The first few $V_\alpha$ are as follows:
- $V_1 = \lbrace \varnothing \rbrace$
- $V_2 = \lbrace \varnothing, \lbrace \varnothing \rbrace \rbrace$
- $V_3 = \lbrace \varnothing, \lbrace \varnothing \rbrace, \lbrace \lbrace \varnothing \rbrace \rbrace, \lbrace \varnothing, \lbrace \lbrace \varnothing\rbrace \rbrace \rbrace$
- $V_\omega = \mathsf{HF}$
The collection of all $V_\alpha$ for every ordinal $\alpha$ is called the Von Neumann universe.
\[V = \bigcup_{\alpha \in \mathrm{Ord}} V_\alpha\]When $x \in y \in z$ implies $x \in z$, we call $z$ a transitive set. This is an important property of $V$.
Theorem.
- For $\alpha \in \mathrm{Ord}$, $V_\alpha$ is transitive.
- $V$ is transitive.
Proof. By transfinite induction.
Accordingly, we can also define $V$ as follows:
- $V_0 = \varnothing$
- $V_{\alpha + 1} = \mathcal{P}(V_\alpha)$
- When $\lambda$ is a limit ordinal, $V_\lambda = \bigcup_{\alpha < \lambda}V_\alpha$
Intuitively, $V$ appears to contain all sets. Indeed, we can prove the following:
Theorem. If $x$ is a set, then $x \in V$.
Proof. For a set $x$, we define the transitive closure $\bar{x}$ of $x$ as the smallest transitive set containing $x$ as an element. Note that this is well-defined as the intersection of transitive sets is transitive.
Assume $x \notin V$. By the axiom of separation, $y = \lbrace u \in \bar{x} : u \notin V \rbrace$ is a set, and by the axiom of foundation, there exists an $\in$-minimal element $z$ of $y$. If there exists $w \in z$ such that $w \notin V$, then by transitivity $w \in y$, contradicting the $\in$-minimality of $z$. Therefore, all elements of $z$ are in $V$, and by the axiom of replacement, $\Omega = \lbrace \alpha \in \mathrm{Ord} \mid \exists w \in z : w \in V_\alpha\rbrace$ is a set. Let $\beta = \bigcup_{\alpha \in \Omega}\alpha$. Then $\beta$ is an ordinal, and $z \in V_{\beta + 1}$. (This is where the definition of von Neumann universe $V_{\beta + 1} = \mathcal{P}(V_\beta)$ is invoked.) This yields a contradiction. ■
Consequently, $V$ is not a set. Therefore, while $V$ is a model of ZFC in the sense that it contains all sets, many mathematicians require models to be sets, so it is not a model in the strict sense. (This explains why our proof that $V$ is a ‘model’ of ZFC does not contradict Gödel’s incompleteness theorems; within ZFC, $V$ is not recognised as a valid set-theoretic object.) However, for convenience, in this article, we shall refer to $V$ as a model of set theory. Moreover, we shall understand $x \in V$ as a formal expression for “$x$ is a set”.
1.2. Gödel Constructible Universe
First, we define constructibility as follows:
Definition. Let $\mathfrak{A}$ be an $\mathcal{L}$-structure and let $A$ be the underlying domain of $\mathfrak{A}$. $u$ is constructible from $\mathfrak{A}$ if there exist some $\mathcal{L}$-formula $\phi(y, x_1, \dots, x_n)$ and $a_1, \dots, a_n \in A$ such that the following holds:
\[y \in u \iff y \in A \land \mathfrak{A} \vDash \phi(y, a_1, \dots, a_n)\]
Sometimes we abuse the notation and say that $u$ is constructible from $A$.
For example, with respect to the standard model of arithmetics, the following constructs $u = \lbrace 1, 2 \rbrace$:
- $\phi(y, x_1, x_2) : (y = x_1) \lor (y = x_2)$
- $a_1 = 1, a_2 = 2$
The following constructs $u = \lbrace 2, 5, 10, 17, \dots \rbrace$:
- $\phi(y, x_1) : \exists z (z \cdot z + x_1 = y)$
- $a_1 = 1$
Gödel’s constructibility differs from constructibility in the general sense, namely expressibility in language. For instance, since the set of real numbers expressible in language is countable, some real numbers cannot be expressed in language. Let such a real number be $r$. With respect to the standard model of real numbers, the following “constructs” $u = \lbrace r \rbrace$:
- $\phi(y, x_1) : x_1 = y$
- $a_1 = r$
That is, Gödel’s constructibility is more versatile than linguistic constructibility in that it allows initialisation of free variables to arbitrary elements. Nonetheless, it is constrained to have only finite number of free variables.
We now define $\lbrace L_\alpha \rbrace$ using transfinite recursion:
- $L_0 = \varnothing$
- $L_{\alpha + 1} = \lbrace x : x \text{ is constructible from } L_\alpha \rbrace$
- When $\lambda$ is a limit ordinal, $L_\lambda = \bigcup_{\alpha < \lambda} L_\alpha$
- $L = \bigcup_{\alpha < \lambda} L_\alpha$
We can easily show that $L_\alpha = V_\alpha$ when $\alpha < \omega$. Specifically, when $\alpha = n$, we can construct $x \in V_\alpha$ with at most $n$ disjunctions. Therefore:
- $L_1 = \lbrace \varnothing \rbrace$
- $L_2 = \lbrace \varnothing, \lbrace \varnothing \rbrace \rbrace$
- $L_3 = \lbrace \varnothing, \lbrace \varnothing \rbrace, \lbrace \lbrace \varnothing \rbrace \rbrace, \lbrace \varnothing, \lbrace \lbrace \varnothing\rbrace \rbrace \rbrace$
- $L_\omega = \mathsf{HF}$
However, $L_{\omega + 1} \subsetneq V_{\omega + 1}$. This is because although $\mathcal{P}(\mathbb{N}) \subset V_{\omega + 1}$ is uncountable, since the set of first-order logical sentences and $L_\omega$ are both countable, $L_{\omega + 1}$ is countable. In general, when $\alpha$ is countable, $L_\alpha$ is countable.
Nevertheless, $L$ shares many properties with $V$. For instance:
Theorem. For $\alpha \in \mathrm{Ord}$, the following hold:
- $L_\alpha$ is transitive. (Therefore $L$ is transitive)
- $\alpha \in L_{\alpha + 1} \setminus L_{\alpha}$
Proof. By transfinite induction.
Note that $L$ is not a set since it contains all ordinals. However, there exists a first-order formula $\mathsf{IsInL}_\alpha(x)$ that expresses $x \in L_\alpha$. The proof is intricate and involves arithmetising propositions using Gödel numbers. (See link) At any rate, this means that we may understand $x \in L$ as a formal expression expressing $\exists \alpha \in \mathrm{Ord} :\mathsf{IsInL}_\alpha(x)$. The two will be co-extensional for models of ZF.
2. Relativisation
2.1. Relativisation of Formulas
Definition. Let $T$ be an $\mathcal{L}$-theory and $\psi$ an $\mathcal{L}$-formula. We define the relativisation $\phi^\psi$, read as the relativisaion of $\phi$ respect to $\psi$, as the formula where all quantifiers in $\phi$ are restricted to satisfy $\psi$.
Using $\mathsf{PA}$ as an example, if $\psi(x) : \exists z(z + z = x)$ and $\phi(x) : \exists z(z \cdot z = x)$, then:
\[\phi^\psi(x) : \exists z (\psi(z) \land z \cdot z = x)\]Semantically, $\phi(x)$ expresses “$x$ is a perfect square” while $\phi^\psi(x)$ expresses “$x$ is a square of an even number”.
When it is clear that what $\psi(x)$ is supposed to express is $x \in S$, then we abuse the notation and write $\phi^S$ instead of $\phi^\psi$. Hence in the case of the previous example, we may write $\phi^E$ instead, where $E$ is the set of even numbers. That is,
\[\phi^E(x) : \exists z \in E (z \cdot z = x)\]To use a bit of metaphoric expression, $\phi^S$ is how $\phi$ is “seen from” $S$.
For example, let $o(x)$ be the first-order formula expressing “$x$ is an ordinal”. Specifically, it is defined as:
\[o(x) : \mathrm{tr}(x) \land \forall y \in x \; \mathrm{tr}(y)\]where $\mathrm{tr}(x) : \forall y \in x \; \forall z \in y (z \in x)$ expresses “$x$ is transitive”. By the abuse of notation, we may write $\phi^{\mathrm{Ord}}$ instead of $\phi^o$. $\phi^{\mathrm{Ord}}$ is how $\phi$ is “seen from” the class of all ordinals. Define:
- $\phi_1 : \forall x \exists y \forall z (z \subset x \rightarrow z \in y)$
- $\phi_2 : \forall x \forall y \exists z (z = x \cup y)$
That is, $\phi_1$ expresses closure under power set operation and $\phi_2$ expresses closure under set union. We have:
- $\mathsf{ZFC} \not\vdash \phi_1^\mathrm{Ord}$
- $\mathsf{ZFC} \vdash \phi_2^\mathrm{Ord}$,
since the set of ordinals is closed under union but not under power set. Put in another way, $\phi_1$ successfully distinguishes the class of all sets — what ZFC tries to describe — and the class of ordinals, while $\phi_2$ cannot. Generalising this observation, for a theory $T$ and a set $A$, the more formulas $\phi$ such that $T \vdash \phi \leftrightarrow \phi^A$, the better $A$ “conforms” to the description of $T$.
This leads us to the following definition.
Definition. For an $\mathcal{L}$-theory $T$ and a set $A$, $\phi$ is said to be absolute with respect to $A$ if for every $\mathcal{L}$-formula $\phi$,
\[T \vdash \forall x_1, \dots, x_n \in A (\phi(x_1, \dots, x_n) \leftrightarrow \phi^A(x_1, \dots, x_n))\]
Note that the definition simply becomes $T \vdash \phi^A$ when $\phi$ has no free variables, and it is given that $T \vdash \phi$.
2.2. $L$-Relativisation
Our goal now is to show that the axioms of ZF are absoulte with respect to $L$. That is:
Theorem 1. If $\phi$ is an axiom of ZF, then $\mathsf{ZF} \vdash \phi^L$.
That is to say,
“When seen from $L$, $L$ is a model of ZF” can be proved in ZF.
Of course, we only know that $L \subset V$ and do not know whether $V = L$, which leaves open the possibility of some set $x$ not belonging to $L$. Yet according to Theorem 1 states is that, even if there exists such a set $x$, its abscence does not break the internal consistency of $L$.
For example, suppose some set $x = \lbrace y, z \rbrace$ is absent from $L$. At first glance, the absence of $x$ seems to suggest that $L$ does not satisfy the pairing axiom $\mathsf{Pair}$:
\[\mathsf{Pair} := \forall y, z \; \exists x \; \forall w: w \in x \leftrightarrow (w = y \lor w = z)\]However, the pairing axiom as viewed from inside $L$ is:
\[\mathsf{Pair}^L := \forall y, z \in L \; \exists x \in L \; \forall w \in L: w \in x \leftrightarrow (w = y \lor w = z)\]Note that the quantification $\forall y, z$ is also restricted to $L$. That is, the absence of $x = \lbrace y, z \rbrace$ causes problems in $L$ only when $y, z \in L$. Conversely, if $x = \lbrace y, z \rbrace \notin L$ implies $y, z \notin L$, then $L$ satisfies $\mathsf{Pair}^L$. This is, $L$ lacks sets only in a way that maintains internal consistency.
Although we do not give the full proof, we highlight that the key reason Theorem 1 holds is that $L$, like $V$, is a transitivie class of sets, which leads to the following lemma.
Lemma. The following predicates are absolute with respect to $L$ in ZF:
- $x \in y$
- $x \subset y$
- $x = \bigcup y$
- $x = \lbrace y, z \rbrace$
- $\alpha \in \mathrm{Ord}$
- $x$ is transitive
- $\Delta_0$ formulas
From this lemma, it is not too difficult to prove Theorem 1. Moreover, we can prove:
Theorem 2. $\mathsf{ZF} \vdash (V = L)^L$
Here, $V = L$ is a formal expression standing for $\forall x (x \in L)$. At first glance it may seem that $(V = L)^L$ is thus the trivial proposition $\forall x \in L (x \in L)$. However, when we actually expand $V = L$ as a first-order formula, we have:
\[\forall x \; \exists \alpha \; (\alpha \in \mathrm{Ord} \land x \in L_\alpha)\]so $(V = L)^L$ becomes:
\[\forall x \in L \; \exists \alpha \in L \; (\alpha \in \mathrm{Ord})^L \land (x \in L_\alpha)^L\]Note particularly that since $\alpha \in \mathrm{Ord}$ and $x \in L_\alpha$ are formal expressions of first-order formulas rather than a genuine $\in$-relation, they must likewise be relativised to $L$. Thus, to prove $(V = L)^L$ in ZF, we must prove that $\alpha \in \mathrm{Ord}$ and $x \in L_\alpha$ are also absolute. The former follows from the previous lemma, and the latter also “almost” follows from the lemma, except that $x \in L_\alpha$ is a $\Sigma_1$-sentence, so slightly more argument is required to secure its absoluteness.
From Theorems 1 and 2, we can prove:
Theorem 3. $\mathsf{ZFL} \vdash \phi \implies \mathsf{ZF} \vdash \phi^L$
Proof. We prove by induction on the proof length of $\mathsf{ZFL} \vdash \phi$. When the proof length is 0, $\phi$ is an axiom of ZFL. When $\phi$ is an axiom of ZF, it follows from Theorem 1, and when $\phi$ is $V = L$, it follows from Theorem 2.
Now assume $\phi$ is proved by applying an inference rule to $\lbrace \psi_1, \dots, \psi_n \rbrace$. The proof length of $\psi_k$ is smaller than that of $\phi$, so by the induction hypothesis $\mathsf{ZF} \vdash \psi_k^L$. We can easily show that logical axioms and inference rules are absolute with respect to $L$. Using modus ponens as an example, this means that:
\[\mathsf{ZF} \vdash ((\phi \land \phi \rightarrow \psi) \rightarrow \psi)^L\]Therefore, if $(\psi_1 \land \dots \land \psi_n) \rightarrow \phi$ is logically valid, then $(\psi_1^L \land \dots \land \psi_n^L) → \phi^L$ is also logically valid, and consequently $\mathsf{ZF} \vdash \phi^L$. ■
As a corollary of Theorem 3, we obtain Theorem 4:
Theorem 4. If ZF is consistent, then ZFL is also consistent.
Proof. If ZFL is inconsistent, then $\mathsf{ZFL} \vdash \varnothing \neq \varnothing$, and by Theorem 3, $\mathsf{ZF} \vdash (\varnothing \neq \varnothing)^L \iff \mathsf{ZF} \vdash \varnothing \neq \varnothing$, which contradicts the consistency of ZF. ■
Therefore, V = L is consistent with ZF.
초한귀납과 초한재귀
05 Dec 20241. 초한귀납법
정리. $P$가 서수 위에서 정의된 속성이고 임의의 $\alpha \in \mathrm{Ord}$에 대해
\[[ \forall \beta < \alpha : P(\beta)] → P(\alpha)\]가 성립할 때, $P$는 모든 서수에 대해 참이다.
Remark. $P$의 정의역인 $\mathrm{Ord}$는 집합이 아닌 진모임proper class이므로 “술어” 대신 “속성”이란 표현을 사용한다.
증명. 서수가 정렬 순서라는 사실과 귀류법을 사용한다.
$\lnot P(\lambda)$인 $\lambda$가 존재한다고 하자. $\Omega = \lbrace \alpha \in \lambda : \lnot P(\alpha) \rbrace$는 공집합이 아닌 정렬 집합이므로 최소 원소 $\alpha_0$가 존재한다. 이때 $\forall \beta < \alpha_0 : P(\beta)$이므로 가정에 의해 $P(\alpha_0)$가 되어 모순이다. ■
응용. 폰 노인만 계층에서 $V_\alpha$는 추이적이다. 따라서 $V_{\alpha + 1} = V_\alpha \cup \mathcal{P}(V_\alpha)$ 대신 $V_{\alpha + 1} = \mathcal{P}(V_\alpha)$로 정의할 수 있다.
2. 초한재귀적 정의
Motivation. 자연수의 재귀적 정의를 생각해 보자. $n$개의 집합 $x_1, \dots , x_n$이 주어졌을 때 집합을 출력하는 함수 $g$가 존재한다면 다음과 같이 $f: \mathbb{N} → V$을 정의할 수 있을 것이다.
\[f(n) = g(f(0), \dots, f(n - 1))\]문제는 $g$가 고정된 수의 매개변수만을 가질 수 있다는 것이다. 따라서 다음과 같이 $g$의 매개변수를 순서쌍으로 묶는다.
\[f(n) = g(\langle f(0), \dots, f(n - 1) \rangle)\]이 순서쌍은 $\lbrace (0, f(0)), \dots, (n - 1, f(n - 1)) \rbrace = f \upharpoonright n$과 같이 표현할 수 있다. 즉,
\[f(n) = g(f \upharpoonright n).\]이를 서수에 대해서 일반화하면 다음과 같다.
정리. $G: V → V$가 모임함수(class function)이라고 하자. 다음을 만족하는 모임함수 $F: \mathrm{Ord} → V$가 존재한다.
\[F(\alpha) = G(F \upharpoonright \alpha)\]
증명. 초한귀납법을 겁나게 쓰면 된다. (불친절해서 ㅈㅅ)
Transfinite Induction and Transfinite Recursion
05 Dec 20241. Transfinite Induction
Theorem. Let $P$ be a property defined on ordinals, and suppose that for any $\alpha \in \mathrm{Ord}$,
\[[ \forall \beta < \alpha : P(\beta)] → P(\alpha).\]Then $P$ is true for all ordinals.
Remark. Since $\mathrm{Ord}$, the domain of $P$, is a proper class rather than a set, we use the term “property” instead of “predicate”.
Proof. Suppose there exists $\lambda$ such that $\lnot P(\lambda)$. Then $\Omega = \lbrace \alpha \in \lambda : \lnot P(\alpha) \rbrace$ is a non-empty well-ordered set, so it has a minimal element $\alpha_0$. Since $\forall \beta < \alpha_0 : P(\beta)$, by hypothesis we have $P(\alpha_0)$, which is a contradiction. ■
Application. Show that the von Neumann hierarchy may be defined as $V_{\alpha + 1} = \mathcal{P}(V_\alpha)$ instead of $V_{\alpha + 1} = V_\alpha \cup \mathcal{P}(V_\alpha)$.
2. Transfinite Recursive Definition
Motivation. Consider recursive definitions on natural numbers. Given $n$ sets $x_1, \dots , x_n$ and a function $g$ that outputs a set, we would like to define $f: \mathbb{N} → V$ as follows:
\[f(n) = g(f(0), \dots, f(n - 1))\]The problem is that $g$ can only take a fixed number of parameters. Therefore, we group the parameters of $g$ into an ordered pair:
\[f(n) = g(\langle f(0), \dots, f(n - 1) \rangle)\]This ordered pair can be represented as $\lbrace (0, f(0)), \dots, (n - 1, f(n - 1)) \rbrace = f \upharpoonright n$. That is,
\[f(n) = g(f \upharpoonright n).\]Generalising this to ordinals, we obtain the following:
Theorem. Let $G: V → V$ be a class function. There exists a class function $F: \mathrm{Ord} → V$ satisfying
\[F(\alpha) = G(F \upharpoonright \alpha)\]
Proof. Apply transfinite induction extensively. (Sorry for the brevity, lol.) It is worth remarking that the proof does not depend on the axiom of choice, for the well-orderedness of ordinals is provable from ZF. Note, however, that the proof that every well-ordered set is order isomorophic to an ordinal does require AC.
콤팩트성과 그물
01 Dec 2024콤팩트성
정의. $X$가 위상공간이라고 하자.
- 임의의 열린 덮개가 유한한 부분덮개를 가질 때 $X$를 콤팩트하다고 한다.
- 임의의 점렬 $\lbrace x_n \in X \rbrace$가 수렴하는 부분점렬을 가질 때 $X$를 점렬 콤팩트sequentially compact하다고 한다.
- 임의의 무한집합 $S \subset X$가 극점을 가질 때 $X$를 극점 콤팩트limit point compact하다고 한다.
정리.
- 콤팩트 $\rightarrow$ 극점 콤팩트
- 점렬 콤팩트 $\rightarrow$ 극점 콤팩트
- 극점 콤팩트 $\not\rightarrow$ 콤팩트
- 극점 콤팩트 $\not\rightarrow$ 점렬 콤팩트
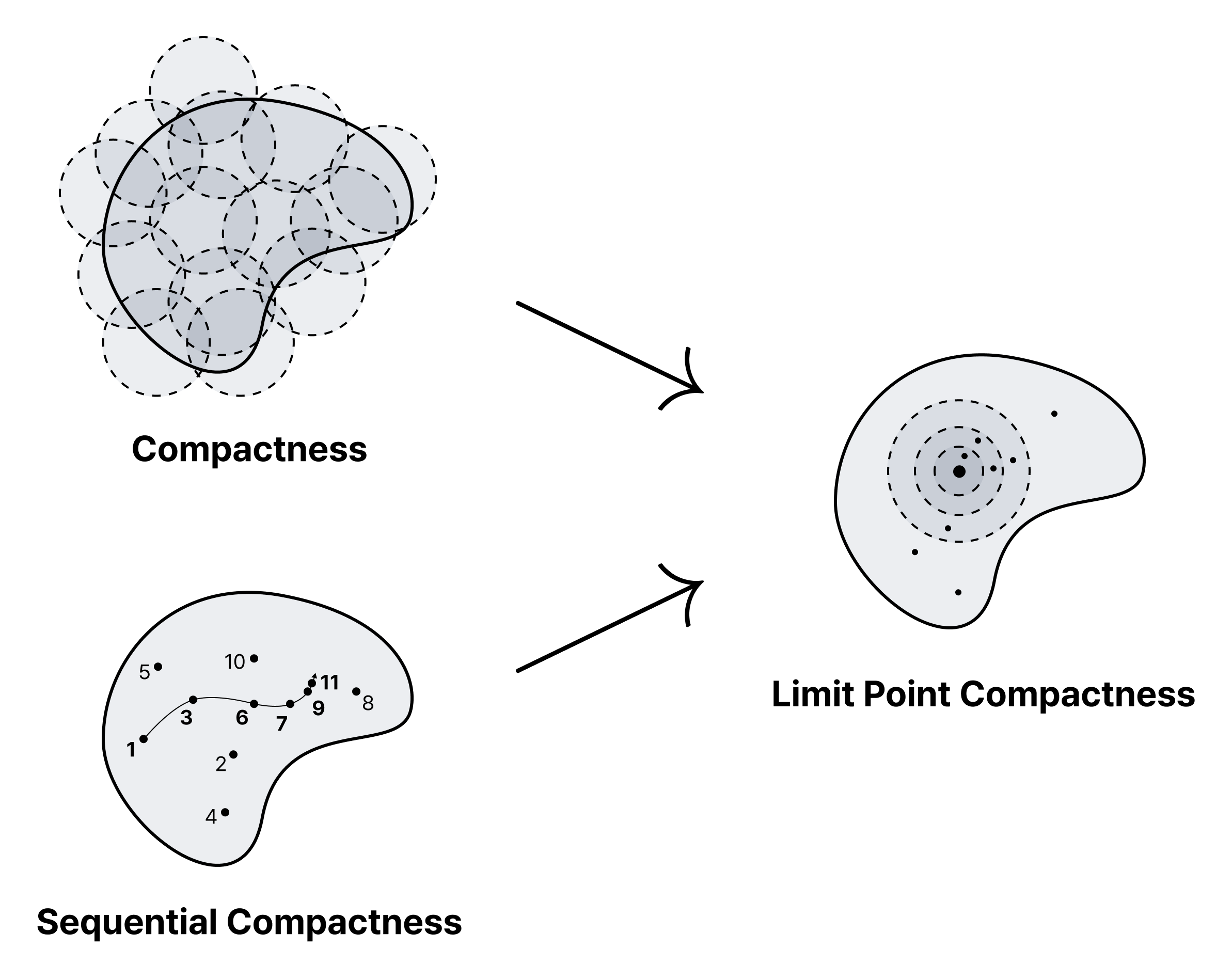
증명.
- $S \subset X$가 극점이 없는 무한집합이라고 하자. $\overline{S} = S \cup S’ = S$이므로 $S$는 닫힌 집합이며, $X \setminus S$는 열린 집합이다. 임의의 $s \in S$에 대해, $s$가 극점이 아니므로 $U_s \cap S = \lbrace s \rbrace$인 $s$의 근방 $U_s$가 존재한다. 따라서 다음 $X$의 열린 덮개는 유한한 부분덮개를 가지지 않는다.
- $S \subset X$가 무한집합이라고 하자. $S$의 원소들을 임의로 추출하여 점렬 $\lbrace s_n \rbrace \;(n \neq m \implies s_n \neq s_m)$을 만든다. $X$가 점렬 콤팩트하므로 $\lbrace s_n \rbrace → s$이며, $s$는 $S$의 극점이다.
- 순서 토폴로지가 주어진 $\omega_1$은 극점 콤팩트하지만 콤팩트하지 않다.
- $X = \mathbb{N} \times \lbrace 0, 1 \rbrace$, $\mathbb{N}$에는 이산 토폴로지가 주어지고 $\lbrace 0, 1\rbrace$에는 자명한 토폴로지가 주어짐.
Remark. 4의 올바르지 못한 “증명”
$X$가 극점 콤팩트하다고 하자. 점렬 $(x_n)$이 주어졌을 때, $S = \lbrace x_n : n \in \mathbb{N}\rbrace$이 유한집합이라면 $(x_n)$은 수렴하는 부분점렬을 자명하게 가진다. $S$가 무한집합이라면 $X$의 극점 콤팩트성에 의해 $x \in S’$가 존재한다. 이제 다음 조건을 만족하는 $x$의 근방들의 가산 모임 $\mathcal{U} = \lbrace U_n \rbrace$을 정의한다.
- $n < m \implies U_n \supset U_m$
- $V$가 $x$의 근방일 때, $\exists U \in \mathcal{U} : U \subset V$
이로부터 다음 조건을 만족하는 함수 $k: \mathbb{N} → \mathbb{N}$을 정의할 수 있다.
- $x_{k(n)} \in U_n$
- $n < m \implies k(n) < k(m)$
- $n \neq m \implies x_{k(n)} \neq x_{k(m)}$
2가 가능한 이유는 $k(i)$가 $i \leq n$까지 정의되었을 때 $T = S \setminus \lbrace x_i : i \leq k(n) \rbrace$가 여전히 $x$를 극점으로 가지기 때문이다. 즉, $(x_n)$은 수렴하는 부분점렬 $(x_{k(n)})$을 가진다.
위 증명이 올바르지 않은 이유는 볼드체 부분이 일반적으로 가능하지 않기 때문이다. 대신 다음이 성립한다.
정리. 1차 가산 $T_1$ 공간에서 극점 콤팩트성과 점렬 콤팩트성은 동치이다.
$T_1$은 조건 3을 일반적으로 성립시키는 데 필요하다.
그물과 점렬
정의. $(J, \leq)$가 원순서preorder라고 하자. 임의의 $x, y \in J$에 대해 $x, y \leq z$인 $z \in J$가 존재한다면 $(J, \leq)$를 방향 집합directed set이라고 한다.
정의. $K$가 $(J, \leq)$의 부분집합이라고 하자. 임의의 $x \in J$에 대해 $x \leq y$인 $y \in K$가 존재한다면 $K$를 공종cofinal이라고 한다.
Remark 1. $(J, \leq)$가 방향 집합이면 $J$는 $J$에서 자명하게 공종이다. 한편 $K \subset J$가 공종이라면 $(K, \leq)$ 또한 방향 집합이다.
Remark 2. 이후 드러나듯이, 방향성은 수렴의 일반화와 관련되는 조건이다.
정의. $(J, \leq)$가 방향 집합이라고 하자. 위상공간 $X$에 대해 $J$에서 $X$로 가는 함수 $f: J → X$를 그물net이라고 한다. 특히, $\alpha \in J$에 대해 $f(\alpha)$를 $x_\alpha$와 같이 표기한다.
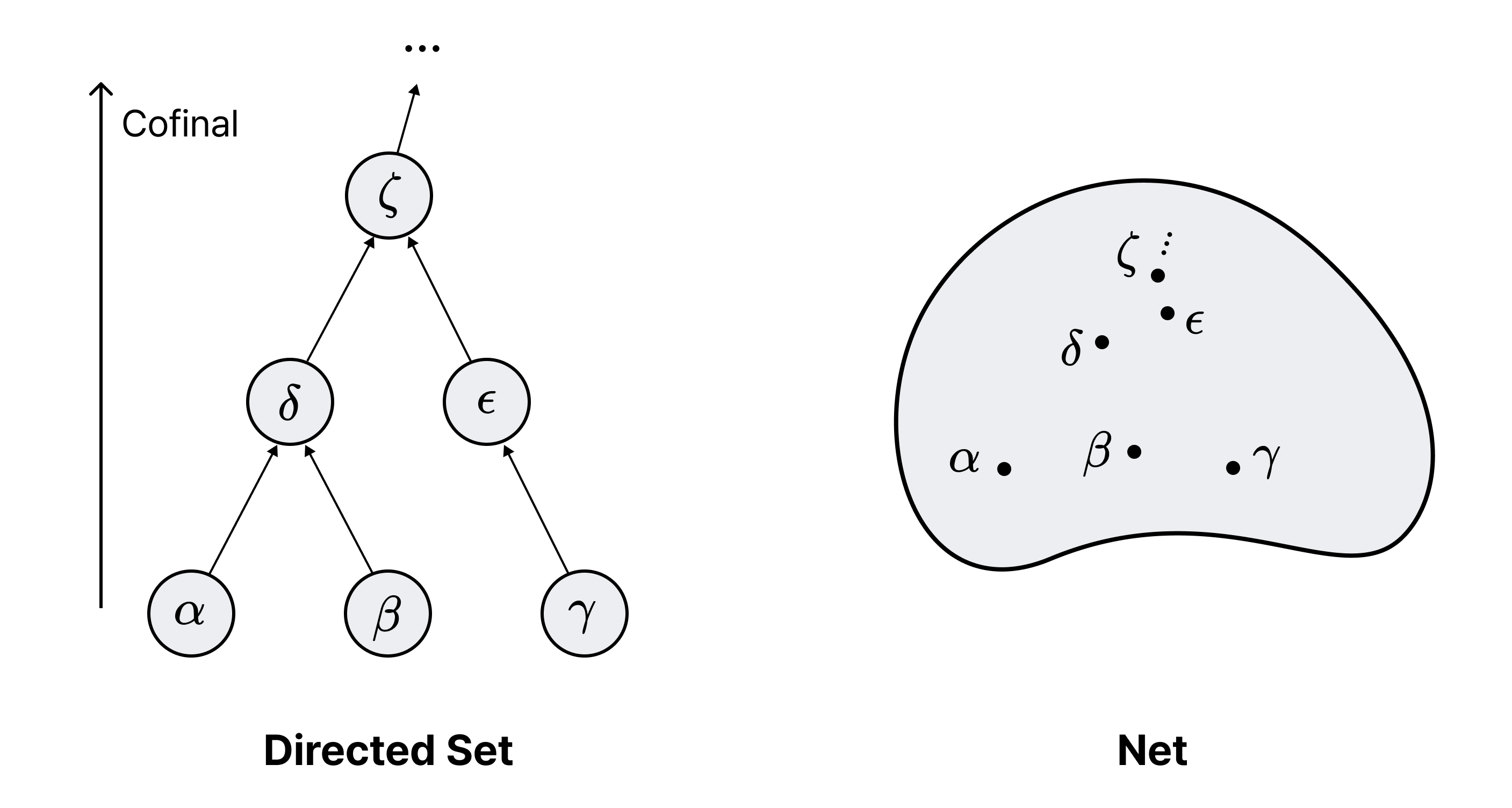
정의. 그물 $(x_\alpha)$가 $x$로 수렴한다는 것은, 임의의 $x$의 근방 $U$에 대해 어떤 $\alpha \in J$가 존재하여
\[\alpha \leq \beta \implies x_\beta \in U\]인 것이다.
방향성에 의해, 특정한 $\alpha \in J$에 대해 $\alpha \leq \beta$인 $\beta$들만 고려해도 $\mathrm{im} f$ 전체를 포섭할 수 있음을 유의하라. 즉, 임의의 $x_\gamma$에 대해 $\alpha, \gamma \leq \beta$인 $\beta$가 존재한다. 달리 말해, 그물이 $x$로 수렴한다는 것은 임의의 $x$의 근방 $U$가 주어졌을 때, 그물의 어느 원소에서 시작하든 간에 위로 충분히 올라가다 보면 어느 지점부터 이후의 모든 원소가 $U$에 속한다는 것이다.
일반 위상 공간에서의 그물의 수렴은 1차 가산 공간에서 점렬의 수렴과 대응된다. 즉,
정리. $X$가 1차 가산 공간이라고 하자.
- $A \subset X$에 대해, $x \in \bar{A}$일 필요충분조건은 $x$로 수렴하는 점렬 $(x_n)$이 존재하는 것이다.
- $f: X → Y$에 대해, $f$가 연속일 필요충분조건은 임의의 점렬 $(x_n)$에 대해 $x_n → x$라면 $f(x_n) → f(x)$인 것이다.
정리. $X$가 위상 공간이라고 하자.
- $A \subset X$에 대해, $x \in \bar{A}$일 필요충분조건은 $x$로 수렴하는 그물 $(x_\alpha)$가 존재하는 것이다.
- $f: X → Y$에 대해, $f$가 연속일 필요충분조건은 임의의 그물 $(x_\alpha)$에 대해 $x_\alpha → x$라면 $f(x_\alpha) → f(x)$인 것이다.
증명.
- $\mathcal{U}_x$를 $x$의 근방들의 집합이라고 하자. 역포함관계로 $\mathcal{U}_x$에 순서 $\leq$를 준다. $x \in \bar{A}$라면 임의의 $U_\alpha \in \mathcal{U}_x$에 대해 $x_\alpha \in U_\alpha \cap A, x_\alpha \neq x$인 $x_\alpha$가 존재한다. $x_\alpha → x$임을 확인하라.
정의. $(x_\alpha)_{\alpha \in J}$가 그물이라고 하자. $(I, \preceq)$가 방향 집합이고, $g: (I, \preceq) → (J, \leq)$가 순서 보존이며, $\operatorname{im}g$가 공종일 때, $(x_{g(\beta)})_{\beta \in I}$를 $(x_\alpha)$의 부분그물이라고 한다.
정리. $X$가 콤팩트할 필요충분조건은 임의의 그물이 수렴하는 부분그물을 가지는 것이다.
Remark. ”수렴하는 점렬이 존재한다“는 ”수렴하는 그물이 존재한다“보다 강한 조건이지만, ”임의의 점렬이 수렴하는 부분점렬을 가진다”는 “임의의 그물이 수렴하는 부분그물을 가진다”보다 강하지도, 약하지도 않은 조건임에 유의하라. 주어는 후자가 더 강하고, 술어는 전자가 더 강하다. 따라서 콤팩트성과 점렬 콤팩트성은 일반적으로 시사 관계가 없다. 구체적으로,
정리.
- 콤팩트 $\not\rightarrow$ 점렬 콤팩트
- 점렬 콤팩트 $\not\rightarrow$ 콤팩트
증명.
- $[0, 1]^{[0, 1]}$은 티호노프 정리에 의해 콤팩트하지만 점렬 콤팩트하지 않다.
- Long line과 $\omega_1$은 점렬 콤팩트하지만 콤팩트하지 않다.
Compactness and Nets
01 Dec 2024Compactness
Definition. Let $X$ be a topological space.
- $X$ is said to be compact if every open cover has a finite subcover.
- $X$ is said to be sequentially compact if every sequence $\lbrace x_n \in X \rbrace$ has a convergent subsequence.
- $X$ is said to be limit point compact if every infinite set $S \subset X$ has a limit point.
Theorem.
- Compact $\rightarrow$ Limit point compact
- Sequentially compact $\rightarrow$ Limit point compact
- Limit point compact $\not\rightarrow$ Compact
- Limit point compact $\not\rightarrow$ Sequentially compact

Proof.
- Let $S \subset X$ be an infinite set with no limit points. Since $\overline{S} = S \cup S’ = S$, $S$ is a closed set and $X \setminus S$ is an open set. For any $s \in S$, since $s$ is not a limit point, there exists a neighbourhood $U_s$ of $s$ such that $U_s \cap S = \lbrace s \rbrace$. Therefore, the following open cover of $X$ has no finite subcover:
- Let $S \subset X$ be an infinite set. Arbitrarily extract elements of $S$ to form a sequence $\lbrace s_n \rbrace \;(n \neq m \implies s_n \neq s_m)$. Since $X$ is sequentially compact, $\lbrace s_n \rbrace → s$, and $s$ is a limit point of $S$.
- $\omega_1$ with the order topology is limit point compact but not compact.
- $X = \mathbb{N} \times \lbrace 0, 1 \rbrace$, where $\mathbb{N}$ is given the discrete topology and $\lbrace 0, 1\rbrace$ is given the trivial topology.
Remark. An incorrect “proof” of 4
Suppose $X$ is limit point compact. Given a sequence $(x_n)$, if $S = \lbrace x_n : n \in \mathbb{N}\rbrace$ is a finite set, then $(x_n)$ trivially has a convergent subsequence. If $S$ is an infinite set, then by the limit point compactness of $X$, there exists $x \in S’$. Now we define a countable collection of neighbourhoods of $x$, $\mathcal{U} = \lbrace U_n \rbrace$, satisfying the following conditions:
- $n < m \implies U_n \supset U_m$
- For any neighbourhood $V$ of $x$, $\exists U \in \mathcal{U} : U \subset V$
From this, we can define a function $k: \mathbb{N} → \mathbb{N}$ satisfying the following conditions:
- $x_{k(n)} \in U_n$
- $n < m \implies k(n) < k(m)$
- $n \neq m \implies x_{k(n)} \neq x_{k(m)}$
Condition 2 is possible because when $k(i)$ is defined for $i \leq n$, $T = S \setminus \lbrace x_i : i \leq k(n) \rbrace$ still has $x$ as a limit point. Thus, $(x_n)$ has a convergent subsequence $(x_{k(n)})$.
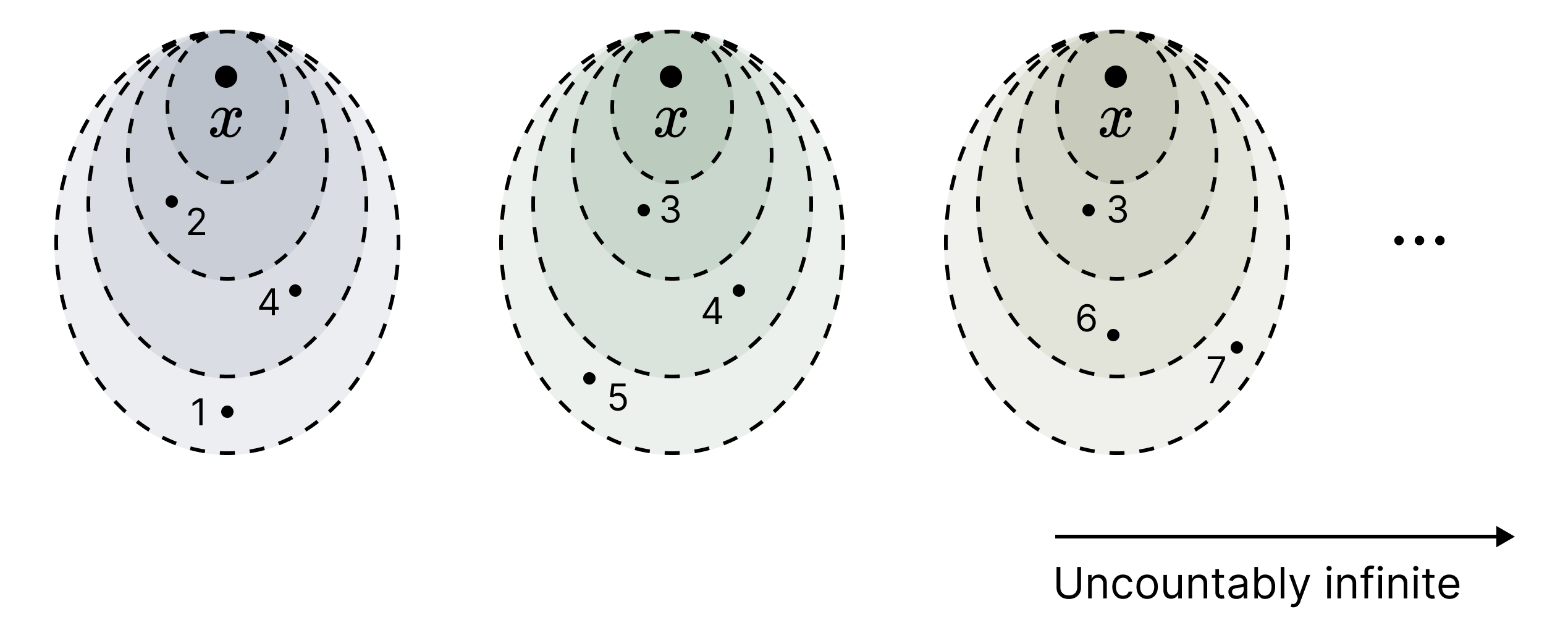
The above proof is incorrect because the bold portion is not generally possible. Consider, for instance, a topological space where $x \in S’$ has uncountably many neighbourhoods which form uncountably infinite distinct classes of containment chain. Hence, in the diagram below, the same-coloured sets contain one or the other properly, but distinct-coloured sets do not, although they need not be strictly disjoint either. Such a space may be limit point compact yet not be sequentially compact, for there is no guaranteed way to enumerate the points of $S$ into a series such that whichever open set one chooses, for a large enough index, all points after that index is included in that open set. (Exercise: Convince yourself that this is not the case if the open sets can be arranged to form only finite distinct classes of chain, or countably infinite distinct classes of chain.)
Instead, the following holds:
Theorem. In first countable $T_1$ spaces, limit point compactness and sequential compactness are equivalent.
Note that $T_1$-ness is also required, for without it Condition 3 cannot be guaranteed.
Nets and Sequences
Definition. Let $(J, \leq)$ be a preorder. If for any $x, y \in J$, there exists $z \in J$ such that $x, y \leq z$, then $(J, \leq)$ is called a directed set.
Definition. Let $K$ be a subset of $(J, \leq)$. If for any $x \in J$, there exists $y \in K$ such that $x \leq y$, then $K$ is said to be cofinal.
Remark 1. If $(J, \leq)$ is a directed set and $K \subset J$ is cofinal, then $(K, \leq)$ is also a directed set.
Remark 2. As will be shown, cofinality is related with the generalisation of convergence.
Definition. Let $(J, \leq)$ be a directed set. For a topological space $X$, a function $f: J → X$ is called a net. In particular, for $\alpha \in J$, we denote $f(\alpha)$ as $x_\alpha$.

Definition. A net $(x_\alpha)$ converges to $x$ if, for any neighbourhood $U$ of $x$, there exists some $\alpha \in J$ such that
\[\alpha \leq \beta \implies x_\beta \in U\]
The convergence of nets in general topological spaces corresponds to the convergence of sequences in first countable spaces. That is,
Theorem. Let $X$ be a first countable space.
- For $A \subset X$, $x \in \bar{A}$ if and only if there exists a sequence $(x_n)$ converging to $x$.
- For $f: X → Y$, $f$ is continuous if and only if for any sequence $(x_n)$, if $x_n → x$ then $f(x_n) → f(x)$.
Theorem. Let $X$ be a topological space.
- For $A \subset X$, $x \in \bar{A}$ if and only if there exists a net $(x_\alpha)$ converging to $x$.
- For $f: X → Y$, $f$ is continuous if and only if for any net $(x_\alpha)$, if $x_\alpha → x$ then $f(x_\alpha) → f(x)$.
Proof.
- Let $\mathcal{U}_x$ be the set of neighbourhoods of $x$. Give $\mathcal{U}_x$ the order $\leq$ by reverse inclusion. If $x \in \bar{A}$, then for any $U_\alpha \in \mathcal{U}_x$, there exists $x_\alpha \in U_\alpha \cap A, x_\alpha \neq x$. Verify that $x_\alpha → x$.
Definition. Let $(x_\alpha)_{\alpha \in J}$ be a net. If $(I, \preceq)$ is a directed set, $g: (I, \preceq) → (J, \leq)$ is order-preserving, and $\operatorname{im}g$ is cofinal, then $(x_{g(\beta)})_{\beta \in I}$ is called a subnet of $(x_\alpha)$.
Theorem. $X$ is compact if and only if every net has a convergent subnet.
Remark. Note that “there exists a convergent sequence” is a stronger condition than “there exists a convergent net”, but “every sequence has a convergent subsequence” is neither stronger nor weaker than “every net has a convergent subnet”. The subject (for every sequence v. for every net) is stronger in the latter case, while the predicate (there exists a subsequence v. there exists a subnet) is stronger in the former case. Therefore, compactness and sequential compactness have no implication relation in general. Specifically,
Theorem.
- Compact $\not\rightarrow$ Sequentially compact
- Sequentially compact $\not\rightarrow$ Compact
Proof.
- $[0, 1]^{[0, 1]}$ is compact by Tychonoff’s theorem but not sequentially compact.
- The long line and $\omega_1$ are sequentially compact but not compact.
베르 범주 정리
01 Dec 20241. 베르 공간
정리. $S$가 위상공간 $X$의 부분집합일 때, 다음은 동치이다.
- $\left( \operatorname{cl}S \right)^\circ$가 공집합이다.
- $(\operatorname{cl}S)^c$가 조밀하다.
- $S$는 어떠한 $X$의 열린 집합에서도 조밀하지 않다.
이때, $S$를 희박(rare)하다고 한다.
정의. 희박한 닫힌 집합들의 가산 합집합 $\bigcup F_n$이 희박한 공간 $X$를 베르 공간이라고 한다.
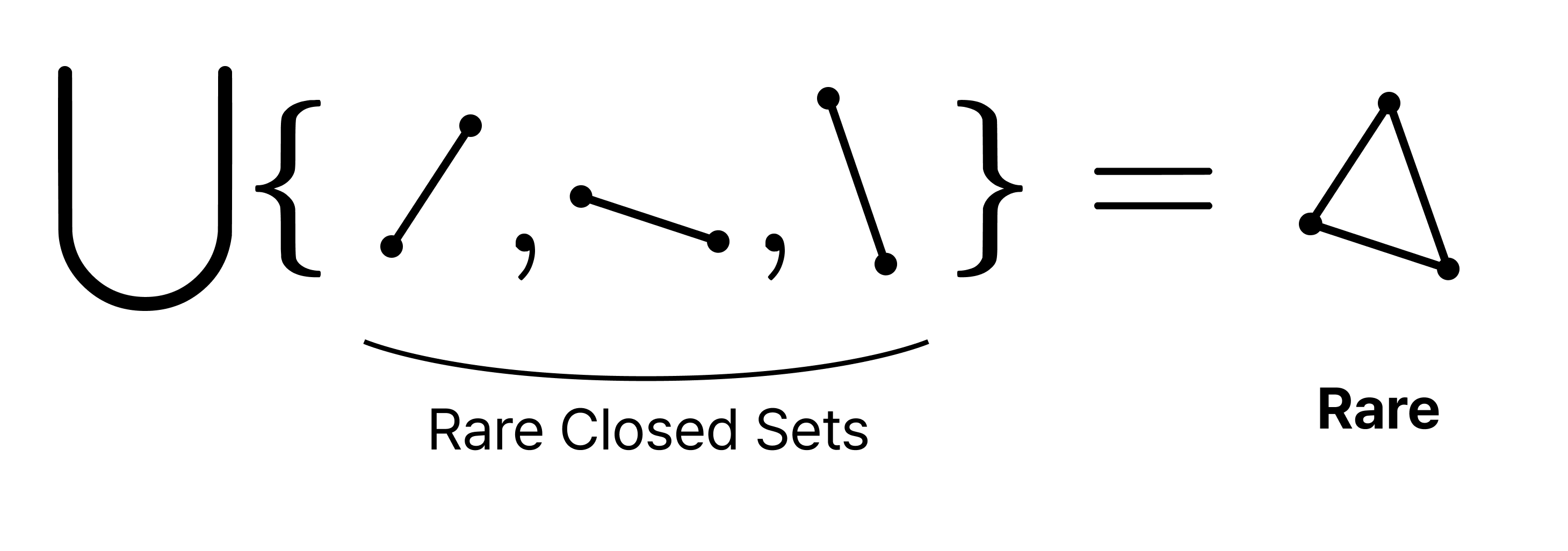
Remark. $X$가 베르 공간이다 iff $X$의 열린 조밀 집합들의 가산 교집합은 조밀하다.
예시. $\mathbb{Q}$는 베르 공간이 아니다.
- $\lbrace q \rbrace$는 닫힌 희박 집합이지만 $\bigcup_{q \in \mathbb{Q}} \lbrace q\rbrace = \mathbb{Q}$는 희박하지 않다.
- $\mathbb{Q} \setminus \lbrace q \rbrace$는 열린 조밀 집합이지만 $\bigcap_{q \in \mathbb{Q}} \left( \mathbb{Q} \setminus \lbrace q \rbrace \right) = \varnothing$은 조밀하지 않다.
2. 베르 범주 정리
콤팩트 공간에서의 칸토어 축소 정리. 다음은 동치이다.
- $X$가 콤팩트하다.
- 임의의 유한 교집합 속성을 가진 닫힌 집합들의 모임 $\mathcal{C}$에 대해 $\bigcap_{C \in \mathcal{C}} C \neq \varnothing$이다.
완비 거리 공간에서의 칸토어 축소 정리. 다음은 동치이다.
- $X$가 완비 거리 공간이다.
- 임의의 공집합이 없는 닫힌 집합열 $C_1 \supset C_2 \supset \cdots$에 대해 $\bigcap C_n \neq \varnothing$이며, 특히 $\operatorname{diam}C_n \to 0$일 때 $\bigcap C_n$은 홑원소 집합이다.
Remark. 2는 4를 함의한다. 이로부터 콤팩트 거리 공간은 완비임을 보일 수 있다. 역은 성립하지 않는다.
정리. 완비 거리 공간과 콤팩트 하우스도르프 공간은 베르 공간이다.
증명.
$X$가 완비 거리 공간 또는 콤팩트 하우스도르프 공간이라고 하자. 희박한 닫힌 집합들의 가산 모임 $\lbrace F_n \rbrace$이 주어졌을 때, 임의의 열린 집합 $U$에 대해 $U \not\subset \bigcup F_n$임을 보이면 된다. 이를 위해 $\forall n : x \not\in F_n$인 $x \in U$를 찾을 것이다.
$F_1$이 희박하므로 $x_1 \in U \setminus F_1$이 존재한다. $X$는 정칙 공간이므로 $x_1 \in U_1$, $\overline{U_1} \cap F_1 = \varnothing$인 열린 집합 $U_1$이 존재한다. 귀납적으로 다음과 같이 정의할 수 있다.
- $x_n \in U_n \setminus F_n$
- $U_n \subset U_{n - 1}$
- $\overline{U_n} \cap F_n = \varnothing$

칸토어 축소 정리에 의해 $x \in \bigcap \overline{U_n}$인 $x$가 존재한다.
3. 베르 범주 정리의 응용
연속함수열의 수렴은 거의 연속이다. $\lbrace f_n : X → (Y, d) \rbrace$가 $f$로 수렴하는 연속함수열일 때,
\[S = \lbrace x \in X : f\text{ is continuous at } x \rbrace\]는 $X$에서 조밀하다.
KAIST POW2024-20. $f$가 연속함수이고,
\[\forall x \geq 0 : \lim_{n \to \infty} f(nx) = 0\]라면 $\lim_{x \to \infty} f(x) = 0$이다.
병리적 함수의 존재성. $h : [0, 1] → \mathbb{R}$가 연속함수라고 하자. 임의의 $ε > 0$에 대해 다음을 만족하는 함수 $g : [0,1] → \mathbb{R}$가 존재한다.
- $\lVert h − g\rVert < ε$이다.
- $g$는 전 구간에서 연속이다.
- $g$는 전 구간에서 미분 불가능하다.