유리수와 실수의 집합론적 정의

20 Nov 2024

1. 칸토어의 동형성 정리

칸토어의 동형성 정리. 가산이고 양끝점이 없으며 조밀한 전순서 집합은 순서 동형에 대해 유일하다.

증명 1. (Back-and-Forth Argument)

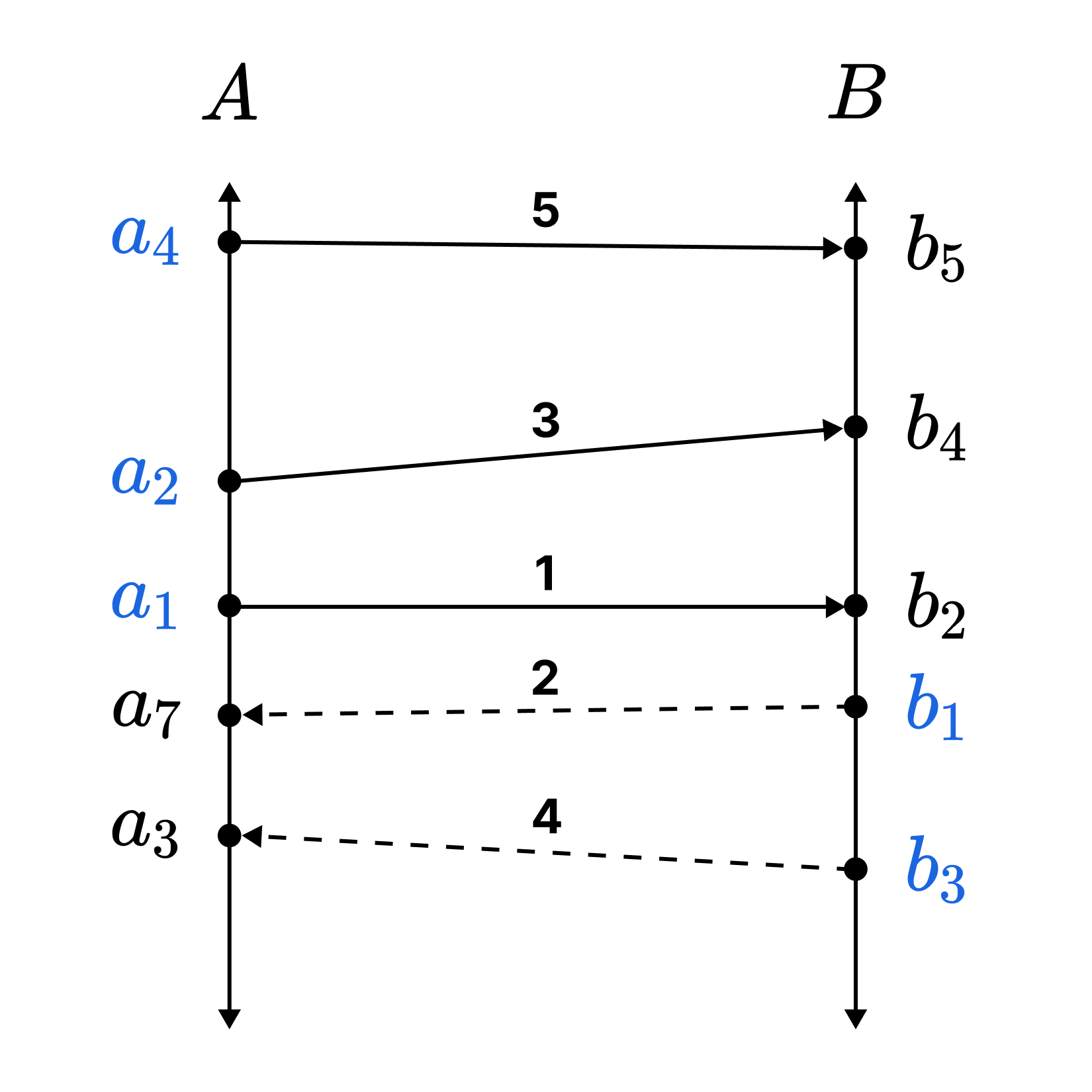
$n$번째 단계에서 $\mathrm{argmin}_k a_k \in A \setminus \mathrm{dom} f_n$을 순서 동형성을 만족하게끔 $b \in B \setminus \mathrm{im} f_n$과 대응시키고, $\mathrm{argmin}_{l}b_l \in B \setminus (\mathrm{im} f_n \cup \lbrace b \rbrace)$ 을 순서 동형성을 만족하게끔 임의의 $a \in A \setminus (\mathrm{dom}f_n \cup \lbrace a_k\rbrace)$ 와 대응시킨다.

증명 2. (Only-Forth Argument)

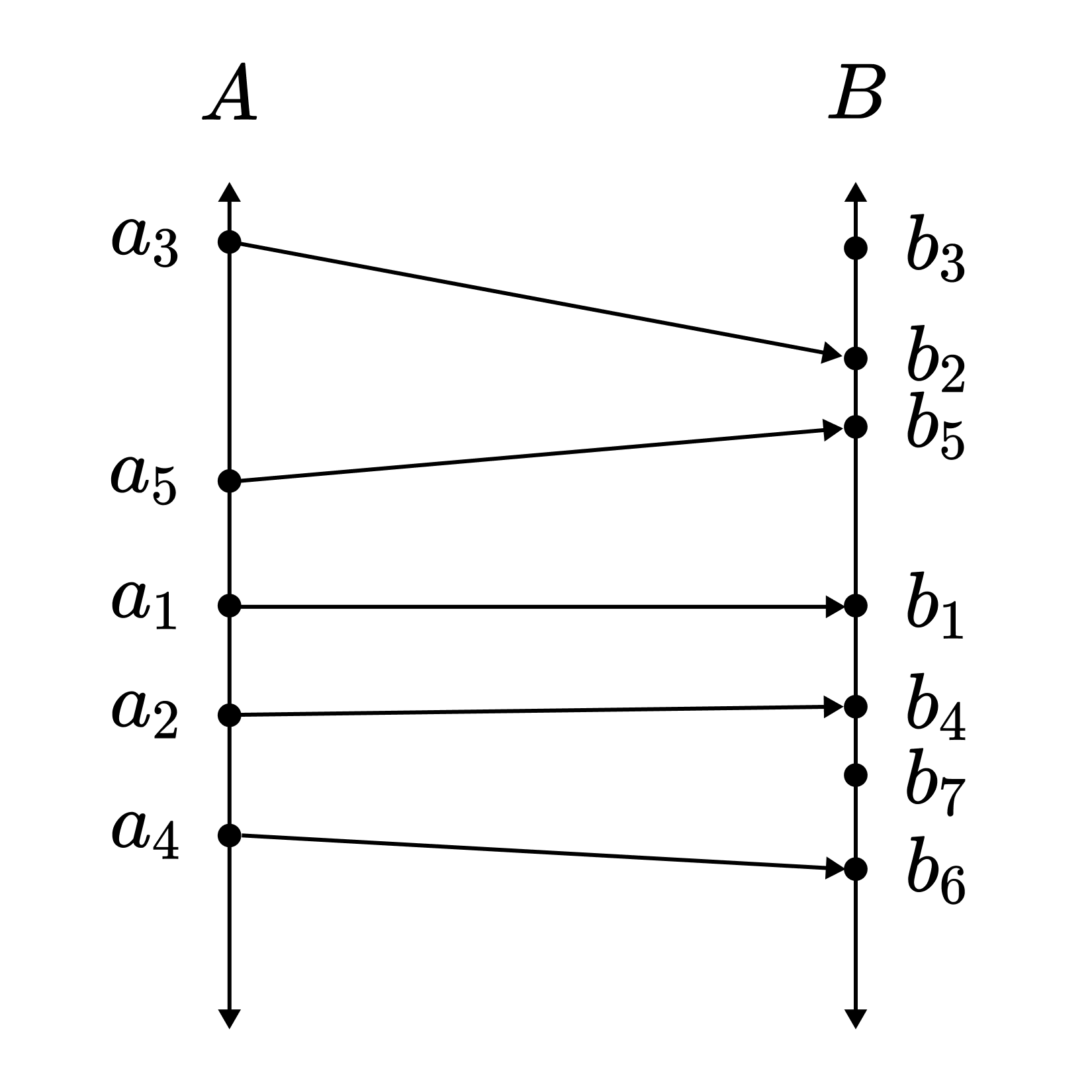
$n$ 번째 단계에서 $\mathrm{argmin}_k a_k \in A \setminus \mathrm{dom} f_n$을 순서 동형성을 만족하게끔 $b \in B \setminus \mathrm{im}f_n$ 중에서 가장 인덱스가 작은 $b_l$과 대응시킨다.

잘못된 증명. (Incorrect Only-Forth Argument)

$n$번째 단계에서 $\mathrm{argmin}_k a_k \in A \setminus \mathrm{dom} f_n$을 순서 동형성을 만족하게끔 임의의 $b \in B \setminus \mathrm{im}f_n$와 대응시킨다.

잘못된 이유: $\mathrm{im} \left[ \bigcup f_n \right]$이 $B$ 전체를 소진한다는 보장이 없다. 일례로 모든 경우 선택된 $b$의 인덱스가 짝수인 경우가 가능하다.

2. 데데킨트 절단

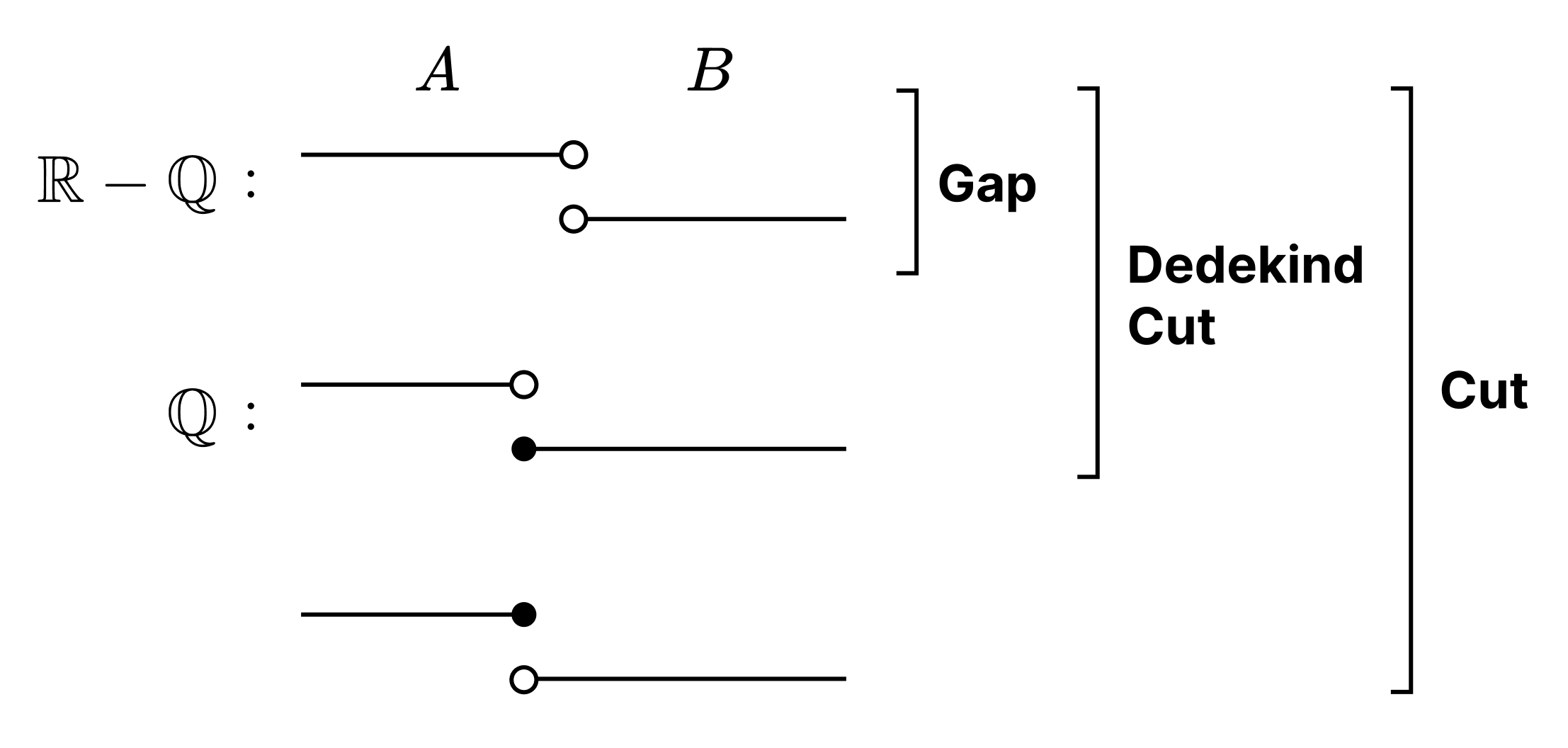
정의. 전순서 집합 $(P, <)$에 대하여 $P$의 부분집합 $A, B$가 다음을 만족할 때 $(A, B)$를 절단이라고 한다.

1. $A \sqcup B = P$
2. 임의의 $a \in A, b \in B$에 대해 $a < b$이다.

추가로 다음을 만족할 때 데데킨트 절단이라고 한다.

1. $A$는 최대 원소를 가지지 않는다.

추가로 다음까지 만족할 때 틈이라고 한다.

1. $B$는 최소 원소를 가지지 않는다.

Remark 1. $P$가 완비이다 ⇔ $P$는 틈을 가지지 않는다. Remark 2. $P = \mathbb{Q}$일 때 틈은 무리수 집합을, 데데킨트 절단은 실수 집합을 나타낸다.

3. 완비화 정리

완비화 정리. $(P, <)$가 양끝점이 없는 조밀한 전순서라면 다음을 만족하는 완비 전순서 $(C, \prec)$가 순서 동형에 대해 유일하게 존재한다.

1. $P \subseteq C$
2. $\prec$는 $P$에서 $<$와 일치한다.
3. $P$는 $C$에서 조밀하다. 즉, $c_1 < c_2 \in C$에 대해 $c_1 < p < c_2$를 만족하는 $p \in P$가 언제나 존재한다.
4. $C$는 양끝점이 없다.

유일성 증명. $(C, \prec)$와 $(C^\ast, \prec^\ast)$가 조건을 만족하는 완비 전순서라고 하자. 다음과 같이 정의된 $\phi: C → C^\ast$는 순서 동형 사상이다.

1. $c \in P$라면 $\phi(c)=c$
2. $c \notin P$라면 $\phi(c) = \sup^\ast \lbrace p \in P : p \prec c \rbrace$

존재성 증명. 다음과 같이 정의한다.

\[\begin{gather} \mathcal{G} = \lbrace (A, B) : (A, B) \text{ is a gap of } P \rbrace \\ \mathcal{D} = \lbrace (A, B) : (A, B) \text{ is a Dedekind cut of } P \rbrace \\ \mathcal{P} = \mathcal{D} \setminus \mathcal{G} \end{gather}\]

라고 하자. 다음과 같이 $\mathcal{D}$에 순서를 준다.

\[(A_1, B_1) \prec (A_2, B_2) \iff A_1 \subset A_2\]

$(A, B) \in \mathcal{P}$라면 어떤 $p$에 대해 $B = \lbrace x \in P : x \geq p \rbrace$이며, 이때 $(A, B) = [p]$라고 적자. 즉,

\[\mathcal{P} = \lbrace [p] : p \in P \rbrace\]

$(\mathcal{P}, \prec) \sim (P, <)$임을 쉽게 확인할 수 있다. 이제 다음을 보인다.

Claim. $\mathcal{D}$는 $\mathcal{P}$에 대해 완비화 정리의 4가지 조건을 모두 만족하는 확장이다.

1, 2, 4는 자명하다. 3을 보인다.

$\mathfrak{d}_1 = (A_1, B_1), \mathfrak{d}_2 = (A_2, B_2) \in \mathcal{D}$에 대해 $\mathfrak{d_1} \prec \mathfrak{d}_2$, 즉 $A_1 \subset A_2$라고 하자. $p \in A_2 \setminus A_1$이며 $p$가 $B$의 최소 원소가 아닌 $p \in P$가 존재한다. 그러한 $p$에 대해 $\mathfrak{d}_1 \prec [p] \prec \mathfrak{d}_2$이다. □

마지막으로 다음을 보인다.

Claim. $(\mathcal{D}, \prec)$는 완비이다.

$\mathcal{S}$가 위로 유계인 $\mathcal{D}$의 공집합이 아닌 부분집합이라고 하자. 다음과 같이 정의한다.

\[\begin{gather} A_\mathcal{S} = \bigcup \lbrace A : (A, B) \in \mathcal{S} \rbrace\\ B_\mathcal{S} = \bigcap \lbrace B : (A, B) \in \mathcal{S} \rbrace \end{gather}\]

$(A_\mathcal{S}, B_\mathcal{S}) \in \mathcal{D}$이며, $\mathcal{S}$의 최소 상계임을 확인할 수 있다. ◾

집합론적 실수의 정의. 다음을 만족하는 집합 $(R, <)$은 순서 동형에 대해 유일하다.

1. 완비 전순서 집합이다.
2. 양끝점이 없다.
3. 분리 가능하다(separable). 즉, $Q \subset R$이 존재하여 $Q$는 가산집합이고 $R$에서 조밀하다.

증명. 칸토어의 동형성 정리와 완비화 정리로부터 따라 나온다.