디멘의 블로그 이데아를 여행하는 히치하이커

베르 범주 정리

01 Dec 2024
수학
위상수학

1. 베르 공간

정리. $S$가 위상공간 $X$의 부분집합일 때, 다음은 동치이다.

  • $\left( \operatorname{cl}S \right)^\circ$가 공집합이다.
  • $(\operatorname{cl}S)^c$가 조밀하다.
  • $S$는 어떠한 $X$의 열린 집합에서도 조밀하지 않다.

이때, $S$를 희박(rare)하다고 한다.

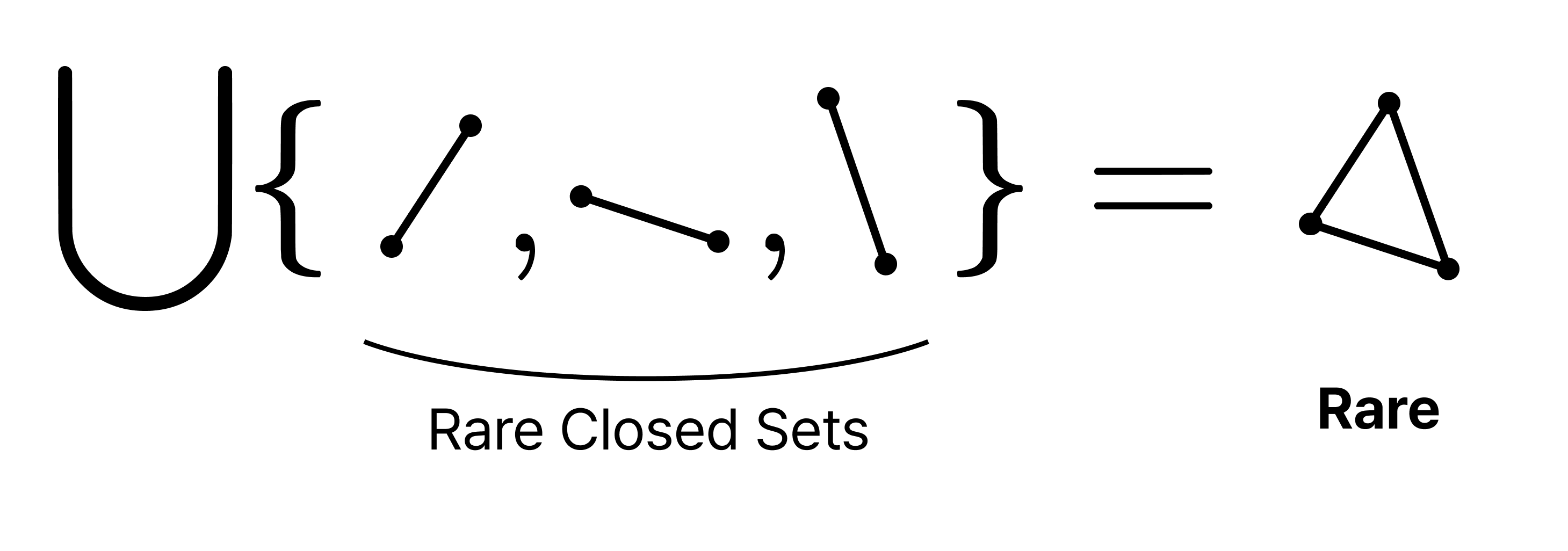
정의. 희박한 닫힌 집합들의 가산 합집합 $\bigcup F_n$이 희박한 공간 $X$를 베르 공간이라고 한다.

Remark. TFAE:

  • $X$가 베르 공간이다.
  • $X$의 열린 조밀 집합들의 가산 교집합은 조밀하다.

예시. $\mathbb{Q}$는 베르 공간이 아니다.

  • $\lbrace q \rbrace$는 닫힌 희박 집합이지만 $\bigcup_{q \in \mathbb{Q}} \lbrace q\rbrace = \mathbb{Q}$는 희박하지 않다.
  • $\mathbb{Q} \setminus \lbrace q \rbrace$는 열린 조밀 집합이지만 $\bigcap_{q \in \mathbb{Q}} \left( \mathbb{Q} \setminus \lbrace q \rbrace \right) = \varnothing$은 조밀하지 않다.

2. 베르 범주 정리

콤팩트 공간에서의 칸토어 축소 정리. 다음은 동치이다.

  1. $X$가 콤팩트하다.
  2. 임의의 유한 교집합 속성을 가진 닫힌 집합들의 모임 $\mathcal{C}$에 대해 $\bigcap_{C \in \mathcal{C}} C \neq \varnothing$이다.

완비 거리 공간에서의 칸토어 축소 정리. 다음은 동치이다.

  1. $X$가 완비 거리 공간이다.
  2. 임의의 공집합이 없는 닫힌 집합열 $C_1 \supset C_2 \supset \cdots$에 대해 $\bigcap C_n \neq \varnothing$이며, 특히 $\operatorname{diam}C_n \to 0$일 때 $\bigcap C_n$은 홑원소 집합이다.

Remark. 2는 4를 함의한다. 이로부터 콤팩트 거리 공간은 완비임을 보일 수 있다. 역은 성립하지 않는다.

정리. 완비 거리 공간과 콤팩트 하우스도르프 공간은 베르 공간이다.

증명.

$X$가 완비 거리 공간 또는 콤팩트 하우스도르프 공간이라고 하자. 희박한 닫힌 집합들의 가산 모임 $\lbrace F_n \rbrace$이 주어졌을 때, 임의의 열린 집합 $U$에 대해 $U \not\subset \bigcup F_n$임을 보이면 된다. 이를 위해 $\forall n : x \not\in F_n$인 $x \in U$를 찾을 것이다.

$F_1$이 희박하므로 $x_1 \in U \setminus F_1$이 존재한다. $X$는 정칙 공간이므로 $x_1 \in U_1$, $\overline{U_1} \cap F_1 = \varnothing$인 열린 집합 $U_1$이 존재한다. 귀납적으로 다음과 같이 정의할 수 있다.

  • $x_n \in U_n \setminus F_n$
  • $U_n \subset U_{n - 1}$
  • $\overline{U_n} \cap F_n = \varnothing$

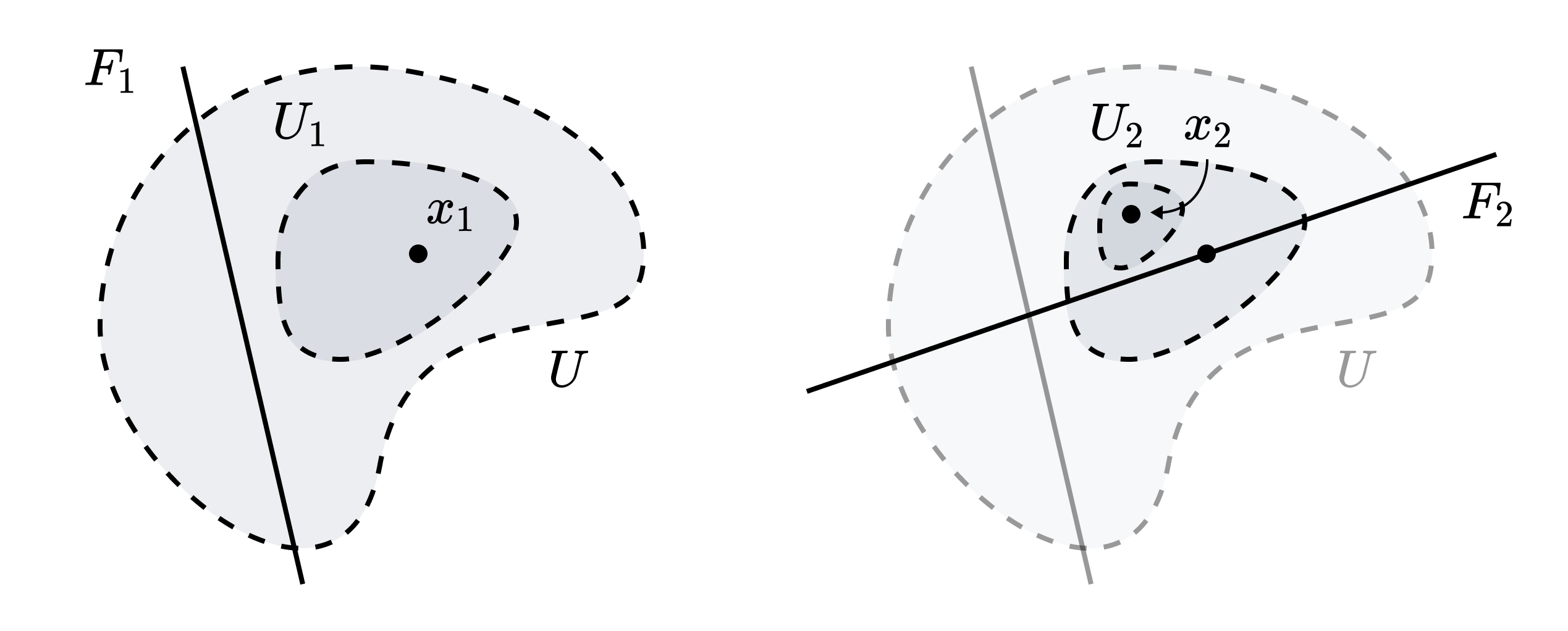
칸토어 축소 정리에 의해 $x \in \bigcap \overline{U_n}$인 $x$가 존재한다.

3. 베르 범주 정리의 응용

연속함수열의 수렴은 거의 연속이다. $\lbrace f_n : X → (Y, d) \rbrace$가 $f$로 수렴하는 연속함수열일 때,

\[S = \lbrace x \in X : f\text{ is continuous at } x \rbrace\]

는 $X$에서 조밀하다.

KAIST POW2024-20. $f$가 연속함수이고,

\[\forall x \geq 0 : \lim_{n \to \infty} f(nx) = 0\]

라면 $\lim_{x \to \infty} f(x) = 0$이다.

병리적 함수의 존재성. $h : [0, 1] → \mathbb{R}$가 연속함수라고 하자. 임의의 $ε > 0$에 대해 다음을 만족하는 함수 $g : [0,1] → \mathbb{R}$가 존재한다.

  • $\lVert h − g\rVert < ε$이다.
  • $g$는 전 구간에서 연속이다.
  • $g$는 전 구간에서 미분 불가능하다.