칸토어-슈뢰더-베른슈타인 정리
19 Nov 2024정리. 두 집합 $X, Y$에 대해 $|X| \leq |Y|$, $|X| \geq |Y|$라면 $|X| = |Y|$이다.
매우 당연해 보이지만 $\leq$가 단사함수의 존재성으로, $=$가 전단사함수의 존재성으로 정의된다는 점에서 트리키한 함수 핸들링을 요구한다.
여담으로 “칸토어-베른슈타인 정리(위키피디아)” 또는 “슈뢰더-베른슈타인 정리(나무위키)”라고도 부르는데 “칸토어-슈뢰더 정리”라고 부르는 경우는 못 봤다. 홍대병에 취해 있다면 “칸토어-슈뢰더 정리”라고 불러보자.
첫 번째 증명
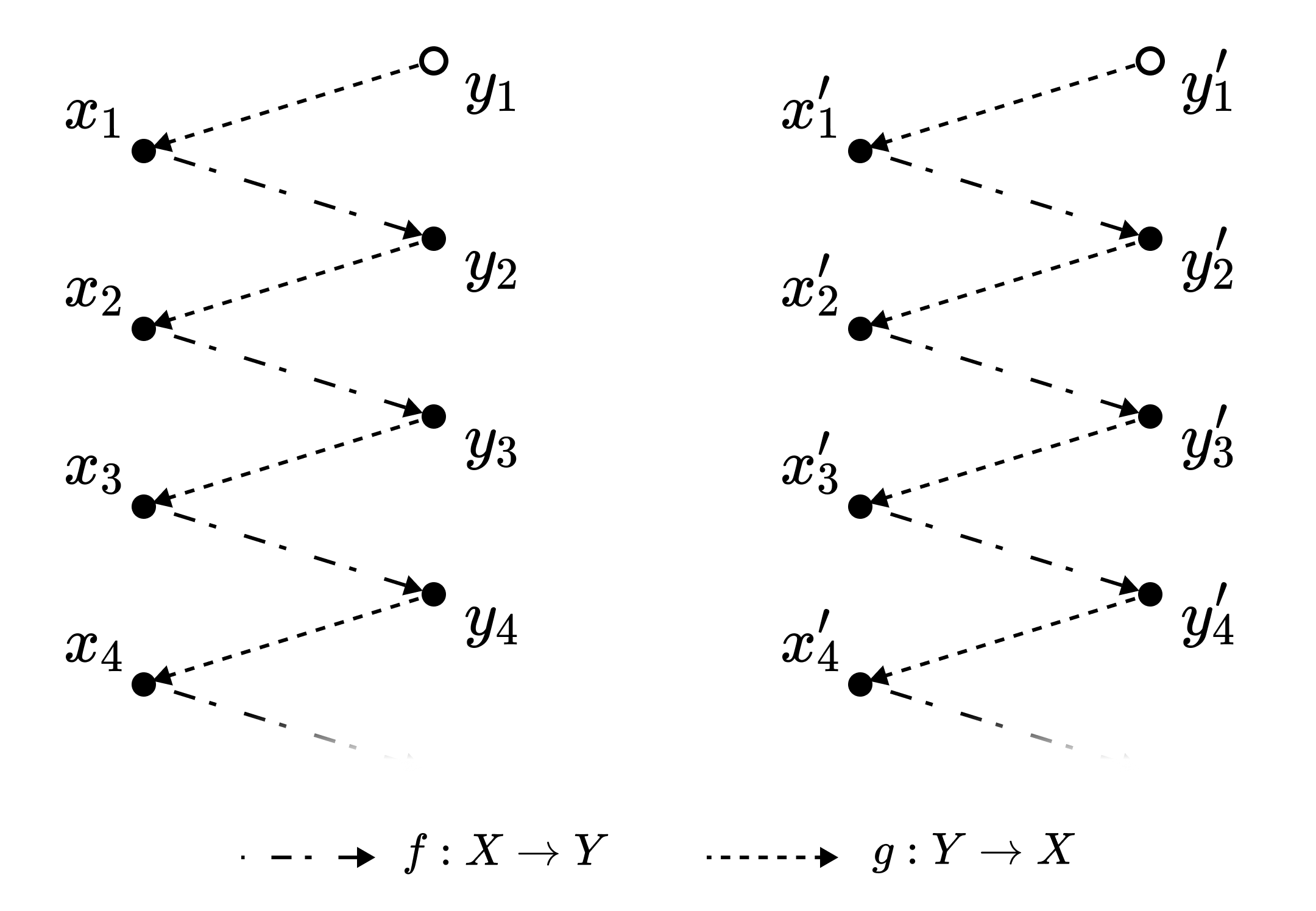
조건에 의해 단사함수 $f: X \to Y, g: Y \to X$가 존재한다. $Z := \mathrm{Im} f$가 $Y$와 같다면 증명이 끝나므로 $Z \subsetneq Y$라고 하자.
임의의 $y \in Z \setminus Y$ (그림에서 빈 점으로 표시) 에 대해,
- $x_1^y = g^{-1}(y)$
- $x_{n+1}^y = g(f(x_n))$
와 같이 두어, $h: X \to Y$를 다음과 같이 정의한다.
- $h_y(x_1^y) = y$
- $h_y(x_{n+1}^y) = f(x_n)$
다음이 성립함을 확인하라.
\[x^y_n = x^z_m \iff y = z, n = m\]따라서 다음의 함수 $h: X → Y$는 well-defined이다.
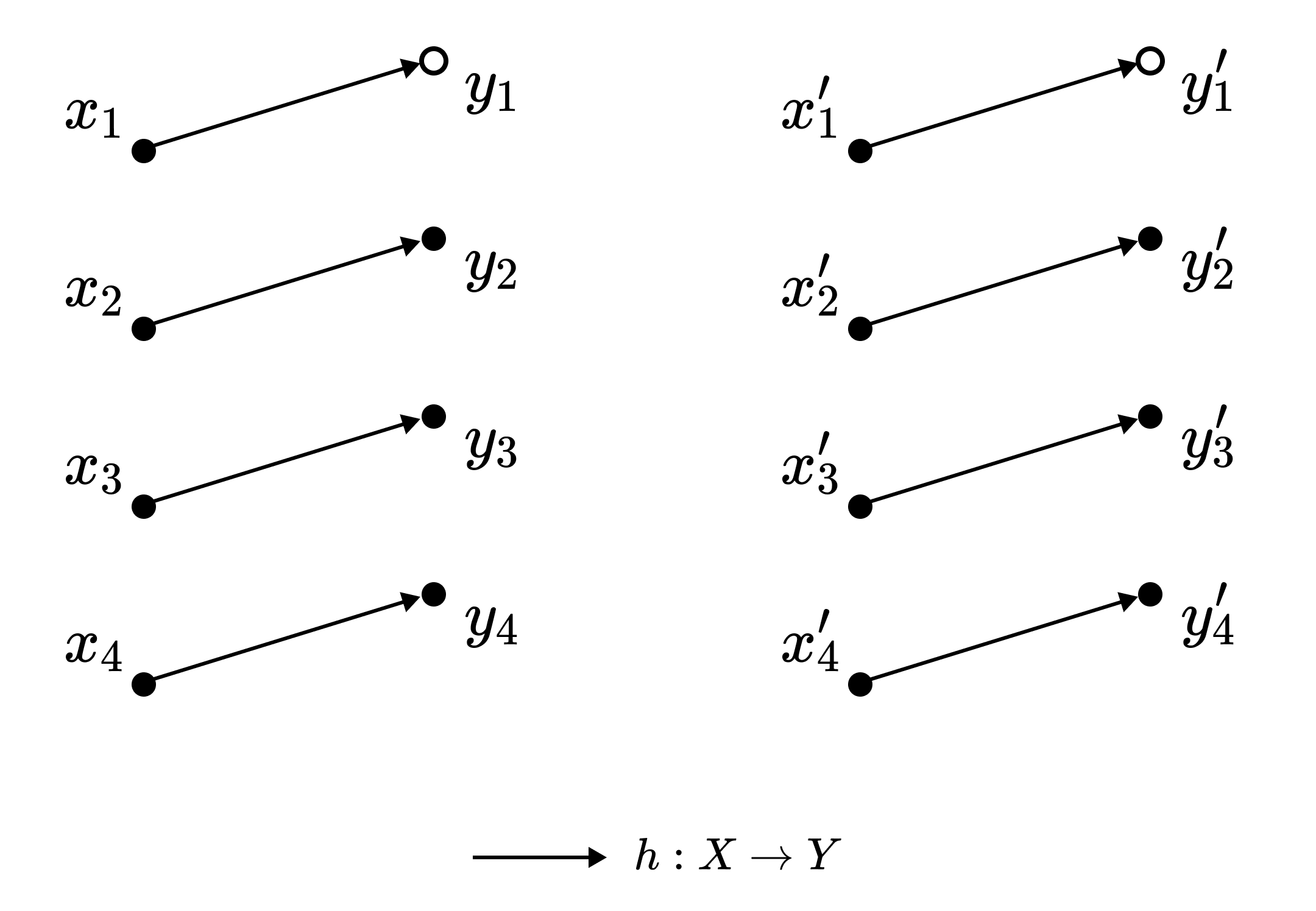
$h$가 전단사임을 확인하라. ◾
두 번째 증명
보조정리 (기수의 샌드위치 정리). $A_1 \supseteq B \supseteq A_2$에 대해 $|A_1| = |A_2|$라면 $|A_1| = |B| = |A_2|$이다.
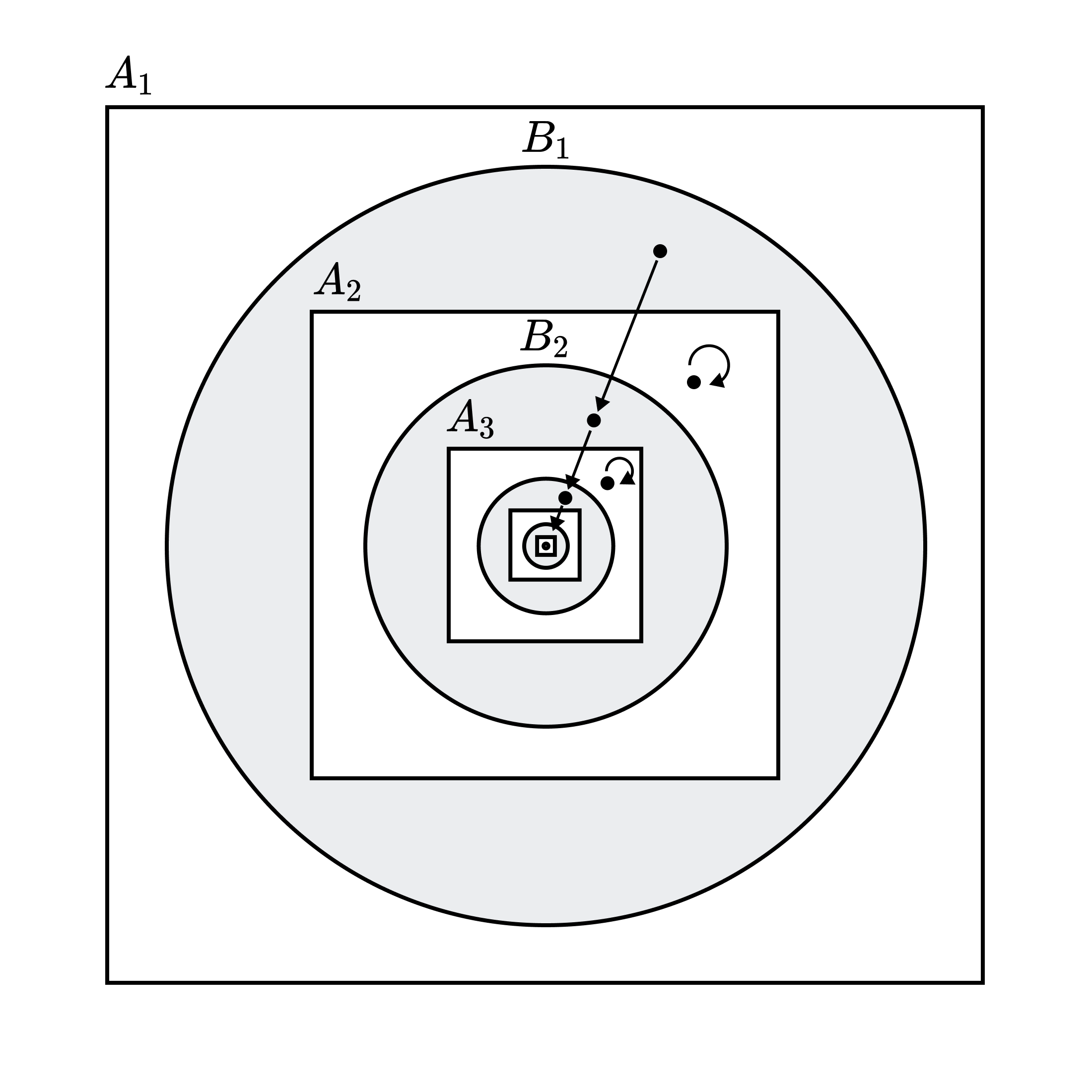
증명. $f: A_1 → A_2$가 전단사라고 하자. $B_1 = B$로 둔다. 다음과 같이 $\lbrace A_n\rbrace , \lbrace B_n\rbrace , \lbrace C_n\rbrace $을 정의한다.
\[\begin{gather} A_{n+1} = f[A_n]\\ B_{n+1} = f[B_n]\\ C_n = A_n \setminus B_n \end{gather}\]$C = \bigcup C_n$ (그림에서 색칠되지 않은 영역), $D = A_1 \setminus C$ (그림에서 색칠된 영역) 라고 하자. $f[C] \subset C, f[D] \subset D$임을 확인하라. 따라서 다음의 $g: B_1 → A_2$는 전단사이다. (화살표)
본 정리의 증명. $f: X → Y, g: Y → X$가 전사일 때 $gf[X] \subseteq g[Y] \subseteq X$이고, $| gf[X] | = | X |$이므로, 보조정리에 의해 $|g[Y]| = |Y| = |X|$이다. ◾
잘 생각해 보면 두 증명은 사실 같다.