Cantor–Schröder–Bernstein Theorem

19 Nov 2024

Theorem. For two sets $X, Y$, if $|X| \leq |Y|$ and $|X| \geq |Y|$, then $|X| = |Y|$.

Although this may seem obvious, it requires some delicate function handling, since $\leq$ is defined by the existence of an injective function, while $=$ is defined by the existence of a bijective function.

As a side note, the theorem is often called the “Cantor–Bernstein theorem” or the “Schröder–Bernstein theorem”, but I’ve never seen it called the “Cantor–Schröder theorem.” If you’re feeling a bit pretentious, it’s an open option.

First Proof

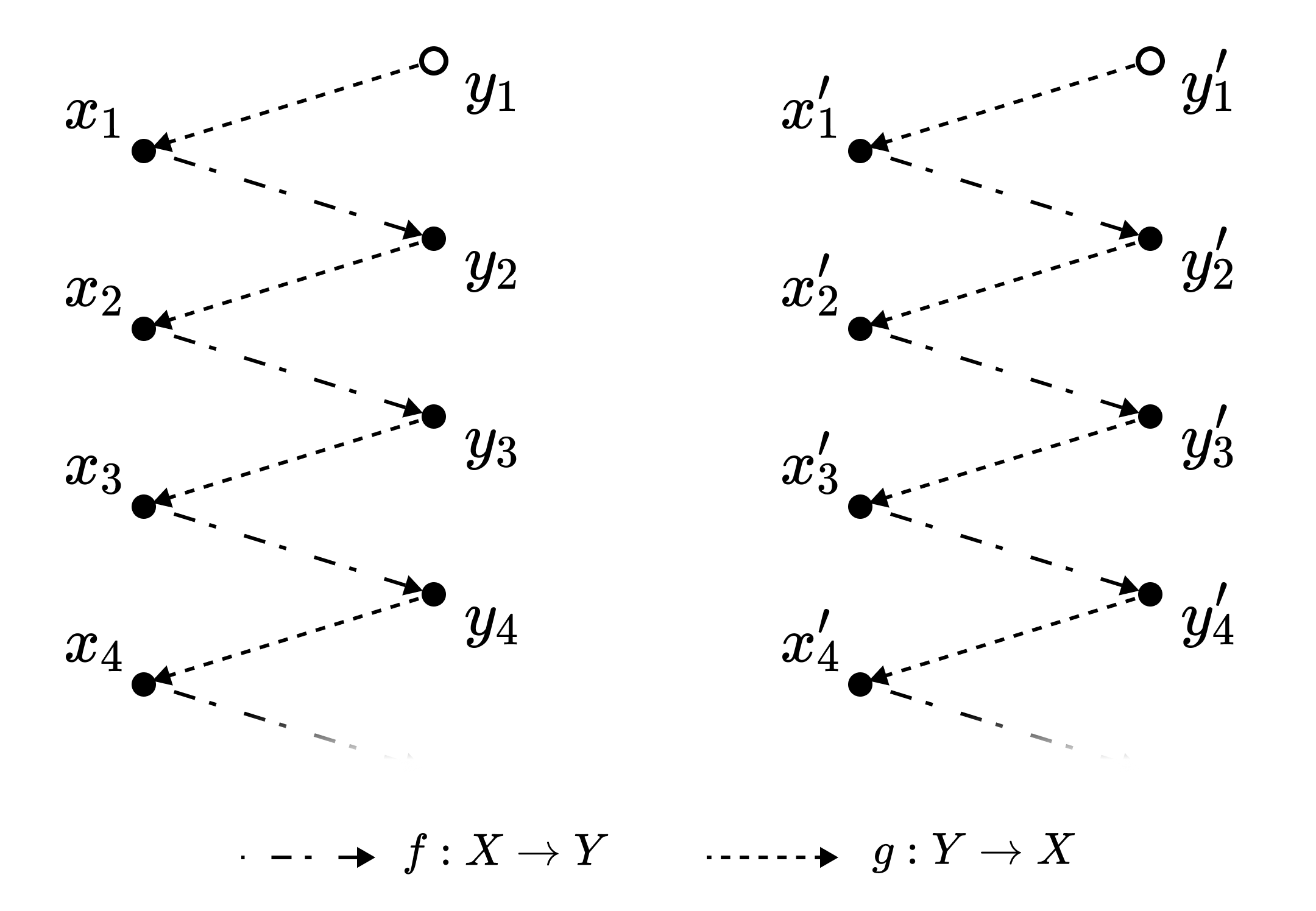
By assumption there exists $f: X \to Y, g: Y \to X$ injective. If $Z := \mathrm{Im} f$ equals $Y$, the proof is done, so let us assume $Z \subsetneq Y$.

For any $y \in Z \setminus Y$ (represented as an empty dot in the diagram),

• let $x_1^y = g^{-1}(y)$
• let $x_{n+1}^y = g(f(x_n))$

Now define a function $h: X \to Y$ as follows:

• $h_y(x_1^y) = y$
• $h_y(x_{n+1}^y) = f(x_n)$

Check that the following holds:

\[x^y_n = x^z_m \iff y = z, n = m\]

Thus, the function $h: X \to Y$ defined by

\[h(x) = \begin{cases} h_y(x) &x = x^y_n \text{ for some } y, n \\\\ f(x) &\text{otherwise} \end{cases}\]

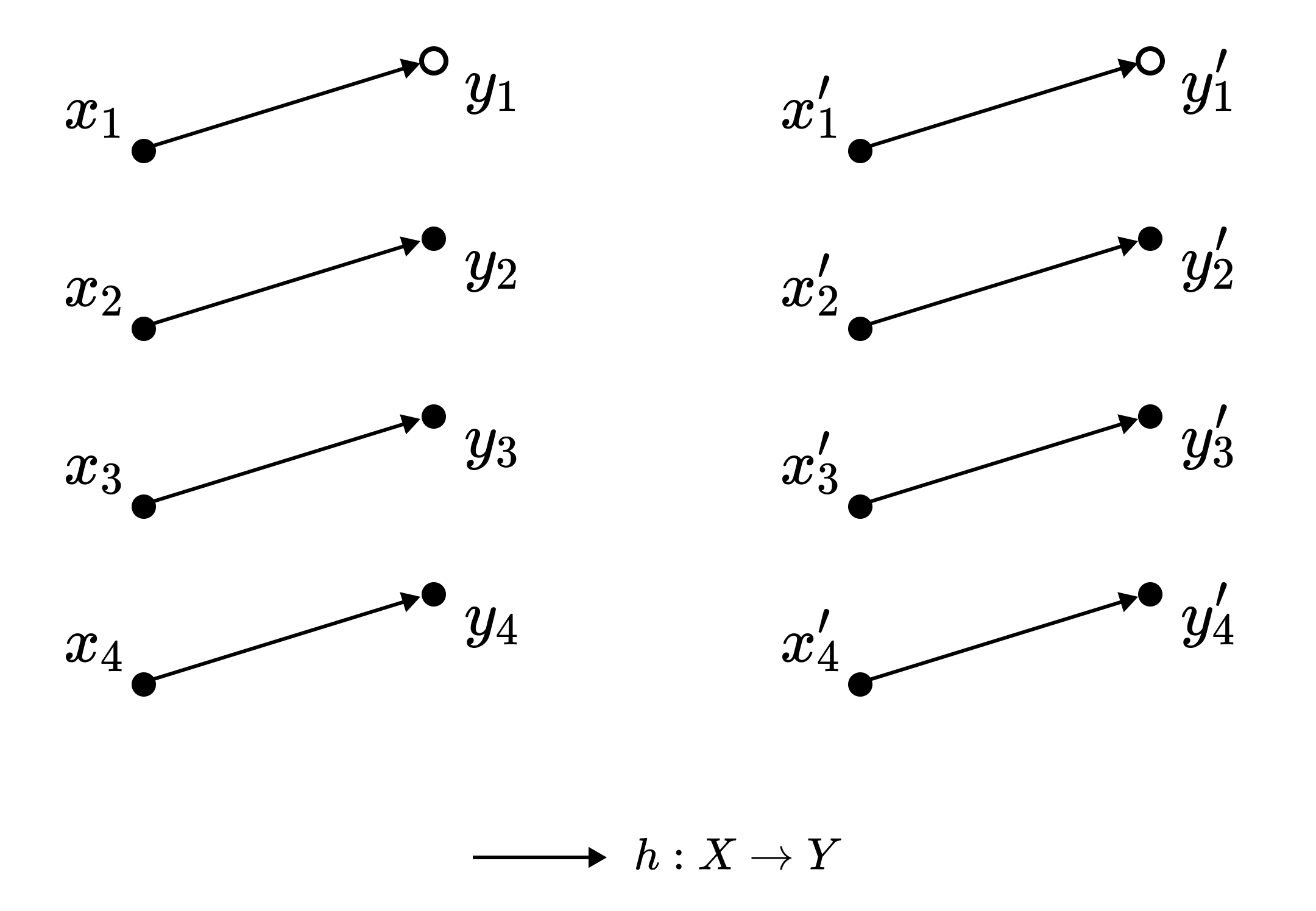
is well-defined. Verify that $h$ is bijective. ◾

Second Proof

Lemma (Sandwich Theorem for Cardinals). If $A_1 \supseteq B \supseteq A_2$ and $|A_1| = |A_2|$, then $|A_1| = |B| = |A_2|$.

Proof. Assume $f: A_1 \to A_2$ is bijective. Let $B_1 = B$. Define the sequences $\lbrace A_n\rbrace , \lbrace B_n\rbrace , \lbrace C_n\rbrace$ as follows:

\[\begin{gather} A_{n+1} = f[A_n]\\ B_{n+1} = f[B_n]\\ C_n = A_n \setminus B_n \end{gather}\]

Let $C = \bigcup C_n$ (the unshaded region in the diagram) and $D = A_1 \setminus C$ (the shaded region). Verify that $f[C] \subset C$ and $f[D] \subset D$. Then, define $g: B_1 \to A_2$ as follows (represented as arrows in the diagram).

\[g(x) = \begin{cases} x & x \in C\\ f(x) & x \in D \end{cases}\]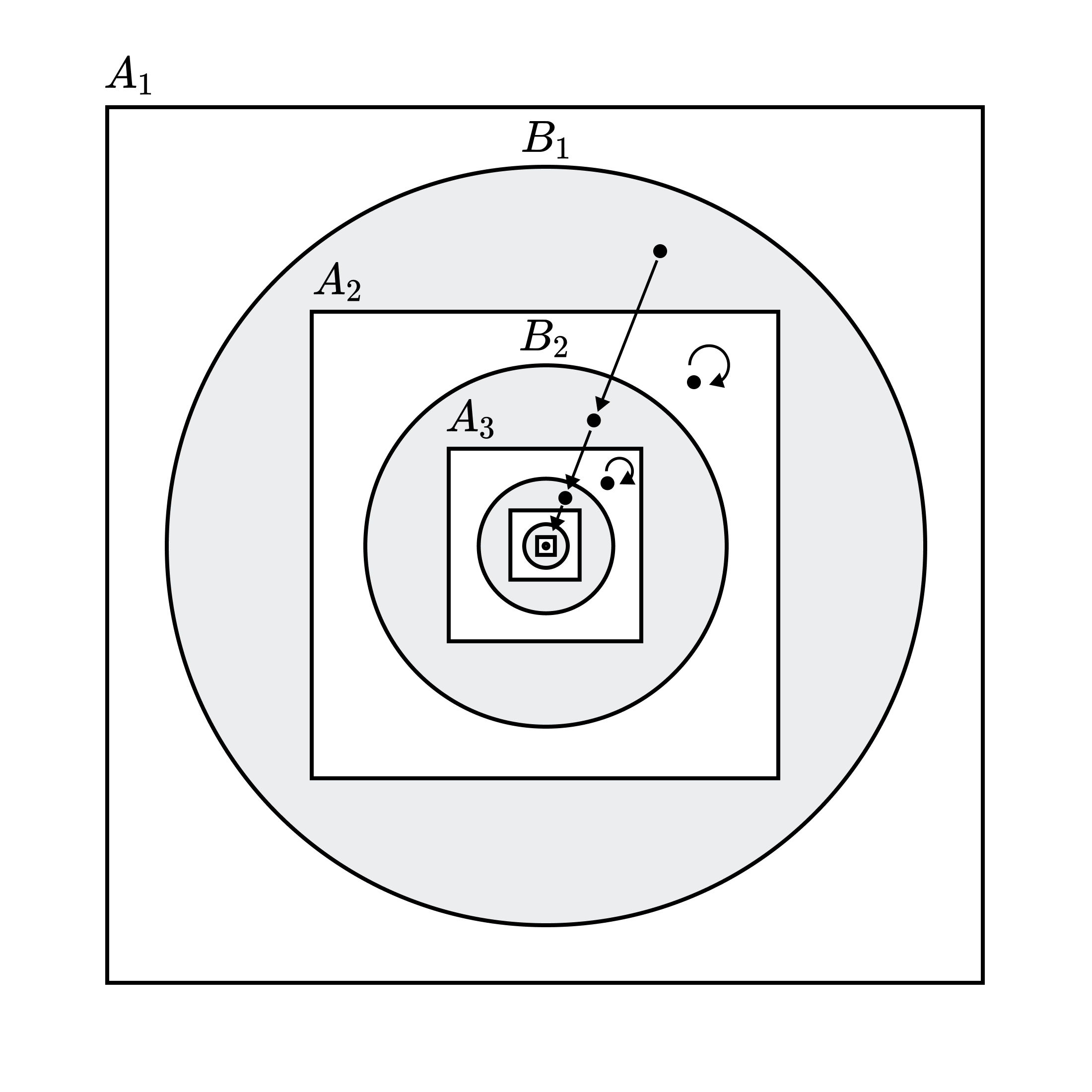

Then $g$ is bijective.

Proof of the main theorem. Given $f: X \to Y$ and $g: Y \to X$ are injective, we have $gf[X] \subseteq g[Y] \subseteq X$ and $| gf[X] | = | X |$. By the lemma, we obtain $|g[Y]| = |Y| = |X|$. ◾

Upon closer reflection, the two proofs are essentially the same.