디멘의 블로그
Dimen's Blog
이데아를 여행하는 히치하이커
Alice in Logicland
On Reference — Definite Descriptions
18 Jan 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
4. Definite Descriptions
Unlike names, the primary question raised concerning definite descriptions is whether definite descriptions actually refer. Frege held that definite descriptions, like names, possess both sense (the content of the definite description) and reference (the object that uniquely satisfies that content), while Russell maintained that definite descriptions do not have referents.
4.1. Russell’s Theory of Descriptions
Russell’s Claim
According to Russell, definite descriptions do not refer to objects. Rather, definite descriptions are semantically equivalent to second-order predicates. In other words, just as we can think of a predicate P as
P: object → truth value
when D is a definite description, we have
D: (object → truth value) → truth value (i.e. predicate → truth value)
According to this view, “the present King of Britain” does not refer to Charles III, but rather is a second-order predicate that returns true for “x is male”, “x is British”, “x is the son of Elizabeth II”, etc., and returns false for “x is female”, “x is American”, “x is the son of James I”, etc.
The strength of Russell’s theory of descriptions lies in its ability to explain how definite descriptions lacking referents can be used meaningfully in sentences such as “The present King of France is bald” (according to Frege this sentence would be meaningless, but according to Russell this sentence is simply false), and to resolve Frege’s puzzle.
Furthermore, Russell claims that all names except ‘this’ and ‘I’ are disguised definite descriptions. while this claim has the advantage of making the semantics of language elegantly simple, it fails to adequately explain Kripke’s modal and semantic arguments. Therefore, this essay shall examine only Russell’s claim that “definite descriptions do not refer”.
Remark. However, there remains doubt as to whether Russell’s theory of descriptions truly resolves Frege’s puzzle. If we adopt an extensional definition for predicates, then ‘the morning star’ and ‘the evening star’ become exactly the same (second-order) predicate. The arguments of Quine and others regarding intensionalism and extensionalism are also worth considering.
Strawson’s Theory
Consider the following sentence:
The table is covered with books.
This sentence appears to be true when, for instance, the speaker is in a room, there is exactly one table in the room, and that table is covered with books. However, according to Russell’s theory of descriptions, since there is more than one table in the universe, the sentence is false.
In response, Strawson argues that there are cases where definite descriptions genuinely refer. When a definite description is used referentially, the definite description refers to the object amongst those satisfying the descriptive content that is most salient in the given context. Conversely, when a definite description is used attributively, the description functions as in Russell’s theory.
Donnellan’s Theory
Consider the following sentence:
Who is the man drinking a martini?
Suppose that the man the speaker intends to refer to is actually drinking water, not a martini. In this case, according to Strawson, “the man drinking a martini” cannot be used referentially (since there is no man drinking a martini in the relevant context), nor can it be used attributively (since there are multiple men currently drinking martinis worldwide).
Therefore, Donnellan argues that definite descriptions can also refer to objects that do not satisfy their descriptive content. What matters is the speaker’s intention to designate a particular object with the definite description. Donnellan’s theory appears to fall into the problem of rigidity concerning definite descriptions, and being conscious of this, Donnellan appeals to Gricean theories of meaning.
Kripke’s Theory
Kripke argues that if we understand sentences such as “Who is the man drinking a martini?” pragmatically, we can maintain a strong Russellian position that definite descriptions never refer under any circumstances.
Kripke appears to hold that reference must be achieved purely through convention (though it might be more appropriate to understand this as an algorithm). For instance, Kripke’s theory of names precisely specifies, given a name $N$, the object that this name designates through causal theory. However, given that strong conventionalism about names fails to properly explain names with multiple bearers or the principle of impure indexicals, Kripke’s conventionalism lacks solid foundation, and consequently Kripke’s argument against Donnellanism is also weakly grounded.
Definite Descriptions v. Indefinite Descriptions
Recently, the very distinction between definite descriptions (the F) and indefinite descriptions (a F) has come under question. Not only has precisely defining the difference between them proved to be extremely challenging, but numerous languages have been reported that do not grammatically distinguish between the two. If the distinction between definite and indefinite descriptions proves to be unfounded, this could strengthen Russellian views that definite descriptions do not refer. (Alternatively, one would have to advance the highly controversial claim that indefinite descriptions also refer.)
5. Referential Scepticism
Descriptivism, Millianism, and indexical theories agree in their position that reference is a philosophically worthy subject of enquiry and that meaningful analysis thereof is possible. However, there also exist so-called “referentially sceptical” positions that argue reference is an essentially meaningless or vacuous concept.
Quinean Scepticism
Quine argues through the indeterminacy of translation thesis that referential expressions such as ‘gavagai’ are incomprehensible. Regarding the indeterminacy of translation thesis, the present author has written previously, which may be consulted.
The Problem of the Many
The problem of the many concerns how to define the boundaries of the object that a referential expression refers to. For example, I can refer to the present Gyeongbokgung Palace with ‘Gyeongbokgung’. Now imagine that one day an incident occurs in which the roof tiles of Gyeongbokgung are burnt away. Even after the fire incident, it seems I can still refer to Gyeongbokgung (now without roof tiles) with ‘Gyeongbokgung’. Can we then say that ‘Gyeongbokgung’ before and after the fire incident has the same referent? How much of Gyeongbokgung must be burnt away before it can no longer be the referent of ‘Gyeongbokgung’? This problem raises doubts about the general schema that referential expressions have referents.
Davidson’s Theory of Truth
The reason philosophers pursue theories of reference is that they are necessary for establishing the semantics of language. That is, the referent of each expression appearing in a sentence must be determined in order to determine the truth value of that sentence.
However, Davidson argues that this puts the cart before the horse. Davidson claims that merely providing a theory of truth for sentences suffices to establish the semantics of the relevant language, and that reference theory is therefore unnecessary. Philosophical discussions of truth shall be organised in a separate series hereafter.
지시에 대하여 — 특성 모델과 의도주의
13 Jan 20253. 지표사
지표사란 ‘나’, ‘너’, ’여기‘, ’지금‘, ’그‘, ’이것‘, ’저것‘과 같은 표현을 일컫는다. 지표사는 ’나‘, ’너‘, ’여기‘, ’지금‘과 같이 맥락이 주어졌을 때 지시체가 비교적 분명한 순수 지표사와 ’그’, ‘이것’, ’저것’과 같이 지시체가 비교적 불분명한 불순 지표사로 구분하는 것이 일반적이나, 모든 학자가 이 구분을 유의미하게 받아들이는 것은 아니다.
3.1. 순수 지표사
3.1.1. 기술주의는 순수 지표사를 적절히 설명하는가?
일면 기술주의는 ‘나’의 지시체가 “이 발화의 화자”라는 기술적 내용을 통해 결정된다고 주장함으로써 순수 지표사를 적절히 설명하는 것으로 보인다. 그런데 여기에는 두 가지 문제가 있다.
첫째, “이 발화의 화자”가 기술구에 해당하는지 불분명하다. 보통 기술구는 순전히 그 내용만으로 해당하는 대상을 특정해 내며, 그렇기에 기술(description)이라고 불린다. 그런 점에서 “이 발화의 화자”는 일반적인 기술구로 보기에 문제가 있다.
일례로 어느 날 침대에서 일어난 당신 앞에 다음과 같은 쪽지가 있었다고 하자.
브렉시트를 시행한 영국의 전 총리 는 누구인가?
그럼 당신은 — 혼란스럽기야 하겠지만 — ‘보리스 존슨’이라고 답할 것이다. 그러나 쪽지에 적힌 질문이 다음과 같았다면 어떨까?
이 문장의 화자 는 누구인가?
위 쪽지만 가지고서는 이 문장의 화자 가 지시하는 바를 알 수 없다. 즉, 이 문장의 화자 는 의미론적 계층을 넘어, 언어의 구체적인 사용과 관련된 화용론적 계층에 호소한다.
이와 연관된 두 번째 문제는, “이 발화의 화자”가 ‘나’의 의미일 경우 ‘나’의 사용과 관련하여 이상한 예측을 내놓는다는 점이다. 일례로 앨리스와 밥이 ”나는 배고프다“라고 발화한 경우, 앨리스와 밥은 서로 다른 바를 주장했다고 보는 편이 자연스럽다. 그러나 기술주의는 앨리스와 밥이 둘 다 ”이 발화의 화자는 배고프다“라는 동등한 내용을 주장했다는 예측을 내놓는다.
3.1.2. 라이헨바흐의 해결법: 사례 재귀성
라이헨바흐는 지표사가 사례 재귀적(token reflexive)이라고 주장함으로써 기술주의와 지표사 사이의 간극을 메꾸고자 했다. 즉, 앨리스가 2025년 1월 13일 오후 4시 53분 광화문에서 ”나는 배고프다“라고 발화했다면 이 문장에서 ‘나’와 결부되는 기술구는 2025년 1월 13일 오후 4시 53분 광화문에서 “나는 배고프다”라고 발화한 화자 이다.
3.1.3. 캐플런의 해결법: 특성 모델
캐플런은 라이헨바흐의 접근법을 밀주의적으로 변형시켰다. 캐플런은 두 가지 유형의 의미를 구분한다. 내용(content)는 우리가 지금까지 의미라고 불렀던 것으로, 밀주의자 캐플런에게 있어 이름의 내용은 그 지시체이다. 한편 특성(character)은 사용 규칙으로서, 주어진 맥락에서 표현의 내용이 무엇인지 결정한다.
캐플런은 엄격한 의미에서 동명인 이인이 존재하지 않는다는 입장이기 때문에 그에 따르면 이름은 불변 특성(constant character)을 가진다. 예를 들어 ‘보리스 존슨ᵢ ’의 내용은 모든 맥락에서 보리스 존슨ᵢ을 지시체로 산출하라 이다.
반면 순수 지표사의 특성은 이 화자를 산출하라, 이 발화의 위치를 산출하라 등과 같다. 캐플런의 입장을 받아들이면 우리는 ”나는 지금 여기에 있다“가 어떻게 논리적으로는 필연적이지만(’나‘, ’지금‘, ’여기‘의 특성은 이 문장이 모든 맥락에서 참임을 보장한다) 형이상학적으로는 필연적이지 않은지(주어진 맥락에서 ’나‘, ’지금‘, ’여기‘를 그 내용으로 대치한 문장은 필연적으로 참이 아니다) 설명할 수 있으며, 앨리스와 밥의 사례 또한 해결한다.
Remark. 캐플런의 이론에 대한 유명한 반박으로 자동응답기 역설을 찾아보라.
3.1.4. 인과 이론과 특성 모델의 융합
인과 이론과 특성 모델은 밀주의 이론이라는 공통점을 갖기에 둘을 융합하여 이름에 대한 보다 정교한 이론을 제시할 수 있다.
앞서 말했듯이 캐플런은 (1) 이름을 심적 현상으로 간주하며, (2) 이에 따라 다수의 담지자를 가지는 이름은 존재하지 않으므로 (3) 이름의 특성은 불변이라고 주장했다. 그러나 이름을 심리 현상으로 보는 입장은 다소 부담스럽다. 대신 (1), (2), (3)을 다음과 같이 수정해 봄직하다.
- 이름은 언어적 현상이다.
- 다수의 담지자를 가지는 이름이 존재한다.
- 이름의 특성은 그 이름의 담지자 집합 중, 현 맥락에서 가장 두드러지는(most salient) 대상을 지시체로 산출하는 것이다.
여기에 더불어 인과 이론적인 4번 논제를 추가한다.
- 이름의 담지자 집합은 그 이름가 결부되는 인과적 사슬 중 최초로 명명된 대상들의 집합이다.
이같은 인과 이론과 특성 모델의 융합은 매력적이지만 한계가 없는 것은 아니다. 특히, 인과 이론의 강점인 “이름의 전달만으로 피전달자가 이름으로 지시할 수 있게 되는 원리”를 완벽히 보존하지 못한다. (필자왈: 뭐 그렇다고 한다 내가 보기에 이 이론은 완벽한 거 같은데~)
3.2. 불순 지표사
‘그’, ‘그녀’와 같은 불순 지표사, 또는 ‘이것’, ‘저것’과 같은 ‘진정한 지표사’의 의미는 순수 지표사보다 더 불분명하다. 웨트스타인과 앨리슨 마운트는 불순 지표사가 지시하는 대상은 해당 맥락에서 가장 두드러지는 인물/대상이라는 노선의 이론을 발전시켰다.
그렇다면 무엇이 특정 대상을 ‘해당 맥락에서 가장 두드러지는 대상’으로 만드는가? 아무래도 화자 또는 청자의 관심이라고 보는 편이 가장 자연스럽다. 하지만 누구의 편을 들어줘야 할까?
1. 마운트: 상호 두드러짐의 원리
주장. 마운트는 불순 지표사가 대상 $c$를 지시할 필요충분조건은 화자와 청자의 관심이 일치하며 둘에게 공통적으로 두드러지는 대상이 A인 것이라고 주장한다.
문제. 이 견해는 화자와 청자의 관심이 갈라지는 경우, 또는 청자가 우연히 화자의 말에 집중하지 않고 있었을 경우 지표사의 지시는 실패한다는 반직관적인 결론을 함의한다.
2. 캐플런: 의도주의
주장. 캐플런은 불순 지표사가 대상 $c$를 지시할 필요충분조건은 화자가 $c$을 지시하고자 하는 겨냥 의도로 지표사를 사용하는 것이라고 주장한다.
문제. 화자의 겨냥 의도가 무한히 유연할 수 있는 경우 험티덤티 문제가 발생한다. 예컨데 화자가 충분한 의도를 가지고 있는 한 화자는 도널드 트럼프의 사진을 가리키며 루돌프 카르납을 지시할 수 있게 되는데, 이것은 매우 반직관적이다.
또한 캐플런은 다음의 복잡한 험티덤티 사례를 제시한다.
한 철학 교사는 교탁 뒤에 루돌프 카르납의 사진을 걸어 두었다. 그런데 어느 날 장난꾸러기 학생이 교사 몰래 카르납의 사진을 도널드 트럼프의 사진으로 바꿨다. 이 사실을 눈치채지 못한 교사는 학생들이 교실로 들어오자 자신의 등 뒤를 가리키며 ”저것은 20세기 가장 위대한 철학자 중 한 명이다“라고 말했다.
위 사례에서 교사는 ‘저것’이라는 지표사로 루돌프 카르납의 사진을 지시하고자 하는 의도를 가지고 있으나, 청자인 학생들은 이 의도를 잡아낼 수 없다. 그렇다면 여기서 의문이 든다. 교사의 발화는 참인가 거짓인가?
강한 의도주의에 따르면 교사가 카르납을 지시하려는 의도를 가지고 ‘저것’이라고 발화했으므로 ‘저것’은 카르납을 지시하며, 따라서 교사의 발화는 참이다.
3. 그라이스식 의도주의
게일 스타인은 그라이스의 의미론을 의도주의에 접목시켜 캐플런의 딜레마에 대한 다른 해답을 제공한다. 지표사 $i$가 대상 $c$를 지시하는 데 성공하기 위해서 화자는 세 가지 의도를 가져야 한다. 화자는 1) $i$로 $c$를 지시하려는 의도를 가져야 하고, 2) $i$로 청자에게 $c$를 지시체로 식별시키려는 의도를 가져야 하고, 3) 자신의 의도를 청자가 인식함으로써 청자에게 $c$를 지시치로 식별시키려는 의도를 가져야 한다.
그라이스식 의도주의는 험티덤티 문제를 해소한다. 캐플런의 험티덤티 문제를 해소하기 위해 스타인은 직접 지시와 간접 지시의 구분을 제시한다. 캐플런의 사례의 경우, 교사는 루돌프 카르납을 지시하려는 의도를 가지고 있으나 이 의도는 자신의 뒤에 있는 그림을 지시하려는 의도를 통해 이루어진다. 따라서 전자는 간접적 지시, 후자가 직접적 지시이다. 스타인은 간접적 지시체 직접적 지시체가 충돌할 경우 직접적 지시체가 우선권을 가진다고 주장한다. 즉, 교사의 발언은 거짓이다.
4. 라이머식 의도주의
그라이스식 의도주의는 ’상대가 내 마음을 읽을 수 있다고 믿는 화자‘의 경우와 같이 충분히 이상한 믿음을 가진 화자의 경우 험티덤티 문제를 제거하지 못한다는 한계(?)를 가진다.
이에 대해 라이머는 의도주의에 제약을 가하기 위한 다른 전략을 택하는데, 그의 전략은 제스처 우선순위로 요약할 수 있다. 라이머의 제약된 의도주의는 기대 이상으로 많은 험티덤티 문제를 명쾌하게 해결하는 것으로 보인다.
On Reference — Character Model and Intentionalism
13 Jan 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
3. Indexicals
Indexicals refer to expressions such as ‘I’, ‘you’, ‘here’, ‘now’, ‘he’, ‘this’, and ‘that’. It is common to distinguish between pure indexicals like ‘I’, ‘you’, ‘here’, and ‘now’, whose referents are relatively clear when context is given, and impure indexicals like ‘he’, ‘this’, and ‘that’, whose referents are relatively unclear. However, not all scholars accept this distinction as meaningful.
3.1. Pure Indexicals
3.1.1. Does Descriptivism Adequately Explain Pure Indexicals?
At first glance, descriptivism appears to adequately explain pure indexicals by claiming that the referent of ‘I’ is determined through the descriptive content “the speaker of this utterance”. However, there are two problems with this approach.
Firstly, it is unclear whether “the speaker of this utterance” constitutes a description. Typically, descriptions specify their corresponding objects purely through their content, and are thus called descriptions. In this respect, “the speaker of this utterance” is problematic as a general description.
For instance, suppose you wake up one day to find the following note in front of you:
Who is the former British Prime Minister who implemented Brexit?
You would answer ‘Boris Johnson’, albeit with some confusion. However, what if the question on the note were:
Who is the speaker of this sentence?
With only this note, one cannot determine what the speaker of this sentence refers to. That is, the speaker of this sentence appeals beyond the semantic level to the pragmatic level concerning the concrete use of language.
The second problem related to this is that if “the speaker of this utterance” is the meaning of ‘I’, it makes strange predictions regarding the use of ‘I’. For instance, when Alice and Bob both utter “I am hungry”, it seems natural to view them as making different claims. However, descriptivism predicts that Alice and Bob both made equivalent claims: “the speaker of this utterance is hungry”.
3.1.2. Reichenbach’s Solution: Token Reflexivity
Reichenbach attempted to bridge the gap between descriptivism and indexicals by claiming that indexicals are token reflexive. That is, if Alice uttered “I am hungry” at Gwanghwamun at 4:53 PM on 13th January 2025, then the description associated with ‘I’ in this sentence is the speaker who uttered “I am hungry” at Gwanghwamun at 4:53 PM on 13th January 2025.
3.1.3. Kaplan’s Solution: Character Models
Kaplan modified Reichenbach’s approach in a Millian direction. Kaplan distinguishes between two types of meaning. Content is what we have hitherto called meaning; for the Millian Kaplan, the content of a name is its referent. Meanwhile, character is a rule of use that determines what the content of an expression is in a given context.
Since Kaplan holds that there are no co-referential names in the strict sense, names have constant character according to him. For example, the content of ‘Boris Johnsonᵢ’ is produce Boris Johnsonᵢ as referent in all contexts.
In contrast, the character of pure indexicals is produce this speaker, produce the location of this utterance, and so forth. If we accept Kaplan’s position, we can explain how “I am here now” is logically necessary (the character of ‘I’, ‘now’, and ‘here’ ensures that this sentence is true in all contexts) but not metaphysically necessary (the sentence obtained by substituting ‘I’, ‘now’, and ‘here’ with their content in a given context is not necessarily true), and also resolve the case of Alice and Bob.
Remark. For a famous objection to Kaplan’s theory, see the answering machine paradox.
3.1.4. Fusion of Causal Theory and Character Models
Since both causal theory and character models are Millian theories, they can be fused to present a more sophisticated theory of names.
As mentioned earlier, Kaplan claimed that (1) names are mental phenomena, (2) accordingly, names with multiple bearers do not exist, and therefore (3) the character of names is constant. However, viewing names as psychological phenomena is somewhat burdensome. Instead, we might modify (1), (2), and (3) as follows:
- Names are linguistic phenomena.
- Names with multiple bearers exist.
- The character of a name produces as referent the most salient object in the current context from the set of that name’s bearers.
In addition to this, we add a fourth thesis from causal theory:
- The set of bearers of a name is the set of objects initially named in the causal chains associated with that name.
Such a fusion of causal theory and character models is attractive but not without limitations. In particular, it does not perfectly preserve the strength of causal theory: “the principle by which the mere transmission of a name enables the recipient to refer with that name”. (Author’s note: Well, so they say, but this theory seems perfect to me~)
3.2. Impure Indexicals
The meaning of impure indexicals such as ‘he’ and ‘she’, or ‘genuine indexicals’ such as ‘this’ and ‘that’, is more unclear than that of pure indexicals. Wettstein and Alison Mount developed theories along the lines that impure indexicals refer to the most salient person/object in the relevant context.
What then makes a particular object ‘the most salient object in the relevant context’? It seems most natural to view it as the interest of the speaker or hearer. But whose side should we take?
1. Mount: Principle of Mutual Salience
Claim. Mount argues that the necessary and sufficient condition for an impure indexical to refer to object $c$ is that the interests of speaker and hearer coincide and that the object commonly salient to both is A.
Problem. This view implies the counterintuitive conclusion that when the interests of speaker and hearer diverge, or when the hearer happens not to be paying attention to the speaker’s words, the reference of the indexical fails.
2. Kaplan: Intentionalism
Claim. Kaplan argues that the necessary and sufficient condition for an impure indexical to refer to object $c$ is that the speaker uses the indexical with a directing intention to refer to $c$.
Problem. When the speaker’s directing intention can be infinitely flexible, the Humpty Dumpty problem arises. For instance, provided the speaker has sufficient intention, the speaker could point to a photograph of Donald Trump and refer to Rudolf Carnap, which is highly counterintuitive.
Kaplan also presents the following complex Humpty Dumpty case:
A philosophy teacher had hung a photograph of Rudolf Carnap behind the lectern. However, one day a mischievous student secretly replaced Carnap’s photograph with one of Donald Trump. Unaware of this fact, when students entered the classroom, the teacher pointed behind himself and said “That is one of the greatest philosophers of the 20th century”.
In the above case, the teacher has the intention to refer to Rudolf Carnap’s photograph with the indexical ‘that’, but the hearers (the students) cannot grasp this intention. This raises the question: is the teacher’s utterance true or false?
According to strong intentionalism, since the teacher uttered ‘that’ with the intention to refer to Carnap, ‘that’ refers to Carnap, and therefore the teacher’s utterance is true.
3. Gricean Intentionalism
Gail Stine provides a different solution to Kaplan’s dilemma by grafting Grice’s semantics onto intentionalism. For indexical $i$ to successfully refer to object $c$, the speaker must have three intentions: the speaker must 1) have the intention to refer to $c$ with $i$, 2) have the intention to get the hearer to identify $c$ as the referent with $i$, and 3) have the intention to get the hearer to identify $c$ as referent through the hearer’s recognition of the speaker’s intention.
Gricean intentionalism resolves the Humpty Dumpty problem. To resolve Kaplan’s Humpty Dumpty problem, Stine presents the distinction between direct reference and indirect reference. In Kaplan’s case, the teacher has the intention to refer to Rudolf Carnap, but this intention is achieved through the intention to refer to the picture behind him. Therefore, the former is indirect reference and the latter is direct reference. Stine argues that when indirect referent and direct referent conflict, the direct referent takes priority. That is, the teacher’s statement is false.
4. Reimer-style Intentionalism
Gricean intentionalism has the limitation(?) that it cannot eliminate the Humpty Dumpty problem in cases of speakers with sufficiently strange beliefs, such as ‘a speaker who believes the other party can read their mind’.
In response, Reimer takes a different strategy for constraining intentionalism, which can be summarised as gesture priority. Reimer’s constrained intentionalism appears to resolve many more Humpty Dumpty problems than expected with remarkable clarity.
지시에 대하여 — 기술주의와 인과 이론
07 Jan 2025해당 글은 스탠퍼드 철학백과의 지시 항목을 요약 및 정리한 글이다.
1. 서론
”저것은 금성이다“, “영국의 마지막 여왕은 엘리자베스 2세이다”에서 ‘저것‘, ’금성’, ’영국의 마지막 여왕‘, ‘엘리자베스 2세’는 이 세상에서 오직 하나의 대상을 특정하여 지시하는 표현들이다. 그러나 이들 표현이 특정 대상을 지시하게 되는 구체적 원리는 철학적 의문으로 가득하다.
이 글에서 다루는 질문은 여섯 가지이다.
- 지시의 주체: 화자인가 단어인가?
- 지시 표현의 의미: 기술구인가, 지시체인가, 그 외의 것인가?
- 지시의 메커니즘: 지시 표현은 어떻게 특정 인물/대상에 결부되는가?
- 지시 이론의 범위: 모든 지시 표현은 공통의 메커니즘을 가지는가?
- 지시의 사적성: 지시는 화자의 사적 특징(e.g. 심리 상태)에 얼마나 의존하는가?
- 지시 이론의 의의: 지시 관계라는 것이 실제로 있는가? 철학적으로 유의미한가?
이 글에서 다루는 이론은 기술주의, 인과 이론, 특성 모델, 의도주의의 네 가지이며, 추가로 지시 회의주의를 짧게 다룬다.
| 기술주의 | 인과 이론 | 특성 모델 | 의도주의 | |
|---|---|---|---|---|
| 주체 | 화자 | 지시어 | 다원적 | 화자 |
| 의미 | 기술적 내용 | 지시체 | 특성과 내용 | |
| 메커니즘 | 단어는 구체적인 기술적 내용과 결부되어 그에 부합하는 대상을 지시한다. | 단어는 지시체의 명명식으로 거슬러 올라가는 인과적 사슬과 결부되어 지시한다. | 단어는 통상적 지시 규칙(특성)과 결부되어 대상(내용)을 지시한다. | 단어는 특정 대상을 지시하려는 의도와 결부되어 지시한다. |
| 범위 | 넓음 | 좁음(이름) | 보통 | 넓음 |
| 사적성 | 강한 사적성 | 약한 사적성 | 보통 사적성 | 강한~보통 사적성 |
| 학자 | (프레게), 러셀, 스트로슨, 라이헨바흐 | 밀, 크립키, 캐플런 | 캐플런 | 캐플런, 그라이스, 라이머 |
| 강점 | 프레게의 퍼즐을 설명 | 크립키의 논증을 해결 | 순수지표사의 원리를 해명 | 불순지표사의 원리를 해명 |
| 단점 | 크립키의 양상 논증 및 의미론적 논증 | 다수의 담지자를 가지는 이름의 문제 | 불순지표사에서 화자-청자 딜레마 발생 | 험티덤티 문제 |
2. 고유이름
2.1. 고유이름에 대한 기술주의 이론
기술주의 논제.
- 고유이름 $n$은 특정 기술적 내용 $P$와 결부된다.
- $n$이 $P$와 결부되는 이유는 화자가 마음속에서 $n$을 $P$와 결부하기 때문이다.
- $P$를 만족하는 대상 $c$가 유일하게 존재할 때, $n$은 $c$를 지시한다.
- $n$의 의미와 $n$의 지시체는 구별되며, 전자가 후자를 결정한다.
- $n$의 의미는 $P$이다.
예를 들어 ‘금성‘이라는 이름에 “태양계의 두 번째 행성”이라는 기술적 내용을 결부하는 화자는, 해당 기술적 내용을 만족하는 대상이 유일하며 그 대상이 금성이기 때문에 ’금성‘을 사용하여 금성을 지시한다.
Remark.
-
기술적 내용은 기술구로 이해하는 것이 표준적이지만, 설(Searle) 등은 기술적 내용이 언어적으로 명시 가능한 것뿐 아니라 지각에 기반할 수도 있다고 주장한다.
-
기술적 내용은, 그것을 만족시키는 대상이 불변한다는 특징을 가진다. 후술하다시피 이것은 기술주의가 지표사를 적절히 설명하지 못하는 원인이다.
-
$n$의 의미는 대언적이다. 후술하다시피 이것은 기술주의가 양상 반론에 직면하는 원인이다.
-
1번, 3번, 4번, 5번 논제는 이름의 의미론 — 즉, 이름을 정의역으로 가지는 의미 함수 $M$의 공역이 무엇인지 설명하는 이론 — 을 제공하고, 2번 논제는 이름의 메타의미론 — 즉, 각 이름 $n$에 대해 사상 $n \mapsto M(n)$은 어떻게 정의되는지 설명하는 이론 — 을 제공한다.
논변 1. 여러 담지자를 가지는 이름의 사례
A와 B가 ’보리스 존슨‘이라는 이름을 가진 두 명의 사람을 아는 경우를 고려하자. 한 명은 A와 B의 직장 동료이고, 다른 한 명은 영국의 전 총리이다. A가 B에게 “보리스 존슨은 중대한 실수를 저질렀다.”라고 말하자, B는 “어느 보리스 존슨을 의미하는가?”라고 묻는다. 이에 대해 A는 “영국의 전 총리”라고 대답한다.
위 사례에서 ’보리스 존슨‘이 지시하는 바는 (1) 화자인 A에게 결정권이 있으며, 이 결정은 (2) 화자가 마음속으로 염두에 두고 있는 기술적 내용을 매개로 이루어지는 것으로 보인다.
논변 2. 프레게의 퍼즐
다음 예문을 보자.
- 샛별은 개밥바라기이다.
- 산타클로스는 북극에 산다.
- 프레드는 마크 트웨인이 미국인이었다고 믿지만 새뮤얼 클레먼스가 미국인이었다고는 믿지 않는다.
1은 참이지만 선험적(a priori)이지 않다. 2는 무의미(nonsense)하지 않다. 3의 경우 프레드의 믿음은 정합적(consistent)이다.
만약 이름의 의미가 그 지시체라면 1은 자기동일성 법칙에 따라 선험적이어야 하고, 2는 지시체(의미)가 결여된 문장이므로 무의미해야 하고, 3의 경우 마크 트웨인과 새뮤얼 클래먼스의 의미가 같으므로 프레드의 믿음은 비정합적이어야 한다. 그러나 기술주의는 이름의 의미와 지시체를 구별함으로써 세 예문에 대한 적절한 설명을 내놓는다.
반론 1. 양상 논증
만약 내가 ‘보리스 존슨’에 대해 “브렉시트를 시행한 영국의 전 총리”라는 기술구를 결부시킨다 해도 나는 아래 문장을 참이라고 주장할 수 있다.
1. 보리스 존슨은 브렉시트를 시행하지 않을 수 있었다.
그러나 이름의 의미가 기술구와 동등하다면 1은 2와 동치이다.
2. 다음이 사실일 수 있었다: 브렉시트를 시행한 영국의 전 총리는 브렉시트를 시행하지 않았다.
그러나 2는 거짓이다. 따라서 이름의 의미는 기술적 내용이 아니다.
Remark. 이름의 의미가 대상(re)이 아닌 기술적 내용(dicto)이므로, 1 → 2는 De Dicto 치환이다. De Re 치환의 경우 1은 3이 된다.
3. 브렉시트를 시행한 영국의 전 총리가 $c$일 때, 다음이 사실일 수 있었다: $c$는 브렉시트를 시행하지 않았다.
2와 달리 3은 참으로 간주하는 데 문제가 없다.
Remark. 양상 논증에 대처하기 위해 기술주의자는 3번, 4번 논제를 수정하고 5번 논제를 기각할 수 있다.
-
$P$를 만족하는 대상 $c$가 현실 세계에서 유일하게 존재할 때, $n$은 $c$를 지시한다.
-
$n$의 의미는 $n$의 지시체, 즉 $c$이다. (즉, $n$의 의미는 대물적이다)
그러나 이렇게 수정된 기술주의는 프레게의 퍼즐을 적절히 설명하지 못할 뿐더러, 다음의 의미론적 논증 또한 적절히 설명하지 못한다는 점에서 한계가 많은 이론이다.
반론 2. 의미론적 논증
의미론적 논증은 방금 제시한 수정 기술주의를 비롯, 기술주의에 속하는 일군의 이론을 반박하는 논증이다. 요지는, 많은 경우 화자가 이름 $n$에 결부하는 기술적 내용 $P$는 세계에서 특정 대상을 유일하게 집어내지 못하며(즉, 기술은 불충분하며), 애초에 기술적 내용은 지시에 불필요하다는 것이다.
먼저 기술적 내용이 불충분함을 보여주는 사례로서 크립키가 제시한 파인만-겔만 사고실험이 있다. 대부분의 사람이 ‘파인만’이라는 이름에 결부하는 기술적 내용은 “미국의 유명한 물리학자” 정도이다. 이는 겔만 또한 해당하는 기술이다. 그러나 우리는 ‘파인만’이라는 이름으로 파인만을 성공적으로 지시하는 듯하다.
나아가 기술적 내용이 불필요함을 보여주는 사례로서 마찬가지로 크립키가 제시한 괴델-슈미트 사고실험을 보자. 크립키는 다음의 상황을 가정한다.
사실 산술의 불완전성을 처음 증명한 수학자는 괴델이 아닌 슈미트라는 무명의 수학자다. 그러나 증명을 발표하기 전, 슈미트는 의문스러운 죽음을 당했고 그의 증명은 괴델의 손에 들어가 괴델의 이름으로 발표되었다.
(이 괴상한 사고실험에 대해서는 자기보다 위대한 논리학자인 괴델을 시기했던 크립키의 분풀이라는 카더라가 전해진다)
만약 (P1) 위 가정이 사실이고, (P2) 기술주의가 올바르며, (P3) 대부분의 사람이 ’괴델‘이라는 이름에 결부하는 기술적 내용이 ”산술의 불완전성을 처음 증명한 수학자“라면, (C) 대부분의 사람이 ’괴델‘이라는 이름으로 지시하는 대상은 괴델이 아닌 슈미트라는 결론이 도출된다. 그러나 이것은 반직관적이다. 따라서 기술주의는 올바르지 않다.
Remark. 의미론적 논증을 극복하기 위해기술주의자는 다음 두 노선 중 하나를 택할 수 있다.
-
이름에 결부되는 기술적 내용은 화자에게 개인적으로 이용 가능한 정보를 초월할 수 있다.
-
이름에 결부되는 기술적 내용으로 “나에게 이 이름을 전달해 준 사람이 그 이름으로 지시하고자 했던 사람”을 채택할 수 있다.
스트로슨은 1번 노선을 선택한다. 그에 따르면 화자는 이름과 결부되어야 하는 기술적 내용을 제시하는 작업을 타인에게 의존할 수 있다. 이 경우, ‘파인만’ 또는 ‘괴델’의 의미는 파인만 전문가, 또는 괴델 전문가가 각 이름에 결부하는 기술적 내용이다. 그러나 스트로슨주의는 화자의 지시 의도를, 실제로 이루어지는 지시와 무관한 것으로 만든다는 점에서 반직관적이라는 한계가 있다.
2번 노선은 인과 이론과 밀접하게 닿아있다. 해당 이론을 살펴보도록 하자.
2.2. 고유이름에 대한 밀주의 및 인과 이론
밀주의 논제. 고유이름의 의미는 곧 지시체이다.
“밀주의”라는 이름에서 알 수 있듯이 이 입장은 존 스튜어트 밀로 거슬러 올라간다. 밀주의 이론들은 “샛별은 개밥바라기이다”와 같은 동일성 진술이 후험적이지만 필연적으로 참임을 함의한다.
Remark. 크립키는 선험적이지만 우연적으로 참인 문장 또한 존재한다고 주장하며, “미터 원기의 길이는 1m이다”를 그 사례로 든다.
밀주의 논제는 이름에 대한 의미론을 제공한다. 이를 보충하는 대표적인 메타의미론으로 인과 이론이 있다.
인과 이론.
- 처음으로 대상 $c$를 이름 $n$으로 부르는 사건인 명명식이 있다.
- 명명식에 참여한 사람을 시초로 하여, $n$으로 $c$를 지시하는 화자는 의사소통을 통해 해당 용례를 다른 화자에게 전달한다. 이같은 용례의 전달은 이름의 인과적 사슬을 형성한다.
- 이름 $n$의 의미(지시체)는 $n$의 인과적 사슬의 시발점에 이루어진 명명식에서 명명된 대상이다.
인과 이론의 미묘한 문제 중 하나는 어떤 의사소통 전달이 인과적 사슬에 실질적으로 참여하는지를 구별하는 문제이다. 일례로 내가 직장 동료에게 거만한 나의 고양이를 ’나폴레옹‘으로 불렀다고 해서 이 의사소통이 ’나폴레옹‘이라는 이름의 인과적 사슬에 실질적으로 참여하지는 않는다(이름의 가식적 사용). 또한 마다가스카르 사례와 같이 이름의 지시체가 도중에 바뀌는 경우도 있다(이름의 혼동된 사용). 여기서는 이 문제에 대한 논의를 생략한다.
2.3. 다수의 담지자가 있는 이름의 문제
앞선 ‘보리스 존슨‘의 사례와 같이 다수의 담지자가 있는 이름의 경우, 지시의 결정권은 화자에게 있는 듯하다. 이 사실은 고전적 기술주의의 경우 문제가 되지 않는다. 그러나 스트로슨주의와 인과 이론에게 이 문제는 골칫거리이다.
스트로슨주의의 경우 이름 $n$의 지시체는 전문가 집단에 의해 유일하게 결정되므로 최대 1개의 지시체만을 가질 수 있다. 그러나 다수의 담지자가 있는 이름이 분명 가능하므로, 스트로슨주의는 이름을 더 세분화해서 생각해야 한다. 즉, 문자적으로 동등하지만($\ulcorner n_1 \urcorner = \ulcorner n_2 \urcorner$) 의미론적으로 다른($n_1 \mapsto c_1, n_2 \mapsto c_2, c_1 \neq c_2$) 이름들이 가능하다고 보는 것이다. 그러나 이 경우, 화자가 $\ulcorner n_i \urcorner$를 발화할 때 $i$를 결정하는 원리가 무엇이냐는 문제가 생긴다. 해당 원리가 화자의 내면 기술구일 수는 없는데, $\ulcorner n_i \urcorner$을 사용하여 $c_1$ 또는 $c_2$를 지시할 수 있으나 $c_1$과 $c_2$를 구별해 내는 데 충분한 지시적 내용을 갖추지 못한 화자를 떠올릴 수 있기 때문이다.
필자는 이탤릭체 내용을 받아들이지 못했다. 그런 경우가 정말로 있나?
밀주의에도 비슷한 문제가 발생한다. 이 문제를 극복하기 위해 캐플런은 이름을 심리 현상으로 간주한다. 즉, 이름 $n$은 문자적 내용 $\ulcorner n \urcorner$과, $\ulcorner n \urcorner$으로 $c$를 지시하려는 의도가 얽힌 심리 현상이며, 인과적 사슬을 통해 전달되는 것은 이 심리 현상이다. 이에 따르면 다수의 담지자를 가지는 이름은 $n_1 = (\ulcorner n \urcorner, c_1), n_2 = (\ulcorner n \urcorner, c_2)$과 같이 구별되는 이름이며, $n_1$과 $n_2$를 성공적으로 습득한 화자는 자신의 의도에 따라 $n_1$ 또는 $n_2$를 선택하여 사용할 수 있다.
캐플런과 구별되는 또 하나의 노선은 다수의 담지자 문제를 인과 이론과 지표사 이론의 혼합으로 해결하려는 시도이다. 이 노선은 르카나티, 펠처, 래인스버리 등에 의해 채택되었으며, 다음 글에서 살펴 볼 지표사 이론에 대한 이해를 요구한다.
On Reference — Descriptivism and Causal Theory
07 Jan 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
This article is a summary and analysis of the Stanford Encyclopedia of Philosophy entry on reference.
1. Introduction
In “That is Venus” and “The last Queen of England is Elizabeth II”, the expressions ‘that’, ‘Venus’, ‘the last Queen of England’, and ‘Elizabeth II’ are expressions that refer to exactly one object in this world by specifying it. However, the specific principles by which these expressions come to refer to particular objects are shrouded with philosophical puzzles.
This article addresses six questions:
- The subject of referring: Is reference done by the speaker via their intention, or by the word via its meaning?
- The meaning of referring expressions: Is it a (defininte) description, the referent, or something else?
- The mechanism of reference: What grounds the correspondence between referring expressions and referred objects?
- The scope of theories of reference: Do all referring expressions share a common mechanism?
- The privacy of reference: To what extent does reference depend on the speaker’s private states (e.g. intentions to refer)?
- The significance of theories of reference: Does the reference relation actually exist? Is it philosophically significant?
This article examines four theories: descriptivism, causal theory, character model, and intentionalism, and briefly discusses referential scepticism.
| Descriptivism | Causal Theory | Character Model | Intentionalism | |
|---|---|---|---|---|
| Subject | Speaker | Referring expression | Pluralistic | Speaker |
| Meaning | Descriptive content | Referent | Character and content | |
| Mechanism | Words are associated with specific descriptive content and refer to objects that satisfy them. | Words are associated with causal chains that trace back to the referent’s initial baptism. | Words are associated with conventional referential rules (character) to refer its referent (content). | Words are epiphenomenal to the speaker’s intention to refer to a specific objects. |
| Scope | Broad | Narrow (names) | Moderate | Broad |
| Privacy | Strong privacy | Weak privacy | Moderate privacy | Strong~moderate privacy |
| Scholars | (Frege), Russell, Strawson, Reichenbach | Mill, Kripke, Kaplan | Kaplan | Kaplan, Grice, Reimer |
| Strengths | Solves Frege’s puzzle | Solves Kripke’s arguments | Explains how pure indexicals work | Explains how impure indexicals work |
| Weaknesses | Kripke’s modal and semantic arguments | Problems with names having multiple bearers | Speaker-hearer dilemma arises with impure indexicals | Humpty Dumpty problem |
2. Proper Names
2.1. Descriptivist Theory of Proper Names
Descriptivist Thesis.
- A proper name $n$ is associated with specific descriptive content $P$.
- $n$ is associated with $P$ because the speaker privately (mentally) associates $n$ with $P$.
- When there exists a unique object $c$ that satisfies $P$, $n$ refers to $c$.
- The meaning of $n$ ($P$) and the referent of $n$ ($c$) are distinct, with the former determining the latter.
For example, a speaker who associates the name ‘Venus’ with the descriptive content “the second planet of the solar system” refers to Venus using ‘Venus’ because there is a unique object satisfying that descriptive content, and that object is Venus.
Remark.
-
while it is standard to understand descriptive content as descriptions, scholars such as Searle argue that descriptive content need not be linguistically specifiable but may also be based on perception.
-
The satisfaction relation of descriptive content is speaker-independent. As we shall see, this spells problem in explaining indexicals.
-
Furthermore, the satisfaction relation is de dicto. As we shall see, this spells problem in dealing with modality.
-
Theses 1, 3, 4 provide a semantics for names — a theory specifing the domain (names) and codomain (descriptive content) of the meaning function $M$ — while thesis 2 provides a metasemantics for names — a theory explaining how the map $n \mapsto M(n)$ is defined for each name $n$.
Argument 1. Cases of Names with Multiple Bearers
Consider a case where A and B know two people named ‘Boris Johnson’. One is a colleague of A and B, and the other is the former Prime Minister of Britain. When A says to B, “Boris Johnson has made a grave mistake,” B asks, “Which Boris Johnson do you mean?” To this, A replies, “The former Prime Minister of Britain.”
In the above case, it appears that (1) the speaker A has the authority to determine what ‘Boris Johnson’ refers to, and this determination is made (2) via the descriptive content that the speaker has in mind.
Argument 2. Frege’s Puzzle
Consider the following examples:
- The morning star is the evening star.
- Santa Claus lives at the North Pole.
- Fred believes that Mark Twain was American but does not believe that Samuel Clemens was American.
Let us first make some remarks. Statement 1 is true but not a priori. Statement 2 is not incomprehensible. Fred’s belief expressed in Statement 3 is not inconsistent.
If the meaning of a name were its referent, then 1 would be a priori by the law of self-identity, 2 would be nonsense as it has as its subject an expression lacking a referent, and in case 3, Fred’s belief would be inconsistent since Mark Twain and Samuel Clemens share the same referent. On the other hand, descriptivism provides adequate explanations for all three statements by distinguishing between the meaning and referent of names.
Objection 1. The Modal Argument
Even if I associate the description “the former British Prime Minister who implemented Brexit” with ‘Boris Johnson’, I can still assert the following sentence as true:
1. Boris Johnson might not have implemented Brexit.
However, if the meaning of a name is equivalent to a description, then 1 is equivalent to 2.
2. The following might have been the case: the former British Prime Minister who implemented Brexit did not implement Brexit.
But 2 is false. Therefore, the meaning of a name is not descriptive content.
Remark. Since the meaning of the name is de dicto, the inference from 1 to 2 is a de dicto substitution. In the case of de re substitution, 1 becomes 3.
3. Let $c$ be that person who is the former British Prime Minister who implemented Brexit. Then the following might have been the case: $c$ did not implement Brexit.
Unlike 2, there is no problem in regarding 3 as true. Hence, to deal with the modal argument, descriptivists may attempt to modify theses 3 and 4.
-
When there exists a unique object $c$ that satisfies $P$ in the actual world, $n$ refers to $c$.
-
The meaning of $n$ is the referent of $n$, i.e., $c$. (That is, the meaning of $n$ is de re)
However, this modified descriptivism not only fails to adequately explain Frege’s puzzle but also fails to adequately explain the following semantic argument, making it a theory with many limitations.
Objection 2. The Semantic Argument
The semantic argument is an argument that refutes a group of theories belonging to descriptivism, including the modified descriptivism just presented. The gist is that in many cases, the descriptive content $P$ that a speaker associates with a name $n$ fails to uniquely pick out a specific object in the world (i.e., the description is insufficient), and descriptive content is unnecessary for reference in the first place.
As a case showing that descriptive content is insufficient, there is the Feynman-Gell-Mann thought experiment presented by Kripke. The descriptive content that most people associate with the name ‘Feynman’ is something like “a famous American physicist”. This description also applies to Gell-Mann. However, we seem to successfully refer to Feynman with the name ‘Feynman’.
Furthermore, as a case showing that descriptive content is unnecessary, consider the Gödel-Schmidt thought experiment likewise presented by Kripke. Kripke assumes the following situation:
In fact, the mathematician who first proved the incompleteness of arithmetic was not Gödel but an unknown mathematician named Schmidt. However, before publishing the proof, Schmidt died under mysterious circumstances, and his proof fell into Gödel’s hands and was published under Gödel’s name.
(Regarding this bizarre thought experiment, there is a rumour that it was Kripke’s way of venting his jealousy towards Gödel, a logician greater than himself)
If (P1) the above assumption is true, (P2) descriptivism is correct, and (P3) the descriptive content that most people associate with the name ‘Gödel’ is “the mathematician who first proved the incompleteness of arithmetic”, then (C) the object that most people refer to with the name ‘Gödel’ is Schmidt, not Gödel. However, this is counterintuitive. Therefore, descriptivism is not correct.
Remark. To overcome the semantic argument, descriptivists can take one of two approaches:
-
The descriptive content associated with a name can transcend information personally available to the speaker.
-
The descriptive content associated with a name can adopt “the person whom the person who transmitted this name to me intended to refer to with that name”.
Strawson chooses approach 1. According to him, speakers can rely on others for the task of providing the descriptive content that should be associated with names. In this case, the meaning of ‘Feynman’ or ‘Gödel’ is the descriptive content that Feynman experts or Gödel experts associate with each name. However, Strawsonian theory has the limitation of being counterintuitive in that it makes the speaker’s referential intention irrelevant to the actual reference.
Approach 2 is closely connected to causal theory. Let us examine this theory.
2.2. Millianism and Causal Theory of Proper Names
Millian Thesis. The meaning of a proper name is its referent.
As the name suggests, this position traces back to John Stuart Mill. Millian theories imply that identity statements such as “The morning star is the evening star” are a posteriori but necessarily true.
Remark. Kripke also argues that there exist sentences that are a priori but contingently true, citing “The length of the standard metre is 1m” as an example.
The Millian thesis provides semantics for names. A representative metasemantics supplementing this is the causal theory.
Causal Theory.
- There is an initial baptism, an event in which object $c$ is first called by name $n$.
- Starting with those who participated in the initial baptism, speakers who refer to $c$ with $n$ transmit this usage to other speakers through communication. Such transmission of usage forms a causal chain of the name.
- The meaning (referent) of name $n$ is the object named in the initial baptism that occurred at the starting point of $n$’s causal chain.
One subtle problem with causal theory is distinguishing which communicative transmissions substantially participate in the causal chain. For instance, if I called my arrogant cat ‘Napoleon’ to a work colleague, this communication does not substantially participate in the causal chain of the name ‘Napoleon’ (parasitic use of names). There are also cases where the referent of a name changes along the way, such as the Madagascar case (confused use of names). We omit discussion of this problem here.
2.3. The Problem of Names with Multiple Bearers
In cases of names with multiple bearers, such as the earlier ‘Boris Johnson’ example, the authority to determine reference seems to lie with the speaker. This fact poses no problem for classical descriptivism. However, this
In cases of names with multiple bearers, such as the earlier ‘Boris Johnson’ example, the authority to determine reference seems to lie with the speaker. This fact poses no problem for classical descriptivism. However, this spells trouble for Strawsonian and causal theories.
In the case of Strawson’s theory, the referent of a name $n$ is uniquely determined by a group of experts, so it can have at most one referent. However, since names with multiple bearers are clearly possible, Strawson’s theory must consider names in a more nuanced way. That is, it must acknowledge the possibility of names that are literally equivalent ($\ulcorner n_1 \urcorner = \ulcorner n_2 \urcorner$) but semantically different ($n_1 \mapsto c_1, n_2 \mapsto c_2, c_1 \neq c_2$). However, this raises the question of what principle determines $i$ when the speaker utters $\ulcorner n_i \urcorner$. This principle cannot be the speaker’s internal description, as one can imagine a speaker who can refer to either $c_1$ or $c_2$ using $\ulcorner n_i \urcorner$, but lacks sufficient descriptive content to distinguish between $c_1$ and $c_2$.
I cannot accept the italicised content. Are there really such cases?
A similar problem arises in Millianism. To overcome this issue, Kaplan considers names as psychological phenomena. That is, a name $n$ is a psychological phenomenon intertwined with the literal content $\ulcorner n \urcorner$ and the intention to refer to $c$ using $\ulcorner n \urcorner$, and what is transmitted through the causal chain is this psychological phenomenon. According to this view, names with multiple bearers are distinguished as $n_1 = (\ulcorner n \urcorner, c_1), n_2 = (\ulcorner n \urcorner, c_2)$, and a speaker who has successfully acquired $n_1$ and $n_2$ can choose to use either $n_1$ or $n_2$ according to their intention.
Another approach that differs from Kaplan’s is the attempt to resolve the problem of multiple bearers through a combination of causal theory and indexical theory. This approach has been adopted by Lucanati, Pelcher, and Rainsbury, and requires an understanding of the indexical theory that will be examined in the following text.
대각선 논법 없이 실수의 비가산성 증명하기
26 Dec 2024정리. $\mathbb{R}$은 비가산이다. 즉, $\mathbb{N}$에서 $\mathbb{R}$로 가는 전사함수는 존재하지 않는다.
수학과 2학년 정도 되면 한번쯤은 들어 봤을 정리이다. 가장 널리 알려진 증명은 칸토어의 대각선 논법이다. 하지만 대각선 논법 없이 이 정리를 증명하는 방법이 있다. 각각 $\mathbb{R}$의 순서적 특징과, 위상적 특징을 이용한다.
1. 동형성 정리를 이용한 증명
칸토어의 동형성 정리에 따르면 다음을 만족하는 전순서 집합 $(S, \leq)$는 모두 순서 동형이다.
- $S$는 가산이다.
- $S$는 조밀하다. 즉, $x, y \in S$에 대해 $x < y$라면 $x < z < y$인 $z \in S$가 존재한다.
- $S$는 상계 및 하계를 가지지 않는다.
$(\mathbb{Q}, \leq)$는 위 세 조건을 모두 만족하고, $(\mathbb{R}, \leq)$는 2와 3을 만족한다. 따라서 만약 $\mathbb{R}$이 가산이면 $(\mathbb{R}, \leq)$는 $(\mathbb{Q}, \leq)$와 순서 동형이다. 하지만 전자는 완비인데 반해 후자는 그렇지 않으므로 $\mathbb{R}$은 비가산이다. ■
2. 콤팩트성을 이용한 증명
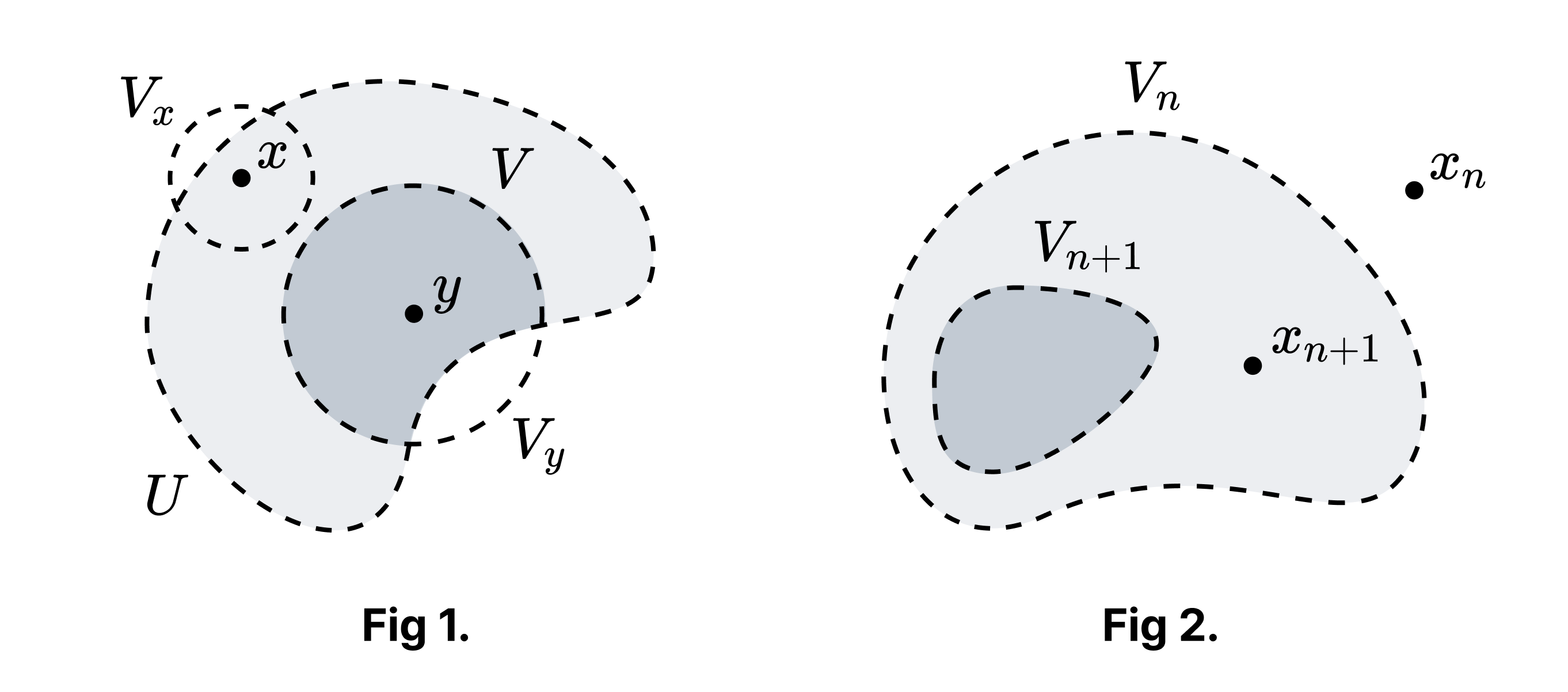
$X$가 고립점이 없는 콤팩트한 하우스도르프 공간이라고 하자. 또한 $X \neq \varnothing$이라고 하자.
Claim 1. $U \neq \varnothing$가 $X$의 열린 집합이라고 하자. $x \in X$에 대해 $x \notin \bar{V}$이면서 $V \subset U$인 열린 집합 $V$가 존재한다.
Proof of Claim 1. $x \neq y$이며 $y \in U$가 존재한다. 왜냐하면 $x \in U$인 경우 $X$가 고립점을 가지지 않으므로 존재하고, $x \notin U$인 경우 $U$가 공집합이 아니기 때문에 존재하기 때문이다. $X$가 하우스도르프이므로 $x, y$를 근방 $V_x, V_y$로 분리할 수 있다. $V = V_y \cap U$가 얻고자 하는 집합이다 (Fig 1에서 짙게 색칠된 영역). □
Claim 2. $X$는 비가산이다.
Proof of Claim 2. $X$가 가산이라고 하자. $X$의 원소들을 $\lbrace x_n \rbrace_{n \in \mathbb{Z}^+}$와 같이 나열한다. $V_0 = X$라고 하자. Claim 1에 의해 각 $n$에 대해 $x_n \notin \bar{V_n}$인 열린 집합 $V_n$이고 $V_n \subset V_{n-1}$인 열린 집합 $V_n$이 존재한다 (Fig 2). $X$가 콤팩트하므로 유한 교집합 성질에 의해
\[K = \bigcap_{n \in \mathbb{Z}^+} \bar{V}_n \neq \varnothing\]이다. 하지만 $x_n \in K$라면 $x_n \in \bar{V}_n$이 되어 모순이다. 따라서 $X$는 비가산이다. □
Claim 3. $\mathbb{R}$은 비가산이다.
Proof of Claim 3. $[0, 1]$은 고립점을 가지지 않는 콤팩트 하우스도르프 공간이다. 따라서 비가산이다. 이에 따라 $\mathbb{R}$은 비가산이다. ■
Proving the Uncountability of Real Numbers Without the Diagonal Argument
26 Dec 2024Theorem. $\mathbb{R}$ is uncountable. That is, there exists no surjective function from $\mathbb{N}$ to $\mathbb{R}$.
This is a theorem that any sophomore student would have encountered at least once. The most widely known proof is Cantor’s diagonal argument. However, there are methods to prove this theorem without the diagonal argument. These utilise the order-theoretic and topological properties of $\mathbb{R}$, respectively.
1. Proof Using the Isomorphism Theorem
Cantor’s isomorphism theorem states that all totally ordered sets $(S, \leq)$ satisfying the following conditions are order isomorphic:
- $S$ is countable.
- $S$ is dense. That is, for $x, y \in S$ with $x < y$, there exists $z \in S$ such that $x < z < y$.
- $S$ has neither an upper bound nor a lower bound.
$(\mathbb{Q}, \leq)$ satisfies all three conditions above, while $(\mathbb{R}, \leq)$ satisfies conditions 2 and 3. Therefore, if $\mathbb{R}$ were countable, then $(\mathbb{R}, \leq)$ would be order isomorphic to $(\mathbb{Q}, \leq)$. However, the former is complete while the latter is not, so $\mathbb{R}$ is uncountable. ■
2. Proof Using Compactness

Let $X$ be a compact Hausdorff space with no isolated points. Also assume that $X \neq \varnothing$.
Claim 1. Let $U \neq \varnothing$ be an open subset of $X$. For $x \in X$, there exists an open set $V$ such that $x \notin \bar{V}$ and $V \subset U$.
Proof of Claim 1. There exists $y \in U$ where $x \neq y$. This is because if $x \in U$, then since $X$ has no isolated points such a $y$ must exist, and if $x \notin U$, then such a $y$ exists because $U$ is non-empty. Since $X$ is Hausdorff, we can separate $x$ and $y$ by neighbourhoods $V_x$ and $V_y$. Then $V = V_y \cap U$ is the desired set (the dark shaded region in Fig 1). □
Claim 2. $X$ is uncountable.
Proof of Claim 2. Suppose $X$ is countable. Enumerate the elements of $X$ as $\lbrace x_n\rbrace _{n \in \mathbb{Z}^+}$. Let $V_0 = X$. By Claim 1, for each $n$ there exists an open set $V_n$ such that $x_n \notin \bar{V_n}$ and $V_n \subset V_{n-1}$ (Fig 2). Since $X$ is compact, by the finite intersection property we have
\[K = \bigcap_{n \in \mathbb{Z}^+} \bar{V}_n \neq \varnothing.\]However, if $x_n \in K$, then $x_n \in \bar{V}_n$, which is a contradiction. Therefore, $X$ is uncountable. □
Claim 3. $\mathbb{R}$ is uncountable.
Proof of Claim 3. $[0, 1]$ is a compact Hausdorff space with no isolated points. Therefore, it is uncountable. Consequently, $\mathbb{R}$ is uncountable. ■
칸토어-벤딕슨 정리와 폴란드 공간
25 Dec 2024정의. 위상공간 $X$의 집합 $P$에 대해 $P’ = P$일 때 $P$를 완벽한 집합perfect set이라고 한다. ($P’$은 $P$의 집적점들의 집합)
Remark. 모든 완벽한 집합은 닫힌 집합이지만, 역은 성립하지 않는다. 일반적으로 $S \not\subset S’$ ($S$가 고립점을 가짐), $S’ \not\subset S$ ($S$가 닫힌 집합이 아님) 임에 유의하라. 뒤집어 말해, 완벽한 집합은 고립점이 없는 닫힌 집합이다.
정의. $X$의 임의의 부분공간이 린델뢰프일 때 $X$를 세습적 린델뢰프hereditarily Lindelöf라고 한다.
약한 칸토어-벤딕슨 정리. $X$가 세습적 린델뢰프 공간이라고 하자. $F \subset X$가 닫힌 집합일 때 어떤 완벽한 집합 $P$와 가산집합 $C$가 존재하여 $F = P \sqcup C$이다.
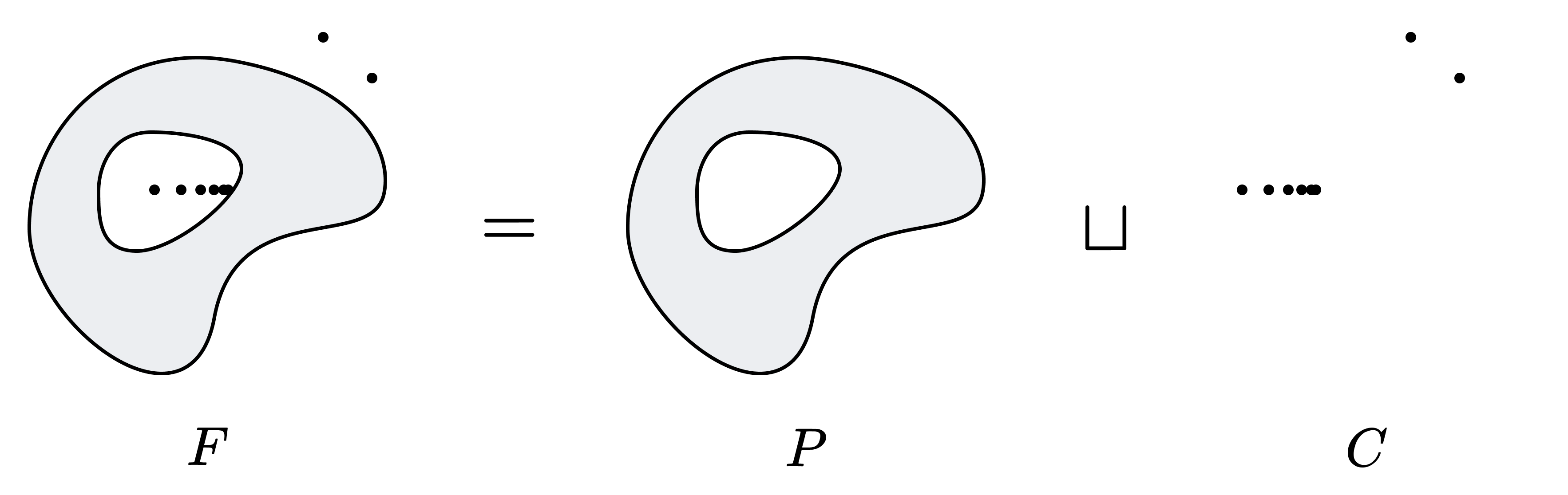
완벽한 집합은 고립점이 없는 닫힌 집합이므로, 위 정리는 “닫힌 집합은 최대 가산 개의 고립점을 가진다”로 재진술할 수 있다.
증명. 다음과 같이 $P, C$를 정의한다.
\[P = \lbrace x \in F : \text{For all nbd $U$ of $x$, $U \cap F$ is uncountable} \rbrace\] \[C = \lbrace x \in F : \text{There exists a nbd $U$ of $x$ s.t. $U \cap F$ is countable} \rbrace\]$F = P \sqcup C$임에 주목하라.
Claim 1. $C$는 $F$에서 열린 집합이다.
Proof of Claim. $x \in C$일 때 어떤 $x$의 근방 $U$가 존재하여 $U \cap F$가 가산이다. 즉, 임의의 $y \in U \cap F$에 대해 $U$는 $y$의 근방이고 $U \cap F$가 가산이므로 $y \in C$이다. 따라서 $U \cap F \subset C$이다. □
Claim 2. $C$는 가산이다.
Proof of Claim. $F$의 부분공간 토폴로지를 생각하자. 가정에 의해 이 토폴로지는 린델뢰프이다. 임의의 $x \in C$에 대해 $U_x \cap F$가 가산인 $x$의 근방 $U_x$를 찾을 수 있다. 그러면 $\lbrace U_x \rbrace_{x \in C}$는 $C$의 $F$-열린 덮개이며, 린델뢰프 가정에 의해 $C = \bigcup_{\alpha \in J} U_\alpha$ ($J$는 가산)이다. $U_\alpha$가 가산이므로 $C$는 가산이다. □
Claim 3. $P$는 완벽하다.
Proof of Claim. Claim 1에 의해 $P$는 $F$에서 닫힌 집합이며, $F$가 닫힌 집합이므로 $P$는 $X$에서 닫힌 집합이다. 따라서 $P’ \subset P$이다. 역을 보이기 위해 $x \in P$라고 하자. 임의의 $x$의 근방 $U$에 대해 $U \cap F = (U \cap C) \sqcup (U \cap P)$가 비가산이다. $C$가 가산이므로, $U \cap P$가 비가산이어야 한다. 따라서 $U$는 $P$와 $\lbrace x \rbrace$보다 큰 교집합을 가지며, $x \in P’$이다. ■
정의. 분리 가능한separable 완비 거리화 가능 공간을 폴란드 공간Polish space이라고 한다.
거리화 가능 공간에서 분리 가능성, 2차 가산, 그리고 린델뢰프는 동치이므로 해당 세 가지 조건 중 하나로 정의를 대체할 수 있다. ‘폴란드 공간’이라는 이름은 해당 공간을 처음으로 연구한 학자들인 시에르핀스키, 쿠라토프스키, 타르스키 등이 폴란드인들인 데에서 유래했다.
$X$가 폴란드 공간이라는 더 강한 조건이 주어지면 칸토어-벤딕슨 분해가 유일함을 증명할 수 있다.
강한 칸토어-벤딕슨 정리. $X$가 폴란드 공간이라고 하자. $F \subset X$가 닫힌 집합일 때 어떤 완벽한 집합 $P$와 가산집합 $C$가 존재하여 $F = P \sqcup C$이다. 또한, 해당 분해는 유일하다.
또한 다음이 성립한다.
정리. 폴란드 공간의 완벽한 집합은 $2^{\aleph_0}$의 크기를 가진다.
증명. 추후 기술적 집합론에 대한 글에서 따로 다룰 예정.
이로부터 다음의 결론이 따라 나온다.
따름정리: 실수의 닫힌집합에서의 연속체 가설. 실수의 닫힌집합은 가산이거나 $2^{\aleph_0}$의 크기를 가진다.
증명. 실수는 폴란드 공간이므로 칸토어-벤딕슨 정리에 의해 모든 닫힌집합이 가산집합과 완벽한 집합의 서로소 합으로 분해된다. 후자가 공집합일 경우 해당 닫힌집합은 가산이며, 그렇지 않을 경우 $2^{\aleph_0}$이다. ■
칸토어는 위 정리의 증명으로부터 일반적인 연속체 가설을 증명할 수 있으리라는 희망을 품었지만 잘 알려져 있다시피 그 희망은 실현되지 못했다.
The Cantor-Bendixson Theorem and Polish Space
25 Dec 2024This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
Definition. A set $P$ in a topological space $X$ is perfect when $P’ = P$. Here, $P’$ denotes the set of limit points of $P$.
Remark. Every perfect set is a closed set, but the converse does not hold. Recall that in general $S \not\subset S’$ (when $S$ has isolated points) and $S’ \not\subset S$ (when $S$ is not a closed set). It follows that a perfect set is a closed set with no isolated points.
Definition. A topological space $X$ is hereditarily Lindelöf when every subspace of $X$ is Lindelöf.
Weak Cantor-Bendixson Theorem. Let $X$ be a hereditarily Lindelöf space. For any closed set $F \subset X$, there exist a perfect set $P$ and a countable set $C$ such that $F = P \sqcup C$.

Since a perfect space is a closed space with no isolated points, the above theorem can be restated as: A closed subspace of a hereditarily Lindelöf space has at most countable isolated points.
Proof. We define $P$ and $C$ as follows:
\[P = \lbrace x \in F : \text{For all nbd $U$ of $x$, $U \cap F$ is uncountable} \rbrace\] \[C = \lbrace x \in F : \text{There exists a nbd $U$ of $x$ s.t. $U \cap F$ is countable} \rbrace\]Note that $F = P \sqcup C$.
Claim 1. $C$ is open in $F$.
Proof of Claim. When $x \in C$, there exists a neighbourhood $U$ of $x$ such that $U \cap F$ is countable. That is, for any $y \in U \cap F$, $U$ is a neighbourhood of $y$ and $U \cap F$ is countable, so $y \in C$. Therefore $U \cap F \subset C$. □
Claim 2. $C$ is countable.
Proof of Claim. Consider the subspace topology on $F$. By hypothesis, this topology is Lindelöf. For any $x \in C$, we can find a neighbourhood $U_x$ of $x$ such that $U_x \cap F$ is countable. Then $\lbrace U_x \rbrace_{x \in C}$ is an $F$-open cover of $C$, and by the Lindelöf hypothesis, $C = \bigcup_{\alpha \in J} U_\alpha$ where $J$ is countable. Since each $U_\alpha$ is countable, $C$ is countable. □
Claim 3. $P$ is perfect.
Proof of Claim. By Claim 1, $P$ is a closed set in $F$, and since $F$ is a closed set, $P$ is a closed set in $X$. Therefore $P’ \subset P$. To show the reverse inclusion, let $x \in P$. For any neighbourhood $U$ of $x$, we have that $U \cap F = (U \cap C) \sqcup (U \cap P)$ is uncountable. Since $C$ is countable, $U \cap P$ must be uncountable. Therefore $U$ has intersection with $P$ larger than $\lbrace x \rbrace$, and hence $x \in P’$. ■
Definition. A separable complete metrisable space is called a Polish space.
In metrisable spaces, separability, second countability, and the Lindelöf property are equivalent, so the definition can be replaced with any of these three conditions. The name ‘Polish space’ derives from the fact that the mathematicians who first studied these spaces — Sierpiński, Kuratowski, Tarski — were Polish.
When the stronger condition that $X$ is a Polish space is given, one can prove that the Cantor-Bendixson decomposition is unique.
Strong Cantor-Bendixson Theorem. Let $X$ be a Polish space. For any closed set $F \subset X$, there exist a perfect set $P$ and a countable set $C$ such that $F = P \sqcup C$. Moreover, this decomposition is unique.
The following also holds:
Theorem. A perfect set in a Polish space has cardinality $2^{\aleph_0}$.
Proof. This will be treated separately in a future article on descriptive set theory.
From this, the following conclusion follows:
Corollary: The Continuum Hypothesis for Closed Sets of Real Numbers. A closed set of real numbers is either countable or has cardinality $2^{\aleph_0}$.
Proof. Since the real numbers form a Polish space, by the Cantor-Bendixson theorem every closed set decomposes as a disjoint union of a countable set and a perfect set. If the latter is empty, then the closed set is countable; otherwise it has cardinality $2^{\aleph_0}$. ■
Cantor had hoped that from the proof of the above theorem he might be able to prove the general continuum hypothesis, but as is well known, this hope was not realised.
어드조인트에 대한 직관적 이해
16 Dec 2024카테고리 이론의 핵심 개념 중 하나는 어드조인트adjoint이다.
정의. $\mathcal{A}, \mathcal{B}$가 카테고리이고, $F: \mathcal{A} \to \mathcal{B}, G: \mathcal{B} \to \mathcal{A}$가 함자functor라고 하자. $F$가 $G$의 좌 어드조인트left adjoint라는 것은 임의의 $A \in \mathcal{A}, B \in \mathcal{B}$에 대해 $\mathcal{B}(F(A), B)$와 $\mathcal{A}(A, G(B))$가 자연스럽게 일대일 대응될 수 있다는 것이다. 즉,
\[\begin{gather} (F(A) \xrightarrow{g} B) \quad \mapsto \quad (A \xrightarrow{\bar{g}} G(B))\\ (A \xrightarrow{f} G(B)) \quad \mapsto \quad (F(A) \xrightarrow{\bar{f}} B) \end{gather}\]또한 $G$를 $F$의 우 어드조인트right adjoint라고 한다. 기호로 $F \dashv G$로 표기한다.
이 정의는 다소 추상적으로 느껴질 수 있지만, 이해를 돕는 몇 가지 직관이 있다.
1. 근사로서의 어드조인트
$F \dashv G$일 때 $F, G$는 $\mathcal{A}$과 $\mathcal{B}$의 원소들을 서로 근사하는 방법으로 생각할 수 있다. 특히 좌 어드조인트는 ‘좌측에서 우측으로‘의 근사이고, 우 어드조인트는 ‘우측에서 좌측으로’의 근사이다.
예를 들어 $\mathbf{Z}$가 정수를 원소로 가지고, $x \leq y$일 때 그리고 오직 그 경우에만 $x \to y$ 사상이 유일하게 존재하는 카테고리라고 하자. 또한 $\mathbf{R}$이 실수를 원소로 가지고, $x \leq y$일 때 그리고 오직 그 경우에만 $x \to y$ 사상이 유일하게 존재하는 카테고리라고 하자. 이때 $\lceil \cdot \rceil, \lfloor \cdot \rfloor$는 표준적인 방식으로 함자 $\mathbf{R} → \mathbf{Z}$가 되고, 포함 사상 $\iota$는 함자 $\mathbf{Z} → \mathbf{R}$이 된다. 또한 $\lceil \cdot \rceil \dashv \iota \dashv \lfloor \cdot \rfloor$임을 확인할 수 있다.
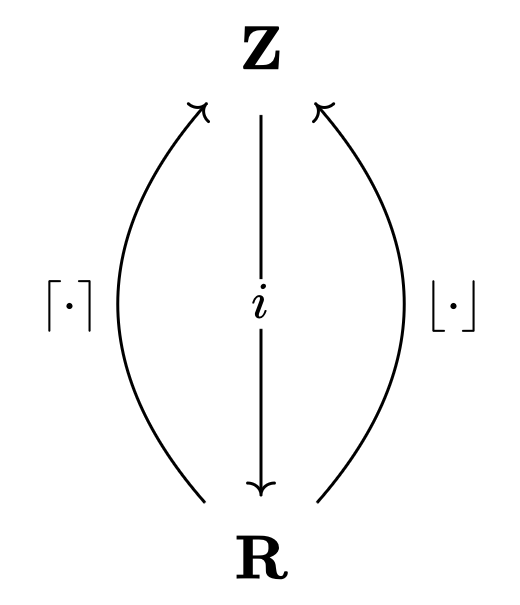
즉 $\lceil \cdot \rceil$는 $r$을 $r \leq \lceil r \rceil$로 ‘좌측에서 우측으로 끌어올리는’ 변환이고, $\lfloor \cdot \rfloor$은 $r$을 $\lfloor r \rfloor \leq r$로 ‘우측에서 좌측으로 잡아당기는’ 변환이다.
또한 $I, T$가 각각 $\mathcal{A}$의 초기 대상initial object 및 종단 대상terminal object라고 하자. 즉, 임의의 $A \in \mathcal{A}$에 대해
- 사상 $I \to A$가 유일하게 존재한다.
- 사상 $A \to T$가 유일하게 존재한다.
일례로 $\mathbf{Set}$에서 공집합은 초기 대상이고 홑원소 집합은 종단 대상이다.
홑원소 카테고리 $\mathcal{U}$에 대해 함자 $F: \mathcal{A} \to \mathcal{U}$가 유일하게 존재한다. $G_I, G_T: \mathcal{U} \to \mathcal{A}$가 각각 상이 $I, T$인 함자라고 하자. 이때 앞선 경우와 비슷한 원리로 $G_T \dashv F \dashv G_I$가 됨을 확인하라. (종단 대상은 가장 “오른쪽”에 있는 대상이므로 $G_T$는 “왼쪽에서 오른쪽으로”의 근사이며, 초기 대상은 가장 “왼쪽”에 있는 대상이므로 $G_I$는 “오른쪽에서 왼쪽으로”의 근사이다.)
2. 구축과 파괴로서의 어드조인트
좌 어드조인트는 구축을, 우 어드조인트는 파괴를 의미한다. 따라서 일반적으로 자유함자free functor는 좌 어드조인트, 망각함자forgetful functor는 우 어드조인트이다.
일례로 군의 카테고리를 $\mathbf{Grp}$, 모노이드의 카테고리를 $\mathbf{Mon}$이라 하자. $F$를 자유함자, $U$를 망각함자라고 하자. 그리고 $R: \mathbf{Mon} → \mathbf{Grp}$를 다음과 같이 정의한다.
- $R(M) = \lbrace m \in M : \exists m^{-1} \in M \rbrace$
- $R(f): m \mapsto f(m)$
이때, 다음 다이어그램이 성립하여 $F \dashv U \dashv R$이다.
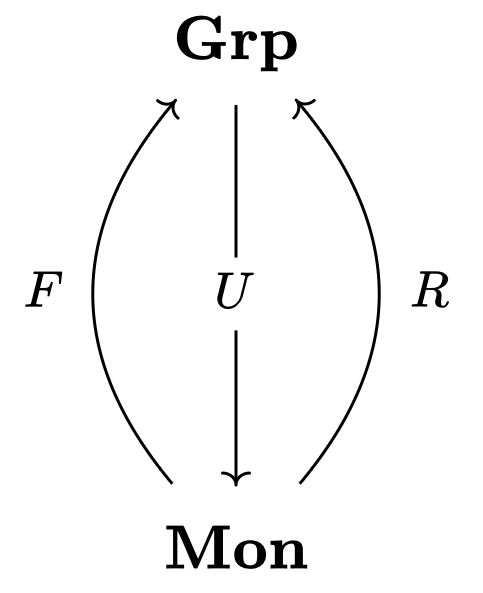
$R$이 $U$보다 더 파괴적이기 때문에 $U \dashv R$인 것으로 이해할 수 있다.