Set-theoretic Definitions of Rational and Real Numbers

20 Nov 2024

1. Cantor’s Isomorphism Theorem

Cantor’s Isomorphism Theorem. Any countable, dense, linear order without endpoints is unique up to order isomorphism.

Proof 1. (Back-and-Forth Argument)

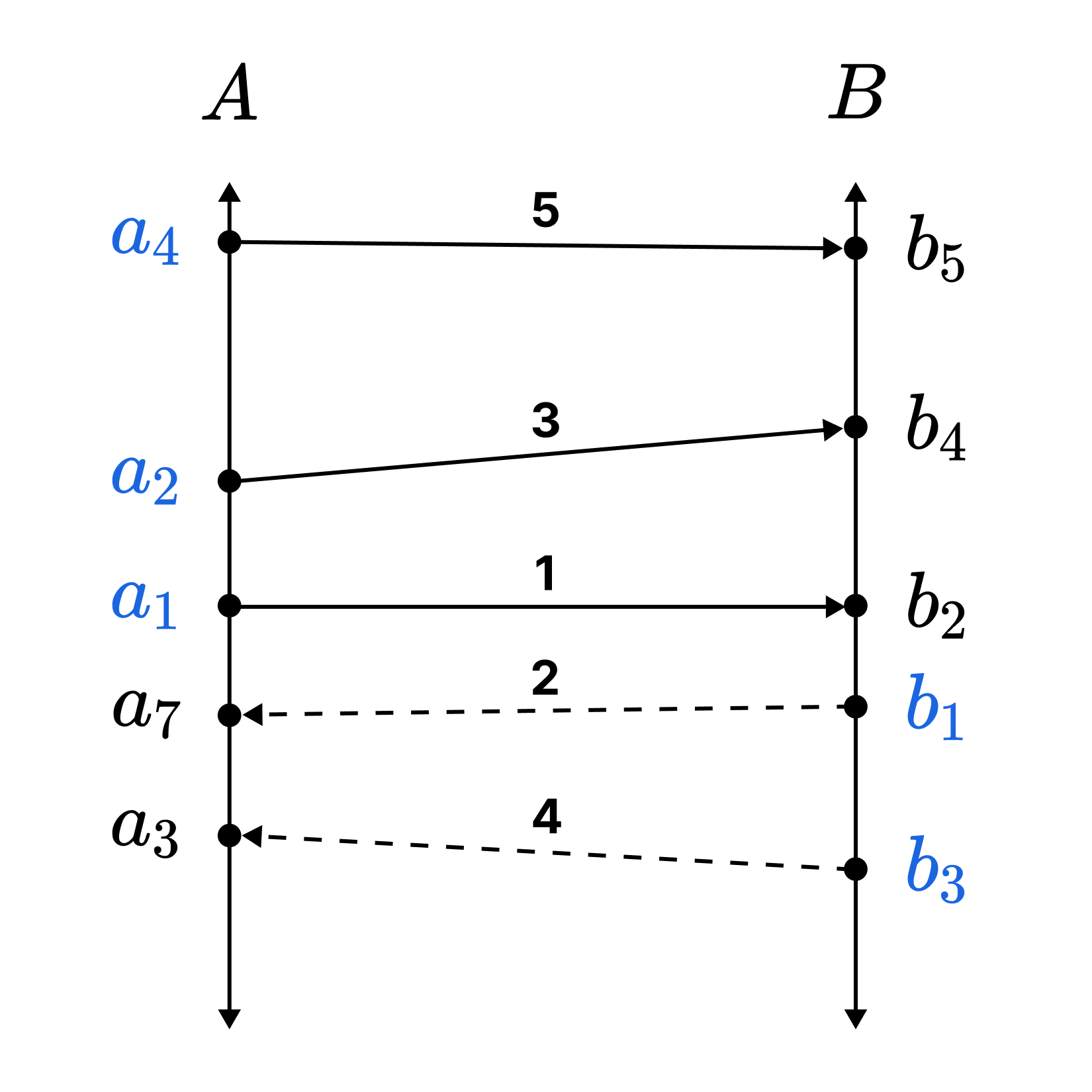
At the $n$-th step, map the least-indexed $a_k \in A \setminus \mathrm{dom} f_n$ to an arbitrary $b \in B \setminus \mathrm{im} f_n$ so that order isomorphism is preserved, and then map the least-indexed $b_l \in B \setminus (\mathrm{im} f_n \cup \lbrace b \rbrace)$ to an arbitrary $a \in A \setminus (\mathrm{dom}f_n \cup \lbrace a_k\rbrace)$ so that order isomorphism is preserved. (In the diagram, blue indicates the ‘least-indexed’ elements.)

Proof 2. (Only-Forth Argument)

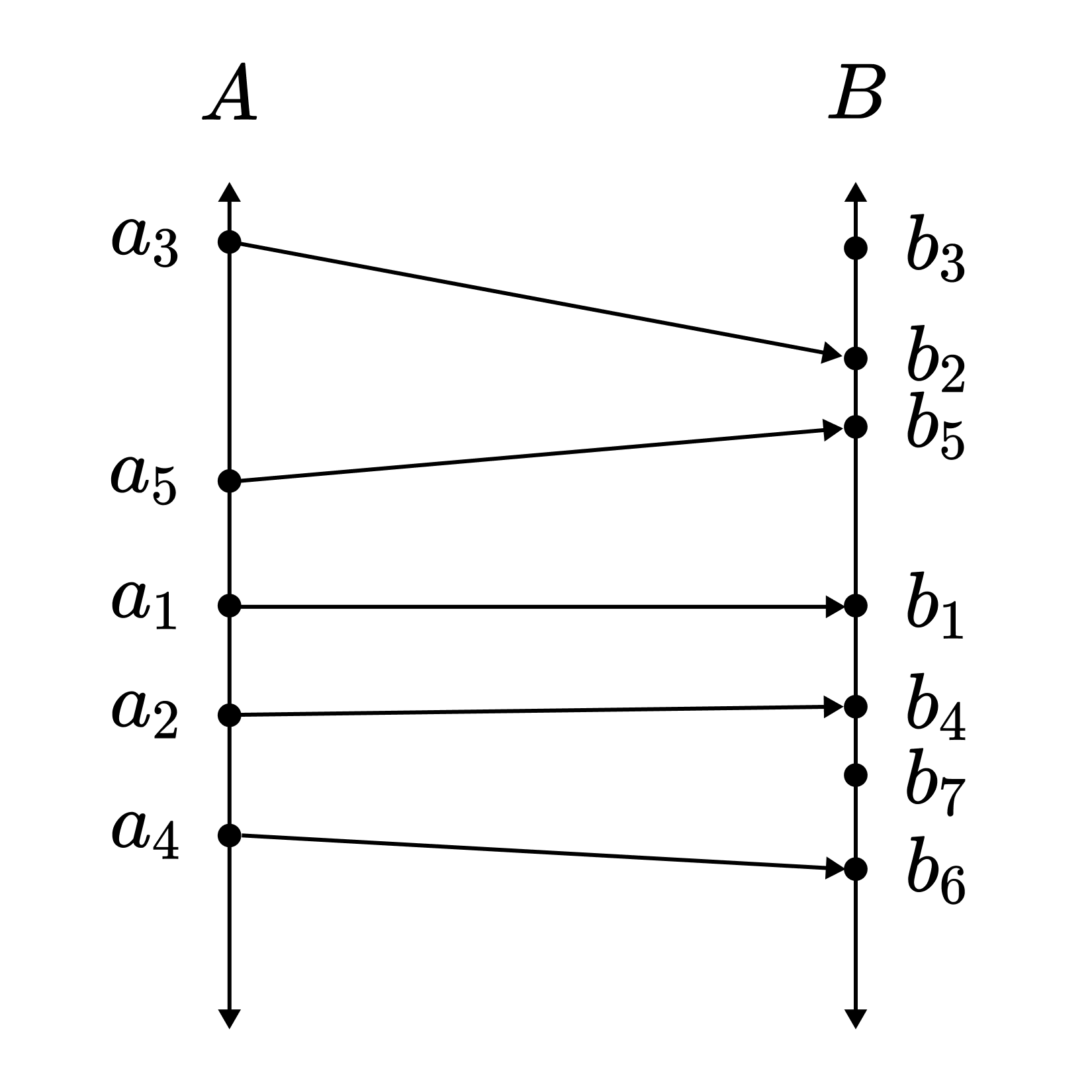
At the $n$-th step, map the least-indexed $a_k \in A \setminus \mathrm{dom} f_n$ to the least-indexed $b_l \in B \setminus \mathrm{im}f_n$ so that order isomorphism is preserved.

Incorrect Proof. (Incorrect Only-Forth Argument)

At the $n$-th step, match the least-index $a_k \in A \setminus \mathrm{dom} f_n$ to an arbitrary $b \in B \setminus \mathrm{im}f_n$ so that order isomorphism is preserved.

Why this is incorrect: There is no guarantee that $\mathrm{im} \left[ \bigcup f_n \right]$ exhausts all of $B$. For example, it is possible that only $b$’s with even indices are chosen in every step.

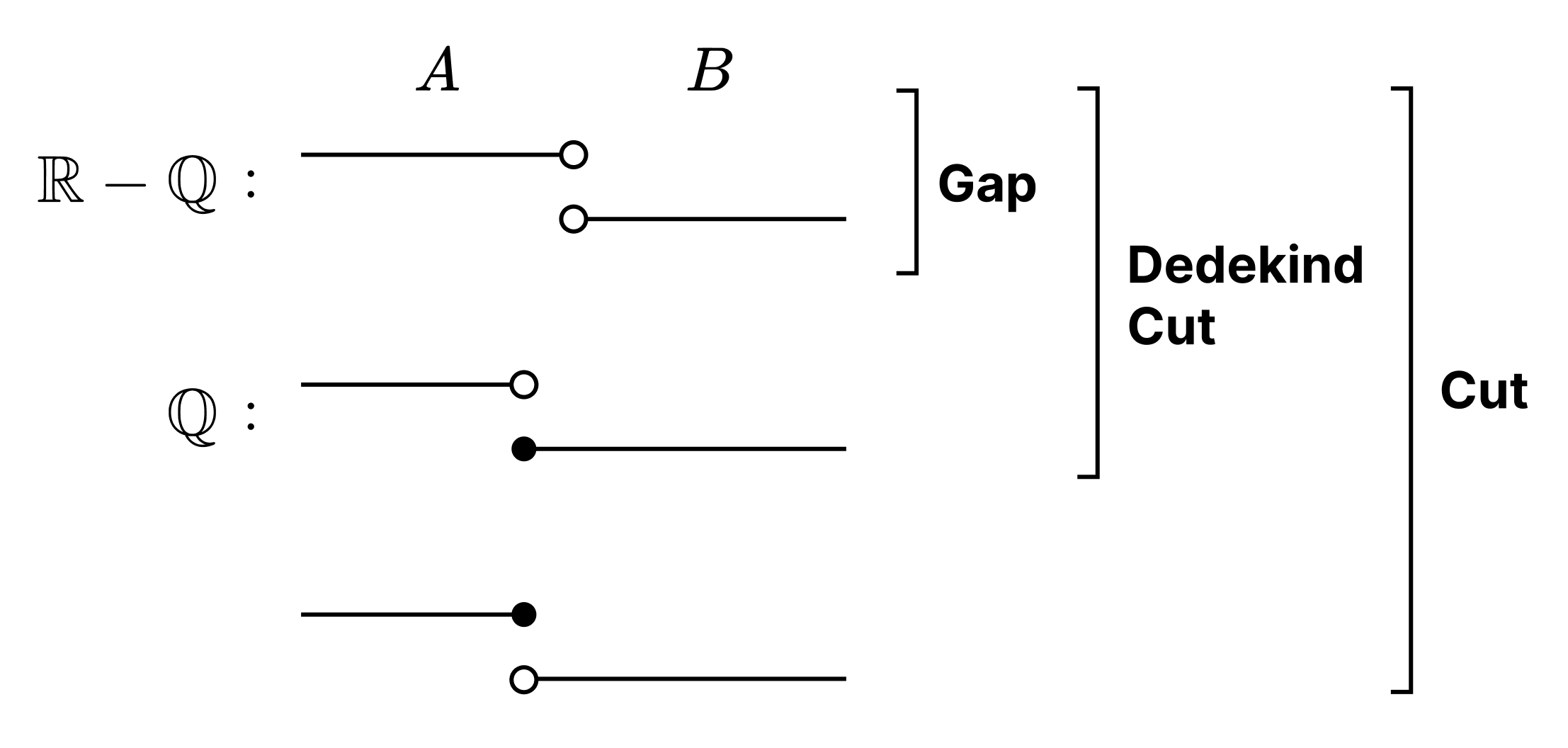
2. Dedekind Cuts

Definition. For a linearly ordered set $(P, <)$, a pair of subsets $A, B$ of $P$ is called a cut if:

1. $A \sqcup B = P$
2. For any $a \in A, b \in B$, $a < b$.

Furthermore, it is a Dedekind cut if:

1. $A$ has no greatest element.

It is called a gap if, in addition:

1. $B$ has no least element.

Remark

1. $P$ is complete ⇔ $P$ has no gaps.
2. As will be seen, for $P = \mathbb{Q}$, gaps correspond to irrational numbers while Dedekind cuts correspond to real numbers.

3. Completion Theorem

Completion Theorem. If $(P, <)$ is a dense linear order without endpoints, then there exists a unique (up to order isomorphism) complete linear order $(C, \prec)$ satisfying:

1. $P \subseteq C$
2. $\prec$ coincides with $<$ on $P$
3. $P$ is dense in $C$: for any $c_1 < c_2 \in C$, there exists $p \in P$ with $c_1 < p < c_2$
4. $C$ has no endpoints.

Uniqueness Proof. Suppose $(C, \prec)$ and $(C^\ast, \prec^\ast)$ are complete linear orders satisfying the conditions. Define $\phi: C \to C^\ast$ as follows:

1. If $c \in P$, then $\phi(c)=c$
2. If $c \notin P$, then $\phi(c) = \sup^\ast \lbrace p \in P : p \prec c \rbrace$

This $\phi$ is an order isomorphism.

Existence Proof. Define:

\[\begin{gather} \mathcal{G} = \lbrace (A, B) : (A, B) \text{ is a gap of } P \rbrace \\ \mathcal{D} = \lbrace (A, B) : (A, B) \text{ is a Dedekind cut of } P \rbrace \\ \mathcal{P} = \mathcal{D} \setminus \mathcal{G} \end{gather}\]

Define an order on $\mathcal{D}$ by:

\[(A_1, B_1) \prec (A_2, B_2) \iff A_1 \subset A_2\]

If $(A, B) \in \mathcal{P}$, then for some $p$, $B = \lbrace x \in P : x \geq p \rbrace$, and we write $(A, B) = [p]$. That is,

\[\mathcal{P} = \lbrace [p] : p \in P \rbrace\]

It is easy to check that $(\mathcal{P}, \prec) \sim (P, <)$. Now, we show the following:

Claim. $\mathcal{D}$ is an extension of $\mathcal{P}$ satisfying all four conditions of the Completion Theorem.

Conditions 1, 2, and 4 are clear. We show 3.

Let $\mathfrak{d}_1 = (A_1, B_1), \mathfrak{d}_2 = (A_2, B_2) \in \mathcal{D}$ with $\mathfrak{d}_1 \prec \mathfrak{d}_2$, i.e., $A_1 \subset A_2$. There exists $p \in A_2 \setminus A_1$ such that $p$ is not the least element of $B$, i.e., $p \in P$. For such $p$, we have $\mathfrak{d}_1 \prec [p] \prec \mathfrak{d}_2$. □

Finally, we show:

Claim. $(\mathcal{D}, \prec)$ is complete.

Let $\mathcal{S}$ be a nonempty, upward-bounded subset of $\mathcal{D}$. Define:

\[\begin{gather} A_\mathcal{S} = \bigcup \lbrace A : (A, B) \in \mathcal{S} \rbrace\\ B_\mathcal{S} = \bigcap \lbrace B : (A, B) \in \mathcal{S} \rbrace \end{gather}\]

Then $(A_\mathcal{S}, B_\mathcal{S}) \in \mathcal{D}$ and is the least upper bound of $\mathcal{S}$. ◾

Set-theoretic Definition of the Real Numbers. A set $(R, <)$ satisfying the following is unique up to order isomorphism:

1. It is a complete linear order.
2. It has no endpoints.
3. It is separable; i.e., there exists $Q \subset R$ which is countable and dense in $R$.

Proof. This follows from Cantor’s Isomorphism Theorem and the Completion Theorem.