디멘의 블로그
Dimen's Blog
이데아를 여행하는 히치하이커
Alice in Logicland
Arithmetic Hierarchy
07 Feb 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
Warning. This article was written informally and may therefore lack rigour or even contain incorrect content.
The arithmetic hierarchy is a classification of propositions in arithmetic — more precisely, first-order Peano arithmetic — according to the complexity of their quantifiers. The arithmetic hierarchy is a central concept in proof theory and computational complexity theory, and is also related to descriptive set theory.
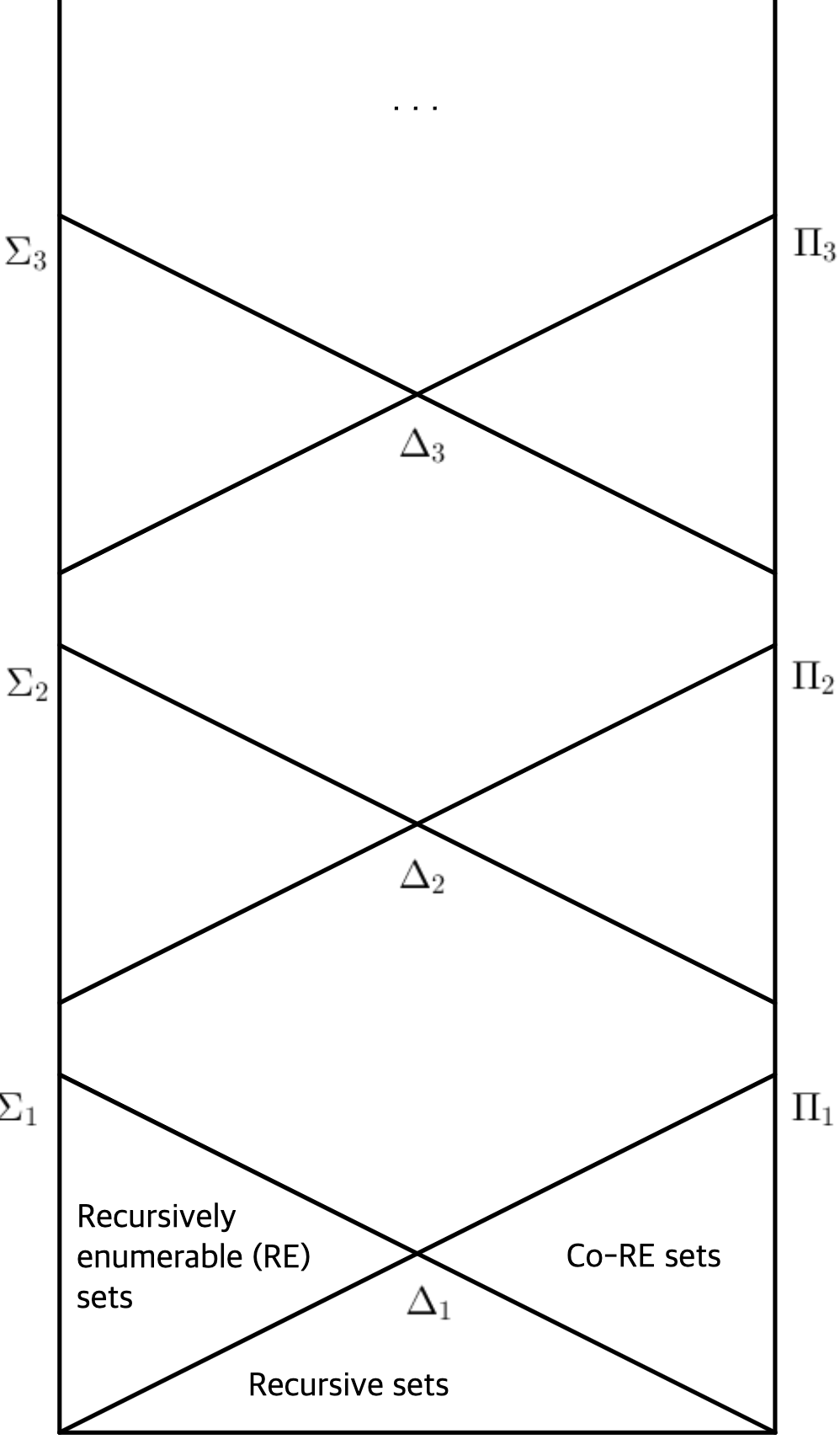
1. $\Delta_0$ Propositions
1.1. Definition
Definition. $\Sigma_0 = \Pi_0 = \Delta_0$ is the set of propositions containing only bounded quantifiers.
Why the same class of propositions is referred to by three names will become clear shortly. In this article, unless there is a specific reason otherwise, we shall use $\Delta_0$ as the representative name among the three.
For example, the following four propositions are all $\Delta_0$.
\[\begin{gather} \phi_1 : 0 = 1\\ \phi_2(x) : \exists y < x \; [y + y = x] \\ \phi_3(x, y) : \exists z \leq y \;[ xz = y ] \\ \end{gather}\]$\phi_1$ is a false statement. $\phi_2$ is true when $x$ is even, and $\phi_3$ is true when $x$ is a divisor of $y$.
Since $\Delta_0$ propositions have bounded quantifiers, it is possible to determine whether an arbitrary $x$ satisfies the corresponding proposition using a Turing machine. For instance, a Turing machine that determines whether $x$ satisfies $\phi_2$ is as follows:
for y < x:
if y + y == x:
return true;
return false;
The above Turing machine halts within $x$ iterations. Therefore, $\Delta_0$ propositions are decidable, recursive, or computable (the three expressions are synonymous). However, as we shall explain in detail later, not all decidable propositions are $\Delta_0$.
According to Gödel’s representability theorem, decidable true propositions are provable. In this article, when we say that $\phi$ is ‘true’, we mean $\mathcal{N} \vDash \phi$ for the standard model of arithmetics $\mathcal{N}$, rather than $\mathsf{PA} \vDash \phi$.
The following holds:
Theorem. The set of true $\Delta_0$ sentences is complete. (That is, if $\phi$ is a true $\Delta_0$ sentence, then $\mathsf{PA} \vdash \phi$.)
1.2. $\Delta_0$ in Computational Theory
From a programming language perspective, $\Delta_0$ sentences correspond to the set of code that permits only the following:
- Conditional statements
- Bounded loops
- Addition and multiplication
It should be noted that unbounded loops and variable reassignment are not permitted. For example, the following code demonstrates that primality testing is $\Delta_0$:
for y < x:
for z <= y:
if yz == x:
return false;
return true;
However, the following code that computes $x^y$ does not correspond to $\Delta_0$:
let a = 1
for 1<= z <= y:
a = a * x
return a
So is exponentiation not $\Delta_0$? Not necessarily. Although complex, there are methods to express exponentiation with a $\Delta_0$ proposition. This case demonstrates that determining whether a given operation or predicate is $\Delta_0$ can be intricate. For instance, the following is known:
Theorem. Factorial is $\Delta_0$, but tetration is not $\Delta_0$.
However, tetration is decidable. Therefore, not all decidable propositions are $\Delta_0$.
2. Moving Up One Level
Definition.
\[\begin{gather} \Sigma_1 := \{ \exists x_1 \cdots \exists x_n \;\phi : \phi \in \Pi_0 \}\\ \Pi_1 := \{ \forall x_1 \cdots \forall x_n \;\phi : \phi \in \Sigma_0 \}\\ \Delta_1 := \Sigma_1 \cap \Pi_1 \end{gather}\]
2.1. $\Sigma_1$ Propositions
The following propositions are $\Sigma_1$:
\[\begin{gather} \phi_1(x): \exists y \; \underbrace{[y^2 + y + 1 = x]}_{\Pi_0}\\ \phi_2(x): ∃y\; ∃z\; \underbrace{(y \text{ is prime} ∧ z \text{ is prime} ∧ x = y + z ∧ x \text{ is even})}_{\Pi_0} \end{gather}\]$\phi_1$ is true in the set $\lbrace 1, 3, 7, 13, \ldots\rbrace $. $\phi_2$ is Goldbach’s conjecture; it is not known whether all $x$ satisfy this.
$\Sigma_1$ is the collection of recursively enumerable sets. That is, if $\phi \in \Sigma_1$, then there exists a Turing machine $M$ such that:
- If $\phi(c)$ is true, then $M$ is guaranteed to decide $\phi(c)$.
- If $\phi(c)$ is false, then $M$ is not guaranteed to decide $\phi(c)$.
For example, the following Turing machine shows that $\phi_2$ is recursively enumerable:
for y > 1:
for z > 1:
if isPrime(y) & isPrime(z) & x = y + z & isEven(x):
return true;
return false;
Although there is a return false statement, since there is no break statement to exit the loop, return false is unreachable. That is, if $\phi_2(c)$ is true, the above Turing machine returns true, but if it is false, it falls into an infinite loop.
If $\phi \in \Sigma_1$ is a sentence that is true in the standard model of arithmetics, then $\mathsf{PA} \vdash \phi$. A proposition of the form $\phi : \exists x \; \psi(x)$ being true in the standard model of arithmetics means that $\psi(c)$ is true for some $c \in \mathbb{N}$, and since $\psi(c)$ is a true $\Pi_0$ sentence, it is provable. Therefore, the following holds:
Theorem. The set of true $\Sigma_1$ sentences is complete.
2.2. $\Sigma_1 \setminus \Delta_0$ Propositions
However, I have in fact been misleading the reader thus far. The propositions I listed earlier as examples of $\Sigma_1$ can actually be written as $\Delta_0$:
\[\begin{gather} \phi_1: \exists y<x \;{[y^2 + y + 1 = x]}\\ \phi_2(x): ∃y<x\; ∃z<x\; {(y \text{ is prime} ∧ z \text{ is prime} ∧ x = y + z ∧ x \text{ is even})} \end{gather}\]So what do propositions that strictly belong to $\Sigma_1$ look like? One answer can be found in the halting problem.
First, let $\mathrm{HaltsIn}(x, n)$ be a predicate that determines whether “the Turing machine with Gödel number $x$” produces an output within $n$ operations. This predicate can be easily defined from the Kleene predicate, and the Kleene predicate is known to be $\Sigma_0$. For example, if the Gödel number of a Turing machine that computes the square of 3 in 2 operations is $123$, then $\mathrm{HaltsIn}(123, 3)$ is true but $\mathrm{HaltsIn}(123, 1)$ is false.
Now consider the following proposition:
\[\phi_1(x): \exists y \;[ \mathrm{HaltsIn}(x, y) ]\]What this proposition states is that the Turing machine with Gödel number $x$ eventually halts. That is, the above proposition is equivalent to the halting problem. However, the halting problem is undecidable. Since we showed earlier that all $\Delta_0$ propositions are decidable, $\phi$ is a $\Sigma_1$ proposition that does not belong to $\Delta_0$.
As another example, consider the following proposition:
\[\phi_2(x): \exists y \; [ \mathrm{Proves}(x, y) ]\]Here, $\mathrm{Proves}(x, y)$ is a predicate that is true when the Gödel number of “a proof of the sentence with Gödel number $x$” is $y$. That is, $\phi_2(x)$ is a predicate stating that the sentence with Gödel number $x$ is provable. However, this predicate is not decidable. If $\phi_2$ were decidable, then (under the assumption that PA is consistent) there would exist a proof in PA that $\phi_2(\ulcorner 0 = 1 \urcorner)$ is false, which would conflict with Gödel’s incompleteness theorem.
2.3. $\Pi_1$ Propositions
If $\Sigma_1$ propositions are the collection of recursively enumerable propositions, then $\Pi_1$ propositions are the collection of co-recursively enumerable propositions. That is, a $\Pi_1$ sentence is decidable if false, but not necessarily decidable if true. For example, the following two propositions are $\Pi_1$ sentences that are not $\Delta_0$:
\[\begin{gather} \phi_3(x): \forall y \;[ \lnot \mathrm{HaltsIn}(x, y) ] \\ \phi_4(x): \forall y \; [ \lnot \mathrm{Proves}(x, y) ] \end{gather}\]Unlike the case of $\Sigma_1$, $\Pi_1$ is not complete. Since the negation of a $\Sigma_1$ sentence is $\Pi_1$, if $\Pi_1$ were also complete, then $\Sigma_1 = \Pi_1 =$ (collection of decidable propositions).
Theorem. The set of true $\Pi_1$ sentences is not complete.
2.4. $\Delta_1$ Propositions
$\Delta_1$ propositions belong to both $\Sigma_1$ and $\Pi_1$. Therefore, $\Delta_1$ is the collection of decidable propositions. The tetration we saw earlier is a $\Delta_1$ proposition that is not $\Delta_0$.
3. Moving Up Another Level
Definition.
\[\begin{gather} \Sigma_2 := \{ \exists x_1 \cdots \exists x_n \;\phi : \phi \in \Pi_1 \}\\ \Pi_2 := \{ \forall x_1 \cdots \forall x_n \;\phi : \phi \in \Sigma_1 \}\\ \Delta_2 := \Sigma_2 \cap \Pi_2 \end{gather}\]
I believe the pattern should now be clear. As an example of a $\Sigma_2$ proposition, consider the following:
\[\phi_5(x) : \exists y \; [ \mathrm{DoesNotHaltOn}(x, y)]\]Here, $\mathrm{DoesNotHaltOn}(x, y)$ is a predicate that is true if “the Turing machine with Gödel number $x$” does not halt when given input $y$. From the preceding discussion, it is not difficult to see that $\mathrm{DoesNotHaltOn}$ is $\Pi_1$.
Theorem. $\phi_5 \notin \Pi_1$
Proof. Suppose $\phi_5 \in \Pi_1$. Our goal is to show that this assumption implies “the set of true $\Pi_1$ sentences is complete”.
Let $\psi(x)$ be an arbitrary $\Delta_0$ proposition. Then $\theta : \forall x \;\psi(x)$ is a $\Pi_1$ sentence. Consider the following Turing machine $M$:
if ψ(x):
return 1;
while True:
This Turing machine halts for value $x$ if $\psi(x)$ is true and does not halt if it is false. Therefore, $\theta$ being true is equivalent to $M$ halting for all $x$, which is equivalent to $\phi_5(\ulcorner M \urcorner)$ being false. By assumption, $\phi_5 \in \Pi_1$, so if $\phi_5(\ulcorner M \urcorner)$ is false, then $\mathsf{PA} \vdash \lnot \phi(\ulcorner M \urcorner)$. That is, $\mathsf{PA} \vdash \theta$, making all true $\Pi_1$ sentences provable. This is a contradiction. ■
Remark. Strictly speaking, one should show that the above proof is expressible within PA.
We said earlier that $\Sigma_1$ propositions are decidable when true, and $\Pi_1$ propositions are decidable when false. However, since $\Sigma_2$ sentences have mixed $\forall$ and $\exists$ quantifiers, there may be sentences that are undecidable both when true and when false.
3.1. Oracles
Definition. When $\mathcal{O}$ can obtain the result of problem $P$ in a single operation, we call $\mathcal{O}$ an oracle for $P$.
For example, an oracle for the halting problem is a truly divine entity that can determine whether a given Turing machine halts in a single operation.
Ascending the arithmetic hierarchy is equivalent to being given increasingly powerful oracles. We saw earlier the following as an example of a $\Sigma_1$ proposition:
\[\phi_1(x): \exists y \;[ \mathrm{HaltsIn}(x, y) ]\]However, if a halting problem oracle $\mathcal{O}$ were given, $\phi_1$ could be expressed simply as a $\Delta_0$ proposition:
\[\phi_1(x) : \mathcal{O}(x)\]Also, we saw earlier the following as an example of a $\Sigma_2$ proposition:
\[\phi_5(x) : \exists y \; [ \mathrm{DoesNotHaltOn}(x, y)]\]If a halting problem oracle $\mathcal{O}$ were given, $\phi_5$ could be expressed as a $\Sigma_1$ proposition:
\[\phi_5(x): \exists y \; \lnot \mathcal{O}(x|_y)\]Here, $x|_y$ is the Gödel number of the state where input $y$ is given to the Turing machine with Gödel number $x$. That is, $\Sigma_2$ propositions reduce to $\Sigma_1$ propositions when given an oracle for the halting problem. By similar principles, $\Pi_2$ and $\Delta_2$ propositions reduce to $\Pi_1$ and $\Delta_1$ propositions, respectively, when given an oracle for the halting problem.
Furthermore, we can define second-order oracles. A second-order halting problem oracle is a halting problem oracle for Turing machines that use halting problem oracles. For example, while $\mathcal{O}$ is limited to determining whether the following code halts:
for x > 0:
for y > 0:
for z > 0:
for n > 2:
if x^n + y^n == z^n:
return True;
return False;
$\mathcal{O}^2$ can also determine whether the following code halts. The following code takes as input the Gödel number $x$ of an NP Turing machine, halts if there exists a P Turing machine whose output matches $x$, and does not halt if no such machine exists:
let x ∈ NP;
for y ∈ P:
if !Halts(
let z = 0
while x(z) == y(z):
z = z + 1
):
return 1; // halts when x is an NP that belongs to P
In general, the following holds:
Theorem. Propositions in $\Pi_n$, $\Sigma_n$, $\Delta_n$ become propositions in $\Pi_{n-k}$, $\Sigma_{n-k}$, $\Delta_{n-k}$, respectively, when given a $k$-th order oracle.
곱군과 위수에 관한 노트: 페르마 소수 정리와 윌슨의 정리
05 Feb 2025Remarks
| 곱군 | 합군 |
|---|---|
| 1이 항등원 | 0이 항등원 |
| $x$의 위수가 $r$일 때, $x^r = 1$ | $x$의 위수가 $r$일 때, $rx = 0$ |
- 소수 $p$에 대해 $p - 1$에 대한 정보가 주어졌다면 위수가 $p - 1$인 곱군 $(\mathbb{Z}/p\mathbb{Z})^\times$을 생각해 보자.
- 유한체의 곱군은 순환군이다.
- 순환적 곱군 $G$에 대해 $nm \mid |G|$는, $x^{nm} = 1$이지만 $x^n, x^m \neq 1$인 원소 $x$의 존재성과 동치이다.
- 위수는 주기와 다르다. 일반적으로 (주기) = (위수) + 1이다.
페르마 소수 정리
정리. 소수 $p$가 두 정수 $a, b$에 대해 $p = a^2 + b^2$ 꼴로 나타내어질 필요충분조건은 $p \bmod 1 = 4$인 것이다.
증명.
(⇒) 자명
(⇐) $G = (\mathbb{Z}/p\mathbb{Z})^\times$라고 하자. 조건에 의해 $4 \mid |G|$이다. 따라서 $n^4 = 1$이지만 $n^2 \neq 1$인 원소 $n$이 존재한다. 즉, $n^2 = -1$이다. 따라서 $p \mid n^2 + 1$이다. 이제 $\mathbb{Z}[i]$에서 생각해 보면 $p \mid (n + i)(n - i)$이다. 만약 $p$가 $\mathbb{Z}[i]$에서 기약이었다면 $p \mid n + i$ 또는 $p \mid n - i$인데 둘 다 불가능하다. 따라서 $p$는 기약이 아니며, 켤레성에 의해
\[p = (a + bi)(a - bi) = a^2 + b^2\]이다. ■
윌슨의 정리
정리. $p$가 소수일 필요충분조건은 $(p - 1)! \equiv -1 \mod p$인 것이다.
증명.
(⇒) $G = (\mathbb{Z}/p\mathbb{Z})^\times$라고 하자. $G$의 원소를 모두 곱한 값은 $(p - 1)!$이다. $x^2 = 1$의 근인 $\pm 1$을 제외한 $G$의 모든 원소는 자기 자신을 역원으로 가지지 않는다. 따라서 $(p - 1)! \equiv -1$이다.
(⇐) $N = (p - 1)! + 1$이라고 하자. 조건에 의해 $p \mid N$이다. 만약 $p$가 소수가 아니라면 어떤 소수 $q < p$에 대해 $q \mid N$이다. 그러나 $N \bmod q = 1$이므로 모순이다. ■
Notes on Multiplicative Groups and Order: Fermat's Theorem on Primes and Wilson's Theorem
05 Feb 2025Remarks
| Multiplicative Group | Additive Group |
|---|---|
| 1 is the identity element | 0 is the identity element |
| When the order of $x$ is $r$, $x^r = 1$ | When the order of $x$ is $r$, $rx = 0$ |
- For a prime $p$, if information about $p - 1$ is given, consider the multiplicative group $(\mathbb{Z}/p\mathbb{Z})^\times$ of order $p - 1$.
- The multiplicative group of a finite field is cyclic.
- For a cyclic multiplicative group $G$, $nm \mid |G|$ is equivalent to the existence of an element $x$ such that $x^{nm} = 1$ but $x^n, x^m \neq 1$.
- Order is different from period. In general, (period) = (order) + 1.
Fermat’s Theorem on Primes
Theorem. A prime $p$ can be expressed in the form $p = a^2 + b^2$ for two integers $a, b$ if and only if $p \equiv 1 \pmod{4}$.
Proof.
(⇒) Trivial.
(⇐) Let $G = (\mathbb{Z}/p\mathbb{Z})^\times$. By the condition, $4 \mid |G|$. Therefore, there exists an element $n$ such that $n^4 = 1$ but $n^2 \neq 1$. That is, $n^2 = -1$. Hence, $p \mid n^2 + 1$. Now, considering in $\mathbb{Z}[i]$, we have $p \mid (n + i)(n - i)$. If $p$ were irreducible in $\mathbb{Z}[i]$, then $p \mid n + i$ or $p \mid n - i$ (note that the fact that $\mathbb{Z}[i]$ is UFD is used here) but both are impossible. Therefore, $p$ is not irreducible, and by conjugacy,
\[p = (a + bi)(a - bi) = a^2 + b^2\]■
Wilson’s Theorem
Theorem. $p$ is prime if and only if $(p - 1)! \equiv -1 \pmod{p}$.
Proof.
(⇒) Let $G = (\mathbb{Z}/p\mathbb{Z})^\times$. The product of all elements of $G$ is $(p - 1)!$. Except for $\pm 1$, which are the roots of $x^2 = 1$, all other elements of $G$ do not have themselves as their inverse. Therefore, $(p - 1)! \equiv -1$.
(⇐) Let $N = (p - 1)! + 1$. By the condition, $p \mid N$. If $p$ were not prime, then for some prime $q < p$, we would have $q \mid N$. However, $N \equiv 1 \pmod{q}$, which is a contradiction. ■
베타 함수를 통한 페아노 산술에서의 괴델 수 정의
25 Jan 2025요약. 1차 페아노 산술은 술어에 대한 양화를 허용하지 않기 때문에 덧셈과 곱셈 공리를 별도로 요구한다. 그러나 지수나 계승 등의 추가적인 연산은 — 튜플을 페아노 산술에서 정의할 수 있는 한 — 별도의 공리 없이 정의 가능하다. 그리고 튜플은 베타 암호화를 통해 페아노 산술에서 정의 가능하기 때문에, 페아노 산술은 지수, 계승, 소인수분해, 나아가 괴델 수까지 형식화할 수 있다.
1. 서론
정의. 페아노 산술(Peano arithmetics, PA)은 $(0, S, +, \cdot)$를 부호수(signature)로 가지는 이론으로, 공리는 다음과 같다.
- $\forall x : S(x) \neq 0$
- $\forall x, y : S(x) = S(y) \rightarrow x = y$
- $\forall x : x + 0 = x$
- $\forall x, y : x + S(y) = S(x + y)$
- $\forall x, y : x \cdot 0 = 0$
- $\forall x, y : x \cdot S(y) = (x \cdot y) + x$
추가로 다음의 귀납 공리꼴(axiom schema)을 가진다. 임의의 1차 논리식 $\phi(x)$에 대해,
7. $\big[ \phi(0) \land \forall x \; [ \phi(x) \rightarrow \phi(S(x)) ] \big] \rightarrow \forall x \;\phi(x)$
추가적으로 편의를 위해 $<, -, \bmod$를 다음과 같이 정의한다.
\[\begin{aligned} &x < y : &&\exists z \neq 0\; [x + z = y]\\ &x - y = z : &&x = y + z \\ &x \bmod y = z: && (z < y) \land \exists q \;[ qy + z = x ] \end{aligned}\]역사적으로 데데킨트가 처음 제시한 페아노 산술은 2차 논리 이론이었기 때문에 귀납 공리꼴 대신 귀납 공리가 있었다. 또한 3번부터 7번 공리가 없었다.
정의. 2차 논리 페아노 산술은 $(0, S)$를 부호수(signature)로 가지는 이론으로, 공리는 다음과 같다.
- $\forall x : S(x) \neq 0$
- $\forall x, y : S(x) = S(y) \rightarrow x = y$
- $\forall \phi \bigg[ \big[ \phi(0) \land \forall x \; [ \phi(x) \rightarrow \phi(S(x)) ] \big] \rightarrow \forall x \;\phi(x)\bigg]$
나머지 공리가 불필요한 이유는, 2차 논리는 술어에 대한 양화를 허용하기 때문에 2차 논리식만으로 덧셈과 곱셈을 정의할 수 있기 때문이다. 예를 들어 $w = u + v$는 다음 논리식과 동치이다.
\[\forall \phi \bigg[ \forall x, y, z \big[ \phi(x, 0, x) \land (\phi(x, S(y), z) \rightarrow \phi(x, y, S(z)) \big] \rightarrow \phi(u, v, w) \bigg]\]그러나 2차 논리는 수많은 수학적 · 철학적 허점을 가지는 것으로 드러났기 때문에 서두에서 소개한 1차 논리 페아노 산술이 표준으로 선택되었다. 이 선택의 함의는 첫째로 귀납 공리가 귀납 공리꼴이 된다는 것이고, 둘째는 덧셈과 곱셈을 별도의 공리를 통해 정의해야 한다는 것이다.
그런데 이런 의문이 남는다. 덧셈과 곱셈 말고 다른 연산은 따로 정의할 필요가 없는 것일까? 예를 들어 지수, 소인수분해, 계승과 같은 연산은 별도의 공리 없이 정의 가능할까? 나아가, 임의의 논리식을 자연수에 대응시키는 괴델 수 기법은 페아노 산술만으로 정의 가능할까?
2. 튜플
이 의문에 답하는 혜안은, 튜플을 페아노 산술에서 정의할 수 있다면 기타 수많은 연산이 정의 가능해진다는 사실이다. 여기서 튜플이란 $(1, 4, 2)$와 같은 유한한 자연수의 나열을 말한다.
일례로 다음과 같은 술어와 함수들이 정의되어 있다고 가정하자.
- $\mathrm{Tup}(\tau):$ $\tau$가 튜플이다.
- $\mathrm{At}(\tau, i):$ $\tau$가 튜플일 때, $\tau$의 $i$번째 자연수를 반환한다.
- $\mathrm{Len}(\tau):$ $\tau$의 길이를 반환한다.
편의를 위해 $\mathrm{At}(\tau, i)$를 $\tau[i]$로 쓰도록 하자. 예를 들어 $\tau = (1, 4, 2)$라면 다음이 성립한다. (인덱스는 0부터 시작하는 것으로 생각한다)
\[\mathrm{Tup}(\tau) \; \land \; \mathrm{Len}(\tau) = 3 \;\land\; \tau[1] = 4\]튜플을 사용하면 다음과 같이 $z = x^y$를 정의할 수 있다.
\[\forall \tau \bigg[ \big[ \mathrm{Tup}(\tau)\; \land \; \tau[0] = 1 \;\land \forall i < y (\tau[i + 1] = \tau[i] \cdot x) \big] \rightarrow \tau[y] = z \bigg]\]3. 베타 암호화
그렇다면 튜플을 덧셈과 곱셈, 그리고 1차 논리식만으로 정의할 수 있을까? 이에 대한 답은 “가능하다”이다. 아니나다를까역시나적시나 이 결과를 처음 증명한 사람은 괴델이다. 먼저 다음의 정리를 상기하자.
중국인의 나머지 정리. $(n_1, \dots, n_k)$가 켤레서로소(pairwise coprime)라고 하자. $0 \leq r_i < n_i$인 임의의 $(r_1, \dots, r_k)$에 대해 다음을 만족하는 수 $x$가 언제나 존재한다.
\[x \bmod n_i = r_i\]
괴델의 아이디어는 중국인의 나머지 정리에서 $x$에 해당하는 수를 튜플 $(r_1, \dots, r_k)$의 코드로 생각하는 것이다. 그런데 여기에는 문제가 있다. $x$로부터 $(r_1, \dots, r_k)$를 복호화하기 위해서는 $(n_1, \dots, n_k)$가 주어져야 하는데, 이는 또다시 튜플을 요구하기 때문이다.
이 문제를 해결하기 위해 괴델은 다음의 보조정리를 꺼내든다.
보조정리. $n!+ 1, 2n! + 1, \dots, n \cdot n! + 1$은 켤레서로소이다.
증명. $1 \leq a < b \leq n$에 대해 $u = an! + 1, v = bn! + 1$이라고 하자. 유클리드 호제법에 의해,
\[\mathrm{gcd}(u, v) = \mathrm{gcd}(u, v - u) = \mathrm{gcd}(an! + 1, (b - a)n!)\]이다. $(b - a)n!$의 모든 약수의 집합은 $\lbrace 1, 2, \dots, n\rbrace $이다. 그런데 이중 어느 원소도 $an! + 1$의 약수가 아니므로 $\mathrm{gcd}(an! + 1, (b - a)n!) = \mathrm{gcd}(u, v) = 1$이다. □
이제 우리는 튜플을 순서쌍으로서 정의할 수 있다.
정의. 튜플 $(r_1, \dots, r_k)$를 다음과 같이 순서쌍 $\langle a, b \rangle$로 표현한다.
- $b = n! \quad \text{where} \quad n = \max(r_1, \dots, r_k, k)$
- $a \bmod (kb + 1) = r_k$
단, $a$는 2번 조건을 만족하는 자연수 중 가장 작은 자연수로 선택한다.
한편 튜플은 칸토어 대응을 통해 자연수로 표현이 가능하다.
정의.
\[\langle a, b \rangle = \frac{(a + b)(a + b + 1)}{2} + b\]
이로써 우리는 튜플 $\tau$를 자연수 $n$으로 암호화(coding)할 수 있다. 그리고 역으로 $n$이 주어지면 덧셈, 곱셈, 그리고 나머지 연산만을 사용하여 $\tau$를 복호화해낼 수 있다. 그리고 나머지 연산은 덧셈, 곱셈, 그리고 1차 논리로부터 쉽게 정의가 가능하므로, 목표가 달성되었다.
역사적으로 괴델이 증명한 정리는 다음과 같다.
$\beta$-함수 보조정리. 임의의 자연수열 $(n_1, \dots, n_k)$에 대해, 어떤 자연수 $a, b$가 존재하여 $1 \leq i \leq k$에 대해 $\beta(a, b, i) = n_i$이다. 여기서 $\beta$는 다음과 같이 정의된 함수이다.
\[\beta(x, y, i) = x \bmod (iy + 1)\]
이런 이유로 지금까지의 과정을 베타 암호화(Beta coding)라고 부른다. 괴델은 베타 암호화를 이용하여 지수 연산과 소인수분해를 PA에서 성공적으로 정의했으며, 이로부터 괴델 수와 비롯된 여러 술어를 PA에서 형식화할 수 있었다. 제목에서 드러나다시피 원래 이 글의 목표는 이 과정을 모두 개괄하는 것이었으나 때늦게 찾아온 필자의 귀찮음 이슈와, 글을 여기까지 읽은 독자라면 이후 내용은 어렵지 않게 유추 가능하리라는 생각으로 이만 줄인다.
Defining Gödel Numbers in Peano Arithmetic via the Beta Function
25 Jan 2025Summary. First-order Peano arithmetic does not permit quantification over predicates, hence it requires separate axioms to define addition and multiplication. However, further operations such as exponentiation and factorial are definable without separate axioms, provided that tuples can be defined in Peano arithmetic. And since tuples are definable in Peano arithmetic through beta encoding, Peano arithmetic can formalise exponentiation, factorial, prime factorisation, and ultimately Gödel numbering.
1. Introduction
Definition. Peano arithmetic (PA) is a theory with signature $(0, S, +, \cdot)$, where the axioms are as follows:
- $\forall x : S(x) \neq 0$
- $\forall x, y : S(x) = S(y) \rightarrow x = y$
- $\forall x : x + 0 = x$
- $\forall x, y : x + S(y) = S(x + y)$
- $\forall x, y : x \cdot 0 = 0$
- $\forall x, y : x \cdot S(y) = (x \cdot y) + x$
Additionally, it has the following induction axiom schema. For any first-order formula $\phi(x)$:
7. $\big[ \phi(0) \land \forall x \; [ \phi(x) \rightarrow \phi(S(x)) ] \big] \rightarrow \forall x \;\phi(x)$
For convenience, we define $<, -, \bmod$ as follows:
\[\begin{aligned} &x < y : &&\exists z \neq 0\; [x + z = y]\\ &x - y = z : &&x = y + z \\ &x \bmod y = z: && (z < y) \land \exists q \;[ qy + z = x ] \end{aligned}\]Historically, the Peano arithmetic first presented by Dedekind was a second-order logic theory, hence it had an induction axiom rather than induction axiom schema.
Definition. Second-order Peano arithmetic is a theory with signature $(0, S)$, where the axioms are as follows:
- $\forall x : S(x) \neq 0$
- $\forall x, y : S(x) = S(y) \rightarrow x = y$
- $\forall \phi \bigg[ \big[ \phi(0) \land \forall x \; [ \phi(x) \rightarrow \phi(S(x)) ] \big] \rightarrow \forall x \;\phi(x)\bigg]$
Note that second-order formalisation omits axioms 3-6. The reason they are unnecessary is that second-order logic permits quantification over predicates, enabling addition and multiplication to be defined using second-order formulae alone. For instance, $w = u + v$ is equivalent to the following formula:
\[\forall \phi \bigg[ \forall x, y, z \big[ \phi(x, 0, x) \land (\phi(x, S(y), z) \rightarrow \phi(x, y, S(z)) \big] \rightarrow \phi(u, v, w) \bigg]\]However, since second-order logic was found to have numerous mathematical and philosophical shortcomings, the first-order Peano arithmetic introduced at the beginning became the standard norm. The implications of the transition from second to first are, firstly, that the induction axiom becomes an axiom schema, and secondly, that addition and multiplication must be defined through separate axioms.
This raises the question: are there no other operations besides addition and multiplication that need separate definition? For example, can operations such as exponentiation, prime factorisation, and factorial be defined without additional axioms? Furthermore, can Gödel numbering, which maps formulae to natural numbers one-to-one, be defined using Peano arithmetic alone?
2. Tuples
The insight that answers this question is that if tuples can be defined in Peano arithmetic, then numerous other operations become definable. Here, a tuple refers to a finite sequence of natural numbers such as $(1, 4, 2)$.
For instance, suppose the following predicates and functions are defined:
- $\mathrm{Tup}(\tau):$ $\tau$ is a tuple.
- $\mathrm{At}(\tau, i):$ When $\tau$ is a tuple, returns the $i$-th index of $\tau$.
- $\mathrm{Len}(\tau):$ Returns the length of $\tau$.
For convenience, let us write $\mathrm{At}(\tau, i)$ as $\tau[i]$. For example, if $\tau = (1, 4, 2)$, then the following holds (assuming the index starts from 0):
\[\mathrm{Tup}(\tau) \; \land \; \mathrm{Len}(\tau) = 3 \;\land\; \tau[1] = 4\]Using tuples, we can define $z = x^y$ as follows:
\[\forall \tau \bigg[ \big[ \mathrm{Tup}(\tau)\; \land \; \tau[0] = 1 \;\land \forall i < y (\tau[i + 1] = \tau[i] \cdot x) \big] \rightarrow \tau[y] = z \bigg]\]3. Beta Encoding
Can tuples be defined using only addition, multiplication, and first-order formulae? The answer is yes. As might be expected, it was Gödel who first proved this result. Let us first recall the following theorem:
Chinese Remainder Theorem. Let $(n_1, \dots, n_k)$ be pairwise coprime. For any $(r_1, \dots, r_k)$ with $0 \leq r_i < n_i$, there always exists a number $x$ satisfying:
\[x \bmod n_i = r_i\]
Gödel’s idea was to think of the number $x$ from the Chinese Remainder Theorem as a code for the tuple $(r_1, \dots, r_k)$. However, there is a problem here. To decode $(r_1, \dots, r_k)$ from $x$, we need $(n_1, \dots, n_k)$ to be given, which itself is a tuple.
To solve this problem, Gödel produced the following lemma:
Lemma. $n!+ 1, 2n! + 1, \dots, n \cdot n! + 1$ are pairwise coprime.
Proof. For $1 \leq a < b \leq n$, let $u = an! + 1, v = bn! + 1$. By the Euclidean algorithm,
\[\mathrm{gcd}(u, v) = \mathrm{gcd}(u, v - u) = \mathrm{gcd}(an! + 1, (b - a)n!)\]The set of all divisors of $(b - a)n!$ is $\lbrace 1, 2, \dots, n\rbrace $. Since none of these elements divides $an! + 1$, we have $\mathrm{gcd}(an! + 1, (b - a)n!) = \mathrm{gcd}(u, v) = 1$. □
With this lemma, instead of individually specifying $n$ pairwise coprime numbers, we can simply let $n$ be an arbitrary number, and from it, $n$ pairwise coprime numbers $n! + 1, 2n! + 1, \dots, n \cdot n! + 1$ can be chosen canonically. We can now define tuples as an ordered pair.
Definition. We represent the tuple $(r_1, \dots, r_k)$ as an ordered pair $\langle a, b \rangle$ as follows:
- $b = n! \quad \text{where} \quad n = \max(r_1, \dots, r_k, k)$
- $a \bmod (kb + 1) = r_k$
where $a$ is chosen to be the smallest natural number satisfying the second condition.
Meanwhile, tuples can be represented as natural numbers through a well-defined injection from $\mathbb{N}^2$ to $\mathbb{N}$. The following is an example:
\[\pi(a, b) = \frac{(a + b)(a + b + 1)}{2} + b\]Check that $b$ is injective. Hence we can define as follows:
Definition.
\[\langle a, b \rangle = \frac{(a + b)(a + b + 1)}{2} + b\]
This establishes that we can encode a tuple $\tau$ as a natural number $n$. Conversely, given $n$, we can decode $\tau$ using only addition, multiplication, and the modulo operation. Since the modulo operation is easily definable from addition, multiplication, and first-order logic, our goal is achieved.
Historically, Gödel’s theorem was as follows:
$\beta$-function Lemma. For any sequence of natural numbers $(n_1, \dots, n_k)$, there exist natural numbers $a, b$ such that $\beta(a, b, i) = n_i$ for $1 \leq i \leq k$, where $\beta$ is the function defined as follows:
\[\beta(x, y, i) = x \bmod (iy + 1)\]
For this reason, the entire process is called beta encoding. Gödel used beta encoding to successfully define exponentiation and prime factorisation in PA, enabling the formalisation of Gödel numbers and various related predicates in PA. As indicated by the title, the original goal of this article was to provide an overview of this entire process. However, due to the author’s tardily arising laziness and the belief that readers who have come this far can easily infer the subsequent content, let me finish off here.
워시의 정리
25 Jan 2025이전 글에서 이어지는 내용이다.
5. 초자연수의 비표준적 특징
지금까지 우리가 살펴본 초자연수는 $[0], [1], [2], \dots$와 같이 표준 자연수와 상응하는 것들이었다. 이제 표준 자연수와는 괴리가 있는 초자연수들을 살펴 보자.
다음의 초자연수 $\mathfrak{n}$을 보자.
\[(1, 2, 3, 4, \dots) \in \mathfrak{n}\]초자연수의 정의가 동치류이기 때문에 등호가 아닌 포함 관계로 표현함에 유의하라. 초자연수에서 부등호의 정의를 상기하면, 자연수 $n$에 대해 $[n] < \mathfrak{n}$임을 알 수 있다. 즉, $\mathfrak{n}$은 모든 자연수보다 큰 초자연수이다. 따라서 초자연수에서는 다음이 성립한다.
\[\phi_1 : \exists x \; ( \lbrace y : y < x \rbrace \text{ is infinite } )\]위 명제는 자연수에서는 성립하지 않는다.
이번에는 다음의 초자연수 $\mathfrak{m}$을 보자.
\[(1, 2!, 3!, 4!, \dots) \in \mathfrak{m}\]표준 자연수 $n$에 대해 $\mathfrak{m}$은 $[n]$으로 나누어떨어진다. 즉, $\mathfrak{m}$은 모든 자연수를 약수로 가진다. 따라서 초자연수에서는 다음이 성립한다.
\[\phi_2 : \exists x \; (\lbrace y : y \mid x \rbrace \text{ is infinite })\]위 명제 또한 자연수에서는 성립하지 않는다.
그런데 이상한 점이 있다. 저번 글의 서론에서 필자는 자연수와 초자연수가 논리적으로 구분 불가능하다고 했다. 그러나 $\phi_1$과 $\phi_2$는 $\mathbb{N}^*$에서는 참이지만 $\mathbb{N}$에서는 거짓이므로, 둘은 논리적으로 구분 가능한 것으로 보인다. 필자가 거짓말을 한 것일까?
그렇지 않다. 이 표면적인 역설을 해결하는 실마리는, $\phi_1$과 $\phi_2$가 1차 논리로 표현 불가능한 문장이라는 사실이다. 콤팩트성 정리에 의해 “…가 유한하다”는 1차 논리로 표현 불가능하기 때문이다.
$\mathbb{N}^*$과 $\mathbb{N}$이 논리적으로 구분 불가능하다는 말의 엄밀한 의미는 다음과 같다.
정의. 언어 $\mathcal{L}$의 모형 $\mathcal{M}_1$과 $\mathcal{M}_2$가 초등적으로 동등(elementarily equivalent)하다는 것은 임의의 (1차 논리) 문장 $\phi$에 대해
\[\mathcal{M_1} \vDash \phi \iff \mathcal{M}_2 \vDash \phi\]가 성립하는 것이다.
정리. $\mathbb{N}$과 $\mathbb{N}^*$은 초등적으로 동등하다.
위 정리는 워시의 정리의 특수한 결과이다. 워시의 정리를 소개하기 앞서, 일반화된 초곱의 개념을 먼저 살펴보자.
6. 초곱
집합 $I$와, $I$ 위의 자유 초필터 $\mathcal{U}$가 주어졌다고 하자. 또한, 언어 $\mathcal{L}$의 모형 $\lbrace \mathcal{M}_i \rbrace_{i \in I}$가 주어졌다고 하자. 이때, 초곱(ultraproduct) $\mathcal{M}^* = \prod \mathcal{M}_i / \mathcal{U}$를 다음과 같이 정의한다.
초곱의 원소
$\mathcal{M}^*$의 원소는 $\lbrace (a_i)_{i\in I} : a_i \in \mathcal{M}_i \rbrace$가 $\sim$에 대해 이루는 동치류이다. 여기서 $\sim$은 다음과 같이 정의된다.
\[(a_i)_{i\in I} \sim (b_i)_{i \in I} \iff \lbrace i \in I : a_i = b_i \rbrace \in \mathcal{U}\]초곱 위의 연산
$f(x)$가 $\mathcal{L}$의 함수라고 하자. $\mathcal{M}^*$의 원소 $\mathfrak{a} = [(a_i)_{i\in I}]$에 대해 다음과 같이 정의한다.
\[f(\mathfrak{a}) = [(f(a_i))_{i \in I}]\]위 정의는 자연스러운 방식으로 $n$항 함수로 일반화된다.
초곱 위의 술어
$P(x, y)$가 $\mathcal{L}$의 술어라고 하자. $\mathcal{M}^*$의 두 원소 $\mathfrak{a} = [(a_i)_{i\in I}]$와 $\mathfrak{b} = [(b_i)_{i\in I}]$에 대해 다음과 같이 정의한다.
\[\mathcal{M}^* \vDash P(\mathfrak{a}, \mathfrak{b}) \iff \lbrace i \in I : \mathcal{M}_i \vDash P(a_i, b_i) \rbrace \in \mathcal{U}\]위 정의는 자연스러운 방식으로 $n$항 술어로 일반화된다.
초곱 위의 연산과 술어를 정의할 때, 연산과 술어의 결과가 동치류에서 어떤 원소를 대표자로 선택하든 상관없이 같음을 보여야 한다. 이것은 $\mathcal{U}$의 교집합 속성으로부터 어렵지 않게 얻어진다.
연습문제. 주 초필터로 취한 초곱은 원소가 유한함을 보이시오. (이것은 우리가 초자연수를 정의할 때 프레셰 필터와 같은 자유 초필터를 사용해야 하는 이유이다)
이로써 우리는 초자연수를, $I, \mathcal{U}, \mathcal{L}, \mathcal{M}_i$가 각각 다음과 같을 때 도출되는 초곱으로 재정의할 수 있다.
- $I = \mathbb{N}$
- $\mathcal{U} =$ 프레셰 초필터
- $\mathcal{L} = (0, S, <)$
- $\mathcal{M}_i = \mathbb{N}$
비슷한 방식으로 초실수hyperreals를 정의할 수 있다.
- $I = \mathbb{N}$
- $\mathcal{U} =$ 프레셰 초필터
- $\mathcal{L} = (0, 1, +, ⋅, <)$
- $\mathcal{M}_i = \mathbb{R}$
7. 워시의 정리
워시Łoś의 정리. 초곱 $\mathcal{M}^* = \prod \mathcal{M}_i / \mathcal{U}$가 주어졌을 때, 임의의 $\mathcal{L}$-문장 $\phi$에 대해 다음이 성립한다.
\[\mathcal{M}^* \vDash \phi \iff \lbrace i \in I : \mathcal{M}_i \vDash \phi \rbrace \in \mathcal{U}\]
Proof. $\phi$에 대한 구조적 귀납법으로 증명한다.
1. $\phi$가 원자 명제이다
“초곱 위의 술어” 정의에 의해 자명하게 성립한다.
2. $\phi := \psi \land \theta$
\[\begin{aligned} &\mathcal{M}^* ⊨ φ\\ &\iff \mathcal{M}^* ⊨ ψ \land \mathcal{M}^* ⊨ θ\\ &\iff \lbrace i ∈ I \mid \mathcal{M}_i ⊨ ψ \rbrace ∈ \mathcal{U} \land \lbrace i ∈ I \mid \mathcal{M}_i ⊨ θ \rbrace ∈ \mathcal{U} &&(*) \\ &\iff \lbrace i ∈ I \mid \mathcal{M}_i ⊨ ψ \rbrace \cap \lbrace i ∈ I \mid \mathcal{M}_i ⊨ θ \rbrace ∈ \mathcal{U} &&(**) \\ &\iff \lbrace i ∈ I \mid \mathcal{M}_i ⊨ ψ \land \mathcal{M}_i ⊨ θ \rbrace ∈ \mathcal{U}\\ &\iff \lbrace i ∈ I \mid \mathcal{M}_i ⊨ ψ∧θ \rbrace ∈ \mathcal{U}\\ &\iff \lbrace i ∈ I \mid \mathcal{M}_i ⊨ φ \rbrace ∈ \mathcal{U} \end{aligned}\]$(*)$는 귀납 가정에 의해 성립하고, $(**)$는 $\mathcal{U}$의 교집합 닫힘 속성으로 성립한다.
3. $\phi := \lnot \psi$
2와 비슷한 방법으로 하면 된다. 단, 귀납 가정과 $\mathcal{U}$의 초필터 속성($A \in \mathcal{U} \lor A^c \in \mathcal{U}$)를 사용한다.
4. $\phi := \exists x\; \psi$
2와 비슷한 방법으로 하면 된다. 단, 귀납 가정만 사용해도 충분하다.
모든 명제는 1, 2, 3, 4로 구성할 수 있으므로 귀납법에 의해 정리가 증명되었다. ■
따름정리. $\mathbb{N}$과 $\mathbb{N}^*$은 초등적으로 동등하다.
Proof. 워시의 정리에 의해 $\mathbb{N}^* \vDash \phi$일 필요충분조건은 $\lbrace i \in \mathbb{N} : \mathbb{N}^\ast_i \vDash \phi \rbrace \in \mathcal{U}$인 것이다. 그런데 $\mathbb{N}^*_i = \mathbb{N}$이므로, 필요충분조건은 $\mathbb{N} \vDash \phi$로 환원된다. ■
Łoś's Theorem
25 Jan 2025This post continues from the previous post.
5. Nonstandard Characteristics of Hypernatural Numbers
The hypernatural numbers we have examined so far — $[0], [1], [2], \dots$ — correspond to standard natural numbers. We shall now examine some bizarre hypernatural numbers.
Consider the following hypernatural number $\mathfrak{n}$:
\[\mathfrak{n} = [(1, 2, 3, 4, \dots)]\]Recalling how binary relation is defined for hypernaturals, for any natural number $n$, we have $[n] < \mathfrak{n}$. That is, $\mathfrak{n}$ is a hypernatural number greater than all natural numbers. That is, the following holds for hypernaturals:
\[\phi_1 : \exists x \; ( \lbrace y : y < x \rbrace \text{ is infinite } )\]This sentence does not hold in the natural numbers.
Now consider the following hypernatural number $\mathfrak{m}$:
\[\mathfrak{m} = [(1, 2!, 3!, 4!, \dots)]\]For any standard natural number $n$, $\mathfrak{m}$ is divisible by $[n]$. That is, $\mathfrak{m}$ has every natural number as a divisor. Therefore, the following holds for hypernaturals:
\[\phi_2 : \exists x \; (\lbrace y : y \mid x \rbrace \text{ is infinite })\]Again, this sentence does not hold in the natural numbers.
This may seem to contradict the promise delivered in the previous essay. There, I stated that the natural numbers and hypernatural numbers are logically indistinguishable. Yet $\phi_1$ and $\phi_2$, both of which seem to be a cogent logical formula, are true in $\mathbb{N}^*$ but false in $\mathbb{N}$. Have I been misleading?
Of course not. The key to this apparent paradox lies in the fact that $\phi_1$ and $\phi_2$ cannot be expressed in first-order logic. By the compactness theorem, “… is finite” is inexpressible in first-order logic.
For a more precise statement, let us define the following:
Definition. Two $\mathcal{L}$-models $\mathcal{M}_1$ and $\mathcal{M}_2$ of a language $\mathcal{L}$ are elementarily equivalent if for any $\mathcal{L}$-sentence $\phi$,
\[\mathcal{M_1} \vDash \phi \iff \mathcal{M}_2 \vDash \phi\]
Theorem. $\mathbb{N}$ and $\mathbb{N}^*$ are elementarily equivalent.
This theorem is a special case of Łoś’s theorem. But before we state Łoś’s theorem, let us first rigorously define ultraproducts.
6. Ultraproducts
Let a set $I$ and a free ultrafilter $\mathcal{U}$ on $I$ be given. Furthermore, let models $\lbrace \mathcal{M}_i \rbrace_{i \in I}$ of a language $\mathcal{L}$ be given. We define the ultraproduct $\mathcal{M}^* = \prod \mathcal{M}_i / \mathcal{U}$ as follows:
Elements of the Ultraproduct
The elements of $\mathcal{M}^*$ are equivalence classes of $\lbrace (a_i)_{i\in I} : a_i \in \mathcal{M}_i \rbrace$ under the relation $\sim$, where $\sim$ is defined as:
\[(a_i)_{i\in I} \sim (b_i)_{i \in I} \iff \lbrace i \in I : a_i = b_i \rbrace \in \mathcal{U}\]Operations on the Ultraproduct
Let $f(x)$ be a function in $\mathcal{L}$. For an element $\mathfrak{a} = [(a_i)_{i\in I}]$ of $\mathcal{M}^*$, we define:
\[f(\mathfrak{a}) = [(f(a_i))_{i \in I}]\]This definition generalises naturally to $n$-ary functions.
Relations on the Ultraproduct
Let $P(x, y)$ be a relation in $\mathcal{L}$. For two elements $\mathfrak{a} = [(a_i)_{i\in I}]$ and $\mathfrak{b} = [(b_i)_{i\in I}]$ of $\mathcal{M}^*$, we define:
\[\mathcal{M}^* \vDash P(\mathfrak{a}, \mathfrak{b}) \iff \lbrace i \in I : \mathcal{M}_i \vDash P(a_i, b_i) \rbrace \in \mathcal{U}\]This definition generalises naturally to $n$-ary predicates.
When defining operations and relation on the ultraproduct, one needs to show that the definition is irrelevant to which element is chosen as a representative for each equivalence class. This follows readily from the intersection property of $\mathcal{U}$, so we leave it as an exercise.
We can now redefine the hypernatural numbers as the ultraproduct arising when $I, \mathcal{U}, \mathcal{L}, \mathcal{M}_i$ are respectively:
- $I = \mathbb{N}$
- $\mathcal{U} =$ Fréchet ultrafilter
- $\mathcal{L} = (0, S, <)$
- $\mathcal{M}_i = \mathbb{N}$
Similarly, we can define the hyperreal numbers:
- $I = \mathbb{N}$
- $\mathcal{U} =$ Fréchet ultrafilter
- $\mathcal{L} = (0, 1, +, ⋅, <)$
- $\mathcal{M}_i = \mathbb{R}$
7. Łoś’s Theorem
Łoś’s Theorem. Given an ultraproduct $\mathcal{M}^* = \prod \mathcal{M}_i / \mathcal{U}$, for any $\mathcal{L}$-sentence $\phi$, the following holds:
\[\mathcal{M}^* \vDash \phi \iff \lbrace i \in I : \mathcal{M}_i \vDash \phi \rbrace \in \mathcal{U}\]
Proof. We prove this by structural induction on $\phi$.
1. $\phi$ is an atomic proposition
This follows trivially from the definition of predicates on ultraproducts.
2. $\phi := \psi \land \theta$
\[\begin{aligned} &\mathcal{M}^* ⊨ φ\\ &\iff \mathcal{M}^* ⊨ ψ \land \mathcal{M}^* ⊨ θ\\ &\iff \lbrace i ∈ I \mid \mathcal{M}_i ⊨ ψ \rbrace ∈ \mathcal{U} \land \lbrace i ∈ I \mid \mathcal{M}_i ⊨ θ \rbrace ∈ \mathcal{U} &&(*) \\ &\iff \lbrace i ∈ I \mid \mathcal{M}_i ⊨ ψ \rbrace \cap \lbrace i ∈ I \mid \mathcal{M}_i ⊨ θ \rbrace ∈ \mathcal{U} &&(**) \\ &\iff \lbrace i ∈ I \mid \mathcal{M}_i ⊨ ψ \land \mathcal{M}_i ⊨ θ \rbrace ∈ \mathcal{U}\\ &\iff \lbrace i ∈ I \mid \mathcal{M}_i ⊨ ψ∧θ \rbrace ∈ \mathcal{U}\\ &\iff \lbrace i ∈ I \mid \mathcal{M}_i ⊨ φ \rbrace ∈ \mathcal{U} \end{aligned}\]$(*)$ holds by the inductive hypothesis, and $(**)$ holds by the intersection closure property of $\mathcal{U}$.
3. $\phi := \lnot \psi$
This can be proved by a similar method to case 2, using the inductive hypothesis and the ultrafilter property of $\mathcal{U}$ ($A \in \mathcal{U} \lor A^c \in \mathcal{U}$).
4. $\phi := \exists x\; \psi$
This can be proved by a similar method to case 2, though the inductive hypothesis alone suffices.
Since every proposition can be constructed from cases 1, 2, 3, and 4, the theorem is proved by induction. ■
Corollary. $\mathbb{N}$ and $\mathbb{N}^*$ are elementarily equivalent.
Proof. By Łoś’s theorem, the necessary and sufficient condition for $\mathbb{N}^* \vDash \phi$ is that $\lbrace i \in \mathbb{N} : \mathbb{N}^\ast_i \vDash \phi \rbrace \in \mathcal{U}$. However, since $\mathbb{N}^*_i = \mathbb{N}$, the necessary and sufficient condition reduces to $\mathbb{N} \vDash \phi$. ■
프레셰 필터와 비표준 자연수
22 Jan 2025뢰벤하임-스콜렘 정리에 따르면 표준 산술 모형과 초등적으로 동등elementarily equivalent하지만 구조적으로 상이nonisomorphic한 모형이 존재한다. 달리 말해, 자연수가 만족하는 모든 1차 논리 명제를 만족하지만 자연수가 아닌 수 체계가 존재한다.
이 글에서는 초곱ultraproduct을 이용하여 대표적인 산술의 비표준적 모형인 초자연수hypernaturals를 구성하고, 이것이 표준 산술 모형과 초등적으로 동등함을 보증하는 워시의 정리Łoś’s theorem를 증명한다.
1. 개괄
콤팩트성 정리에 의해 우리는 1차 논리가 유한과 무한을 구별하지 못함을 안다. 따라서 무한을 적절히 사용함으로써 자연수와 1차 논리적으로 구분 불가능한 모델을 정의할 수 있으리라 기대해봄직하다.
이에 따라 다음과 같이 초자연수 $[0], [1], [2], \dots$를 정의하자.
\[\begin{aligned} [][0] &= (0, 0, 0, 0, 0, \dots) \\ [1] &= (1, 1, 1, 1, 1, \dots) \\ [2] &= (2, 2, 2, 2, 2, \dots) \end{aligned}\]그런데 생각해 보면 모든 항이 0으로 차 있어야 $[0]$으로 간주하는 것은 지나치게 엄격하다. 예를 들어 처음 두 개의 항만 1이고 나머지 항은 모두 0인 튜플 $(1, 1, 0, 0, 0, \dots)$ 또한 $[0]$으로 보는 것이 자연스럽다. 따라서 유한 개의 항을 제외한 모든 항이 $n$이라면 그 튜플 또한 $[n]$으로 간주하도록 하자. 즉,
\[[n] = \lbrace (x_1, x_2, x_3, \dots) \in \mathbb{N}^\omega : \lbrace i \in \mathbb{N}: x_i \neq n \rbrace \text{ is finite} \rbrace\]하지만 이제 다음의 문제가 생긴다. 다음 튜플은 $[0]$으로 간주해야 하는가, $[1]$로 간주해야 하는가?
\[(0, 1, 0, 1, 0, 1, \dots)\]이 모호함을 제거하기 위해 우리는 짝수 집합과 홀수 집합 중 하나를 임의로 채택할 것이다. 만약 짝수 집합을 채택했다면 위 튜플은 $[0]$이 되고(인덱스는 0부터 시작하는 것으로 전제한다) 홀수 집합을 채택했다면 $[1]$이 될 것이다.
하지만 이 채택의 과정에는 주의가 필요하다. 만약 6의 배수의 집합이 채택되었다면, 3의 배수의 집합 또한 채택되어야 논리적으로 일관된다. 후자를 만족하는 튜플은 자명하게 전자를 만족하기 때문이다. 그리고 3의 배수의 집합이 채택되었으므로, 3의 배수가 아닌 수의 집합은 기각되어야 한다. 자연수의 모든 부분집합에 대해 이같은 채택과 기각의 과정을 거친 결과물은 초필터ultrafilter라고 불리는 구조와 상응될 것이다. 적절한 초필터가 주어지면 그것을 토대로 임의의 튜플을 초자연수에 대응시킬 수 있으며, 이 전체적인 과정을 초곱ultraproduct이라고 부른다.
2. 초필터의 정의
정의. $X$가 집합이라고 하자. $X$의 부분집합들로 이루어진 집합 $\mathcal{F}$가 다음을 만족할 때, $X$의 필터라고 부른다.
- $X \in \mathcal{F}$
- $\varnothing \not\in \mathcal{F}$
- 상위집합 닫힘: $A \in \mathcal{F}, A \subset B \implies B \in \mathcal{F}$
- 유한 교집합 닫힘: $A, B \in \mathcal{F} \implies A \cap B \in \mathcal{F}$
직관적으로 필터는 “큰 집합들의 모임”이다. 이 관점에서 보면 1번과 2번 공리는 전체집합은 크고 공집합은 작다는 자명한 원리를 진술한다. 3번 공리는 큰 집합을 포함하는 집합은 크다는 원리를, 4번 공리는 큰 집합끼리 유한 번 교집합을 해도 여전히 크다는 원리를 진술한다.
여담으로 필터는 초곱뿐 아니라 퍼지 논리의 모형을 고전 논리의 모형으로 변환하는 데도 쓰인다. 이때 필터는 “큰 집합들의 모임”이 아닌 “참인 문장들의 모임”이 된다. 그리고 퍼지 논리에서 고전 논리로의 변환은 코헨의 강제법을 이해하는 한 가지 방식이기도 하다.
하세 다이어그램Hasse diagram을 통해 필터를 더 직관적으로 이해할 수 있다. 색칠된 영역은 $X = \lbrace 0, 1, 2 \rbrace$의 필터이다. 하세 다이어그램을 $\varnothing$에서 $X$로 가는 물줄기의 흐름으로 이해하면, 특정 지점에 잉크를 떨어뜨렸을 때 그 잉크가 퍼져 나가는 영역은 필터를 이룬다.
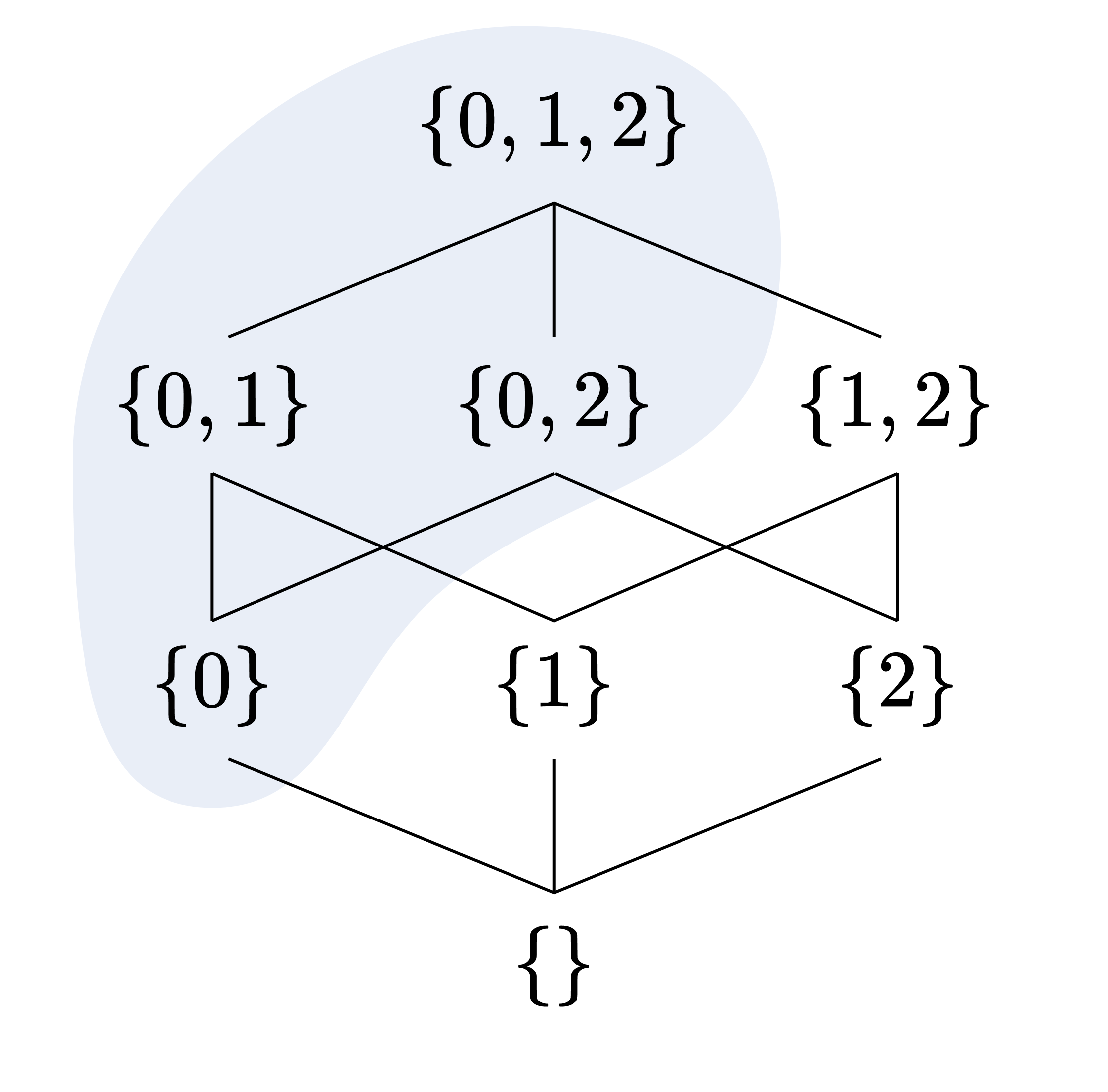
2번 공리와 4번 공리에 의해, $A \in \mathcal{F}$라면 $A^c := X \setminus A \notin \mathcal{F}$이다. 이 사실을 강화하여, $X$의 모든 부분집합에 대해 그 집합 또는 여집합이 필터에 있을 것을 요구하면 초필터의 정의를 얻는다.
정의. $X$의 필터 $\mathcal{F}$가 다음을 만족할 때 $\mathcal{F}$는 초필터이다.
\[\forall A \in \mathcal{P}(X) : A \in \mathcal{F} \lor A^c \in \mathcal{F}\]
앞선 그림의 필터는 초필터이다. 초필터는 하세 다이어그램의 정확히 절반을 차지한다는 사실에 주목하라.
3. 무한집합에서의 초필터
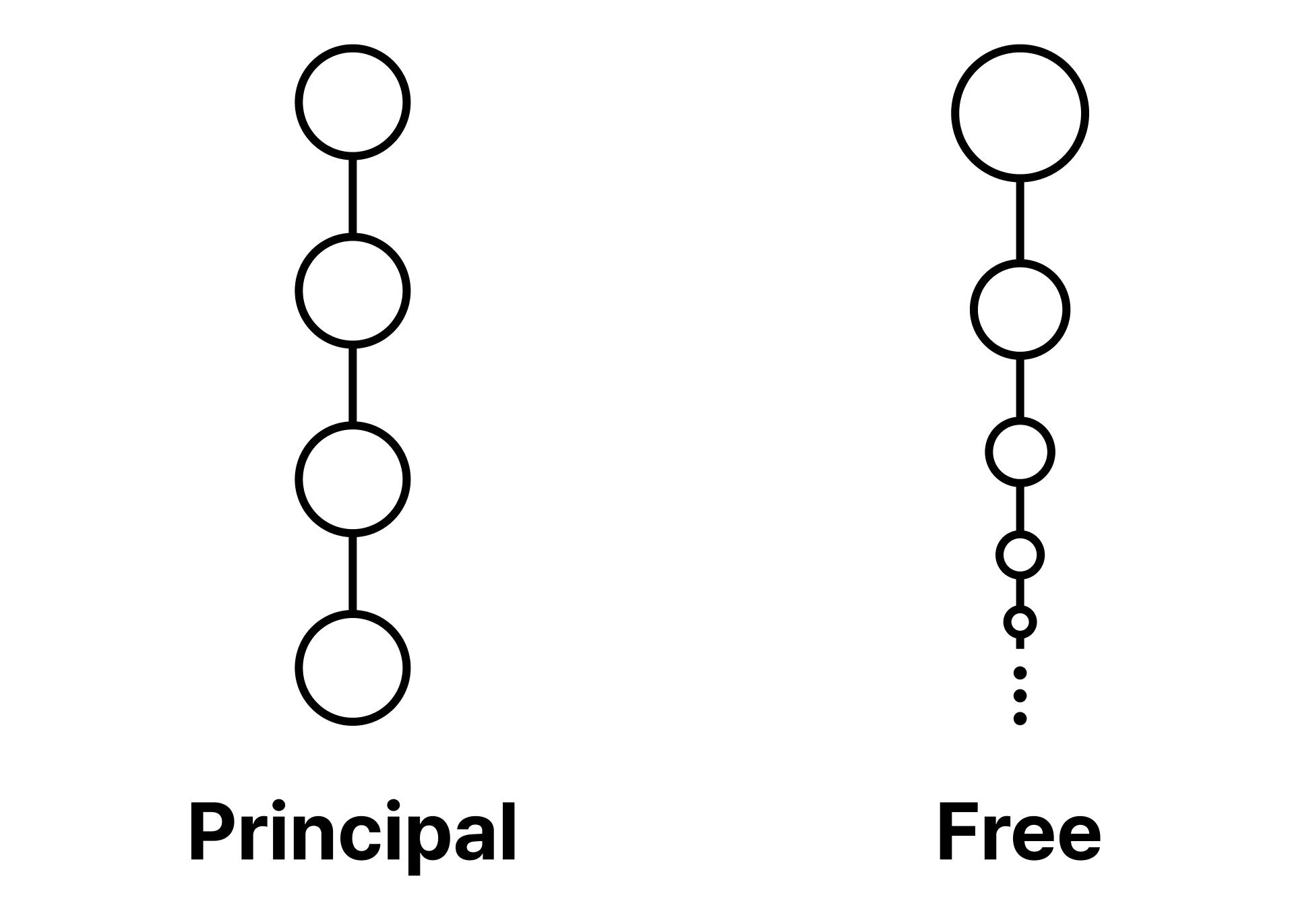
최소 원소를 가지는 필터를 주 필터principal filter라고 하며, 주 필터가 아닌 필터를 자유 필터free filter라고 한다. 지금까지 우리가 본 모든 필터는 주 필터로, “특정 지점에 떨어뜨린 잉크가 퍼져 나가는 영역”의 이미지와 완전히 부합한다.
연습문제. 모든 주 초필터는 홑원소 집합을 원소로 가짐을 보이시오.
주 필터와 달리 자유 필터는 직관적으로 포착하기 힘들다. 다음의 정리 때문이다.
정리. 유한집합 위의 필터는 모두 주 필터이다.
Proof. $A_0 \in \mathcal{F}$가 최소 원소가 아니라고 하자. 그러면 어떤 $B \in \mathcal{F}$가 존재하여 $A_1 = A_0 \cap B \subsetneq A$이다. 즉, $|A_1| < |A_0 |$이다. $A_1$이 최소 원소라면 증명이 끝나고, 아니라면 똑같은 과정을 반복한다. 주어진 집합의 크기가 유한하므로 이 과정은 계속 반복될 수 없으며, 최소 원소에 종착하게 된다. ■
위 정리는 이렇게 이해할 수도 있다. 자유 필터는 그 내부에 무한히 이어지지만 (따라서 유한 교집합만으로 최소 원소에 도달할 수 없다) 공집합에 도달하지는 않는 부분집합의 체인을 가지는 필터이다. 이에 따라 무한집합 위의 필터만이 자유 필터가 될 수 있다.
그 실례를 살펴보자.
정의. $X$가 무한집합이라고 하자. $A \subset X$가 여유한cofinite하다는 것은 $X \setminus A$가 유한집합인 것이다.
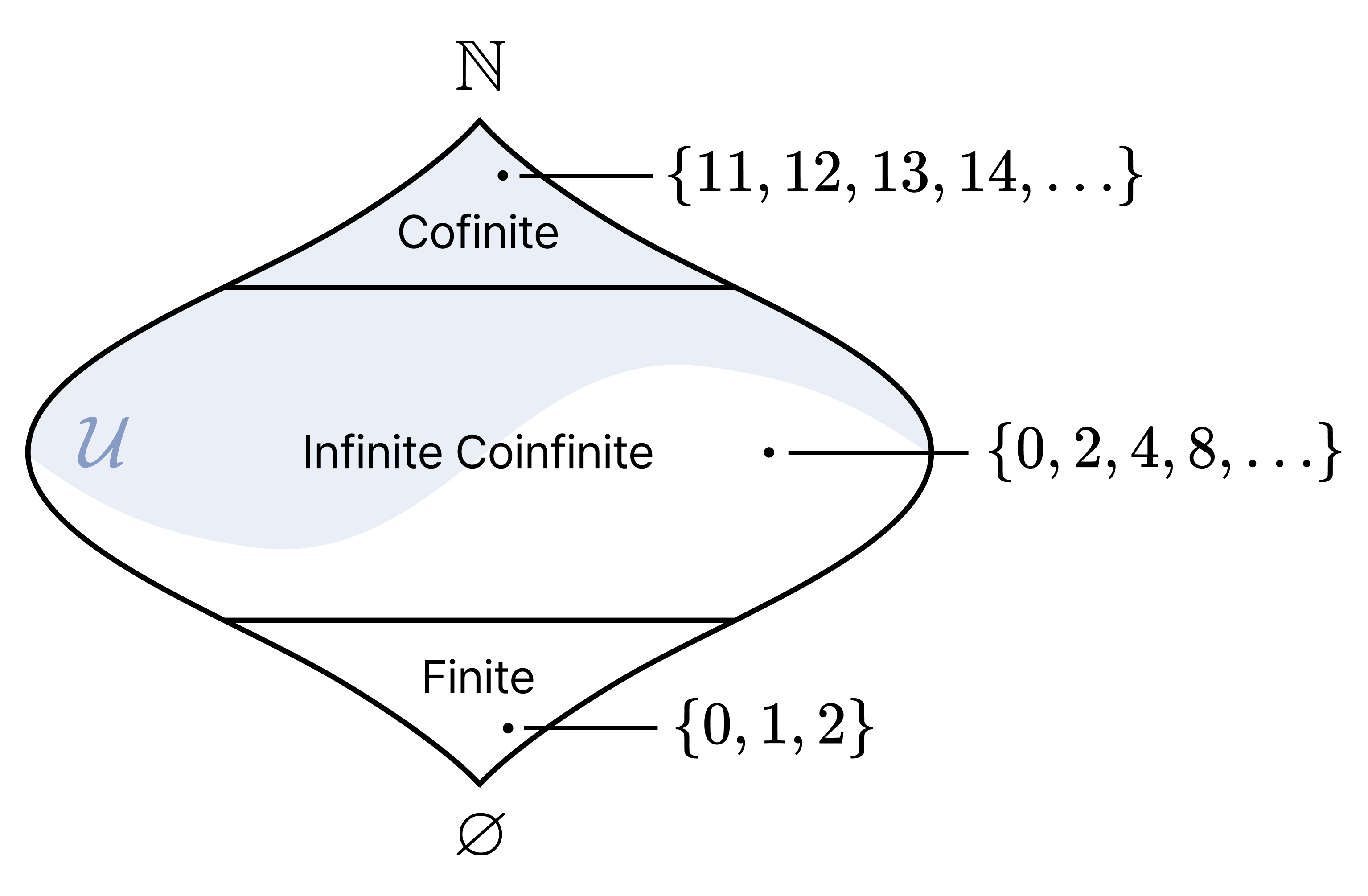
정리. $\mathbb{N}$의 모든 여유한 부분집합의 모임을 $\mathcal{F}$라고 하자. $\mathcal{F}$는 자유 필터이다.
증명은 연습문제로 남긴다. 위 정리의 $\mathcal{F}$를 프레셰 필터Fréchet filter라고 부른다. 일례로 10보다 큰 수들의 집합 $\lbrace 11, 12, 13, 14, \dots \rbrace$은 $\mathcal{F}$의 원소이지만, 짝수의 집합은 $\mathcal{F}$의 원소가 아니다.
프레셰 필터는 초필터가 아니다. 하지만 다음 정리에 의해 초필터로 확장할 수 있다.
정리. 모든 필터는 초필터로 확장될 수 있다.
Proof. $X$의 모든 필터들의 모임 $\Omega$에 포함 관계로 정의되는 순서를 주자. 이 순서 하에서 체인을 이루는 필터들의 합집합은 필터임을 어렵지 않게 보일 수 있다. 따라서 초른의 보조정리에 의해 $\Omega$는 극대 원소 $\mathcal{U}$를 가진다. 만약 $\mathcal{U}$가 초필터가 아니라면, 어떤 $A_0 \subset X$가 존재하여 $A_0, A_0^c \notin U$이다. 이제 다음과 같이 $\mathcal{V}$를 정의한다.
\[\mathcal{V} = \mathcal{U} \cup \lbrace A \subset X : A_0 \subset A \rbrace \cup \lbrace A_0 \cap U : U \in \mathcal{U} \rbrace\]$\mathcal{V}$는 필터임을 확인할 수 있다. 이것은 $\mathcal{U}$의 극대성에 위배된다. 따라서 $\mathcal{U}$는 초필터이다. ■
따라서 자연수 집합은 프레셰 필터로부터 확장되는 자유 초필터를 가진다. 이 필터를 프레셰 초필터라고 부르자.
4. 초자연수
지금까지의 논의를 정리하자면, 프레셰 초필터를 비롯한 자유 초필터는 다음의 성질을 가진다.
- 모든 여유한 집합을 원소로 가진다.
- 유한집합은 원소로 가지지 않는다.
- $A \subset \mathbb{N}$일 때 $A$가 필터의 원소이거나 $A^c$가 필터의 원소이다.
위 세 성질 덕분에 프레셰 초필터는 서론에서 초곱의 기초적인 아이디어를 개괄했을 때 맞닥뜨렸던 모호성의 문제를 해결하는 데 안성맞춤이다. 이제 우리는 다음과 같이 초자연수를 정의할 수 있다.
$\mathcal{U}$가 자유 초필터라고 하자. $\mathbb{N}^\omega$ 위에 다음의 동치 관계를 정의한다.
\[(n_0, n_1, n_2, \dots) \sim (m_0, m_1, m_2, \dots) \iff \lbrace i \in \mathbb{N} : n_i = m_i \rbrace \in \mathcal{U}\]이것이 동치 관계임은 어렵지 않게 확인할 수 있다. 따라서 다음과 같이 동치류를 취할 수 있다.
\[\mathbb{N}^* := \mathbb{N}^\omega/\sim\]$\mathbb{N}^*$을 초자연수라고 한다. 초자연수의 정의가 동치류인 것은 서론에서 초자연수를 $[n]$으로 적은 이유이다. 이제 남은 것은 초자연수의 연산과 술어 관계를 정의하는 것이다.
초자연수의 덧셈은 다음과 같이 자연스럽게 정의한다.
\[(n_0, n_1, \dots) + (m_0, m_1, \dots) = (n_0 + m_0, n_1 + m_1, \dots)\]여기에는 한 가지 미묘한 문제가 있다. 초자연수의 정의가 동치류이기 때문에, 동치류의 어떤 원소를 택하더라도 위 덧셈의 결과에 영향을 주지 않음을 보여야 한다. 즉,
\[\begin{gather} (n_0, n_1, \dots), (n_0', n_1', \dots) \in [n]\\ (m_0, m_1, \dots), (m_0', m_1', \dots) \in [m] \end{gather}\]에 대해,
\[(n_0, n_1, \dots) + (m_0, m_1, \dots), (n_0', n_1', \dots) + (m_0', m_1', \dots) \in [n + m]\]임을 보여야 한다. 다행히 이는 어렵지 않다.
곱셈과 역원 또한 비슷하게 정의하면 된다. 한편 $<$와 같은 이항 관계는 다음과 같이 정의한다.
\[(n_0, n_1, n_2, \dots) < (m_0, m_1, m_2, \dots) \iff \lbrace i \in \mathbb{N} : n_i < m_i \rbrace \in \mathcal{U}\]이 정의는 자연스럽게 삼항, 사항 관계로 일반화할 수 있다.
이로써 우리는 초자연수를 정의했다. 다음 글에서는 초자연수의 여러 비표준적인 특징과, 그런 비표준성에도 불구하고 초자연수와 자연수를 1차 논리로 구분할 수 없음을 보이는 워시의 정리를 살펴볼 것이다.
Fréchet Filters and Nonstandard Natural Numbers
22 Jan 2025Löwenheim-Skolem theorem states that there exist models that are elementarily equivalent yet nonisomorphic to the standard model of arithmetics. In other words, there exist number systems that satisfy all first-order sentences of arithmetics, yet are not “the” natural numbers.
In this article, we construct the hypernaturals, a representative nonstandard model of arithmetic, using ultraproducts, and prove Łoś’s theorem, which states that this model is elementarily equivalent to the standard model of arithmetics.
1. Overview
By the compactness theorem, we know that first-order logic cannot distinguish between the finite and the infinite. Therefore, we might reasonably expect to be able to define a model that is indistinguishable from the standard model with respect to every first-order formula by a clever use of infinity.
To this end, we may tro to define the hypernaturals $[0], [1], [2], \dots$ as follows:
\[\begin{aligned} [0] &= (0, 0, 0, 0, 0, \dots) \\ [1] &= (1, 1, 1, 1, 1, \dots) \\ [2] &= (2, 2, 2, 2, 2, \dots) \end{aligned}\]This definition makes sense, but upon reflection, requiring all entries to be 0 in order to regard it as $[0]$ is excessively stringent. For instance, it would be natural to regard the tuple $(1, 1, 0, 0, 0, \dots)$, where the only the first two entries are nonzero, as $[0]$ as well. Therefore, let us consider a tuple as $[n]$ if all but finitely many entries equal $n$. That is,
\[[n] = \lbrace (x_1, x_2, x_3, \dots) \in \mathbb{N}^\omega : \lbrace i \in \mathbb{N}: x_i \neq n \rbrace \text{ is finite} \rbrace\]However, this now gives rise to the following problem. Should the following tuple be considered as $[0]$ or as $[1]$?
\[(0, 1, 0, 1, 0, 1, \dots)\]To resolve this ambiguity, we shall arbitrarily choose one among the set of even numbers and the set of odd numbers. If we choose the even numbers, the above tuple becomes $[0]$ (indices begin at 0), while if we choose the odd numbers it becomes $[1]$.
This “choosing” requires some intricacy. For example, if the set of multiples of 6 is chosen, then the set of multiples of 3 must also be chosen for consistency, since tuples satisfying the latter trivially satisfy the former. Moreover, since the set of multiples of 3 is chosen, the set of numbers that are not multiples of 3 must be rejected. The end result of this process of choosing and rejecing for all subsets of the natural numbers will give rise to a structure called an ultrafilter. Given an appropriate ultrafilter, we can map any tuple to a hypernatural, and this entire process is called an ultraproduct.
2. Definition of Ultrafilters
Definition. Let $X$ be a set. A collection $\mathcal{F}$ of subsets of $X$ is called a filter on $X$ if it satisfies the following:
- $X \in \mathcal{F}$
- $\varnothing \not\in \mathcal{F}$
- Upward closure: $A \in \mathcal{F}, A \subset B \implies B \in \mathcal{F}$
- Finite intersection closure: $A, B \in \mathcal{F} \implies A \cap B \in \mathcal{F}$
Intuitively, a filter is a “collection of large sets”. From this perspective, axioms 1 and 2 express the trivial principle that the whole set is large and the empty set is small. Axiom 3 expresses the principle that a set containing a large set is large, while axiom 4 expresses the principle that finite intersections of large sets remain large.
As a side note, filters are used not only in ultraproducts but also in converting models of fuzzy logic into models of classical logic. In this context, filters become “collections of true statements” rather than “collections of large sets”. And indeed, the conversion from fuzzy logic to classical logic is also one way of understanding Cohen’s forcing method.
Filters can be understood more intuitively through Hasse diagrams. The shaded region represents a filter on $X = \lbrace 0, 1, 2 \rbrace$. If we understand the Hasse diagram as representing a stream of water from $\varnothing$ to $X$, the region an ink dropped at a particular point spreads over forms a filter.

By axioms 2 and 4, if $A \in \mathcal{F}$, then $A^c := X \setminus A \notin \mathcal{F}$. Strengthening this fact by requiring that for every subset of $X$, either the set or its complement is in the filter, we obtain the definition of an ultrafilter.
Definition. A filter $\mathcal{F}$ on $X$ is an ultrafilter if it satisfies:
\[\forall A \in \mathcal{P}(X) : A \in \mathcal{F} \lor A^c \in \mathcal{F}\]
The filter in the previous diagram is an ultrafilter. Note that an ultrafilter occupies exactly half of the Hasse diagram.
3. Ultrafilters on Infinite Sets
A filter with the least element is called a principal filter, while a filter that is not principal is called a free filter. All filters we have seen so far are principal filters, which perfectly match the image of “the region an ink dropped at a particular point spreads over”.
Exercise.
- Show that the least element of a principal filter is a singleton.
- Show that “a filter with a minimal element” is an equivalent definition of the principal filter.
Unlike principal filters, free filters are difficult to visualise intuitively, due to the following theorem:
Theorem. Every filter on a finite set is principal.
Proof. Suppose $A_0 \in \mathcal{F}$ is not a minimal element. Then there exists some $B \in \mathcal{F}$ such that $A_1 = A_0 \cap B \subsetneq A$. That is, $|A_1| < |A_0 |$. If $A_1$ is a minimal element, the proof is complete; otherwise, we repeat the same process. Since the given set has finite cardinality, this process cannot continue indefinitely and must terminate at a minimal element. ■
This theorem can also be understood as follows: a free filter is one that contains an infinitely descending chain of subsets within it. It thus does not reach a minimal element nor the empty set through finite intersections. Hence, only filters on infinite sets can be free.

Let us examine a concrete example.
Definition. Let $X$ be an infinite set. A subset $A \subset X$ is cofinite if $X \setminus A$ is finite.
Theorem. Let $\mathcal{F}$ be the collection of all cofinite subsets of $\mathbb{N}$. Then $\mathcal{F}$ is a free filter.
The proof is left as an exercise. The $\mathcal{F}$ in the above theorem is called the Fréchet filter. For instance, the set of numbers greater than 10 is an element of $\mathcal{F}$, but the set of even numbers is not.
Fréchet filter is not an ultrafilter. However, it can be extended to an ultrafilter by the following theorem:
Theorem. Every filter can be extended to an ultrafilter.
Proof. Let $\Omega$ be the collection of all filters on $X$, ordered by inclusion. Under this ordering, the union of filters forming a chain is itself a filter, as can be shown without much difficulty. Therefore, by Zorn’s lemma, $\Omega$ has a maximal element $\mathcal{U}$. We now claim that $\mathcal{U}$ is an ultrafilter. Assuming otherwise, there exists some $A_0 \subset X$ such that $A_0, A_0^c \notin U$. Define $\mathcal{V}$ as follows:
\[\mathcal{V} = \mathcal{U} \cup \lbrace A \subset X : A_0 \subset A \rbrace \cup \lbrace A_0 \cap U : U \in \mathcal{U} \rbrace\]One can verify that $\mathcal{V}$ is a filter. This contradicts the maximality of $\mathcal{U}$. Therefore, $\mathcal{U}$ is an ultrafilter. ■
Hence, the set of natural numbers possesses a free ultrafilter extending from the Fréchet filter. Let us call this filter the Fréchet ultrafilter.

4. The Hypernaturals
To summarise our discussion thus far, free ultrafilters, including the Fréchet ultrafilter, possess the following properties:
- They contain all cofinite sets as elements.
- They do not contain finite sets as elements.
- For $A \subset \mathbb{N}$, either $A$ is an element of the filter or $A^c$ is an element of the filter.
These three properties make the Fréchet ultrafilter perfectly suited for resolving the ambiguity problem we encountered when outlining the basic idea of ultraproducts in the introduction. We can now define the hypernaturals as follows.
Let $\mathcal{U}$ be a free ultrafilter. Define the following equivalence relation on $\mathbb{N}^\omega$:
\[(n_0, n_1, n_2, \dots) \sim (m_0, m_1, m_2, \dots) \iff \lbrace i \in \mathbb{N} : n_i = m_i \rbrace \in \mathcal{U}\]It is not difficult to verify that this is indeed an equivalence relation. Therefore, we can take equivalence classes:
\[\mathbb{N}^* := \mathbb{N}^\omega/\sim\]We call $\mathbb{N}^*$ the hypernaturals. This reveals why the hypernaturals were written as $[n]$ in the introduction — a hypernatural number is an equivalence class. Indeed, it would have more accurate to write $[n]$ ans $[(n, n, n, \dots)]$, but let us allow ourselves some abuse of notation.
What remains now is to define operations and relations on the hypernaturals. Addition of hypernaturals is defined naturally as follows:
\[[(n_0, n_1, \dots)] + [(m_0, m_1, \dots)] = [(n_0 + m_0, n_1 + m_1, \dots)]\]There is one subtle issue here. Since hypernaturals are equivalence classes, we need to show that the above operation is well-defined regardless of which representative of an equivalence class we choose. That is, for
\[\begin{gather} (n_0, n_1, \dots), (n_0', n_1', \dots) \in [n]\\ (m_0, m_1, \dots), (m_0', m_1', \dots) \in [m], \end{gather}\]we need to show that
\[(n_0, n_1, \dots) + (m_0, m_1, \dots), (n_0', n_1', \dots) + (m_0', m_1', \dots) \in [n + m]\]Fortunately, this is not too difficult to establish and is left as an exercise.
Multiplication and successor can be defined similarly. Binary relations such as $<$ are defined as follows:
\[(n_0, n_1, n_2, \dots) < (m_0, m_1, m_2, \dots) \iff \lbrace i \in \mathbb{N} : n_i < m_i \rbrace \in \mathcal{U}\]This definition can be naturally generalised to ternary and quaternary relations.
We have thus defined the hypernaturals. In the next article, we shall examine various nonstandard features of the hypernaturals and Łoś’s theorem, which shows that despite such nonstandardness, the hypernaturals and natural numbers cannot be distinguished by first-order logic.
지시에 대하여 — 한정 기술구
18 Jan 20254. 한정 기술구
이름과 달리 한정 기술구와 관련하여 제기되는 일차적인 질문은 과연 한정 기술구는 지시를 하느냐는 것이다. 프레게는 한정 기술구 또한 이름과 마찬가지로 뜻(한정 기술구의 내용)과 지시체(해당 내용을 유일하게 만족하는 대상)를 가진다고 봤지만, 러셀은 한정 기술구가 지시체를 가지지 않는다고 보았다.
4.1. 러셀의 기술주의
러셀의 주장
러셀에 따르면 한정 기술구는 대상을 지시하지 않는다. 오히려 한정 기술구는 2차 술어와 의미론적으로 동등하다. 요컨데 술어 P를
P: 대상 → 진릿값
와 같은 함수로 생각할 수 있듯이, D가 한정 기술구일 때
D: (대상 → 진릿값) → 진릿값 (i.e. 술어 → 진릿값)
이다. 이 관점에 따르면 “현재 영국의 왕”은 찰스 3세를 지시하는 것이 아닌, ”x는 남자이다”, “x는 영국인이다”, “x는 엘리자베스 2세의 아들이다” 등에 대해서는 참을 반환하고, “x는 여자이다”, “x는 미국인이다”, “x는 제임스 1세의 아들이다”에 대해서는 거짓을 반환하는 2차 술어이다.
러셀의 기술주의의 강점은 “현재 프랑스의 왕은 대머리이다“와 같이 지시체를 결여하는 한정 기술구가 어떻게 유의미한 문장에서 쓰일 수 있는지(프레게에 따르면 이 문장은 무의미하지만 러셀에 따르면 이 문장은 그저 거짓이다), 그리고 프레게의 퍼즐을 설명할 수 있다는 것이다.
나아가 러셀은 ‘이것’과 ‘나’를 제외한 모든 이름이 위장된 한정 기술구라고 주장한다. 이 주장은 언어의 의미론을 단순명료하게 만드는 장점이 있지만 크립키의 양상 및 의미론적 논증을 잘 설명하지 못한다. 따라서 이 글에서는 “한정 기술구는 지시하지 않는다”라는 러셀의 주장만 살펴 보기로 한다.
Remark. 하지만 러셀의 기술주의가 정말로 프레게의 퍼즐을 설명하는가에 대해서는 의문의 여지가 있다. 술어에 대한 외연적 정의를 택할 경우, ’샛별‘과 ’개밥바라기‘는 정확히 같은 (2차) 술어가 되기 때문이다. 내포주의와 외연주의에 대한 콰인 등의 논변도 참고할 만하다.
스트로슨의 이론
다음 문장을 보자.
그 책상은 책에 덮여 있다. (The table is covered with books.)
이 문장은, 예컨데 화자가 방에 있고, 방에 책상이 딱 하나 있으며, 그 책상이 책에 덮여 있을 때 참인 듯하다. 그러나 러셀의 기술주의에 따르면 이 우주에는 책상이 하나보다 많으므로 문장은 거짓이다.
이에 대해 스트로슨은 한정 기술구가 진정으로 지시를 하는 경우가 있다고 주장한다. 한정 기술구가 지시적 사용으로 사용되면, 한정 기술구는 기술의 내용을 만족하는 대상 중 해당 맥락에서 가장 두드러지는 대상을 지시한다. 반면 한정 기술구가 속성적 사용으로 사용될 때 기술구는 러셀의 이론처럼 작동한다.
도넬란의 이론
다음 문장을 보자.
마티니를 마시는 그 남자는 누구인가? (Who is the man drinking a martini?)
이 문장의 화자가 지시하려고 하는 남자가 사실은 마티니가 아닌 물을 마시고 있었다고 하자. 이 경우 스트로슨에 따르면 “the man drinking a martini”는 지시적으로 사용될 수 없으며(해당 맥락에서 마티니를 마시고 있는 남자가 없으므로), 속성적으로 사용될 수도 없다(전 세계에서 현재 마티니를 마시고 있는 남자가 여러 명이므로).
따라서 도넬란은 한정 기술구가 그 기술적 내용을 만족하지 않는 대상 또한 지시할 수 있다고 주장한다. 중요한 것은 화자가 한정 기술구로써 특정 대상을 지칭하려는 의도이다. 도넬란의 이론은 한정 기술구에 대한 험티덤티 문제로 빠지는 듯하며, 이를 의식한 도넬란은 그라이스식 의미 이론에 호소한다.
크립키의 이론
크립키는 우리가 “마티니를 마시는 그 남자는 누구인가?”와 같은 문장을 화용론적으로 이해하면 그 어떤 경우에도 한정 기술구는 지시하지 않는다는 강한 러셀주의를 견지할 수 있다고 주장한다.
크립키는 지시가 순전히 규약(convention — 알고리즘으로 이해하는 것이 더 적절할 수 있다)으로 이루어져야 한다고 보는 듯하다. 일례로 크립키의 이름 이론은 이름 $N$이 주어졌을 때, 이 이름이 지칭하는 대상이 인과 이론으로 정확하게 특정된다. 그러나 이름에 대한 강한 규약주의가 다수의 담지자를 가지는 이름이나 불순 지표사의 원리를 제대로 설명하지 못한다는 점을 보았을 때 크립키의 규약주의는 근거가 미약하며, 이에 따라 도넬란주의를 거부하는 크립키의 주장 또한 근거가 미약하다.
한정 기술구 v. 비한정 기술구
최근에는 한정 기술구(the F)와 비한정 기술구(a F)의 구분 자체가 의문시되고 있다. 둘의 차이를 정확하게 정의하기가 매우 까다로운 일로 드러났을 뿐더러, 둘을 문법적으로 구분하지 언어가 수많이 보고되었기 때문이다. 만약 한정 기술구와 비한정 기술구의 구분이 부당한 것으로 드러난다면, 이것은 한정 기술구가 지시를 하지 않는다는 러셀주의를 보강할 수 있을 것이다. (또는, 비한정 기술구 또한 지시를 한다는 매우 논란적인 주장을 개진해야 할 것이다)
5. 지시 회의주의
기술주의, 밀주의, 그리고 지표사 이론들은 지시가 철학적으로 탐구할 만한 주제이며 이에 대한 의미 있는 분석이 가능하다는 입장에서 일치한다. 그러나 지시가 본질적으로 무의미하거나 공허한 개념이라고 주장하는, 이른바 “지시 회의주의적” 입장들도 존재한다.
콰인의 회의주의
콰인은 번역 불확정성 논제를 통해 ‘가바가이’와 같은 지시 표현들이 불가해하다고 주장한다. 번역 불확정성 논제에 대해서는 필자가 이전에 쓴 바가 있으니 그쪽을 참고.
다수의 문제
다수의 문제는 지시 표현이 지시하는 대상의 경계를 어떻게 정의해야 하는가에 대한 문제이다. 예를 들어 나는 ‘경복궁’으로 현재의 경복궁을 지시할 수 있다. 그런데 어느 날 경복궁의 기와가 불타 없어지는 사건이 일어났다고 상상해 보자. 화재 사건 이후에도 나는 ’경복궁‘으로 (이제는 기와가 없는) 경복궁을 지시할 수 있는 듯하다. 그렇다면 화재 사건 이전과 이후의 ‘경복궁’은 동일한 지시체를 가진다고 말할 수 있는가? 경복궁이 얼마나 불타 없어져야 더이상 그것은 ‘경복궁’의 지시체가 될 수 없는가? 이 문제는 지시 표현이 지시체를 가진다는 일반적인 도식에 의혹을 제기한다.
데이비드슨의 참 이론
철학자들이 지시에 대한 이론을 추구하는 이유는 그것이 언어의 의미론을 세우는 데 필요하기 때문이다. 즉, 문장에 등장하는 각 표현의 지시체가 결정되어야 해당 문장의 진릿값을 결정할 수 있다.
그러나 데이비드슨은 이것이 본말을 전도하는 것이라고 주장한다. 데이비드슨은 문장에 대한 참 이론을 제시하는 것만으로 해당 언어의 의미론을 세울 수 있고, 이에 따라 지시 이론은 불필요하다고 주장한다. 참에 대한 철학적 논의는 이후 별개의 시리즈로 정리하도록 하겠다.