The Cantor-Bendixson Theorem and Polish Space

25 Dec 2024

This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.

Definition. A set $P$ in a topological space $X$ is perfect when $P’ = P$. Here, $P’$ denotes the set of limit points of $P$.

Remark. Every perfect set is a closed set, but the converse does not hold. Recall that in general $S \not\subset S’$ (when $S$ has isolated points) and $S’ \not\subset S$ (when $S$ is not a closed set). It follows that a perfect set is a closed set with no isolated points.

Definition. A topological space $X$ is hereditarily Lindelöf when every subspace of $X$ is Lindelöf.

Weak Cantor-Bendixson Theorem. Let $X$ be a hereditarily Lindelöf space. For any closed set $F \subset X$, there exist a perfect set $P$ and a countable set $C$ such that $F = P \sqcup C$.

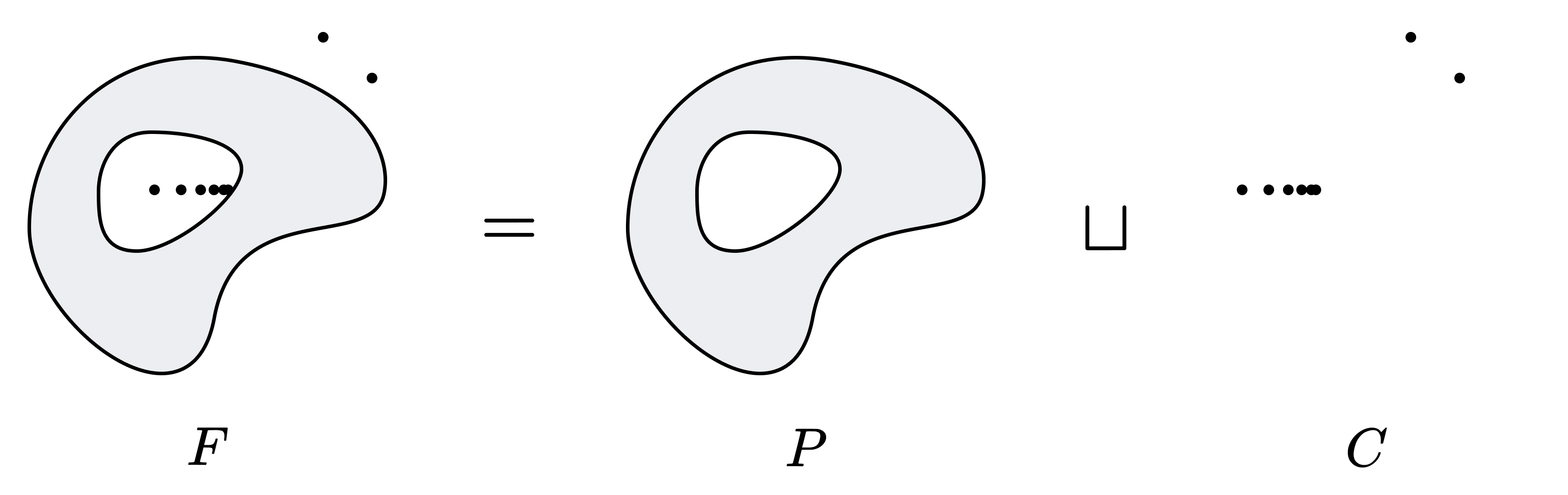
Since a perfect space is a closed space with no isolated points, the above theorem can be restated as: A closed subspace of a hereditarily Lindelöf space has at most countable isolated points.

Proof. We define $P$ and $C$ as follows:

\[P = \lbrace x \in F : \text{For all nbd $U$ of $x$, $U \cap F$ is uncountable} \rbrace\] \[C = \lbrace x \in F : \text{There exists a nbd $U$ of $x$ s.t. $U \cap F$ is countable} \rbrace\]

Note that $F = P \sqcup C$.

Claim 1. $C$ is open in $F$.

Proof of Claim. When $x \in C$, there exists a neighbourhood $U$ of $x$ such that $U \cap F$ is countable. That is, for any $y \in U \cap F$, $U$ is a neighbourhood of $y$ and $U \cap F$ is countable, so $y \in C$. Therefore $U \cap F \subset C$. □

Claim 2. $C$ is countable.

Proof of Claim. Consider the subspace topology on $F$. By hypothesis, this topology is Lindelöf. For any $x \in C$, we can find a neighbourhood $U_x$ of $x$ such that $U_x \cap F$ is countable. Then $\lbrace U_x \rbrace_{x \in C}$ is an $F$-open cover of $C$, and by the Lindelöf hypothesis, $C = \bigcup_{\alpha \in J} U_\alpha$ where $J$ is countable. Since each $U_\alpha$ is countable, $C$ is countable. □

Claim 3. $P$ is perfect.

Proof of Claim. By Claim 1, $P$ is a closed set in $F$, and since $F$ is a closed set, $P$ is a closed set in $X$. Therefore $P’ \subset P$. To show the reverse inclusion, let $x \in P$. For any neighbourhood $U$ of $x$, we have that $U \cap F = (U \cap C) \sqcup (U \cap P)$ is uncountable. Since $C$ is countable, $U \cap P$ must be uncountable. Therefore $U$ has intersection with $P$ larger than $\lbrace x \rbrace$, and hence $x \in P’$. ■

Definition. A separable complete metrisable space is called a Polish space.

In metrisable spaces, separability, second countability, and the Lindelöf property are equivalent, so the definition can be replaced with any of these three conditions. The name ‘Polish space’ derives from the fact that the mathematicians who first studied these spaces — Sierpiński, Kuratowski, Tarski — were Polish.

When the stronger condition that $X$ is a Polish space is given, one can prove that the Cantor-Bendixson decomposition is unique.

Strong Cantor-Bendixson Theorem. Let $X$ be a Polish space. For any closed set $F \subset X$, there exist a perfect set $P$ and a countable set $C$ such that $F = P \sqcup C$. Moreover, this decomposition is unique.

The following also holds:

Theorem. A perfect set in a Polish space has cardinality $2^{\aleph_0}$.

Proof. This will be treated separately in a future article on descriptive set theory.

From this, the following conclusion follows:

Corollary: The Continuum Hypothesis for Closed Sets of Real Numbers. A closed set of real numbers is either countable or has cardinality $2^{\aleph_0}$.

Proof. Since the real numbers form a Polish space, by the Cantor-Bendixson theorem every closed set decomposes as a disjoint union of a countable set and a perfect set. If the latter is empty, then the closed set is countable; otherwise it has cardinality $2^{\aleph_0}$. ■

Cantor had hoped that from the proof of the above theorem he might be able to prove the general continuum hypothesis, but as is well known, this hope was not realised.