칸토어-벤딕슨 정리와 폴란드 공간
25 Dec 2024정의. 위상공간 $X$의 집합 $P$에 대해 $P’ = P$일 때 $P$를 완벽한 집합perfect set이라고 한다. ($P’$은 $P$의 집적점들의 집합)
Remark. 모든 완벽한 집합은 닫힌 집합이지만, 역은 성립하지 않는다. 일반적으로 $S \not\subset S’$ ($S$가 고립점을 가짐), $S’ \not\subset S$ ($S$가 닫힌 집합이 아님) 임에 유의하라. 뒤집어 말해, 완벽한 집합은 고립점이 없는 닫힌 집합이다.
정의. $X$의 임의의 부분공간이 린델뢰프일 때 $X$를 세습적 린델뢰프hereditarily Lindelöf라고 한다.
약한 칸토어-벤딕슨 정리. $X$가 세습적 린델뢰프 공간이라고 하자. $F \subset X$가 닫힌 집합일 때 어떤 완벽한 집합 $P$와 가산집합 $C$가 존재하여 $F = P \sqcup C$이다.
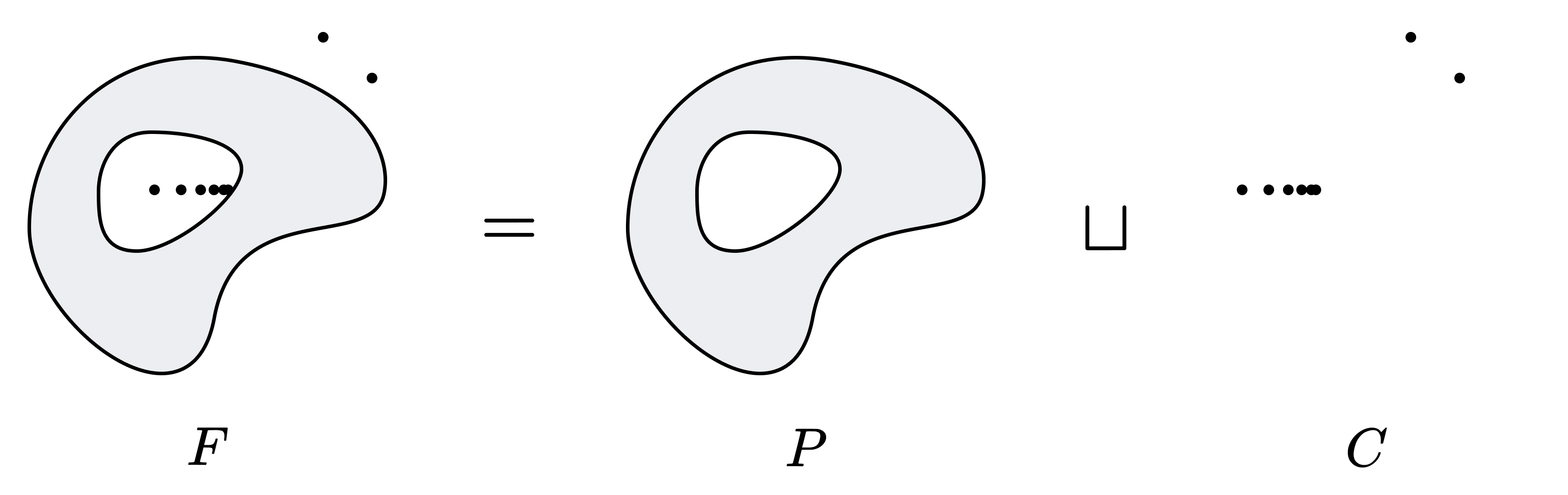
완벽한 집합은 고립점이 없는 닫힌 집합이므로, 위 정리는 “닫힌 집합은 최대 가산 개의 고립점을 가진다”로 재진술할 수 있다.
증명. 다음과 같이 $P, C$를 정의한다.
\[P = \lbrace x \in F : \text{For all nbd $U$ of $x$, $U \cap F$ is uncountable} \rbrace\] \[C = \lbrace x \in F : \text{There exists a nbd $U$ of $x$ s.t. $U \cap F$ is countable} \rbrace\]$F = P \sqcup C$임에 주목하라.
Claim 1. $C$는 $F$에서 열린 집합이다.
Proof of Claim. $x \in C$일 때 어떤 $x$의 근방 $U$가 존재하여 $U \cap F$가 가산이다. 즉, 임의의 $y \in U \cap F$에 대해 $U$는 $y$의 근방이고 $U \cap F$가 가산이므로 $y \in C$이다. 따라서 $U \cap F \subset C$이다. □
Claim 2. $C$는 가산이다.
Proof of Claim. $F$의 부분공간 토폴로지를 생각하자. 가정에 의해 이 토폴로지는 린델뢰프이다. 임의의 $x \in C$에 대해 $U_x \cap F$가 가산인 $x$의 근방 $U_x$를 찾을 수 있다. 그러면 $\lbrace U_x \rbrace_{x \in C}$는 $C$의 $F$-열린 덮개이며, 린델뢰프 가정에 의해 $C = \bigcup_{\alpha \in J} U_\alpha$ ($J$는 가산)이다. $U_\alpha$가 가산이므로 $C$는 가산이다. □
Claim 3. $P$는 완벽하다.
Proof of Claim. Claim 1에 의해 $P$는 $F$에서 닫힌 집합이며, $F$가 닫힌 집합이므로 $P$는 $X$에서 닫힌 집합이다. 따라서 $P’ \subset P$이다. 역을 보이기 위해 $x \in P$라고 하자. 임의의 $x$의 근방 $U$에 대해 $U \cap F = (U \cap C) \sqcup (U \cap P)$가 비가산이다. $C$가 가산이므로, $U \cap P$가 비가산이어야 한다. 따라서 $U$는 $P$와 $\lbrace x \rbrace$보다 큰 교집합을 가지며, $x \in P’$이다. ■
정의. 분리 가능한separable 완비 거리화 가능 공간을 폴란드 공간Polish space이라고 한다.
거리화 가능 공간에서 분리 가능성, 2차 가산, 그리고 린델뢰프는 동치이므로 해당 세 가지 조건 중 하나로 정의를 대체할 수 있다. ‘폴란드 공간’이라는 이름은 해당 공간을 처음으로 연구한 학자들인 시에르핀스키, 쿠라토프스키, 타르스키 등이 폴란드인들인 데에서 유래했다.
$X$가 폴란드 공간이라는 더 강한 조건이 주어지면 칸토어-벤딕슨 분해가 유일함을 증명할 수 있다.
강한 칸토어-벤딕슨 정리. $X$가 폴란드 공간이라고 하자. $F \subset X$가 닫힌 집합일 때 어떤 완벽한 집합 $P$와 가산집합 $C$가 존재하여 $F = P \sqcup C$이다. 또한, 해당 분해는 유일하다.
또한 다음이 성립한다.
정리. 폴란드 공간의 완벽한 집합은 $2^{\aleph_0}$의 크기를 가진다.
증명. 추후 기술적 집합론에 대한 글에서 따로 다룰 예정.
이로부터 다음의 결론이 따라 나온다.
따름정리: 실수의 닫힌집합에서의 연속체 가설. 실수의 닫힌집합은 가산이거나 $2^{\aleph_0}$의 크기를 가진다.
증명. 실수는 폴란드 공간이므로 칸토어-벤딕슨 정리에 의해 모든 닫힌집합이 가산집합과 완벽한 집합의 서로소 합으로 분해된다. 후자가 공집합일 경우 해당 닫힌집합은 가산이며, 그렇지 않을 경우 $2^{\aleph_0}$이다. ■
칸토어는 위 정리의 증명으로부터 일반적인 연속체 가설을 증명할 수 있으리라는 희망을 품었지만 잘 알려져 있다시피 그 희망은 실현되지 못했다.