대각선 논법 없이 실수의 비가산성 증명하기

26 Dec 2024

정리. $\mathbb{R}$은 비가산이다. 즉, $\mathbb{N}$에서 $\mathbb{R}$로 가는 전사함수는 존재하지 않는다.

수학과 2학년 정도 되면 한번쯤은 들어 봤을 정리이다. 가장 널리 알려진 증명은 칸토어의 대각선 논법이다. 하지만 대각선 논법 없이 이 정리를 증명하는 방법이 있다. 각각 $\mathbb{R}$의 순서적 특징과, 위상적 특징을 이용한다.

1. 동형성 정리를 이용한 증명

칸토어의 동형성 정리에 따르면 다음을 만족하는 전순서 집합 $(S, \leq)$는 모두 순서 동형이다.

1. $S$는 가산이다.
2. $S$는 조밀하다. 즉, $x, y \in S$에 대해 $x < y$라면 $x < z < y$인 $z \in S$가 존재한다.
3. $S$는 상계 및 하계를 가지지 않는다.

$(\mathbb{Q}, \leq)$는 위 세 조건을 모두 만족하고, $(\mathbb{R}, \leq)$는 2와 3을 만족한다. 따라서 만약 $\mathbb{R}$이 가산이면 $(\mathbb{R}, \leq)$는 $(\mathbb{Q}, \leq)$와 순서 동형이다. 하지만 전자는 완비인데 반해 후자는 그렇지 않으므로 $\mathbb{R}$은 비가산이다. ■

2. 콤팩트성을 이용한 증명

$X$가 고립점이 없는 콤팩트한 하우스도르프 공간이라고 하자. 또한 $X \neq \varnothing$이라고 하자.

Claim 1. $U \neq \varnothing$가 $X$의 열린 집합이라고 하자. $x \in X$에 대해 $x \notin \bar{V}$이면서 $V \subset U$인 열린 집합 $V$가 존재한다.

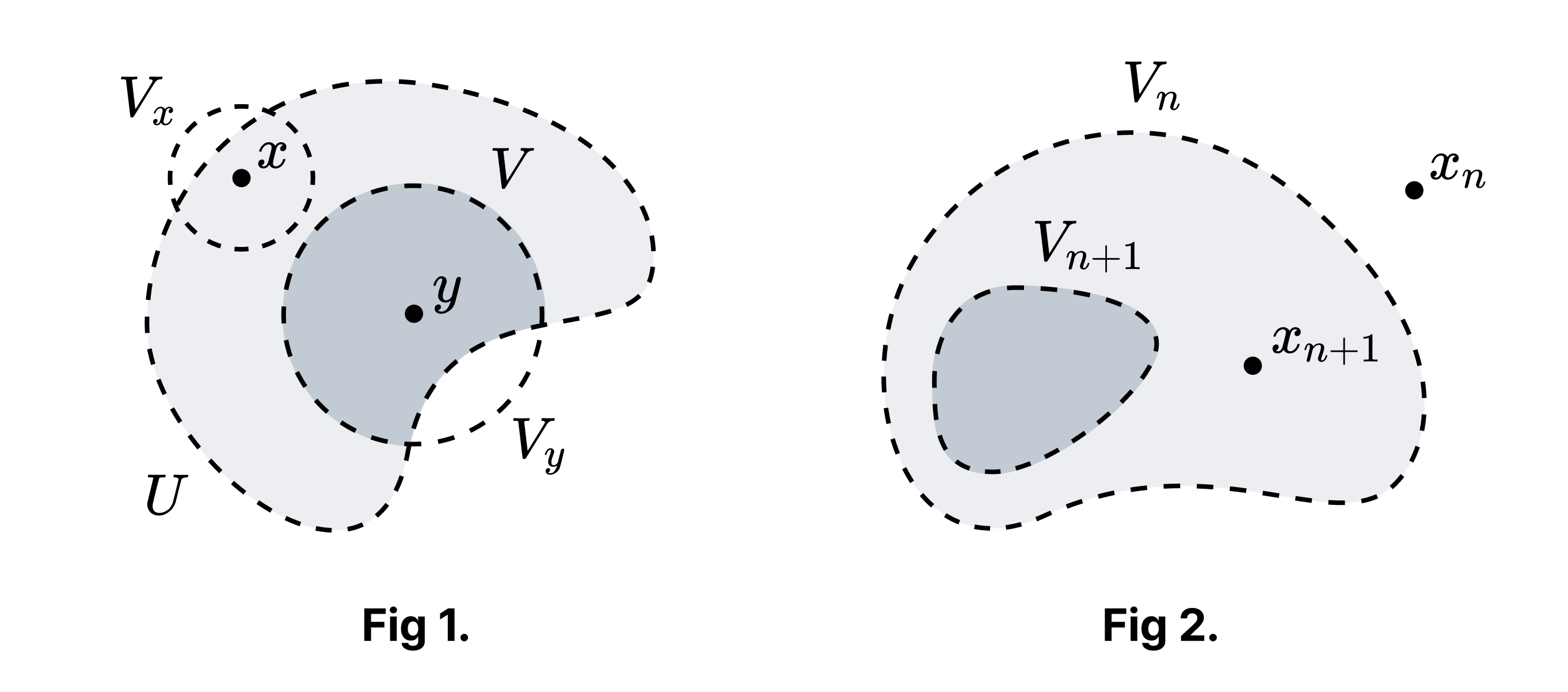
Proof of Claim 1. $x \neq y$이며 $y \in U$가 존재한다. 왜냐하면 $x \in U$인 경우 $X$가 고립점을 가지지 않으므로 존재하고, $x \notin U$인 경우 $U$가 공집합이 아니기 때문에 존재하기 때문이다. $X$가 하우스도르프이므로 $x, y$를 근방 $V_x, V_y$로 분리할 수 있다. $V = V_y \cap U$가 얻고자 하는 집합이다 (Fig 1의 색칠된 부분). □

Claim 2. $X$는 비가산이다.

Proof of Claim 2. $X$가 가산이라고 하자. $X$의 원소들을 $\lbrace x_n \rbrace_{n \in \mathbb{Z}^+}$와 같이 나열한다. $V_0 = X$라고 하자. Claim 1에 의해 각 $n$에 대해 $x_n \notin \bar{V_n}$인 열린 집합 $V_n$이고 $V_n \subset V_{n-1}$인 열린 집합 $V_n$이 존재한다 (Fig 2). $X$가 콤팩트하므로 유한 교집합 성질에 의해

\[V = \bigcap_{n \in \mathbb{Z}^+} \bar{V}_n \neq \varnothing\]

이다. 하지만 $x_n \in V$라면 $x_n \in \bar{V}_n$이 되어 모순이다. 따라서 $X$는 비가산이다. □

Claim 3. $\mathbb{R}$은 비가산이다.

Proof of Claim 3. $[0, 1]$은 고립점을 가지지 않는 콤팩트 하우스도르프 공간이다. 따라서 비가산이다. 이에 따라 $\mathbb{R}$은 비가산이다. ■