Proving the Uncountability of Real Numbers Without the Diagonal Argument

26 Dec 2024

Theorem. $\mathbb{R}$ is uncountable. That is, there exists no surjective function from $\mathbb{N}$ to $\mathbb{R}$.

This is a theorem that any sophomore student would have encountered at least once. The most widely known proof is Cantor’s diagonal argument. However, there are methods to prove this theorem without the diagonal argument. These utilise the order-theoretic and topological properties of $\mathbb{R}$, respectively.

1. Proof Using the Isomorphism Theorem

Cantor’s isomorphism theorem states that all totally ordered sets $(S, \leq)$ satisfying the following conditions are order isomorphic:

1. $S$ is countable.
2. $S$ is dense. That is, for $x, y \in S$ with $x < y$, there exists $z \in S$ such that $x < z < y$.
3. $S$ has neither an upper bound nor a lower bound.

$(\mathbb{Q}, \leq)$ satisfies all three conditions above, whilst $(\mathbb{R}, \leq)$ satisfies conditions 2 and 3. Therefore, if $\mathbb{R}$ were countable, then $(\mathbb{R}, \leq)$ would be order isomorphic to $(\mathbb{Q}, \leq)$. However, the former is complete while the latter is not, so $\mathbb{R}$ is uncountable. ■

2. Proof Using Compactness

Let $X$ be a compact Hausdorff space with no isolated points. Also assume that $X \neq \varnothing$.

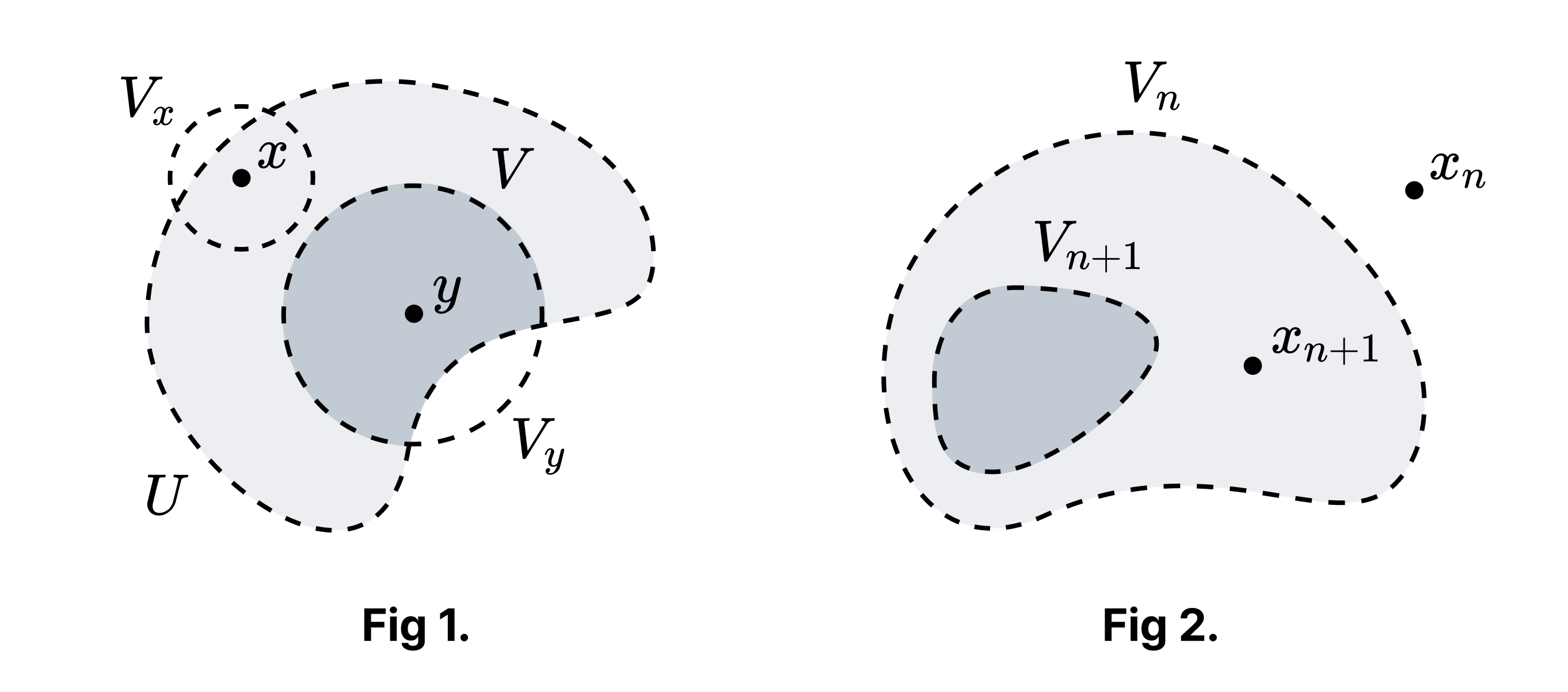
Claim 1. Let $U \neq \varnothing$ be an open subset of $X$. For $x \in X$, there exists an open set $V$ such that $x \notin \bar{V}$ and $V \subset U$.

Proof of Claim 1. There exists $y \in U$ where $x \neq y$. This is because if $x \in U$, then since $X$ has no isolated points such a $y$ must exist, and if $x \notin U$, then such a $y$ exists because $U$ is non-empty. Since $X$ is Hausdorff, we can separate $x$ and $y$ by neighbourhoods $V_x$ and $V_y$. Then $V = V_y \cap U$ is the desired set (the dark shaded region in Fig 1). □

Claim 2. $X$ is uncountable.

Proof of Claim 2. Suppose $X$ is countable. Enumerate the elements of $X$ as $\lbrace x_n\rbrace _{n \in \mathbb{Z}^+}$. Let $V_0 = X$. By Claim 1, for each $n$ there exists an open set $V_n$ such that $x_n \notin \bar{V_n}$ and $V_n \subset V_{n-1}$ (Fig 2). Since $X$ is compact, by the finite intersection property we have

\[K = \bigcap_{n \in \mathbb{Z}^+} \bar{V}_n \neq \varnothing.\]

However, if $x_n \in K$, then $x_n \in \bar{V}_n$, which is a contradiction. Therefore, $X$ is uncountable. □

Claim 3. $\mathbb{R}$ is uncountable.

Proof of Claim 3. $[0, 1]$ is a compact Hausdorff space with no isolated points. Therefore, it is uncountable. Consequently, $\mathbb{R}$ is uncountable. ■