디멘의 블로그
Dimen's Blog
이데아를 여행하는 히치하이커
Alice in Logicland
Robinson, Craig, and Beth's Theorems
08 May 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
Elementary Amalgamation Property
Theorem. Let $\mathfrak{A}$ be an $\mathcal{L}$-structure and $\mathfrak{B}$ be an $\mathcal{L}’$-structure such that the $\mathcal{L}$-reduct of $\mathfrak{B}$ is elementarily equivalent to $\mathfrak{A}$. Then there exists an $\mathcal{L}’$-structure $\mathfrak{C}$ such that $f: \mathfrak{A} \to \mathfrak{C}$ is an elementary embedding in $\mathcal{L}$ and $g: \mathfrak{B} \to \mathfrak{C}$ is an elementary embedding in $\mathcal{L}’$.
Proof. Following the notation of this post, consider the theory $E(\mathfrak{A})$ in language $L_\mathfrak{A}$ and the theory $E(\mathfrak{B})$ in language $L’\mathfrak{B}$. Let $T = E(\mathfrak{A}) \cup E(\mathfrak{B})$ be a theory in the language $\mathcal{L}’{\mathfrak{AB}} = \mathcal{L}\mathfrak{A} \cup \mathcal{L}’\mathfrak{B}$. We shall show that $T$ has a model $\mathfrak{C}$.
Suppose $T$ has no model. Then $T$ is inconsistent. By the compactness theorem, there exist some $\mathcal{L}$-formula $\phi$ and $\mathcal{L}’$-formula $\psi$ such that for appropriate ${a_i} \subset \mathcal{L}\mathfrak{A}$ and ${b_j} \subset \mathcal{L}\mathfrak{B}$,
\[\{\phi(a_1, \dots, a_n), \psi(b_1, \dots, b_m)\}\]has no model. Since $\mathfrak{B} \vDash \psi(b_1, \dots, b_m)$, there must be no way to assign the constants $a_1, \dots, a_n$ to elements of the domain of $\mathfrak{B}$ such that $\mathfrak{B} \vDash \phi(a_1, \dots, a_n)$. That is,
\[\mathfrak{B} \not\vDash \exists x_1, \dots x_n \; \phi(x_1, \dots, x_n)\]However, since the $\mathcal{L}$-reduct of $\mathfrak{B}$ is elementarily equivalent to $\mathfrak{A}$, and the right-hand side above is an $\mathcal{L}$-sentence that is satisfied by $\mathfrak{A}$, this yields a contradiction. Therefore, $T$ has a model $\mathfrak{C}$. Since $\mathfrak{C}$ is a model of both $E(\mathfrak{A})$ and $E(\mathfrak{B})$, both $\mathfrak{A}$ and $\mathfrak{B}$ are naturally elementarily embedded into $\mathfrak{C}$. ■
Robinson Consistency Theorem
Theorem. Let $\mathcal{L} = \mathcal{L}_1 \cap \mathcal{L}_2$. Suppose $T$ is a (semantically) complete theory in $\mathcal{L}$, and $T_1$ and $T_2$ are consistent theories in $\mathcal{L}_1$ and $\mathcal{L}_2$ respectively, each extending $T$. Then $T_1 \cup T_2$ is consistent as a theory in $\mathcal{L}_1 \cup \mathcal{L}_2$.
Proof. It suffices to construct a model of $T_1 \cup T_2$.
Since $T_1$ and $T_2$ are consistent, they have models $\mathfrak{A}_0$ and $\mathfrak{B}_0$ respectively. Since $T = T_1 \cap T_2$ is complete, the $\mathcal{L}$-reducts of $\mathfrak{A}_0$ and $\mathfrak{B}_0$ are elementarily equivalent. Therefore, by the elementary amalgamation property, there exist an $\mathcal{L}$-elementary embedding $f_0$ and an $\mathcal{L}_2$-elementary embedding $h_0$ such that the following holds:
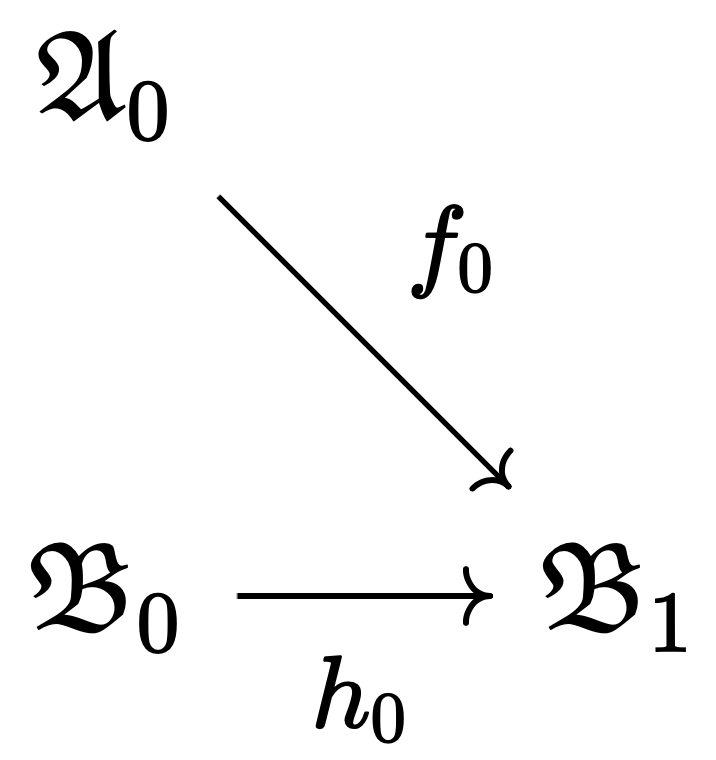
Now considering the $\mathcal{L}$-reduct of $\mathfrak{B}_1$, this is elementarily equivalent to $\mathfrak{A}_0$, so again by the elementary amalgamation property, there exist an $\mathcal{L}$-elementary embedding $g_0$ and an $\mathcal{L}_1$-elementary embedding $k_0$ such that the following holds:
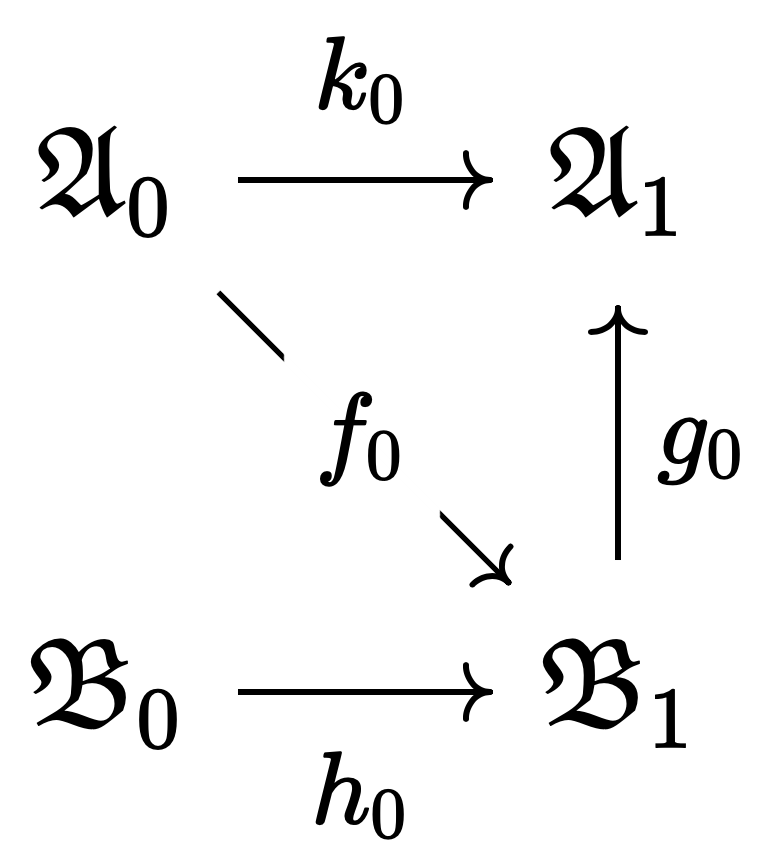
Repeating this process, we obtain the following directed system of structures:
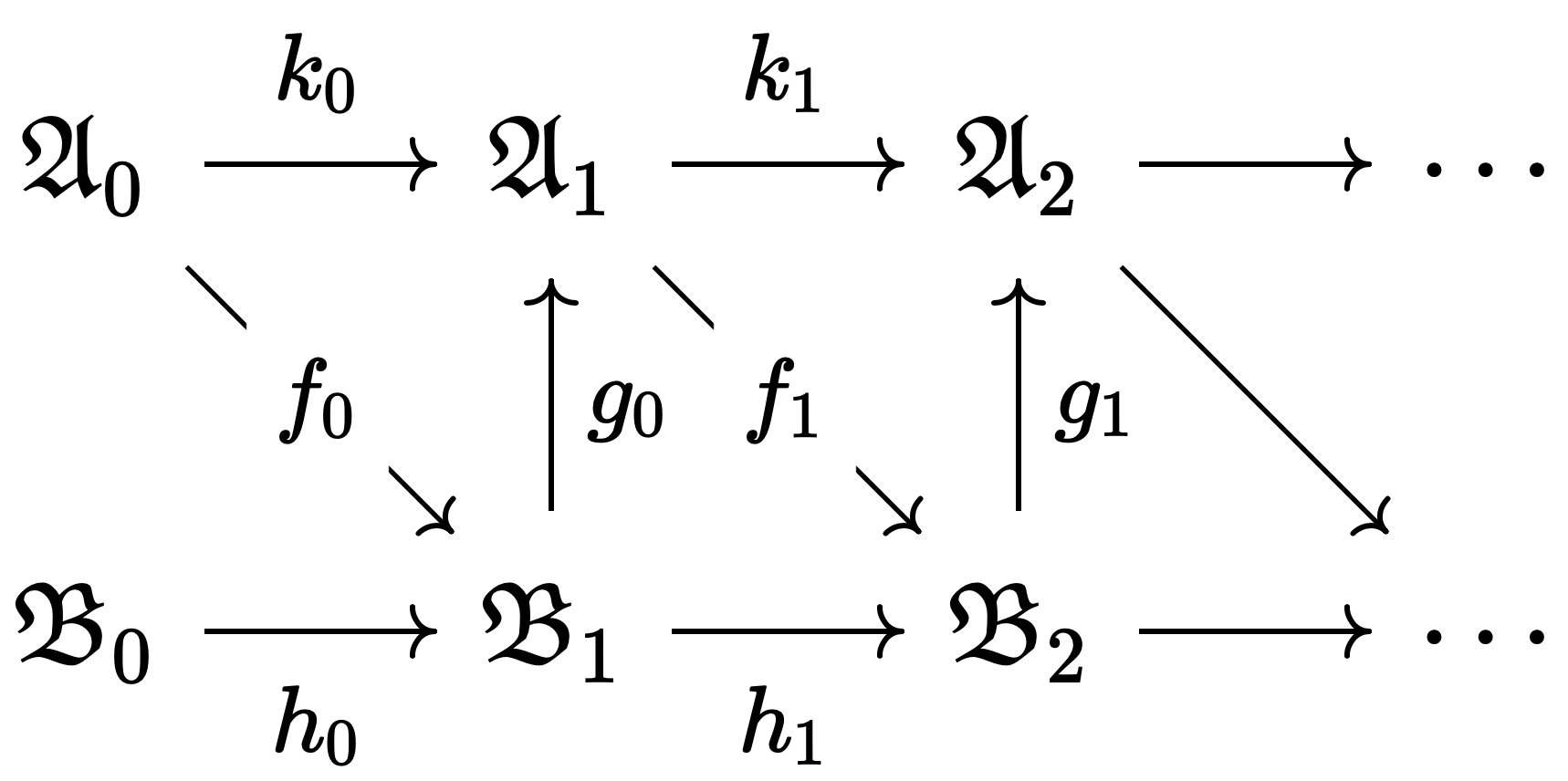
| Map | Property |
|---|---|
| $f, g$ | $\mathcal{L}$-elementary embedding |
| $k$ | $\mathcal{L}_1$-elementary embedding |
| $h$ | $\mathcal{L}_2$-elementary embedding |
Reducing all models in the above directed system to $\mathcal{L}$ gives an $\mathcal{L}$-structure directed system. Let $\mathfrak{C}$ be the colimit of this directed system. $\mathfrak{C}$ is also the colimit of the directed system consisting of ${\mathfrak{A}_i}$, since the parts of the original directed system shown in grey all project to one of the ${\mathfrak{A}_i}$. Therefore, $\mathfrak{C}$ is an $\mathcal{L}_1$-structure that elementarily embeds $\mathfrak{A}_0$.
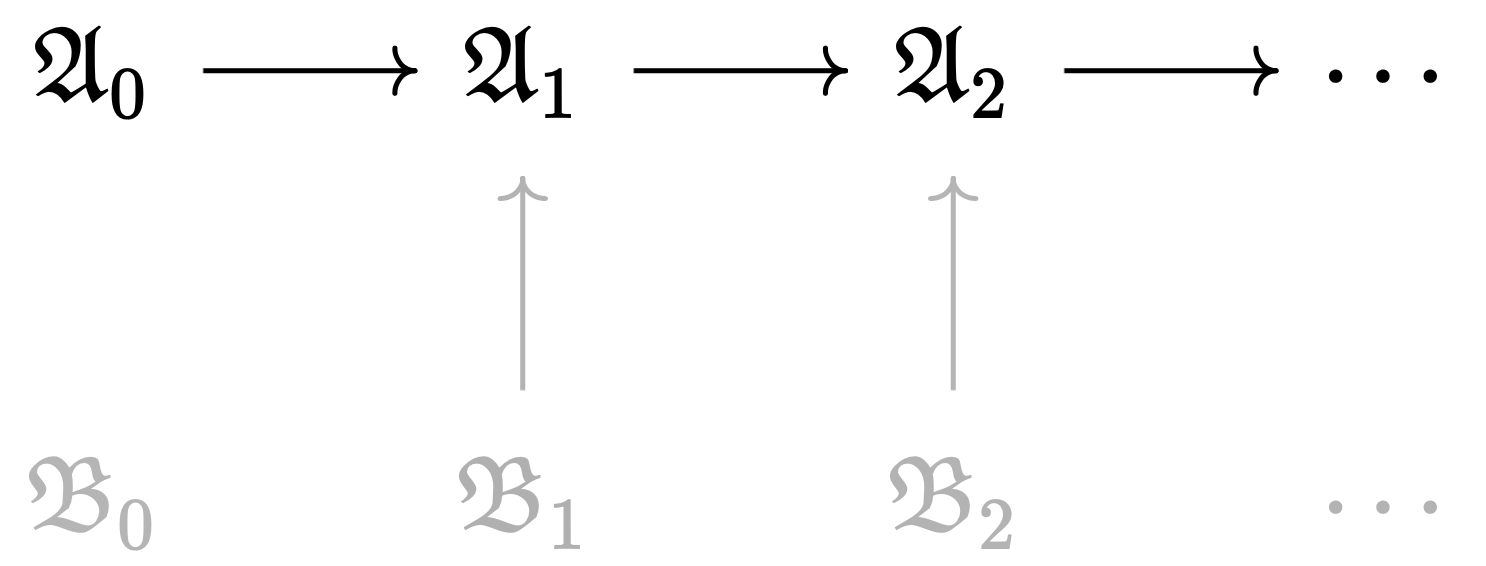
For the same reason, $\mathfrak{C}$ is also the colimit of the directed system consisting of ${\mathfrak{B}_i}$. Therefore, $\mathfrak{C}$ is an $\mathcal{L}_2$-structure that elementarily embeds $\mathfrak{B}_0$.

That is, $\mathfrak{C}$ embeds both $\mathfrak{A}$ and $\mathfrak{B}$, from which it follows that it is a model of $T_1 \cup T_2$. ■
Craig Interpolation Theorem
Theorem. For $\mathcal{L}$-sentences $\phi$ and $\psi$, if $\phi \vDash \psi$, then there exists an $\mathcal{L}$-sentence $\theta$ such that $\phi \vDash \theta$ and $\theta \vDash \psi$. Moreover, the non-logical symbols (constants, predicates, functions) contained in $\theta$ are those common to both $\phi$ and $\psi$.
$\theta$ is called a Craig interpolant of $\phi$ and $\psi$.
Proof. We prove by contradiction. Suppose no Craig interpolant exists. Then $\phi$ has a model, for if $\phi$ had no model, then $\perp$ would be a Craig interpolant of $\phi$ and $\psi$. Also, $\lnot \psi$ has a model, for otherwise $\top$ would be a Craig interpolant.
Let $\mathcal{L}’$ be the language consisting of the non-logical symbols common to both $\phi$ and $\psi$. Let $\Gamma$ be the set of $\mathcal{L}’$-sentences $\sigma$ such that either $\phi \vDash \sigma$ or $\lnot \psi \vDash \sigma$.
We show that $\Gamma \cup {\phi}$ is consistent. Suppose it is inconsistent. Then by the compactness theorem, there exist $\mathcal{L}’$-sentences $\sigma_1$ and $\sigma_2$ such that $\phi \vDash \sigma_1$, $\lnot\psi \vDash \sigma_2$, and ${\sigma_1, \sigma_2, \phi}$ is inconsistent. Since $\phi \vDash \sigma_1$, we have $\phi \vDash \lnot\sigma_2$. By contraposition, from $\lnot\psi \vDash \sigma_2$ we obtain $\lnot\sigma_2 \vDash \psi$. Thus $\lnot\sigma_2$ is a Craig interpolant of $\phi$ and $\psi$, contradicting our assumption.
Therefore, $\Gamma \cup {\phi}$ is consistent, and by the same reasoning, $\Gamma \cup {\lnot\psi}$ is also consistent. Now applying Zorn’s lemma, define $\overline{\Gamma}$ as the maximum of the following ordered set of $\mathcal{L}’$-theories:
\[\{ \Gamma' : \Gamma \subseteq \Gamma', \Gamma' \cup \{\phi\} \text{ and } \Gamma' \cup \{\lnot \psi\} \text{ are consistent} \}\]We show that $\overline{\Gamma}$ is complete. Suppose $\overline{\Gamma}$ is not complete. Then there exists an $\mathcal{L}’$-sentence $\sigma$ such that $\sigma \notin \overline{\Gamma}$, and either $\overline{\Gamma} \cup {\sigma, \phi}$ or $\overline{\Gamma} \cup {\sigma, \lnot \psi}$ is consistent.
In the former case, by the compactness theorem, there exists a sentence $\theta$ in $\overline{\Gamma}$ such that $\phi \vDash \theta \rightarrow \lnot \sigma$. By the definition of $\Gamma$, we have $\theta \rightarrow \lnot \sigma \in \Gamma \subseteq \overline{\Gamma}$. Therefore, $\overline{\Gamma} \cup {\sigma, \phi}$ proves $\lnot\phi$, which is a contradiction. The latter case yields a similar contradiction. Therefore, $\overline{\Gamma}$ is complete.
Since $\overline{\Gamma}$ is complete and $\overline{\Gamma} \cup {\phi}$ and $\overline{\Gamma} \cup {\lnot\psi}$ are consistent, by Robinson’s consistency theorem, $\overline{\Gamma} \cup {\phi, \lnot \psi}$ is consistent. But this contradicts $\phi \vDash \psi$. Therefore, by contradiction, $\phi$ and $\psi$ have a Craig interpolant. ■
Beth Definability Theorem
Consider a language $\mathcal{L}$ and a predicate $P$ not contained in $\mathcal{L}$. Let $T$ be a theory in $\mathcal{L} \cup {P}$. We say that $T$ implicitly defines $P$ when there is a unique way to extend any $\mathcal{L}$-structure $\mathfrak{A}$ satisfying $T$ to $\mathcal{L} \cup {P}$.
This can also be stated as follows. Let $T(P’)$ be the theory in $\mathcal{L} \cup {P’}$ obtained by replacing every occurrence of $P$ in $T$ with $P’$. Then $T$ implicitly defines $P$ if and only if the following holds:
\[T \cup T(P') \vDash \forall x_1, \dots, x_n \; P(x_1, \dots, x_n) \leftrightarrow P'(x_1, \dots, x_n)\]On the other hand, $T$ explicitly defines $P$ if there exists an $\mathcal{L}$-formula $\phi$ satisfying:
\[T \vDash \forall x_1, \dots, x_n \; P(x_1, \dots, x_n) \leftrightarrow \phi(x_1, \dots, x_n)\]For example, consider the following theory $T$, which adds axioms concerning a predicate $P(x, y)$ to the theory $\mathsf{PA}$ in the language $\mathcal{L} = (0, S, +, \cdot)$:
\[T = \mathsf{PA} \cup \Big\{ \forall x, y \big[ P(x, y) \rightarrow x + y = S(0) \big] \Big\}\]$T(P’)$ is as follows:
\[T(P') = \mathsf{PA} \cup \Big\{ \forall x, y \big[ P'(x, y) \rightarrow x + y = S(0) \big] \Big\}\]That $T$ implicitly defines $P$ means the following holds:
\[T \cup T(P') \vDash \forall x, y \big[ P(x, y) \leftrightarrow P'(x, y) \big]\]This follows naturally from the induction axiom schema. But $P$ can also be explicitly defined in $T$ as follows:
\[\begin{gather} T \vDash \forall x, y \big[ P(x, y) \leftrightarrow \phi(x, y) \big] \\\\ \text{where}\\\\ \phi(x, y) : \forall z \big[ x + z = S(0) \rightarrow z = y \big] \end{gather}\]This is no coincidence.
Theorem. For a language $\mathcal{L}$, if a theory $T$ in $\mathcal{L} \cup {P}$ implicitly defines $P$, then $T$ explicitly defines $P$.
Proof. Suppose $P$ is an $n$-ary predicate. Let $\mathcal{L}’$ be the language obtained by adding new constants $c_1, \dots, c_n$ to $\mathcal{L}$. Since $T$ implicitly defines $P$, we have:
\[T \cup T(P') \vDash P(c_1, \dots, c_n) \rightarrow P'(c_1, \dots, c_n)\]By the compactness theorem, there exists an $\mathcal{L} \cup {P}$-sentence $\psi$ such that $T \vdash \psi$ and the following holds:
\[\psi \land \psi(P') \vDash P(c_1, \dots, c_n) \rightarrow P'(c_1, \dots, c_n)\]Using the deduction theorem and rearranging:
\[\psi \land P(c_1, \dots, c_n) \vDash \psi(P') \rightarrow P'(c_1, \dots, c_n)\]The left-hand side is a sentence in $\mathcal{L}’ \cup {P}$, and the right-hand side is a sentence in $\mathcal{L}’ \cup {P’}$. Therefore, by Craig’s interpolation theorem, there exists an $\mathcal{L}’$-formula $\theta$ such that:
\[\begin{gather} \psi \land P(c_1, \dots, c_n) \vDash \theta(c_1, \dots, c_n), \\\\ \theta(c_1, \dots, c_n) \vDash \psi(P') \rightarrow P'(c_1, \dots, c_n) \end{gather}\]Rearranging again and substituting $P$ for $P’$:
\[\begin{gather} \psi \vDash P(c_1, \dots, c_n) \rightarrow \theta(c_1, \dots, c_n), \\\\ \psi \vDash \theta(c_1, \dots, c_n) \rightarrow P(c_1, \dots, c_n) \end{gather}\]Therefore, $\theta$ explicitly defines $P$. ■
정칙 기수와 특이 기수, 그리고 도달 불가능 기수
04 May 2025이 글에서 $\kappa$는 무한 기수이다. 또한, 기수를 초기 서수initial ordinal로 정의하는 방식을 택한다(이 글의 3번). 이에 따라 모든 기수는 서수이기도 하다.
정의. $\theta$가 $\kappa$보다 작은 극한 서수라고 하자. 각 $\nu$에 대해 $\alpha_\nu < \kappa$인 증가하는 서수열 $\langle \alpha_\nu : \nu < \theta \rangle$에 대하여, 언제나 $\lim_{\nu \to \theta} \alpha_\nu < \kappa$일 때, $\kappa$를 정칙 기수regular cardinal라고 한다. 정칙 기수가 아닌 기수를 특이 기수singular cardinal라고 한다.
Remark. $\alpha_\nu$와 $\theta$는 일반적으로 기수가 아니라 서수이다.
예를 들어 $\aleph_0$는 정칙 기수이다. $\aleph_0$개보다 적은 개수의 — 즉, 유한한 — $\aleph_0$보다 작은 기수들 — 즉, 자연수 — 의 상한은 $\aleph_0$에 달하지 않기 때문이다.
반면 $\aleph_\omega$는 특이 기수이다. 다음 기수열에서 각각의 기수는 $\aleph_\omega$보다 작고, 기수열의 길이 또한 $\aleph_0 < \aleph_\omega$이지만, 그 상한은 $\aleph_\omega$이기 때문이다.
\[\aleph_0 \quad \aleph_1 \quad \aleph_2 \quad \aleph_3 \quad \cdots\]정리. (특이 기수 판별법) $\kappa$가 특이 기수일 필요충분조건은 $\kappa$가 $\kappa$개보다 적은 개수의 $\kappa$보다 작은 기수들의 합일 것이다. 즉, $|I| < \kappa$, $\kappa_i < \kappa \;(\forall i \in I)$에 대하여,
\[\sum_{i \in I} \kappa_i = \kappa\]
Remark. $\kappa_i$는 일반적인 서수가 아닌 기수이다. 그리고 $\sum$은 서수 덧셈이 아니라 기수 덧셈이다.
증명.
($\Rightarrow$) $\kappa$가 특이 기수라면 어떤 서수열 $\langle \alpha_\nu : \nu < \theta\rangle$이 존재하여,
\[\lim_{\nu \to \theta} \alpha_\nu = \sup \alpha_\nu = \bigcup_{\nu < \theta}\alpha_\nu = \kappa\]이다. 일반적으로 서수 $\alpha$는 자기보다 작은 서수 $\beta < \alpha$들의 합집합이다. 따라서 다음이 성립한다.
\[\kappa = \bigcup_{\nu < \theta}\alpha_\nu = \bigcup_{\nu < \theta}\left( \alpha_\nu - \bigcup_{\xi < \nu} \alpha_\xi \right)\]$A_\nu = \alpha_\nu - \bigcup_{\xi < \nu} \alpha_\xi$라고 하자. $A_\nu$는 더이상 서수가 아니지만 그건 중요하지 않다. 중요한 것은 $\lbrace A_\nu \rbrace $가 쌍으로 서로소라는 것이다. 따라서 $\kappa_\nu = |A_\nu|$라고 하면 기수 덧셈의 정의에 의해,
\[\sum_{\nu < \theta} \kappa_\nu = \left| \bigcup_{\nu < \theta} A_\nu \right| = \kappa\]이다.
($\Leftarrow$) $\kappa = \sum_{i \in I}\kappa_i$라고 하자. $|I| = \lambda$라고 하면 기수 덧셈의 성질에 의해 $\kappa = \lambda \cdot \sup \kappa_i$이다. $\lambda < \kappa$이므로, 기수 곱셈의 성질에 의해 $\kappa = \sup \kappa_i$이다. 각 $i \in I$에 대해 $\kappa_i < \kappa$인데 $\sup \kappa_i = \kappa$이므로, 초한귀납법을 통해 증가하는 기수열
\[\langle \kappa_\nu : \kappa_\nu = \kappa_i \text{ for some } i \in I, \nu < \theta\rangle\]을 구축할 수 있으며, $\theta \leq \lambda$이므로 정리가 보여졌다. ■
정의. 어떤 $\alpha \in \mathrm{Ord}$에 대해 $\kappa = \aleph_{\alpha + 1}$일 때, $\kappa$를 계승 기수successor cardinal라고 한다. 계승 기수가 아닌 기수를 극한 기수limit cardinal라고 한다.
정리. 모든 계승 기수는 정칙이다.
증명. $\kappa = \aleph_{\alpha + 1}$이라고 하자. $\kappa$가 특이 기수라면, 특이 기수 판별법에 의해 $\kappa = \sum_{i \in I} \kappa_i$이며 $\kappa_i, |I| < \kappa$이다. 이는 $\kappa_i , |I| \leq \aleph_\alpha$와 같다. 그런데
\[\sum_{i \in I} \kappa_i \leq \sum_{i \in I} \aleph_\alpha = |I| \cdot \aleph_\alpha \leq \aleph_\alpha \cdot \aleph_\alpha = \aleph_\alpha < \kappa\]이므로 모순이다. ■
따라서 모든 특이 기수는 극한 기수이다. 그러나 모든 극한 기수가 특이 기수인 것은 아니다. $\aleph_0$는 정칙인 극한 기수이기 때문이다. 그러나 $\aleph_0$ 이외에 정칙인 극한 기수가 존재할까?
정의. 비가산 정칙 극한 기수를 도달 불가능 기수inaccessible cardinal라고 한다.1
$\aleph_\alpha$가 도달 불가능 기수라고 하자. 다음의 증가 기수열의 극한은 $\aleph_\alpha$이다.
\[\langle \aleph_\beta : \beta < \alpha \rangle : \aleph_0 \quad \aleph_1 \quad \aleph_2 \quad \cdots \quad \to \aleph_\alpha\]따라서 $\aleph_\alpha$가 정칙이기 위해서는 위 기수열의 길이인 $\alpha$가 $\aleph_\alpha$보다 작아서는 안 된다. 그런데 $\alpha \leq \aleph_\alpha$이므로, $\alpha = \aleph_\alpha$임이 따라 나온다.
정리. $\aleph_\alpha$가 도달 불가능할 필요조건은 $\alpha = \aleph_\alpha$인 것이다.
이는 $\alpha$가 무지막지하게 큰 기수임을 시사한다. 일례로 다음의 기수열 $\langle \alpha_n : n \in \omega \rangle$을 보자.
\[\alpha_0 = \aleph_0, \alpha_{n + 1} = \aleph_{\alpha_n}\]위 기수열의 상한을 $\kappa$라고 하자. 상한의 정의에 의해 $\lambda < \kappa$라면 $\alpha_n > \lambda$인 $n$이 존재한다. 따라서 $\aleph_\lambda = \alpha_{n+1} < \kappa$이며,
\[\aleph_\kappa = \sum_{\lambda < \kappa} \aleph_\lambda \leq \sum_{\lambda < \kappa} \kappa = \kappa\]이다. 다시 말해, $\alpha = \aleph_\alpha$를 만족하는 기수는 적어도 다음에 비견되는 크기를 가진다.
\[\kappa = \aleph_{\aleph_{\aleph_{\aleph_{\ddots}}}}\]여기서 집고 넘어갈 점이 있다. 비록 $\kappa$가 $\kappa = \aleph_\kappa$를 보이긴 했지만, $\kappa$가 도달 불가능함을 보인 것은 아니다. 오히려 $\kappa$는 특이 기수이다. 길이가 $\omega$인 기수열 $\alpha_n$의 극한이기 때문이다.
사실 도달 불가능 기수의 존재성은 ZFC와 독립적이다.
정리. 도달 불가능 기수의 존재성은 ZFC와 독립이다.
따라서 도달 불가능 기수의 존재는 공리로서 가정해야 한다. 도달 불가능 기수의 존재를 가정하는 부류의 공리들을 큰 기수 공리large cardinal axioms라고 부르며, 이와 관련된 연구는 집합론의 중요한 부분을 이룬다.
1. 엄밀히 말해 이는 약한 도달 불가능 기수weakly inaccessible cardinal에 해당한다. $\kappa$가 강한 도달 불가능 기수strongly inaccessible cardinal라는 것은 $\kappa$가 약한 도달 불가능 기수이며, 추가로 $\lambda < \kappa$일 때 $2^\lambda < \kappa$인 것이다. 연속체 가설을 인정할 때 약한 도달 불가능성과 강한 도달 불가능성은 동치이다.
Regular Cardinals, Singular Cardinals, and Inaccessible Cardinals
04 May 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
In this article, $\kappa$ denotes an infinite cardinal. Moreover, we adopt the approach of defining cardinals as initial ordinals (see method 3 in this post). Accordingly, every cardinal is also an ordinal.
Definition. Let $\theta$ be a limit ordinal less than $\kappa$. For each $\nu$, consider an increasing sequence of ordinals $\langle \alpha_\nu : \nu < \theta \rangle$ where $\alpha_\nu < \kappa$. If we always have $\lim_{\nu \to \theta} \alpha_\nu < \kappa$, then $\kappa$ is called a regular cardinal. A cardinal that is not regular is called a singular cardinal.
Remark. $\alpha_\nu$ and $\theta$ are generally ordinals, not necessarily cardinals.
For example, $\aleph_0$ is a regular cardinal. This is because the supremum of fewer than $\aleph_0$ many—that is, finitely many—cardinals less than $\aleph_0$—that is, natural numbers—does not reach $\aleph_0$.
In contrast, $\aleph_\omega$ is a singular cardinal. This is because in the following sequence of cardinals, each cardinal is less than $\aleph_\omega$, and the length of the sequence is also $\aleph_0 < \aleph_\omega$, yet their supremum is $\aleph_\omega$.
\[\aleph_0 \quad \aleph_1 \quad \aleph_2 \quad \aleph_3 \quad \cdots\]Theorem. (Characterisation of Singular Cardinals) $\kappa$ is a singular cardinal if and only if $\kappa$ is the sum of fewer than $\kappa$ many cardinals, each less than $\kappa$. That is, for $|I| < \kappa$ and $\kappa_i < \kappa \;(\forall i \in I)$, we have
\[\sum_{i \in I} \kappa_i = \kappa\]
Remark. $\kappa_i$ denotes cardinals, not general ordinals. Moreover, $\sum$ denotes cardinal addition, not ordinal addition.
Proof.
($\Rightarrow$) If $\kappa$ is a singular cardinal, then there exists a sequence of ordinals $\langle \alpha_\nu : \nu < \theta\rangle$ such that
\[\lim_{\nu \to \theta} \alpha_\nu = \sup \alpha_\nu = \bigcup_{\nu < \theta}\alpha_\nu = \kappa\]In general, an ordinal $\alpha$ is the union of all ordinals $\beta < \alpha$ that are less than it. Therefore, the following holds:
\[\kappa = \bigcup_{\nu < \theta}\alpha_\nu = \bigcup_{\nu < \theta}\left( \alpha_\nu - \bigcup_{\xi < \nu} \alpha_\xi \right)\]Let $A_\nu = \alpha_\nu - \bigcup_{\xi < \nu} \alpha_\xi$. while $A_\nu$ is no longer an ordinal, this is not important. What matters is that $\lbrace A_\nu \rbrace $ are pairwise disjoint. Therefore, letting $\kappa_\nu = |A_\nu|$, by the definition of cardinal addition, we have
\[\sum_{\nu < \theta} \kappa_\nu = \left| \bigcup_{\nu < \theta} A_\nu \right| = \kappa\]($\Leftarrow$) Let $\kappa = \sum_{i \in I}\kappa_i$. Setting $|I| = \lambda$, by the properties of cardinal addition, we have $\kappa = \lambda \cdot \sup \kappa_i$. Since $\lambda < \kappa$, by the properties of cardinal multiplication, we have $\kappa = \sup \kappa_i$. For each $i \in I$, we have $\kappa_i < \kappa$, yet $\sup \kappa_i = \kappa$. Therefore, by transfinite induction, we can construct an increasing sequence of cardinals
\[\langle \kappa_\nu : \kappa_\nu = \kappa_i \text{ for some } i \in I, \nu < \theta\rangle\]Since $\theta \leq \lambda$, the theorem is proved. ■
Definition. When $\kappa = \aleph_{\alpha + 1}$ for some $\alpha \in \mathrm{Ord}$, we call $\kappa$ a successor cardinal. A cardinal that is not a successor cardinal is called a limit cardinal.
Theorem. Every successor cardinal is regular.
Proof. Let $\kappa = \aleph_{\alpha + 1}$. If $\kappa$ is a singular cardinal, then by the characterisation of singular cardinals, we have $\kappa = \sum_{i \in I} \kappa_i$ where $\kappa_i, |I| < \kappa$. This is equivalent to $\kappa_i , |I| \leq \aleph_\alpha$. However,
\[\sum_{i \in I} \kappa_i \leq \sum_{i \in I} \aleph_\alpha = |I| \cdot \aleph_\alpha \leq \aleph_\alpha \cdot \aleph_\alpha = \aleph_\alpha < \kappa\]which is a contradiction. ■
Therefore, every singular cardinal is a limit cardinal. However, not every limit cardinal is singular. This is because $\aleph_0$ is a regular limit cardinal. But do there exist other regular limit cardinals beyond $\aleph_0$?
Definition. An uncountable regular limit cardinal is called an inaccessible cardinal.1
Let $\aleph_\alpha$ be an inaccessible cardinal. The limit of the following increasing sequence of cardinals is $\aleph_\alpha$:
\[\langle \aleph_\beta : \beta < \alpha \rangle : \aleph_0 \quad \aleph_1 \quad \aleph_2 \quad \cdots \quad \to \aleph_\alpha\]Therefore, for $\aleph_\alpha$ to be regular, the length of the above sequence, namely $\alpha$, must not be less than $\aleph_\alpha$. Since $\alpha \leq \aleph_\alpha$, it follows that $\alpha = \aleph_\alpha$.
Theorem. A necessary condition for $\aleph_\alpha$ to be inaccessible is that $\alpha = \aleph_\alpha$.
This suggests that $\alpha$ is an enormously large cardinal. For instance, consider the following sequence of cardinals $\langle \alpha_n : n \in \omega \rangle$:
\[\alpha_0 = \aleph_0, \alpha_{n + 1} = \aleph_{\alpha_n}\]Let $\kappa$ be the supremum of this sequence. By the definition of supremum, if $\lambda < \kappa$, then there exists $n$ such that $\alpha_n > \lambda$. Therefore, $\aleph_\lambda = \alpha_{n+1} < \kappa$, and
\[\aleph_\kappa = \sum_{\lambda < \kappa} \aleph_\lambda \leq \sum_{\lambda < \kappa} \kappa = \kappa\]In other words, a cardinal satisfying $\alpha = \aleph_\alpha$ has a magnitude at least comparable to the following:
\[\kappa = \aleph_{\aleph_{\aleph_{\aleph_{\ddots}}}}\]There is an important point to note here. Although $\kappa$ satisfies $\kappa = \aleph_\kappa$, we have not shown that $\kappa$ is inaccessible. Indeed, $\kappa$ is a singular cardinal, as it is the limit of a sequence $\alpha_n$ of length $\omega$.
In fact, the existence of inaccessible cardinals is independent of ZFC.
Theorem. The existence of inaccessible cardinals is independent of ZFC.
Therefore, the existence of inaccessible cardinals must be assumed as an axiom. The class of axioms that assume the existence of inaccessible cardinals are called large cardinal axioms, and research related to these forms an important part of set theory.
1. Strictly speaking, this corresponds to a weakly inaccessible cardinal. A cardinal $\kappa$ is called strongly inaccessible if it is weakly inaccessible and additionally satisfies $2^\lambda < \kappa$ whenever $\lambda < \kappa$. Under the continuum hypothesis, weak and strong inaccessibility are equivalent.
준동형 사상, 임베딩, 초등적 임베딩
01 May 2025이 글에서는 편의를 위해 술어와 함수를 별도의 대상으로 생각하는 대신, 함수식 $f(a) = c$를 이항 술어 $F(a, c)$로 환원하는 접근을 택한다.
정의. $\mathfrak{A}, \mathfrak{B}$가 언어 $\mathcal{L}$의 구조라고 하자. 다음을 만족하는 사상 $f: \mathfrak{A} \to \mathfrak{B}$을 준동형 사상homomorphism이라고 부른다. $R$이 $\mathcal{L}$의 관계일 때, 임의의 $a_1, \dots, a_n \in \mathfrak{A}$에 대해,
\[R^\mathfrak{A}(a_1, \dots, a_n) \implies R^\mathfrak{B}(f(a_1), \dots, f(a_n))\]이다.
추가로, 준동형사상 $f$가 단사이고 다음을 만족할 때 $f$를 임베딩embedding이라고 부른다.
\[R^\mathfrak{A}(a_1, \dots, a_n) \iff R^\mathfrak{B}(f(a_1), \dots, f(a_n))\]
단사 준동형사상이라고 해서 임베딩인 것은 아니다. 일례로 하나의 이항 관계 $<$를 가지는 언어 $\mathcal{L}$의 다음의 두 구조를 보자. $<$를 만족시키는 대상은 화살표로 표시되었다. 즉, $b_1 <^\mathfrak{B} b_2$이다.
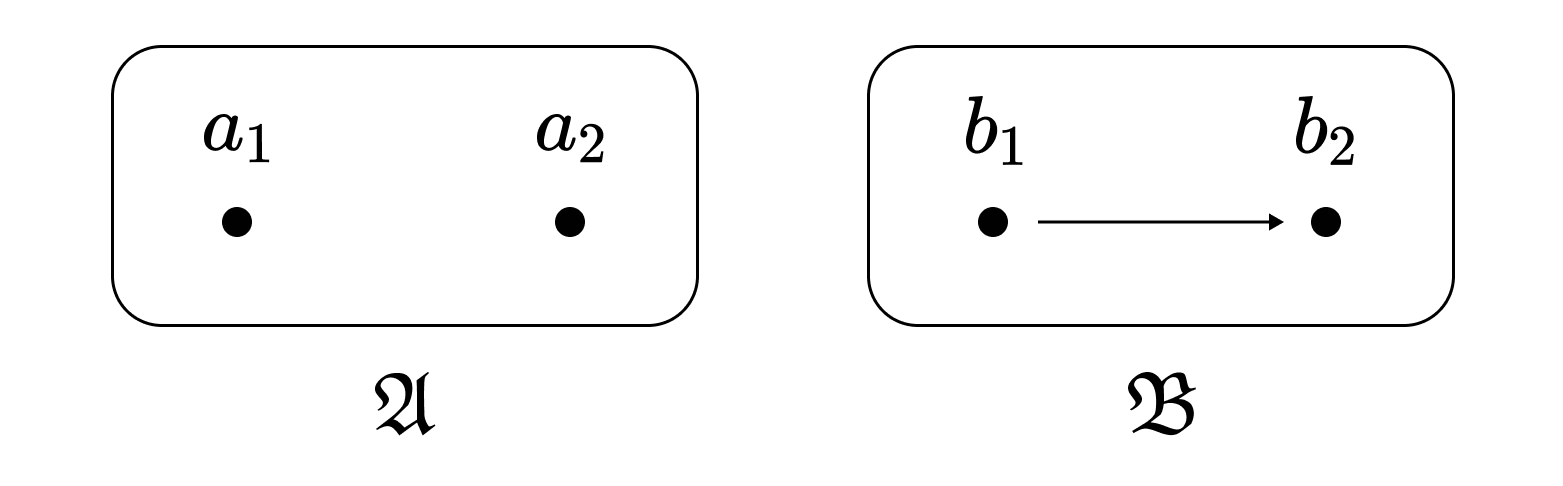
$\mathfrak{A}$의 원소들은 $<^\mathfrak{A}$를 만족시키는 경우가 없으므로 $f: a_1 \mapsto b_1, a_2 \mapsto b_2$는 자명하게 준동형사상이며, 단사이다. 그러나 $f$는 임베딩이 아니다. $f$가 임베딩이라면 $b_1 <^\mathfrak{B} b_2$으로부터 $a_1 <^\mathfrak{A} a_2$가 성립해야 하기 때문이다. 즉, 임베딩은 $\mathfrak{A}$의 원소들뿐 아니라 원소들 간의 관계까지 그대로 $\mathfrak{B}$에 대응시켜야 한다. 이런 면에서 임베딩은 범주론에서의 포화된 함자full functor와 비슷하다.
정의. $\mathfrak{A}$가 언어 $\mathcal{L}$의 구조라고 하자. $\mathcal{L}_\mathfrak{A}$를 $\mathcal{L}$에 $\mathfrak{A}$의 정의역 크기만큼의 상수를 추가한 언어로 정의한다.
페아노 산술로 예를 들자면, $\mathcal{L} = (0, S, +)$이고 $\mathfrak{A}$가 산술의 표준 모형일 때, $\mathcal{L}_\mathfrak{A} = (0, 1, 2, 3, \dots, S, +)$이다.
정의. $\mathfrak{A}$가 만족시키는 모든 $\mathcal{L}_\mathfrak{A}$-원자명제들의 집합을 $\Delta_\mathfrak{A}^+$로 적는다. 즉,
\[\Delta_\mathfrak{A}^+ = \{ R(c_1, \dots, c_n) \mid R, c_i \in \mathcal{L}_\mathfrak{A}, \; \mathfrak{A} \vDash R^{\mathfrak{A}}(c_1^\mathfrak{A}, \dots, c_n^\mathfrak{A}) \}\]추가로, $\Delta_\mathfrak{A}^+$에다 $\mathfrak{A}$가 만족시키지 않는 모든 $\mathcal{L}$-원자명제들의 부정까지 추가한 집합을 $\Delta_\mathfrak{A}$로 적는다. 즉,
\[\Delta_\mathfrak{A} = \Delta_\mathfrak{A}^+ \cup \{ \lnot R(c_1, \dots, c_n) \mid R, c_i \in \mathcal{L}_\mathfrak{A}, \; \mathfrak{A} \not\vDash R^{\mathfrak{A}}(c_1^\mathfrak{A}, \dots, c_n^\mathfrak{A}) \}\]
$\Delta$라는 표기법은 산술 위계와 관련이 있다.
$\Delta_\mathfrak{A}^+$에 빠진 원자명제들의 부정을 추가한 것이 곧 $\Delta_\mathfrak{A}$이기 때문에, 두 집합이 내포하는 정보량은 사실상 같다. 그럼에도 두 집합을 구분하여 정의하는 것은 다음의 정리 때문이다.
정리. $\mathfrak{A}, \mathfrak{B}$가 $\mathcal{L}$-구조라고 하자.
- 단사 준동형사상 $f: \mathfrak{A} \to \mathfrak{B}$가 존재할 필요충분조건은 $\mathfrak{B}$가 $\Delta_\mathfrak{A}^+$의 $\mathcal{L}_\mathfrak{A}$-모델인 것이다.
- 임베딩 $f: \mathfrak{A} \to \mathfrak{B}$가 존재할 필요충분조건은 $\mathfrak{B}$가 $\Delta_\mathfrak{A}$의 $\mathcal{L}_\mathfrak{A}$-모델인 것이다.
즉, $\mathfrak{B}$가 $\Delta_\mathfrak{A}^+$를 만족할 경우 $\mathfrak{B}$가 원자명제들을 ‘과도하게’ 만족시켜서, $\mathfrak{A}$가 $\mathfrak{B}$로 임베딩되지 못할 가능성이 있다. 그러나 $\mathfrak{B}$가 $\Delta_\mathfrak{A}$를 만족할 경우, $\mathfrak{B}$가 만족시킬 수 있는 원자명제에 한계가 걸리기 때문에 임베딩 가능성이 보장된다.
이전 글에서 초등적 부분모델이라는 개념을 소개한 바 있다. 이로부터 다음의 개념을 정의할 수 있다.
정의. $f: \mathfrak{A} \to \mathfrak{B}$가 임베딩이고, $f[\mathfrak{A}]$가 $\mathfrak{B}$의 초등적 부분모델일 때, $f$를 초등적 임베딩이라고 한다.
초등적 임베딩과 관련된 문장 집합은 다음과 같다.
정의. $\mathfrak{A}$가 만족시키는 모든 $\mathcal{L}_\mathfrak{A}$-명제들의 집합을 $E(\mathfrak{A})$로 적는다. 즉,
\[E(\mathfrak{A}) = \{ \phi : \mathfrak{A} \vDash \phi \}\]
$E(\mathfrak{A})$가 $\Delta_\mathfrak{A}$와 가장 구별되는 특징은 양화사가 있는 문장 또한 포함한다는 것이다.
정리. $\mathfrak{A}, \mathfrak{B}$가 $\mathcal{L}$-구조라고 하자. 초등적 임베딩 $f: \mathfrak{A} \to \mathfrak{B}$가 존재할 필요충분조건은 $\mathfrak{B}$가 $E(\mathfrak{A})$의 $\mathcal{L}_\mathfrak{A}$-모델인 것이다.
마지막으로 다음의 문장 집합을 언급할 만하다.
정의. $\mathfrak{A}$가 $\mathcal{L}$-구조라고 하자. $\mathfrak{A}$에서 참인 모든 $\mathcal{L}$-문장들의 집합을 $\mathrm{Th}(\mathfrak{A})$라고 한다.
정리. $\mathfrak{A}, \mathfrak{B}$가 $\mathcal{L}$-구조라고 하자. $\mathfrak{A}$와 $\mathfrak{B}$가 초등적으로 동등할 필요충분조건은 $\mathrm{Th}(\mathfrak{A}) = \mathrm{Th}(\mathfrak{B})$인 것이다.
사실 이는 초등적 동등성의 정의나 다름이 없어서 정리라고 부르기는 무색하지만, 이 글에서 소개한 나머지 정리들과 일관성을 유지하기 위해 소개하였다.
표로 정리하면 이렇다.
| 정의 | 예시 | 사상 | |
|---|---|---|---|
| $\Delta_\mathfrak{A}^+$ | $\mathfrak{A}$가 만족시키는 $\mathcal{L}_\mathfrak{A}$-원자명제 | $0 < 1$ | 전사 준동형 |
| $\Delta_\mathfrak{A}$ | $\mathfrak{A}$가 만족시키는 $\Delta_0$ $\mathcal{L}_\mathfrak{A}$-명제 | $\lnot(1 < 0)$ | 임베딩 (부분모델) |
| $\mathrm{Th}(\mathfrak{A})$ | $\mathfrak{A}$가 만족시키는 $\mathcal{L}$-명제 | $\forall x \exists y (x < y)$ | 초등적 동등성 |
| $E(\mathfrak{A})$ | $\mathfrak{A}$가 만족시키는 $\mathcal{L}_\mathfrak{A}$-명제 | $\not \exists x (x < 0)$ | 초등적 임베딩 (초등적 부분모델) |
예를 들어 $\mathfrak{A} = (\mathbb{N}, <)$은 $\mathfrak{B} = (\mathbb{Z}, <)$에 임베딩되지만, 초등적으로 임베딩되지는 않는다. $\mathfrak{B}$가 $E(\mathfrak{A})$의 문장인 $\not \exists x (x < 0)$을 만족하지 않기 때문이다.
Homomorphisms, Embeddings, and Elementary Embeddings
01 May 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
For convenience, this article takes the approach of reducing function expressions $f(a) = c$ to binary predicates $F(a, c)$, rather than treating predicates and functions as separate objects.
Definition. Let $\mathfrak{A}, \mathfrak{B}$ be structures of language $\mathcal{L}$. A mapping $f: \mathfrak{A} \to \mathfrak{B}$ satisfying the following is called a homomorphism. For any relation $R$ in $\mathcal{L}$ and arbitrary $a_1, \dots, a_n \in \mathfrak{A}$,
\[R^\mathfrak{A}(a_1, \dots, a_n) \implies R^\mathfrak{B}(f(a_1), \dots, f(a_n))\]Additionally, when a homomorphism $f$ is injective and satisfies the following, we call $f$ an embedding.
\[R^\mathfrak{A}(a_1, \dots, a_n) \iff R^\mathfrak{B}(f(a_1), \dots, f(a_n))\]
An injective homomorphism is not necessarily an embedding. For example, consider the following two structures of language $\mathcal{L}$ with one binary relation $<$. Objects satisfying $<$ are indicated by arrows. That is, $b_1 <^\mathfrak{B} b_2$.

Since no elements in $\mathfrak{A}$ satisfy $<^\mathfrak{A}$, the mapping $f: a_1 \mapsto b_1, a_2 \mapsto b_2$ is trivially a homomorphism and is injective. However, $f$ is not an embedding. If $f$ were an embedding, then from $b_1 <^\mathfrak{B} b_2$ it would follow that $a_1 <^\mathfrak{A} a_2$. That is, an embedding must preserve not only the elements of $\mathfrak{A}$ but also the relationships between elements in $\mathfrak{B}$. In this respect, embeddings are similar to full functors in category theory.
Definition. Let $\mathfrak{A}$ be a structure of language $\mathcal{L}$. Define $\mathcal{L}_\mathfrak{A}$ as the language obtained by adding to $\mathcal{L}$ as many constants as the size of the domain of $\mathfrak{A}$.
For example with Peano arithmetic, when $\mathcal{L} = (0, S, +)$ and $\mathfrak{A}$ is the standard model of arithmetic, then $\mathcal{L}_\mathfrak{A} = (0, 1, 2, 3, \dots, S, +)$.
Definition. Let $\Delta_\mathfrak{A}^+$ denote the set of all $\mathcal{L}_\mathfrak{A}$-atomic propositions satisfied by $\mathfrak{A}$. That is,
\[\Delta_\mathfrak{A}^+ = \{ R(c_1, \dots, c_n) \mid R, c_i \in \mathcal{L}_\mathfrak{A}, \; \mathfrak{A} \vDash R^{\mathfrak{A}}(c_1^\mathfrak{A}, \dots, c_n^\mathfrak{A}) \}\]Additionally, let $\Delta_\mathfrak{A}$ denote the set obtained by adding to $\Delta_\mathfrak{A}^+$ the negations of all $\mathcal{L}$-atomic propositions not satisfied by $\mathfrak{A}$. That is,
\[\Delta_\mathfrak{A} = \Delta_\mathfrak{A}^+ \cup \{ \lnot R(c_1, \dots, c_n) \mid R, c_i \in \mathcal{L}_\mathfrak{A}, \; \mathfrak{A} \not\vDash R^{\mathfrak{A}}(c_1^\mathfrak{A}, \dots, c_n^\mathfrak{A}) \}\]
The notation $\Delta$ is related to the arithmetic hierarchy.
Since $\Delta_\mathfrak{A}$ is obtained by adding the negations of atomic propositions missing from $\Delta_\mathfrak{A}^+$, the two sets contain essentially the same information. Nevertheless, we define the two sets separately because of the following theorem.
Theorem. Let $\mathfrak{A}, \mathfrak{B}$ be $\mathcal{L}$-structures.
- There exists an injective homomorphism $f: \mathfrak{A} \to \mathfrak{B}$ if and only if $\mathfrak{B}$ is an $\mathcal{L}\mathfrak{A}$-model of $\Delta\mathfrak{A}^+$.
- There exists an embedding $f: \mathfrak{A} \to \mathfrak{B}$ if and only if $\mathfrak{B}$ is an $\mathcal{L}\mathfrak{A}$-model of $\Delta\mathfrak{A}$.
That is, when $\mathfrak{B}$ satisfies $\Delta_\mathfrak{A}^+$, there is a possibility that $\mathfrak{B}$ satisfies atomic propositions ‘excessively’, preventing $\mathfrak{A}$ from being embedded into $\mathfrak{B}$. However, when $\mathfrak{B}$ satisfies $\Delta_\mathfrak{A}$, there are constraints on which atomic propositions $\mathfrak{B}$ can satisfy, thus guaranteeing the possibility of embedding.
In a previous article, we introduced the concept of elementary submodel. From this, we can define the following concept.
Definition. When $f: \mathfrak{A} \to \mathfrak{B}$ is an embedding and $f[\mathfrak{A}]$ is an elementary submodel of $\mathfrak{B}$, we call $f$ an elementary embedding.
The set of sentences related to elementary embeddings is as follows.
Definition. Let $E(\mathfrak{A})$ denote the set of all $\mathcal{L}_\mathfrak{A}$-propositions satisfied by $\mathfrak{A}$. That is,
\[E(\mathfrak{A}) = \{ \phi : \mathfrak{A} \vDash \phi \}\]
The most distinguishing feature of $E(\mathfrak{A})$ from $\Delta_\mathfrak{A}$ is that it also includes sentences with quantifiers.
Theorem. Let $\mathfrak{A}, \mathfrak{B}$ be $\mathcal{L}$-structures. There exists an elementary embedding $f: \mathfrak{A} \to \mathfrak{B}$ if and only if $\mathfrak{B}$ is an $\mathcal{L}_\mathfrak{A}$-model of $E(\mathfrak{A})$.
Finally, the following set of sentences is worth mentioning.
Definition. Let $\mathfrak{A}$ be an $\mathcal{L}$-structure. Let $\mathrm{Th}(\mathfrak{A})$ denote the set of all $\mathcal{L}$-sentences true in $\mathfrak{A}$.
Theorem. Let $\mathfrak{A}, \mathfrak{B}$ be $\mathcal{L}$-structures. $\mathfrak{A}$ and $\mathfrak{B}$ are elementarily equivalent if and only if $\mathrm{Th}(\mathfrak{A}) = \mathrm{Th}(\mathfrak{B})$.
In fact, this is nothing more than the definition of elementary equivalence, so it hardly deserves to be called a theorem, but it has been included here to maintain consistency with the other theorems introduced in this article.
Summarising in a table:
| Definition | Example | Mapping | |
|---|---|---|---|
| $\Delta_\mathfrak{A}^+$ | $\mathcal{L}_\mathfrak{A}$-atomic propositions satisfied by $\mathfrak{A}$ | $0 < 1$ | Surjective homomorphism |
| $\Delta_\mathfrak{A}$ | $\Delta_0$ $\mathcal{L}_\mathfrak{A}$-propositions satisfied by $\mathfrak{A}$ | $\lnot(1 < 0)$ | Embedding (submodel) |
| $\mathrm{Th}(\mathfrak{A})$ | $\mathcal{L}$-propositions satisfied by $\mathfrak{A}$ | $\forall x \exists y (x < y)$ | Elementary equivalence |
| $E(\mathfrak{A})$ | $\mathcal{L}_\mathfrak{A}$-propositions satisfied by $\mathfrak{A}$ | $\not \exists x (x < 0)$ | Elementary embedding (elementary submodel) |
For example, $\mathfrak{A} = (\mathbb{N}, <)$ embeds into $\mathfrak{B} = (\mathbb{Z}, <)$, but does not embed elementarily. This is because $\mathfrak{B}$ does not satisfy the sentence $\not \exists x (x < 0)$ from $E(\mathfrak{A})$.
연속체 가설과 동치인 색칠 문제
24 Apr 2025문제. 좌표평면을 가산 개의 색깔을 사용하여 칠했을 때, 세 꼭짓점이 같은 색깔인 직각삼각형이 언제나 존재하는가?
예를 들어 다음의 색칠은 3개의 색깔을 사용하는데, 세 꼭짓점이 모두 같은 색인 직각삼각형을 쉽게 찾을 수 있다.
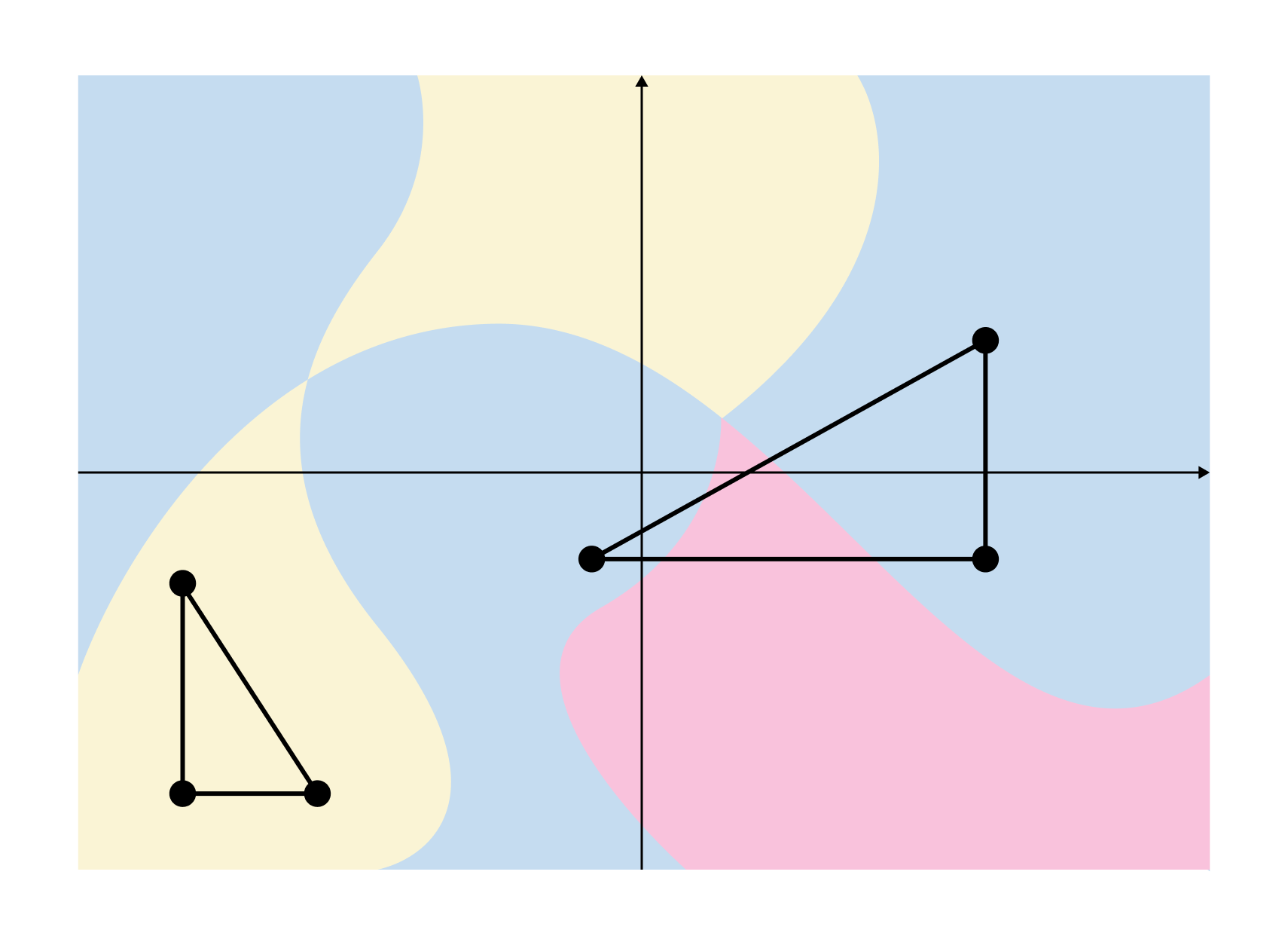
물론 위의 경우는 단순한 경우이고, 아래와 같이 무한히 많은 색깔들이 매우 불규칙적으로 칠해져 있는 경우에도 문제의 직각삼각형이 존재하는지를 따져야 한다.
놀랍게도 언뜻 자명해 보이는 이 문제는 연속체 가설과 동치이다.
연속체 가설. 자연수보다 크고 실수보다 작은 무한집합은 존재하지 않는다.
가장 작은 무한집합인 자연수의 기수를 $\aleph_0$, 자연수보다 큰 무한집합 중 가장 작은 무한집합의 기수를 $\aleph_1$이라고 정의한다. 한편 실수는 자연수의 멱집합과 크기가 같음을 쉽게 보일 수 있으며 집합 $X$의 멱집합은 크기가 $2^{|X|}$이므로, 실수의 기수는 $2^{\aleph_0}$이다. 따라서 연속체 가설의 진술은 $\aleph_1 = 2^{\aleph_0}$와 같다.
정리. 문제의 반례가 존재할 필요충분조건은 $\aleph_1 = 2^{\aleph_0}$이다.
참고로 아래 증명은 필자가 구상한 것이기 때문에 오류가 있을 수도 있다.
증명. $\aleph_1 = 2^{\aleph_0}$라면 문제의 반례가 존재함과, 문제의 반례가 존재하면 $\aleph_1 = 2^{\aleph_0}$임을 각각 보인다.
$\aleph_1 = 2^{\aleph_0}$라면 문제의 반례가 존재한다.
가장 작은 비가산 서수 $\omega_1$에 대해, $\omega_1^2$은 세 꼭짓점이 같은 색인 직각삼각형이 존재하지 않도록 색칠하는 다음의 방법이 존재한다. 먼저 가산 개의 색을 정수와 일대일 대응시킨다. $\alpha < \omega_1$은 가산 서수이므로, 빨간색 선분 $\lbrace (\beta, \alpha) : 0 \leq \beta \leq \alpha \rbrace $의 모든 점을 서로 다른 가산 개의 색으로 칠할 수 있다. 이들 점을 양의 정수에 대응되는 색들로 칠한다. 한편 파란색 선분 $\lbrace (\alpha, \beta) : 0 \leq \beta < \alpha \rbrace $의 점들은 음의 정수에 대응되는 색들로 칠한다.
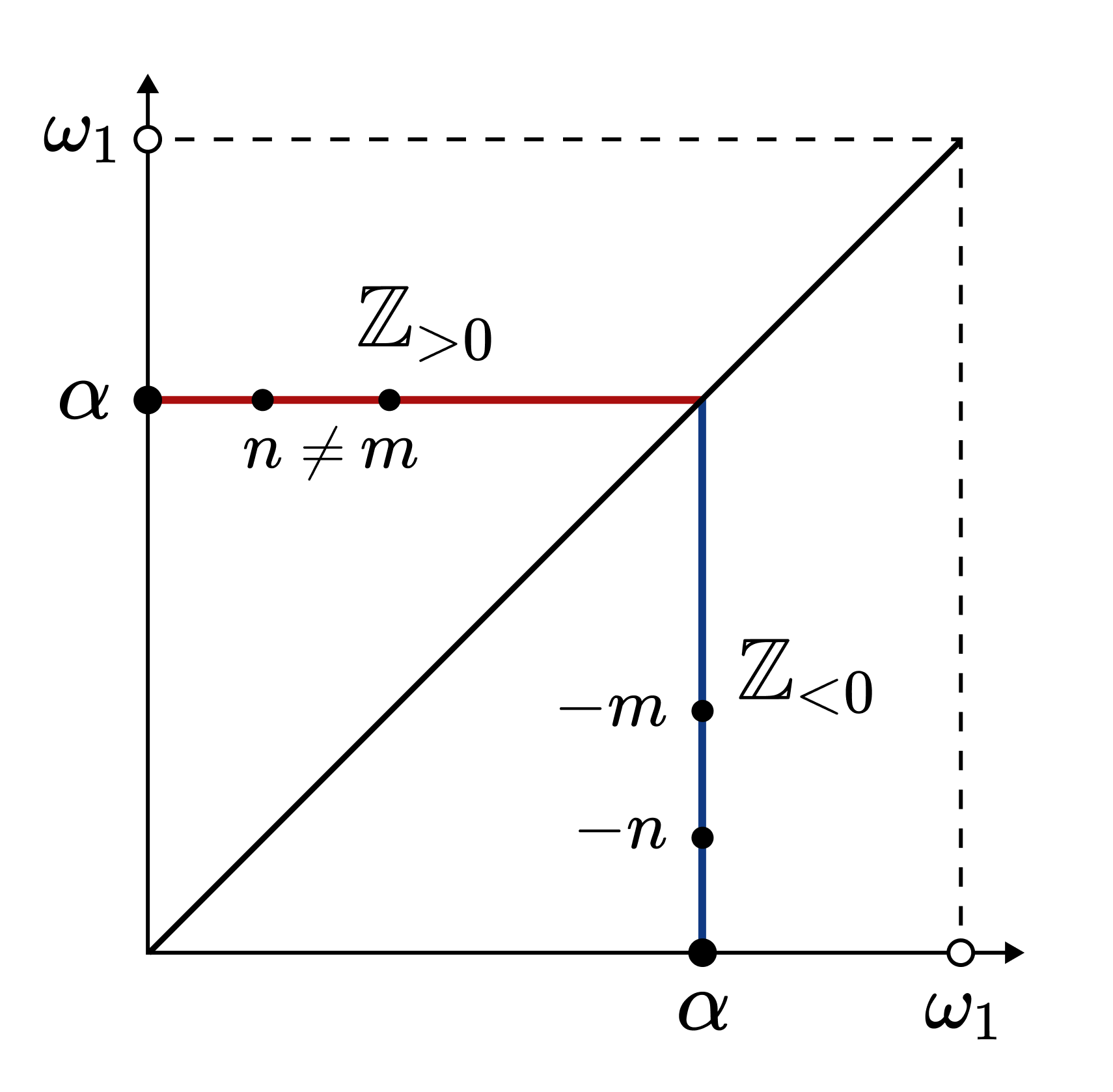
위와 같이 색칠했을 때 세 꼭짓점이 모두 같은 색인 직각삼각형이 없음을 쉽게 보일 수 있다.
만약 $\aleph_1 = 2^{\aleph_0}$라면, 어떤 일대일 대응 $f: \mathbb{R} \to \omega_1$이 존재한다. 이제 평면의 색칠을 다음과 같이 정의한다. 점 $p = (x, y) \in \mathbb{R}^2$을 점 $f(p) = (f(x), f(y)) \in \omega_1^2$와 같은 색으로 칠한다. $f$가 일대일 대응이기 때문에, 만약 해당 색칠해서 점 $p_1, p_2, p_3$가 색깔이 같은 직각삼각형의 세 꼭짓점이라면 $f(p_1), f(p_2), f(p_3)$ 또한 색깔이 같은 직각삼각형의 세 꼭짓점이다. 그런데 그러한 삼각형은 $\omega_1^2$에서 존재하지 않음을 보였으므로, 평면 또한 해당 색칠에서 요구되는 직각삼각형을 가지지 않는다.
문제의 반례가 존재한다면 $\aleph_1 = 2^{\aleph_0}$이다.
$2^{\aleph_0} > \aleph_1$이라고 가정하고 모순을 이끌어 내자. $I$가 크기 $\aleph_1$인 실수의 부분집합이라고 하자. 평면의 부분집합 $X = I \times \mathbb{R}$을 고려하자.
$x$축과 평행인 $X$의 직선들의 집합을 $L_0$라고 하자. $l \in L_0$에 대해, $l$을 이루는 점들 중 색깔 $c$로 칠해진 점의 개수가 $\aleph_1$ 이상일 때, $c \in \aleph_1(l)$이라고 적자. 임의의 $l \in L_0$에 대해, $|l| = \aleph_1$이므로 비둘기집의 원리에 의해 $c \in \aleph_1(l)$인 색깔 $c$가 직선마다 적어도 하나 존재함을 확인하라.
또한 $|L_0| = 2^{\aleph_0}$이므로 비둘기집의 원리에 의해 어떤 색깔 $c_0$가 존재하여, $c_0 \in \aleph_1(l)$을 만족하는 직선 $l$의 개수가 $2^{\aleph_0}$이다. 그러한 직선들의 집합 $L_0’$을 고려하자. $L_0’$의 직선들을 지나는 수직선을 그었을 때 어느 두 교점의 색이 $c_0$라면, 세 꼭짓점의 색이 모두 $c_0$인 직각삼각형이 존재하게 된다. 따라서 임의의 수직선과 $L_0’$의 직선들이 이루는 교점 중 $c_0$로 칠해진 점은 최대 1개이다. 수직선의 개수가 총 $|I| = \aleph_1$개이므로, $L_0’$에는 총 $\aleph_1$개의 $c_0$ 점들이 존재한다.
해당 점들을 모두 빼면 듬성듬성한 직선들의 집합이 된다. 이 집합을 $L_1$이라고 하자.
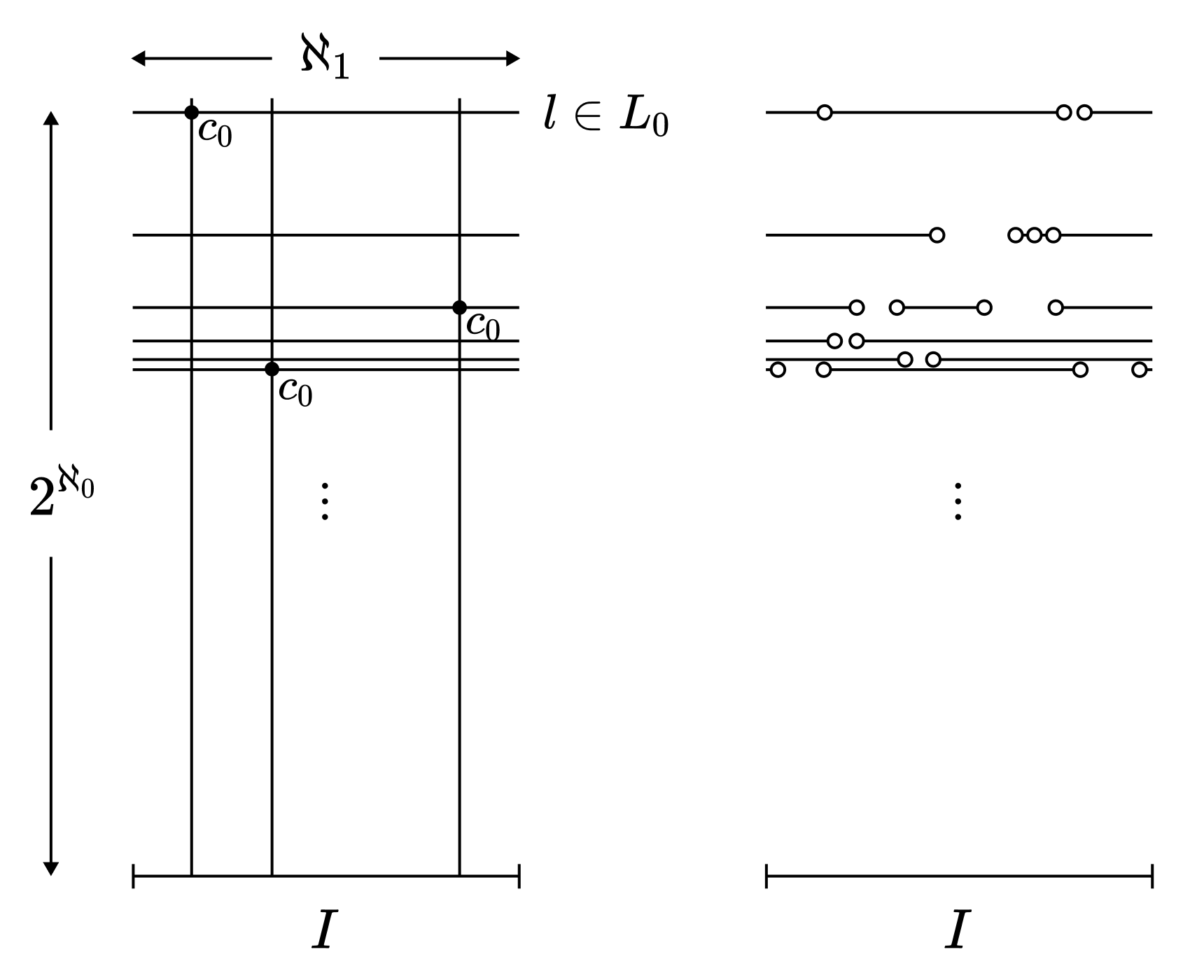
두 가지 경우가 가능하다. a) $L_1$의 직선들 중 $\aleph_1$개의 점들을 가지는 직선이 $2^{\aleph_0}$개이다. b) $L_1$의 직선들 중 $\aleph_1$개의 점들을 가지는 직선이 $\aleph_1$개 이하이다.
a의 경우, 다시 비둘기집의 원리에 의해 $c_1 \in \aleph_1(l)$을 만족하는 직선 $l \in L_1$의 개수가 $2^{\aleph_0}$인 색깔 $c_1$이 존재한다. 그러한 $L_1$의 직선들의 집합을 $L_1’$이라고 하자. 앞선 논의에 의해 $L_1’$에는 총 $\aleph_1$개의 $c_1$ 점들이 존재한다. 이 점들을 뺀 집합을 $L_2$라고 하자. 이같은 과정을 b가 될 때까지 반복한다. (색깔이 가산 개 있기 때문에 언젠가는 b에 도달함을 확인하라)
b가 되었을 때 $L_n$은 최대 $\aleph_1$개의 점들을 가진다. 그런데 $L$이 $L_n$이 되는 과정에서 빠진 점들의 개수는 $\aleph_1 \cdot \aleph_0 = \aleph_1$을 넘지 않는다. 한편 $L$은 $2^{\aleph_0}$개의 점들을 가지고 있었기 때문에, 이는 $\aleph_1 < 2^{\aleph_0}$에 모순된다. ■
A Colouring Problem Equivalent to the Continuum Hypothesis
24 Apr 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
Problem. When the coordinate plane is coloured using countably many colours, does there always exist a right triangle whose three vertices are of the same colour?
For instance, the following colouring uses 3 colours, and one can easily find a right triangle whose three vertices are all of the same colour.

Of course, the above case is a simple one, and we must consider whether the required right triangle exists even when infinitely many colours are applied in a highly irregular manner, as shown below.

Remarkably, this problem, which appears trivial at first glance, is equivalent to the continuum hypothesis.
Continuum Hypothesis. There exists no infinite set whose cardinality is greater than that of the natural numbers but smaller than that of the real numbers.
We define $\aleph_0$ as the cardinality of the smallest infinite set, namely the natural numbers, and $\aleph_1$ as the cardinality of the smallest infinite set larger than the natural numbers. Meanwhile, the real numbers can easily be shown to have the same cardinality as the power set of the natural numbers, and since the power set of a set $X$ has cardinality $2^{|X|}$, the cardinality of the real numbers is $2^{\aleph_0}$. Therefore, the statement of the continuum hypothesis is equivalent to $\aleph_1 = 2^{\aleph_0}$.
Theorem. A counterexample to the problem exists if and only if $\aleph_1 = 2^{\aleph_0}$.
Note that the following proof is conceived by the author and may contain errors.
Proof. We shall show that if $\aleph_1 = 2^{\aleph_0}$, then a counterexample to the problem exists, and conversely, if a counterexample to the problem exists, then $\aleph_1 = 2^{\aleph_0}$.
If $\aleph_1 = 2^{\aleph_0}$, then a counterexample to the problem exists.
For the smallest uncountable ordinal $\omega_1$, there exists a method of colouring $\omega_1^2$ such that no right triangle with three vertices of the same colour exists. First, we establish a one-to-one correspondence between countably many colours and the integers. Since $\alpha < \omega_1$ is a countable ordinal, we can colour all points of the red segment $\lbrace (\beta, \alpha) : 0 \leq \beta \leq \alpha \rbrace $ with countably many distinct colours. We colour these points with colours corresponding to positive integers. Meanwhile, the points of the blue segment $\lbrace (\alpha, \beta) : 0 \leq \beta < \alpha \rbrace $ are coloured with colours corresponding to negative integers.

It can easily be shown that with this colouring, there exists no right triangle whose three vertices are all of the same colour.
If $\aleph_1 = 2^{\aleph_0}$, then there exists a one-to-one correspondence $f: \mathbb{R} \to \omega_1$. We now define a colouring of the plane as follows. A point $p = (x, y) \in \mathbb{R}^2$ is coloured with the same colour as the point $f(p) = (f(x), f(y)) \in \omega_1^2$. Since $f$ is a one-to-one correspondence, if points $p_1, p_2, p_3$ form the three vertices of a right triangle of the same colour under this colouring, then $f(p_1), f(p_2), f(p_3)$ also form the three vertices of a right triangle of the same colour. However, since we have shown that no such triangle exists in $\omega_1^2$, the plane also lacks the required right triangle under this colouring.
If a counterexample to the problem exists, then $\aleph_1 = 2^{\aleph_0}$.
Suppose $2^{\aleph_0} > \aleph_1$ and derive a contradiction. Let $I$ be a subset of the real numbers with cardinality $\aleph_1$. Consider the subset $X = I \times \mathbb{R}$ of the plane.
Let $L_0$ denote the set of lines in $X$ parallel to the $x$-axis. For $l \in L_0$, we write $c \in \aleph_1(l)$ when the number of points in $l$ coloured with colour $c$ is at least $\aleph_1$. For any $l \in L_0$, since $|l| = \aleph_1$, verify that by the pigeonhole principle, there exists at least one colour $c$ such that $c \in \aleph_1(l)$ for each line.
Moreover, since $|L_0| = 2^{\aleph_0}$, by the pigeonhole principle there exists some colour $c_0$ such that the number of lines $l$ satisfying $c_0 \in \aleph_1(l)$ is $2^{\aleph_0}$. Consider the set $L_0’$ of such lines. When vertical lines are drawn through the lines in $L_0’$, if any two intersection points have colour $c_0$, then there exists a right triangle whose three vertices are all of colour $c_0$. Therefore, amongst the intersection points of any vertical line with the lines in $L_0’$, at most one point is coloured $c_0$. Since there are $|I| = \aleph_1$ vertical lines in total, there exist $\aleph_1$ points of colour $c_0$ in $L_0’$.
Removing all these points yields a sparse set of lines. Let this set be $L_1$.

Two cases are possible: a) There are $2^{\aleph_0}$ lines in $L_1$ that contain $\aleph_1$ points. b) There are at most $\aleph_1$ lines in $L_1$ that contain $\aleph_1$ points.
In case a), again by the pigeonhole principle, there exists a colour $c_1$ such that the number of lines $l \in L_1$ satisfying $c_1 \in \aleph_1(l)$ is $2^{\aleph_0}$. Let $L_1’$ denote the set of such lines in $L_1$. By the previous argument, there exist $\aleph_1$ points of colour $c_1$ in $L_1’$. Let $L_2$ denote the set obtained by removing these points. Repeat this process until case b) is reached. (Verify that case b) is eventually reached since there are countably many colours.)
When case b) is reached, $L_n$ contains at most $\aleph_1$ points. However, the number of points removed in the process from $L$ to $L_n$ does not exceed $\aleph_1 \cdot \aleph_0 = \aleph_1$. Meanwhile, since $L$ originally contained $2^{\aleph_0}$ points, this contradicts $\aleph_1 < 2^{\aleph_0}$. ■
기수의 정의에 관한 노트
20 Apr 2025정의. $X$에서 $Y$로 가는 단사 사상이 존재할 때, $|X| \leq |Y|$라고 적는다. 전단사 사상이 존재할 때, $|X| = |Y|$라고 적는다.
집합론을 처음 공부하는 학생들이 흔히 하는 오해는, 위 정의의 $|\cdot|$과 $\leq$를 복소수에서의 $|\cdot|$과 $\leq$와 유사한 것으로 은연 중에 취급하는 것이다. 요컨대 복소수 $z$에 대해 $|z|$가 실수이고 $\leq$가 실수의 대소 관계이듯이, 집합 $X$에 대해 $|X|$는 집합의 크기 — 이른바 기수cardinality이고, $\leq$는 기수의 대소 관계라고 생각하는 것이다.
그러나 이는 문제의 여지가 많은 접근이다. 왜냐하면 위 정의만으로는 기수라는 수학적 대상을 정의할 수 있다는 보장이 없기 때문이다. 우리가 정의한 것은 이항 관계에 불과하다.
이해를 위한 예시를 들어보자. $A$가 $B$를 좋아할 때, $|A| \leq |B|$라고 적을 수 있을 것이다. 그러나 이렇게 적었다고 해서, $|A|$는 ‘$A$의 호감도’를 의미하며 $\leq$가 호감도의 대소 관계라고 해석한다면 완전히 틀린 것이다. 이와 마찬가지로 $|X| \leq |Y|$는 단사 관계의 유무로 정의되는 이항 관계일 뿐, 이 관계 자체가 기수의 개념을 시사하는 것은 아니다.
특히 ZFC에서는 모든 것이 집합이기 때문에, 만약 기수를 정의하고 싶다면 다음의 사실을 논증해야 한다.
정리 1. 임의의 집합 $X, Y$에 대해, 어떤 집합 $\mathrm{Card}(X), \mathrm{Card}(Y)$가 존재하여, 다음이 성립한다.
- $|X| \leq |Y|$ iff $\mathrm{Card}(X) \subseteq \mathrm{Card}(Y)$
- $|X| = |Y|$ iff $\mathrm{Card}(X) = \mathrm{Card}(Y)$
$\mathrm{Card}(X)$를 $X$의 기수라고 부른다.
즉 ① $\mathrm{Card}(X)$를 정의해야 하고, ② 해당 정의에 대해 위 진술이 성립함을 보여야 한다.
표현의 편의를 위해 $|X| \leq |Y|$와 $|X| = |Y|$를 “$Y$가 $X$보다 작지 않다”, ”$X$와 $Y$의 크기가 같다“라고 부르자. ①부터 살펴 보자면, 크게 네 가지 접근이 가능하다. 짤막하게 알아보자면 이렇다.
-
칸토어의 정의
- 정의: $\mathrm{Card}(X)$를 $X$와 크기가 같은 집합들의 집합으로 정의한다.
- 장점: 정의가 가장 직관적임
- 단점: $\mathrm{Card}(X)$는 사실 집합이 아니라 모임class임
-
스콧의 트릭Scott’s trick
- 정의: $X$와 크기가 같은 집합 중 폰 노이만 위계에서 가장 먼저 등장하는 집합의 랭크가 $V_\alpha$일 때, $\mathrm{Card}(X)$를 $V_\alpha$로 정의한다.
- 장점: 모임의 문제 없이 기수를 정의함
- 단점: 정의가 직관적이지 않고 ad-hoc적인 면모가 있음
-
정렬 원리well-ordering theorem를 사용하여 기수를 정의하기
- 정의: $X$의 정렬에 대응되는 서수ordinal들보다 작지 않은 서수 중 가장 작은 서수를 $\mathrm{Card}(X)$로 정의한다.
- 장점: 정의가 다소 직관적이고, 모임의 문제가 없음
- 단점: 선택 공리 없이는 임의의 집합에 대해 해당 집합의 정렬이 존재함을 보장할 수 없음
-
하르토그스 수Hartogs number를 사용하여 기수를 정의하기
- 정의: $X$의 정렬 가능한 부분집합들에 대응되는 서수들보다 큰 서수 중 가장 작은 서수를 $X$의 하르토그수 수로 정의한다.
- 장점: 정의가 어느 정도 직관적이고, 모임의 문제가 없으며, 선택 공리에 의존적이지 않음
- 단점: 다루기 불편하고 제약이 많음
사실 4를 정의로 채택하는 경우는 없지만, 한 가지 가능성으로서 소개했다. 현대 집합론에서는 2 또는 3을 기수의 정의로 채택한다. 두 경우 모두 정리 1이 성립함을 ZFC에서 보일 수 있다.
흥미로운 것은, 스콧의 트릭을 사용하여 기수를 정의하면 선택 공리가 필요하지는 않지만, 스콧의 트릭으로 정의된 기수가 정리 1을 만족함을 보일 때에는 선택 공리가 필요하다는 사실이다. 왜냐하면 다음이 선택 공리와 동치이기 때문이다.
정리 2. 임의의 집합 $X, Y$에 대해, $|X| \leq |Y|$이거나 $|Y| \leq |X|$이다.
즉, 선택 공리를 사용하지 않더라도 a) 스콧의 트릭을 통해 $\mathrm{Card}(X)$를 정의하거나, b) 단사 사상의 유무를 통해 $|X| \leq |Y|$를 정의할 수 있지만, a)와 b)가 맞물린다는 사실을 보일 때는 선택 공리가 필요하다.
Notes on the Definition of Cardinality
20 Apr 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
Definition. When there exists an injective mapping from $X$ to $Y$, we write $|X| \leq |Y|$. When there exists a bijective mapping, we write $|X| = |Y|$.
A common misunderstanding amongst students first studying set theory is to implicitly treat the $|\cdot|$ and $\leq$ in the above definition as analogous to $|\cdot|$ and $\leq$ for complex numbers. In other words, just as $|z|$ is a real number for a complex number $z$ and $\leq$ is the ordering relation on real numbers, they think that $|X|$ for a set $X$ is the size of the set—the so-called cardinality—and $\leq$ is the ordering relation on cardinalities.
However, this is a problematic approach. This is because there is no guarantee that we can define cardinality as a mathematical object using only the definition above. What we have defined is merely a binary relation.
Let us consider an example for understanding. When $A$ likes $B$, we might write $|A| \leq |B|$. However, if we interpret this notation to mean that $|A|$ represents ‘$A$’s affection level’ and $\leq$ is the ordering relation on affection levels, this would be completely incorrect. Similarly, $|X| \leq |Y|$ is merely a binary relation defined by the existence of an injective mapping; the relation itself does not suggest the concept of cardinality.
In particular, since everything is a set in ZFC, if we wish to define cardinality, we must prove the following fact.
Theorem 1. For any sets $X, Y$, there exist sets $\mathrm{Card}(X), \mathrm{Card}(Y)$ such that the following holds:
- $|X| \leq |Y|$ iff $\mathrm{Card}(X) \subseteq \mathrm{Card}(Y)$
- $|X| = |Y|$ iff $\mathrm{Card}(X) = \mathrm{Card}(Y)$
We call $\mathrm{Card}(X)$ the cardinality of $X$.
That is, we must ① define $\mathrm{Card}(X)$, and ② show that the above statement holds for this definition.
For convenience of expression, let us refer to $|X| \leq |Y|$ and $|X| = |Y|$ as “$Y$ is not smaller than $X$” and “$X$ and $Y$ have the same size”, respectively. Regarding ①, there are broadly four possible approaches. Let us briefly examine them:
-
Cantor’s definition
- Definition: Define $\mathrm{Card}(X)$ as the collection of all sets having the same size as $X$.
- Advantage: The definition is most intuitive
- Disadvantage: $\mathrm{Card}(X)$ is actually a class, not a set
-
Scott’s trick
- Definition: When the rank of the first set to appear in the von Neumann hierarchy amongst sets having the same size as $X$ is $V_\alpha$, define $\mathrm{Card}(X)$ as $V_\alpha$.
- Advantage: Defines cardinality without the class problem
- Disadvantage: The definition is not intuitive and has ad-hoc aspects
-
Defining cardinality using the well-ordering theorem
- Definition: Define $\mathrm{Card}(X)$ as the smallest ordinal that is not smaller than the ordinals corresponding to well-orderings of $X$.
- Advantage: The definition is somewhat intuitive and avoids the class problem
- Disadvantage: Without the axiom of choice, we cannot guarantee the existence of a well-ordering for arbitrary sets
-
Defining cardinality using Hartogs numbers
- Definition: Define the Hartogs number of $X$ as the smallest ordinal greater than the ordinals corresponding to well-orderable subsets of $X$.
- Advantage: The definition is reasonably intuitive, avoids the class problem, and is not dependent on the axiom of choice
- Disadvantage: Inconvenient to handle and has many limitations
In fact, 4 is never used as a definition, but I’ve listed it for reference purpose. In modern set theory, either 2 or 3 is adopted as the definition of cardinality. In both cases, one can prove that Theorem 1 holds in ZFC.
What is interesting is that while the axiom of choice is not required to define cardinality using Scott’s trick, the axiom of choice is needed to prove that cardinality defined by Scott’s trick satisfies Theorem 1. This is because the following is equivalent to the axiom of choice:
Theorem 2. For any sets $X, Y$, either $|X| \leq |Y|$ or $|Y| \leq |X|$.
That is, even without using the axiom of choice, we can a) define $\mathrm{Card}(X)$ through Scott’s trick, or b) define $|X| \leq |Y|$ through the existence of injective mappings, but the axiom of choice is required to prove that a) and b) mesh together.
무한 죄수 모자 문제
18 Apr 2025아마 여러분은 죄수들이 자신의 모자 색을 맞히는 내용의 퍼즐을 제법 보았을 것이다. 예시는 다음과 같다.
3명의 죄수 A, B, C가 일렬로 서 있다. 간부는 검은 모자 2개와 흰 모자 3개 중 세 개를 골라 각 죄수에게 씌우고는, 만약 어느 한 명이라도 자신의 모자의 색을 맞히면 모두 풀려나지만 틀릴 경우 모두 사형에 처해질 것이라고 말한다. 죄수는 자기 앞에 있는 죄수들의 모자 색은 볼 수 있지만, 자신의 모자 색이나 자기 뒤에 있는 죄수들의 모자 색은 볼 수 없다. 오랜 침묵이 흐른 후, 한 죄수가 자신의 모자 색을 정확히 맞혔다. 문제를 맞힌 죄수는 누구인가?
C가 정답을 맞힌다.
만약 B와 C의 모자 색이 모두 검은색이었다면 A는 자신의 모자가 흰색임을 맞혔을 것이다. 그러나 "오랜 침묵"이 흘렀으므로, A는 자신의 모자 색을 맞히지 못하는 상황이며 이는 B, C의 모자 색이 (흰, 검), (검, 흰), (흰, 흰)의 경우 중 하나임을 시사한다.
이 사실을 고려했을 때, 만약 C의 모자 색이 검정색이었다면 B는 자신의 모자 색이 흰색임을 맞혔을 것이다. 그럼에도 "오랜 침묵"이 흘렀다는 것은 B 또한 자신의 모자 색을 맞히지 못하는 상황임을 의미하므로, C의 모자 색은 흰색이다.
조금 더 어려운 문제도 있다.
100명의 죄수가 일렬로 서 있다. 간부는 각 죄수에게 검은 모자와 흰 모자를 무작위로 씌우고는, 1번 죄수부터 차례대로 자신의 모자 색을 맞히게 시킨다. 맞히는 사람은 풀려나지만 틀린 사람은 사형에 처해진다. 죄수들은 사전에 전략을 의논할 수 있지만 모자가 씌워진 이후부터는 정답을 외치는 것 이외의 모든 발언과 행동이 금지된다. 최대 몇 명의 생존을 확실히 보장할 수 있는가?
첫 번째 죄수를 제외한 99명의 생존을 보장할 수 있다.
첫 번째 죄수를 제외한 99명의 생존을 보장할 수 있다.
첫 번째 죄수는 자신을 제외한 99명의 모자 색을 볼 수 있다. 그 중 검은색 모자가 짝수 개라면 자신의 모자 색을 검은색으로 맞히고, 홀수 개라면 흰색으로 맞힌다. 그러면 두 번째 죄수는 첫 번째 죄수가 전달한 정보와, 자기 앞에 있는 모자들 중 검은색 모자의 홀짝성을 비교함으로서 자신의 모자 색을 정확히 맞힐 수 있다. 세 번째 죄수 또한 첫 번째 죄수가 전달한 정보와, 두 번째 죄수가 자신의 모자 색을 맞혔다는 사실로부터 자신의 모자 색을 정확히 맞힐 수 있고, 이같은 식으로 99명이 모두 풀려날 수 있다.
이제 문제를 더 괴랄하게 만들어 보자.
무한히 많은 죄수가 일렬로 서 있다. 간부는 각 죄수에게 검은 모자와 흰 모자를 무작위로 씌우고는, 1번 죄수부터 차례대로 자신의 모자 색을 맞히게 시킨다. 맞히는 사람은 풀려나지만 틀린 사람은 사형에 처해진다. 죄수들은 사전에 전략을 의논할 수 있지만 모자가 씌워진 이후부터는 정답을 외치는 것 이외의 모든 발언과 행동이 금지된다. 가능한 적은 죄수가 죽도록 하는 전략은 무엇인가? 단, 모든 죄수는 무한한 연산 능력을 가지며, 수학적으로 전지전능하다고 가정한다. 즉, $f$가 수학적으로 존재하는 함수일 때, 죄수들은 $f$의 함숫값을 언제나 계산할 수 있으며, 사전에 전략을 의논할 때 $f$를 사용하자고 합의할 수 있다.
첫 번째 죄수를 제외한 전원의 생존을 보장할 수 있다.
선택 공리를 사용한다.
검은색 모자를 0, 흰색 모자를 1로 적으면 죄수들의 모자 배열은 101011... 와 같은 무한 숫자열로 표현할 수 있다. 앞에 소숫점을 찍고 이진법으로 읽으면 죄수들의 모자 배열은 0 이상 1 이하의 실수와 일대일 대응된다.
실수 $a, b \in [0, 1]$에 대해, $a$와 $b$의 이진 전개가 차이나는 자릿수의 개수가 유한할 때 $a \sim b$라고 하자. 예를 들어,
$$ 0.11111\dots \sim 0.01111\dots, \; 0.10101\dots \not\sim 0.01010\dots $$$\sim$은 동치 관계임을 쉽게 보일 수 있다. 따라서 동치류 $[0, 1]/\sim$을 취할 수 있다. 선택 공리에 의해 $[0, 1]/\sim$의 선택 함수 $\iota$가 존재한다. 죄수들이 수학적으로 전지전능하다고 가정했으므로 사전에 죄수들은 어떤 선택 함수 $\iota$를 사용할지 합의할 수 있다.
모자 맞히기가 시작되었을 때 $n$번째 죄수는 $n$개의 모자를 제외한 모든 모자의 색을 볼 수 있다. 즉, 죄수들의 모자 배열에 대응되는 실수가 $r$일 때, $n$번째 죄수는 $r$의 소숫점 아래 $n$개 자릿수 이외의 모든 자릿수를 알고 있다. 즉, 그는 $r$이 $[0, 1]/\sim$의 어떤 동치류에 속하는지 알며, $r$이 속하는 동치류를 $[r]$이라고 했을 때 $\iota([r])$을 계산할 수 있다.
이제 다음의 전략을 취한다. $\sim$의 정의에 의해 $r$과 $\iota([r])$은 유한한 개수의 자릿수에서만 차이가 난다. 첫 번째 죄수는 자신이 보는 모자들의 배열과 $\iota([r])$에 대응되는 모자들의 배열이 짝수만큼 차이가 나면 자신의 모자색을 검정색으로 맞히고, 홀수만큼 차이가 나면 흰색으로 맞힌다. 이제 나머지 죄수들은 100명의 죄수 문제와 같은 방식으로 자신의 모자 색을 맞힐 수 있다.
즉, 선택 공리는 $N$명의 죄수 문제에서 $N \to \infty$를 취했을 때에도 첫 번째 죄수를 제외한 전원이 생존할 수 있다는 결론이 존속되도록 보장하는 원리이다.
위 퍼즐도 상당히 신기하지만, 다음의 퍼즐은 더 기묘하다.
무한히 많은 죄수가 일렬로 서 있다. 간부는 각 죄수에게 검은 모자와 흰 모자를 무작위로 씌우고는, 1번 죄수부터 차례대로 자신의 모자 색을 맞히게 시킨다. 맞히는 사람은 풀려나지만 틀린 사람은 사형에 처해진다. 죄수들은 사전에 전략을 의논할 수 있지만 모자가 씌워진 이후부터는 정답을 외치는 것 이외의 모든 발언과 행동이 금지된다. 또한, 모자가 씌워지는 순간 죄수들은 청력을 완전히 상실하여 아무런 정보를 주고받을 수 없다. 오직 유한한 수의 죄수만이 죽도록 하는 전략이 있는가? (마찬가지로 죄수는 무한한 연산 능력을 가지며 수학적으로 전지전능하다.)
이전 문제와 같이 $\iota$를 $[0, 1]/\sim$의 선택 함수라고 하자. 다음의 전략을 취한다. $n$번째 죄수는 자신의 모자 색을 $\iota([r])$의 $n$번째 자릿수에 대응되는 색으로 맞힌다. 그러면 $\sim$의 정의에 의해 유한한 수의 죄수를 제외한 전원이 정답을 맞힌다.
위 퍼즐이 특히 기묘한 이유는, 청력 상실 조건에 의해 서로 다른 두 죄수가 모자를 맞히는 사건이 독립이므로, 각각의 죄수가 정답을 맞힐 확률은 $p$로 동일해야 할 듯하기 때문이다. 이 경우 총 $N$명의 죄수가 정답을 맞히는 확률은 $p^N$이 되므로, $N \to \infty$에 따라 확률은 0으로 수렴한다. 그러나 실제로는 무한히 많은 죄수들이 정답을 맞힌다.
이 역설의 뿌리는, 임의의 죄수가 정답을 맞히는 확률이 정의되지 않는다는 데 있다. 잘 생각해 보면, 임의의 죄수가 정답을 맞히는 사건은 주어진 실수 $r \in [0, 1]$이 비탈리 집합에 포함되는 사건과 동일한데, 비탈리 집합은 비가측 집합이므로 이 사건에는 확률을 정의할 수 없기 때문이다.