어드조인트에 대한 직관적 이해

16 Dec 2024

카테고리 이론의 핵심 개념 중 하나는 어드조인트_adjoint이다.

정의. $\mathcal{A}, \mathcal{B}$가 카테고리이고, $F: \mathcal{A} \to \mathcal{B}, G: \mathcal{B} \to \mathcal{A}$가 함자_functor라고 하자. $F$가 $G$의 좌 어드조인트_{left adjoint}라는 것은 임의의 $A \in \mathcal{A}, B \in \mathcal{B}$에 대해 $\mathcal{B}(F(A), B)$와 $\mathcal{A}(A, G(B))$가 자연스럽게 일대일 대응될 수 있다는 것이다. 즉,

\[\begin{gather} (F(A) \xrightarrow{g} B) \quad \mapsto \quad (A \xrightarrow{\bar{g}} G(B))\\ (A \xrightarrow{f} G(B)) \quad \mapsto \quad (F(A) \xrightarrow{\bar{f}} B) \end{gather}\]

또한 $G$를 $F$의 우 어드조인트_{right adjoint}라고 한다. 기호로 $F \dashv G$로 표기한다.

이 정의는 다소 추상적으로 느껴질 수 있지만, 이해를 돕는 몇 가지 직관이 있다.

1. 근사로서의 어드조인트

$F \dashv G$일 때 $F, G$는 $\mathcal{A}$과 $\mathcal{B}$의 원소들을 서로 근사하는 방법으로 생각할 수 있다. 특히 좌 어드조인트는 ‘좌측에서 우측으로‘의 근사이고, 우 어드조인트는 ‘우측에서 좌측으로’의 근사이다.

예를 들어 $\mathbf{Z}$가 정수를 원소로 가지고, $x \leq y$일 때 그리고 오직 그 경우에만 $x \to y$ 사상이 유일하게 존재하는 카테고리라고 하자. 또한 $\mathbf{R}$이 실수를 원소로 가지고, $x \leq y$일 때 그리고 오직 그 경우에만 $x \to y$ 사상이 유일하게 존재하는 카테고리라고 하자. 이때 $\lceil \cdot \rceil, \lfloor \cdot \rfloor$는 표준적인 방식으로 함자 $\mathbf{R} → \mathbf{Z}$가 되고, 포함 사상 $\iota$는 함자 $\mathbf{Z} → \mathbf{R}$이 된다. 또한 $\lceil \cdot \rceil \dashv \iota \dashv \lfloor \cdot \rfloor$임을 확인할 수 있다.

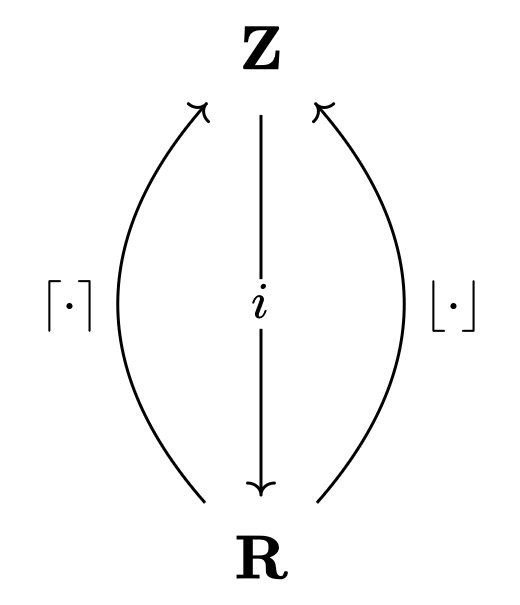
즉 $\lceil \cdot \rceil$는 $r$을 $r \leq \lceil r \rceil$로 ‘좌측에서 우측으로 끌어올리는’ 변환이고, $\lfloor \cdot \rfloor$은 $r$을 $\lfloor r \rfloor \leq r$로 ‘우측에서 좌측으로 잡아당기는’ 변환이다.

또한 $I, T$가 각각 $\mathcal{A}$의 초기 대상_{initial object} 및 종단 대상_{terminal object}라고 하자. 즉, 임의의 $A \in \mathcal{A}$에 대해

• 사상 $I \to A$가 유일하게 존재한다.
• 사상 $A \to T$가 유일하게 존재한다.

일례로 $\mathbf{Set}$에서 공집합은 초기 대상이고 홑원소 집합은 종단 대상이다.

홑원소 카테고리 $\mathcal{U}$에 대해 함자 $F: \mathcal{A} \to \mathcal{U}$가 유일하게 존재한다. $G_I, G_T: \mathcal{U} \to \mathcal{A}$가 각각 상이 $I, T$인 함자라고 하자. 이때 앞선 경우와 비슷한 원리로 $G_T \dashv F \dashv G_I$가 됨을 확인하라. (종단 대상은 가장 “오른쪽”에 있는 대상이므로 $G_T$는 “왼쪽에서 오른쪽으로”의 근사이며, 초기 대상은 가장 “왼쪽”에 있는 대상이므로 $G_I$는 “오른쪽에서 왼쪽으로”의 근사이다.)

2. 구축과 파괴로서의 어드조인트

좌 어드조인트는 구축을, 우 어드조인트는 파괴를 의미한다. 따라서 일반적으로 자유함자_{free functor}는 좌 어드조인트, 망각함자_{forgetful functor}는 우 어드조인트이다.

일례로 군의 카테고리를 $\mathbf{Grp}$, 모노이드의 카테고리를 $\mathbf{Mon}$이라 하자. $F$를 자유함자, $U$를 망각함자라고 하자. 그리고 $R: \mathbf{Mon} → \mathbf{Grp}$를 다음과 같이 정의한다.

• $R(M) = \lbrace m \in M : \exists m^{-1} \in M \rbrace$
• $R(f): m \mapsto f(m)$

이때, 다음 다이어그램이 성립하여 $F \dashv U \dashv R$이다.

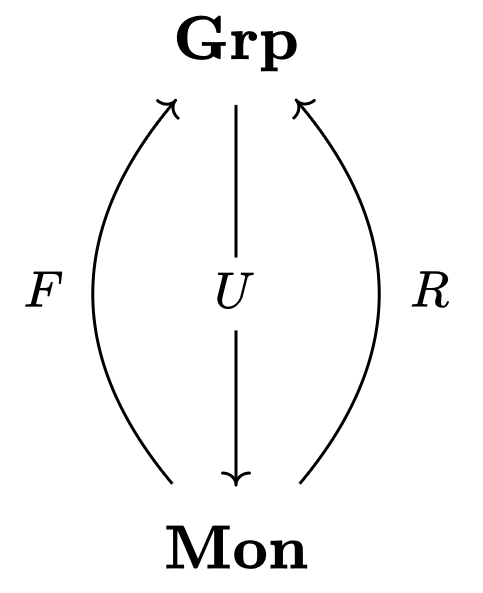
$R$이 $U$보다 더 파괴적이기 때문에 $U \dashv R$인 것으로 이해할 수 있다.