디멘의 블로그 이데아를 여행하는 히치하이커

콤팩트성과 그물

01 Dec 2024
수학
위상수학

콤팩트성

정의. $X$가 위상공간이라고 하자.

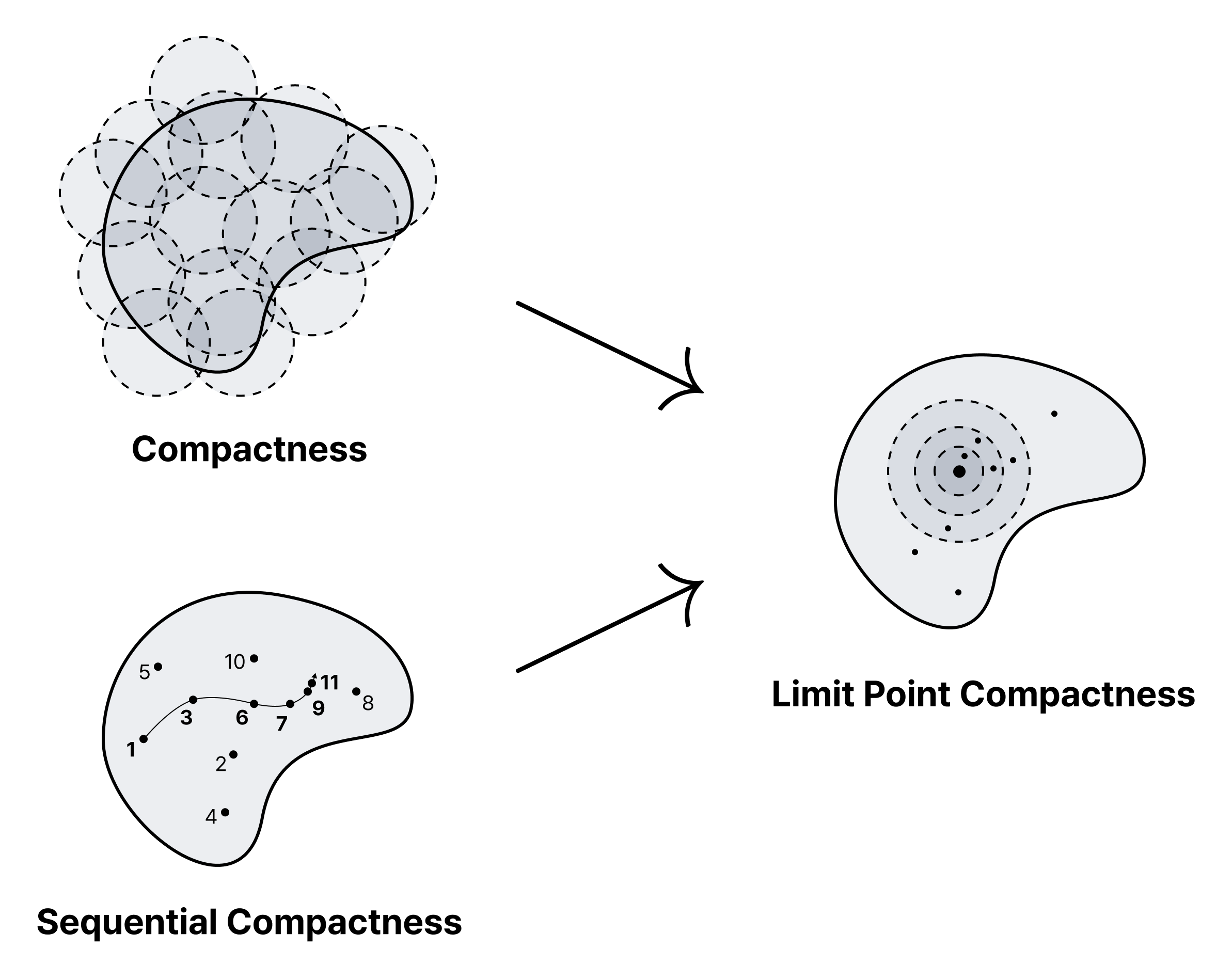
  1. 임의의 열린 덮개가 유한한 부분덮개를 가질 때 $X$를 콤팩트하다고 한다.
  2. 임의의 점렬 $\lbrace x_n \in X \rbrace$가 수렴하는 부분점렬을 가질 때 $X$를 점렬 콤팩트하다고 한다.
  3. 임의의 무한집합 $S \subset X$가 극점을 가질 때 $X$를 극점 콤팩트하다고 한다.

정리.

  1. 콤팩트 $\rightarrow$ 극점 콤팩트
  2. 점렬 콤팩트 $\rightarrow$ 극점 콤팩트
  3. 극점 콤팩트 $\not\rightarrow$ 콤팩트
  4. 극점 콤팩트 $\not\rightarrow$ 점렬 콤팩트

증명.

  1. $S \subset X$가 극점이 없는 무한집합이라고 하자. $\overline{S} = S \cup S’ = S$이므로 $S$는 닫힌 집합이며, $X \setminus S$는 열린 집합이다. 임의의 $s \in S$에 대해, $s$가 극점이 아니므로 $U_s \cap S = \lbrace s \rbrace$인 $s$의 근방 $U_s$가 존재한다. 따라서 다음 $X$의 열린 덮개는 유한한 부분덮개를 가지지 않는다.
\[\mathcal{C} = \lbrace X \setminus S \rbrace \cup \bigcup_{s \in S} \lbrace U_s \rbrace\]
  1. $S \subset X$가 무한집합이라고 하자. $S$의 원소들을 임의로 추출하여 점렬 $\lbrace s_n \rbrace \;(n \neq m \implies s_n \neq s_m)$을 만든다. $X$가 점렬 콤팩트하므로 $\lbrace s_n \rbrace → s$이며, $s$는 $S$의 극점이다.
  2. 순서 토폴로지가 주어진 $\omega_1$은 극점 콤팩트하지만 콤팩트하지 않다.
  3. $X = \mathbb{N} \times \lbrace 0, 1 \rbrace$, $\mathbb{N}$에는 이산 토폴로지가 주어지고 $\lbrace 0, 1\rbrace$에는 자명한 토폴로지가 주어짐.

Remark. 4의 올바르지 못한 “증명”

$X$가 극점 콤팩트하다고 하자. 점렬 $(x_n)$이 주어졌을 때, $S = \lbrace x_n : n \in \mathbb{N}\rbrace$이 유한집합이라면 $(x_n)$은 수렴하는 부분점렬을 자명하게 가진다. $S$가 무한집합이라면 $X$의 극점 콤팩트성에 의해 $x \in S’$가 존재한다. 이제 다음 조건을 만족하는 $x$의 근방들의 가산 모임 $\mathcal{U} = \lbrace U_n \rbrace$을 정의한다.

  1. $n < m \implies U_n \supset U_m$
  2. $V$가 $x$의 근방일 때, $\exists U \in \mathcal{U} : U \subset V$

이로부터 다음 두 조건을 만족하는 함수 $k: \mathbb{N} → \mathbb{N}$을 정의할 수 있다.

  1. $x_{k(n)} \in U_n$
  2. $n < m \implies k(n) < k(m)$

2가 가능한 이유는 $k(i)$가 $i \leq n$까지 정의되었을 때 $T = S \setminus \lbrace x_i : i \leq k(n) \rbrace$가 여전히 $x$를 극점으로 가지기 때문이다. 즉, $(x_n)$은 수렴하는 부분점렬 $(x_{k(n)})$을 가진다.

위 증명이 올바르지 않은 이유는 볼드체 부분이 일반적으로 가능하지 않기 때문이다. 대신 다음이 성립한다.

정리. 1차 가산 T₁ 공간에서 극점 콤팩트성과 점렬 콤팩트성은 동치이다.

그물과 점렬

정의. $(J, \leq)$가 전순서라고 하자. 임의의 $x, y \in J$에 대해 $x, y \leq z$인 $z \in J$가 존재한다면 $(J, \leq)$를 방향 집합(directed set)이라고 한다.

정의. $K$가 $(J, \leq)$의 부분집합이라고 하자. 임의의 $x \in J$에 대해 $x \leq y$인 $y \in K$가 존재한다면 $K$를 공종(cofinal)이라고 한다.

Remark. $(J, \leq)$가 방향 집합이고 $K \subset J$가 공종이라면 $(K, \leq)$ 또한 방향 집합이다.

정의. $(J, \leq)$가 방향 집합이라고 하자. 위상공간 $X$에 대해 $J$에서 $X$로 가는 함수 $f: J → X$를 그물(net)이라고 한다. 특히, $\alpha \in J$에 대해 $f(\alpha)$를 $x_\alpha$와 같이 표기한다.

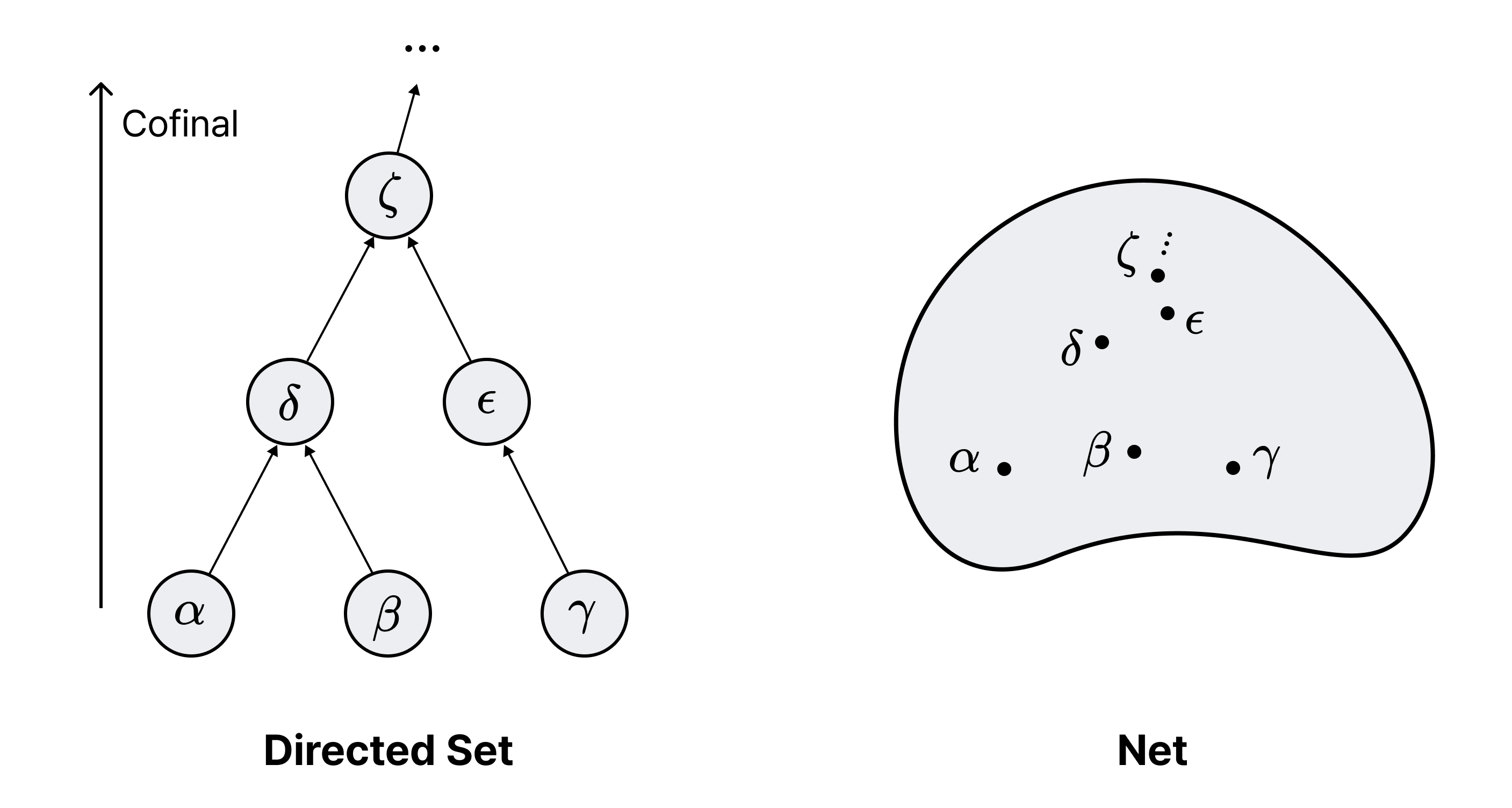
정의. 그물 $(x_\alpha)$가 $x$로 수렴한다는 것은, 임의의 $x$의 근방 $U$에 대해 어떤 $\alpha \in J$가 존재하여

\(\alpha \leq \beta \implies x_\beta \in U\) 인 것이다.

일반 위상 공간에서의 그물의 수렴은 1차 가산 공간에서 점렬의 수렴과 대응된다. 즉,

정리. $X$가 1차 가산 공간이라고 하자.

  1. $A \subset X$에 대해, $x \in \bar{A}$일 필요충분조건은 $x$로 수렴하는 점렬 $(x_n)$이 존재하는 것이다.
  2. $f: X → Y$에 대해, $f$가 연속일 필요충분조건은 임의의 점렬 $(x_n)$에 대해 $x_n → x$라면 $f(x_n) → f(x)$인 것이다.

정리. $X$가 위상 공간이라고 하자.

  1. $A \subset X$에 대해, $x \in \bar{A}$일 필요충분조건은 $x$로 수렴하는 그물 $(x_\alpha)$가 존재하는 것이다.
  2. $f: X → Y$에 대해, $f$가 연속일 필요충분조건은 임의의 그물 $(x_\alpha)$에 대해 $x_\alpha → x$라면 $f(x_\alpha) → f(x)$인 것이다.

증명.

  1. $\mathcal{U}_x$를 $x$의 근방들의 집합이라고 하자. 역포함관계로 $\mathcal{U}_x$에 순서 $\leq$를 준다. $x \in \bar{A}$라면 임의의 $U_\alpha \in \mathcal{U}_x$에 대해 $x_\alpha \in U_\alpha \cap A, x_\alpha \neq x$인 $x_\alpha$가 존재한다. $x_\alpha → x$임을 확인하라.

정의. $(x_\alpha)_{\alpha \in J}$가 그물이라고 하자. $(I, \preceq)$가 방향 집합이고, $g: (I, \preceq) → (J, \leq)$가 순서 보존이며, $\operatorname{im}g$가 공종일 때, $(x_{g(\beta)})_{\beta \in I}$를 $(x_\alpha)$의 부분그물이라고 한다.

정리. $X$가 콤팩트할 필요충분조건은 임의의 그물이 수렴하는 부분그물을 가지는 것이다.

Remark. ”수렴하는 점렬이 존재한다“는 ”수렴하는 그물이 존재한다“보다 강한 조건이지만, ”임의의 점렬이 수렴하는 부분점렬을 가진다”는 “임의의 그물이 수렴하는 부분그물을 가진다”보다 강하지도, 약하지도 않은 조건임에 유의하라. 주어는 후자가 더 강하고, 술어는 전자가 더 강하다. 따라서 콤팩트성과 점렬 콤팩트성은 일반적으로 시사 관계가 없다. 구체적으로,

정리.

  1. 콤팩트 $\not\rightarrow$ 점렬 콤팩트
  2. 점렬 콤팩트 $\not\rightarrow$ 콤팩트

증명.

  1. $[0, 1]^{[0, 1]}$은 티호노프 정리에 의해 콤팩트하지만 점렬 콤팩트하지 않다.
  2. Long line과 $\omega_1$은 점렬 콤팩트하지만 콤팩트하지 않다.