Compactness and Nets

01 Dec 2024

Compactness

Definition. Let $X$ be a topological space.

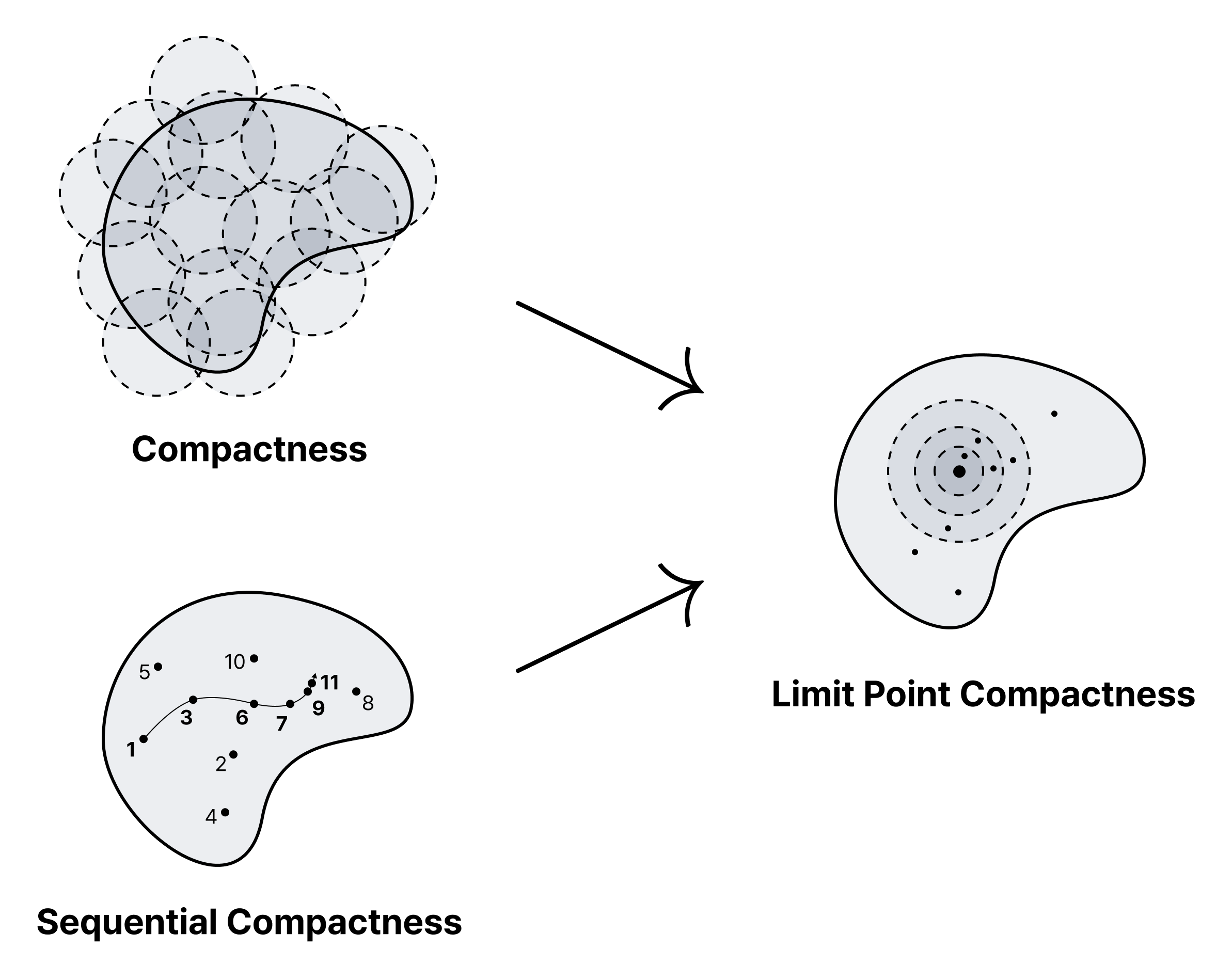
1. $X$ is said to be compact if every open cover has a finite subcover.
2. $X$ is said to be sequentially compact if every sequence $\lbrace x_n \in X \rbrace$ has a convergent subsequence.
3. $X$ is said to be limit point compact if every infinite set $S \subset X$ has a limit point.

Theorem.

1. Compact $\rightarrow$ Limit point compact
2. Sequentially compact $\rightarrow$ Limit point compact
3. Limit point compact $\not\rightarrow$ Compact
4. Limit point compact $\not\rightarrow$ Sequentially compact

Proof.

1. Let $S \subset X$ be an infinite set with no limit points. Since $\overline{S} = S \cup S’ = S$, $S$ is a closed set and $X \setminus S$ is an open set. For any $s \in S$, since $s$ is not a limit point, there exists a neighbourhood $U_s$ of $s$ such that $U_s \cap S = \lbrace s \rbrace$. Therefore, the following open cover of $X$ has no finite subcover:

\[\mathcal{C} = \lbrace X \setminus S \rbrace \cup \bigcup_{s \in S} \lbrace U_s \rbrace\]

1. Let $S \subset X$ be an infinite set. Arbitrarily extract elements of $S$ to form a sequence $\lbrace s_n \rbrace \;(n \neq m \implies s_n \neq s_m)$. Since $X$ is sequentially compact, $\lbrace s_n \rbrace → s$, and $s$ is a limit point of $S$.
2. $\omega_1$ with the order topology is limit point compact but not compact.
3. $X = \mathbb{N} \times \lbrace 0, 1 \rbrace$, where $\mathbb{N}$ is given the discrete topology and $\lbrace 0, 1\rbrace$ is given the trivial topology.

Remark. An incorrect “proof” of 4

Suppose $X$ is limit point compact. Given a sequence $(x_n)$, if $S = \lbrace x_n : n \in \mathbb{N}\rbrace$ is a finite set, then $(x_n)$ trivially has a convergent subsequence. If $S$ is an infinite set, then by the limit point compactness of $X$, there exists $x \in S’$. Now we define a countable collection of neighbourhoods of $x$, $\mathcal{U} = \lbrace U_n \rbrace$, satisfying the following conditions:

1. $n < m \implies U_n \supset U_m$
2. For any neighbourhood $V$ of $x$, $\exists U \in \mathcal{U} : U \subset V$

From this, we can define a function $k: \mathbb{N} → \mathbb{N}$ satisfying the following conditions:

1. $x_{k(n)} \in U_n$
2. $n < m \implies k(n) < k(m)$
3. $n \neq m \implies x_{k(n)} \neq x_{k(m)}$

Condition 2 is possible because when $k(i)$ is defined for $i \leq n$, $T = S \setminus \lbrace x_i : i \leq k(n) \rbrace$ still has $x$ as a limit point. Thus, $(x_n)$ has a convergent subsequence $(x_{k(n)})$.

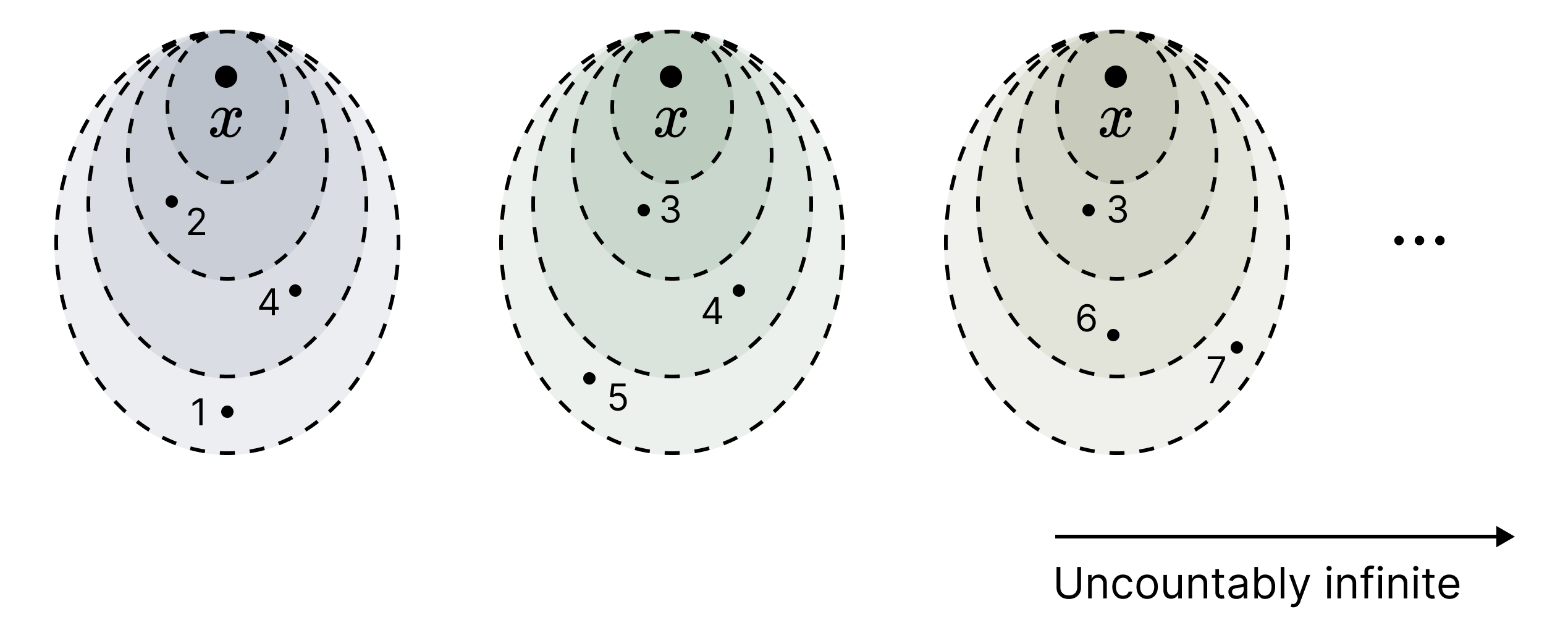
The above proof is incorrect because the bold portion is not generally possible. Consider, for instance, a topological space where $x \in S’$ has uncountably many neighbourhoods which form uncountably infinite distinct classes of containment chain. Hence, in the diagram below, the same-coloured sets contain one or the other properly, but distinct-coloured sets do not, although they need not be strictly disjoint either. Such a space may be limit point compact yet not be sequentially compact, for there is no guaranteed way to enumerate the points of $S$ into a series such that whichever open set one chooses, for a large enough index, all points after that index is included in that open set. (Exercise: Convince yourself that this is not the case if the open sets can be arranged to form only finite distinct classes of chain, or countably infinite distinct classes of chain.)

Instead, the following holds:

Theorem. In first countable $T_1$ spaces, limit point compactness and sequential compactness are equivalent.

Note that $T_1$-ness is also required, for without it Condition 3 cannot be guaranteed.

Nets and Sequences

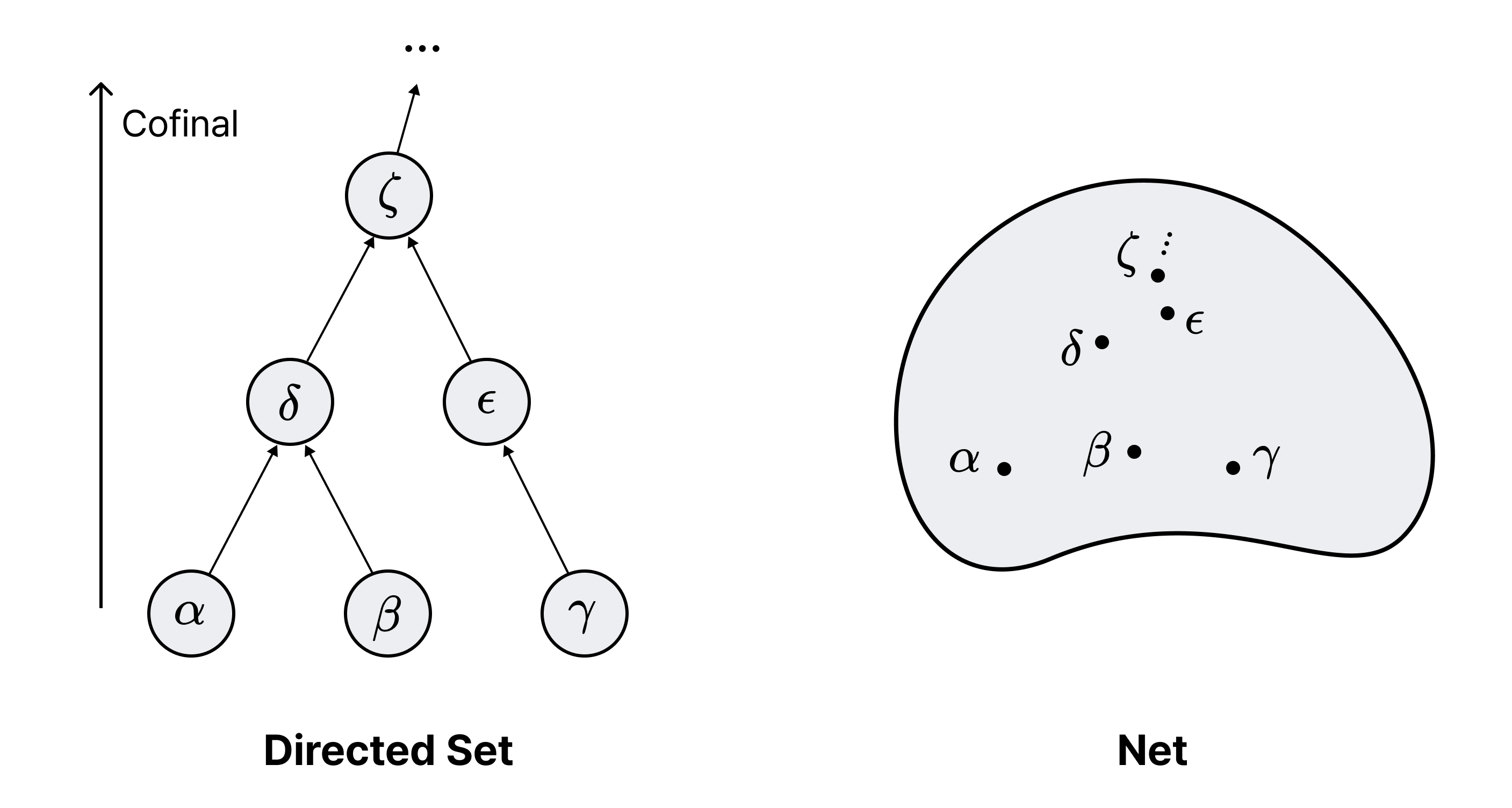
Definition. Let $(J, \leq)$ be a preorder. If for any $x, y \in J$, there exists $z \in J$ such that $x, y \leq z$, then $(J, \leq)$ is called a directed set.

Definition. Let $K$ be a subset of $(J, \leq)$. If for any $x \in J$, there exists $y \in K$ such that $x \leq y$, then $K$ is said to be cofinal.

Remark 1. If $(J, \leq)$ is a directed set and $K \subset J$ is cofinal, then $(K, \leq)$ is also a directed set.

Remark 2. As will be shown, cofinality is related with the generalisation of convergence.

Definition. Let $(J, \leq)$ be a directed set. For a topological space $X$, a function $f: J → X$ is called a net. In particular, for $\alpha \in J$, we denote $f(\alpha)$ as $x_\alpha$.

Definition. A net $(x_\alpha)$ converges to $x$ if, for any neighbourhood $U$ of $x$, there exists some $\alpha \in J$ such that

\[\alpha \leq \beta \implies x_\beta \in U\]

The convergence of nets in general topological spaces corresponds to the convergence of sequences in first countable spaces. That is,

Theorem. Let $X$ be a first countable space.

1. For $A \subset X$, $x \in \bar{A}$ if and only if there exists a sequence $(x_n)$ converging to $x$.
2. For $f: X → Y$, $f$ is continuous if and only if for any sequence $(x_n)$, if $x_n → x$ then $f(x_n) → f(x)$.

Theorem. Let $X$ be a topological space.

1. For $A \subset X$, $x \in \bar{A}$ if and only if there exists a net $(x_\alpha)$ converging to $x$.
2. For $f: X → Y$, $f$ is continuous if and only if for any net $(x_\alpha)$, if $x_\alpha → x$ then $f(x_\alpha) → f(x)$.

Proof.

1. Let $\mathcal{U}_x$ be the set of neighbourhoods of $x$. Give $\mathcal{U}_x$ the order $\leq$ by reverse inclusion. If $x \in \bar{A}$, then for any $U_\alpha \in \mathcal{U}_x$, there exists $x_\alpha \in U_\alpha \cap A, x_\alpha \neq x$. Verify that $x_\alpha → x$.

Definition. Let $(x_\alpha)_{\alpha \in J}$ be a net. If $(I, \preceq)$ is a directed set, $g: (I, \preceq) → (J, \leq)$ is order-preserving, and $\operatorname{im}g$ is cofinal, then $(x_{g(\beta)})_{\beta \in I}$ is called a subnet of $(x_\alpha)$.

Theorem. $X$ is compact if and only if every net has a convergent subnet.

Remark. Note that “there exists a convergent sequence” is a stronger condition than “there exists a convergent net”, but “every sequence has a convergent subsequence” is neither stronger nor weaker than “every net has a convergent subnet”. The subject (for every sequence v. for every net) is stronger in the latter case, whilst the predicate (there exists a subsequence v. there exists a subnet) is stronger in the former case. Therefore, compactness and sequential compactness have no implication relation in general. Specifically,

Theorem.

1. Compact $\not\rightarrow$ Sequentially compact
2. Sequentially compact $\not\rightarrow$ Compact

Proof.

1. $[0, 1]^{[0, 1]}$ is compact by Tychonoff’s theorem but not sequentially compact.
2. The long line and $\omega_1$ are sequentially compact but not compact.