디멘의 블로그
Dimen's Blog
이데아를 여행하는 히치하이커
Alice in Logicland


논리학, 철학, 수학 등을 다루는 블로그입니다.
아래에서 저의 가장 최근 글들을 읽을 수 있습니다.
To read in English, toggle the button in the header.


A blog on logic, philosophy, mathematics, et cetra.
You can read my most recent posts below.
교환법칙, 분배법칙, 지수법칙의 범주론적 증명
27 Dec 2025정리.
- 분배법칙: $(A + B) \times C = A \times C + B \times C$
- 지수법칙: $(A \times B)^C = A^C \times B^C$
이전 글에서 범주론적 합과 곱을 살펴 보았다. 합은 쌍극한의 일종이고, 곱은 극한의 일종이다. 이 관찰로부터, 분배법칙과 지수법칙을 다음 정리로 일반화할 수 있다.
정리. 좌 어드조인트는 쌍극한colimit을, 우 어드조인트는 극한limit을 보존한다.
이 정리의 정확한 의미는 다음과 같다. $F: \mathcal{A} \to \mathcal{B}, G: \mathcal{B} \to \mathcal{A}$에 대해 $F \dashv G$라고 하자. $G$가 극한을 보존preserves limits한다는 것은, 임의의 작은 범주small category $\mathbf{I}$와 함자 $D : \mathbf{I} \to \mathcal{B}$에 대해 다음이 성립한다는 것이다.
$\big(B \xrightarrow{q_I} D(I)\big)_{I \in \mathbf{I}}$가 $\mathcal{B}$에서 극한 고깔limit cone일 때, $\big(G(B) \xrightarrow{G(q_I)} GD(I)\big)_{I \in \mathbf{I}}$가 $\mathcal{A}$에서 극한 고깔이다.
이로부터, $G$가 극한을 보존할 때 다음이 성립함을 알 수 있다.
\[G\left(\lim_{\leftarrow \mathbf{I}} D\right) \cong \lim_{\leftarrow \mathbf{I}} G \circ D\]쌍극한의 경우에는 고깔을 쌍고깔로 바꿔 정의한다.
한편, 임의의 $X, Y, Z \in \mathbf{Set}$에 대해 $\hom(X \times Y, Z) \cong \hom(X, Z^Y)$가 성립한다 (이는 함수형 프로그래밍에서 자주 등장하는 커링Currying 기법이다). 이로부터 다음의 어드조인트 관계가 따라 나온다.
\[(-) \times Y \dashv (-)^Y\]따라서 함자 $(-) \times Y$는 쌍극한을 보존하고, $(-)^Y$는 극한을 보존한다. 이로부터 일반화된 분배법칙과 지수법칙을 얻을 수 있다.
정리. 집합 $A, B, Y$에 대해, $A, B$가 서로소라면 다음이 성립한다.
- $(A + B) \times Y \cong (A \times Y) + (B \times Y)$
- $(A \times B)^Y \cong A^Y \times B^Y$
여기서 $+$는 서로소 집합의 합집합으로, $\sqcup$과 의미가 같으나 분배법칙과의 유사성을 강조하기 위해 사용되었다. 좌변이 $G\left(\lim_{\leftarrow \mathbf{I}} D\right)$에, 우변이 $\lim_{\leftarrow \mathbf{I}} G \circ D$에 대응된다. 위 정리에 집합의 크기 연산을 취하면 자연수에서의 분배법칙과 지수법칙을 얻는다.
참고로 극한에 대한 다음 성질 또한 알려져 있다 ($\bullet, -$ 표기법은 이 글을 참고)
정리. $\mathbf{I}, \mathbf{J}$가 작은 범주이고, $\mathcal{S}$가 $\mathbf{I}, \mathbf{J}$ 모양의 극한들을 가지는 국소적으로 작은 범주라고 하자. $D: \mathbf{I} \times \mathbf{J} \to \mathcal{S}$에 대해, 다음이 성립한다.
\[\lim_{\leftarrow \mathbf{J}}\lim_{\leftarrow \mathbf{I}} D(\bullet, -) \cong \lim_{\leftarrow \mathbf{I} \times \mathbf{J}} D \cong \lim_{\leftarrow \mathbf{I}}\lim_{\leftarrow \mathbf{J}} D(-, \bullet)\]
즉, 극한끼리는 교환법칙을 만족한다. 이것은 덧셈의 교환법칙과 곱셈의 교환법칙을 일반화한 것으로 생각할 수 있다.
서슬린의 문제와 다이아몬드 원리
26 Dec 2025이전 글에서 다음 정리를 소개했다.
집합론적 실수의 정의. 다음을 만족하는 순서 집합 $(R, <)$은 순서 동형에 대해 유일하다.
- 완비 전순서 집합이다.
- 양끝점이 없다.
- 분리 가능separable하다. 즉, 어떤 가산인 $Q \subset R$이 존재하여 $Q$가 $R$에서 조밀dense하다.
3번 성질로부터 다음이 따라 나온다.
정리. $\mathcal{C}$가 $\mathbb{R}$의 개구간들의 모임이라고 하자. $\mathcal{C}$의 원소들이 쌍으로 서로소pairwise disjoint라면 $\mathcal{C}$는 가산이다.
증명. $\mathcal{C}$의 원소들이 쌍으로 서로소이므로, 각 $(x, y) \in \mathcal{C}$를 $q \in (x, y) \cap \mathbb{Q}$에 대응시키는 단사 사상 $\mathcal{C} \to \mathbb{Q}$가 존재한다. 따라서 $\mathcal{C}$는 가산이다. ■
쌍으로 서로소인 개구간들의 모임이 기껏 가산인 순서 집합은 가산 체인 성질countable chain condition을 가진다고 한다. 이 특이한 이름의 이유는 뒤에서 설명할 것이다.
서슬린의 문제Suslin’s problem는 집합론적 실수의 정의에서 분리 가능성을 가산 체인 성질로 약화시킬 수 있는지를 묻는다.
정의. 양끝점이 없고 가산 체인 성질을 가지는 완비 전순서 집합 중 실수와 순서 동형이 아닌 순서 집합을 서슬린 선Suslin line이라고 한다.
따라서 서슬린 선은 분리 가능하지 않아야 한다.
서슬린의 문제. 서슬린 선이 존재하는가?
1920년에 제기된 이 문제는, 1971년 솔로베이Solovay와 테넨바움Tennenbaum에 의해 ZFC와 독립적임이 증명되었다. 이 글에서는 독립성 증명을 살펴보는 대신, 서슬린 선의 조합론적 버전인 서슬린 트리에 대해서 알아보고자 한다. 우선 다음의 유명한 정리를 보자.
쾨니히 보조정리König’s lemma. 트리 $T$에 대해, $T$의 높이가 $\omega$이고, $T$의 각 노드가 유한한 수의 자식을 가진다면, $T$는 길이가 $\omega$인 가지를 가진다.
증명. $\alpha_0$를 루트 노드라고 하고, 다음과 같이 귀납적으로 노드열을 정의한다. $\alpha_n$이 주어졌을 때, $\alpha_n$의 자식 노드의 수는 유한하므로, 어떤 자식 노드에 대해 해당 노드를 루트로 하는 트리는 높이가 무한하다. 그러한 자식 노드 중 하나를 선택하여 (여기서 선택 공리가 필요하다) $\alpha_{n + 1}$로 정의한다. $\lbrace a_n \rbrace $은 길이가 무한한 가지이다. ■
$T$의 노드가 가산 수의 자식을 가질 수 있다면 다음과 같이 $T$의 모든 가지가 유한 길이임에도 $T$의 높이는 $\omega$일 수 있다.

자연스러운 질문은, 쾨니히 보조정리를 비가산 기수에 대해 확장할 수 있는지이다. 그러나 이 질문에 대한 답은 부정적이다.
아론샤인 정리Aronszajn theorem. 높이가 $\omega_1$이고, 각 노드가 가산 수의 자식을 가지지만, 길이가 $\omega_1$인 가지가 없는 트리가 존재한다. (그러한 트리를 높이 $\omega_1$의 아론샤인 트리라고 한다.)
따라서 쾨니히 보조정리를 비가산 기수로 확장하기 위해서는 “각 노드가 가산 수의 자식을 가진다”보다 더 강력한 조건이 필요하다. 이를 위해 다음의 정의를 도입한다.
정의. 트리 $T$의 부분집합 $S$에 대해, $S$의 원소들이 서로 비교 불가능mutually incomparable할 때, $S$를 반체인antichain이라고 한다. $T$의 모든 반체인이 가산일 때, $T$가 가산 체인 성질을 가진다고 한다.
예를 들어 다음 트리의 색칠된 노드들은 반체인을 이룬다.
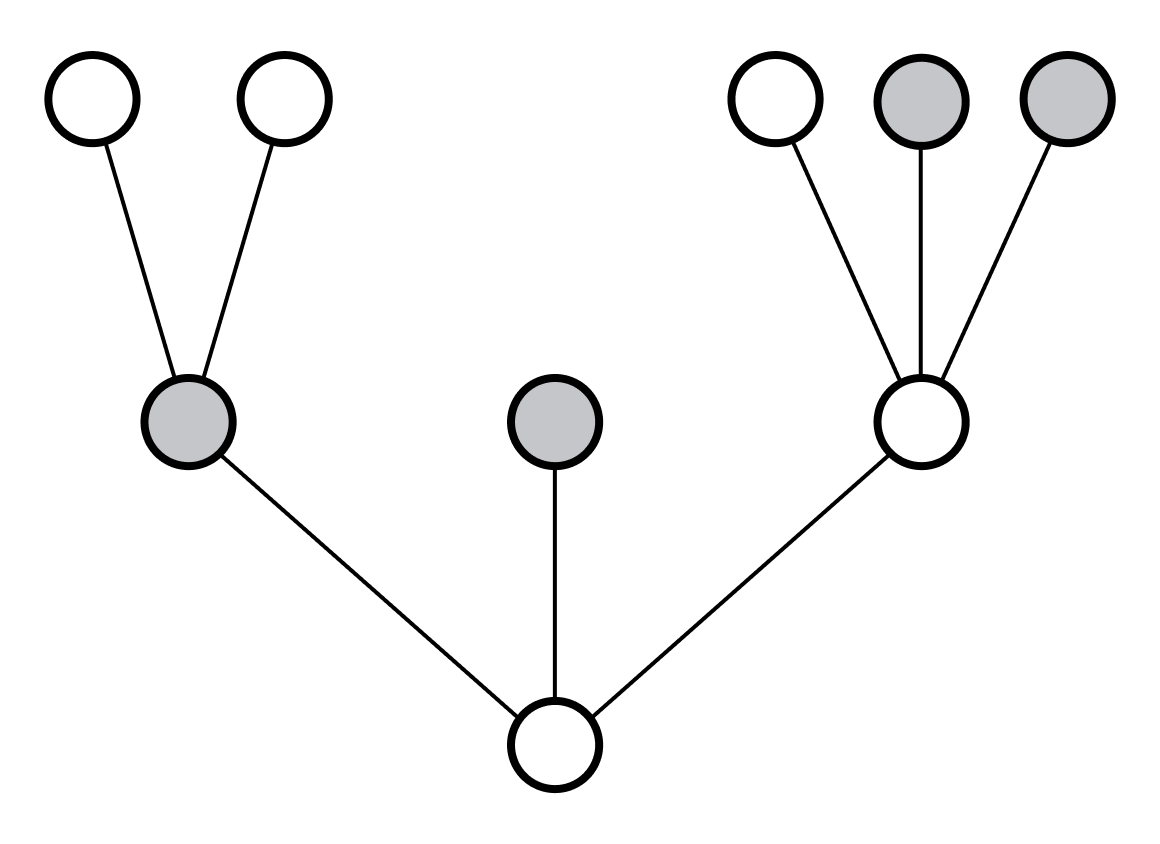
“각 노드가 가산 수의 자식을 가진다”가 국소적 성질이라면, 가산 체인 성질은 트리 전체에 관한 전역적 성질이다. 즉, 가산 체인 성질은 직관적으로 트리의 “너비”가 $\omega_1$보다 작다는 의미이다. 참고로 가산 반체인 성질이 아니라 가산 체인 성질이라고 부르는 것은 역사적 이유이기 때문에 크게 신경 쓸 필요는 없다.
앞서 쌍으로 서로소인 실수의 개구간들의 모임이 기껏 가산인 성질 또한 가산 체인 성질이라고 부른다고 했는데, 두 용법은 밀접한 관련이 있다. 반체인의 일반적인 정의는 다음과 같다.
정의. $(P, \leq)$가 부분순서라고 하자. $x, y \in P$가 비교 불가능하다는 것은, $z \leq x, z \leq y$인 $z \in P$가 존재하지 않는다는 것이다. $S \subseteq P$의 원소들이 서로 비교 불가능할 때 $S$를 반체인이라고 한다. $P$의 모든 반체인이 가산일 때, $P$가 가산 체인 성질을 가진다고 한다.
트리 $T$에서, 노드 $x$가 노드 $y$의 후손일 때 $x \leq y$라고 하자. 이때 트리의 노드로서 $x, y$가 비교 불가능한 것은 $(T, \leq)$의 원소로서 $x, y$가 비교 불가능한 것과 동치이다.
정의. 가산 체인 성질을 가지는 아론샤인 트리를 서슬린 트리라고 한다.
서슬린 트리의 존재성은 서슬린 선의 존재성과 동치이기 때문에 ZFC와 독립적이다. 동치가 되는 개략적인 이유는 각 성질이 다음 표와 같이 대응하기 때문이다.
| 서슬린 선 | 서슬린 트리 |
|---|---|
| 분리 불가능성 | 트리의 높이가 $\omega_1$ |
| 개구간의 가산 체인 성질 | 트리의 가산 체인 성질 |
분리 불가능성이 높이 $\omega_1$ 성질에 대응되는 개략적인 이유는, 어떤 집합 $D$가 존재하여 $|D| \leq \aleph_0$이고 임의의 개구간 $(a, b)$가 $D$와 교차한다는 사실이 (분리 가능성), 어떤 서수 $\alpha$가 존재하여 $\alpha < \omega_1$이고 임의의 노드 $x \in T$에 대해 $x$가 $T^{(\alpha)}$의 노드들로 이루어진 노드열의 극한이라는 사실과 (트리의 높이가 가산) 대응되기 때문이다.
서슬린 트리와 관련하여, 집합론의 다음 비표준 공리를 살펴보자.
다이아몬드 원리. 어떤 집합열 $\langle W_\alpha : \alpha < \omega_1 \rangle$가 존재하여 $W_\alpha \subseteq \mathcal{P}(\alpha)$이고, 각 $W_\alpha$가 가산집합이며, 임의의 $X \subseteq \omega_1$에 대해 $\lbrace \alpha : \alpha < \omega_1, X \cap \alpha \in W_\alpha \rbrace $가 정상 집합stationary set이다.
다이아몬드 원리는 $\Diamond$로 자주 표기한다. 또한 다이아몬드 원리의 $\langle W_\alpha \rangle$을 다이아몬드 열이라고 부른다.
$X \cap \alpha$는 $\alpha$라는 “거울”을 통해 “비춰” 보인 $X$의 모습으로 생각될 수 있다. 이 경우, 다이아몬드 원리는 $\omega_1$보다 작은 서수들에서 $X$의 반사된 모습이 $\langle W_\alpha \rangle$에서 충분히 자주 나타난다는 의미로 이해될 수 있다 (이 글에서 정상 집합이 “측도 > 0”의 집합론적 버전임을 설명했다).
따라서 다이아몬드 원리는 반사 원리reflection principle의 일종이며, $V = L$ 공리와 비슷하게 집합론적 우주를 규제하는 역할을 한다 (실제로 $V = L$은 $\Diamond$를 함의한다). 그리고 집합론적 우주를 규제하는 공리들이 그렇듯이, 다이아몬드 원리는 연속체 가설을 함의한다.
정리. $\Diamond \implies \mathsf{CH}$
증명. $X \subseteq \omega \subset \omega_1$이라고 하자. $X$가 $< \omega_1$에서 정상적으로 반사되므로, 어떤 $\alpha > \omega$에 대해 $X \cap \alpha = X \in W_\alpha$이다. 따라서 $\omega$의 부분집합들은 모두 $\bigcup_{\alpha < \omega_1} W_\alpha$에 속하는데, 후자의 기수가 $\aleph_1$이므로 $2^{\aleph_0} = \aleph_1$이다. ■
정리. $\Diamond$라면 서슬린 선이 존재한다.
증명. Hrbacek & Jech (3rd ed), Chapter 12, Section 5를 참고하라. 참고로 원문에는 다음의 오타가 있으니 주의하라.
(원문) Lemma 5.3. $\Diamond$ implies that there exists a sequence $\langle Z_\alpha : \alpha < \omega_1 \rangle$ such that, for each $\alpha < \omega_1$, $Z_\alpha \subseteq \omega^{<\alpha}$, $Z_\alpha$ is at most countable, and for any $X \subseteq \omega^{<\omega_1}$ the set $\lbrace \alpha < \omega_1 : X \cap \omega^{<\alpha} \rbrace $ is stationary.
Proof. We note that […] Clearly, $Z_\alpha \subseteq \omega^{<\alpha}$ and is at most countable.
(수정) Lemma 5.3. $\Diamond$ implies that there exists a sequence $\langle Z_\alpha : \alpha < \omega_1 \rangle$ such that, for each $\alpha < \omega_1$, $Z_\alpha \subseteq \mathcal{P}(\omega^{<\alpha})$, $Z_\alpha$ is at most countable, and for any $X \subseteq \omega^{<\omega_1}$ the set $\lbrace \alpha < \omega_1 : X \cap \omega^{<\alpha} \rbrace $ is stationary.
Proof. We note that […] Clearly, $Z_\alpha \subseteq \mathcal{P}(\omega^{<\alpha})$ and is at most countable.
또한 Claim 5.5 직전에 나오는 문장 “Let $\lbrace C_n : n \in \mathbb{N} \rbrace $ be the at most countable collection of those elements of $Z_\alpha$ which happen to be maximal antichains in $T^{(\alpha)}$.”의 의미는, 각 $n$에 대해 $C_n \in Z_\alpha$이고, $C_n \subseteq \omega^\alpha$이며, $C_n$의 원소들을 $T^{(\alpha)}$의 노드로 간주했을 때 $C_n$이 반체인이라는 것이다. ■
따름정리. $V = L$이라면 서슬린 선이 존재한다.
따라서 서슬린 선의 존재성은 집합론적 우주의 규제와 관련이 있다. 이 사실이 모순적으로 느껴질 수 있지만, 서슬린 선의 조건 중 하나가 가산 조밀 집합의 “비”존재라는 사실을 고려하면 그렇게 이상한 것은 아니다. 서슬린 선은 가산 체인 성질까지만 얻고 가산 조밀 집합은 발생시키지 않는 것이 가능한 “허술한” 집합론적 우주의 특징인 것이다.
오일러-푸앵카레 정리
23 Nov 2025독자 분은 어렸을 때 다음의 정리를 배웠을 것이다.
오일러 공식. 볼록다면체의 꼭짓점, 모서리, 면의 개수를 $v, e, f$라고 할 때, $v - e + f= 2$이다.
예를 들어 정육면체의 경우 $v = 8, e = 12, f = 6$이므로 $v - e + f = 2$가 성립한다. 볼록다면체라는 조건은 중요한데, 만약 다면체에 “구멍”이 있으면 공식이 성립하지 않기 때문이다. 예를 들어 아래의 구멍 난 프리즘의 경우 $v = 16, e = 32, f = 16$이므로 $v - e + f = 0$이다.

이로부터 우리는 $v - e + f$의 값이 도형의 위상에 의해 결정된다고 추측할 수 있다. 이것이 오일러-푸앵카레 정리의 내용이다. 정리를 진술하기 앞서, 먼저 다음의 개념을 정의하자.
정의. 위상공간 $X$에 대해, $X$의 호몰로지 군 $H_p(X)$의 자유 부분free part의 랭크를 $X$의 $p$번째 베티 수Betti number라고 하며 $R_p(X)$라고 적는다.
원래 $b_p(X)$라고 적는 것이 관행인데, 이 글에서는 $b_p$를 다른 의미로 사용할 것이기 때문에 다른 표기법을 채택했다. 호몰로지 군은 위상 불변이므로 베티 수 또한 위상 불변이다.
예를 들어 토러스의 호몰로지 군은 다음과 같다.
- $H_0(X) = \mathbb{Z}$
- $H_1(X) = \mathbb{Z} \oplus \mathbb{Z}$
- $H_2(X) = \mathbb{Z}$
따라서 토러스의 0차, 1차, 2차 베티 수는 각각 1, 2, 1이다. 베티 수는 직관적으로 구멍의 의미를 가진다 (이전 글 참조). 특히, 0차 베티 수는 $K$를 이루는 연결 요소들의 수이다. 즉, 두 개의 사면체를 하나의 단체 복합체로 간주한다면 이 복합체의 0차 베티 수는 2이다.
오일러-푸앵카레 정리. $n$-단체 복합체 $K$에 대해, $\alpha_p \; (p \leq n)$를 $K$의 $p$-단체들의 개수라고 하자. 다음이 성립한다.
\[\sum^n_{p = 0} (-1)^p\alpha_p = \sum^n_{p=0}(-1)^p R_p(K)\]
위 정리의 증명에서는 $p$-체인들을 자유군의 원소로 보는 것보다 선형 공간의 원소로 보는 것이 더 자연스럽기 때문에 이 접근을 취한다.
증명. $K$의 $p$-체인, 고리, 경계가 각각 유리수체에 대해 이루는 선형 공간을 $C_p, Z_p, B_p$라고 하자. $\lbrace d^i_p \rbrace $가 고리를 선형 생성하지 않는 $C_p$의 극대 부분집합이라고 하고, $\lbrace d^i_p \rbrace $가 생성하는 선형공간을 $D_p$라고 하자. 다음이 성립한다 ($\oplus$는 벡터 공간의 직합).
\[\begin{gather} C_p = D_p \oplus Z_p\\\\ \alpha_p = \dim C_p = \dim D_p + \dim Z_p \end{gather}\]$p \leq n - 1$에 대해, $b^i_p = \partial d^i_{p + 1}$라고 하자. $\lbrace b^i_p \rbrace $가 생성하는 선형 공간을 $B_p$라고 하자. $\partial$은 선형 연산자이므로, $\lbrace d^i_{p +1} \rbrace $가 $D_{p + 1}$의 선형 기저라는 사실로부터 $\lbrace b^i_p \rbrace $가 $B_p$의 선형 기저라는 사실이 따라 나온다. 다음의 보조정리를 증명한다.
보조정리. $B_p$는 $K$의 모든 $p$-경계들을 포함한다.
증명. 만약 $b_p$가 $K$의 $p$-경계라면, 어떤 $c_{p + 1} \in C_{p + 1}$에 대해 $\partial c_{p + 1} = b_p$이다. $C_{p + 1} = D_{p + 1} \oplus Z_{p + 1}$ 관계에 의해 어떤 유일한 $d_{p + 1} \in D_{p + 1}, z_{p + 1} \in Z_{p + 1}$이 존재하여 $c_{p + 1 } = d_{p + 1} + z_{p + 1}$이다. 그런데 $\partial z_{p + 1} = 0$이므로 $\partial d_{p + 1} = b_p$이다. 따라서 $b_p \in B_p$이다. □
$\lbrace z^i_p \rbrace $가 $B_p$의 원소를 선형 생성하지 않는 $Z_p$의 극대 부분집합이라고 하고, $\lbrace z^i_p \rbrace $가 생성하는 선형공간을 $G_p$라고 하자. 보조정리에 의해 다음이 성립한다.
\[\dim G_p = R_p\]따라서 다음이 성립한다.
\[\begin{gather} Z_p = B_p \oplus G_p\\\\ \dim Z_p = \dim B_p + \dim G_p = \dim D_{p + 1} + R_p \end{gather}\]앞선 결과와 연립하면 다음을 얻는다 ($p \leq n - 1$).
\[\alpha_p = \dim D_{p + 1} + \dim D_p + R_p\]$p = n$일 때 $\alpha_n = \dim D_n + R_n$이고, $p = 0$일 때 $\alpha_0 = \dim D_1 + R_0$이다. 따라서 다음을 얻는다 (wlog, $n$은 짝수).
\[\begin{alignat}{3} &\alpha_n &&= \;\cancel{\dim D_n} + R_p \\ &-\alpha_{n-1} &&= \;\cancel{-\dim D_{n}} \cancel{- \dim D_{n - 1}} - R_{n - 1} \\ &\alpha_{n-2} &&= \;\cancel{\dim D_{n - 1}} \cancel{ + \dim D_{n - 2}} + R_{n - 2} \\ &&\vdots \\ &-\alpha_{1} &&= \;\cancel{-\dim D_{2}} \cancel{-\dim D_{1}} - R_{1} \\ &\alpha_{0} &&= \;\cancel{\dim D_{1}} + R_{0} \\ \hline &\sum_{p = 0}^n (-1)^p \alpha_p &&= \;\sum_{p=0}^n (-1)^p R_p(K) \quad \blacksquare \end{alignat}\]정의. 위상공간 X에 대해, 다음 값을 오일러 종수Euler characteristic라고 한다.
\[\xi(X) = \sum (-1)^p R_p(X)\]
베티 수가 위상 불변이므로 오일러 종수 또한 위상 불변이다.
따름정리. 다면체 $P$의 꼭짓점, 모서리, 면의 개수를 $v, e, f$라고 하자. 2차원 위상공간으로서의 $P$의 표면을 $X$라고 하자. 다음이 성립한다.
\[v - e + f = \xi(X)\]
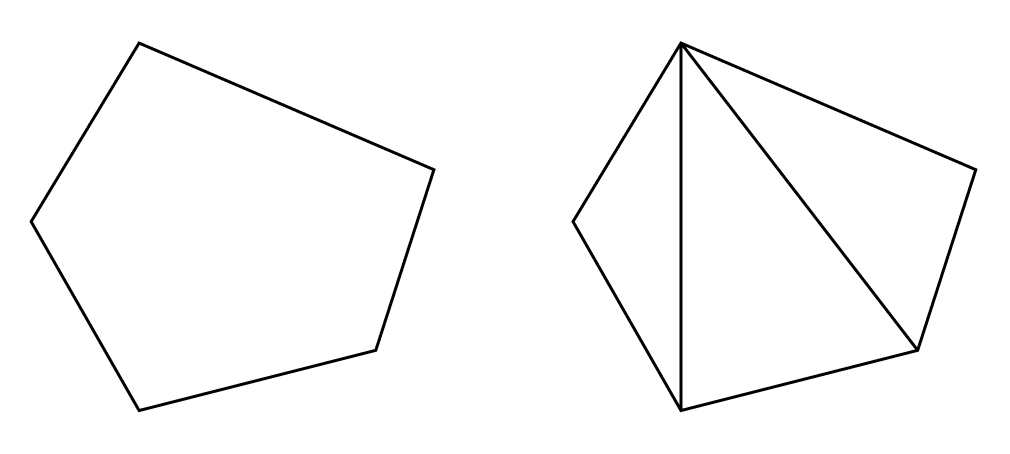
증명. $k$각형의 삼각화는 $k - 3$개의 모서리를 추가함으로써 얻을 수 있는데, 이 과정에서 $k - 3$개의 면이 생긴다. 따라서 $P$는 $P$의 삼각화와 $v - e + f$ 값이 같으며, 이는 오일러 종수와 같다. ■
앞서 우리는 구멍이 하나 있는 다면체의 경우 $v - e + f = 0$임을 보았다. 실제로 토러스의 0차, 1차, 2차 베티 수는 1, 2, 1이며, $1 - 2 + 1 = 0$이다. 한편 구의 호몰로지 군은 다음과 같다.
- $H_0(K) = \mathbb{Z}$
- $H_1(K) = 0$
- $H_2(K) = \mathbb{Z}$
따라서 구의 0차, 1차, 2차 베티 수는 1, 0, 1이며, $1 - 0 + 1 = 2$이다. 따라서 볼록다면체의 경우 $v - e + f = 2$이다.
클럽 집합과 정상 집합
11 Nov 2025클럽 집합
정의. $C \subseteq \omega_1$이 클럽 집합club set이라는 것은 $C$가 닫히고 무계closed and unbounded라는 것이다. 즉,
- 임의의 서수열 $(\alpha_n)_{n \in \omega} \subseteq C$에 대해 $\alpha_n \to \alpha$라면 $\alpha \in C$이다.
- 임의의 $\gamma < \kappa$에 대해 $\alpha > \gamma$인 $\alpha \in C$가 존재한다.
그야말로 정직한 네이밍이 아닐 수 없다.
정리. $C_1, C_2 \subseteq \omega_1$이 두 클럽 집합일 때, $C = C_1 \cap C_2$ 또한 클럽 집합이다.
증명. $C$가 닫힘이라는 것은 쉽게 보여진다. $C$가 무계임을 보이기 위해 임의의 $\gamma \in \omega_1$를 잡자. $C_1$이 무계이므로 $\gamma < \alpha_0$을 만족하는 가장 작은 $\alpha_0 \in C_1$가 있다. $C_2$가 무계이므로 $\alpha_0 < \beta_0$인 가장 작은 $\beta_0 \in C_2$가 있다. 다시 $C_1$이 무계이므로 $\beta_0 < \alpha_1$인 $\alpha_1 \in C_1$가 있다. 이 과정을 계속 반복하여 서수열 $\lbrace \alpha_n \rbrace $과 $\lbrace \beta_n \rbrace $을 얻는다. 두 서수열은 같은 서수 $\delta$로 수렴하므로 $\delta \in C$이며, $\delta > \gamma$이다. (p.s. “가장 작은”은 불필요한 선택 공리의 사용을 피하기 위해 사용되었다) ■
위 증명을 살짝 변형하면 다음 정리를 얻을 수 있다.
정리. $\lbrace C_n \rbrace _{n < \omega}$가 클럽 집합들의 가산 모임일 때, $C = \bigcap C_n$ 또한 클럽 집합이다.
증명. 연습문제 (힌트: 삼각형을 사용한다) ■
따라서 가산 개의 클럽 집합들이 주어지면 교집합을 취함으로써 새로운 클럽 집합을 얻을 수 있다. 한편, 비가산 개의 클럽 집합들이 주어지면 다음을 사용할 수 있다.
정리. $\lbrace C_\xi \rbrace _{\xi < \omega_1}$이 클럽 집합들의 모임일 때, $\lbrace C_\xi \rbrace $의 대각 교집합diagonal intersection을 다음과 같이 정의한다.
\[\Delta_{\xi < \omega_1} C_\xi = \{ \alpha \in \omega_1 : \forall \xi < \alpha \;\; \alpha \in C_\xi \}\]$D$는 클럽 집합이다.
증명. $D$가 닫혀 있음을 먼저 보이자. 서수열 $(\alpha_n)_{n \in \omega} \subseteq D$에 대해 $\alpha_n \to \alpha$라고 하자. 임의의 $\xi < \alpha$에 대해 $\xi < \alpha_n$인 $n \in \omega$가 존재하며, 대각 교집합의 정의에 의해 $C_\xi$은 $\lbrace \alpha_m : m \geq n \rbrace $을 포함한다. 따라서 $\sup \lbrace \alpha_m : m \geq n \rbrace = \alpha \in C_\xi$이므로 $\alpha \in D$이다.
이제 $D$가 무계임을 보이자. 임의의 $\gamma < \omega_1$에 대해, $D_0 = \bigcap_{\xi < \gamma} C_\xi$는 클럽 집합이므로 무계이다. 따라서 $\alpha_0 > \gamma$를 만족하는 가장 작은 $\alpha_0 \in D_0$가 존재한다. 마찬가지로 $D_1 = \bigcap_{\xi < \alpha_0} C_\xi$가 클럽 집합이므로 $\alpha_1 > \alpha_0$를 만족하는 가장 작은 $\alpha_1 \in D_1$이 존재한다. 이 과정을 귀납적으로 반복하여 얻은 서수열 $(\alpha_n)$의 극한이 $\alpha$라고 하자. 임의의 $\xi < \alpha$에 대해, 어떤 $n$이 존재하여 $\xi < \alpha_n$이므로 임의의 $m \geq n$에 대하여 $\alpha_m \in C_\xi$이다. 따라서 $\alpha \in C_\xi$이며 $\alpha \in D$이다. ■
$\Delta C_\xi \supseteq \bigcap C_\xi$임을 확인하라.
참고로 지금까지의 정의와 정리들은 다음과 같이 일반화될 수 있다. $\kappa$가 $\operatorname{cf}\kappa > \omega$인 비가산 기수라고 하자.
정의. $C \subseteq \kappa$가 클럽 집합club set이라는 것은 $C$가 닫히고 무계closed and unbounded라는 것이다. 즉,
- 임의의 $\alpha < \kappa$에 대해 $\sup (C \cap \alpha) = \alpha$라면 (즉 $C$가 $\alpha$에서 무계라면) $\alpha \in C$이다.
- 임의의 $\gamma < \kappa$에 대해 $\alpha > \gamma$인 $\alpha \in C$가 존재한다.
정리. $\lambda < \operatorname{cf}\kappa$에 대해 $\lbrace C_\xi \rbrace _{\xi < \lambda}$가 클럽 집합들의 모임일 때, $C = \bigcap C_\xi$ 또한 클럽 집합이다.
정리. $\kappa$가 정칙regular이라면, $\lbrace C_\xi \rbrace _{\xi < \kappa}$가 클럽 집합들의 모임일 때, $\lbrace C_\xi \rbrace $의 대각 교집합 또한 클럽 집합이다.
증명. $\kappa = \omega_1$인 경우와 거의 같다. ■
정상 집합
유한 교집합 닫힘에 의해 클럽 집합들의 모임은 필터를 생성한다. 해당 필터의 쌍대dual 아이디얼에 속하지 않는 집합을 정상 집합stationary set이라고 한다. 다른 말로 하자면 다음과 같다.
정의. $S \subseteq \omega_1$이라고 하자. 임의의 클럽 집합 $C \subseteq \omega_1$에 대해 $C \cap S \neq \varnothing$이라면 $S$는 정상 집합이다.
어떤 클럽 집합 $C$에 대해 $C \cap S = \varnothing$이라면 $S^c \subseteq C$이므로 $C$는 쌍대 아이디얼의 원소이다. 따라서 두 정의는 동치이다.
정상 집합은 $\omega_1$의 부분집합 중 “유의미하게 큰” 집합들을 포착한다. 이 사실은 다음의 (엄밀하지는 않은) 유비를 통해 더 잘 이해할 수 있다. $\omega_1$의 측도가 1이라고 할 때, 클럽 집합은 $\mu(C) = 1$인 집합에, 정상 집합은 $\mu(S) > 0$인 집합에 대응된다.
다음의 사실들은 쉽게 증명될 수 있다 (1번과 3번이 측도 유비와 자연스럽게 연결되는 것에 주목하라).
정리. 다음이 성립한다.
- 모든 클럽 집합은 정상 집합이다.
- 모든 정상 집합은 무계이다.
- $\bigcup_{n < \omega} A_n$가 정상 집합이라면 어떤 $m \in \omega$에 대해 $A_m$은 정상 집합이다.
정상 집합의 이름이 stationary인 이유는 다음의 정리 때문이다.
정리. $S \subseteq \omega_1$에 대해, $f: S \to \omega_1$이 퇴행적regressive이라는 것은 임의의 $\alpha \in S$에 대해 $f(\alpha) < \alpha$라는 것이다. 다음이 동치이다.
- $S$는 정상 집합이다.
- 임의의 퇴행적 함수 $f: S \to \omega_1$에 대해, $f$는 어떤 무계 집합 $T \subseteq S$ 위에서 상수constant이다.
- 임의의 퇴행적 함수 $f: S \to \omega_1$에 대해, $f$는 어떤 정상 집합 $T \subseteq S$ 위에서 상수이다.
증명. 3 ⇒ 2는 자명하므로, 1 ⇒ 3과 2 ⇒ 1을 증명하면 된다.
1 ⇒ 3
대우를 증명한다. 어떤 퇴행적 함수 $f: S \to \omega_1$에 대해, $S$의 모든 정상 부분집합 위에서 $f$가 상수가 아니라고 하자. 즉, 임의의 $\xi \in \omega_1$에 대하여 $A_\xi = f^{-1}(\lbrace \xi \rbrace )$는 정상 집합이 아니다. 따라서 $A_\xi \cap C_\xi = \varnothing$인 클럽 집합 $C_\xi$가 존재한다.
$D = \Delta_{\xi < \omega_1} C_\xi$라고 하자. $D$는 클럽 집합이므로, 만약 $S$가 정상 집합이라면 $D \cap S \neq \varnothing$이다. $\alpha \in D \cap S$라고 하자. $\alpha \in D$이므로 임의의 $\xi < \alpha$에 대하여 $\alpha \in C_\xi$이다. 즉, $\alpha \notin A_\xi$이므로 $f(\alpha) \neq \xi$이다. 그런데 $\alpha \in S$이므로 $f(\alpha) < \alpha$이다. 이는 모순이므로 $S$는 정상 집합이 아니다. □
2 ⇒ 1
마찬가지로 대우를 증명한다. $S$가 정상 집합이 아니라고 하자. 그러면 어떤 클럽 집합 $C$에 대해 $S \cap C = \varnothing$이다. 다음의 함수를 정의하자.
\[f(\alpha) = \sup (C \cap \alpha)\]임의의 $\alpha \in S$에 대하여 $f(\alpha) \leq \alpha$이다. 만약 $f(\alpha) = \alpha$라면, $C$는 $\alpha$로 수렴하는 서수열을 가진다. 그런데 $C$는 닫힌 집합이므로, $\alpha \in C$이다. 이는 $S \cap C = \varnothing$에 모순이다. 따라서 $f(\alpha) < \alpha$이며, $f$는 퇴행적이다.
만약 어떤 무계 집합 $T$ 위에서 $f$의 값이 $\gamma < \omega_1$로 일정했다면, 어떤 무계인 서수열 $(\alpha_n)$에 대해 $\sup (C \cap \alpha_n) = \gamma$이다. 그런데 $C$는 무계이므로, 이는 $\sup \alpha_n = \gamma$를 함축한다. 그런데 $(\alpha_n)$이 무계이므로 $\sup \alpha_n = \omega_1$이다. 이는 모순이다. 따라서 $f$는 어떠한 무계 집합 위에서도 상수가 아닌 퇴행적 함수이다. ■
위 정리는 다음의 정리로 일반화될 수 있다.
포더 보조정리Fodor’s lemma. $\kappa$가 비가산 정칙 기수라고 하자. 임의의 $S \subseteq \kappa$에 대해 다음이 동치이다.
- $S$는 정상 집합이다.
- 임의의 퇴행적 함수 $f: S \to \omega_1$에 대해, $f$는 어떤 무계 집합 $T \subseteq S$ 위에서 상수이다.
- 임의의 퇴행적 함수 $f: S \to \omega_1$에 대해, $f$는 어떤 정상 집합 $T \subseteq S$ 위에서 상수이다.
정상 집합의 응용
정상 집합의 한 응용으로서 조합론의 다음 정리를 보자.
Δ-계 보조정리Δ-system lemma. $\lbrace A_\xi\rbrace _{\xi < \omega_1}$가 $\omega_1$의 유한부분집합들의 모임이라고 하자. 어떤 무계인 $I \subseteq \omega_1$와 유한집합 $A$가 존재하여, 임의의 $i, j \in I, i \neq j$에 대해 $A_i \cap A_j = A$이다.
증명. 비둘기집의 원리에 의해 일반성을 잃지 않고, 임의의 $\xi < \omega_1$에 대해 $|A_\xi | = n$이라고 가정할 수 있다. 다음과 같이 정의하자.
\[C = \{ \alpha < \omega_1 : \forall \xi < \alpha \;\; \operatorname{max}C_\xi < \alpha \}\]$C$는 클럽 집합이다. 또한 $0 \leq k \leq n$에 대해 다음과 같이 정의하자.
\[T_k = \{ \alpha \in C : |A_\alpha \cap \alpha | = k \}\]$\bigcup_{0 \leq k \leq n} T_k = C$이므로 어떤 $m$에 대해 $T_m$은 정적 집합이다. 이제 $0 \leq l < m$에 대해 다음의 함수를 정의하자.
\[f_l(\alpha) : T_m \to \omega_1; \quad \alpha \mapsto \text{$l$th element of $A_\alpha$}\]$|A_\alpha \cap \alpha| > l$이므로 $f_l(\alpha) < \alpha$이다. 따라서 각 $l$에 대해 $f_l$는 퇴행적이다. 이제 다음의 단계를 반복한다.
- $f_0$가 상수가 되는 정적 집합 $S_0 \subseteq T_m$이 존재한다.
- $f_1 |_{S_0}$이 상수가 되는 정적 집합 $S_1 \subseteq S_0$가 존재한다.
- $f_2 |_{S_1}$이 상수가 되는 정적 집합 $S_2 \subseteq S_1$이 존재한다.
- …
- $f_{m-1} |_{S_{m-2}}$가 상수가 되는 정적 집합 $S_{m-1} \subseteq S_{m-2}$가 존재한다.
그러면 임의의 $0 \leq l < m$에 대해 $f_l$은 $S_{m-1}$에서 상수이다. 이제 $S_{m-1} = I$가 찾고자 하는 집합임을 쉽게 확인할 수 있다. ■
수학과 윤리학은 같은 배를 탔는가? 진화론 논변을 중심으로
07 Nov 2025이 글은 Justin Clarke-Doane, Morality and Mathematics: The Evolutionary Challenge (2012)를 정리한 것이다. “저자”는 논문의 저자를, “필자”는 이 글의 필자를 가리킨다. “도덕”과 “윤리”의 혼용을 방지하기 위해 “윤리”로 표현을 통일했다.
개요
윤리 실재론에 대한 반론 중 하나는 진화론 논변The Evolutionary Challenge이다. 진화론 논변에 따르면, 오늘날의 인류가 가지는 윤리적 믿음들은 진화적 압력evolutionary forces에 의해 형성되었다. 그러나 진화의 원리는 윤리적 사실들과 무관하므로, 윤리적 사실들이 완전히 다른 반사실적 세계에서도 인류는 동일한 윤리적 믿음들을 가지도록 진화했을 것이다. 그러므로 만약 우리의 윤리적 믿음들이 참이라면 이는 진화의 결과와 윤리의 명제들이 굉장한 우연으로 일치하게 된 것이다. 따라서 진화론 논변을 옹호하는 자들은 윤리 실재론이 굉장한 우연을 날것 그대로 받아들이거나, 혹은 우리의 윤리적 믿음들이 참이라고 생각할 근거가 없음을 인정해야 한다고 주장한다.
예를 들어 우리가 “타인을 배려해야 한다”라는 윤리적 믿음을 가지게 된 이유는, 아마 인류의 진화에 있어 상호 협력을 중시하는 집단이 이기주의를 중시하는 집단보다 생존 확률이 높았기 때문일 것이다. 그런데 상호 협력이 이기주의보다 생존 확률이 높다는 것은 윤리적 사실이 아니라, 두 전략의 기댓값에 대한 게임이론적 내지는 수학적 사실이다. 따라서 설령 상호 협력보다 이기주의가 윤리적이었다고 하더라도, 우리는 “타인을 배려해야 한다”라는 믿음을 가지도록 진화했을 것이다.
한편으로 진화론 논변은 수학 실재론을 위협하지는 않는 것으로 받아들여져 왔다. 왜냐하면 진화의 원리는 수학적 참에 의존적인 것으로 보이기 때문이다. 예를 들어 1 + 1 = 2임을 믿는 개체들은 그렇지 않은 개체보다 생존에 유리한데, 이는 1 + 1 = 2가 실제로 참이기 때문이다. 이를 조이스는 다음과 같이 설명한다.
수풀 A 뒤에 사자 한 마리가 있고 수풀 B 뒤에 사자 한 마리가 있다고 하자. 우리의 선조 P와 Q가 수풀 C 뒤에 숨어 있다. P는 사자 한 마리와 다른 사자 한 마리는 총 사자 두 마리가 된다고 믿고, Q는 사자 한 마리와 다른 사자 한 마리가 총 사자 0마리가 된다고 믿는다. 그렇다면 P가 Q보다 죽을 확률이 적으며, 자신의 유전자를 남길 확률이 크다. 왜냐하면 P는 Q보다 수풀 C에서 걸어나와 두 마리의 사자에게 잡아먹힐 확률이 적기 때문이다. 그러나 이 사실[이탤릭체로 표시된 사실]에 대한 설명은, 사자 한 마리와 다른 사자 한 마리가 정말로 0마리가 아니라 두 마리의 사자라는 사실을 전제한다.
그러나 논문에서 저자는 이것이 잘못된 생각이라고 주장한다. 저자는 진화론 논변이 윤리 실재론을 위협하는 것과 같은 정도로 수학 실재론을 위협한다고 주장한다. 결론적으로 저자는 윤리 실재론과 수학 실재론 중 하나만 받아들이는 입장은 비정합적이라고 피력한다.
1. 실재론은 정확히 무엇인가?
본 논증에 들어가기 앞서 저자는 윤리 실재론과 수학 실재론이 정확히 무엇을 의미하는지를 해명하고자 한다. 일반적으로, 저자는 어떤 논의 영역area of discourse D에 대해, D-실재론을 다음 네 입장의 연언으로 정의한다.
- D-참-적합성D-Truth-Aptness. D의 문장들은 진릿값을 가진다.
- D-참D-Truth. 어떤 D의 원자명제 또는 존재 양화 명제는 참이다.
- D-독립성D-Independence. D의 문장들의 진릿값은 정신과 언어에 유의미한 의미에서 독립적이다.
- D-액면성D-Literalness. D의 문장들은 문자 그대로 받아들여져야 한다.
D를 윤리학으로 설정할 경우 1은 에이어의 감정주의emotivism1를 기각하고, 2는 매키의 오류 이론error theory2을 기각하고, 3은 구성주의constructivism3를 기각하고, 4는 하먼의 상대주의4를 기각한다. D를 수학으로 설정할 경우 1은 힐베르트의 형식주의formalism5를 기각하고, 2는 필드의 허구주의fictionalism6를 기각하고, 3은 브라우어르 구성주의7를 기각하고, 4는 만약주의if-thenism8를 기각한다.
이 논문에서는 윤리 실재론과 수학 실재론을 기본적으로 전제한 뒤, 이들이 진화론 논변을 극복할 수 있는지 검토한다. 추가로 우리의 윤리적, 수학적 믿음들은 대부분 참이라고 전제한다.
2. 윤리 실재론에 대한 진화론 논변
실재론의 구성 요건을 밝혔으니, 진화론 논변이 어떻게 윤리 실재론을 공격하는지 살펴보자. 진화론 논변의 전제는 다음과 같다.
강한 전제. 우리의 윤리적 믿음은 참-독립적인 진화적 압력에 의해 형성되었다.
강한 전제는 다음 두 전제로 이루어져 있다.
E. 우리의 윤리적 믿음은 진화적으로 형성되었다.
NTT. 윤리적 믿음의 진화는 참-독립적non-truth-tracking으로 이루어졌다.
NTT의 정확한 의미는 다음의 반사실적 조건문이다.
P. 나머지 사실은 모두 유지된 채 오직 윤리적 사실만이 현실과 아주 달랐다고 하자. 그럼에도 우리는 현실에서 참인 윤리적 믿음들을 가지도록 진화했을 것이다.
혹자는 P 대신 Q를 2의 의미로 해명할 수 있다고 지적할 수 있다.
Q. 우리는 틀린 윤리적 믿음들을 가지도록 진화할 수 있었다.
그러나 저자는 Q가 견지될 수 없는 입장이라고 주장한다. 물론, 다윈이 일찍이 지적했듯이 인류가 꿀벌과 같은 환경에서 발생했다면 인류는 결혼하지 않은 여성이 형제를 죽이는 것을 용인했을지 모른다. 그러나 이 사례 자체는 Q를 예증하지 않는다. 해당 사례가 Q를 예증하기 위해서는 “꿀벌과 같은 환경에서 결혼하지 않은 여성이 형제를 죽이는 것은 잘못되었다”가 윤리적 참이라는 추가적인 가정이 필요한데, 이는 자명한 가정이 아니기 때문이다. (기아가 빈번했던 전근대 사회에서의 영아 살해와 현대의 영아 살해가 가지는 윤리적 무게를 고려해 보라.) 따라서 저자는 Q를 예증하고자 할 경우 “고통은 좋다”, “쾌는 나쁘다”와 같이 기초적explanatorily basic으로 틀린 윤리적 믿음들을 가지게 되는 경우를 제시해야 한다고 주장한다. 그러나 고통이 좋고 쾌가 나쁘다고 믿는 개체들은 진화론적으로 절멸했을 것이므로 Q는 견지될 수 없다. 따라서 P가 NPP의 올바른 해명이다.
그러나 P에도 문제가 있다. 많은 윤리 실재론자들은 윤리적 속성과 기술적descriptive 속성의 동일시가 형이상학적으로 필연적metaphysically necessary이라고 주장한다. 예를 들어 “쾌는 좋다”가 참이라면, 이 참은 형이상학적으로 필연적이다. 이 관점에 따르면 기술적 사실들이 고정된 채 윤리적 사실들만 달라지는 것은 형이상학적으로 불가능하다. 따라서 P에 대한 다음의 독해는 견지될 수 없다.
P1. 형이상학적인 의미에서 나머지 사실은 모두 유지된 채 오직 윤리적 사실만이 현실과 아주 달랐다고 하자. 그럼에도 우리는 현실에서 참인 윤리적 믿음들을 가지도록 진화했을 것이다.
대신 저자는 P를 다음과 같이 이해해야 한다고 주장한다.
P2. 나머지 사실은 모두 유지된 채 오직 윤리적 사실만이 현실과 아주 다른 상황을 정합적으로 상상해 보자intelligibly imagine. 그럼에도 우리는 현실에서 참인 윤리적 믿음들을 가지도록 진화했을 것이다.
수학을 예시로 들어, $\zeta(-1)$을 구하는 문제의 답을 $-1/12$로 찍어서 맞힌 아이의 경우를 생각해 보자. $\zeta(-1) = -1/12$은 필연적이므로, “이 문제의 답이 달랐더라도 아이는 정답을 맞혔을 것이다 (아이의 대답은 참-의존적truth-tracking이었다)”라는 반사실적 가정문은 형이상학적으로 공허참이다. 그럼에도 우리는 $\zeta(-1) = -1/12$이 아닌 경우를 상상할 수 있으며, 이 상상을 정합적으로intelligibly 전개한다면 아이는 문제를 틀렸을 것이다. 이런 의미에서 아이의 대답은 참-독립적이었다.
E와 NTT의 의미가 해명되었으므로, 강한 전제로부터 어떻게 윤리 실재론에 대한 반박을 유도하는지 살펴보자. 스트리트 등은 다음의 논변을 제시한다.
- 윤리적 사실이 아주 달라지는 것이 형이상학적으로는 불가능하더라도 그런 경우를 상상할 수는 있다.
- 우리가 상상할 수 있는 한에서, 윤리적 사실이 아주 달랐더라도 우리가 진화론적으로 형성하게 된 윤리적 믿음들은 동일했을 것이다.
- 따라서 현실의 우리가 윤리적으로 참인 믿음들을 가지게 되었다는 것은 설명될 수 없는 우연이다.
그러나 저자는 2로부터 3이 따라 나오지는 않는다고 주장한다. 2로부터 3을 도출하기 위해서는 다음의 일반적인 원리를 전제해야 한다.
D에 대한 기본적인 사실들이 달라지더라도 D에 대한 믿음들 중 달라지지 않는 믿음들의 참은 우연적이다.
저자는 위 원리에 대한 다음 반례를 든다. 철수는 자신을 향해 날아오는 농구공을 보며, “농구공이 내 눈앞으로 날라오고 있다”라고 믿는다. 여기서 농구공이 농구공처럼 배열된 원자들atoms arranged basketballwise과 같다는 것은 형이상학적으로 필연적이다. 그러나 우리는 물질이 원자가 아닌 다른 요소로 구성된 세계를 상상할 수 있다. 그런 세계에 사는 철수 앞으로 농구공이 날라오더라도 철수는 동일한 믿음, 즉 “농구공이 내 눈앞으로 날라오고 있다”라고 믿을 것이다. 이처럼 농구공에 대한 기본적인 사실들이 달라지더라도 철수는 동일한 믿음을 견지하지만, 그럼에도 불구하고 현실의 철수가 “농구공이 내 앞으로 날라오고 있다”라고 믿는 것은 참이며, 이 참은 우연적이지 않다.
필자 주: 필자는 저자가 잘못된 유비를 들었다고 생각한다. 농구공이 원자로 구성된 세계의 철수가 “농구공이 내 앞으로 날라오고 있다”라고 믿는 것과, 농구공이 연속체로 구성된 세계의 철수가 “농구공이 내 앞으로 날라오고 있다”라고 믿는 것은 동일한 믿음이 아니다. 왜냐하면 두 철수에게 있어 “농구공”의 의미는 지시ostension를 통해 결정되기 때문이다. 따라서 전자의 철수는 “농구공”으로 “농구공처럼 배열된 원자들”을 의미하고, 후자의 철수는 “농구공”으로 “농구공처럼 응축된 연속체”를 의미한다. 이렇듯 농구공에 대한 기본적인 사실이 달라지면 철수는 그에 상응하는 다른 믿음을 가지게 된다. 반면 윤리적 언어의 의미는 지시로 결정되지 않는 것으로 보인다.
그러나 저자는 비록 스트리트의 논증이 그 자체로는 우리가 참인 윤리적 믿음들을 가지는 것에 대한 설명이 완전히 불가능함을 보이지 않더라도, 적어도 다음의 두 설명은 잘못되었음을 입증한다고 지적한다.
- 진화적 설명evolutionary explanation. 우리가 참된 윤리적 믿음들을 가지는 이유는 우리가 참된 윤리적 믿음들을 가지도록 (자연)선택되었기 때문이다.
- 자명한 설명trivial explanation. 우리가 참된 윤리적 믿음들을 가지는 이유는 현재의 윤리적 사실들이 유일하게 가능한 윤리적 사실들이며, 그 사실들을 믿는 개체들이 진화에 더 유리하기 때문이다.
진화적 설명과 자명한 설명의 차이에 집중하라. 진화적 설명은 윤리적 사실이 “쾌는 좋다”에서 “고통은 좋다”로 — 형이상학적이지는 않을지언정 상상 속에서 — 바뀌었다면 우리 또한 “고통은 좋다”라는 믿음을 가지도록 진화했을 것이라고 주장한다. 반면 자명한 설명은 “쾌는 좋다”라는 윤리적 사실이 “고통은 좋다”로 바뀌는 것이 — 형이상학적인 의미에서나 상상 속에서나 — 불가능하다고 견지하며, 이에 따라 진화가 어떻게 현실의 윤리적 사실들을 믿는 개체를 탄생시키는지 설명한다면 그것으로 모든 문제는 해결된다고 주장한다.
필자 주: 자명한 설명은 개요에서 언급한 게임 이론적 설명을 전제하는 듯하다. 즉, 자명한 설명은 윤리 실재론에 대한 진화론 논변을 (i) 윤리적 사실들의 강한 필연성과, (ii) 해당 윤리적 사실들이 진화적으로 유리하다는 수학적 사실, 그리고 (iii) 수학적 사실들의 필연성이라는 세 전제를 통해 극복하고자 한다. 이는 (ii)라는 다리 원리를 통해 윤리적 믿음들의 참에 대한 설명을 수학적 믿음들의 참에 대한 설명에 정초하는 시도로 보인다.
그런데 진화적 설명과 자명한 설명이 잘못되었음을 주장하는 것이 진화론 논변의 목적이라면, 진화론 논변은 E ∧ NTT를 전제할 필요 없이 E → NTT만 전제해도 그 목적을 달성할 수 있다. 즉, 진화론 논변은 다음과 같다.
진화론 논변. E → NTT라면, 우리가 참된 윤리적 믿음들을 가진다는 사실을 진화적 설명 또는 자명한 설명으로 설명하는 것은 잘못되었다.
저자는 위와 같이 진화론 논변을 정리한 뒤, 해당 논변이 수학에서는 얼마나 유효한지를 검토한다.
3. 수학은 진화에 영향을 주는가?
통상적으로 수학은 진화론 논변의 대상이 되지 않는다고 생각된다. 윤리적 참이 진화와 무관한 것과 달리 (윤리적 참이 달라지더라도 진화에는 영향이 없다) 수학적 참은 진화에 영향을 준다고 생각되기 때문이다. 앞서 소개한 조이스는 사례를 다시 보자.
수풀 A 뒤에 사자 한 마리가 있고 수풀 B 뒤에 사자 한 마리가 있다고 하자. 우리의 선조 P와 Q가 수풀 C 뒤에 숨어 있다. P는 사자 한 마리와 다른 사자 한 마리는 총 사자 두 마리가 된다고 믿고, Q는 사자 한 마리와 다른 사자 한 마리가 총 사자 0마리가 된다고 믿는다. 그렇다면 P가 Q보다 죽을 확률이 적으며, 자신의 유전자를 남길 확률이 크다. 왜냐하면 P는 Q보다 수풀 C에서 걸어나와 두 마리의 사자에게 잡아먹힐 확률이 적기 때문이다. 그러나 이 사실[이탤릭체로 표시된 사실]에 대한 설명은, 사자 한 마리와 다른 사자 한 마리가 정말로 0마리가 아니라 두 마리의 사자라는 사실을 전제한다.
그러나 저자는 조이스의 논증에 두 가지 문제가 있다고 지적한다. 첫 번째 문제는, 조이스의 논증이 다음의 원리에 기반한다는 사실에 기인한다.
우리가 D에 관한 특정 믿음들을 가지는 것에 대한 진화적 설명이 해당 믿음들의 내용을 전제하면, 우리는 D에 관한 참인 믿음들을 가지도록 선택되었다.
그러나 저자는 우리가 참인 D-믿음들을 가지도록 선택되지 않았더라도 (즉 우리의 D-믿음들이 참이 아니거나, 참-독립적으로 형성되었다고 하더라도) 우리의 D-믿음들에 관한 진화적 설명이 우리의 D-믿음들의 내용을 전제할 수 있다고 주장한다. 가령 모든 유형의 설명은 우리의 논리적 믿음들에 대한 내용을 전제하지만, 그럼에도 불구하고 우리가 참인 논리적 믿음들을 가지도록 선택되었는지는 의문으로 남는 듯하다 (필자의 소논문 참고).
그럼에도 혹자는 콰인-퍼트넘 등의 전체론적 인식론을 채택함으로써, 수학적 사실이 우리의 수학적 믿음들을 설명하는 기반이 된다는 고찰을 해당 수학적 사실이 참인 잠정적 근거로 볼 수 있다고 반론할 수 있다. 이에 저자는 두 번째, 더 심각한 문제를 지적한다. 바로 우리의 수학적 믿음들에 관한 진화적 설명은 애당초 수학적 사실과는 관련이 없다는 것이다. 저자는 진화적 설명이 수학적 사실이 아닌 1차 논리적 사실과만 관련 있다고 주장한다. 앞선 사자의 사례를 보면, P가 Q보다 생존할 확률이 높았던 것은 M이 참이기 때문이 아니라 L이 참이기 때문이라는 것이다.
M. 1 + 1 = 2
L. 수풀 A 뒤에 사자 한 마리가 있고, 수풀 B 뒤에 사자 한 마리가 있고, 어떠한 수풀 A 뒤에 있는 사자도 수풀 B 뒤에 있는 사자와 같지 않다면, 수풀 A와 수풀 B 뒤에는 사자 두 마리가 있다.
L은 다음과 같이 1차 논리식으로 풀어쓸 수 있다.
\[\begin{align} &\;\exists! x A(x) \land \exists! y B(y) \land \forall x, y (A(x) \land B(y) \rightarrow x \neq y) \\ &\rightarrow \exists x, y \big((x \neq y) \land (A(x) \lor B(x)) \land (A(y) \lor B(y)) \\ &\quad \quad \land\; \forall z ( (A(z) \lor B(z)) \rightarrow (z = x) \lor (z = y))\big) \end{align}\]많은 수학자와 철학자가 수학이 논리로 환원될 수 있다는 입장을 견지하기는 하지만, 환원의 종착지가 1차 논리라고 주장하는 학자는 없다. 따라서 우리의 수학적 믿음들에 대한 진화적 설명이 수학적 사실이 아닌 1차 논리적 사실에만 의존한다면, 진화적 설명은 우리가 참인 수학적 믿음들을 가지도록 선택되었다는 결론을 확정적으로도, 잠정적으로도 도출해내지 못한다.
또한 수학 실재론자는 M과 L을 단순히 동일시할 수도 없다. 왜냐하면 실재론의 요건 중 D-액면성이 있기 때문이다. 1 + 1 = 2의 진술은 문자 그대로 받아들여져야 하며, 문자 그대로 받아들여졌을 때 이 진술은 1과 2라는 수가 존재하며, 해당 수들이 덧셈에 대해 특정 관계에 있다는 진술이다.
결론적으로, P가 Q보다 생존 확률이 높은 이유는 P가 가진 수학적 믿음 M의 내용이 참이기 때문이 아니라, 그 믿음에 대응되는 논리적 내용 L이 참이기 때문이다. 그리고 M이 L에 대응된다는 사실은 수학적 실재론을 전제하지 않더라도 충분히 해명될 수 있다. 전반부에서 언급된 여러 반실재론적 입장들 — 형식주의, 허구주의, 구성주의, 만약주의 — 은 각자 정도의 차이는 있지만 모두 M과 L의 대응을 수학적 대상을 가정하지 않으면서 설명해 낸다.
물론 우리는 1차 논리로 포착될 수 없는 수학적 믿음들 또한 가지고 있다. 귀납 공리에 대한 믿음이 한 예시이다. 그러나 저자는 귀납 공리가 직접적인 진화의 외압으로 인해 형성된 믿음이 아님을 지적한다. 귀납 공리는 17세기 전까지는 명시적으로 표현된 적조차 없었다. 귀납 공리에 대한 믿음은 기초적인 산술 믿음들을 형식화하여 정립하는 과정에서 발생한 것이다. 즉 우리가 귀납 공리를 믿는 이유는 기초적인 산술에 대한 믿음 때문이고, 그 믿음들은 수학적 사실이 아닌 1차 논리적 사실로 인해 형성된 것이다. 결론적으로, 논리를 초월하는 수학적 사실들은 정작 수학적 믿음의 진화적 형성에 아무런 영향을 미치지 않는다 (다음의 그림 참조: A → B는 “A로 인해 B를 믿는 개체가 진화한다”는 의미이다).
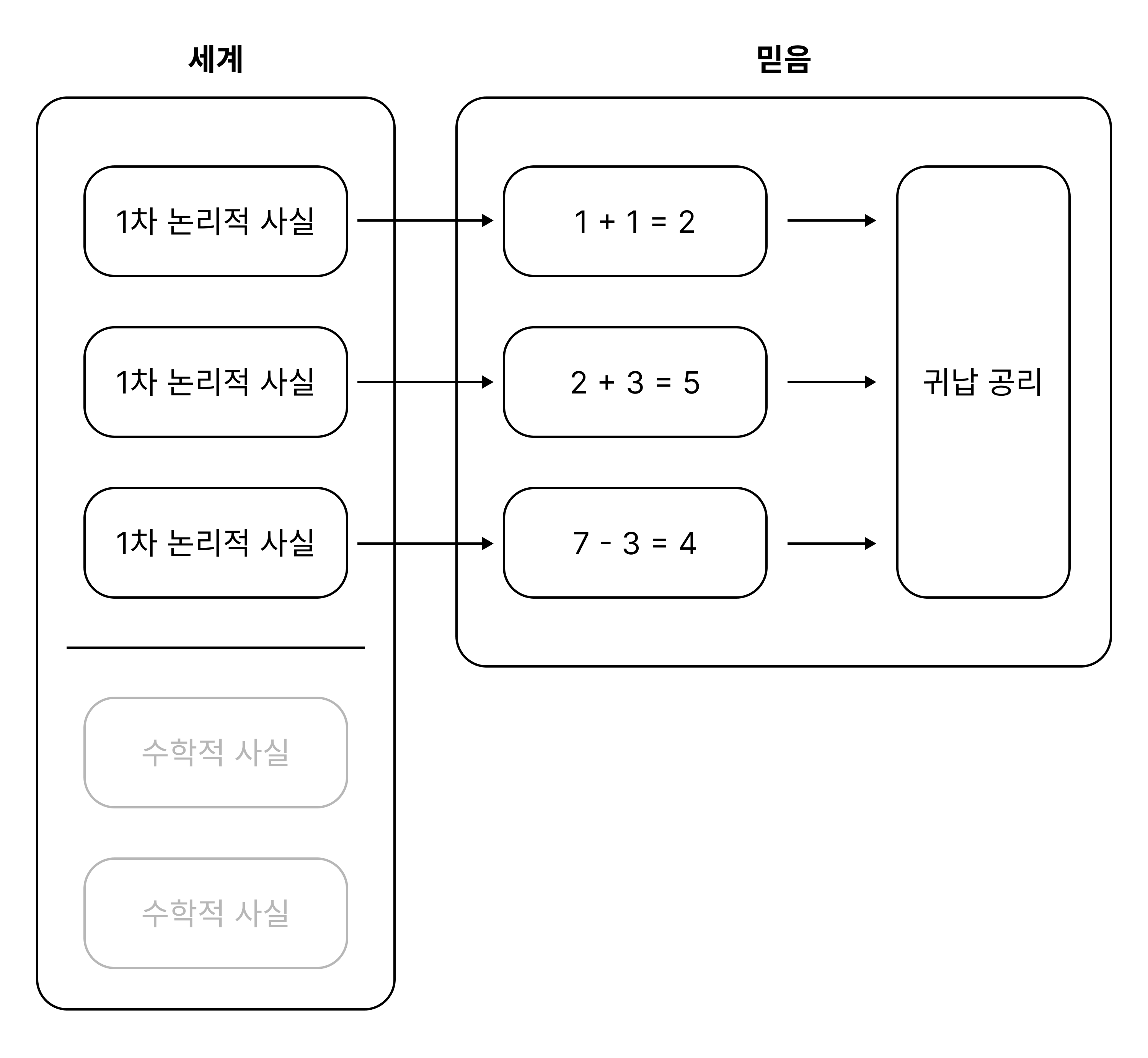
여기서 저자는 짧게 다음의 질문을 제시한다. 그렇다면 지금까지의 논의는 우리가 참인 1차 논리적 믿음들을 가지도록 진화했다는 것을 보여주는가? 저자는 이 질문의 답이 “아니오”일 것이라고 생각한다. 왜냐하면 논리적 사실들은 5 + 7 = 12와 같은 단순한 산술적 사실만 되어도 굉장히 복잡해지기 때문이다. 따라서 진화론적으로는 단순히 수학적 믿음을 가지는 개체가, 수학적 믿음, 논리적 믿음, 그리고 각각의 수학적 명제를 논리적 명제로 어떻게 번역할지에 관한 믿음을 가지는 개체보다 유리할 것으로 보인다. 즉, 논리적 사실들이 달랐더라면 우리의 수학적 믿음들 또한 달라졌을 것이지만 우리의 논리적 믿음들이 어떻게 되었을지는 불분명하다(— 라고 저자는 생각하는 듯한데, 사실 이 부분에 관한 저자의 코멘트가 너무 함축적이라서 잘 모르겠다. 논리적 믿음의 형성을 진화론적으로 설명할 수 없다는 별도의 논증으로 필자의 소논문을 참고하라.)
4. 또다른 수학은 상상 가능한가?
수학에 대한 진화적 설명을 기각한 저자는 자명한 설명으로 논의를 돌린다. 자명한 설명은, 현재의 수학적 사실들이 유일하게 가능한 수학적 사실들임을 주장한다.
통상적으로 윤리에 대한 자명한 설명은 설득력이 없는 것으로 간주되었다. 왜냐하면 윤리의 영역에서는 충분히 합리적인 개인들이 상충하는 입장을 가지는 경우가 자주 있기 때문이다. 서로 다른 윤리적 사실을 견지하는 합리적 개인들이 존재한다면, 현실과 다른 윤리적 사실을 가진 세계는 충분히 정합적으로 상상될 수 있다. 반면 수학의 경우에는 그런 상충이 거의 보이지 않는다. 트롤리 딜레마와 피타고라스 정리에 대한 사람들의 견해차를 비교해 보라.
그러나 저자는 이것이 윤리 실재론자에게 불리하도록 선별된 비교라고 주장한다. 우리는 윤리 실재론자들 사이에서 이견이 없는 명제들 — 이를테면 “아이를 재미로 고문하는 것은 정당하지 않다” — 을 찾을 수 있다. 반대로, 수학 실재론자들 사이에서 이견이 있는 수학의 공리들 또한 찾을 수 있다. 유한주의는 임의의 자연수보다 큰 자연수가 언제나 존재한다는 공리를 부정하고, 선택 공리는 전통적으로 굉장히 많은 논란을 야기했으며, 연속체 가설은 지금까지도 논란이 되고 있다. 따라서 저자는 현실과 다른 윤리적 참을 가지는 세계를 상상할 수 있는 것과 같은 정도로, 현실과 다른 수학적 참을 가지는 세계 — 이를테면 무한집합이 존재하지 않는 세계 — 를 상상할 수 있다고 주장한다.
5. 결론
저자는 진화론 논변이 윤리 실재론을 위협하는 것으로 여겨졌지만, 동일한 위협이 수학 실재론에도 가해짐을 논증했다. 저자는 수학 실재론 말고 오직 윤리 실재론만 위협하는 다른 논증이 있을 수도 있다는 사실을 인정한다. 일례로 하먼은 경험과학에서 수학의 필수불가결성indispensability으로부터 수학적 참을 경험적으로 정당화하는 콰인-퍼트넘 논증이 윤리에서는 적용되지 않는다는 점을 지적했다. 하지만 저자는 경험과학-수학 불가결성에 대한 근래의 회의주의와 경험과학-윤리 불가결성에 대한 새로운 논증들, 그리고 베나세라프 등의 인식론적 고려들을 제시하며, 수학 실재론과 윤리 반실재론을 동시에 견지하는 것이 점점 어려워지고 있음을, 어쩌면 불가능해질지도 모른다고 결론 내린다.
-
윤리적 문장은 감정의 발화라는 입장. 이 입장은 윤리학을 환호 및 야유와 동일시한다. 예를 들어 “도둑질은 나쁘다”는 “도둑질 우우!”와 동등하다 (“나는 도둑질을 싫어한다”와 동등하지는 않음에 유의하라). ↩
-
모든 윤리적 문장은 거짓이라는 입장. 이 입장은 윤리학을 플로지스톤 이론과 동일시한다. 플로지스톤이 존재하지 않으므로 플로지스톤 이론의 모든 문장이 틀렸듯이, 선함이 존재하지 않으므로 윤리학의 모든 문장은 틀렸다. ↩
-
인간의 정신이 윤리적 대상과 속성을 구성한다는 입장. 이 입장은 윤리학을 색깔 이론과 동일시한다. 색깔 이론의 객관성과 유용성과는 별개로 모든 인간이 사라지면 색의 개념도 사라지듯이, 모든 인간이 사라지면 선함의 개념도 사라진다. ↩
-
모든 윤리적 문장에는 생략된 전제구가 있다는 입장. 예를 들어 “트롤리의 선로를 바꿔야 한다”에서 생략된 전제구가 “공리주의에 따르면”이라면 이 문장은 참이고, “의무론에 따르면”이라면 거짓이다. ↩
-
수학은 규칙이 정해진 게임 활동이라는 입장. 이 입장은 수학을 체스의 수와 동일시한다. 가령 “1 + 1” 뒤에 “= 2”를 쓰는 것은 킹과 룩 사이를 비운 뒤 캐슬링을 하는 행위와 동등하다 (“킹과 룩 사이가 비어 있으면 캐슬링이 가능하다”와 동등하지는 않음에 유의하라). ↩
-
모든 수학적 문장은 거짓이라는 입장. 주석 2 참조. 필드는 유명론과 허구주의를 견지하면서도 수학이 과학에 유용할 수 있는 이유를 “다리 원리”를 통해 설명할 수 있다고 주장했다. ↩
-
인간의 정신이 수학적 대상과 속성을 구성한다는 입장. 주석 3 참조. 브라우어르의 구성주의는 수학이 인간의 시공간 인식에 정초되어야 한다고 주장한다. ↩
-
모든 수학적 명제에는 생략된 전제구가 있다는 입장. 예를 들어 “삼각형의 세 내각의 합은 180도이다”에서 생략된 전제구가 “유클리드 기하학에서”라면 이 문장은 참이고, “쌍곡 기하학에서”라면 거짓이다. ↩
단체 호몰로지
05 Nov 2025정의. $K$가 순수 $k$-단체 복합체pure simplicial complex이고, $p \leq k$에 대해 $C_p(K)$가 $K$의 $p$-체인chain들의 집합이라고 하자.
- $z \in C_p(K)$가 $K$의 $p$-고리cycle라는 것은 $z \in \ker \partial_p$라는 것이다.
- $b \in C_p(K)$가 $K$의 $p$-경계boundary라는 것은 $b \in \operatorname{im} \partial_{p + 1}$이라는 것이다.
$p$-고리들의 집합을 $Z_p(K)$, $p$-경계들의 집합을 $B_p(K)$라고 적는다.
$C_p(K)$를 자유 아벨군으로 보았을 때 $Z_p(K)$와 $B_p(K)$는 $C_p(K)$의 부분군이다. 자유 아벨군의 부분군은 언제나 자유 아벨군이므로 $Z_p(K)$와 $B_p(K)$는 자유 아벨군이다. 또한 $\partial_p \partial_{p+1} = 0$이므로 $B_p(K) \leq Z_p(K)$이며, 아벨군의 부분군은 정규부분군이므로 몫군 $Z_p(K)/B_p(K)$를 취할 수 있다. 이 목군을 호몰로지 군homology group이라고 하며 $H_p(K)$라고 적는다.
쉬운 언어로 설명하자면, 두 1-고리 $z_1, z_2$가 같은 호몰로지 군의 원소에 대응된다는 것은 $z_1 - z_2$가 어떤 2-체인의 경계를 이룬다는 것이다. 예를 들어 띠cylinder의 삼각화인 다음 복합체 $K$를 보자.
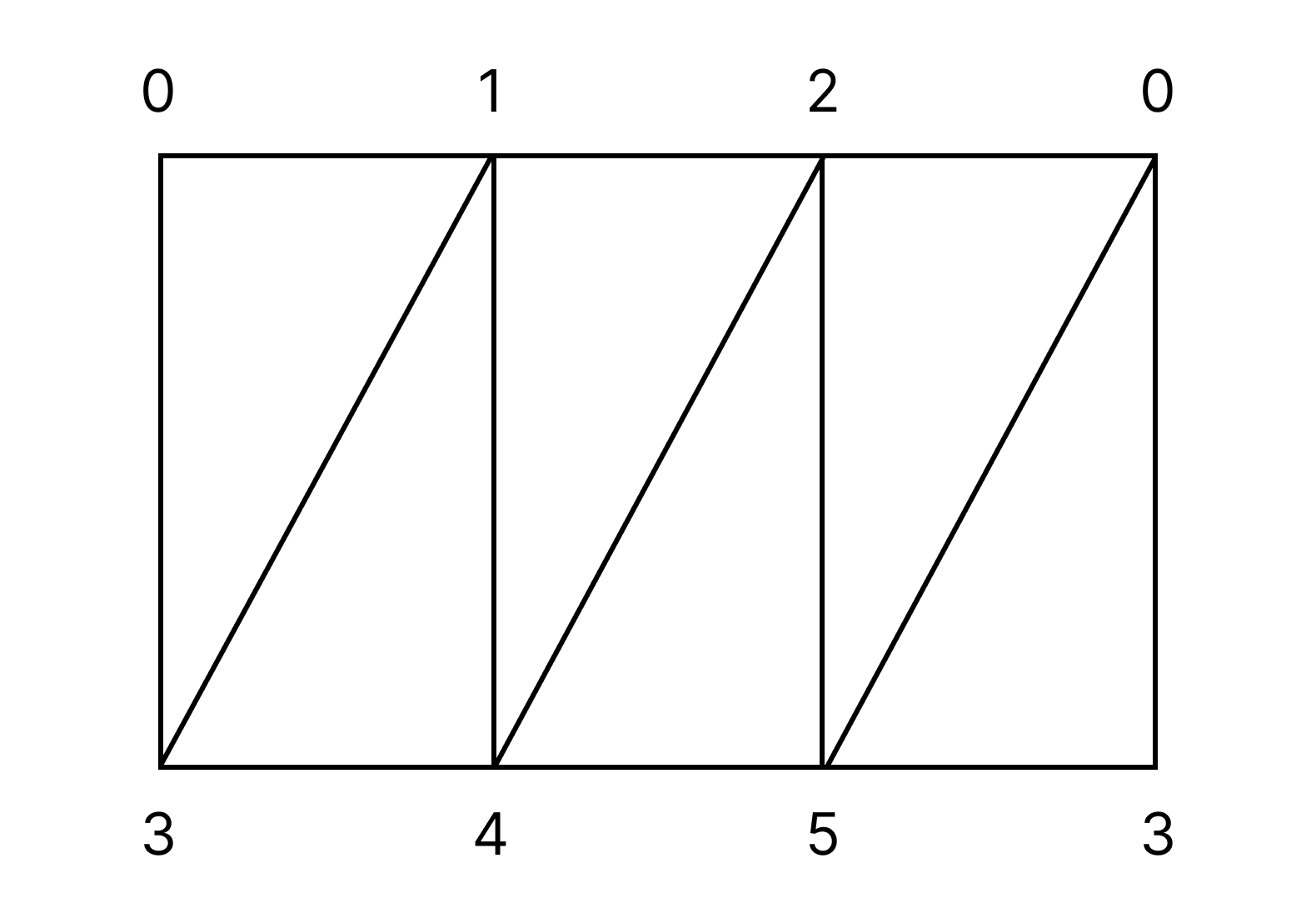
$z_1 = \langle 01 \rangle + \langle 12 \rangle + \langle 20 \rangle, z_2 = \langle 34 \rangle + \langle 45 \rangle + \langle 53 \rangle$이라고 하자. $z_1 - z_2$는 오른쪽과 같다.
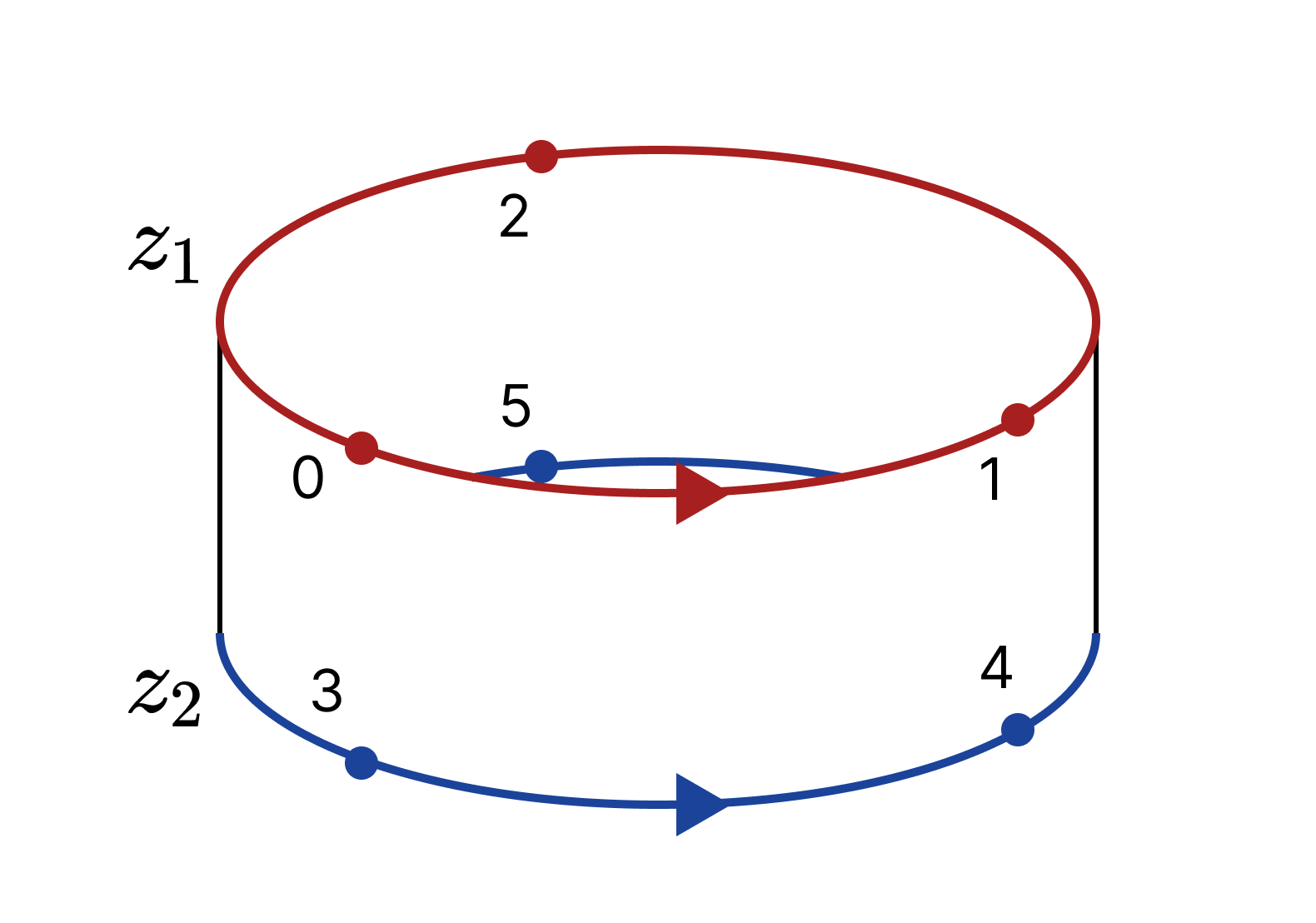
그런데 이는 띠 전체의 경계와 같다. 구체적으로,
\[\begin{align*} &\partial (\langle 013 \rangle + \langle 143 \rangle + \langle 124 \rangle + \langle 254 \rangle + \langle 205 \rangle + \langle 035 \rangle) \\ &= (\langle 01 \rangle + \langle 12 \rangle + \langle 20 \rangle) - ( \langle 34 \rangle + \langle 45 \rangle + \langle 53 \rangle) \\ &= z_1 - z_2 \end{align*}\]따라서 $z_1$과 $z_2$는 같은 호몰로지 군의 원소에 대응된다. 그러나 $n, m \in \mathbb{Z}$에 대해 $n \neq m$이라면 $n \cdot z_1$과 $m \cdot z_1$은 서로 다른 호몰로지 군의 원소에 대응된다. $(n - m) \cdot z_1$이 $B_1(K)$에 속하지 않기 때문이다. 이로부터 띠의 1-호몰로지 군이 $\mathbb{Z}$임을 유추할 수 있으며, 이 유추는 올바르다.
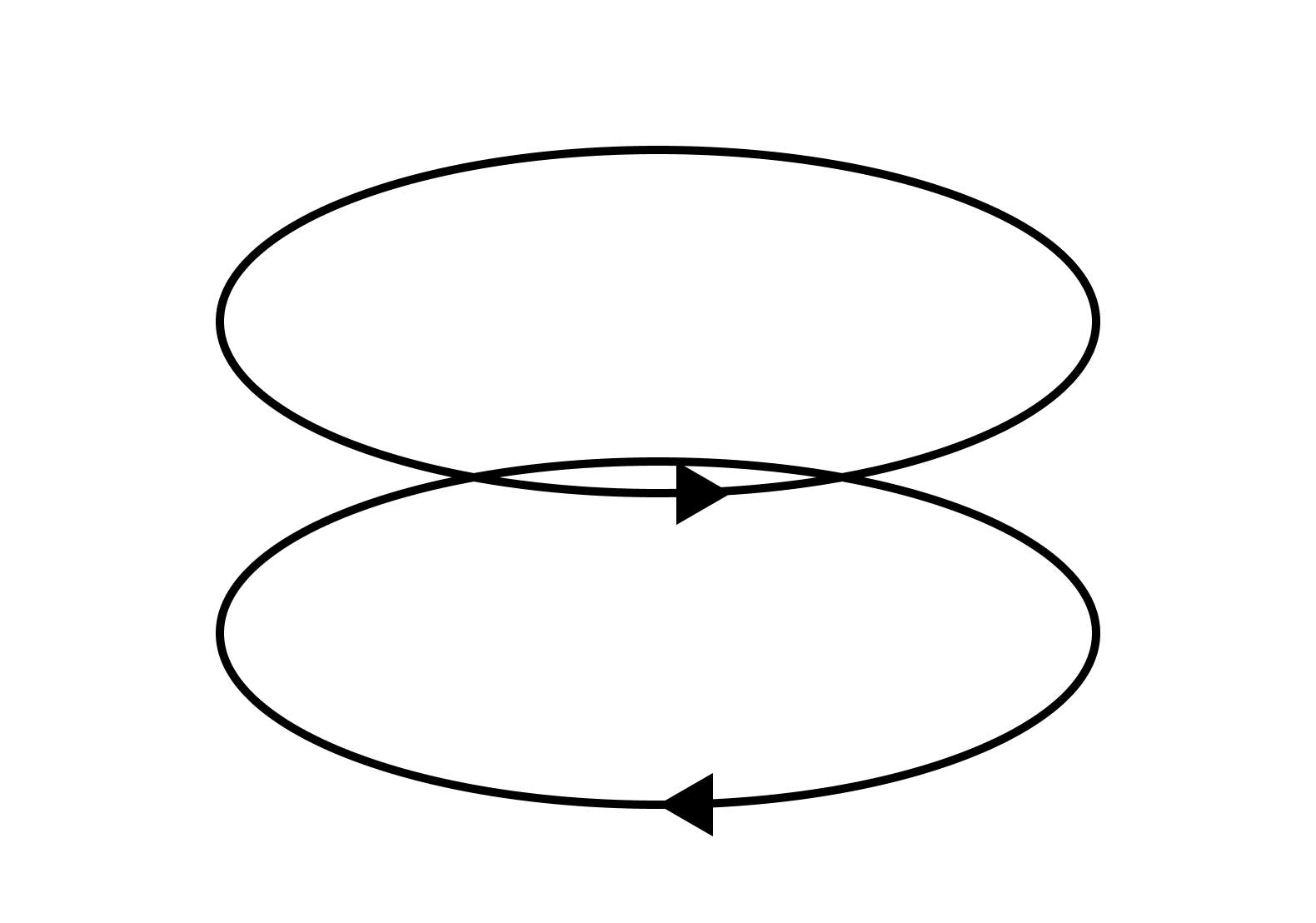
반면 토러스의 경우, 다음의 $w_1$과 $w_2$는 서로 다른 호몰로지 군의 원소에 대응된다. $w_1 - w_2$가 어떠한 2-체인의 경계도 아님을 직관적으로 파악할 수 있을 것이다. 실제로 토러스의 1-호몰로지 군은 $\mathbb{Z} \oplus \mathbb{Z}$이다.
호몰로지 군의 랭크rank는 직관적으로 구멍의 의미를 가진다. 띠의 1-호몰로지 군의 랭크가 1이라는 것은 띠의 1차원 구멍이 하나 있다는 것이고, 토러스의 1-호몰로지 군의 랭크가 2라는 것은 토러스의 1차원 구멍이 2개 있다는 것이다. (여기서 $n$차원 구멍이라 함은 $n$차원 경로에 의해 둘러질 수 있는 구멍을 말한다.)

닫힌집합과 보렐 집합에서의 연속체 가설
25 Sep 2025연속체 가설은 $\aleph_1 = 2^{\aleph_0}$가 성립하는지에 관한 질문이다. 이는 비가산 집합 중 실수 집합보다 크기가 작은 집합이 있는지에 관한 질문과 같다. 잘 알려져 있듯이 연속체 가설은 ZFC에서 증명과 반증이 불가능하지만, 몇몇 제한적인 경우에 대해서는 증명할 수 있다. 일찍이 칸토어는 연속체 가설을 실수의 닫힌집합으로 제한할 경우 성립함을 증명했다.
정리. $F \subseteq \mathbb{R}$이 닫힌집합이라면 $|F| = \aleph_0$이거나 $|F| = 2^{\aleph_0}$이다.
이 정리의 증명은 완벽한 집합perfect set이라는 개념을 사용한다. 이에 관해서는 예전에 칸토어-벤딕슨 정리를 다루며 소개한 적 있지만 다시 소개하겠다.
정의. 위상공간 $X$에 대해 $P \subseteq X$가 완벽하다는 것은 $P = P’$이라는 것이다. ($P’$은 $X$에 대한 $P$의 극점limit point들의 집합)
일반적으로 부분집합 $A \subseteq X$에 대해 $A$와 $A’$이 서로 포함 관계가 아닌 이유는 두 가지이다:
- $x$가 $A$의 고립점일 경우 $x \in A$이지만 $x \notin A’$
- $x$가 $A$에 속하지 않는 극점일 경우 $x \notin A$이지만 $x \in A’$
따라서 완벽한 집합은 고립점을 가지지 않는 닫힌집합이다. 이에 따라, 어떤 닫힌집합 $F$가 주어졌을 때 $F$의 고립점들을 모두 ‘덜어’ 내면 완벽한 집합이 되지 않을까 기대할 수 있다. 문제는, 고립점을 덜어 낸 집합이 또다시 고립점을 가질 수 있다는 것이다. 예를 들어,
\[F = \mathbb{N} \cup \lbrace m - 1/n : m \geq 0, n > 1 \rbrace\]일 때, $F$의 고립점들을 덜어 낸 집합은 $\mathbb{N}$으로 또다시 가산 개의 고립점을 가진다. 그러나 이같이 고립점을 ‘덜어’ 내는 과정을 초한귀납적으로 반복한다면 다음의 흥미로운 결과를 얻을 수 있다.
칸토어-벤딕슨 정리. $F \subseteq \mathbb{R}$가 닫힌집합이라면 어떤 가산집합 $C$와 완벽한 집합 $P$가 존재하여 $F = P \sqcup C$이다.
증명. 앞선 링크에 증명이 소개되어 있지만, 여기서는 칸토어의 증명을 소개한다.
초한귀납적으로 다음과 같이 정의하자.
\[\begin{gather} F_0 = F \\ F_{\alpha + 1} = F_\alpha' \\ F_\lambda = \bigcap_{\alpha < \lambda} F_\alpha \quad (\lim \lambda) \end{gather}\]다음을 관찰하라.
- 각 $F_\alpha$는 닫힌집합이다.
- $\alpha \leq \beta$라면 $F_\alpha \supseteq F_\beta$이다.
- $F_\alpha \setminus F_{\alpha + 1}$은 $F_\alpha$의 고립점들의 집합이다.
- $\alpha \neq \beta$라면 $F_{\alpha} \setminus F_{\alpha + 1}$와 $F_{\beta} \setminus F_{\beta+1}$는 서로소이다.
만약 모든 $\alpha \in \mathrm{Ord}$에 대해 $F_{\alpha} \setminus F_{\alpha+1} \neq \varnothing$이었다면 $\mathcal{P}(F)$의 하르토그 수 $\gamma$에 대해 $f : \gamma \to \mathcal{P}(F); \alpha \mapsto F_{\alpha} \setminus F_{\alpha + 1}$가 단사이므로 모순이다. 따라서 $F_{\xi} \setminus F_{\xi+1} = \varnothing$인 $\xi$가 존재한다. 따라서 $P = F_\xi$로 두면 $P$는 공집합이거나 완벽한 집합이다.
$C = F \setminus P$라고 하자. $\mathcal{B} = \lbrace B_n \rbrace $이 $\mathbb{R}$의 가산 기저라고 하자. 다음과 같이 $f: C \to \omega$를 정의한다.
\[f(x) = \mathop{\arg \min}\limits_{n \in \omega} : B_n \cap F_\alpha = \{ x \} \quad (x \in F_\alpha \setminus F_{\alpha + 1})\]$f$가 well-defined이며 단사임을 확인하라. ■
정리. $P \subseteq \mathbb{R}$이 공집합이 아닌 완벽한 집합이라면 $|P| = 2^{\aleph_0}$이다.
증명. 다음의 두 보조정리를 증명한다.
보조정리. $P \subseteq \mathbb{R}$이 공집합이 아닌 완벽한 집합이라면, 어떤 공집합이 아니며 완벽한 서로소 집합 $P_1, P_2 \subset P$가 존재한다.
증명. $\alpha = \inf P, \beta = \sup P$라고 하자 ($\alpha, \beta$는 $\pm \infty$일 수도 있다). $(\alpha, \beta) \subset P$라면 $\alpha < r < s < \beta$인 임의의 $r, s$에 대해 $P \cap (-\infty, r], P \cap [s, \infty)$가 조건을 만족한다. $(\alpha, \beta) \not\subset P$라면, 어떤 $x \in (\alpha, \beta)$가 존재하여 $x \notin P$이다. $P = P’$이므로, $x$는 $P$의 극점이 아니다. 따라서 어떤 충분히 작은 $\delta > 0$가 존재하여 $(x - \delta, x + \delta)$가 $F$와 서로소이고 $\alpha < x - \delta, x + \delta < \beta$이다. 이때 $P \cap (-\infty, x - \delta], P \cap [x + \delta, \infty)$가 조건을 만족한다. □
보조정리. $P \subseteq \mathbb{R}$이 공집합이 아닌 완벽한 집합이라면, 임의의 $n > 0$에 대해 어떤 공집합이 아니며 완벽한 집합 $P’ \subset P$가 존재하여 $\mathrm{diam} P’ < 1/n$이다.
증명. $\mathcal{J} = \lbrace (m/n, (m+1)/n) : m \in \mathbb{Z} \rbrace $에 대해, 어떤 $(k/n, (k+1)/n) \in \mathcal{J}$가 존재하여 $J \cap F \neq \varnothing$이다 (만약 그렇지 않다면 $P = \lbrace m/n : m \in \mathbb{Z} \rbrace $이므로 완벽하지 않다). $a = \inf F \cap (k/n, (k+1)/n)$, $b = \sup F \cap (k/n, (k+1)/n)$라고 하고 $E = F \cap [a, b]$로 두자. $E = F \cap [k/n, (k+1)/n]$이라고 하자. $E$는 닫힌집합이므로, $E$가 고립점을 가지지 않는다면 $E$는 완벽하다. 귀류법에 따라 $x \in E$가 고립점이라고 하자. 상한과 하한의 정의에 의해 $x \neq a, b$이다. 따라서 어떤 충분히 작은 $\delta > 0$가 존재하여 $E \cap (x - \delta, x + \delta) = \lbrace x\rbrace $이고 $k/n < x - \delta, x + \delta < (k + 1)/n$이다. 이때 $F \cap (x - \delta, x + \delta) = \lbrace x\rbrace $이므로 $x$는 $F$의 고립점이다. 이는 모순이므로, $E$는 완벽하다. □
$P$가 공집합이 아닌 완벽한 집합이라고 하자. 위 두 보조정리로부터, 선택 공리를 사용함으로써 다음과 같이 귀납적으로 정의할 수 있다.
- $P_1, P_2 \subset P, P_1 \cap P_2 = \varnothing, \mathrm{diam} P_1, \mathrm{diam} P_2 < 1/2$
- $P_{11}, P_{12} \subset P_1, P_{11} \cap P_{12} = \varnothing, \mathrm{diam} P_{11}, \mathrm{diam} P_{12} < 1/4$
- $P_{21}, P_{22} \subset P_2, P_{21} \cap P_{22} = \varnothing, \mathrm{diam} P_{21}, \mathrm{diam} P_{22} < 1/4$
- $P_{111}, P_{112} \subset P_{11}, P_{111} \cap P_{112} = \varnothing, \mathrm{diam} P_{111}, \mathrm{diam} P_{112} < 1/8$
- …
모든 $P_i$의 교집합을 $A$라고 하자. $A$는 칸토어 집합과 크기가 같다. 그런데 칸토어 집합은 실수와 크기가 같으므로, $|P| = 2^{\aleph_0}$이다. ■
위 정리와 칸토어-벤딕슨 정리로부터 다음 결과가 얻어진다.
따름정리. $F \subseteq \mathbb{R}$이 닫힌집합이라면 $|F| = \aleph_0$이거나 $|F| = 2^{\aleph_0}$이다.
참고로 칸토어-벤딕슨 정리와 비슷한 결과가 보렐 집합에서 성립한다.
정리. $B \subseteq \mathbb{R}$이 비가산 보렐 집합이라면 $B$는 완벽한 집합을 포함한다.
증명. 생략.
따라서 보다 일반적으로 다음이 성립한다.
따름정리. $B \subseteq \mathbb{R}$이 보렐 집합이라면 $|B| = \aleph_0$이거나 $|B| = 2^{\aleph_0}$이다.
The Continuum Hypothesis for Closed Sets and Borel Sets
25 Sep 2025The continuum hypothesis (CH) asks whether $\aleph_1 = 2^{\aleph_0}$ holds. This is equivalent to asking whether there exists an uncountable set whose cardinality is smaller than that of the real numbers. As is well known, CH is neither provable nor disprovable in ZFC, but it can be proven for certain restricted cases. Cantor proved that CH holds when restricted to closed subsets of the real numbers.
Theorem. If $F \subseteq \mathbb{R}$ is a closed set, then $|F| = \aleph_0$ or $|F| = 2^{\aleph_0}$.
The proof of this theorem uses the concept of a perfect set. I previously introduced this when discussing the Cantor-Bendixson theorem, but let me reintroduce it here.
Definition. For a topological space $X$, a subset $P \subseteq X$ is said to be perfect if $P = P’$, where $P’$ is the set of limit points of $P$ in $X$.
In general, for a subset $A \subseteq X$, there are two reasons why $A$ and $A’$ may not include one or the other.
- If $x$ is an isolated point of $A$, then $x \in A$ but $x \notin A’$
- If $x$ is a limit point of $A$ that does not belong to $A$, then $x \notin A$ but $x \in A’$
Therefore, a perfect set is a closed set with no isolated points. Accordingly, when given a closed set $F$, one might expect that removing all isolated points from $F$ would yield a perfect set. The problem is that the set obtained after removing isolated points may itself have isolated points. For example,
\[F = \mathbb{N} \cup \lbrace m - 1/n : m \geq 0, n > 1 \rbrace\]The set obtained by removing the isolated points of $F$ is $\mathbb{N}$, each of whose points is isolated. However, if we repeat this process of ‘removing’ isolated points transfinitely, we obtain the following interesting result.
Cantor-Bendixson Theorem. If $F \subseteq \mathbb{R}$ is a closed set, then there exist a countable set $C$ and a perfect set $P$ such that $F = P \sqcup C$.
Proof. Although a proof is presented in the previous link, here we present Cantor’s alternate proof.
Define transfinitely as follows:
\[\begin{gather} F_0 = F \\ F_{\alpha + 1} = F_\alpha' \\ F_\lambda = \bigcap_{\alpha < \lambda} F_\alpha \quad (\lim \lambda) \end{gather}\]Observe the following:
- Each $F_\alpha$ is a closed set.
- If $\alpha \leq \beta$, then $F_\alpha \supseteq F_\beta$.
- $F_\alpha \setminus F_{\alpha + 1}$ is the set of isolated points of $F_\alpha$.
- If $\alpha \neq \beta$, then $F_{\alpha} \setminus F_{\alpha + 1}$ and $F_{\beta} \setminus F_{\beta+1}$ are disjoint.
If $F_{\alpha} \setminus F_{\alpha+1} \neq \varnothing$ for all $\alpha \in \mathrm{Ord}$, then for the Hartogs number $\gamma$ of $\mathcal{P}(F)$, the function $f : \gamma \to \mathcal{P}(F); \alpha \mapsto F_{\alpha} \setminus F_{\alpha + 1}$ would be injective, which is a contradiction. Therefore, there exists $\xi$ such that $F_{\xi} \setminus F_{\xi+1} = \varnothing$. Setting $P = F_\xi$, we have that $P$ is either empty or perfect.
Let $C = F \setminus P$. Let $\mathcal{B} = \lbrace B_n \rbrace $ be a countable basis for $\mathbb{R}$. Define $f: C \to \omega$ as follows:
\[f(x) = \mathop{\arg \min}\limits_{n \in \omega} : B_n \cap F_\alpha = \{ x \} \quad (x \in F_\alpha \setminus F_{\alpha + 1})\]Verify that $f$ is well-defined and injective. ■
Theorem. If $P \subseteq \mathbb{R}$ is a non-empty perfect set, then $|P| = 2^{\aleph_0}$.
Proof. We prove the following two lemmas.
Lemma. If $P \subseteq \mathbb{R}$ is a non-empty perfect set, then there exist non-empty perfect disjoint sets $P_1, P_2 \subset P$.
Proof. Let $\alpha = \inf P$ and $\beta = \sup P$ (where $\alpha, \beta$ may be $\pm \infty$). If $(\alpha, \beta) \subset P$, then for any $r, s$ with $\alpha < r < s < \beta$, the sets $P \cap (-\infty, r]$ and $P \cap [s, \infty)$ satisfy the conditions. If $(\alpha, \beta) \not\subset P$, then there exists some $x \in (\alpha, \beta)$ such that $x \notin P$. Since $P = P’$, $x$ is not a limit point of $P$. Therefore, there exists sufficiently small $\delta > 0$ such that $(x - \delta, x + \delta)$ is disjoint from $F$ and $\alpha < x - \delta, x + \delta < \beta$. In this case, $P \cap (-\infty, x - \delta]$ and $P \cap [x + \delta, \infty)$ satisfy the conditions. □
Lemma. If $P \subseteq \mathbb{R}$ is a non-empty perfect set, then for any $n > 0$, there exists a non-empty perfect set $P’ \subset P$ such that $\mathrm{diam} P’ < 1/n$.
Proof. For $\mathcal{J} = \lbrace (m/n, (m+1)/n) : m \in \mathbb{Z} \rbrace $, there exists $(k/n, (k+1)/n) \in \mathcal{J}$ such that $J \cap F \neq \varnothing$ (otherwise $P = \lbrace m/n : m \in \mathbb{Z} \rbrace $, which is not perfect). Let $a = \inf F \cap (k/n, (k+1)/n)$ and $b = \sup F \cap (k/n, (k+1)/n)$ and take $E = F \cap [a, b]$. Since $E$ is a closed set, if $E$ has no isolated points, then $E$ is perfect. For contradiction, assume that $x \in E$ is an isolated point of $E$. By the definition of supremum and inifimum, $x \neq a, b$. Hence there exists sufficiently small $\delta > 0$ such that $E \cap (x - \delta, x + \delta) = \lbrace x\rbrace $ and $k/n < x - \delta, x + \delta < (k + 1)/n$. In this case, $F \cap (x - \delta, x + \delta) = \lbrace x\rbrace $, so $x$ is an isolated point of $F$, which is a contradiction. Hence, $E$ is perfect. □
Let $P$ be a non-empty perfect set. From the two lemmas above, using the axiom of choice, we can inductively define:
- $P_1, P_2 \subset P, P_1 \cap P_2 = \varnothing, \mathrm{diam} P_1, \mathrm{diam} P_2 < 1/2$
- $P_{11}, P_{12} \subset P_1, P_{11} \cap P_{12} = \varnothing, \mathrm{diam} P_{11}, \mathrm{diam} P_{12} < 1/4$
- $P_{21}, P_{22} \subset P_2, P_{21} \cap P_{22} = \varnothing, \mathrm{diam} P_{21}, \mathrm{diam} P_{22} < 1/4$
- $P_{111}, P_{112} \subset P_{11}, P_{111} \cap P_{112} = \varnothing, \mathrm{diam} P_{111}, \mathrm{diam} P_{112} < 1/8$
- …
Let $A$ be the intersection of all $P_i$. $A$ has the same cardinality as the Cantor set. Since the Cantor set has the same cardinality as the real numbers, $|P| = 2^{\aleph_0}$. ■
From the above theorem and the Cantor-Bendixson theorem, we obtain the following result.
Corollary. If $F \subseteq \mathbb{R}$ is a closed set, then $|F| = \aleph_0$ or $|F| = 2^{\aleph_0}$.
Incidentally, a result similar to the Cantor-Bendixson theorem holds for Borel sets.
Theorem. If $B \subseteq \mathbb{R}$ is an uncountable Borel set, then $B$ contains a perfect set.
Proof. Omitted.
Therefore, more generally, the following holds.
Corollary. If $B \subseteq \mathbb{R}$ is a Borel set, then $|B| = \aleph_0$ or $|B| = 2^{\aleph_0}$.
기수 연산
16 Sep 2025이 글에서 모든 집합과 기수는 무한하다.
1. 기수 덧셈
기수 산술cardinal arithmetics을 다룰 때에는 각 연산의 정의를 정확히 아는 것이 중요하다. 정의와 정리를 혼동하기가 쉽기 때문이다. 먼저 기수 덧셈부터 보자.
정의. $A, B$가 각각 기수가 $\kappa, \lambda$인 서로소 집합이라고 하자. $\kappa + \lambda$를 $|A \cup B |$로 정의한다.
정리. 기수의 유한 덧셈은 교환법칙과 결합법칙을 만족한다.
위 정의가 well-defined임을 보이기 위해서는 $\kappa + \lambda$가 $A, B$의 선택에 의존적이지 않음을 보여야 한다. 이는 ZF에서 쉽게 증명 가능하다. 또한 유한한 기수 덧셈은 그저 최대 기수를 구하는 것이기 때문에 계산하기가 상당히 용이하다.
정리.
\[\kappa + \lambda = \mathrm{max}(\kappa, \lambda)\]
증명. “2. 기수 곱셈”의 보조정리와 칸토어-베른슈타인 정리에 의해, $\aleph_\alpha = \aleph_\alpha + \aleph_\alpha$이다. 따라서 $|A| \leq |B|$라면 $|B| \leq |A + B| \leq |B + B| = |B|$이다. ■
기수 덧셈의 정의를 무한한 경우로 확장하면,
정의. 각 $i \in I$에 대해 $A_i$가 기수 $\kappa_i$인 쌍으로 서로소인 집합족 $\lbrace A_i \rbrace $가 주어졌을 때, 다음과 같이 정의한다.
\[\sum_{i \in I} \kappa_i = \left| \bigcup_{i \in I}A_i \right|\]
유의할 점은, 위 정의가 well-defined임을 보이는 데는 선택 공리가 필요하다는 점이다. 각 $i \in I$에 대해 일대일 대응 $A_i \to \kappa_i$을 선택할 수 있어야 하기 때문이다. 그래서 기수 산술을 다룰 때에는 거의 언제나 선택 공리를 전제한다.
$\kappa + \lambda = \mathrm{max}(\kappa, \lambda)$ 관계식으로부터 다음의 관계식을 유도하고 싶을 수 있지만, 성립하는 식이 아님에 주의해야 한다.
주의. $\sum_{i \in I} \kappa_i = \sup \kappa_i$는 일반적으로 성립하지 않는다.
2. 기수 곱셈
그렇다면 무한한 기수 덧셈은 어떻게 계산해야 할까? 이를 알아보기 위해, 먼저 기수 곱셈을 정의하자.
정의. $A, B$가 각각 기수가 $\kappa, \lambda$인 집합이라고 하자. $\kappa \cdot \lambda$를 $| A \times B|$로 정의한다.
정리. 기수의 유한 곱셈은 교환법칙과 결합법칙을 만족한다.
아주 용이하게도 유한 기수 곱셈의 계산은 유한 기수 덧셈의 계산과 같다.
정리.
\[\kappa \cdot \lambda = \mathrm{max}(\kappa, \lambda)\]
증명. 다음의 보조정리로부터 따라 나온다. ■
보조정리. 임의의 $\alpha \in \mathrm{Ord}$에 대해, $\aleph_\alpha \cdot \aleph_\alpha = \aleph_\alpha$
증명 개요는 다음과 같다. 임의의 $\alpha \in \mathrm{Ord}$에 대해, 다음과 같이 정의된 순서 $\prec$가 $\omega_\alpha \times \omega_\alpha$의 정렬 순서임을 보인다. $\hat{x} = \mathrm{max}(x_1, x_2), \hat{y} = \mathrm{max}(y_1, y_2)$일 때,
\[(x_1, x_2) \prec (y_1, y_2) \iff \begin{cases} \hat{x} < \hat{y}\\ x_1 < y_1 \quad (\text{if }\hat{x} < \hat{y}) \\ x_2 < y_2 \quad (\text{if }\hat{x} < \hat{y}, x_1 = y_1) \\ \end{cases}\]즉, $\prec$은 최댓값 우선 후 사전식 순서이다. 초한귀납법에 따라 모든 $\beta < \alpha$에 대해 $\aleph_\beta \cdot \aleph_\beta = \aleph_\beta$일 때 $\aleph_\alpha \cdot \aleph_\alpha = \aleph_\alpha$임을 보인다. 이를 위해 $(\omega_\alpha \times \omega_\alpha, \prec)$의 순서형order type이 $\omega_\alpha$를 넘지 않음을 보이면 된다. 이를 위해 임의의 $(\gamma_1, \gamma_2) \in \omega_\alpha \times \omega_\alpha$에 대해
\[X = \{ (\xi_1, \xi_2) : (\xi_1, \xi_2) \prec (\gamma_1, \gamma_2) \}\]라면 $|X| < \aleph_\alpha$임을 보이면 된다. $\gamma = \mathrm{max}(\gamma_1, \gamma_2) + 1$이라고 하자. $\omega_\alpha$는 극한 서수이므로 $\gamma \in \omega_\alpha$이며, 따라서 $|\gamma| = \aleph_\delta \; (\delta < \alpha)$이다. 한편으로 $X \subseteq \gamma \times \gamma$이므로 $|X| \leq \aleph_\delta \cdot \aleph_\delta$이며 이는 귀납 가정에 의해 $\aleph_\delta$이다. ■
기수 곱셈의 정의는 기수 덧셈과 아무 관련이 없다. 즉, 기수 곱셈의 정의에는 “$\kappa$를 $\lambda$번 더한다”와 같은 의미가 없다. 그럼에도 다음 정리에 의해 기수 곱셈을 기수 덧셈과 연관지을 수 있다.
정리.
\[\sum_{i \in I} \kappa = |I| \cdot \kappa\]
증명. $\lbrace A_i \rbrace $가 쌍으로 서로소이며 $|A_i| = \kappa$인 집합족이라고 하자. 좌변은 $\bigcup_{i \in I} A_i$의 기수이고, 우변은 $I \times A$의 기수이다 $(|A| = \kappa)$. 선택 공리에 의해 각 $i \in I$에 대해 일대일 대응 $f_i : A_i \to A$를 정의할 수 있다. 다음의 대응 $f: \bigcup_{i \in I} A_i \to I \times A$을 정의하자.
\[f(x) = (i, f_i(x)) \quad (\text{if } x \in A_i)\]위 함수가 일대일 대응임은 쉽게 확인할 수 있다. 따라서 (좌변) = (우변)이다. ■
이로부터 앞선 언급한 “주의”에 해당되는 올바른 관계식을 증명할 수 있다.
정리.
\[\sum_{i \in I} \kappa_i = |I| \cdot \sup \kappa_i\]
증명. $\kappa = \sup \lbrace \kappa_i : i \in I \rbrace $라고 하고, 좌변을 $L$, 우변을 $R$이라고 하자. 앞선 정리에 의해 $|I| \cdot \kappa = \sum_{i \in I} \kappa$이고 $\kappa_i \leq \kappa$이므로 $L ≤ R$이다. 반대로, $| I | = \sum_{i \in I} 1 \leq L$이고, $\kappa = \sup \kappa_i \leq L$이다. 글 하단의 보조정리에 의해 $L = L \cdot L$이므로 $L \geq | I | \cdot \kappa = R$이다. 따라서 칸토어-베른슈타인 정리에 의해 $L = R$이다. (이 증명에는 선택 공리가 암시적으로 많이 사용되었으니 관심 있는 독자는 생략된 논증을 자세히 써 봐도 좋을 것이다) ■
이제 기수 곱셈도 무한 경우로 일반화하자.
정의. 각 $i \in I$에 대해 $A_i$가 기수 $\kappa_i$인 집합족 $\lbrace A_i \rbrace $가 주어졌을 때, 다음과 같이 정의한다.
\[\prod_{i \in I} \kappa_i = \left| \prod_{i \in I}A_i \right|\]
기수 곱셈을 계산할 때 쾨니히 정리König’s Theorem가 유용하게 사용될 수 있다.
쾨니히 정리. 인덱스 집합 $I$에 대해 $\kappa_i < \lambda_i$라고 하자. 다음이 성립한다.
\[\sum \kappa_i < \prod \lambda_i\]
당연한 거 아니냐고 생각할 수 있겠지만, 일반적으로 1, 2는 고사하고 3도 성립하지 않는다는 사실에 유의하라.
- $\kappa_i < \lambda_i$라면 $\sum \kappa_i < \sum \lambda_i$
- $\kappa_i < \lambda_i$라면 $\prod \kappa_i < \prod \lambda_i$
- $\kappa_i \leq \lambda_i$일 때 $\sum \kappa_i < \prod \lambda_i$
물론 1, 2, 3에서 결론부의 부등호를 $<$에서 $\leq$로 약화하면 모두 성립한다. 쾨니히 정리의 특징은 결론부가 엄격한 부등호라는 것이다.
증명. $\lbrace A_i \rbrace , \lbrace B_i \rbrace $가 각각 기수가 $\kappa_i, \lambda_i$인 (쌍으로 서로소인) 집합들의 모임이라고 하자. 귀류법에 따라, $f: \prod B_i \to \cup A_i$인 단사함수가 존재한다고 하자. 임의의 $i \in I$에 대해, $f$의 단사성으로부터 $|f^{-1}(A_i)| = |A_i|$이다. 그런데 $|A_i| < |B_i|$이므로 $\pi_i (f^{-1}(A_i)) \subset B_i$는 $B_i$보다 크기가 엄격히 작으며, 이에 따라 $b_i \in B_i \setminus \pi_i (f^{-1}(A_i))$가 존재한다. 각 $i$에 대해 그러한 $b_i$를 고른 뒤, $b = (b_i)_{i \in I}$를 생각하면, 임의의 $i \in I$에 대해 $\pi_i(b) = b_i$이므로 $f(b) \notin \cup A_i$가 되어 모순이다. ■
3. 기수 지수
정의. $A, B$가 각각 기수가 $\kappa, \lambda$인 집합이라고 하자. $\kappa^\lambda$를 $|A^B |$로 정의한다. ($A^B$는 $B$에서 $A$로 가는 함수들의 집합이다)
기수 곱셈의 경우와 마찬가지로, 비록 기수 지수의 정의는 기수 곱셈과 아무 관련이 없지만, 다음 정리에 의해 둘 사이에 다리를 놓을 수 있다.
정리.
\[\prod_{i \in I} \kappa = \kappa^{|I|}\]
또한 기수 지수는 일반적인 지수의 여러 좋은 성질을 공유한다.
정리. 기수의 지수 연산은 지수법칙을 만족한다. 즉,
- $\kappa^{\lambda + \mu} = \kappa^\lambda \cdot \kappa^\mu$
- $(\kappa^\lambda)^\mu = \kappa^{\lambda \cdot \mu}$
- $(\kappa \cdot \lambda)^{\mu} = \kappa^\mu \cdot \lambda^\mu$
그럼에도 기수 지수를 정확히 계산하기란 굉장히 까다로운데, 일반화된 연속체 가설Generalized Continuum Hypothesis을 전제하지 않으면 얻을 수 있는 결과가 제한적이기 때문이다. 우선 일반화된 연속체 가설 없이 증명할 수 있는 정리들을 보자.
정리.
- $2^{\aleph_\alpha} > \aleph_\alpha$
- $\alpha \leq \beta \implies \kappa^{\aleph_\alpha} \leq \kappa^{\aleph_\beta}$
- $\mathrm{cf}(\kappa^{\aleph_\alpha}) > \aleph_\alpha$
$\mathrm{cf}(\kappa) \leq \kappa$이므로 3이 1을 함의한다는 사실에 주목하라.
증명. 1은 칸토어의 정리이고, 2는 선택 공리를 사용하면 자명하다. 3의 증명은 쾨니히 정리를 사용한다. $\mathrm{cf}(\kappa^{\aleph_\alpha}) = \aleph_\lambda$라고 하자. $\mathrm{cf}$의 정의에 의해 $\xi_i < \kappa^{\aleph_\alpha}$이며 $\sum_{i < \omega_\lambda} \xi_i = \kappa^{\aleph_\alpha}$을 만족하는 $\lbrace \xi_i \rbrace _{i < \omega_\lambda}$가 존재한다. 쾨니히 정리에 의해 다음이 성립한다.
\[\kappa^{\aleph_\alpha} = \sum_{i < \omega_\lambda} \xi_i < \prod_{i < \omega_\lambda} \kappa^{\aleph_\alpha} = \kappa^{\aleph_\alpha \cdot \aleph_\lambda}\]그런데 만약 $\aleph_\lambda = \aleph_\alpha$라면 $\kappa^{\aleph_\alpha \cdot \aleph_\lambda} = \kappa^{\aleph_\alpha}$이므로 $<$가 성립하지 않는다. 따라서 $\aleph_\lambda > \aleph_\alpha$이다. ■
다음의 두 정리는 특히 유용하다.
정리.
\[\aleph_\alpha^{\aleph_\beta} = \begin{cases} 2^{\aleph_\beta} & (\aleph_\alpha \leq \aleph_\beta) \\ \mathrm{card} \{ A \subseteq \omega_\alpha : |A| = \aleph_\beta \} & (\aleph_\beta < \aleph_\alpha) \end{cases}\]
증명. $\aleph_\alpha \leq \aleph_\beta$인 경우의 증명은 다음과 같다.
\[2^{\aleph_\beta} \leq \aleph_\alpha^{\aleph_\beta} \leq (2^{\aleph_\alpha})^{\aleph_\beta} = 2^{\aleph_\alpha \cdot \aleph_\beta} = 2^{\aleph_\beta}\]$\aleph_\alpha > \aleph_\beta$인 경우를 증명하자. 좌변의 집합을 $S$라고 하자. 각 $S$의 원소는 $\aleph_\beta$에서 $\aleph_\alpha$로 가는 단사함수로 생각할 수 있으므로 $|S| \leq {\aleph_\alpha}^{\aleph_\beta}$이다. 역방향을 보이기 위해 먼저 $\aleph_\beta < \aleph_\alpha$이므로 $\aleph_\alpha = \aleph_\beta \cdot \aleph_\alpha$임을 관찰하자. 따라서,
\[|S| = |T| \quad \text{where} \quad T = \{ A \subseteq \omega_\beta \times \omega_\alpha : |A| = \aleph_\beta \}\]그런데 $T$의 각 원소는 $\omega_\alpha$에서 중복을 허용하고 $\aleph_\beta$개의 원소를 뽑는 경우의 수로 생각될 수 있다. 이는 $T$에서 ${\aleph_\alpha}^{\aleph_\beta}$로 가는 전사 관계를 정의한다. 따라서 ${\aleph_\alpha}^{\aleph_\beta} = |S|$이다. ■
이의 따름정리는 하우스도르프 정리이다.
하우스도르프 정리.
\[\aleph_{\alpha+1}^{\aleph_\beta} = \aleph_\alpha^{\aleph_\beta} \cdot \aleph_{\alpha + 1}\]
증명. $\beta > \alpha$라면 앞선 정리에 의해 정리가 자명하게 성립한다. 따라서 $\beta \leq \alpha$라고 하자. $\aleph_{\alpha+1}^{\aleph_\beta} \geq \aleph_\alpha^{\aleph_\beta}, \aleph_{\alpha + 1}$이므로 $\geq$ 방향은 자명하게 성립한다. 따라서 $\leq$ 방향을 보이면 충분하다.
$\aleph_{\alpha + 1}$은 계승자 기수successor cardinal이므로 정칙regular이며, 이에 따라 $\aleph_\beta < \mathrm{cf}(\aleph_{\alpha + 1})$이다. 따라서 $f \in \omega_\alpha^{\omega_\beta}$는 상계를 가진다. 즉,
\[\aleph_{\alpha+1}^{\aleph_\beta} = \bigcup_{\gamma < \omega_{\alpha + 1}} \gamma^{\omega_\beta}\]여기서 각 $\gamma$는 기수가 $\aleph_\alpha$ 이하이다. 따라서 다음이 성립한다.
\[\aleph_{\alpha+1}^{\aleph_\beta} \leq \sum_{\gamma < \omega_{\alpha + 1}} |\gamma|^{\aleph_\beta} \leq \sum_{\gamma < \omega_{\alpha + 1}} {\aleph_\alpha}^{\aleph_\beta} = {\aleph_\alpha}^{\aleph_\beta} \cdot \aleph_{\alpha + 1} \quad \blacksquare\]4. 일반화된 연속체 가설 하에서
일반화된 연속체 가설을 전제하면 훨씬 더 강력한 결과들을 증명할 수 있다.
정리. $\aleph_\alpha$가 정칙 기수인 경우, 다음이 성립한다.
\[\aleph_\alpha^{\aleph_\beta} = \begin{cases} \aleph_{\beta + 1} & \aleph_\alpha \leq \aleph_\beta \\ \aleph_{\alpha} & \aleph_\beta < \aleph_\alpha \end{cases}\]
증명. $\aleph_\alpha \leq \aleph_\beta$인 경우 $\aleph_\alpha^{\aleph_\beta} = 2^{\aleph_\beta}$이므로 GCH에 의해 성립한다. $\aleph_\alpha > \aleph_\beta$인 경우,
\[\aleph_\alpha^{\aleph_\beta} = |S| \quad \text{where} S = \{ A \subseteq \omega_\alpha : |A| = \aleph_\beta \}\]이다. $\aleph_\alpha$가 정칙이므로 $S$의 각 원소는 유계이다. 따라서,
\[S \subseteq \bigcup_{\lambda \in \omega_\alpha} \mathcal{P}(\lambda)\]이다. 임의의 $\lambda \in \omega_\alpha$에 대해 $|\lambda| = \aleph_\delta$라고 하면, $\aleph_\delta < \aleph_\alpha$이므로 $2^{|\lambda|} = \aleph_{\delta + 1} < \aleph_\alpha$이다. 따라서 다음이 성립한다.
\[\begin{align} |S| &\leq \sum_{\lambda \in \omega_\alpha} 2^{|\lambda} \\ &\leq \sum_{\lambda \in \omega_\alpha} \aleph_\alpha \\ &= \aleph_\alpha \cdot \aleph_\alpha = \aleph_\alpha \quad \blacksquare \end{align}\]정리. $\aleph_\alpha$가 특이 기수인 경우, 다음이 성립한다.
\[\aleph_\alpha^{\aleph_\beta} = \begin{cases} \aleph_{\beta + 1} & \aleph_\alpha \leq \aleph_\beta \\ \aleph_{\alpha + 1} & \mathrm{cf}(\aleph_\alpha) \leq \aleph_\beta < \aleph_\alpha \\ \aleph_{\alpha} & \aleph_\beta < \mathrm{cf}(\aleph_\alpha) \end{cases}\]
증명. 첫 번째 경우와 세 번째 경우는 이전 정리의 증명과 거의 같으므로, 두 번째 경우만 살펴보자. 다음이 성립한다.
\[\aleph_\alpha \leq \aleph_\alpha^{\aleph_\beta} \leq \aleph_\alpha^{\aleph_\alpha} = 2^{\aleph_\alpha} = \aleph_{\alpha+1}\]따라서 $\aleph_\alpha < \aleph_\alpha^{\aleph_\beta}$임을 보이면 충분하다. 만약 $\aleph_\alpha = \aleph_\alpha^{\aleph_\beta}$라면 $\mathrm{cf}(\aleph_\alpha) = \mathrm{cf}(\aleph_\alpha^{\aleph_\beta}) > \aleph_\beta$인데, 가정에 의해 $\mathrm{cf}(\aleph_\alpha) \leq \aleph_\beta$이므로 모순이다. ■
Cardinal Arithmetic
16 Sep 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
In this article, all sets and cardinals are infinite.
1. Cardinal Addition
When dealing with cardinal arithmetic, it is important to know the precise definitions of each operation. It is easy to confuse definitions with theorems. Let us begin with cardinal addition.
Definition. Let $A, B$ be disjoint sets with cardinalities $\kappa, \lambda$ respectively. Define $\kappa + \lambda$ as $|A \cup B |$.
Theorem. Finite cardinal addition satisfies the commutative and associative laws.
To show that the above definition is well-defined, we must prove that $\kappa + \lambda$ does not depend on the choice of $A, B$. This is easily provable in ZF. Moreover, finite cardinal addition is merely finding the maximum cardinal, making it quite easy to compute.
Theorem.
\[\kappa + \lambda = \mathrm{max}(\kappa, \lambda)\]
Proof. By the lemma in “2. Cardinal Multiplication” and the Cantor-Bernstein theorem, $\aleph_\alpha = \aleph_\alpha + \aleph_\alpha$. Therefore, if $|A| \leq |B|$, then $|B| \leq |A + B| \leq |B + B| = |B|$. ■
Extending the definition of cardinal addition to the infinite case,
Definition. Given a family of pairwise disjoint sets $\lbrace A_i \rbrace $ where each $A_i$ has cardinality $\kappa_i$ for $i \in I$, we define:
\[\sum_{i \in I} \kappa_i = \left| \bigcup_{i \in I}A_i \right|\]
Note that proving this definition is well-defined requires the axiom of choice. For each $i \in I$, we must be able to choose a bijection $A_i \to \kappa_i$. Therefore, when dealing with cardinal arithmetic, the axiom of choice is almost always presupposed.
From the relation $\kappa + \lambda = \mathrm{max}(\kappa, \lambda)$, one might wish to derive the following relation, but note that this is not a valid equation.
Warning. $\sum_{i \in I} \kappa_i = \sup \kappa_i$ does not hold in general.
2. Cardinal Multiplication
How then should we compute infinite cardinal addition? To understand this, let us first define cardinal multiplication.
Definition. Let $A, B$ be sets with cardinalities $\kappa, \lambda$ respectively. Define $\kappa \cdot \lambda$ as $| A \times B|$.
Theorem. Finite cardinal multiplication satisfies the commutative and associative laws.
Very conveniently, the computation of finite cardinal multiplication is the same as that of finite cardinal addition.
Theorem.
\[\kappa \cdot \lambda = \mathrm{max}(\kappa, \lambda)\]
Proof. This follows from the lemma below. ■
Lemma. For any $\alpha \in \mathrm{Ord}$, $\aleph_\alpha \cdot \aleph_\alpha = \aleph_\alpha$
The proof outline is as follows. For any $\alpha \in \mathrm{Ord}$, we show that the order $\prec$ defined as follows is a well-ordering of $\omega_\alpha \times \omega_\alpha$. When $\hat{x} = \mathrm{max}(x_1, x_2), \hat{y} = \mathrm{max}(y_1, y_2)$,
\[(x_1, x_2) \prec (y_1, y_2) \iff \begin{cases} \hat{x} < \hat{y}\\ x_1 < y_1 \quad (\text{if }\hat{x} < \hat{y}) \\ x_2 < y_2 \quad (\text{if }\hat{x} < \hat{y}, x_1 = y_1) \\ \end{cases}\]That is, $\prec$ is the maximum-first then lexicographic order. By transfinite induction, we show that $\aleph_\alpha \cdot \aleph_\alpha = \aleph_\alpha$ when $\aleph_\beta \cdot \aleph_\beta = \aleph_\beta$ for all $\beta < \alpha$. For this, it suffices to show that the order type of $(\omega_\alpha \times \omega_\alpha, \prec)$ does not exceed $\omega_\alpha$. We need to show that for any $(\gamma_1, \gamma_2) \in \omega_\alpha \times \omega_\alpha$,
\[X = \{ (\xi_1, \xi_2) : (\xi_1, \xi_2) \prec (\gamma_1, \gamma_2) \}\]satisfies $|X| < \aleph_\alpha$. Let $\gamma = \mathrm{max}(\gamma_1, \gamma_2) + 1$. Since $\omega_\alpha$ is a limit ordinal, $\gamma \in \omega_\alpha$, and therefore $|\gamma| = \aleph_\delta$ for some $\delta < \alpha$. On the other hand, $X \subseteq \gamma \times \gamma$, so $|X| \leq \aleph_\delta \cdot \aleph_\delta$, which equals $\aleph_\delta$ by the induction hypothesis. ■
The definition of cardinal multiplication has no relation to cardinal addition. That is, there is no meaning like “adding $\kappa$ exactly $\lambda$ times” in the definition of cardinal multiplication. Nevertheless, the following theorem allows us to relate cardinal multiplication to cardinal addition.
Theorem.
\[\sum_{i \in I} \kappa = |I| \cdot \kappa\]
Proof. Let $\lbrace A_i \rbrace $ be a family of pairwise disjoint sets with $|A_i| = \kappa$. The left side is the cardinality of $\bigcup_{i \in I} A_i$, and the right side is the cardinality of $I \times A$ where $|A| = \kappa$. By the axiom of choice, for each $i \in I$ we can define a bijection $f_i : A_i \to A$. Define the following correspondence $f: \bigcup_{i \in I} A_i \to I \times A$:
\[f(x) = (i, f_i(x)) \quad (\text{if } x \in A_i)\]It is easily verified that this function is a bijection. Therefore (left side) = (right side). ■
From this, we can prove the correct relation corresponding to the aforementioned “warning”.
Theorem.
\[\sum_{i \in I} \kappa_i = |I| \cdot \sup \kappa_i\]
Proof. Let $\kappa = \sup \lbrace \kappa_i : i \in I \rbrace $, and denote the left side as $L$ and the right side as $R$. By the previous theorem, $|I| \cdot \kappa = \sum_{i \in I} \kappa$, and since $\kappa_i \leq \kappa$, we have $L ≤ R$. Conversely, $| I | = \sum_{i \in I} 1 \leq L$ and $\kappa = \sup \kappa_i \leq L$. By the lemma at the bottom of this article, $L = L \cdot L$, so $L \geq | I | \cdot \kappa = R$. Therefore, by the Cantor-Bernstein theorem, $L = R$. (The axiom of choice is implicitly used extensively in this proof, so interested readers may wish to write out the omitted arguments in detail.) ■
Now let us generalise cardinal multiplication to the infinite case.
Definition. Given a family of sets $\lbrace A_i \rbrace $ where each $A_i$ has cardinality $\kappa_i$ for $i \in I$, we define:
\[\prod_{i \in I} \kappa_i = \left| \prod_{i \in I}A_i \right|\]
König’s theorem can be usefully employed when computing cardinal multiplication.
König’s Theorem. For an index set $I$, suppose $\kappa_i < \lambda_i$. The following holds:
\[\sum \kappa_i < \prod \lambda_i\]
One might think this is obvious, but note that in general, not only do 1 and 2 fail to hold, but even 3 does not hold.
- If $\kappa_i < \lambda_i$, then $\sum \kappa_i < \sum \lambda_i$
- If $\kappa_i < \lambda_i$, then $\prod \kappa_i < \prod \lambda_i$
- If $\kappa_i \leq \lambda_i$, then $\sum \kappa_i < \prod \lambda_i$
Of course, if we weaken the inequality in the conclusion from $<$ to $\leq$ in 1, 2, and 3, they all hold. The distinctive feature of König’s theorem is that the conclusion involves a strict inequality.
Proof. Let $\lbrace A_i \rbrace , \lbrace B_i \rbrace $ be collections of (pairwise disjoint) sets with cardinalities $\kappa_i, \lambda_i$ respectively. By contradiction, suppose there exists an injective function $f: \prod B_i \to \cup A_i$. For any $i \in I$, by the injectivity of $f$, $|f^{-1}(A_i)| = |A_i|$. But since $|A_i| < |B_i|$, $\pi_i (f^{-1}(A_i)) \subset B_i$ has strictly smaller cardinality than $B_i$, and accordingly there exists $b_i \in B_i \setminus \pi_i (f^{-1}(A_i))$. Choosing such $b_i$ for each $i$ and considering $b = (b_i)_{i \in I}$, we have $\pi_i(b) = b_i$ for any $i \in I$, so $f(b) \notin \cup A_i$, which is a contradiction. ■
3. Cardinal Exponentiation
Definition. Let $A, B$ be sets with cardinalities $\kappa, \lambda$ respectively. Define $\kappa^\lambda$ as $|A^B |$, where $A^B$ is the set of functions from $B$ to $A$.
As in the case of cardinal multiplication, although the definition of cardinal exponentiation has no relation to cardinal multiplication, the following theorem allows us to bridge the two.
Theorem.
\[\prod_{i \in I} \kappa = \kappa^{|I|}\]
Moreover, cardinal exponentiation shares several nice properties of ordinary exponentiation.
Theorem. Cardinal exponentiation satisfies the laws of exponents. That is,
- $\kappa^{\lambda + \mu} = \kappa^\lambda \cdot \kappa^\mu$
- $(\kappa^\lambda)^\mu = \kappa^{\lambda \cdot \mu}$
- $(\kappa \cdot \lambda)^{\mu} = \kappa^\mu \cdot \lambda^\mu$
Nevertheless, computing cardinal exponentiation precisely is quite challenging, as the results obtainable without assuming the Generalised Continuum Hypothesis are limited. Let us first examine theorems that can be proved without the Generalised Continuum Hypothesis.
Theorem.
- $2^{\aleph_\alpha} > \aleph_\alpha$
- $\alpha \leq \beta \implies \kappa^{\aleph_\alpha} \leq \kappa^{\aleph_\beta}$
- $\mathrm{cf}(\kappa^{\aleph_\alpha}) > \aleph_\alpha$
Note that since $\mathrm{cf}(\kappa) \leq \kappa$, property 3 implies 1.
Proof. 1 is Cantor’s theorem, and 2 is trivial using the axiom of choice. The proof of 3 uses König’s theorem. Let $\mathrm{cf}(\kappa^{\aleph_\alpha}) = \aleph_\lambda$. By the definition of $\mathrm{cf}$, there exists $\lbrace \xi_i \rbrace _{i < \omega_\lambda}$ such that $\xi_i < \kappa^{\aleph_\alpha}$ and $\sum_{i < \omega_\lambda} \xi_i = \kappa^{\aleph_\alpha}$. By König’s theorem, the following holds:
\[\kappa^{\aleph_\alpha} = \sum_{i < \omega_\lambda} \xi_i < \prod_{i < \omega_\lambda} \kappa^{\aleph_\alpha} = \kappa^{\aleph_\alpha \cdot \aleph_\lambda}\]But if $\aleph_\lambda = \aleph_\alpha$, then $\kappa^{\aleph_\alpha \cdot \aleph_\lambda} = \kappa^{\aleph_\alpha}$, so the strict inequality $<$ does not hold. Therefore $\aleph_\lambda > \aleph_\alpha$. ■
The following two theorems are particularly useful.
Theorem.
\[\aleph_\alpha^{\aleph_\beta} = \begin{cases} 2^{\aleph_\beta} & (\aleph_\alpha \leq \aleph_\beta) \\ \mathrm{card} \{ A \subseteq \omega_\alpha : |A| = \aleph_\beta \} & (\aleph_\beta < \aleph_\alpha) \end{cases}\]
Proof. The proof for the case $\aleph_\alpha \leq \aleph_\beta$ is as follows:
\[2^{\aleph_\beta} \leq \aleph_\alpha^{\aleph_\beta} \leq (2^{\aleph_\alpha})^{\aleph_\beta} = 2^{\aleph_\alpha \cdot \aleph_\beta} = 2^{\aleph_\beta}\]Let us prove the case $\aleph_\alpha > \aleph_\beta$. Let $S$ denote the set on the left. Each element of $S$ can be thought of as an injective function from $\aleph_\beta$ to $\aleph_\alpha$, so $|S| \leq {\aleph_\alpha}^{\aleph_\beta}$. To show the reverse direction, first observe that since $\aleph_\beta < \aleph_\alpha$, we have $\aleph_\alpha = \aleph_\beta \cdot \aleph_\alpha$. Therefore,
\[|S| = |T| \quad \text{where} \quad T = \{ A \subseteq \omega_\beta \times \omega_\alpha : |A| = \aleph_\beta \}\]But each element of $T$ can be thought of as the number of ways to choose $\aleph_\beta$ elements from $\omega_\alpha$ with repetition allowed. This defines a surjective relation from $T$ to ${\aleph_\alpha}^{\aleph_\beta}$. Therefore ${\aleph_\alpha}^{\aleph_\beta} = |S|$. ■
A corollary of this is Hausdorff’s theorem.
Hausdorff’s Theorem.
\[\aleph_{\alpha+1}^{\aleph_\beta} = \aleph_\alpha^{\aleph_\beta} \cdot \aleph_{\alpha + 1}\]
Proof. If $\beta > \alpha$, then by the previous theorem the statement holds trivially. Therefore suppose $\beta \leq \alpha$. Since $\aleph_{\alpha+1}^{\aleph_\beta} \geq \aleph_\alpha^{\aleph_\beta}, \aleph_{\alpha + 1}$, the $\geq$ direction holds trivially. Therefore it suffices to show the $\leq$ direction.
Since $\aleph_{\alpha + 1}$ is a successor cardinal, it is regular, and accordingly $\aleph_\beta < \mathrm{cf}(\aleph_{\alpha + 1})$. Therefore $f \in \omega_\alpha^{\omega_\beta}$ has an upper bound. That is,
\[\aleph_{\alpha+1}^{\aleph_\beta} = \bigcup_{\gamma < \omega_{\alpha + 1}} \gamma^{\omega_\beta}\]where each $\gamma$ has cardinality at most $\aleph_\alpha$. Therefore the following holds:
\[\aleph_{\alpha+1}^{\aleph_\beta} \leq \sum_{\gamma < \omega_{\alpha + 1}} |\gamma|^{\aleph_\beta} \leq \sum_{\gamma < \omega_{\alpha + 1}} {\aleph_\alpha}^{\aleph_\beta} = {\aleph_\alpha}^{\aleph_\beta} \cdot \aleph_{\alpha + 1} \quad \blacksquare\]4. Under the Generalised Continuum Hypothesis
Assuming the Generalised Continuum Hypothesis allows us to prove much stronger results.
Theorem. If $\aleph_\alpha$ is a regular cardinal, the following holds:
\[\aleph_\alpha^{\aleph_\beta} = \begin{cases} \aleph_{\beta + 1} & \aleph_\alpha \leq \aleph_\beta \\ \aleph_{\alpha} & \aleph_\beta < \aleph_\alpha \end{cases}\]
Proof. For the case $\aleph_\alpha \leq \aleph_\beta$, $\aleph_\alpha^{\aleph_\beta} = 2^{\aleph_\beta}$, so it holds by GCH. For the case $\aleph_\alpha > \aleph_\beta$,
\[\aleph_\alpha^{\aleph_\beta} = |S| \quad \text{where} S = \{ A \subseteq \omega_\alpha : |A| = \aleph_\beta \}\]Since $\aleph_\alpha$ is regular, each element of $S$ is bounded. Therefore,
\[S \subseteq \bigcup_{\lambda \in \omega_\alpha} \mathcal{P}(\lambda)\]For any $\lambda \in \omega_\alpha$, let $|\lambda| = \aleph_\delta$. Then $\aleph_\delta < \aleph_\alpha$, so $2^{|\lambda|} = \aleph_{\delta + 1} < \aleph_\alpha$. Therefore the following holds:
\[\begin{align} |S| &\leq \sum_{\lambda \in \omega_\alpha} 2^{|\lambda} \\ &\leq \sum_{\lambda \in \omega_\alpha} \aleph_\alpha \\ &= \aleph_\alpha \cdot \aleph_\alpha = \aleph_\alpha \quad \blacksquare \end{align}\]Theorem. If $\aleph_\alpha$ is a singular cardinal, the following holds:
\[\aleph_\alpha^{\aleph_\beta} = \begin{cases} \aleph_{\beta + 1} & \aleph_\alpha \leq \aleph_\beta \\ \aleph_{\alpha + 1} & \mathrm{cf}(\aleph_\alpha) \leq \aleph_\beta < \aleph_\alpha \\ \aleph_{\alpha} & \aleph_\beta < \mathrm{cf}(\aleph_\alpha) \end{cases}\]
Proof. The first and third cases are almost the same as the proof of the previous theorem, so we examine only the second case. The following holds:
\[\aleph_\alpha \leq \aleph_\alpha^{\aleph_\beta} \leq \aleph_\alpha^{\aleph_\alpha} = 2^{\aleph_\alpha} = \aleph_{\alpha+1}\]Therefore it suffices to show that $\aleph_\alpha < \aleph_\alpha^{\aleph_\beta}$. If $\aleph_\alpha = \aleph_\alpha^{\aleph_\beta}$, then $\mathrm{cf}(\aleph_\alpha) = \mathrm{cf}(\aleph_\alpha^{\aleph_\beta}) > \aleph_\beta$, but by assumption $\mathrm{cf}(\aleph_\alpha) \leq \aleph_\beta$, which is a contradiction. ■