불 대수 구조의 아이디얼과 필터

18 Jul 2025

불 대수

불 대수_{boolean algebra}는 거짓을 의미하는 $0$과 참을 의미하는 $1$ 위에서 정의되는 $\lor, \land, \lnot$ 등의 논리 연산으로 이루어진 대수이다.

$a$	$b$	$a \lor b$	$a \land b$	$\lnot a$
$0$	$0$	$0$	$0$	$1$
$0$	$1$	$1$	$0$	$1$
$1$	$0$	$1$	$0$	$0$
$1$	$1$	$1$	$1$	$0$

여기서 $0$과 $1$을 거짓과 참을 나타내는 형식적 기호로서가 아닌, 대소 비교가 가능한 실제 수로서 간주하면, $\lor$는 $\max$에, $\land$은 $\min$에, $\lnot$은 켤레 연산 $\bar{(\cdot)}: 0 \mapsto 1, 1 \mapsto 0$에 대응됨을 확인할 수 있다.

$a$	$b$	$\max (a, b)$	$\min (a, b)$	$\bar{a}$
$0$	$0$	$0$	$0$	$1$
$0$	$1$	$1$	$0$	$1$
$1$	$0$	$1$	$0$	$0$
$1$	$1$	$1$	$1$	$0$

이에 착안하여, 우리는 불 대수의 정의역을 $\lbrace 0, 1 \rbrace$에서 $[0, 1]$로 자연스럽게 확장할 수 있다. 가령 $0.2 \lor 0.7 = 0.7, 0.3 \land \lnot(0.9) = 0.1$와 같이 말이다. 이 생각을 발전시켜 보면, 적절한 순서 관계가 주어진 집합 위에서는 불 대수와 구조적으로 비슷한 연산을 정의할 수 있으며, 반대로 불 대수와 구조적으로 비슷한 연산이 정의된 집합에는 적절한 순서 관계를 줄 수 있을 듯하다. 이것이 불 대수 구조의 발상이다.

정의. 어떤 두 원소 $0$과 $1$을 가지는 집합 $A$ 위에서 정의된 이항연산 $\lor, \land$과 단항연산 $\lnot$이 다음의 공리를 만족할 때, $(A, 0, 1, \lor, \land, \lnot)$을 불 대수 구조_{Boolean algebraic structure}라고 부른다.

공리	$\lor$	$\land$
결합	$a \lor (b \lor c) = (a \lor b) \lor c$	$a \land (b \land c) = (a \land b) \land c$
교환	$a \lor b = b \lor a$	$a \land b = b \land a$
분배	$a \lor (b \land c) = (a \lor b) \land (a \lor c)$	$a \land (b \lor c) = (a \land b) \lor (a \land c)$
항등원	$a \lor 0 = a$	$a \land 1 = a$
쌍역원	$a \lor \lnot a = 1$	$a \land \lnot a = 0$
흡수	$a \lor (a \land b) = a$	$a \land (a \lor b) = a$

Remark.

• 흡수법칙은 나머지 다섯 공리로부터 증명이 가능하다.

• “쌍역원”이라는 표현은, 원래 $x$에 곱의 역원 $x^{-1}$을 곱하면 곱의 항등원 $1$이 나오고, 합의 역원 $-x$를 더하면 합의 항등원 $0$이 나와야 하지만, 불 대수 구조의 경우 $x \lor \lnot x$의 결과가 $\lor$의 항등원 $0$이 아닌 $\land$의 항등원 $1$이고, $x \land \lnot x$의 결과가 $\land$의 항등원 $1$이 아닌 $\lor$의 항등원 $0$이기 때문에, 혼동의 여지를 줄이고자 도입했다.

서론의 두 예시는 불 대수 구조임을 확인하라. 또다른 예시로, 집합 $X = \lbrace p, q, r \rbrace $의 멱집합 $\mathcal{P}(X)$를 보자. 다음과 같이 두었을 때 $\mathcal{P}(X)$는 불 대수 구조가 됨을 확인하라.

• $a \lor b = a \cup b$
• $a \land b = a \cap b$
• $\lnot a = X \setminus a$
• $1 = X$
• $0 = \varnothing$

$X$가 임의의 집합일 때에도 일반적으로 $X$의 멱집합은 불 대수 구조를 이룬다.

불 대수 구조에는 자연스러운 방식으로 부분순서_{partial order}를 줄 수 있다.

정리. $A$가 불 대수 구조라고 하자. 다음의 이항관계를 정의한다.

\[a \leq b \iff a = a \land b\]

$\leq$는 $A$의 부분순서이다. $1$과 $0$은 각각 $\leq$의 최대 원소, 최소 원소이다. $\lor$와 $\land$는 각각 $\leq$에 대한 상한과 하한을 내놓는 연산이다.

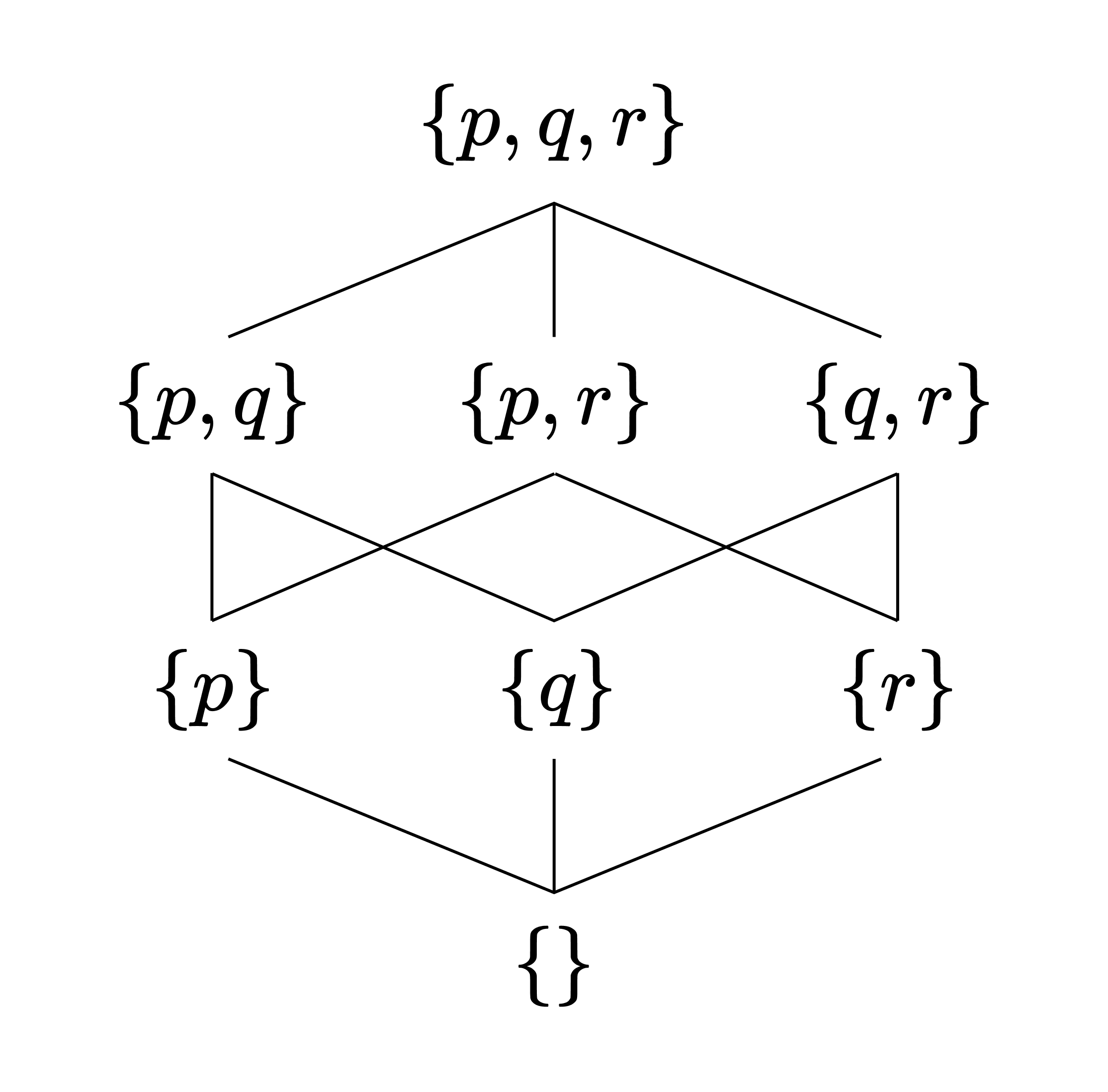
마찬가지로 증명은 생략한다. 이와 같이 불 대수 구조 $A$ 위에는 자연스러운 방식으로 부분순서 $\leq$를 줄 수 있으므로, $\leq$에 따라 $A$의 하세 다이어그램_{Hasse diagram}을 그릴 수 있다. 일례로 앞서 본 $X = \lbrace p, q, r\rbrace $에 대해 $\mathcal{P}(X)$가 이루는 불 대수 구조를 보자.

\[a \leq b \iff a = a \land b \iff a = a \cap b \iff a \subseteq b\]

이므로, 이 경우 불 대수 구조의 하세 다이어그램은 집합의 포함 다이어그램과 같다.

불 환

불 대수 구조는 두 개의 연산과, 각 연산에 해당되는 항등원을 요구한다는 점에서 환_ring과 정의가 비슷하다. 이는 단순한 우연이 아니다.

정의. 환 $R$이 불 환_{Boolean ring}이라는 것은, 임의의 $x \in R$에 대해 $x^2 = x$라는 것이다.

불 대수 구조와 불 환은 일대일 대응된다. 즉, 다음이 성립한다.

정리. $(R, 0, 1, +, \cdot)$가 불 환이라면, $(R, 0, 1, \lor, \cdot, (\cdot)^{-1})$은 불 대수 구조이다. 여기서 $\lor, \lnot$은 다음과 같이 정의된다.

\[\begin{gather} x \lor y = x + y + xy \\ \lnot x = 1 + x \end{gather}\]

역으로, $(A, 0, 1, \lor, \land, \lnot)$이 불 대수 구조라면 $(A, 0, 1, +, \land)$은 불 환이다. 여기서 $+$는 다음과 같이 정의된다.

\[x + y = (x \lor y) \land \lnot (x \land y)\]

증명은 공리를 따라 계산해 보면 되므로 생략한다.

아이디얼

대수학에서 다음의 정의를 상기하자.

정의. 환 $R$에 대해 공집합이 아닌 $I \subseteq R$이 아이디얼_ideal이라는 것은, $I$가 덧셈에 대해 군을 이루며, 임의의 $a \in R$과 $x \in I$에 대해 $ax \in I$라는 것이다. 즉, $aI \subseteq I$이다.

불 대수 구조와 불 환 대응에서 드러난 유사성에 착안하여, 다음과 같이 정의하자.

정의. 불 대수 구조 $A$에 대해 공집합이 아닌 $I \subseteq A$가 아이디얼이라는 것은, $I$가 $\lor$에 대해 닫혀 있고, 임의의 $a \in A$와 $x \in I$에 대해 $a \land x \in I$라는 것이다. 즉, $a \land I \subseteq I$이다.

예를 들어 다음의 색칠된 영역은 $\mathcal{P}(\lbrace p, q, r\rbrace )$의 아이디얼이다.

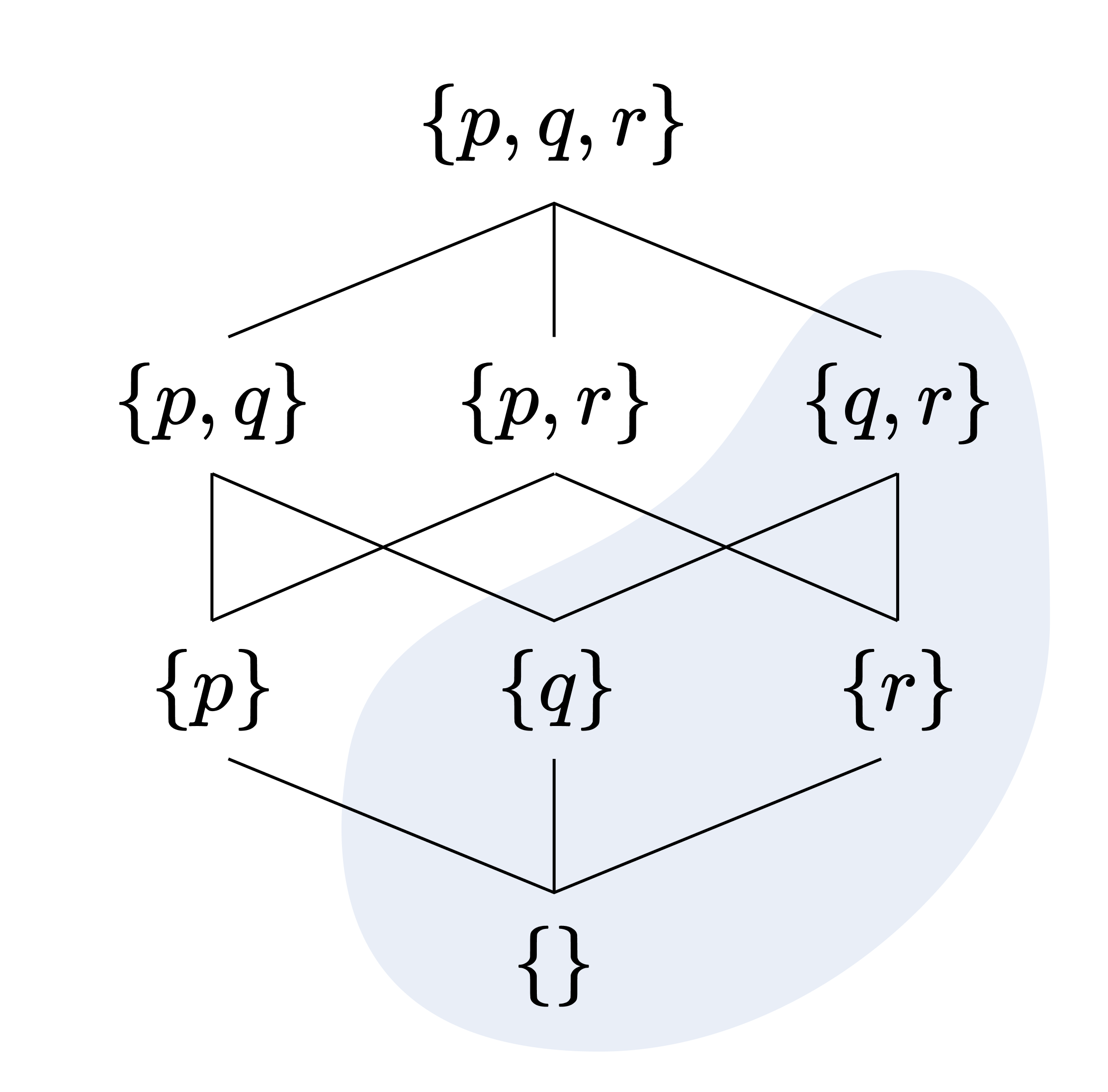
불 대수 구조를 불 환에 대응시키면, $I$가 전자에서 아이디얼이라는 것은 곧 후자에서 아이디얼이라는 것과 같다. 즉 다음이 성립한다.

정리. 불 대수 구조 $A$에 대해 $I \subseteq A$가 (불) 아이디얼일 필요충분조건은, 대응되는 불 환 $A$에서 $I$가 (환) 아이디얼인 것이다.

따라서 불 대수 구조에서도 소 아이디얼_{prime ideal}과 극대 아이디얼_{maximal ideal}을 정의할 수 있다.

정의. $I$가 불 대수 구조 $A$의 아이디얼이라고 하자. $I$가 소 아이디얼이라는 것은, 임의의 $a, b \in A$에 대해, $a \land b \in I$라면 $a \in I$이거나 $b \in I$라는 것이다. $I$가 극대 아이디얼이라는 것은, $J$가 $I$를 엄격히 포함하는 아이디얼일 때, $J = A$라는 것이다.

이들 개념 또한 불 환의 소 아이디얼과 극대 아이디얼에 정확히 상응한다. 앞서 본 아이디얼의 예시는 소 아이디얼인 동시에 극대 아이디얼임을 확인하라. 곧 드러나듯이, 이는 우연이 아니다.

몇 가지 사실을 관찰해 보자. $I \subset A$가 아이디얼이라고 하자.

• 임의의 $a \in I$에 대해, 아이디얼의 정의로부터 $a \land \lnot a = 0 \in I$임이 따라 나온다. 따라서 불 대수의 아이디얼은 항상 $0$을 원소로 가진다.

• 만약 $1 \in I$라면, 임의의 $a \in A$에 대해 $1 \land a = a \in I$임이 따라 나온다. 따라서 $1$을 원소로 가지는 아이디얼은 전체 구조가 유일하다.

• $I$가 소 아이디얼이라면, 임의의 $a \in A$에 대해 $a \land \lnot a = 0 \in I$이므로, $a \in I$ 또는 $\lnot a \in I$이다. 즉, 소 아이디얼은 언제나 임의의 원소 또는 그 부정을 포함한다.

• $I$가 극대 아이디얼이라고 하자. 만약 어떤 $a \in A$가 존재하여 $a \not\in I, \lnot a \not\in I$라면 $I \cup \lbrace x \land a : x \in A \rbrace$가 $I$를 엄격히 포함하며 $A$ 전체는 아닌 아이디얼이므로 $I$는 극대가 아니다. 따라서 극대 아이디얼 또한 언제나 임의의 원소 또는 그 부정을 포함한다.

위 사실로부터 조금의 추론을 거치면 다음을 알 수 있다.

정리. $A$가 불 대수 구조이고 $I$가 $A$의 아이디얼이라고 하자. 다음은 동치이다.

• $I$는 소 아이디얼이다.
• $I$는 극대 아이디얼이다.
• 임의의 $x \in A$에 대해, $x \in I$이거나 $\lnot x \in I$이다.

이런 면에서 불 대수 구조는 환론에서의 PID_{principal ideal domain}와 비슷하다.

필터

필터_filter에 관해서는 이전 글에서 다룬 바가 있다. 정의를 상기해 보자.

정의. $X$가 집합이라고 하자. $X$의 부분집합들로 이루어진 집합 $\mathcal{F}$가 다음을 만족할 때, $X$의 필터라고 부른다.

1. $X \in \mathcal{F}$
2. $\varnothing \not\in \mathcal{F}$
3. 상위집합 닫힘: $A \in \mathcal{F}, A \subset B \implies B \in \mathcal{F}$
4. 유한 교집합 닫힘: $A, B \in \mathcal{F} \implies A \cap B \in \mathcal{F}$

이 정의를 불 대수 구조로 옮기면 다음과 같다.

정의. 불 대수 구조 $A$에 대해 $F \subseteq A$가 필터라는 것은, $F$가 $\land$에 대해 닫혀 있고, 임의의 $a \in A$와 $x \in I$에 대해 $a \lor x \in I$라는 것이다. 즉, $a \lor I \subseteq I$이다.

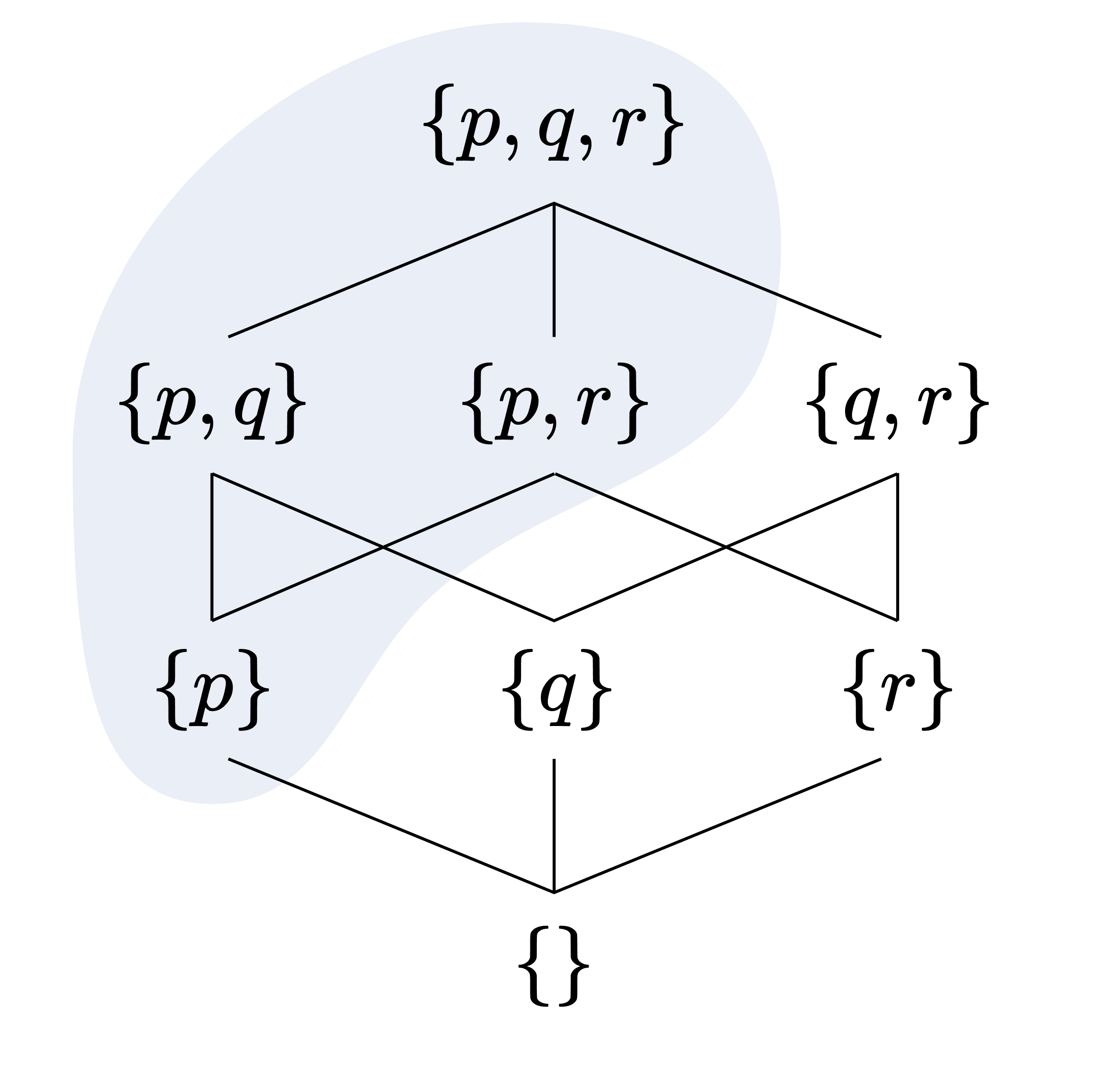
$\land$에 대해 닫혀 있음이 기존의 “유한 교집합 닫힘” 조건에 해당하고, $a \lor I \subseteq I$가 기존의 “상위집합 닫힘” 조건에 해당한다. 특히 $a \lor I \subseteq I$는, 불 대수 구조를 $\leq$ 방향으로 흐르는 일련의 물의 흐름으로 생각했을 때, $x \in I$에서 잉크를 떨어뜨리면 잉크가 퍼져나가는 영역이 모두 $I$에 포섭된다는 의미이다 (이를 이전 글에서 든 잉크의 예시와 비교해 보라). 예를 들어 다음의 색칠된 영역은 $\mathcal{P}(\lbrace p, q, r\rbrace )$의 필터이다.

아이디얼과 필터의 쌍대성

아이디얼과 필터의 정의를 비교해 보면 흥미로운 사실을 발견할 수 있다. 한쪽 정의에서 $\land$과 $\lor$을 맞바꾸면 정확히 다른 쪽 정의가 된다. 이를 두고, 아이디얼과 필터는 서로 쌍대_dual라고 말한다.

쌍대성으로 인해, 한쪽 개념에 대해 증명된 사실은 자연스럽게 다른 쪽 개념에서도 성립한다. 일례로 다음이 성립한다.

정리. $A$가 불 대수 구조이고 $F$가 $A$의 필터라고 하자. 다음은 동치이다.

• $x \lor y \in F$라면 $x \in F$이거나 $y \in F$이다.
• $G$가 $F$를 엄격히 포함하는 필터라면 $G = A$이다.
• 임의의 $x \in A$에 대해, $x \in F$이거나 $\lnot x \in F$이다.

여기서 첫 번째 조건을 만족하는 필터를 소 필터, 두 번째 조건을 만족하는 필터를 극대 필터라고 부른다. 아이디얼의 경우와 달리 필터의 경우에는 세 번째 조건을 만족하는 필터에도 초필터_ultrafilter라는 이름이 붙어있다 (마찬가지로 이전 글 참조).

초필터를 사용한 불 대수 구조의 불 대수화

일반적인 불 대수 구조는, 우리에게 익숙한 불 대수와는 달리, 각각의 원소가 참 또는 거짓으로 이분화되지 않는다. $p$는 $p \land q$에 비해 $1$(참)로부터 같거나 더 가까운 “거리”만큼 떨어져 있지만, 그 자체로는 $0$도 아니고 $1$도 아니다.

그러나 불 대수 구조 $A$의 초필터, 또는 소 아이디얼이 주어졌을 때, 해당 필터(아이디얼)에 속하는 여부에 따라 $A$의 원소들을 “참” 또는 “거짓”으로 이분화할 수 있다. 앞서 본 아이디얼의 예시(왼쪽)와 필터의 예시(오른쪽)을 다시 보자. 왼쪽은 소 아이디얼이고, 오른쪽은 초필터이다.

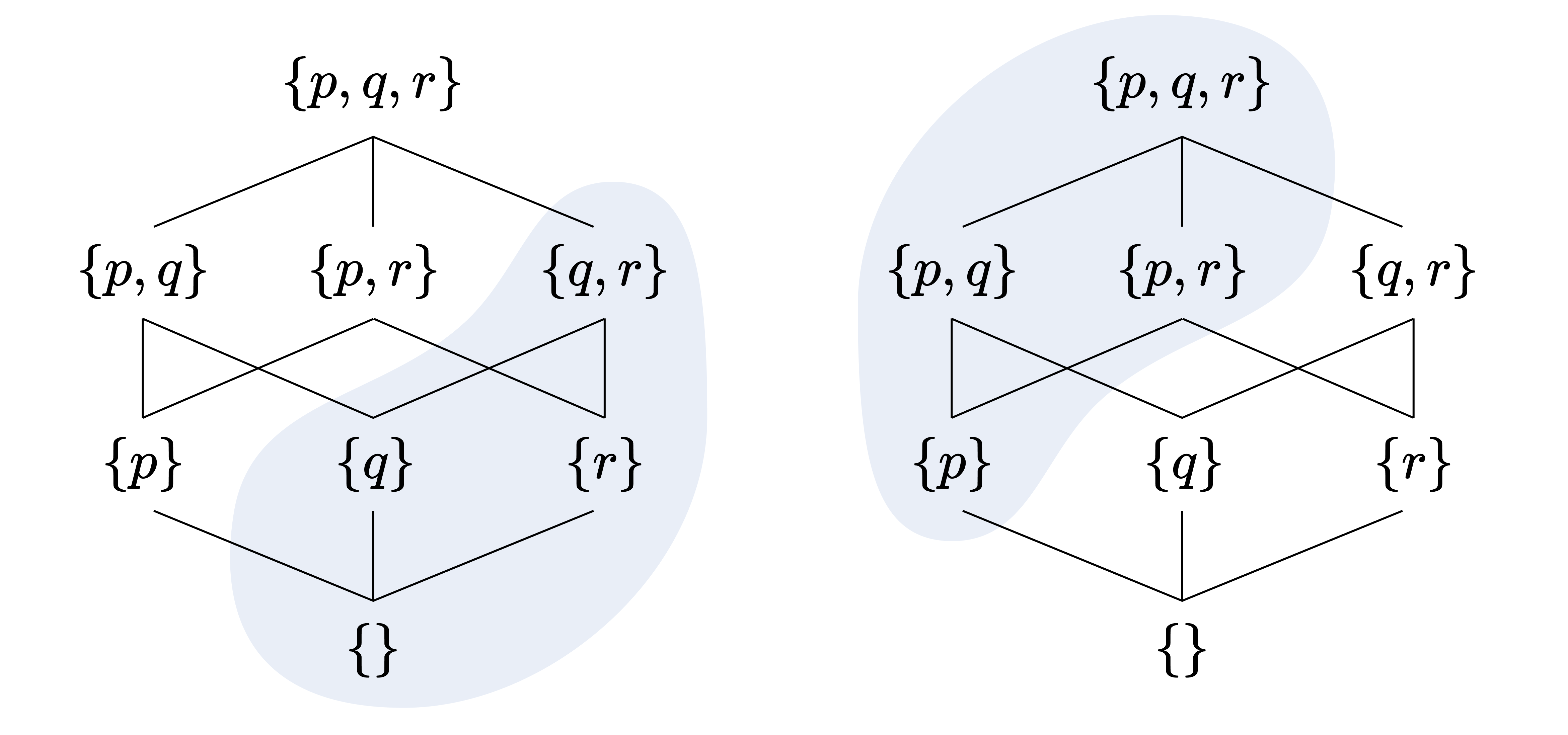
둘은 정확히 서로의 여집합임에 주목하라. 일반적으로 다음이 성립한다.

정리. 불 대수 구조 $A$의 부분집합 $I$에 대해, $I$가 소(극대) 아이디얼일 필요충분조건은 $A \setminus I$가 초(소, 극대) 필터인 것이다.

이에 착안하여, $A$의 원소 중 소 아이디얼 $I$에 속하는 원소는 $0$에, 속하지 않는 원소는 $1$에 대응하자. 또는 $A$의 원소 중 초필터 $F$에 속하는 원소는 $1$에, 속하지 않는 원소는 $0$에 대응하자. 방금의 예시를 사용하면 다음과 같다.

원소	값
$\lbrace \rbrace $	$0$
$\lbrace p\rbrace $	$1$
$\lbrace q\rbrace $	$0$
$\lbrace r\rbrace $	$0$
$\lbrace p, q\rbrace $	$1$
$\lbrace p, r\rbrace $	$1$
$\lbrace q, r\rbrace $	$0$
$\lbrace p, q, r\rbrace $	$1$

이때, 위 대응은 명제 논리의 모델을 이룬다. 특히, $P = \lbrace p \rbrace , Q = \lbrace q \rbrace , R = \lbrace r \rbrace $로 두고, $\cup \leftrightarrow \lor, \cap \leftrightarrow \land$ 대응에 따라 표를 다시 작성하면 다음과 같다.

원소	값
$\varnothing$	$0$
$P$	$1$
$Q$	$0$
$R$	$0$
$P \lor Q$	$1$
$P \lor R$	$1$
$Q \lor R$	$0$
$P \lor Q \lor R$	$1$

이는 $P$가 참이고 $Q, R$은 거짓인 명제 논리의 모델이다. 이와 같이 일반적으로 불 대수 구조에 소 아이디얼 또는 초필터가 주어지면, 해당 정보를 바탕으로 논리적 모델을 구성할 수 있다. 이는 추후 살펴 볼 스톤 표현 정리_{Stone representation theorem}으로 가는 길목이다.