범주론적 관점에서의 곱 위상·상자 위상과 직곱·직합의 차이

02 Apr 2025

곱 위상과 상자 위상

학부 위상에서 곱 위상_{product topology}과 상자 위상_{box topology}을 다루는 부분은 많은 학생에게 난관으로 다가오는 대목이다. 겉보기에는 상자 위상이 훨씬 직관적인데, 교재에서는 상자 위상보다 곱 위상이 다루기에 자연스러운 개념이라고 가르치기 때문이다.

정의. 위상공간의 모임 $\lbrace X_i \rbrace _{i \in I}$에 대해, 상자 위상공간 $\prod X_i$는 다음의 기저로 생성되는 위상공간이다.

\[\left\{ \prod U_i : U_i \text{ is open in } X_i \right\}\]

정의. 위상공간의 모임 $\lbrace X_i \rbrace _{i \in I}$에 대해, 곱 위상공간 $\prod X_i$는 다음의 기저로 생성되는 위상공간이다.

\[\left\{ \prod U_i : U_i \text{ is open in } X_i,\; U_i \neq X_i \text{ for only finitely many } i\right\}\]

일례로 $\mathbb{R}^\omega$에서 $(1, 1, 1, \dots)$의 근방은 각각 다음과 같다.

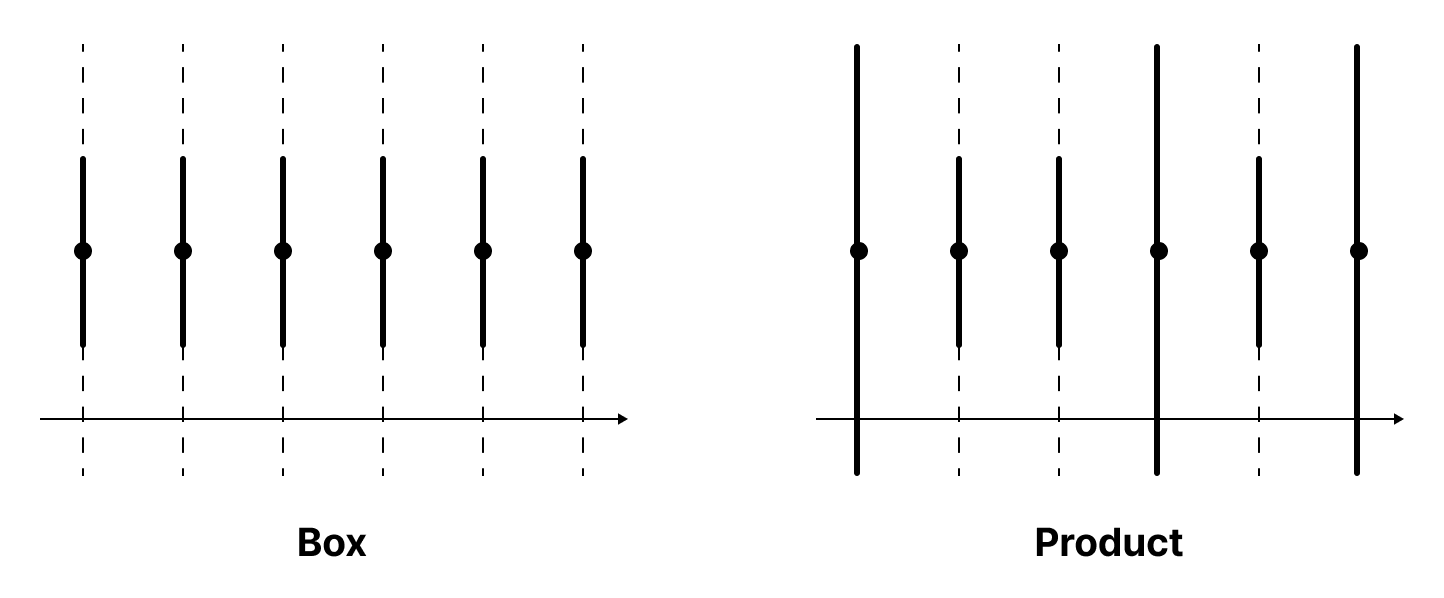
왜 곱 위상은 상자 위상보다 자연스러운 위상으로 간주될까? 그 이유는 범주론에서 대상의 곱을 정의하는 방법과 관련이 있다.

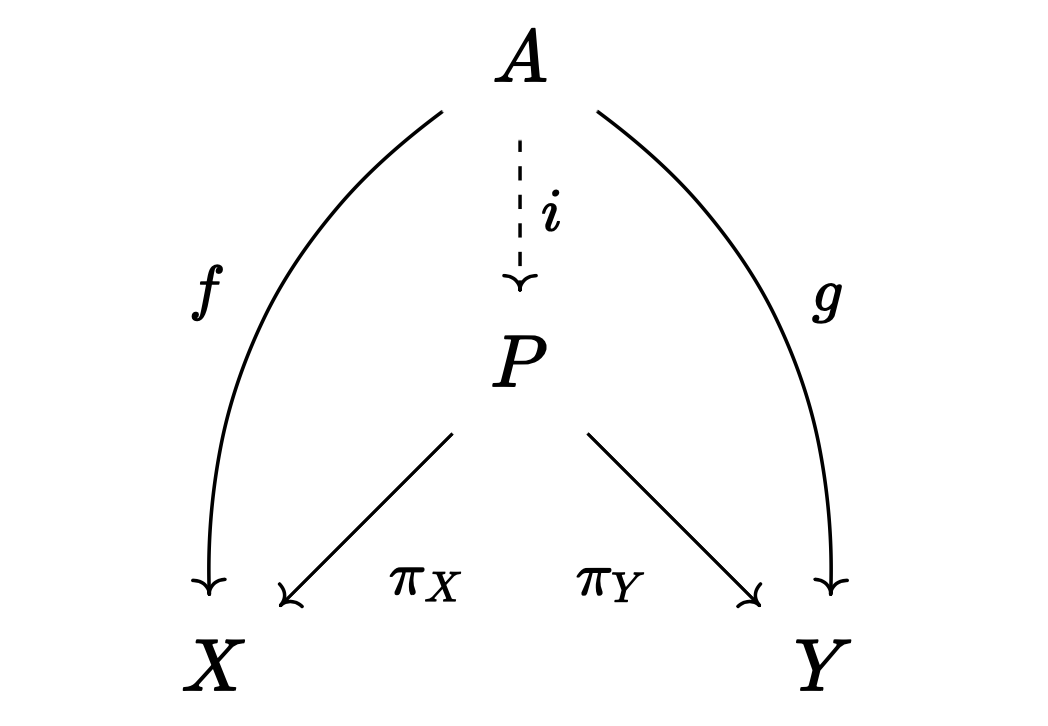
정의. $X, Y$가 범주 $\mathcal{A}$의 대상이라고 하자. $P \in \mathcal{A}$와 사상 $\pi_X : P \to X$, $\pi_Y : P \to Y$에 대해, 다음 조건이 만족될 때 $P$를 $X, Y$의 곱_product이라고 하며, $P = X \times Y$와 같이 적는다.

• 임의의 $A \in \mathcal{A}$와 $f: A \to X$, $g: A \to Y$에 대해 다음 도식이 가환이 되도록 하는 사상 $i: A \to P$가 언제나 유일하게 존재한다.

위의 정의는 자연스러운 방식으로 3개 이상, 또는 무한한 대상들의 곱으로 일반화된다. 극한_limit의 개념이 익숙한 독자라면, 곱은 이산 범주의 극한으로 이해할 수 있다. 또는, 곱은 주어진 대상들의 정보를 온전히 인코딩하는 가장 작은 범주로 이해할 수 있다.

집합들의 범주에서 곱은 곱집합과 같다. 특히 $\pi_X, \pi_Y$는 각각 $(x, y) \mapsto x$, $(x, y) \mapsto y$로 주어진다.

위상공간들의 범주에서 곱은 상자 위상이 아닌 곱 위상이다. 이는 다음의 정리로 보증된다.

정리. 사영함수 $\pi_k : \prod_{i \in I}X_i \to X_k$가 각 $k \in I$에 대해 연속이 되도록 하는 가장 작은 $\prod_{i \in I}X_i$의 위상은 곱 위상이다.

상자 위상도 각 사영함수가 연속이라는 특징을 가지지만, 상자 위상은 곱 위상보다 큰 토폴로지이다. 따라서 상자 위상은 범주론적 곱이 아니다.

상자 위상이 곱이 아님을 보이는 반례를 살펴보자. $\mathbb{R}^\omega$에 상자 위상을 부여하자. 만약 상자 위상이 범주론적 곱이라면, 임의의 연속인 $f_k: \mathbb{R} \to \mathbb{R}$에 대해 $\pi_k \circ i = f_k$가 되도록 하는 연속함수 $i : \mathbb{R} \to \mathbb{R}^\omega$가 존재해야 한다. $f_k: x \mapsto kx$라면 $i$는 $x \mapsto (x, 2x, 3x, \dots)$이다. 상자 위상에서는 $U = (0, 1)^\omega$가 열린 집합이므로, $i$가 연속이면 $i^{-1}(U)$가 열린집합이다. 그런데 $i^{-1}(U) = \lbrace 0 \rbrace $이므로, 상자 위상은 곱의 성질을 만족하지 않는다.

직곱과 직합

상자 위상과 곱 위상의 차이는 전체 공간이 아닌 인덱스가 유한한지의 여부에 있다. 이와 유사한 차이를 대수학에서도 발견할 수 있다.

정의. 벡터 공간들의 모임 $\lbrace V_i \rbrace _{i \in I}$에 대해, 직곱_{direct product} $\prod V_i$를 다음과 같이 정의한다.

\[\prod V_i = \left\{ (v_i)_{i \in I} : v_i \in V_i \right\}\]

정의. 벡터 공간들의 모임 $\lbrace V_i \rbrace _{i \in I}$에 대해, 직합_{direct sum} $\bigoplus V_i$를 다음과 같이 정의한다.

\[\bigoplus V_i = \left\{ (v_i)_{i \in I} : v_i \in V_i,\; v_i \neq 0 \text{ for only finitely many }i \right\}\]

벡터의 연산은 항별_term-wise로 정의한다. 또한 벡터 공간이 아닌 군에 대해서도 같은 방식으로 직곱과 직합을 정의할 수 있다.

직곱과 상자 위상, 직합과 곱 위상의 정의가 비슷하다는 점으로부터 직합이 범주론적 곱에 대응된다고 생각할 수 있지만 그렇지 않다. 대수의 경우 범주론적 곱에 대응되는 것은 직곱이다. 직합은 범주론적 곱의 조건을 일반적으로 만족하지 않는다.

일례로 다음의 경우를 보자. 일차원 실수 공간 $\mathbb{R}$의 직합 $\mathbb{R}^\omega$를 고려하자. 만약 직합이 범주론적 곱이라면, 임의의 선형인 $f_k: \mathbb{R} \to \mathbb{R}$에 대해 $\pi_k \circ i = f_k$가 되도록 하는 연속함수 $i : \mathbb{R} \to \mathbb{R}^\omega$가 존재해야 한다. $f_k: x \mapsto x$라면 $i$는 $x \mapsto (x, x, x, \dots)$이다. 그런데 $i(1) = (1, 1, 1, \dots) \notin \mathbb{R}^\omega$이므로, 직합은 곱의 성질을 만족하지 않는다.

대신 직합은 범주론적 합_sum에 대응된다. 범주론적 합은 곱의 켤레_dual이기 때문에 쌍곱_coproduct이라고도 한다.

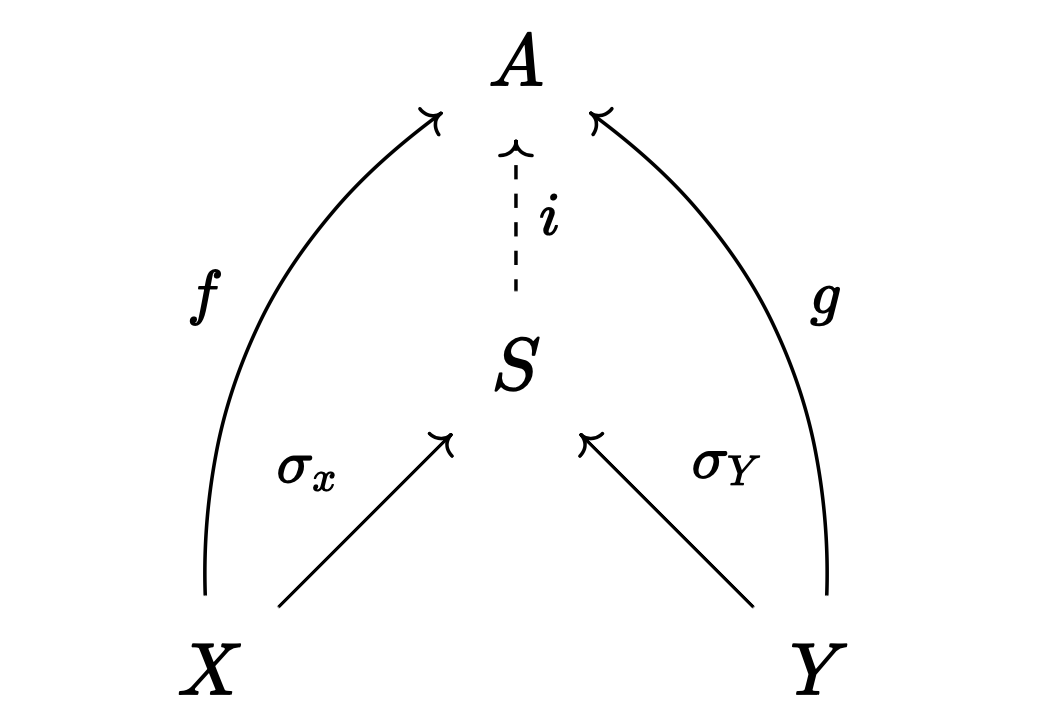
정의. $X, Y$가 범주 $\mathcal{A}$의 대상이라고 하자. $S \in \mathcal{A}$와 사상 $\sigma_X : X \to S$, $\sigma_Y : Y \to S$에 대해, 다음 조건이 만족될 때 $S$를 $X, Y$의 합_sum이라고 하며, $S = X + Y$와 같이 적는다.

• 임의의 $A \in \mathcal{A}$와 $f: X \to A$, $g: Y \to X$에 대해 다음 도식이 가환이 되도록 하는 사상 $i: S \to A$가 언제나 유일하게 존재한다.

앞서 들었던 예시를 다시 보자. 직합 $\bigoplus_\omega \mathbb{R}$를 고려하자. $\sigma_k: \mathbb{R} \to \bigoplus_\omega \mathbb{R}$은 다음과 같이 주어진다.

\[x \mapsto (0, \dots, 0, x, 0, \dots) \quad \text{($x$ is at the $k$th index)}\]

$A = \mathbb{R}$이라고 하고, 항등사상 $f_k : \mathbb{R} \to \mathbb{R}$을 고려하자. $\bigoplus_\omega \mathbb{R}$가 범주론적 합이라면 $i \circ \sigma_k = f_k$가 되도록 하는 연속함수 $i : \bigoplus_\omega \mathbb{R} \to \mathbb{R}$가 존재해야 한다. 실제로 이는 다음과 같이 존재한다.

\[i: (x_i)_{i \in \omega} \mapsto \sum_{i \in \omega} x_i\]

$\bigoplus_\omega \mathbb{R}$의 원소는 오직 유한한 비자명 항을 가지므로 $i$는 잘 정의됨에 주목하라. 반면, 이 예시는 직곱 $\mathbb{R}^\omega$가 범주론적 합이 아님을 보여준다. 직곱의 경우 $i$가 잘 정의되지 않기 때문이다. 이는 $i$에 $(1, 1, 1, \dots)$를 대입해 보면 알 수 있다.

군의 경우 범주론적 곱과 범주론적 합에 대응되는 연산은 일반적인 군의 범주를 따지냐, 아벨군의 범주를 따지냐에 따라 조금 다르다. 이 부분은 간단한 노트 정도로 남겨둔다.

	대수적 정의	범주론적 정의
자유곱	형식적 단어의 집합 + 병치 연산	$\mathbf{Grp}$의 합
직합	유한한 비자명 항을 가지는 튜플의 집합 + 항별 연산	$\mathbf{Ab}$의 합
직곱	튜플의 집합 + 항별 연산	$\mathbf{Grp}$의 곱