The Difference Between Product and Box Topologies, and Direct Product and Direct Sum from a Categorical Perspective

02 Apr 2025

Product Topology and Box Topology

Product topology and box topology often stir confusion among many undergraduate students. For, although the box topology appears more intuitive at first glance, textbooks teach that the product topology is the more “natural” concept to work with.

Definition. For a collection of topological spaces $\lbrace X_i \rbrace _{i \in I}$, the box topological space $\prod X_i$ is the topological space generated by the following basis:

\[\left\{ \prod U_i : U_i \text{ is open in } X_i \right\}\]

Definition. For a collection of topological spaces $\lbrace X_i \rbrace _{i \in I}$, the product topological space $\prod X_i$ is the topological space generated by the following basis:

\[\left\{ \prod U_i : U_i \text{ is open in } X_i,\; U_i \neq X_i \text{ for only finitely many } i\right\}\]

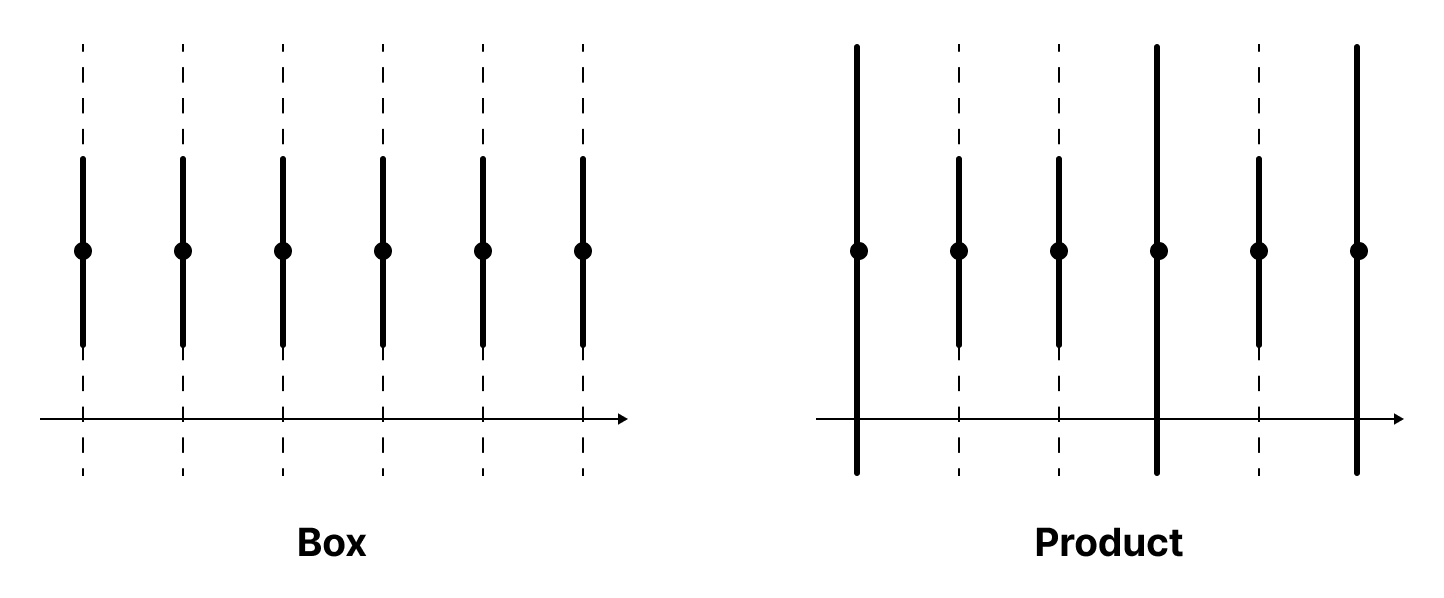
For instance, the neighbourhoods of $(1, 1, 1, \dots)$ in $\mathbb{R}^\omega$ are as follows:

Why is the product topology considered more natural than the box topology? The reason is related to how products of objects are defined in category theory.

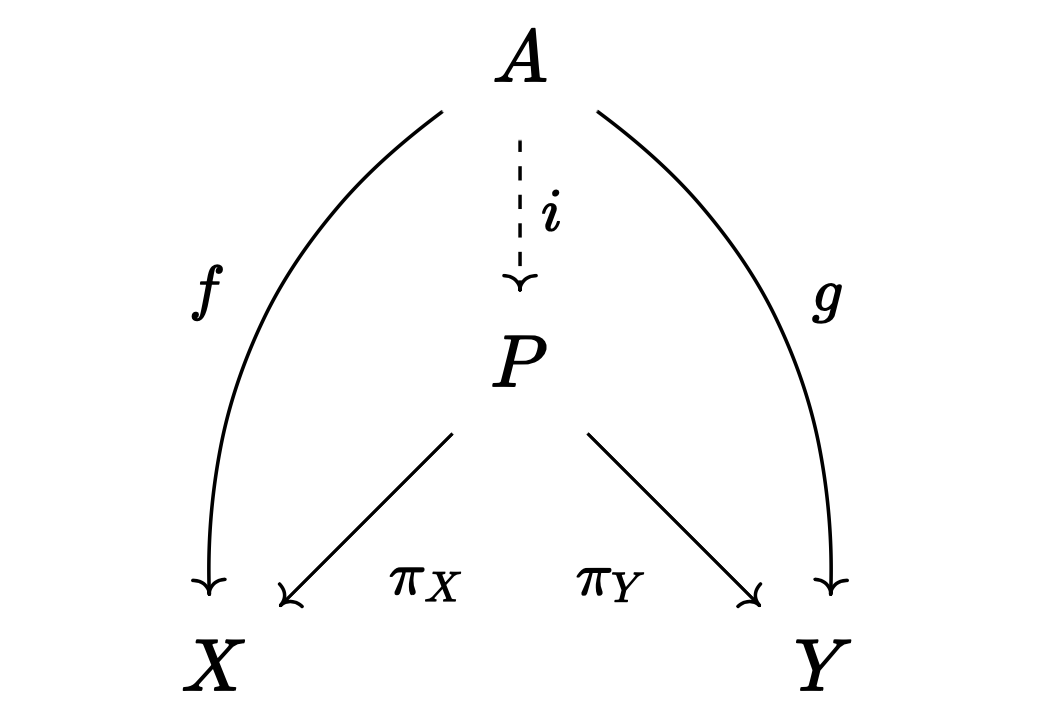
Definition. Let $X, Y$ be objects in category $\mathcal{A}$. For $P \in \mathcal{A}$ and morphisms $\pi_X : P \to X$, $\pi_Y : P \to Y$, we call $P$ the product of $X, Y$ and write $P = X \times Y$ when the following condition is satisfied:

• For any $A \in \mathcal{A}$ and morphisms $f: A \to X$, $g: A \to Y$, there exists a unique morphism $i: A \to P$ such that the following diagram commutes:

The above definition naturally generalises to products of three or more, or infinitely many objects. Readers familiar with the concept of limits will recognise that the product can be understood as the limit of a discrete category. Alternatively, the product can be understood as the smallest category that fully encodes the information of the given objects.

In the category of sets, the product coincides with the Cartesian product. In particular, $\pi_X, \pi_Y$ are given by $(x, y) \mapsto x$ and $(x, y) \mapsto y$ respectively.

In the category of topological spaces, the product is the product topology, not the box topology. This is seen by the following theorem:

Theorem. The smallest topology on $\prod_{i \in I}X_i$ such that the projection functions $\pi_k : \prod_{i \in I}X_i \to X_k$ are continuous for each $k \in I$ is the product topology.

Whilst the box topology also has the property that each projection function is continuous, the box topology is a larger topology than the product topology. Therefore, the box topology is not the categorical product.

Let us examine a counterexample showing that the box topology is not the categorical product. Consider $\mathbb{R}^\omega$ with the box topology. If the box topology were the categorical product, then for any continuous functions $f_k: \mathbb{R} \to \mathbb{R}$, there would exist a continuous function $i : \mathbb{R} \to \mathbb{R}^\omega$ such that $\pi_k \circ i = f_k$. If $f_k: x \mapsto kx$, then $i$ would be $x \mapsto (x, 2x, 3x, \dots)$. In the box topology, $U = (0, 1)^\omega$ is an open set, so if $i$ were continuous, then $i^{-1}(U)$ would be an open set. However, $i^{-1}(U) = \lbrace 0 \rbrace $, so the box topology does not satisfy the property of a product. (Note that in the case of product topology, $U$ is not an open set.)

Direct Product and Direct Sum

The difference between the box topology and product topology lies in whether only finitely many indices are allowed to be non-trivial. A similar difference can be found in algebra.

Definition. For a collection of vector spaces $\lbrace V_i \rbrace _{i \in I}$, the direct product $\prod V_i$ is defined as follows:

\[\prod V_i = \left\{ (v_i)_{i \in I} : v_i \in V_i \right\}\]

Definition. For a collection of vector spaces $\lbrace V_i \rbrace _{i \in I}$, the direct sum $\bigoplus V_i$ is defined as follows:

\[\bigoplus V_i = \left\{ (v_i)_{i \in I} : v_i \in V_i,\; v_i \neq 0 \text{ for only finitely many }i \right\}\]

Vector operations are defined term-wise. The same definitions of direct product and direct sum can be applied to groups as well.

From the similarity between the definitions of direct product and box topology, and direct sum and product topology, one might think that the direct sum corresponds to the categorical product, but this is not the case. In algebra, the direct product corresponds to the categorical product. The direct sum does not generally satisfy the conditions of a categorical product.

Consider the following example: Let us examine the direct sum $\mathbb{R}^\omega$ of one-dimensional real spaces $\mathbb{R}$. If the direct sum were the categorical product, then for any linear maps $f_k: \mathbb{R} \to \mathbb{R}$, there would exist a continuous function $i : \mathbb{R} \to \mathbb{R}^\omega$ such that $\pi_k \circ i = f_k$. If $f_k: x \mapsto x$, then $i$ would be $x \mapsto (x, x, x, \dots)$. However, $i(1) = (1, 1, 1, \dots) \notin \mathbb{R}^\omega$, so the direct sum does not satisfy the property of a product.

Instead, the direct sum corresponds to the categorical sum. The categorical sum is also called a coproduct because it is the dual of the categorical product.

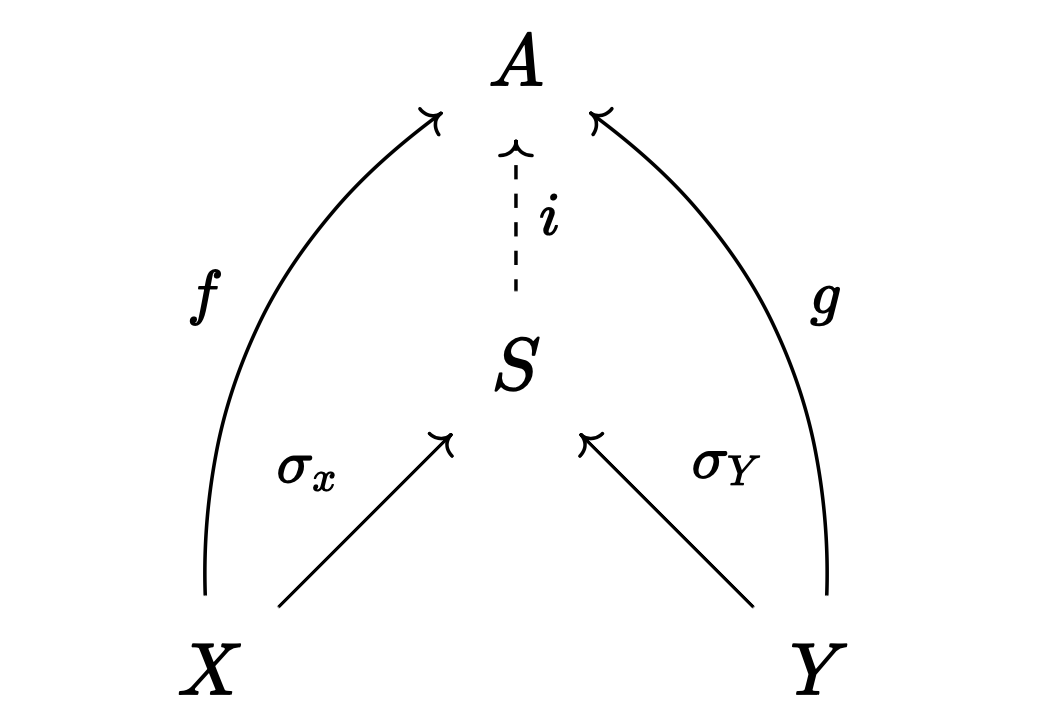
Definition. Let $X, Y$ be objects in category $\mathcal{A}$. For $S \in \mathcal{A}$ and morphisms $\sigma_X : X \to S$, $\sigma_Y : Y \to S$, we call $S$ the sum of $X, Y$ and write $S = X + Y$ when the following condition is satisfied:

• For any $A \in \mathcal{A}$ and morphisms $f: X \to A$, $g: Y \to A$, there exists a unique morphism $i: S \to A$ such that the following diagram commutes:

Let us revisit the earlier example. Consider the direct sum $\bigoplus_\omega \mathbb{R}$. The morphism $\sigma_k: \mathbb{R} \to \bigoplus_\omega \mathbb{R}$ is given by:

\[x \mapsto (0, \dots, 0, x, 0, \dots) \quad \text{($x$ is at the $k$th index)}\]

Let $A = \mathbb{R}$ and consider the identity morphism $f_k : \mathbb{R} \to \mathbb{R}$. If $\bigoplus_\omega \mathbb{R}$ is the categorical sum, then there must exist a continuous function $i : \bigoplus_\omega \mathbb{R} \to \mathbb{R}$ such that $i \circ \sigma_k = f_k$. Indeed, this exists as follows:

\[i: (x_i)_{i \in \omega} \mapsto \sum_{i \in \omega} x_i\]

Note that $i$ is well-defined because elements of $\bigoplus_\omega \mathbb{R}$ have only finitely many non-trivial terms. Conversely, this example shows that the direct product $\mathbb{R}^\omega$ is not the categorical sum. In the case of the direct product, $i$ is not well-defined. This can be seen by substituting $(1, 1, 1, \dots)$ into $i$.

For groups, the operations corresponding to categorical products and categorical sums differ slightly depending on whether we consider the general category of groups or the category of abelian groups. I shall leave this as a brief note.

	Algebraic Definition	Categorical Definition
Free Product	Set of formal words + concatenation operation	Sum in $\mathbf{Grp}$
Direct Sum	Set of tuples with finitely many non-trivial terms + term-wise operation	Sum in $\mathbf{Ab}$
Direct Product	Set of tuples + term-wise operation	Product in $\mathbf{Grp}$