디멘의 블로그
Dimen's Blog
이데아를 여행하는 히치하이커
Alice in Logicland
프란츠 카프카, 「여덟 권의 청색 팔절판 노트」 중 제1권
17 Jun 2025「여덟 권의 청색 팔절판 노트Acht blaue Oktavhefte」는 1917년 말부터 1919년 중순까지 카프카가 작성한 일련의 노트이다. 「팔절판 노트」라는 이름은 카프카의 출판 담당자인 막스 브로트가 그의 사절판 일기장과 구분하기 위해 붙인 것이다. 이후 브로트가 카프카의 일기를 출판했을 때 「팔절판 노트」는 생략되었는데, 카프카의 다른 일기보다 철학적이고 문학적이라는 점에서 성격을 달리한다는 이유에서였다. 이로 인해 「팔절판 노트」는 카프카 특유의 사색적이고 몽환적인 성격에도 불구하고 세간에 잘 알려져 있지 않으며, 특히 국내에서는 전문이 번역된 바가 없다. 이에 필자가 직접 번역을 시도했다. 비전공자의 번역인 점을 감안하여 독일어 원문을 같이 수록했다.

i.
모든 사람은 자신의 내면에 하나의 방을 가지고 다닌다. 이 사실은 심지어 청각의 감각을 통해 증명할 수 있다. 주위가 고요한 밤중에, 서둘러 걸음을 재촉하는 자가 귀를 기울일 때면, 그는 예컨대 벽에 충분히 고정되지 못한 거울이 부딪치는 소리를 듣는 것이다.
ii.
남자는 움츠린 가슴, 튀어나온 어깨, 축 늘어진 팔, 거의 들 수조차 없는 다리, 그리고 한 지점을 응시하는 눈빛으로 서 있다. 그는 화부火夫다. 그는 삽에 석탄을 담아 화염이 치솟는 용광로에 던져 넣는다. 한 아이가 공장의 스무 안뜰을 살금살금 건너와 그의 거적때기에 안긴다. “아버지” — 아이가 말한다 — “제가 수프를 가지고 왔어요.”
iii.
이곳이 저 아래 겨울의 대지보다 따뜻한가? 백색은 온 주위에 쌓여가 오직 나의 들통만이 검다. 이전에 높은 곳에 있었던 나는 이제 깊은 곳에 있으며, 산을 올려다보려는 시도는 나의 목을 골절시킨다. 얼어붙은 백색은 사라진 스케이터들의 궤도를 따라 사방으로 금이 달렸다. 깊고 한 치도 꺼지지 않는 눈 위로, 나는 작은 북극견들의 발자국을 좇는다. 말을 타는 일은 의미를 잃었다. 나는 내려서 들통을 어깨에 메고 걷는다.
iv.
V. W.
베토벤 책에 대해 진심 어린 감사를 보냅니다. 쇼펜하우어는 오늘 시작합니다. 이 책들은 정말 대단한 업적입니다. 당신이 당신의 섬세한 손길과, 참된 진실을 향하는 강렬한 시선과, 절제되었으면서도 위엄한 대지의 불 같은 시적 본성과, 환상적일 정도로 방대한 지식을 통해 앞으로도 이러한 위업을 이룩하여 저에게 형언할 수 없는 기쁨을 주시기를 기원합니다.
Meinen innigsten Dank für das Beethovenbuch. Den Schopenhauer beginne ich heute. Was für eine Leistung, dieses Buch. Möchten Sie doch mit Ihrer allerzartesten Hand, mit Ihrem allerstärksten Blick für die wahrhafte Realität, mit dem gezügelten und mächtigen Grundfeuer Ihres dichterischen Wesens, mit Ihrem phantastisch weiten Wissen noch weiter solche Denkmäler aufrichten — zu meiner unaussprechlichen Freude.
v.
늙고 비대한 육신 속에서, 나는 가벼운 심장 질환을 앓으며, 점심 식사 이후 한 발은 바닥에 떨군 채 소파에 누워 역사책을 읽고 있었다. 하녀가 오더니 삐죽 튀어나온 입술 위로 두 손가락을 얹고는 방문객이 왔다고 일렀다.
“누구인가?” 나는 오후의 커피를 마셔야 할 때에 방문객을 상대해야 한다는 사실에 짜증이 난 목소리로 물었다. “중국인 남자입니다.” 하녀가 말하더니, 경련적으로 몸을 돌리고는 문 앞의 방문객이 들어서는 안 될 웃음을 삼켰다.
“중국인? 나를 보기 위해? 중국 의상을 입고 있나?” 하녀는 여전히 웃음을 억누르며 고개를 끄덕였다. “그에게 나의 이름을 말해주고, 그가 정말로 나를 방문하려는지 물어보거라. 나는 옆집 사람에게도 낯선 이인즉 중국에서는 오죽하겠나.”
하녀는 나에게 몸을 기울이더니 속삭였다. “그는 한 장의 쪽지만을 가지고 있는데, 쪽지에는 그를 들여보내달라는 부탁만 쓰여 있었습니다. 그는 독일어를 할 줄 모르며 알아들을 수 없는 언어로만 말합니다. 저는 쪽지를 그에게서 가져가는 것이 두려울 지경이었습니다.”
“그를 들여보내거라!” 나는 심장 문제가 종종 일으키곤 하는 숨가쁨 속에서 외치며, 책을 바닥 위로 던지고는 하녀의 어색한 접대를 저주했다. 나는 일어나 이처럼 천장이 낮은 방으로 들어오는 방문객이라면 누구든지 경악할 수밖에 없을 거구를 뻗으며 문에 다가섰다. 과연 그 중국인은 나와 눈이 마주치자마자 즉시 들어왔던 길로 미끄러지듯이 돌아갔다. 나는 사뿐히 복도로 손을 뻗어 남자의 비단 저고리를 움켜잡아 내게로 조심히 끌어당겼다. 그는 한눈에 보기에도 학자였으며, 작고, 연약했고, 뿔테 안경을 썼고, 얇고 희끗희끗하고 푸석한 염소 수염을 달고 있었다. 호감상의 난쟁이 — 머리는 한쪽으로 기울인 채 반쯤 감은 눈으로 미소 짓는구나.
vi.
어느 날 아침, 변호사 부케팔루스 박사는 그의 가정부에게 침대로 오게 하고는 그녀에게 말했다. “오늘 내 동생 부케팔루스 대 트롤해타 사社 소송의 큰 재판이 있소. 나는 원고의 편에서 법정에 서지요. 재판이 적어도 수일은 걸릴 테다가, 정말이지 휴식 시간이 없을 것이니, 다음 며칠 동안 나는 집에 전혀 오지 않을 거요. 소송이 끝나거나, 끝날 조짐이 보이는 대로 전화를 주겠소. 지금으로서는 더이상 말할 수도 없고, 어떠한 질문에도 답할 수 없소. 당연히 내 목소리를 최대의 역량으로 보존하는 데 집중해야 하니 말이오. 그런 연유로, 나에게 아침 식사로 두 개의 날달걀과 꿀을 섞은 차를 가져다주겠소?” 그리고, 천천히 등을 베개 속에 묻히며, 눈 위를 손으로 덮은 채, 그는 침묵에 빠졌다.
수다스러울지언정 집주인 앞에 설 때면 두려워 죽을 지경이던 가정부는 이에 실로 당황했다. 그토록 놀라운 소식은 그리 갑작스럽게도 찾아오는 것이었다. 바로 전날 저녁만 하더라도 집주인은 그녀와 말 몇 마디를 나누었건만 곧 다가올 일에 관해서는 아무런 내색도 비치지 않았다. 하지만 재판 일정이 밤중에 정해졌을 수는 없지 않은가? 그리고 날밤을 새우면서 쉼 없이 진행되는 재판이 있던가? 그리고 왜 집주인은 이전에는 일절 알려준 적 없는 피고와 원고의 이름을 언급한 것인가? 그리고 작은 청과물 상점을 운영하는 집주인의 동생 아돌프 부케팔루스가 — 그나저나 그는 집주인과 지난 오랜 기간 좋은 관계로 보이지는 않았다 — 도대체 어떠한 거대한 소송에 연루되었다는 것인가? 그리고 집주인 앞으로 형언하기 힘들 정도의 시련이 닥쳤다는 사실이, 지금 그가 — 이른 새벽빛이 착시를 일으키는 것이 아니라면 — 초췌해진 자신의 얼굴을 손으로 가리는 모습과 어울린다고 정녕 말할 수 있는가? 그리고 그가 늘 원하던, 기력을 완전히 충전시켜 줄 약간의 와인과 햄은 막론하고 오직 차와 달걀만 받고자 한 것은? 그런 생각을 하며 가정부는 부엌으로 물러가, 그녀가 가장 좋아하는, 꽃과 카나리아가 있는 창가의 자리에 잠깐 앉아, 빗장으로 잠긴 창문 너머로 반쯤 벌거벗은 채 함께 뛰놀며 씨름하는 두 아이가 보이는 안뜰 너머를 바라보더니, 이내 일어나 한숨을 쉬고는, 차를 내고, 선반에서 달걀 두 개를 꺼내, 식사를 쟁반에 정돈하고, 차마 어쩔 수 없어 와인 한 병도 준비한 채, 모든 것을 침실로 가져갔다.
방은 비어 있었다. 어떻게, 집주인이 벌써 떠났을 리는 없을 텐데? 단 일 분 만에 옷을 입을 수는 없지 않은가? 하지만 그의 속옷과 양복은 어디에도 보이지 않았다. 도대체 집주인은 뭐 하자는 것인지 환장할 노릇이다. 서둘러 복도로! 코트, 모자, 그리고 지팡이조차 없다. 그렇다면 창문으로! 맙소사, 저기 대문을 나서는 집주인이 있다 — 머리 뒤로 모자를 걸치고, 코트 앞섶은 풀린 채, 손은 서류가방을 꽉 쥐었고, 주머니에 꿴 갈고리 위로 지팡이는 대롱거린다.
vii.
당신은 파리의 트로카데로를 아십니까? 사진만 봐서는 전혀 짐작하지 못할 크기를 자랑하는 이 건물에서, 아주 대단한 재판의 핵심 심리가 지금 이 순간 진행되고 있습니다. 어쩌면 당신은 그토록 큰 건물을 어떻게 이처럼 지독한 겨울에 난방하는 것이 가능한지 궁금할지도 모르겠습니다. 건물은 난방되지 않습니다. 이와 같은 경우에 난방부터 생각하기란, 당신이 인생을 보낸 곳과 같은 안락한 소도시에 사는 사람들에게나 가능한 일이죠. 트로카데로는 난방이 없지만 이것이 심리의 진행을 방해하지는 않습니다. 오히려 모든 방향에서 뿜어져 나오는 한기 속에서, 심리는 그에 정확히 부응하는 빠르기로 진행됩니다. 가로와 세로를 종횡무진 가르며.
viii.
어제 실신失神이 나를 찾아왔다. 그녀는 이웃집에 산다. 나는 예전부터 저녁 무렵이면 종종 그녀가 몸을 굽히며 대문을 지나 사라지는 것을 보았다. 길게 흘러내리는 옷과 깃털이 꽂힌 넓은 모자를 쓴 거구의 여인. 그녀는 마치 죽어가는 환자에게 너무 늦게 도착한 것은 아닌지 두려워하는 의사처럼 급히 문을 열고는 소란스레 들어왔다. “안톤” — 그녀는 공허하면서도 자부하는 듯한 목소리로 외쳤다 — “제가 왔어요, 제가 여기 있어요!” 내가 가리킨 소파에 그녀는 기꺼이 털썩 주저앉았다.
“높이도 사는군요, 높이도 살아요.” 그녀는 신음하듯이 말했다.
나는 내 안락의자에 파묻힌 채 고개를 끄덕였다. 눈앞으로는 내 방으로 이어지는 수많은 계단이 끝없이 일렁이는 물결처럼 앞다투어 튀어 올랐다.
“어찌 이리도 춥나요?” 그녀는 묻더니, 헌 펜싱 장갑처럼 생긴 그녀의 기다란 장갑을 벗어 탁자 위로 던지고는 갸우뚱한 고개로 나를 바라보며 눈을 찡긋했다. 나로서는 한 마리의 참새가 된 듯한 기분이었으니, 계단 위에서 폴짝이며 날갯짓을 연습하는데 그녀가 나의 부드럽고 솜털 같은 회색 깃털을 헝클어뜨리는 것이었다.
“당신이 저에 대한 그리움으로 괴로워한다니 진심으로 유감이에요.” 그녀가 말했다. “이따금 당신이 안뜰에 서서 제 창문을 올려다볼 때면 당신의 피폐한 얼굴에서 깊은 슬픔을 읽곤 했지요. 그래요, 제가 당신에게 적의를 품은 것은 아니랍니다. 비록 당신이 제 마음을 아직 얻지 못했어도, 그것을 쟁취하는 것 또한 불가능하진 않으니까요.”
ix.
사람은 이토록 무관심에 빠질 수 있는가 — 그가 영원히 올바른 길을 잃어버렸다는 그토록 깊은 신념에.
x.
착오. 내가 연 것은 긴 복도 끝 위쪽에 있는 내 방의 문이 아니었다. “착오였습니다,” 라는 말과 함께 나는 다시 나가려고 했다. 그 순간, 나는 방 안쪽으로 수척하고 수염이 없는 사내를 보았다. 입을 굳게 다문 채, 그가 앉은 작은 탁자에는 단 하나의 석유 램프만이 있었다.
xi.
우리의 집 — 변두리에 위치한 이 거대한 건물, 지울 수 없는 중세의 폐허가 스며든 다세대 주택에서, 얼음 같은 안개가 낀 금일의 겨울 아침 이런 공문이 게시되었다.
모든 세입자께 알립니다.
나는 다섯 자루의 장난감 총을 가지고 있습니다. 총은 저마다 고리에 걸린 채 내 장롱에 보관되어 있습니다. 첫 번째 총은 나의 것이지만 나머지는 원하는 사람이 가져가도 좋습니다. 네 명보다 많은 희망자가 있을 시 자신이 소유한 총을 가져 와 장롱에 두어야 합니다. 통일성은 반드시 지켜져야만 하기 때문입니다. 통일성 없이는 우리는 앞으로 나아갈 수 없습니다. 그나저나 내가 가지고 있는 총들이란 죄다 어떤 용도로도 쓸모가 없습니다. 기계 장치는 망가졌고, 노리쇠는 떨어져 나갔으며, 오직 방아쇠만이 여전히 딸깍거릴 뿐입니다. 그러니 필요하다면, 이런 총을 더 많이 구하기란 어려운 일이 아닐 것입니다. 하지만 근본적으로 보면, 첫 시도에는 총이 없는 사람들도 괜찮을 듯합니다. 우리 총을 가진 사람들이 결정적인 순간에 무장하지 않은 자들을 가운데로 몰아넣을 것입니다. 이 전투 방식은 최초의 미국 농부들이 인디언들과 맞설 때 증명된 방법인 만큼, 상황의 유사성을 고려할 때 여기서도 통하지 않을 리 있겠습니까? 생각해 보면 우리는 심지어 오래도록 총을 포기할 수도 있고, 이 다섯 자루조차 꼭 필요한 것은 아닙니다만, 단지 이미 존재하기 때문에 쓰자는 것뿐입니다. 하지만 다른 네 사람이 총을 들기를 원하지 않는다면, 그렇게 하지 않아도 됩니다. 그러면 나 혼자서만 지도자로서 총을 들겠습니다. 그러나 우리는 지도자를 가져서는 안 됩니다. 그래서 나 또한 내 총을 부수거나 내려놓을 것입니다.
이것이 첫 번째 공문이었다. 우리의 집에 사는 사람들은 시간도 없고 공문을 읽거나 숙고할 의욕도 없다. 얼마 안 있어 그 종이쪼가리는 다락방에서 시작해 복도로 터져 나온 더러운 물줄기에 흠뻑 젖은 채로 계단을 따라 쓸려 나가더니 그곳 밑에서 역류하는 물줄기와 싸우는 신세가 되었다. 그러나 일주일 뒤 두 번째 공문이 붙었다.
세입자들이여!
지금까지 아무도 나에게 연락하지 않았습니다. 나는 내 생계에 필수적인 일을 하지 않는 시간에는 항상 집에 머물러 있었습니다. 집을 비울 때는 방문을 열어두어, 원하는 사람은 누구든 이름을 적을 수 있도록 책상 위에 종이를 놓아두었습니다. 아무도 이름을 적지 않았습니다.
xii.
가끔씩 나는, 내가 기계공장에서의 교대근무를 마치고 밤늦게 또는 이른 아침에 집으로 돌아올 때, 내가 저지른, 그리고 저지를, 과거와 미래의 모든 죄가 뼈마디의 통증으로 속죄되는 것은 아닌지 생각한다. 나는 내가 이 일을 견딜 수 있을 정도로 강하지 않다는 사실을 이미 오래전부터 알고 있다. 그러나 나는 아무것도 바꾸지 않는다.
xiii.
우리의 집 — 변두리에 위치한 이 거대한 건물, 중세의 폐허가 스며든 다세대 주택에는, 나와 같은 복도에서 한 노동자 가족과 같이 사는 서기가 있다. 사람들은 그를 공무원이라고 부르지만 실상은 하찮은 서기에 불과하며, 낯선 부부와 그들의 여섯 자식 틈에 끼인 채 바닥에 깔린 밀짚 둥지에서 밤을 보내는 자이다. 그리고 그가 그토록 하찮은 서기라면, 내가 그에게 무슨 신경을 쓰겠는가. 이 집 — 도시가 끓여낸 불행이란 불행은 다 모인 이 집에도, 적어도 백 명은 넘는 사람들이 살거늘…
xiv.
나와 같은 복도에는 한 수선재봉사가 산다. 아무리 조심해도 내 옷은 너무 빨리 닳아서, 최근에도 나는 그에게 다시 외투 하나를 들고 가야만 했다. 그날은 참으로 아름답고 따뜻한 여름 저녁이었다. 재봉사는 자신과 아내, 그리고 여섯 아이까지 모두 단 한 칸의 방 — 그 방은 부엌이기도 하다 — 에서 살고 있다. 그런데도 그는 심지어 한 세무청의 서기를 세입자로 들였다. 이 정도로 들어찬 방은 이미 열악하기 짝이 없는 우리 주택의 기준으로 봐도 지나친 수준이다. 그렇다고는 해도 사람은 각자의 사정이 있고, 재봉사에게 또한 그의 절약에 달아날 수 없는 이유가 분명히 있겠거니, 외부인이 그 이유에 대해 굳이 이야기하려는 일은 없다.
xv.
1917년 2월 19일.
오늘은 헤르만과 도로테아, 그리고 리히터 회고록 약간을 읽었으며, 그의 사진들을 봤고, 마지막으로 하웁트만의 그리젤다에서 나오는 장면을 읽었다. 한 시간이라는 순간 안에 나는 다른 사람이 되어 있었다. 모든 풍경은 여전히 안개처럼 뿌옇지만, 이제는 안개 그림으로 변했다. 오늘 처음 신어 보는 질긴 장화 속에는 — 그 장화는 원래 군사용으로 만들어진 것이었다 — 또다른 사람이 서 있었다.
xvi.
저는 크룸홀츠 씨 댁에 삽니다. 방은 세무청의 한 서기와 나눠 쓰지요. 그 방에서는 크룸홀츠 씨의 두 딸 — 여섯 살, 일곱 살 소녀입니다 — 또한 같은 침대에서 잡니다. 서기가 이사를 해온 첫날부터 — 저로 말하자면 이미 수년 동안 크룸홀츠 씨 댁에 살고 있었습니다 — 저는 그의 첫인상에서 석연찮은 수상함을 느꼈습니다. 평균 신장 이하의 남성. 허약한 체격과, 건강하다고는 할 수 없는 폐. 후줄근한 회색 옷가지. 나이를 가늠할 수 없는 주름진 얼굴. 귀를 덮도록 넘겨진 회갈색의 긴 머리카락. 코끝까지 내려온 안경. 그리고 작고 — 역시나 — 회색인 염소 수염.
xvii.
내가 중부 콩고에서 철도 공사에 종사하며 보냈던 삶은 즐거운 것이 아니었다.
나는 내 오두막집의 차창이 쳐진 베란다에 앉아 있었다. 한쪽으로는 긴 벽 대신 극도로 촘촘한 모기장이 쳐져 있었는데, 그것은 현장 감독관 중 한 명이자 우리의 철도가 지나가는 지역의 족장에게서 얻은 것이었다. 삼베로 만든 그 그물은 튼튼하면서도 섬세하여, 유럽에서는 결코 만들 수 없을 정도였다. 그것은 내 자랑거리였고 많은 이들의 부러움을 샀다. 그 그물이 없었더라면 이렇게 저녁에 베란다에 평화롭게 앉아, 지금처럼 불을 켜고, 오래된 유럽 신문을 샅샅이 펼쳐 읽으며, 파이프를 힘차게 피우는 일은 결코 불가능했을 것이다.
xviii.
나는 — 누가 자신의 능력을 이토록 자부하며 말할 수 있겠는가 — 행복하며 지칠 줄 모르는 늙은 낚시꾼의 손목을 가지고 있다.
나는 예컨대 집에 앉아, 낚시하러 나가기 전에, 고개를 휙 돌려 오른손을 응시하고는, 한 번은 멀리, 한 번은 가까이 손을 거둔다. 그것만으로도 나는 다가올 낚시의 결과를, 때로는 세세한 부분까지도, 내 시각과 촉각 속에서 예지할 수 있다. 평상시에는 힘을 비축하도록 금팔찌 속에 가둬 두는 이 날렵한 손목의 육감. 나는 내 낚시터의 강물을 구체적인 시각의, 구체적인 물살 속에서 본다. 강의 단면이 내 앞으로 드러난다. 분명한 수와 종류로 열 군데, 스무 군데 — 백 군데 지점에서 물고기들이 단면을 향해 밀려오는 모습이 보인다. 이제 나는 어떻게 낚아야 할지를 안다. 어떤 녀석들은 머리로 그 단면을 파고들어 가거늘, 나는 그들 앞에서 낚싯대를 흔들어댈 뿐인데 그들은 낚시고리에 걸려버린다. 내가 집의 책상에 앉아 있을 때도 황홀감을 안겨주는 운명의 순간. 다른 물고기들은 배腹까지 단면에 닿으니 그때가 절정의 기회이다. 나는 몇몇은 여전히 낚아내지만, 다른 물고기들은 꼬리까지 미끄러뜨리며 위험천만한 단면을 지나 내게서 빠져나가고 만다. 하지만 오직 이번뿐이다 — 진정한 낚시꾼은 어떤 물고기도 놓치지 않거늘.
서두의 이미지는 막스 리히터, The Blue Notebooks 의 앨범 커버이다.
Franz Kafka, The Blue Octavo Notebooks, Volume 1
17 Jun 2025
This post is originally a Korean translation of Kafka’s The Blue Octavo Notebooks. Given that there already exists an English translation of the work, I won’t go through the hassle of translating into English again. However, I present the following passage, which I particularly admire.
이탈리안 게임
12 Jun 2025
- e4 e5
- Nf3 Nc6
- Bc4
해당 오프닝을 이탈리안 게임이라고 한다. 백의 아이디어는 흑의 d5를 저지함으로써 강하게 중앙을 컨트롤하는 것이다. 이에 대해 흑은 소극적으로 대응해서는 안 된다. 예를 들어 …h6 (안티 프라이드 리버 어택: 백의 Ng5, Bg5를 저지하는 수)은 권장되지 않는다. 백이 4. d4를 쳤을 때 백의 중앙이 너무 강해지기 때문이다. 흑이 4. ..exd4로 대응할 경우 백은 5. Nxd4로 되잡는다.
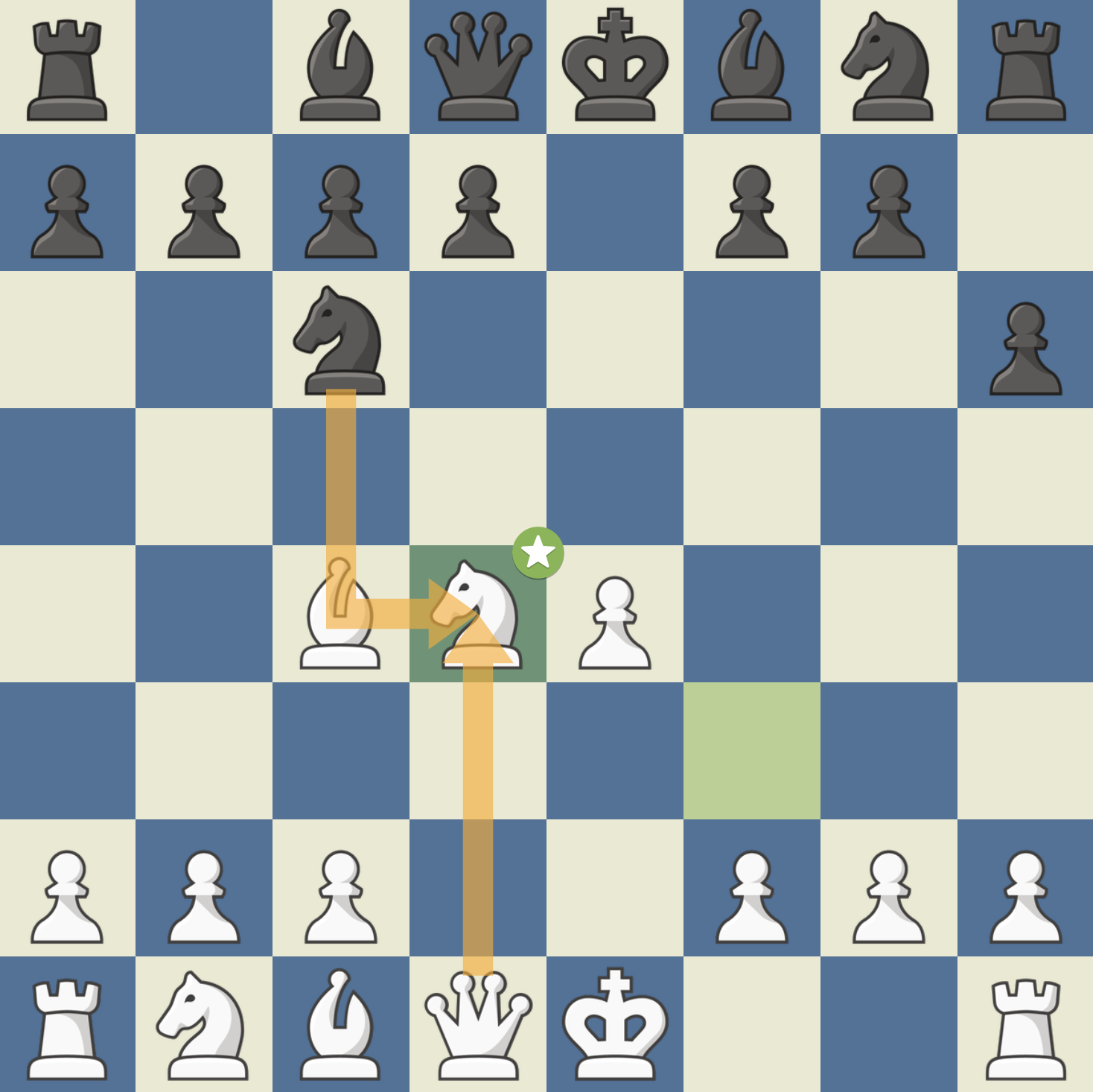
만약 흑이 5. …Nxd4로 나이트까지 교환한다면 백의 6. Qxd4가 강력하다. 흑은 퀸사이드 나이트를 교환했기 때문에 백의 퀸을 쫓아낼 마땅한 방법이 없을 뿐더러 백의 비숍과 퀸에 의해 킹사이드가 노려지고 있어 전개가 상당히 까다로워진다.
3. Bc4에 대한 흑의 정석적인 대응은 두 가지이다.
3. …Bc5

백의 d4를 저지하는 수이다. 이제 백은 d4를 치기 위해 추가적인 지지가 필요하기 때문에 4. c3로 d4를 준비한다. 이 라인을 지우코 피아노라고 부른다. 흑의 정석적인 대응은 …Nf6이다. 백에게 d4를 칠 기회를 주지만, 대신 흑은 e4를 노릴 수 있다. 백은 두 가지 선택지가 있다.
수비적 플레이: 5. d3

백은 e4의 위협을 d3로 수비한다. 이 라인을 지우코 피아니시모이라고 부른다. 이후 백은 킹사이드 캐슬링을 진행하고 나머지 마이너 피스를 전개하여 게임을 안정적으로 운영한다.
공격적 플레이: 5. d4

백은 e4의 위협에 개의치 않고 d4를 친다. 이 라인을 지우코 피아노 메인이라고 부른다. 메인 라인을 들어가게 되면 기물들이 중앙에서 치열하게 뒤엉켜 싸우는 복잡한 게임이 펼쳐진다.
3. …Nf6

백의 e폰을 공격하는 동시에 d5를 지지함으로써 d5 폰브레이크를 준비하는 수이다. 이 라인을 투 나이트 디펜스라고 부른다. 여기서도 백은 선택지가 있다.
수비적 플레이: 4. d3

e폰을 수비하는 동시에 어두운 비숍의 길을 열어주는 수이다. 이후 백은 지우코 피아니시모와 마찬가지로 킹사이드 캐슬링을 진행하고 나머지 마이너 피스를 전개한다.
공격적 플레이: 4. Ng5

Nf7로 퀸과 룩을 포크하는 공격을 준비하는 수이다. 이것을 이탈리안 게임 나이트 어택 바리에이션이라고 한다. 흑의 유일하게 올바른 대응은 d5이다. Bc5 (트렉슬러 카운터어택) 등으로 흑이 역공을 노리는 라인이 있지만, 이 경우 백이 나이트로 공격하는 대신 Bf7+로 킹사이드를 무너뜨리고, Bb3로 안전하게 후퇴하면 된다.
…d5에 대해 백이 5. Bb3 등으로 비숍을 빼면 전개가 너무 느리기 때문에, 5. exd5가 바람직하다. 반면 5. Bxd5는 블런더이다. 5. …Nxd5 6. exd5로 나이트와 비숍이 교환되면 …Qxf5로 나이트가 잡힌다. 백 또한 7. dxc6로 나이트를 잡을 수 있기는 하지만, 이 경우 …Qxg2로 퀸이 킹사이드 진영에 침투하는 것을 막을 수 없다.

5. exd5에 대한 흑의 대응은 흔히 두 가지이다.
5. …Nxd5

흑의 의도는 나이트에 대한 퀸의 공격을 드러내면서 폰을 회수하는 것이다. 그러나 이것은 초보자 경기에서 정말 많이 나오는 실수이다. 백의 강력한 수, 6. Nxf7!!이 있다. 이것을 프라이드 리버 어택이라고 부른다. 흑이 …Kxf7으로 나이트를 잡으면 백은 7. Qf3+로 체크와 동시에 d5 나이트를 공격한다. 여기서 만약 흑이 Kg8으로 피하면 8. Bxd5가 2수 메이트이다.

5. …Na5

나이트가 비숍을 공격하는 폴레리오 디펜스이다. 백의 정석적인 대응은 6. Bb5+로 …c6를 유도하고, 7. dxc6 bxc6로 폰을 교환하는 것이다. (흑이 7. …Nxc6로 되잡을 경우 백은 8. Bc4로 돌아가서 다시 Nf7 공격을 노릴 수 있다. 물론 프라이드 리버 어택도 여전히 가능하다.) 결과적으로 흑은 비숍길이 열리고 중앙에 폰이 있다는 포지션적 이점을 가지는 반면, 백은 원폰업이라는 이점을 가지게 된다.

7. …bxc6로 비숍이 공격받았으므로 백은 비숍을 빼야 하는데, Ba4로 뺴는 것은 블런더이다. (팁: 이거 두면 ‘바보BaFour‘라고 외우면 된다) 흑의 8. …h6 나이트 공격이 강력하기 때문이다.

다음 경우의 수에서 보이듯이 백은 결국 킹사이드 진영이 망가지거나, 비숍-나이트 포크에 걸리거나, 나이트가 트랩 당하거나, 나이트를 원래 자리로 후퇴시키게 된다.
- 9. Nh3 Bg4 10. f3 Bxh3 11. gxh3 (킹사이드 붕괴)
- 9. Nf3 e4 (나이트 공격)
- 10. Ne5 Qd4 (비숍-나이트 포크) 11. Bxc6+ Nxc6 12. Nxc6 Qd5 (나이트 트랩)
- 10. Nh4 d5 (나이트 트랩)
- 10. Ng1 (나이트 후퇴)
대신 백은 8. Be2, 8. Bd3 (9. Ne4), 8. Qf3 (9. Qxa8) 등으로 응수할 수 있다.

스카치 전환: 4. d4

Nxe4의 위협을 d4 폰브레이크로 맞받아치는 수이다. 흑이 4. …exd4로 대응할 경우 이는 스카치 갬빗에서 흑이 4. …Nf6로 대응한 것과 형태가 같다.
스카치 갬빗. 1. e4 e5 2. Nf3 Nc6 3. d4 exd4 4. Bc4
포 나이트 이탈리안: 4. Nc3

이 또한 초보자 경기에서 정말 많이 나오는 실수이다. 이 수의 아이디어는 나이트를 전개하는 동시에 e폰을 지키려는 것이나, 여기서 흑은 4. …Nxe4로 나이트를 희생할 수 있다. 백이 5. Nxe4로 나이트를 되잡으면 흑은 …d5를 쳐서 비숍과 나이트를 포크한다.

백이 대응하는 경우의 수를 살펴보자.
6. Bxd5
백이 데스페라도 전략으로 폰을 먹으면 흑은 …Qxd5로 회수한다. 이 경우 흑과 백은 기물 점수로는 동등하지만 백은 중앙 폰과 쌍비숍 이점을 잃었고, 흑의 퀸 전개까지 도와준 셈이기 때문에 포지션적으로 불리하다. (엔진 기준 -1.1점)

6. Bb5
백은 나이트를 내주는 대신에 흑의 나이트를 핀에 건다. 나이트가 핀에 걸렸으므로 6. …dxe4 이후로 7. Nxe5가 가능할 것 같지만, 이 경우 백은 완전히 불리해진다. 흑이 7. …Qg5로 5 랭크의 나이트와 g폰을 동시에 공격할 수 있기 때문이다.

여기서 백이 당황해서 8. Bxc6를 두면 흑은 사실상 이기게 된다. 비숍이 킹 앞의 e2 칸을 더이상 보호하고 있지 않아, 다음의 치명적인 공격이 가능해진다.
- …bxc6 9. Nxc6 Qxg2 10. Rf1 Bg4 11. f3 Bxf3 12. Rxf3 exf3
여기서 흑은 Qg1# 한수 메이트가 있기 때문에 백은 체크메이트를 피해야 한다. 그러나 체크메이트를 피한다 하더라도, f폰의 프로모션과 그로 인한 디스커버드 체크를 피할 수 없어서 사실상 흑이 이긴 게임이다.
이제 조금 더 드물게 나오는 라인을 알아보자.
3. …d6

e4 폰을 지키는 수이다. 이것은 필리도어 디펜스 (1. e4 e5 2. Nf3 d6) 이후 백이 비숍을 전개하고 흑이 나이트를 전개한 것과 형태가 같다.
이탈리안 필리도어 디펜스와 일반 필리도어 디펜스 모두 백의 대응은 d4를 치는 것이다. 이후 전개는 대략 다음과 같다.
흑이 exd4를 할 경우
백은 Nxd4로 되잡는데. 백은 센터 폰이 있고 나이트의 활동성이 좋다는 이점을 가진다. 반면 흑은 견고한 방어를 구축하게 된다.
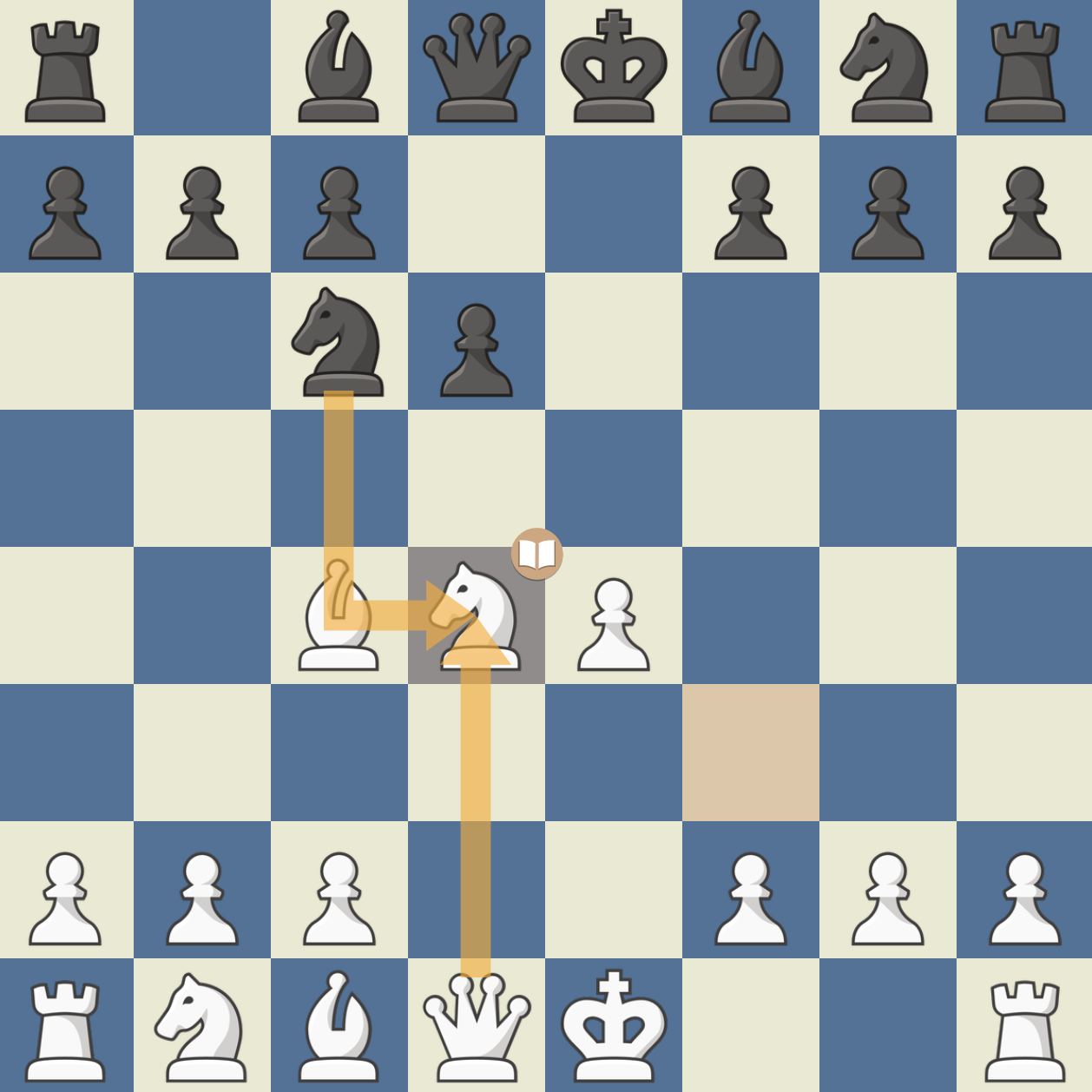
흑이 exd4를 하지 않을 경우
이탈리안의 경우 Nc6 전개가 되어 있기 때문에 5. dxe4 dxe4 이후 6. Qxd8이 들어오더라도 …Nxd8으로 되잡을 수 있어 흑은 캐슬링 권한을 지킬 수 있다. 백 입장에서는 6. Qxd8 대신 6. O-O가 퀸을 유지함으로써 센터 이점을 살리는 데 더 좋다.

3. …Be7

퀸과 비숍을 연결하는 수이다. 이것을 헝가리안 디펜스라고 부른다. 백은 4. d4를 친다. 흑이 4. …exd4로 응수할 경우 이는 스카치 갬빗에서 흑이 4. …Be7을 한 것과 형태가 같다.
그런데 스카치 갬빗에서 4. …Be7은 좋지 않은 대응으로 알려져 있다. 백은 5. Nxd4로 폰을 되잡거나, 스카치 갬빗에서 자주 등장하는 5. c3로 함정을 팔 수 있다. (이 함정의 조건은 f6 칸에 나이트가 없어야 한다는 것이다) 5. c3에 대해 흑이 5. …dxc3로 응수할 경우 6. Qd5로 한수 메이트 Qxf7#를 위협한다.

이를 막기 위한 흑의 유일한 수는 …Nh6인데, 7. Bxh6로 잡으면 흑의 킹사이드 진영이 무너진다.
3. …Nd4

블랙번 실링 갬빗이다. 백 입장에서는 흑이 e5 폰을 내준 것 같지만 이는 함정이다. 흑의 4. …Qg5로 나이트와 g폰이 포크에 걸리기 때문이다.

파훼법은 폰을 잡는 대신 4. Nxd4 exd4로 나이트를 교환하고 캐슬링하는 것이다. 이후 흑이 5. …Bc5로 대응할 경우, 백에게 탁월한 수 6. Bxf7!!이 있다. 킹이 비숍을 잡을 경우 7. Qh5+가 흑의 어두운 비숍을 포크하기 때문에 기물 회수가 가능하다.

3. …f5

루소 갬빗이다. 흑이 f폰을 내주는 것 같지만, 백이 4. exf5를 할 경우 흑의 …e4가 나이트를 공격하게 되고, 나이트는 g칸으로 돌아오는 것밖에 살아남을 구멍이 없어 보인다. 결과적으로 백은 전개에서 뒤지게 된다.

그런데 여기에는 역공 라인이 있다. 백이 g1으로 나이트를 빼는 대신, 5. Ne4로 가는 것이다. 그러면 …Nxe4로 나이트를 잃는 것처럼 보이지만, 6. Qh5+라는 강력한 역공을 넣을 수 있다.

역공을 거는 대신 4. d4로 간단히 응수할 수도 있다. 그러면 흑이 …fxe4로 나이트를 공격하더라도 Nxe5로 전개하면 된다. 한편 흑은 f7-h5 대각선이 약점으로 남는다. (오프닝 때 f폰을 움직이지 말라는 말이 괜히 있는 것이 아니다)
참고자료
슥슥이 유튜브 사랑합니다
슬라보예 지젝, 「소프트 파시즘, 인공지능, 그리고 수치심의 몰락」
06 Jun 2025본 글은 2024년 11월 26일에 이루어진 슬라보예 지젝의 옥스포드 강연을 번역한 것이다. 주석은 역자 주이다. 또한 섹션의 구분도 역자가 독자의 편의를 위해 넣은 것이다. 매끄러운 흐름을 위해 내용을 덧대거나 빼는 수준의 의역과 문장 재배치를 한 부분이 있다.
1. 운명론적 역사관 비판
저는 “우리가 지금 어디에 있는가”라는 질문에 대한 몇 가지 개괄적인 이야기를 하고자 합니다. — 우리는 지금 어디에 있을까요?
저는 양자역학의 개념을 빌려와서 이 사회적 · 역사적 질문에 접근하고 싶습니다. 우선 저의 기본적인 생각은, 자유주의나 마르크스주의에서 피력하는 낙관적인 역사관을 포기해야 한다는 것입니다. 이러한 역사관들은 운명론적인 특징을 가지고 있습니다. 일례로 후쿠야마Francis Fukuyama는 “역사의 종말1”을 주장했습니다. 한편 정통 마르크스주의자들은, 여러 굴곡이 있더라도 궁극적으로는 공산주의 사회가 도래할 것이라고 주장합니다. “미래는 사회주의거나 야만주의다”라고 말한 로자 룩셈부르크Rosa Luxemburg처럼 운명론에서 아주 살짝 비껴난 입장도 있기는 했지요. 여담이지만, 안타깝게도 룩셈부르크는 이 점에 있어 틀렸습니다. 스탈린주의에는 둘 다 있었으니까요.
이런 운명론에 매달리기보다, 저는 다음과 같이 생각합니다. 양자역학에 따르면, 점 A에서 점 B로 이동하는 입자는 A와 B를 잇는 모든 경로를 양자 중첩 상태로 거칩니다. 우리가 관측하는 것은 그러한 중첩 상태에서 붕괴된 하나의 경로이지요. 저는 우리의 현 사회가 붕괴 전의 중첩 상태라고 생각합니다. 과연 누가 앞으로의 인류가 어디로 향할지 알겠습니까? 우리가 아는 것은 우리의 미래에 치명적인 위협들이 있다는 것뿐입니다. 환경, 전쟁, 인구 문제 등이 떠오르네요. 우리는 이러한 위협들이 어떻게 상호작용할지도 오리무중입니다. 어떤 사람들은 환경 위기가 심각해지면 전쟁은 줄어들 것이라고 생각합니다. 저는 이 점에 관해 회의적입니다.
2. 소프트 파시즘과 불량 국가
이러한 위협들에 대응하는 과정에서 어쩌면 미래에는 새로운 사회주의가 도래할지도 모릅니다. 일부 문명만이 섬처럼 고립된 형태의 세계적인 야만주의가 도래할지도 모르지요. 그러나 제가 예상하건대 — 그리고 이 예상은 저를 정말 슬프게 만듭니다 — 가장 도래할 가능성이 높은 미래는 제가 소프트 파시즘Soft Fascism이라고 부르는 것입니다. 여기서 “소프트”라는 표현은 이것이 나치주의와 같은 노골적인 파시즘이 아님을 의미합니다. 제가 생각하기에 파시즘의 가장 괜찮은 정의는 “보수적인 혁명”입니다. 영리한 파시스트들은 자본주의의 활력과 빠른 발전력을 탐내면서도, 방임된 자본주의는 사회 분열을 초래한다는 사실을 알았습니다. 이 문제를 극복하기 위한 파시즘의 발상은, 강력한 국가 권력이 전통 · 종교 · 민족 등의 이데올로기를 통해 자본주의적 경제 구조를 억지로 유지해 내는 사회입니다.
제가 소프트 파시즘의 교과서적인 사례로 생각하는 국가가 있습니다. 바로 중국입니다. 두 달 전, 중국 지도자의 연설이 있었습니다. 그는 우리 세대의 젊은이들이 충분히 교육되지 않았으며 그들을 사상적으로 훈련시켜야 한다고 말했습니다. 저는 그래서 그가 늘 하던 말 — 마르크스를 읽으라는 둥, 마오를 읽으라는 둥 — 을 할 줄 알았습니다. 하지만 아니었습니다. 그가 언급한 것은 유교 전통이었습니다. 통합을 위해서는 유교 정신이 필요하다는 것이었습니다. 같은 일이 인도에서는 모디Narendra Modi에 의해 행해지고 있습니다.2 극도로 야만적인 자본주의 체제가 비자본주의적인 이데올로기를 통해 유지됩니다. 저에게 물어본다면, 이것이 대다수의 국가가 봉착하게 될 미래입니다. 역사는 우리의 편에 서 있지 않습니다.
저를 염려시키는 또다른 사실은, 소위 불량 국가rogue state들이 점점 많아지고 있다는 것입니다. 당황하지 마세요. 제가 말하는 “불량 국가”는 서구의 제국주의적 언어에 해당하지 않습니다.3 제가 정의하는 “불량 국가”란, 현존하는 질서가 자기 자신의 이데올로기적 조건 속에서 스스로를 법적으로 유지할 수 없기 때문에 야만적이고 불법적인 폭력에 의존해야 하는 국가입니다.
아무래도 아이티가 가장 먼저 따오르는 사례군요. 그곳은 국가가 붕괴하여 국토의 80% 이상이 갱단에 의해 경영되고 있습니다. 하지만 굳이 아이티 같은 이례적인 사례에 집착할 필요는 없습니다. 러시아는 어떻습니까? 바그너 그룹은 전형적인 반법半法, 불법 군사 조직으로서, 이제는 러시아 정부의 전폭적인 지지를 받아왔음이 만천하에 드러났습니다. 그럼에도 불구하고 바그너 그룹은 중앙 정부와 언제나 일정한 거리를 두었죠. 그런가 하면 이스라엘은요? 솔직해집시다. 서안 지구4에 정착한 이스라엘인들은 다름아닌 이스라엘의 법에 따라 범법자들입니다. 이스라엘의 비극을 잘 보여주는 사례가 있습니다. 이타마르 벤그리브는 20여년 전에 인종 범죄로 이스라엘 법정에 기소된 바 있습니다. 지금 그는 이스라엘 안보부 장관입니다. 미국도 크게 다르지 않습니다. 현재 미국에는 반이슬람주의자, 반유대주의자, 프라우드 보이즈5와 같은 단체들이 공존하고 있습니다. 그리고 트럼프는 그들과 거리를 두면서도 그들을 통해 사회를 조종합니다. 이들이야말로 실패한 국가들입니다. 이들은 그 자신의 이데올리기와 법적 근거만을 통해서는 질서를 지탱할 수 없는 국가들입니다.
따라서 우리는 현재의 극단적인 혼돈과 비결정성을 인지해야만 합니다. 현재의 상황이 언제까지나 이어질 수 없다는 사실은 명백합니다. 그러나 그 종착지가 어디일지는 그 어떤 의미에서도 결정된 것이 아닙니다. 다시 양자역학의 용어를 빌리자면, 우리의 중첩 상태가 어떠한 하나의 상태로 붕괴할지 전혀 알 수 없습니다. 미래가 가장 바람직한 특정 정치 형태로 나아가리라는 생각은 일종의 착시입니다.
3. 사후성
자세히 말할 시간은 없지만 저는 헤겔이 이것을 내다보았다고 생각합니다. 사후성retroactivity에 관한 헤겔의 논의를 봅시다. 특정한 현실이 자리를 잡으면, 그 현실이 과거를 실질적으로 변화시키지는 않지만 사후적으로는 변화시킵니다. 다시 말해, 현재는 우리가 과거를 인지하는 방식과 과거에 부여하는 서사를 변화시킵니다. 그런 의미에서 우리는 늘 과거를 변화시키고 있습니다. 같은 주장을 마르크스에서도 발견할 수 있습니다. 마르크스는 순진한 진보주의자로 폄하되곤 하지만 — 물론 그에게 이러한 면모가 실제로 있었음은 부정할 수 없습니다 — 그에게는 다른 면모도 있습니다. 예를 들어 그의 ⟪정치경제학 비판 요강⟫에는 이런 대목이 있습니다. “인간의 해부학이 유인원의 해부학을 이해하는 열쇠인 것처럼 자본주의는 역사의 모든 단계를 해석하는 능력을 제공한다.” 마르크스의 이 대목은 놀랍도록 반-운명론적인 것입니다. 여기서 그가 말하려는 것은 “자본주의의 도래는 예정된 것이었다”와 같은 말이 아닙니다. 마르크스의 요점은 훨씬 더 정교합니다. 자본주의가 승리하고 나면, 우리는 사후적으로 역사를 해석하여 과거의 모든 사건들이 마치 자본주의를 향해 왔던 것처럼 재서술한다는 것입니다.
이러한 이유로 저는 데이비드 그레이버David Graeber와 윈그로David Wengrow의 연구를 — 비록 그들의 주장에 완전히 동의하지는 않지만 — 아주 높이 평가합니다. 그들은 고대 잉카 문명에서, 현대의 우리가 처한 것과 같은 중첩 상태를 포착하고자 했습니다. 잘 아시겠지만, 잉카 문명이 언제나 아이들을 희생시키는 식의 공포로 점철된 것은 아니었습니다. 잉카에서는 놀라운 수준의 지역 민주주의 체계가 작동하고 있었습니다. 어느 순간 붕괴했을 뿐이었지요. 이로부터 제가 내리는 교훈은 이것입니다. 일어나는 일들을 이해하기 위해서는, 일어날 수 있었지만 일어나지 않은 일들에 주목해야 합니다. 일어날 수 있었지만 일어나지 않은 일들은 그저 소멸하지 않습니다. 그것은 어쩌면 반동적인, 어쩌면 진보적인, 일종의 염원으로서 사회에 잔존합니다.
4. 인공지능과 인간다움
이러한 이유로 저는 우리가 “진보”를 정의하는 데 있어 매우 조심해야 한다고 생각합니다. 예를 들어 오늘날의 중요한 주제인 인공지능의 사례를 봅시다. 저는 우리가 “인공지능도 사고할 수 있게 될까?”와 같은 질문만 던져서는 인공지능의 문제에 올바르게 접근할 수 없다고 생각합니다. 물론 여기서 말하는 “사고”란 우리 인간과 같은 방식의 사고를 말합니다. 우선 이것은 우리가 답을 알지 못하는 추상적인 질문입니다. 우리는 우리와 같은 방식의 사고 가능성에 집착하지만, 완전히 새로운 형태의 정신이라든가 영혼이 생길 수도 있는 것 아니겠습니까?
대신 제가 여러분을 자극할 만한 정신분석학적 접근을 제시해 보겠습니다. “인공지능이 무엇을 할 수 있는가” — 흔히 있는 멍청한 토론 주제죠 — 라는 질문을 생각해 보면, 당연히 인공지능은 우리보다 훨씬 빠르게 계산할 수 있고, 스스로 학습할 수 있고, 자기 복제할 수 있습니다. 그러나 제 생각에는 인간에게 고유한, 그리고 인간다움의 핵심을 이루는 두 가지 특징이 있습니다.
첫째는 일상에서의 의식, 달리 말하자면 미신적 습관입니다. 개인적인 사례를 들자면 저는 손을 씻고 수도꼭지를 잠굴 때 꼭지에서 물방울이 떨어지고 있지 않다는 것을 똑똑히 보고서도 꼭지에 손을 대서 확인하곤 합니다. 정신분석학자라면 이것을 피임에 대한 무의식적 강박으로 해석할지 모르겠지만 그런 말도 안 되는 소리는 사양하겠습니다. 이것은 단적인 습관일 뿐입니다. 하지만 우리는 모두 이같은 습관을 가지고 있습니다. 제가 애거서 크리스티의 전기에서 읽은 사실인데요, 그는 목욕을 하고 나올 때마다 사과 한 알을 먹었다고 합니다. 도대체 이런 행동에 어떤 의미가 있겠습니까? 이 행동들이 가지는 의미가 있다면 그것은 외양에 불과합니다.6 혹은 의미를 가지지 않는 의미라고 말할 수 있겠습니다. “이 행동의 이면에는 이러한 트라우마가 있다”라든가 “이 행동의 이면에는 이러한 무의식적 동기가 있다”라고 말하는 것은 잘못되었습니다. 애거서 크리스티가 무의식적으로 본인이 에덴 동산의 이브라고 생각했다는 말입니까? 아니죠. 이러한 텅빈 의미의 외양은 우리 인간이 노골적일 정도로 혼란스러운 삶의 무의미에 대응하는 한 가지 방식에 다름 아닙니다.
둘째로, 저는 인공지능이 결코 진정한 의미에서 욕을 할 수 없다고 생각합니다. 저에게 있어 욕은 매우 흥미로운 현상입니다. 욕은 단순히 저급한 언어가 아닙니다. 욕은 인간이 언어 안에 존재하기를 원한다는 증거입니다. 우리의 사고는 언어의 형태로 이루어지지만, 그럼에도 우리는 결코 진정한 의미에서 언어에 거주하지 않습니다. 우리가 욕을 할 때는 단순히 객관적 사건에 대한 불만족을 표출하는 것이 아닙니다. 욕은 그것을 언어로 형성할 수 없는 데에서 오는 분노의 표출입니다. 일례로 십자가에 매달린 예수를 떠올려 보세요. 저는 아무리 예수라고 해도 죽어가면서 욕을 했을 것이라고 생각합니다. 다소 어이없는 생각이긴 하지만, “와 시발…”이라고 중얼거렸을 수도 있지 않을까요? 제 요점은, 언어 안에 완전히 존재할 수 없을 때 느끼는 수치심이야말로 인간다움을 구성하는 본질 중 하나라는 것입니다.
5. 수치심의 몰락
이제 또다른, 어쩌면 놀랍게 들릴 수도 있는 이야기로 마무리를 짓겠습니다. 오늘날 저를 정말로 슬프게 만드는 것은 뻔뻔함shamelessness의 폭증입니다. 10년 전까지만 해도 공적인 장소에서 말하는 것이 불가능했던 말들이 이제는 공공연하게 이루어집니다. 단순히 도널드 트럼프나 보리스 존슨과 같은 뻔한 사례들을 말하려는 것이 아닙니다. 저는 단연코 반유대주의자가 아니지만 — 저는 이스라엘의 입장도 고려하려 합니다 — 최근에 이스라엘에서 일어난 두 가지 일은 저를 충격에 빠뜨렸습니다. 8월에 이스라엘 의회 케네셋에서 논쟁이 있었습니다. 먼저 배경을 말씀드리겠습니다. 예루살렘의 남쪽에 있는 하마스 수용소에서는 간수들이 수감자들을 매우 잔혹하게 다루고 있었습니다. 영상 자료도 유출되었기 때문에 부정할 수 없는 사실이지요. 바늘로 뒤덮인 커다란 철제 막대기를 항문에 쑤셔 넣는 등의 고문으로 인해 많은 수감자가 과다출혈로 사망했습니다. 물론 저는 중립을 지키고 싶기 때문에 하마스 측에서는 무슨 고문을 하고 있을지 누가 아냐는 단서를 남겨두겠습니다. 하지만 저를 정말 슬프게 만드는 것은, 케네셋의 논쟁에서 지배적이었던 의견이 간수들의 잘못을 따지는 것이 아닌, 가혹행위를 한 간수들이 기소되었다는 사실을 치욕으로 여기는 의견이었다는 것입니다. 하마스는 인간도 아니기에 그들에게는 무슨 짓을 해도 괜찮다는 것이었죠. 저는 이런 솔직함보다는 위선이 낫다고 생각합니다.
이제 두 번째 사건을 말해 보겠습니다. 엘리란 미즈라히라는 한 정직하고 올바른 이스라엘 병사가 있었습니다. 가자에서 복무할 당시 그는 끔찍한 명령을 받았습니다. 생사 여부를 따지지 말고 수백 명의 팔레스타인을 트랙터로 깔아뭉개라는 명령이었습니다. 그는 명령을 이행했지만 이후 극심한 혼란에 살다가 이내 자살했습니다. 미즈라히는 윤리적 고결함을 가지고 있었던 것이지요. 그러나 이를 본 이스라엘 방위군의 심리전문가들은 어떻게 병사들을 훈련시켜야 그들이 윤리적 딜레마를 느끼지 않도록 할 수 있을지를 연구하기 시작했습니다. 이것이 제가 말하는 “뻔뻔함”입니다.
그렇다면 이제 정말로 결론을 내리겠습니다. 저에게 무척이나 흥미로운 것은, 저의 스승이라고 부를 수 있을 자크 라캉의 견해입니다. 그는 69-70년에 정신분석학의 다른 측면에 대한 세미나를 진행했었는데요, 그 세미나는 68혁명에 대한 그의 반응이기도 했습니다. 세미나에서 라캉은 학생 저항을 지지하는 대신 이렇게 말했습니다. “당신들에게 결여되어 있는 것은 수치심이다.” 라캉에 따르면, 자유방임적인 오늘날의 사회에서 정신분석학의 궁극적인 목표는 아버지의 억압을 몰아내거나 성적 환상을 실현하는 것이 아닙니다. 오히려 수치의 결여, 그리고 그것이 야기하는 보편적인 도착증perversion이 주제입니다.
도착증은 히스테리아에 비해 훨씬 덜 전복적입니다. 정신분석학에 대해 조금 들은 바가 있다면 아시겠지만, 이 두 증세는 성별과 결부되곤 합니다. 남성 쇼비니즘의 일환입니다만, 요지는 여성은 히스테리적이라 불평을 하면서도 은밀하게 새로운 주인에게 지배받기를 원하고, 남성은 도착적이라서 자신의 꿈을 시행에 옮기기에 급급하다는 것입니다. 하지만 일찍이 프로이트는 알고 있었습니다. 도착증보다 무의식이 더 억압받는 곳은 없으며, 모든 위대한 일은 히스테리아를 통해 발생한다는 사실을 말입니다. 저는 이것이 오늘날의 우리를 위한 교훈이라고 생각합니다.7
제가 젊었을 때 저와 친구들은 촌스러운 좌파였습니다. 우리는 권력자들이 위엄을 지니고 있다고 생각했고, 우리 자신은 온갖 상스러운 손짓과 더러운 말을 주고받았지요. 하지만 이제는 압니다. 권력을 가진 저들이야말로 우리가 상상했던 것 이상으로 상스러운 자들입니다. 지난 선거 때 우리는 완전히 틀렸었습니다. 민주당은 아무것도 배우지 못한 것이죠. 트럼프가 거짓말을 했음이 밝혀졌을 때 민주당은 그의 약점을 잡았다고 생각했어요. 하지만 아니었지요! 오히려 그에게 도움이 됐습니다. 트럼프의 천박함과 거짓말은 그의 정체성을 이룹니다. 사람들은 바로 그 이유에서 그를 사랑했던 것이지요. 따라서 자유방임적인 오늘날의 시대에서 우리가 물어야 하는 질문은 이것입니다. 어떻게 가장 기본적인 수치심의 감각을 되살릴 것인가?
감사합니다.
-
동명의 저술에서 후쿠야마는 자유민주주의와 시장자본주의의 혼합 체계가 사회문화적 진화의 궁극적 단계라는 이론을 주장했다. 이후 후쿠야마는 트럼프를 비롯한 미국 내 극단주의 세력의 부흥을 목격하고 자신의 이론을 폐기했다. ↩
-
모디 정권은 힌두교의 극단주의화를 촉진시키고 인도의 민주주의를 후퇴시켰다는 비판을 받는다. ↩
-
2002년에 부시 미국 대통령이 이라크, 이란, 북한을 “악의 축”으로 부른 것과, 최근에 미국 상원 원내대표가 중국, 러시아, 이란을 “새로운 악의 축”으로 부른 것을 비꼰 것이다. ↩
-
팔레스타인 지역의 일부. 팔레스타인 지역은 크게 이스라엘, 가자 지구, 그리고 서안 지구로 구성되어 있다. ↩
-
미국의 대안우파 단체. 좌익 단체에 대한 폭력적인 반대 활동으로 알려져 있으며, 2021년에 해당 단체의 회원들이 미국 국회의사당 습격 혐의로 기소되었다. ↩
-
더미 텍스트와 같이 통상적으로 어떤 의미를 가지고 있을 것으로 기대되나 — 텍스트, 신호, 행동 등 — 실제로는 의미를 완전히 결여하고 있음을 뜻한다. ↩
-
도착증은 무의식적 긍정성의 발현으로서 자유, 방임, 행동, 능동성 등을 아우르는 개념인 한편, 히스테리아는 무의식적 부정성의 발현으로서 억압, 제약, 금지, 수동성 등을 아우르는 개념이다. 지젝은 본 강연에서 이데올리기와 자본주의가 기형적으로 융합된 “소프트 파시즘”, 인공지능, 그리고 “뻔뻔함의 폭증”을 긍정성의 맹목적인 발현, 즉 도착증이라는 범주 아래에 포섭시키는 것으로 보인다. ↩
Slavoj Žižek, "Soft Fascism, Artificial Intelligence, and Shamelessness"
06 Jun 2025This post is originally a Korean translation of Slavoj Žižek’s Oxford lecture, so there is no separate English version. However, the following personal observation from the original post is reproduced here.
Psychoanalytically, Perversion is a manifestation of subconscious positivity while hysteria is a manifestation of subconscious negativity. Positivity encompasses concepts such as freedom, laissez-faire, liveliness, and activity, while negativity encompasses concepts such as repression, constraint, prohibition, and passivity. In this lecture, Žižek appears to subsume “soft fascism” — the pathological fusion of ideology and capitalism, — artificial intelligence, and the rise of Shamelessness under the category of perversion, namely the uncontrolled manifestation of positivity.
왜 연속함수의 위상적 정의는 “반대”인가?
02 Jun 2025정의. 두 위상공간 $X, Y$에 대해 사상 $f: X \to Y$가 연속이라는 것은, $V \subseteq Y$가 열린 집합이라면 $f^{-1}[V] \subseteq X$ 또한 열린 집합이라는 것이다.
위상수학을 처음 수강하는 학생들은 위 정의에서 혼란을 겪는다. 직관적으로는 “$U \subseteq X$가 열린 집합이라면 $f[U] \subseteq V$ 또한 열린 집합인 사상”이라는 정의가 자연스러운데, 실제 정의는 이와 반대이기 때문이다. 이러한 직관의 “근거”는 대충 다음과 같을 것이다.
1. 엡실론-델타 논법
엡실론-델타 논법에 따르면 $f: X \to Y$가 연속이라는 것은 다음과 같다.
\[\forall \epsilon > 0 \; \exists \delta > 0 : |x - y| < \delta \rightarrow |f(x) - f(y)| < \epsilon\]위 논리식을 보면 조건부에 $x, y \in X$가 있고 결론부에 $f(x), f(y) \in Y$가 있다. 따라서 연속함수의 위상적 정의 또한 조건부에 $U \subseteq X$가 있고 결론부에 $f[U] \subseteq Y$가 있는 것이 자연스러워 보인다.
2. 열린 집합에 대한 직관
처음 위상수학을 배울 때, 열린 집합을 “서로 가까운 점들의 모임”으로 생각하곤 한다. 즉, $U$가 열린 집합이라는 것은 $x, y \in U$라면 $x, y$가 “가깝다”는 것이다. 그렇다면 연속함수는 “가까운 점들을 가까운 점들로 사상시키는 함수”이므로, 열린 집합을 열린 집합으로 사상시키는 함수로 정의하는 것이 자연스러워 보인다.
그러나 위 두 “근거”는 매우 잘못되었다.
3. “엡실론-델타 논법” 근거가 잘못된 이유
$\rightarrow$만을 기준으로 왼쪽이 조건부, 오른쪽이 결론부로 판단하는 것은 오해를 낳기 딱 좋다. 왜냐하면 여기서는 양화사 또한 고려해야 하기 때문이다. 엡실론-델타 논법의 양화사 부분을 언어적으로 읽으면 “임의의 양수 $\epsilon$에 대해, 어떤 양수 $\delta$가 존재한다” 이다. 다른 말로 하자면, U$\epsilon$이 양수라면, 어떤 양수 $\delta$가 존재한다” 이다.
그리고 $\epsilon$과 유관한 공간은 $X$가 아닌 $Y$이다. 즉, $\epsilon$에 대한 서술, 그리고 그에 부수되는 $Y$에 대한 서술이 해당 논리식에서 가장 일차적인 조건부인 것이다. 따라서 위상적 정의에서 $V \subseteq Y$가 조건부에 있는 것은 이상한 일이 아니다.
4. “열린 집합에 대한 직관” 근거가 잘못된 이유
편의를 위해 $x$와 $y$가 “가깝다”는 것을 $x \sim y$로 표기하자. “열린 집합에 대한 직관” 근거는 다음의 잘못된 직관에 기반한다.
열린 집합에 대한 잘못된 직관. $x \in U$에 대해, $y \in U$라면 $x \sim y$이다.
이는 다음과 같이 수정해야 한다.
열린 집합에 대한 올바른 직관. $x \in U$에 대해, $x \sim y$라면 $y \in U$이다.
조금만 생각해 보면 이는 당연하다. 일례로 실수 전체의 집합 $\mathbb{R}$은 열린 집합이다. 그렇다면 임의의 두 실수는 언제나 “가까운” 것인가? 그건 말도 안 된다. 반대 경우를 보면, $\lbrace 0 \rbrace $은 열린 집합이 아니지만 $x, y \in \lbrace 0 \rbrace $일 때 $x = y$이므로 $x$와 $y$는 최대한으로 “가깝다”. 따라서 “잘못된 직관”에 따르면 $\lbrace 0 \rbrace $은 열린 집합이다.
반면 “올바른 직관”으로 보면 $\mathbb{R}$은 열린 집합이고 $\lbrace 0 \rbrace $은 열린 집합이 아닌 것이 분명하게 드러난다. $x \in \mathbb{R}$일 때, $x$와 “가까운” 실수 $y$는 자명하게 $\mathbb{R}$에 포함된다. 한편 $\lbrace 0 \rbrace $은 $0$의 “바로 곁”에 있는 실수들을 포함하고 있지 않으므로 열린 집합이 아니다.
또한 “올바른 직관”으로 보면 연속함수의 위상적 정의가 “뒤집혀야” 하는 이유 또한 분명하다. 먼저 연속함수는 다음과 같이 직관적으로 이해할 수 있다.
연속함수에 대한 올바른 직관. $x \sim y$라면 $f(x) \sim f(y)$이다.
이제 위의 “직관”과 연속함수의 위상적 정의가 동치임을 보이자.
직관적 정의 => 위상적 정의
$f$가 “직관적으로 연속”일 때, 열린 집합 $V$에 대해 $U = f^{-1}[V]$가 열린 집합임을 보이자. $x \in U$, $x \sim y$라고 하자. $f$가 연속이므로 $f(x) \sim f(y)$이다. 그리고 $V$가 열린 집합이며 $f(x) \in V$이므로 $f(y) \in V$이다. 따라서 $y \in U$이다. □
위상적 정의 => 직관적 정의
$f$가 “위상적으로 연속”일 때, $x \sim y$라면 $f(x) \sim f(y)$임을 보이자. $V$가 $f(x)$와 “가까운” 점들만을 포함하는 집합이라고 하자. $V$는 열린 집합이다. 왜냐하면 $z \in V$이고 $z \sim w$일 때, $V$의 정의에 의해 $f(x) \sim z$이므로 ~추이성에 의해~ $f(x) \sim w$, 즉 $w \in V$이기 때문이다. 그리고 $U = f^{-1}[V]$가 $x$를 포함하는 열린 집합이므로 $y \in U$이다. 따라서 $f(y) \in V$, 즉 $f(x) \sim f(y)$이다. ■
물론 위의 논의는 엄밀하게 정의되지 않은 관계 $\sim$을 사용하기 때문에 조금 석연찮기는 하다. 그러나 필자는 $\sim$을 사용하여 열린 집합과 연속성을 이해하는 것이 위상수학을 처음 공부하는 데 있어 유용한 길잡이가 되어준다고 생각한다. 덧붙이자면, 비표준 해석학을 사용하면 $x \sim y$를 $|x - y| = \epsilon$으로 엄밀하게 정의할 수 있다. 이에 관해서는 나중에 기회가 되면 이야기해 보겠다.
Why is Continuity in Topology defined 'Backwards'?
02 Jun 2025Definition. A mapping $f: X \to Y$ is said to be continuous if for any open set $V \subseteq Y$, the preimage $f^{-1}[V] \subseteq X$ is also an open set.
Students learning topology for the first time often experience confusion with this definition. Intuitively, it seems more natural to define continuity as “if $U \subseteq X$ is open, then $f[U] \subseteq V$ is also open,” but the actual definition is the inverse. The reasoning behind this intuition might roughly be as follows.
1. Epsilon-Delta Definition
According to the epsilon-delta definition, a function $f: X \to Y$ is continuous if the following holds:
\[\forall \epsilon > 0 \; \exists \delta > 0 : |x - y| < \delta \rightarrow |f(x) - f(y)| < \epsilon\]Here the antecedent contains $x, y \in X$, and the consequent contains $f(x), f(y) \in Y$. Therefore, it seems natural for the topological definition of continuity to also have $U \subseteq X$ in the antecedent and $f[U] \subseteq Y$ in the consequent.
2. Intuition about Open Sets
When first learning topology, one often thinks of an open set as a “collection of points that are close to each other.” That is, if $U$ is an open set, then $x, y \in U$ implies that $x$ and $y$ are “close.” Thus, if continuous function are those that map “close points” to “close points,” it seems natural to require that they map open sets to open sets.
However, both of these reasonings are fundamentally flawed.
3. Why the Reasoning behind “Epsilon-Delta Definition” is Incorrect
Judging the antecedent and consequent based solely on $\rightarrow$ can easily lead to misunderstandings. One must also consider the quantifiers. The quantifiers of the epsilon-delta definition can be read linguistically as “for any positive $\epsilon$, there exists some positive $\delta$ such that…” In other words, “if $\epsilon$ is a positive number, then there exists some positive $\delta$ such that…”
Here we see that the “true” antecedent regards $\epsilon$\, not $\delta$. And indeed, the space related to $\epsilon$ is not $X$, but $Y$. Therefore, it is only natural that $V \subseteq Y$ appears in the antecedent of the topological definition.
4. Why the Reasoning behind “Intuition about Open Sets” is Incorrect
For convenience, let us denote that $x$ and $y$ are “close” as $x \sim y$. The said reasoning is based on the following incorrect intuition.
Incorrect Intuition about Open Sets. If $x \in U$ and $y \in U$, then $x \sim y$.
This should be corrected as follows:
Correct Intuition about Open Sets. If $x \in U$ and $x \sim y$, then $y \in U$.
A little thought reveals that this is quite trivial. For example, the set of all real numbers $\mathbb{R}$ is an open set. But surely, that does not mean that two arbitrary real numbers are always “close”. Conversely, the set $\lbrace 0 \rbrace $ is not an open set, but when $x, y \in \lbrace 0 \rbrace $, we have $x = y$, so $x$ and $y$ are as “close” as possible. Thus, according to the “incorrect intuition,” $\lbrace 0 \rbrace $ should be an open set.
On the other hand, with the “correct intuition,” it is evident that $\mathbb{R}$ is an open set while $\lbrace 0 \rbrace $ is not. When $x \in \mathbb{R}$, the real number $y$ that is “close” to $x$ is trivially included in $\mathbb{R}$. Meanwhile, $\lbrace 0 \rbrace $ does not include the real numbers that are “not equal to, but in the neighbourhood of” $0$, so it is not an open set.
Furthermore, with the “correct intuition,” the reason why the topological definition of continuous functions should be “backwards” also becomes clear. Let us first note that the following intuition about continuity are indeed correct.
Correct Intuition about Continuous Functions. If $x \sim y$, then $f(x) \sim f(y)$.
Now let us show that this intuitive deifinition of continuity is equivalent to the topological definition of continuity.
Intuitive Definition => Topological Definition
Let $f$ be “intuitively continuous”. We need to show that for an open set $V$, the preimage $U = f^{-1}[V]$ is an open set. Let $x \in U$ and assume $x \sim y$. Since $f$ is continuous, we have $f(x) \sim f(y)$. Moreover, since $V$ is an open set and $f(x) \in V$, it follows that $f(y) \in V$. Therefore, $y \in U$. □
Topological Definition => Intuitive Definition
Let $f$ be “topologically continuous”. We need to show that if $x \sim y$, then $f(x) \sim f(y)$. Let $V$ be a set that contains only points “close” to $f(x)$. Since $V$ is an open set, if $z \in V$ and $z \sim w$, then by the definition of $V$, we have $f(x) \sim z$, which implies by transitivity of $\sim$ that $f(x) \sim w$, hence $w \in V$. Furthermore, since $U = f^{-1}[V]$ is an open set containing $x$, it follows that $y \in U$. Therefore, $f(y) \in V$, which means $f(x) \sim f(y)$. ■
Of course, the above discussion uses the somewhat dubious relation $\sim$, which is not rigorously defined. This may have caused some to feel uneasy in invoking the “transitivity of $\sim$”. However, I think using $\sim$ to understand open sets and continuity serves as a helpful intuition for those studying topology for the first time. Additionally, using non-standard analysis, one can rigorously define $x \sim y$ as $|x - y| = \epsilon$ — but that is a story for another time.
논리적 외계인은 가능한가? 데카르트, 칸트, 프레게, 그리고 《논리철학논고》
02 Jun 2025이 글은 James Conant, The Search for Logically Alien Thought: Descartes, Kant, Frege, and the Tractatus (1991)를 정리한 것이다. 괄호 안의 내용은 필자가 보충한 것이다 (다시 말해 뇌피셜이다).
초록
서양 철학사의 주요 논의 중 하나는 논리 법칙의 필연성에 관한 것이다. 논리 법칙은 필연적으로 필연적인가, 혹은 우연적으로 필연적인가? 즉, 우리의 논리와는 상이한 논리 법칙을 가지는 세계, 또는 상이한 논리 법칙으로 사고하는 외계인이 가능한가?
이에 대한 철학자들의 답변을 개괄하자면 이렇다.
-
아퀴나스는 신 또한 논리 법칙에 의거한다는 점에서 논리 법칙은 필연적으로 필연적이라고 주장했다.
-
그러나 데카르트는 신이 진정으로 권능하다면 신은 논리 법칙 또한 바꿀 수 있어야 하며, 이에 따라 논리 법칙은 우연적으로 필연적이라고 주장했다.
-
칸트는 논리 법칙을 이성적 사고의 초월적1 조건으로서 제시함으로써 데카르트의 입장을 극복했다.
-
그러나 데카르트의 입장은, 논리 또한 인간 사고의 일부이므로 논리학은 심리학으로 환원된다는 심리학주의Psychologism로 살아남었다.
-
프레게는 칸트의 입장을 빌려 심리학주의를 신랄하게 공격했으나, 논리 법칙을 초월적 조건으로 보는 동시에 ‘자연의 가장 보편적인 법칙’으로 보는 그의 입장은 내적 긴장을 일으켰다.
-
비트겐슈타인은 논리 법칙이 무의미Sinnlos하다고 주장했다. 나아가, 프레게의 내적 긴장의 원인은 “논리 법칙은 필연적으로 필연적인가?”라는 질문이 의미를 결여Unsinn하기 때문이라고 진단했다.
이러한 철학사적 흐름을 통해 저자는 비트겐슈타인의 《논고》가 형언할 수 없는 진리에 대한 저술이라는 기존의 해석에 대항하여, 《논고》에는 아무런 철학적 주장도 담겨 있지 않으며 이 사실을 깨닫게 하는 것이 《논고》의 최종 목표라는 “새로운 비트겐슈타인New Wittgenstein” 진영의 해석을 옹호한다.
1. 아퀴나스와 데카르트: 신은 논리에 종속되는가?
스콜라 철학자들에게 논리 법칙의 필연성 논의는 심각한 문제였다. 신의 권능과 논리 법칙의 필연성은 양립할 수 없는 것으로 여겨졌기 때문이다. 아퀴나스는 이 딜레마를 극복하기 위해 절대적 가능possible absolutely과 절대적 불가능impossible absolutely이라고 부를 수 있는 구별을 제시했다. 절대적 가능은 지성체가 이해할 수 있는 사태를 의미하고, 절대적 불가능은 이해조차 불가능한 사태를 의미한다. 신의 권능이 뜻하는 바는 절대적으로 가능한 모든 일 — 이를테면 지구를 평평하게 만드는 일 — 은 신에게 가능하다는 것이며, 절대적으로 불가능한 일 — 이를테면 배중률을 위배하는 일 — 은 신의 권능을 논하는 데 무관하다는 것이 아퀴나스의 주장이다.
그러나 데카르트는 아퀴나스의 주장이 신성 모독적이라고 반박한다. 아퀴나스가 절대적 가능과 절대적 불가능을 구별할 때 근거로 삼은 “지성체”는 인간의 지성임이 암시적으로 전제되어 있다. 즉, 아퀴나스는 인간 지성의 한계 — 우리는 빨간색인 동시에 빨간색이 아닌 사과를 상상할 수 없다 — 와 신의 권능의 한계 — 따라서 신은 빨간색인 동시에 빨간색이 아닌 사과를 창조할 수 없다 — 를 동일시했다. 데카르트는 이것이 인간 지성의 월권이라고 비판한다. 신은 인간이 이해할 수 없는 방식으로도 행할 수 있다. 그러한 신에게 논리 법칙은 자신의 의지대로 변경이 가능한 우연적 산물이라는 것이 데카르트의 주장이다.
그렇다면 어째서 인간은 논리 법칙을 필연적인 것으로 인식하는가? 데카르트의 답변은, 신이 인간에게 내려 준 이성이 논리 법칙을 필연적인 것으로 이해하도록 설계되었기 때문이라는 것이다. 신이 이 세계를 특정 논리 법칙에 따라 창조했다면, 자애로운 신은 이 세계에 거주할 피조물인 인간에게 해당 논리 법칙을 필연적인 것으로 인식하는 지성을 내려 줄 것이다 (이 대목을 데카르트의 유명한 악마 논변과 대조해 보라). 즉, 데카르트에 따르면 논리 법칙의 표면적 필연성은 (신이 내려 준) 이성의 설계에서 기원한다.2 데카르트의 주장에서 신학적인 표현들을 신경생리학적 표현들로 대체하기만 하면, 논리 법칙의 표면적 필연성은 뇌의 작동에서 기원한다는 심리학주의의 주장을 얻는다.
그러나 데카르트주의에는 내적 모순이 있어 보인다. 데카르트는 다음의 세 명제를 동시에 주장하고자 한다.
① 인간은 논리적으로 불가능한 사태를 이해할 수 없다.
② 신은 논리적으로 불가능한 사태를 창조할 수 있다.
③ 인간은 ②의 진술을 이해할 수 있으며 나아가 참인 것으로 판단할 수 있다.
여기서 ①과 ③은 상충하는 것으로 보인다. ’논리적으로 불가능한 사태’가 인간에게 이해 불가능한 개념이라면, 신이 그것을 행할 수 있다는 진술 또한 마찬가지로 이해 불가능하지 않겠는가? 마치 연속체 가설을 이해하지 못하는 사람에게는 ‘연속체 가설이 참인 수학 체계가 가능하다’라는 진술 또한 마찬가지로 이해 불가능하듯이 말이다. 이 문제에 답할 필요를 느낀 데카르트는 이해comprehend와 직관apprehend의 미묘한 구별을 제시했다. 이해가 무언가를 이성 속에서 완전히 파악하는 일이라면, 직관은 이성이 무언가에 닿는 일이다.
나는 신이 만물의 창조주이며, 불변하는 진리가 있으며, 신이 그것의 창조주임을 안다. 나는 내가 이것을 안다고 말하지, 내가 그것을 인식한다든가, 파악한다고 말하지 않는다. 왜냐하면 비록 우리의 정신은 유한하기에 신을 인식하거나 파악할 수 없지만, 신이 무한하며 전능하다는 사실은 알 수 있기 때문이다. 이것은 우리의 손이 산에 닿을 수는 있지만 우리가 두 팔로 산을 감쌀 수는 없는 것과 마찬가지이다.
따라서 데카르트는 ③을 다음과 같이 수정할 것이다.
③ 인간은 ②의 진술을 직관할 수 있으며 나아가 참인 것으로 판단할 수 있다.
나중에 우리는 이와 같이, 엄밀히 따지자면 무의미하지만 그럼에도 유효한 진리로 통하는 명제가 있음을 단어의 미묘한 구별 — 감히 말하자면 말장난 — 을 통해 정당화하려는 시도를 비트겐슈타인의 ⟪논고⟫에 대한 전통적 해석에서 다시 마주할 것이다.
2. 라이프니츠와 칸트: 자유, 이성, 논리
라이프니츠는 신이 논리 법칙을 임의로 창조했다는 데카르트의 주장에 반대했다. 데카르트를 반박하기 위해 라이프니츠는 “신이 행하기 때문에 선한 일인가, 선한 일이기 때문이 신이 행하는 것인가?” 라는 스콜라 철학의 논쟁을 재등장시킨다. 라이프니츠는 후자를 주장한다. 신은 선한 일이기 때문에 그것을 행한다. 그러나 라이프니츠에 따르면 이는 신이 ‘선’의 개념에 얽매여 있음을 시사하지 않는다. 오히려 이 사실은, 그것이 선하다는 것을 신이 이해한다는 것을 보여준다. 즉 ‘선’의 개념은 신의 의지를 선행하지만, 신의 이성에는 포섭된다.
라이프니츠는 신의 의지에 선행되는 ‘선’의 개념이 신의 자유에 반하기는커녕, 신의 자유가 성립하기 위한 조건임을 강조한다. 만약 신의 의지에 선행되는 원리가 전무하다면, 신은 특정 행동을 행할 어떠한 근거도 없을 것이다. (그럼에도 신이 무언가를 행한다면, 그것은 무작위적인 선택에 의한 것이라고밖에 볼 수 없다. 그러나 우리는 무작위적인 행동을 두고 자유의지에 의한 선택이라고 말하지 않는다. 이중 슬릿을 통과하는 전자들이 자유의지에 의해 통과할 슬릿을 선택한다고 말하지 않는 것과 같다. 따라서 자유의지는 무작위랑 구별되기 위한 원리를 요구한다.)
마찬가지로 라이프니츠는 논리 법칙이 신의 이성에 포섭되어 있되 신의 의지에 선행하는 원리이자, 신의 자유가 성립하기 위한 조건이라고 주장한다. 이러한 라이프니츠의 철학은 칸트로 계승된다. 데카르트가 논리 법칙을 이성의 산출물로서 보았다면, 칸트는 데카르트의 주장을 이른바 ‘코페르니쿠스적 전회’를 통해 뒤집는다. 칸트에 따르면 논리 법칙은 이성의 산출물이 아니라 이성의 구성 조건이다. 그리고 라이프니츠적인 의미에서, 자유로운 이성이란 논리 법칙을 따르는 이성이다. 논리 법칙을 따르지 않는 이성은 엄격한 의미에서 이성이라 불릴 수 없다. (이는 마치 체스의 규칙을 따르지 않는 체스는 엄격한 의미에서 체스라 불릴 수 없는 것과 같다.) 이러한 칸트의 논리철학에 대해 퍼트넘은 다음과 같이 적는다.
칸트의 ⟪논리학 강의⟫는 오늘날의 우리가 ‘심리학주의’라고 부르는 입장과 극단적으로 대립하는 입장을 제시하는 선구적인 — 어쩌면 최초의 — 저술이다. […] 나의 관심을 끄는 것은, 비논리적인 생각은 엄격히 말해 애초에 생각이 아니라는 [칸트의] 반복적인 주장이다.
확실히 논리학에는 아무런 형이상학적 가정이 없다. 규범적 의미에서의 생각, 즉 참 [또는 거짓]으로 판명될 수 있는 판단이 논리를 따른다는 것은 형이상학이 설명해야 할 무언가가 아니기 때문이다. 무언가를 설명한다는 것은 논리를 전제한다. 칸트에게 있어 논리는 모든 이성적 활동에 선행한다.
특히 칸트는 논리가 심리학과 엄격히 구별되어야 함을 강조한다. 경험적 사실들에 대한 학문으로서 심리학은 이성의 판단 활동을 통해 도달하는 이론인 반면, 논리학은 그러한 이성의 활동이 가능하기 위해 전제되어야 하는 조건이기 때문이다. 따라서 논리학을 심리학으로 환원하려는 시도는 범주론적 오류이다. 여기서 칸트가 논하는 대상은 ‘인간 이성’이 아닌 이성 일반임에 주목하라.
그러나 칸트는 라이프니츠보다 더 엄격한 논리의 경계를 긋는다. 칸트에 따르면 논리학은 오직 문장의 순수 형식에 관한 것이다. (따라서 배중률, 전건 긍정modus ponens, 대우법 등은 논리의 범주에 속하지만, 오늘날의 우리가 집합론, 모델론, 양상 논리라고 부르는 것은 속하지 않는다.) 이것이 함의하는 바는, 논리학은 세계에 관해 아무것도 진술하는 바가 없다는 것이다. (무한 공리 — 적어도 하나의 무한집합이 존재한다는 공리 — 나 공집합 공리 — 공집합이 존재한다는 공리 — 와 같은 존재론적 진술을 포함하는 집합론과 달리, 칸트적인 의미의 논리학은 어떠한 존재론적 진술도 주장하지 않는다.)
이처럼 논리학은 세계의 사태로부터 유리되어 있으므로, 논리학의 필연성을 정당화하려는 시도나, 논리학으로부터 형이상학적 통찰을 얻으려는 시도는 초험적 비판의 대상이 된다. 그것은 영원의 불멸성에 관한 질문이나 신의 존재에 관한 질문만큼이나 이성의 한계를 벗어난 것이다. 나중에 우리는 비트겐슈타인이 칸트의 주장을 수용하면서도, 그의 주장을 더 원초적인 층위로 옮기는 것을 볼 것이다. 요컨대 칸트가 논리학에 관한 철학적 혼란의 원인을 이성이 그 한계를 넘어섰기 때문으로 진단했다면, 비트겐슈타인은 혼란의 원인이 이성이 부딪히고야 마는 한계가 있다는 환상 때문으로 진단한다.
3. 프레게: 논리적 외계인 사고실험
프레게는 칸트와 마찬가지로 논리학이 이성의 산출물이 아니라 이성 — 인간 이성이 아닌 이성 일반 — 의 구성 조건임을 강조한다. 특히 프레게는 판단의 성립 요건으로서 그것이 참과 거짓의 여부를 따질 수 있는 명제일 것을 주장한다. 판단의 성립 요건을 만족하지 않는 생각은 가짜 생각Scheingedanke이다. 이는 프레게가 논리 법칙으로 내세우는 — 칸트의 경우 유일한 논리 법칙으로 내세우는 — 배중률의 요구이다.
이러한 입장을 바탕으로 프레게는 당대에 유행하던 심리학주의를 강하게 비판했다. 프레게는 심리학주의가 원인의 질문과 정당화의 질문을 혼동한다고 비판한다. 인간의 뇌에 대한 심리적, 생리학적 연구는 우리가 어째서 논리 법칙을 절대적 참으로 받아들이는지에 대한 설명을 제공할 수는 있다. 그러나 그 설명이 어째서 논리 법칙이 절대적으로 참인지를 정당화하는 것은 아니다. 논리 법칙의 정당성은 심리학을 선행한다.
프레게의 논변은 우리가 약한 심리학주의 — 논리 법칙의 절대적 지위를 인정하는 한편 논리학을 심리학으로 환원하려는 입장 — 라고 부를 수 있을 입장을 성공적으로 반박한다. 그러나 강한 심리학주의 — 논리 법칙의 절대적 지위를 인정하지 않고 오로지 심리학만으로 논리학을 환원하려는 입장 — 를 반박하는 데는 아직 부족하다. 강한 심리학주의자는 논리 법칙의 절대성에 관한 질문을 무의미한 질문, 마치 신의 존재에 관한 질문으로 치부할 수 있다.
프레게의 논리적 외계인 사고실험은 강한 심리학주의의 생각에 근본적인 오류가 있음을 지적한다. 강한 심리학주의에 따르면 우리와 다른 뇌 구조를 가지고 있어, 우리의 논리 법칙과 모순되는 논리 법칙을 절대적인 참으로 생각하는 외계인이 가능하다. 실제로 그러한 외계인이 우리 앞에 나타났다고 생각해 보자. 이 상황에서 프레게는 다음 질문을 던진다. 외계인의 논리 법칙과 우리의 논리 법칙 중 무엇이 올바른가?
이 기점에서 사고실험은 두 가지 갈림길로 나눠진다. 첫째 갈림길은 심리학주의자가 프레게의 질문을 유의미한 질문으로 인정하는 경우이다. 이 경우, 심리학주의자는 외계인의 논리 법칙과 우리의 논리 법칙 둘 다를 선행하여, 둘 중 어떤 법칙이 올바른지를 따질 수 있는 논리 체계가 있음을 인정하게 된다. “외계인과 우리 중 누가 올바른가?”라는 질문은 외계인-심리학에도, 인간-심리학에도 속하는 질문이 아니다. 그것은 심리학을 초월해 있으며, 이 질문의 유의미성에 대한 인정 자체가 심리학을 초월해 있는 논리를 인정하는 것이다. 이 상위 논리에 견주었을 때, 외계인의 논리는 다른 논리가 아니라 틀린 논리임이, 즉 애초에 논리가 아님이 드러난다.
(여기서 혹자는 우리의 논리가 틀린 것일수도 있지 않냐고 물을지 모른다. 그러나 이 경우 외계인 사고실험 자체가, 나아가 우리의 모든 이성이 넌센스의 구렁으로 빠져버린다. 논리에 대한 회의주의는 그러한 회의주의를 품게 만든 논증 또한 비논리적인 것으로 만들어 버림으로써 철학적 탐구의 가능성을 완전히 함몰시킨다. 우리는 우리의 논리를 옳은 것으로 간주할 수밖에 없다. 이것은 후술할 프레게의 내적 긴장의 원인이 된다.)
둘째 갈림길은 심리학주의자가 프레게의 질문마저 무의미한 것으로 치부하는 경우이다. 이 경우 심리학주의자는 어느 누구의 논리 법칙도 절대적으로 올바른 것은 아니라고 주장할 것이다. 외계인의 논리 법칙은 외계인에게 올바르고, 인간의 논리 법칙은 인간에게 올바르며, 그 이상 주장할 것은 없다. 그러나 프레게는 이러한 심리학주의자의 태도가 심리학주의자가 견지하고자 하는 입장 — 즉, 우리와 다른 논리 법칙으로 사고하는 외계인의 존재 가능성 — 을 불가해한 입장으로 만들어버림을 지적한다.
프레게의 지적에서 핵심적인 것은, “A와 B는 논리적으로 다르다”라는 명제가 유의미하기 위해서는 A와 B의 동일성을 판별할 수 있는 논리가 전제되어야 한다는 것이다. (이해의 편의를 위해 논리학이 아닌 위상수학으로 예를 들어 보자. 우리가 구와 도넛3이 위상수학적으로 다르다고 말할 수 있는 이유는, 구와 도넛에 대해 공통적으로 유효한 위상수학적 개념 — 이를테면 구멍의 개수4 — 이 존재하여, 구와 토러스가 그 개념에 대해 차이를 보이기 때문이다.)
마찬가지로 우리와 논리적으로 다른 외계인이 존재할 수 있다는 심리학주의자의 주장은 그 자체로 우리의 논리학과 외계인의 논리학의 다름을 성립시키는 배경 논리를 전제하며, 이 경우 우리는 다시 첫째 갈림길로 돌아가게 된다. 한편 심리학주의자가 주장하는 바가 우리와 그저 다른 발화를 하는 외계인의 존재라면, 여기서의 차이는 두 소의 울음소리가 다른 것, 그 이상도 이하도 아니다. 우리와 다른 논리로 사고하는 외계인이 존재한다는 심리학주의의 주장은, 실상 그 외계인은 애초에 사고를 하지 않는다는 것 을 드러낼 뿐이다. (소와 인간은 둘 다 소리를 내지만 오직 후자만이 사고를 한다. 빙고 머신과 계산기는 둘 다 숫자를 출력하지만 오직 후자만이 계산을 한다.)
4. 프레게 논리철학의 내적 긴장
지금까지의 논증을 보았을 때 프레게가 내리는 결론은 “논리적 외계인은 존재할 수 없다”인 듯하다. 정말로 이것이 논증의 결론이라면, 우리의 사고는 다음의 과정을 따랐을 것이다.
- 우리는 논리적 외계인이라는 존재를 상정했다.
- 해당 존재가 가질 특징에 대해 고려했다.
- 이 특징들이 논리의 특성과 양립할 수 없음을 깨달았다.
- 따라서 우리는 논리적 외계인의 가능성을 기각한다.
그러나 — 적어도 프레게 본인이 제시하는 “판단의 성립 요건”에 따르면 — 여기서 우리가 겪는 것은 생각의 환영이 아닌가? 프레게의 논증을 면밀하게 들여다 보면, 그가 말하고자 하는 바는 “논리적 외계인은 이러이러한 이유로 존재할 수 없다”가 아니라 “논리적 외계인의 상정 자체가 불가해하다”는 것임을 알 수 있다. 논리적 외계인의 상정은 우리의 사고를 논리의 범위 밖으로 위치시켜버림으로써, 우리의 사고를 사고가 아닌 것으로 만들어버린다. 비유하자면 그것은 트로이 목마인 것이다.
여기서 궁극적으로 드러나는 사실은, 논리적 외계인에 대한 사고실험 자체가 일종의 가짜 생각Scheingedanke이라는 것이다. “논리적 외계인은 가능하다”는 심리학주의의 주장은 의미를 결여한 문장이다. 그것은 “참 또는 거짓의 여부를 따질 수 있는 명제일 것”이라는 판단의 성립 요건을 만족하지 않는다. 그리고 이것이 함의하는 바는, “논리적 외계인이 불가능하다”는 우리의 주장 또한 의미를 결여한다는 것이다.5
그러나 어떤 의미에서 “논리적 외계인이 불가능하다”는 문장에는 무언가 참인 진술이 있는 듯하다. 그것은 논리의 본성에 관한 어떤 진리를 드러내고 있지 않은가? 단지 우리 언어의 논리적 구조가 그 진리의 발화를 불가능하게 만드는 것이다. 전통적으로 《논고》는 이러한 맥락에서 해석되었다. 특히 해커Hacker, 기치Geach 등의 학자는 《논고》가 반구문론적 명제countersyntactic proposition를 통해 “엄밀한 의미에서는 말해질 수 없는” 진리를 “드러내 보이는” 저술이라고 해석해 왔다. 여기서 반구문론적 명제란, 언어의 자연적 구문론은 따르되 — 이를테면 주어는 서술어를 선행해야 한다 — 어느 시점에서 논리적 구문론을 위배하는 명제이다 — 이를테면 서로 다른 위계에 있는 유형론적 대상들을 같은 술어에 양화시킨다. 예를 들어 대상object과 개념concept의 구분은 엄격한 논리적 언어에서 표현될 수 있는 것이 아니다. 둘은 유형론적으로 다르기 때문이다. 대상과 개념의 구분은 ‘개념’을 대상화함으로써, 러셀의 역설과 같은 유형의 문제를 발생시킨다. 그럼에도 이 구분은 논리의 중요한 특성을 담지하는 것으로 보인다. 전통적 해석에 따르면 《논고》 또한 이러한 반구문론적 명제들 — 엄밀히 말해 무의미하지만 그럼에도 유의미한 진리를 담지하는 명제들 — 로 구성되어 있으며, “사다리를 걷어차야 한다”는 《논고》의 최종적인 메시지는 그 명제들의 반구문론적 특징을 폭로하는 대목이다.
그러나 논문의 저자는 이러한 전통적 해석을 강하게 비판한다. 전통적 해석은 데카르트의 ‘이해’와 ‘파악’의 구분과 같은, 말장난에 불과한 허황된 구분들 — “엄밀히 말해 생각”과 “생각”, “그저 무의미”와 “깊은 무의미”, “사실”과 “사실” — 을 통해 《논고》의 내적 긴장을 해소하는 시늉을 했을 뿐, 실질적으로 그 긴장을 해소하는 데는 완전히 실패했다. 전통적 해석은 이들 구분에 완전히 의존하고 있으면서도, 어떻게 논리적 규칙을 위배하는 문장이 “무의미”하지만 “그저 무의미”하지 않을 수 있는지, 어떻게 “생각은 결코 비논리적일 수 없다(§3.03)”는 《논고》의 구절을 인정하면서도 비논리적인 “생각”이 가능한지를 명료하게 해명하지 못한다. 따라서 논문의 저자는 전통적 해석과 단절된 새 해석을 제시한다. 그것은 소위 “새로운 비트겐슈타인”으로 일컬어지는 해석의 일환이다.
2편에서 계속
1. 이런 걸 신경 쓰는 독자라면, 필자는 ‘a priori’를 ‘선험적’, ‘transzendent’를 ‘초험적’, ‘transzendental’을 ‘초월적’이라고 번역한 아카넷 칸트전집의 용어를 사용한다.
2. 데카르트의 주장은 묘하게 칸트적이다. 실제로 윌슨Margaret Wilson은 논리 법칙에 대한 데카르트의 입장을 칸트의 초월철학과 현대의 자연주의의 시조로 평가한다. 그러나 이후 드러나듯이, 논리 법칙에 대한 데카르트의 입장과 칸트의 입장에는 간과할 수 없는 간극이 있다.
3. 엄밀히는 토러스. 토러스는 도넛의 겉면이다.
4. 엄밀히는 1차 호몰로지 군. 구의 경우 이는 $\mathbb{Z}$이고 토러스의 경우 $\mathbb{Z} \times \mathbb{Z}$이다.
5. 원 논문에서는 다음과 같이 말한다.
If we take the sentences “illogical thought is impossible” or “we cannot think illogically” to indeed present us with thoughts (with senses which we can affirm the truth of), then we concede what a moment ago we wished to deny (namely, that the negation of these sentences preseunt us with a genuine content, one which is able to stand up to the demand for judgment). But if we conclude that these words (which we want to utter in response to the psychologicstic logician) do not express a thought with a sense, then aren’t we, if we judge psychologism to be false, equally victims of an illusion of judgment? This is the problem at the heart of the onion.
즉, 논문의 저자는 다음의 문장이 실제로는 생각thought이 아님을 지적하고 있다.
- 비논리적인 생각은 불가능하다.
이것을 논리식으로 옮기면 다음과 같다.
- $\not\exists x (I(x) \land T(x))$
이제 이를 다음의 문장과 대조해 보자.
- 초록색 생각은 불가능하다.
- $\not\exists x (G(x) \land T(x))$
(1)과 (3)은 형태론적으로 같은 문장이다. 그런데 (3)은 의미가 있는 문장으로 보인다. 그 의미란, 이 세상에 초록색이면서 생각이기도 한 대상이 없다는 것이다. 실증주의자라면 (3)이 반증 가능성 원리 또한 통과한다고 말할지 모른다. 요컨대 세상의 모든 초록색 대상 중 생각에 해당하는 것이 발견되면 (3)은 기각된다는 것이다. 또한 (3)의 논리적 표현인 (4)는 어떠한 논리적 규칙도 위배하지 않는 것으로 보인다.
그러나 필자가 보기에 (1)과 (2)가 유의미하다는 생각은, 프레게의 표현을 빌리자면 “생각의 환영”에 사로잡힌 것이다. 이 입장을 논증하는 가장 효율적인 방법은 (4)에서 등장하는 무제약적 양화사 $\exists x$의 부당함을 피력하는 것이다. $x$의 범위는 어디까지인가? 내 앞의 사과가 $x$에 양화될 수 있다면, 사과의 꼭지 또한 $x$에 양화될 수 있는가? 무언가가 — 이를테면 나뭇잎 — 대상의 부분이 아니라 독립적인 대상으로 고려되어야 하는 기준은 무엇인가? 반대로, 무언가가 — 이를테면 나무 — 대상의 단순한 조합이 아니라 독립적인 대상으로 고려되어야 하는 기준은 무엇인가? 수학적 플라톤주의를 인정하여 ‘자연수 집합’ 또한 양화의 대상으로 고려해야 하는가? ‘신’ 또한 양화의 대상인가?
이렇듯 무제약적 양화사는 사용자로 하여금 강한 존재론적 개입을 요구한다. 이런 난처한 상황을 피하는 한 가지 방법은 무제약적 존재 양화를 사용하는 대신 $x$를 $T$의 진리집합으로 양화시키는 것이다. 요컨대 (4)를 (5)와 같이 수정하는 것이다.
- $\exists x \in \mathrm{Th}\; G(x)$
여기서 $\mathrm{Th}$는 생각들의 집합이다. 그런데 이렇게 적고 나면, (5)는 적형식이 아니게 된다. 문제는 $G$를 정의하는 데 있다. 우리가 무제약적 양화를 피하고자 한다면, $G$의 정의역을 정의하는 데 있어서도 무제약적 양화를 피해야 한다. 즉 a는 가능하지만 b는 불가능하다.
a) G: 물리적 대상 → {T, F} (O)
b) G: 모든 대상 → {T, F} (X)
따라서 (5)는 적형식이 아니다. (5)는 정의역에 속하지 않는 대상을 술어에 적용하고 있으므로 논리적 규칙을 위배한 것이다. 다시 말해, (5)는 의미를 결여한 문장이다.
이는 다음의 수학적 예시를 통해 이해할 수 있다. 독자 분은 $0 < i$가 올바르지 않은 부등식임을 배웠을 것이다. 왜냐하면 해당 맥락에서 $<$는 실수 위에서만 정의되기 관계이기 때문이다. 그리고 $<$가 실수 위에서만 정의 가능한 이유는 실수, 허수, 그리고 $<$가 요구하는 논리적 규칙들과 연관한다. $<$의 규칙에 따르면, 양변에 0보다 큰 수를 곱하면 부등호의 방향이 유지되고, 0보다 작은 수를 곱하면 부등호의 방향이 뒤집힌다. 그런데 만약 $0 < i$라면 $0 = 0 \cdot i < i \cdot i = -1$이 되어 모순이고, $i < 0$이라면 $-1 = i \cdot i > 0 \cdot i = 0$이 되어 모순이다. 따라서 $0 < i$는 의미를 결여한 부등식이다. 이는 $0 < i$가 거짓임을 의미하지 않는다. $0 < i$가 거짓이라면 $0 > i$가 참이어야 하기 때문이다.
Are Logically Alien Beings Possible? Descartes, Kant, Frege, and the Tractus
02 Jun 2025This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
This article is a summary of James Conant, The Search for Logically Alien Thought: Descartes, Kant, Frege, and the Tractatus (1991). THe post includes the author’s supplementary remarks.
Abstract
One of the principal debates in the history of Western philosophy concerns the necessity of logical laws. Are logical laws necessarily necessary, or are they contingently necessary? That is, is a world with logical laws different from ours, or aliens who think according to different logical laws, possible?
The responses of philosophers to this question may be summarised as follows:
-
Aquinas argued that logical laws are necessarily necessary, on the grounds that even God operates according to logical laws.
-
However, Descartes contended that if God is truly omnipotent, He must be able to alter logical laws as well, and accordingly maintained that logical laws are contingently necessary.
-
Kant overcame Descartes’s position by presenting logical laws as transcendental1 conditions of rational thought.
-
However, Descartes’s position survived as psychologismPsychologism, which held that since logic is also part of human thought, logic should be reduced to psychology.
-
Frege, borrowing from Kant’s position, launched a fierce attack on psychologism, but his stance of viewing logical laws simultaneously as transcendental conditions and as ‘the most universal laws of nature’ created internal tension.
-
Wittgenstein argued that logical laws are senselessSinnlos. Furthermore, he diagnosed that the cause of Frege’s internal tension was that the question “Are logical laws necessarily necessary?” lacks senseUnsinn.
Through this philosophical-historical trajectory, the author defends the interpretation of the “New WittgensteinNew Wittgenstein” school, which contends against the traditional interpretation that the Tractus is a work about ineffable truths, arguing instead that the Tractus contains no philosophical claims whatsoever, and that making one realise this fact is the ultimate goal of the Tractus.
1. Aquinas and Descartes: Is God Subject to Logic?
For scholastic philosophers, the debate over the necessity of logical laws was a serious problem, as God’s omnipotence and the necessity of logical laws appeared incompatible. To overcome this dilemma, Aquinas presented a distinction that might be called absolute possibilitypossible absolutely and absolute impossibilityimpossible absolutely. Absolute possibility refers to states of affairs that an intellect can understand, while absolute impossibility refers to states of affairs that are incomprehensible. Aquinas’s claim is that God’s omnipotence means that everything absolutely possible—such as making the Earth flat—is possible for God, while absolutely impossible things—such as violating the law of excluded middle—are irrelevant to discussions of God’s omnipotence.
However, Descartes objects that Aquinas’s claim is blasphemous. When Aquinas distinguishes between absolute possibility and absolute impossibility, the “intellect” upon which he bases this distinction is implicitly presupposed to be human intellect. That is, Aquinas conflates the limitations of human intellect—we cannot imagine an apple that is simultaneously red and not red—with the limitations of God’s omnipotence—therefore God cannot create an apple that is simultaneously red and not red. Descartes criticises this as an overreach of human intellect. God can act in ways that humans cannot understand. For such a God, logical laws are contingent products that can be altered at will, according to Descartes.
Then why do humans perceive logical laws as necessary? Descartes’s answer is that the reason God gave to humans is designed to understand logical laws as necessary. If God created this world according to specific logical laws, a benevolent God would give humans dwelling in this world an intellect that perceives those logical laws as necessary (contrast this passage with Descartes’s famous evil demon argument). That is, according to Descartes, the apparent necessity of logical laws originates in the design of reason (given by God).2 If we merely replace theological expressions with neurophysiological ones in Descartes’s claim, we obtain the psychologist claim that the apparent necessity of logical laws originates in the workings of the brain.
However, Cartesianism appears to contain an internal contradiction. Descartes wishes to assert the following three propositions simultaneously:
① Humans cannot understand logically impossible states of affairs.
② God can create logically impossible states of affairs.
③ Humans can understand the statement in ② and furthermore judge it to be true.
Here ① and ③ seem to conflict. If ‘logically impossible states of affairs’ is a concept incomprehensible to humans, would not the statement that God can accomplish such things be equally incomprehensible? Just as the statement ‘a mathematical system in which the continuum hypothesis is true is possible’ is equally incomprehensible to someone who does not understand the continuum hypothesis. Feeling the need to address this problem, Descartes presented a subtle distinction between comprehensioncomprehend and apprehensionapprehend. If comprehension is the complete grasping of something within reason, apprehension is reason’s touching of something.
I know that God is the creator of all things, that there are immutable truths, and that God is their creator. I say that I know this, not that I perceive or grasp it. For although our mind is finite and thus cannot perceive or grasp God, we can know that God is infinite and omnipotent. This is like how our hands can touch a mountain but we cannot embrace a mountain with our two arms.
Therefore, Descartes would modify ③ as follows:
③ Humans can apprehend the statement in ② and furthermore judge it to be true.
Later, we shall encounter once again in the traditional interpretation of Wittgenstein’s Tractus such attempts to justify through subtle distinctions of words—dare one say, wordplay—the existence of propositions that are, strictly speaking, senseless but nevertheless pass for valid truths.
2. Leibniz and Kant: Freedom, Reason, Logic
Leibniz opposed Descartes’s claim that God arbitrarily created logical laws. To refute Descartes, Leibniz resurrected the scholastic philosophical debate: “Is something good because God does it, or does God do it because it is good?” Leibniz argues for the latter. God acts because something is good. However, according to Leibniz, this does not suggest that God is bound by the concept of ‘good’. Rather, this fact shows that God understands that something is good. That is, the concept of ‘good’ precedes God’s will but is subsumed under God’s reason.
Leibniz emphasises that the concept of ‘good’ that precedes God’s will, far from being contrary to God’s freedom, is a condition for God’s freedom to be established. If there were no principles preceding God’s will, God would have no grounds for performing any particular action. (If God nonetheless acted, it could only be seen as random choice. However, we do not call random behaviour a choice by free will. Just as we do not say that electrons passing through a double slit choose which slit to pass through by free will. Therefore, free will requires principles to distinguish it from randomness.)
Similarly, Leibniz argues that logical laws are principles subsumed under God’s reason while preceding God’s will, and are conditions for God’s freedom to be established. This Leibnizian philosophy is inherited by Kant. Where Descartes viewed logical laws as products of reason, Kant reverses Descartes’s claim through the so-called ‘Copernican revolution’. According to Kant, logical laws are not products of reason but constitutive conditions of reason. And in a Leibnizian sense, free reason is reason that follows logical laws. Reason that does not follow logical laws cannot, in the strict sense, be called reason. (This is like how chess that does not follow the rules of chess cannot, in the strict sense, be called chess.) Putnam writes the following about Kant’s philosophy of logic:
Kant’s Lectures on Logic presents a position that stands in extreme opposition to what we today call ‘psychologism’—a pioneering, perhaps the first, work. […] What interests me is [Kant’s] repeated assertion that illogical thought is not, strictly speaking, thought at all.
Certainly logic contains no metaphysical assumptions. That thought in the normative sense, i.e., judgement that can be proven true [or false], follows logic is not something that metaphysics must explain. To explain something presupposes logic. For Kant, logic precedes all rational activity.
Kant particularly emphasises that logic must be strictly distinguished from psychology. As a science of empirical facts, psychology is a theory reached through rational judgement activity, while logic is a condition that must be presupposed for such rational activity to be possible. Therefore, attempts to reduce logic to psychology constitute a categorical error. Note here that the object of Kant’s discussion is not ‘human reason’ but reason in general.
However, Kant draws stricter boundaries of logic than Leibniz. According to Kant, logic concerns only the pure form of sentences. (Therefore, the law of excluded middle, modus ponensmodus ponens, contraposition, etc., belong to the category of logic, but what we today call set theory, model theory, and modal logic do not.) What this implies is that logic states nothing about the world. (Unlike set theory, which includes ontological statements such as the axiom of infinity—the axiom that at least one infinite set exists—or the empty set axiom—the axiom that the empty set exists—Kantian logic makes no ontological claims.)
Since logic is thus divorced from worldly affairs, attempts to justify the necessity of logic or to gain metaphysical insights from logic become subjects of transcendental critique. This is as much beyond the limits of reason as questions about the immortality of eternity or the existence of God. Later we shall see Wittgenstein accepting Kant’s claim while transposing it to a more fundamental level. In short, where Kant diagnosed the cause of philosophical confusion about logic as reason overstepping its limits, Wittgenstein diagnoses the cause of confusion as the illusion that there are limits that reason inevitably encounters.
3. Frege: The Logically Alien Thought Experiment
Like Kant, Frege emphasises that logic is not a product of reason but a constitutive condition of reason—not human reason but reason in general. Frege particularly argues that for judgement to be established, it must be a proposition whose truth or falsity can be assessed. Thoughts that do not satisfy the conditions for judgement are pseudo-thoughtsScheingedanke. This is a requirement of the law of excluded middle, which Frege—and Kant as the sole logical law—puts forward as a logical law.
Based on this position, Frege strongly criticised the psychologism that was fashionable in his time. Frege criticises psychologism for confusing questions of causation with questions of justification. Psychological and physiological research on the human brain can provide explanations for why we accept logical laws as absolutely true. However, such explanations do not justify why logical laws are absolutely true. The validity of logical laws precedes psychology.
Frege’s argument successfully refutes what we might call weak psychologism—the position that recognises the absolute status of logical laws while attempting to reduce logic to psychology. However, it is still insufficient to refute strong psychologism—the position that does not recognise the absolute status of logical laws and attempts to reduce logic solely to psychology. Strong psychologists can dismiss questions about the absoluteness of logical laws as meaningless questions, like questions about the existence of God.
Frege’s logically alien thought experiment points out that there is a fundamental error in strong psychologism’s thinking. According to strong psychologism, aliens with different brain structures who think of logical laws contradicting ours as absolutely true are possible. Let us suppose that such an alien actually appeared before us. In this situation, Frege poses the following question: Which is correct: the alien’s logical laws or our logical laws?
At this point, the thought experiment divides into two paths. The first path is when the psychologist acknowledges Frege’s question as meaningful. In this case, the psychologist comes to acknowledge that there exists a logical system that precedes both the alien’s logical laws and our logical laws, and can judge which of the two laws is correct. The question “Which is correct, the alien or us?” belongs neither to alien-psychology nor to human-psychology. It transcends psychology, and acknowledging the meaningfulness of this question itself acknowledges logic that transcends psychology. Compared to this higher logic, the alien’s logic is revealed to be not different logic but wrong logic—that is, not logic at all.
(Here someone might ask whether our logic might be wrong. However, in this case, the alien thought experiment itself, and indeed all our reason, falls into a pit of nonsense. Scepticism about logic makes the arguments that led to such scepticism illogical, thereby completely destroying the possibility of philosophical enquiry. We have no choice but to regard our logic as correct. This becomes the cause of Frege’s internal tension, to be discussed below.)
The second path is when the psychologist dismisses even Frege’s question as meaningless. In this case, the psychologist would claim that no one’s logical laws are absolutely correct. The alien’s logical laws are correct for the alien, human logical laws are correct for humans, and there is nothing more to claim. However, Frege points out that such a psychologist’s attitude makes the position the psychologist wishes to maintain—namely, the possibility of aliens who think according to logical laws different from ours—incomprehensible.
What is crucial in Frege’s point is that for the proposition “A and B are logically different” to be meaningful, there must be presupposed a logic that can determine the identity of A and B. (For ease of understanding, let us use an example from topology rather than logic. The reason we can say that a sphere and a torus3 are topologically different is that there exist topological concepts—such as the number of holes4—that are commonly valid for both spheres and tori, and spheres and tori show differences with respect to those concepts.)
Similarly, the psychologist’s claim that aliens who are logically different from us can exist presupposes by itself a background logic that establishes the difference between our logic and the alien’s logic, and in this case we return to the first path. On the other hand, if what the psychologist claims is the existence of aliens who merely make different utterances from us, the difference here is nothing more or less than the difference between the sounds of two cows. The psychologist’s claim that aliens who think according to different logic from ours exist merely reveals that such aliens do not think in the first place. (Cows and humans both make sounds, but only the latter thinks. Bingo machines and calculators both output numbers, but only the latter calculates.)
4. Internal Tension in Frege’s Philosophy of Logic
From the arguments thus far, Frege’s conclusion appears to be “logically alien beings cannot exist”. If this were truly the conclusion of the argument, our thinking would have followed this process:
- We posited the existence of logically alien beings.
- We considered the characteristics such beings would have.
- We realised that these characteristics are incompatible with the nature of logic.
- Therefore, we reject the possibility of logically alien beings.
However—at least according to the “conditions for judgement” that Frege himself presents—is what we experience here not an illusion of thought? If we examine Frege’s argument closely, we can see that what he means to say is not “logically alien beings cannot exist for such and such reasons” but “the very positing of logically alien beings is incomprehensible”. The positing of logically alien beings makes our thinking non-thinking by placing our thought outside the scope of logic. Metaphorically speaking, it is a Trojan horse.
What is ultimately revealed here is that the thought experiment about logically alien beings is itself a kind of pseudo-thoughtScheingedanke. The psychologist’s claim that “logically alien beings are possible” is a sentence that lacks sense. It does not satisfy the condition for judgement that it should be “a proposition whose truth or falsity can be assessed”. And what this implies is that our claim that “logically alien beings are impossible” also lacks sense.5
However, in some sense, the sentence “logically alien beings are impossible” seems to contain something that is a true statement. Does it not reveal some truth about the nature of logic? It is merely that the logical structure of our language makes the utterance of that truth impossible. The Tractus has traditionally been interpreted in this context. Scholars such as HackerHacker and GeachGeach have interpreted the Tractus as a work that “shows” truths that “cannot be said in the strict sense” through counter-syntactic propositionscountersyntactic proposition. Here, counter-syntactic propositions are propositions that follow the natural syntax of language—for instance, the subject must precede the predicate—but at some point violate logical syntax—for instance, quantifying over type-theoretic objects at different levels with the same predicate. For example, the distinction between objectobject and conceptconcept cannot be expressed in strict logical language because they are type-theoretically different. The distinction between object and concept generates problems of the same type as Russell’s paradox by objectifying ‘concept’. Nevertheless, this distinction seems to bear important characteristics of logic. According to traditional interpretation, the Tractus is also composed of such counter-syntactic propositions—propositions that are strictly speaking senseless but nevertheless bear meaningful truths—and the final message of the Tractus to “throw away the ladder” is the passage that exposes the counter-syntactic characteristics of those propositions.
However, the author of the paper strongly criticises such traditional interpretation. Traditional interpretation has merely pretended to resolve the internal tension of the Tractus through spurious distinctions—”strictly speaking thought” and “thought”, “merely senseless” and “deeply senseless”, “fact” and “fact“—that are no more than wordplay, like Descartes’s distinction between ‘understanding’ and ‘grasping’, but has completely failed to actually resolve that tension. Traditional interpretation is completely dependent on these distinctions while failing to clearly explain how sentences that violate logical rules can be “senseless” but not “merely senseless”, how “thought can never be illogical (§3.03)” can be acknowledged while illogical “thought” remains possible. Therefore, the author presents a new interpretation that breaks with traditional interpretation. This is part of the interpretation called the “New Wittgenstein”.
Continued in Part 2
1. Note that in Kantian philosophy, ‘transcendent’ means “beyond the limits of experience,” while ‘transcendental’ means “related to the preconditions of rational judgment.”
2. Descartes’s claim is strangely Kantian. Indeed, Margaret Wilson evaluates Descartes’s position on logical laws as the progenitor of Kant’s transcendental philosophy and modern naturalism. However, as will become apparent later, there is an unbridgeable gap between Descartes’s position on logical laws and Kant’s position.
3. Strictly speaking, a torus. A torus is the surface of a doughnut.
4. Strictly speaking, the first homology group. For a sphere this is $\mathbb{Z}$ and for a torus this is $\mathbb{Z} \times \mathbb{Z}$.
5. The original paper states:
If we take the sentences “illogical thought is impossible” or “we cannot think illogically” to indeed present us with thoughts (with senses which we can affirm the truth of), then we concede what a moment ago we wished to deny (namely, that the negation of these sentences present us with a genuine content, one which is able to stand up to the demand for judgment). But if we conclude that these words (which we want to utter in response to the psychologistic logician) do not express a thought with a sense, then aren’t we, if we judge psychologism to be false, equally victims of an illusion of judgment? This is the problem at the heart of the onion.
That is, the author of the paper is pointing out that the following sentence is not actually a thought:
- Illogical thought is impossible.
Translating this into logical notation:
- $\not\exists x (I(x) \land T(x))$
Now contrast this with the following sentence:
- Green thoughts are impossible.
- $\not\exists x (G(x) \land T(x))$
(1) and (3) are morphologically identical sentences. Yet (3) appears to be a sentence with meaning. That meaning is that there exist no objects in this world that are both green and thoughts. An empiricist might say that (3) also passes the falsifiability principle. In short, if any green object amongst all green objects in the world is discovered to correspond to a thought, then (3) is rejected. Moreover, (4), the logical expression of (3), appears to violate no logical rules.
However, in my view, the idea that (1) and (2) are meaningful is, to borrow Frege’s expression, captivated by an “illusion of thought”. The most efficient way to argue this position is to emphasise the impropriety of the unrestricted quantifier $\exists x$ appearing in (4). What is the range of $x$? If the apple in front of me can be quantified by $x$, can the stem of the apple also be quantified by $x$? What is the criterion by which something—such as a leaf—should be considered an independent object rather than part of an object? Conversely, what is the criterion by which something—such as a tree—should be considered an independent object rather than a simple combination of objects? Should we acknowledge mathematical Platonism and consider ‘the set of natural numbers’ also as an object of quantification? Is ‘God’ also an object of quantification?
Thus unrestricted quantifiers require users to make strong ontological commitments. One way to avoid this awkward situation is to quantify $x$ to the truth set of $T$ instead of using unrestricted existential quantification. In short, modifying (4) as (5):
- $\exists x \in \mathrm{Th}\; G(x)$
Here $\mathrm{Th}$ is the set of thoughts. But having written this, (5) becomes ill-formed. The problem lies in defining $G$. If we wish to avoid unrestricted quantification, we must also avoid unrestricted quantification in defining the domain of $G$. That is, a) is possible but b) is not:
a) G: physical objects → {T, F} (O)
b) G: all objects → {T, F} (X)
Therefore (5) is ill-formed. (5) violates logical rules by applying a predicate to an object that does not belong to its domain. In other words, (5) is a sentence that lacks sense.
This can be understood through the following mathematical example. You will have learnt that $0 < i$ is an incorrect inequality because in that context $<$ is a relation defined only over real numbers. And the reason $<$ can only be defined over real numbers relates to real numbers, imaginary numbers, and the logical rules required by $<$. According to the rules of $<$, multiplying both sides by a number greater than 0 maintains the direction of the inequality, while multiplying by a number less than 0 reverses the direction of the inequality. But if $0 < i$, then $0 = 0 \cdot i < i \cdot i = -1$, which is contradictory, and if $i < 0$, then $-1 = i \cdot i > 0 \cdot i = 0$, which is contradictory. Therefore $0 < i$ is an inequality that lacks sense. This does not mean that $0 < i$ is false, because if $0 < i$ were false, then $0 > i$ would have to be true.
See also the discussion in: https://forum.owlofsogang.com/t/topic/6465
콰인, ⟪경험주의의 두 독단⟫
26 May 2025개요
분석·종합의 구분과 검증가능성 원리는 논리실증주의를 이루는 두 기둥이다. 하지만 콰인은 ⟪경험주의의 두 독단⟫에서 분석·종합의 구분과 검증가능성 원리는 문제적이라고 지적한다. 콰인은 분석성의 정의는 자기순환적이며, 명제는 독립적으로 검증될 수 없고 오로지 믿음의 망web of beliefs 전체가 검증의 대상이 될 수 있다고 주장한다. 콰인이 ⟪두 독단⟫에서 제시하는 논증은 논리실증주의를 와해할 뿐 아니라, 의미의 개념 자체가 허구적이라는 의미 회의주의와, 극단적 전체론을 시사한다. 또한 콰인의 논증에 대한 반론을 검토한다.
1. 분석·종합에 대한 콰인의 공격
콰인은 분석성을 정의하려는 기존의 시도는 모두 만족스럽지 않다고 주장한다. 그 사례로 칸트와 프레게의 정의를 검토한다.
1.1. 칸트의 분석성 정의
분석성에 대한 칸트의 첫 번째 정의는 다음과 같다.
“모든 a는 b이다”는 분석적이다 $\iff$ a가 b에 개념적으로 포함된다
그러나 위 정의는 “개념적으로 포함”이라는 비유적 표현에 의존할 뿐 아니라 주어-술어 구조의 문장만 고려한다는 한계가 있다. 분석성에 대한 칸트의 두 번째 정의는 다음과 같다.
P는 분석적이다 $\iff$ P의 부정이 모순을 시사한다
그러나 이 정의는 모순이 무엇인지 설명해야 한다는 한계를 가진다. 만약 모순을 “분석적으로 거짓인 명제”로 정의한다면 이것은 순환 정의에 불과하다.
1.2. 프레게의 분석성 정의
분석성에 대한 프레게의 정의는 다음과 같다.
P는 분석적이다 $\iff$ P는 논리 법칙이거나, 정의와 논리 법칙만으로부터 도출 가능하다
여기서 논리 법칙이란 논리 연결사를 제외한 문장 성분들을 어떻게 해석하든지 참인 문장을 말한다. 예를 들어 $(φ → ψ) → (¬ψ → ¬φ)$는 $φ$와 $ψ$를 어떻게 해석하든지 참이므로 논리 법칙이다. 이에 따라 “모든 총각은 결혼하지 않았다”는 다음과 같이 “총각”의 정의와 논리 법칙만으로 도출 가능하므로 분석적이다.
- 총각(x) := ¬결혼(x) ∧ 남자(x) (총각의 정의)
- ∀x [ ¬결혼(x) ∧ 남자(x) → ¬결혼(x) ] (논리 법칙)
- ∴ ∀x [ 총각(x) → ¬결혼(x) ] (1과 2로부터 유도)
1.3. 동의성에 대한 콰인의 공격
그러나 콰인은 어떤 단어의 정의가 무엇인지를 어떻게 알 수 있는지를 질문한다. 즉, “a와 b는 동의어이다”가 성립할 조건이 무엇인지 질문한다. 콰인은 이 질문에 대한 가능한 답을 몇 가지 검토한다. 첫 번째 시도는 다음과 같다.
(i) a와 b는 동의어이다 $\iff$ a와 b가 사전에 동의어로 등재되어 있다.
그러나 위 시도는 부적절하다. 왜냐하면 사전은 이미 알려진 동의어의 기록에 불과하기 때문이다. 그러나 우리가 원하는 것은 사전 작성자들이 어떤 기준으로 두 단어를 동의어로 등재하냐이다. 두 번째 시도는 다음과 같다.
(ii) a와 b는 동의어이다 $\iff$ 임의의 술어 P에 대해 P(a)와 P(b)의 진릿값이 같다.
그러나 위 시도 또한 부적절하다. a = “총각”, b = “결혼하지 않는 남성”, P(x): “x는 두 글자이다”일 때 a와 b는 동의어지만 P(a)는 참이고 P(b)는 거짓이기 때문이다.
이에 콰인은 자비의 원칙에 따라 이 문제를 해결하기 위해 인지적 의미cognitive meaning를 도입한다. 인지적 의미란 단어의 길이나 시적 분위기, 화용론적 특징 등과 관련하지 않고 오직 그것이 지시하는 대상이나 개념에 관련하는 의미이다. 이에 따라 다음과 같이 (ii)를 수정해야 한다.
(iii) a와 b는 동의어이다 $\iff$ 인지적 의미에만 관련하는 임의의 술어 P에 대해 P(a)와 P(b)의 진릿값이 같다.
그러나 위 시도 또한 부적절하다. 왜냐하면 “임의의 술어”의 외연이 언어에 상대적이기 때문이다. 일례로 심장을 가진 생물을 cordate, 신장을 가진 생물을 renate라고 하자. 지금까지 보고된 생물종은 모두 심장과 신장을 둘 다 가지거나 둘 다 결여한다. 따라서 L₁이 HasHeart(x)라는 술어만 포함하는 언어라면 HasHeart(Cordate)와 HasHeart(Renate)는 둘 다 참이므로, cordate와 renate는 동의어이다. 반면 L₂가 NecessarilyHasHeart(x)라는 술어를 포함하는 언어라면 NecessarilyHasHeart(cordate)는 참이지만 NecessarilyHasHeart(renate)는 거짓이므로 둘은 동의어가 아니다.
따라서 (iii)는 동의성을 언어에 의존적인 개념으로 만든다. (iii)가 유효한 정의이기 위해서는 “…가 필연적이다”와 같이 양상 표현하는 언어를 배경 언어로 설정해야 한다. 이에 따라 다음과 같이 (iii)를 수정해야 한다.
(iv) a와 b는 동의어이다 $\iff$ 양상 표현이 포함된 언어 L에 속하고 인지적 의미에만 관련하는 임의의 술어 P에 대해 P(a)와 P(b)의 진릿값이 같다.
그러나 콰인에 따르면 위 시도 또한 부적절하다. 왜냐하면 이제는 양상성의 의미를 설명해야 하기 때문이다. 즉, “a는 필연적으로 b이다”가 성립할 조건이 무엇인지 질문한다. 만약 필연성을 다음과 같이 정의하면 순환 논증에 봉착한다.
a는 필연적으로 b이다 $\iff$ 모든 a가 b라는 것은 분석적으로 참이다.
그러므로 분석성에 대한 프레게의 정의는 동의성이나 필연성에 대한 정의가 제시되지 않는 한 순환적이다.
2. 콰인의 공격에 대한 고찰
콰인의 공격은 동의성을 겨냥하고 있지만, 그 함의는 훨씬 광대하다.
2.1. 논리 회의주의
첫째, 콰인의 공격은 논리 법칙에 대한 본인의 정의 또한 공격한다. 일례로 콰인에 따르면 $P(x) ∧ Q(x) → P(x)$ 가 논리 법칙인 이유는 $P, Q, x$에 무엇을 대입하든 참인 문장이 되기 때문이다. 그러나 이 기준이 정합적이기 위해서는 x에 대입하는 단어가 동의적이라는 조건이 필요하다.
예를 들어 P(x): “x는 둥글다”, Q(x): “x는 딱딱하다”, 그리고 x = “배”일 때 P(x) ∧ Q(x) → P(x)는 “둥글고 딱딱한 배는 둥근 배이다”가 된다. 그러나 이 문장이 참이기 위해서는 주어부의 “배”와 술어부의 “배”가 동의어야 한다A round and hard pear is a round pear. 만약 주어부의 “배”가 과일인데, 술어부의 “배”가 선박이라면 거짓인 문장이 되기 때문이다A round and hard pear is a round ship. 따라서 논리 법칙에 대한 콰인의 정의 또한 동의성에 의존한다.
2.2. 의미 회의주의
둘째, 콰인의 공격은 언어 간 번역을 허구적인 것으로 만든다. 누군가 “That apple is red”라는 문장의 번역을 묻는다면 우리는 “저 사과는 빨갛다”라고 말할 것이다. 이것이 올바른 번역인 이유는, ‘that’, ‘apple, ‘red’, ‘is’는 각각 ‘저’, ‘사과’, ‘빨갛다’, ‘이다’와 동의적이기 때문이다. 일반적으로 다음이 성립하는 것으로 보인다.
$φ$의 번역은 $ψ$이다 $\iff$ $φ$는 $ψ$와 동의적이다.
그런데 우변의 정의가 모호하다면 좌변의 정의 또한 모호한 것이 된다. 결론적으로 번역의 기준이 동의성에 의존하는 한 콰인의 공격은 번역, 나아가 의미 자체가 허구적인 개념이라는 의미 회의주의를 시사한다. (번역에 대한 회의주의가 의미에 대한 회의주의로 이어지는 논증에 관해서는 곧 올라올 다른 글을 참고하라)
3. 콰인의 분석·종합 공격에 대한 반론
콰인의 공격은 다음의 구조를 가진다.
개념 C의 정의가 순환적이라면 C는 정당하지 않다unintelligible.
이것을 콰인의 소크라테스적 조건 이라고 부르자. 콰인의 소크라테스적 조건은 지나치게 강한 요구 조건이라는 반박이 가능하다. 예를 들어 “빨강”이나 “파랑”을 순환적이지 않은 방식으로 정의할 수는 없지만 그렇다고 색깔 개념들이 정당하지 않은 것은 아니다. 또한 데이빗슨 등의 논의는 언어가 학습 가능하기 위해서는 무정의 용어가 필요함을 시사한다. 따라서 언어 L의 모든 개념이 소크라테스적 조건은 만족할 경우 L은 학습 불가능하다.
그럼에도 콰인은 모든 개념이 소크라테스적 조건을 만족할 필요는 없지만 특정 개념들은 반드시 소크라테스적 조건을 만족해야 하며, 분석성이 다름아닌 그러한 개념 중 하나라고 주장할 수 있다. 일례로 다음의 문장들을 보자.
모든 초록색인 것은 외연을 가진다.
위 문장이 분석적인지의 여부는 모호하다. 콰인은 이 모호성이 “초록”이나 “외연”의 의미로부터 비롯되는 문제가 아닌, “분석적”의 의미로부터 비롯된다고 주장하며, 이것은 여타 개념과 달리 분석성은 엄밀한 정의 없이는 정당화할 수 없는 개념임을 방증한다고 주장한다.
이에 대해 그라이스와 스트로슨은 “모든 초록색인 것은 외연을 가진다”의 분석성 여부가 모호한 이유는 분석성의 의미가 모호하기 때문이 아니라 “모든 초록색인 것”의 의미가 모호하기 때문이라고 주장한다. 요컨대 “초록색 점멸” 또한 “모든 초록색인 것”에 해당하는지가 모호하므로 문장의 분석성을 결정할 수 없다는 것이다. 오히려 분석성은 거의 모든 사람에 의해 일관적인 방식으로 사용되고 있으므로, 소크라테스적 조건이 요청될 정도로 모호한 개념이라고 볼 이유는 없다고 주장한다.
4. 콰인의 논리실증주의 비판
4.1. 환원주의에 대한 비판
논리실증주의에 따르면 모든 참은 분석적이거나 종합적이다. 이 중 분석적 참은 논리적 분석을 통해 검증할 수 있고, 종합적 참은 감각 자료를 통해 검증할 수 있다. 이에 따라 일반적으로 문장의 의미는 감각 자료의 논리적 복합체logical compound of sense data라는 환원주의적 논제가 얻어진다. 예를 들어 “고양이는 책상 위에 있거나 상자 안에 있다”의 의미는 “고양이”, “책상”, “상자”에 대응하는 감각 자료와 “또는”, “있다” 등의 논리적 연결사로 분석된다.
그러나 콰인은 의미론적 환원주의자는 자연 언어의 문장을 감각 자료의 논리적 복합체로 환원하는 것이 실제로 가능함을 보일 입증 책임burden of proof이 있다고 주장한다. 이에 콰인은 카르납이 ⟪세계의 논리적 구조⟫에서 감각 자료와 논리적 연결사만 가지고서 자연 언어를 구축하려고 시도한 사례를 언급하지만, 카르납의 프로젝트는 본인 스스로도 실패했다고 인정했다.
콰인은 환원주의의 입증 책임이 해소되지 않는 한 환원주의는 정당화될 수 없다고 주장한다.
4.2. 검증가능성에 대한 비판
논리실증주의에 따르면 문장의 의미는 그것의 검증 가능성이다. 이같은 의미의 검증주의적 이론verificationist theory of meaning 하에서 분석성은 다음과 같이 정의할 수 있다.
P는 분석적이다 $\iff$ P는 검증의 결과가 어떻든지 참이다
그러나 콰인은 논리실증주의의 분석성 정의 또한 문제적이라고 주장한다. 콰인에 따르면 개별 명제를 독립적으로 떼 놓고서 검증하기란 불가능하므로, 의미의 검증주의적 이론은 개별 문장의 의미를 해명할 수 없기 때문이다.
예를 들어 다음의 명제를 보자.
(i) 물은 100°C에서 끓는다
위의 명제를 검증하는 한 가지 방법은 끓는 물에 온도계를 넣는 것이다. 그런데 끓는 물에 온도계를 넣어보니 102°C가 나왔다면 우리는 (i)를 기각해야 할까? 그렇지 않다. 우리는 (i)를 기각하는 대신 “온도계가 고장났다”, “순수한 물이 아니었다”, “기포 발생이 저해되어 과가열되었다”, “내가 온도계를 잘못 읽었다” 등 수많은 다른 명제를 대신 선택할 수 있다.
따라서 콰인은 검증의 대상이 되는 것은 언제나 믿음의 망web of beliefs 전체라는 인식론적 전체론epistemological holism을 주장한다. 위의 경우에서 검증되는 것은 “물은 100°C에서 끓는다”는 명제가 아닌, “이것은 순수한 물이고, 온도계는 정상적이고, 과가열이 일어나지 않을 것이며, 물은 100°C에서 끓으며…” 등의 믿음의 망인 것이다.
4.3. 인식론적 전체론의 함의
콰인의 전체론은 모든 명제에 해당한다는 점에서 극단적이다. 콰인에 따르면 믿음의 망에는 분야 간 뚜렷한 경계가 없다. 따라서 수학이라고 해서 과학이나 철학에 비해 독보적인 인식론적 지위를 누리는 것은 아니다. 이것은 콰인의 자연주의로 이어진다.
콰인에 따르면 명제 $φ$가 확실certain하다는 것은, $φ$가 어떤 경우에서도 참이라는 의미가 아니라, $φ$가 믿음의 망 깊숙한 곳에 자리잡고 있다는 의미이다. 믿음의 망에 반하는 검증 결과가 제시되었을 때 우리는 믿음의 망을 수정해야 하는데, 추후에 믿음의 망에 반하는 결과들이 나올 가능성이 최소화되도록 망을 수정하는 것이 가장 실용적이다. 실용성의 원칙에 따라 핵심부에 있는 믿음을 폐기·수정하는 것보다 주변부에 있는 믿음을 폐기·수정하는 것이 바람직하다. 따라서 핵심부에 있는 믿음은 거의 영구적으로 존속하게 되어 확실성의 지위를 획득한다. 그러나 만약 핵심부에 있는 믿음 — 이를테면 논리학의 법칙들 — 을 폐기하는 것이 더욱 실용적인 상황이 닥친다면 콰인은 논리학을 폐기하는 것이 마땅하다고 본다.
4.4. 인식론적 전체론에 대한 반론
라이트Crispin Wright는 콰인의 전체론이 무한 퇴행에 빠지기 때문에 비정합적이라고 주장한다. 예를 들어 다음의 두 가지 요소로 구성된 믿음의 망을 고려하자.
- 세계에 대한 과학적 이론 $T$
- 논리 체계 $\mathcal{S}$
추가로 $p → q$가 $T$와 $\mathcal{S}$로부터 도출 가능한 법칙에 해당한다고 가정하자. 예를 들어 $T$가 뉴턴 역학이고 $\mathcal{S}$가 1차 논리라면, $p$는 “광자는 질량이 없다”이고 $q$는 “광자는 중력의 작용을 받지 않는다”일 수 있다.
이제 $T$와 $\mathcal{S}$에 반하여, $p$와 $¬q$를 시사하는 관찰 결과 — 이를테면 중력 렌즈 효과 — 가 나타났다고 가정하자. 콰인의 전체론을 따르면 다음 네 가지 명제는 모두 기각될 수 있는 명제의 후보이다.
- $p ∧ ¬q$를 기각 (중력 렌즈 효과는 잘못 관찰되었다)
- $T$를 기각 (뉴턴 역학은 틀렸다)
- $\mathcal{S}$를 기각 (1차 논리는 틀렸다)
- $T \vdash_\mathcal{S} p → q$를 기각 (뉴턴 역학과 1차 논리로부터 $p → q$를 도출하는 것은 틀렸다)
위 4개의 후보 중 무엇을 기각할지는 실용성의 기준으로 정해진다. 일례로 실용적 고려가 다음을 시사한다고 하자.
- (4)를 기각하는 것이 가장 실용적이다.
그러나 라이트는 (5) 또한 믿음의 망에 속한다고 지적한다. 그러므로 우리는 (4)를 기각하는 대신, (5)를 기각하기로 선택할 수 있다. 반대로 (5)를 기각하지 않기 위해서는 다음의 믿음이 추가로 요청된다.
- (5)를 기각하지 않는 것이 실용적이다.
그런데 (6)을 기각하지 않기 위해서는 (6)을 기각하지 않는 것이라는 믿음이 추가로 요청되고, 이것은 무한 퇴행로 이어진다. 그러므로 라이트는 인식론이 무한 퇴행에 빠지지 않기 위해서는 (4)와 같은 일부 믿음을 실용주의적 고려의 범위 밖에 위치시켜야 한다고 주장한다.
참고문헌
Quine, Willard V. O. (1951). Two Dogmas of Empiricism. Philosophical Review 60 (1):20–43.
Miller, Alexander (1998). Philosophy of Language. New York: Routledge.
