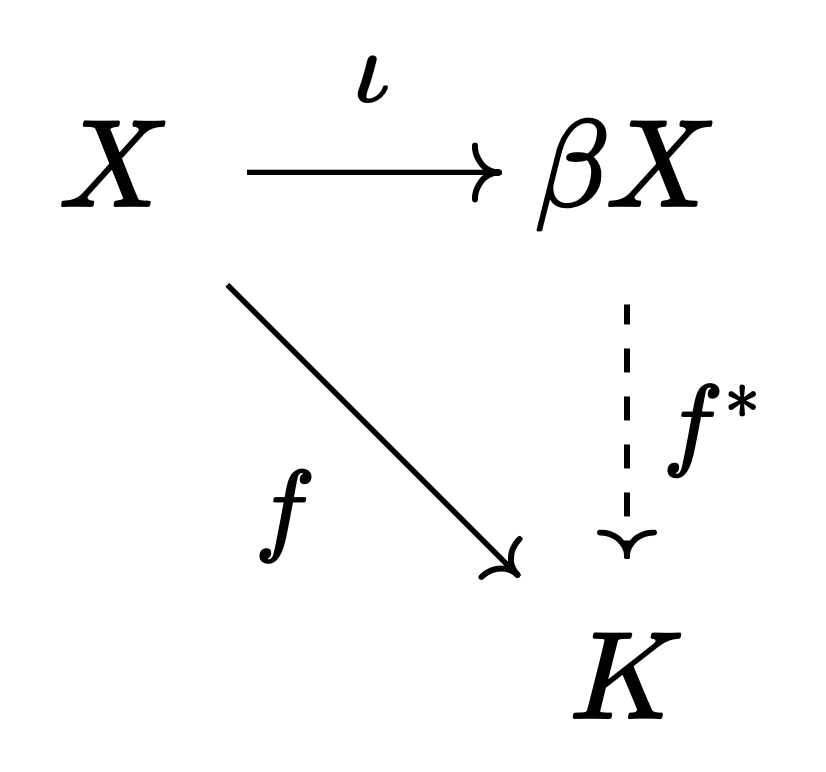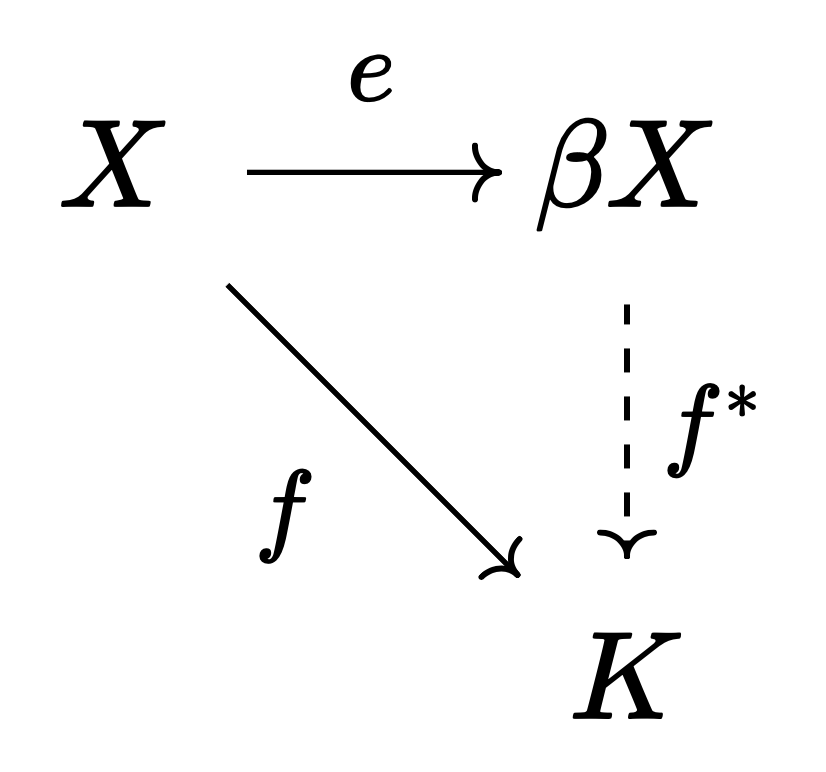사적 언어는 가능한가?

21 Jul 2025

이전 글에서 크립키-비트겐슈타인 역설을 다루었다. 요약하자면, 크립키-비트겐슈타인 역설은 특정 단어가 사용될 수 있는 무한한 사례를 아우르는 규범적 사실이 없다는 고찰에 착안한다. 이로부터 크립키-비트겐슈타인이 내리는 결론은 다음과 같다.

“화자 A가 기호 s를 통해 M을 의미한다”는 대응되는 사태를 가지지 않는다.

그리고 크립키의 독해에 따르면 비트겐슈타인은 이 결론에 대해 “회의주의적 해답”을 제시한다. 즉, 위의 결론을 그대로 받아들이되 — “앨리스는 ‘+’로 덧셈을 의미한다’“에 대응하는 사태는 없다 — 그것이 어떻게 — “앨리스의 생각은 초록색이다”와 달리 — 유의미하게 사용될 수 있는지 해명하는 것이다. 해명의 요지는, 언어의 의미는 그것이 공동체에서 가지는 기능과 불가결하며, 따라서 의미에 대한 논의는 개별 화자 단위에서는 공허하지만 공동체 단위에서는 유효하다는 언어의 공적성을 강조하는 것이다.

1. ⟪논고⟫에서 ⟪탐구⟫로

크립키는 ⟪논리철학논고⟫로 상징되는 전기 비트겐슈타인과, ⟪철학적 탐구⟫로 상징되는 후기 비트겐슈타인 사이에 현격한 차이가 있다고 보는, 소위 “전통적 해석” 학파에 속한다. 크립키는 ⟪논고⟫에서 제시된 언어관의 특징을 다음과 같이 요약한다.

• 논리적 원자주의. 모든 유의미한 명제는 원자명제의 논리적 합성으로 분석된다.
• 그림 이론. 원자명제와 그것이 나타내는 사태는 서로 그림처럼 대응한다. 원자명제가 나타내는 사태가 성립하는 경우 해당 명제는 참이다.
• 진리조건론. 명제의 의미는 그것의 진리조건 — 즉, 해당 명제에 대응되는 사태가 무엇인지 — 에 있다.
• 선험적 접근. 위에서 개괄된 언어의 특징은 선험적_{a priori} 사유를 통해 추론할 수 있다.

반면 ⟪탐구⟫에서는 ⟪논고⟫와 대비되는 두 가지 언어관이 드러난다고 분석한다.

• 주장조건론. 명제의 의미는 그것의 주장조건_{assertability condition} — 즉, 해당 명제가 어떤 상황에서 주장되거나 기각될 수 있는지 — 에 있다.¹
• 실용주의. 특정 명제를 주장하거나 기각하는 것이 우리 삶에서 어떤 역할 또는 기능을 수행하는지에 대한 고찰은 언어의 올바른 이해에 핵심적이다.²

여기서 주장조건론은 비트겐슈타인 이전에도 여타 철학적 입장에서 발견할 수 있는 것이다. 브라우어르의 직관주의 수학, 논리실증주의의 검증론 등이 대표적이다. 크립키는 비트겐슈타인의 독창성이 두 번째 특징, 즉 실용주의에 있다고 본다. 비트겐슈타인은 프레게 등이 요구하는 단어-대상 대응을 비판하며, 그 대신 단어들이 실제로 쓰이는 상황을 고려할 것을 촉구한다. 숫자로 예를 들자면, 프레게는 숫자가 가리키는 대상이 있어야 한다고 주장한다.³ 그러나 비트겐슈타인은 숫자가 쓰이는 실제 상황 — 장터에서 물건을 세는 것, 교사가 학생의 수를 세는 것 — 등을 거론하며, 이들 상황에서 숫자 대신 알파벳을 읊었더라도 언어 행위의 목적은 달성되었을 것임을 강조한다. 요컨데 숫자는 프레게의 말마따나 “자연수를 지칭하는 언어”가 아닌 “물건 등을 세는 활동에 종사하는 언어”인 것이다.

2. 회의주의적 해답

주장조건론에 기반한 비트겐슈타인의 후기 언어관에 입각하여 보면 회의주의 논증은 그 즉시 “앨리스는 ‘+’로 덧셈을 의미한다”가 무의미함을 시사하지 않는다. 해당 명제에 대응되는 사태가 없을지언정, 애초에 사태의 존재 여부는 — 진리조건론 언어관과 달리 — 명제가 유의미할 필요조건이 아니기 때문이다.

한편 실용주의는 “앨리스는 ‘+’로 덧셈을 의미한다”가 유의미한 명제로 간주되기 위한 별도의 필요조건을 제시한다. 즉, 해당 명제는 언어게임에서 유용한 역할을 수행해야 한다. 그리고 크립키는 해당 명제가 수행하는 역할을, ⟪탐구⟫에서 등장하는 또다른 사고실험인 “사적 언어 논증”과 결부지어 설명한다. 그러나 그 전에, 비트겐슈타인의 회의주의적 해답의 특징을 버클리 및 흄의 회의주의와 비교하여 고찰해 보자.

2.1. 버클리의 회의주의

크립키는 “회의주의적 해답”이라는 표현으로, 다음 특징을 가지는 논증들을 아울러 지칭한다.

1. 우리가 자명한 것으로 생각하는 명제 P를 제시한다.
2. 명제 P가 사실 모순적이거나, 불가해하거나, 정당화될 수 없음을 주장하는 “회의주의 역설”을 제시한다.
3. 그러나 회의주의 역설에도 불구하고 우리가 일상에서 P를 정당한 명제로서 간주할 수 있는 이유를, P의 의미를 재해석함으로써 설명한다.
4. 보너스로, 3에서 재해석한 P의 의미가 “진짜 의미”, “일상인의 의미”이고, 2에서 기각된 P의 의미는 “가짜 의미”, “철학자들이 호도한 의미”라고 선전(?)할 수 있다.

예를 들어 버클리의 관념론을 보자. 버클리는 한 개인이 인식할 수 있는 것은 그가 내면에서 발생하는 심상일 뿐임을 지적한다. 따라서 우리는 결코 ‘외부 대상’의 독립적 존재를 증명할 수 없다. 내적 심상들의 집합으로부터 외부 대상의 존재를 추론하는 것은 논리적으로 정당화될 수 없기 때문이다. 위에서 제시한 3단계에 맞추어 이를 개괄하자면,

1. 우리는 “내 손에 사과가 있다”는 명제를 정당한 것으로 간주한다.
2. 그러나 개인이 인식할 수 있는 것은 내적 심상으로 제한되므로 1의 명제는 정당화될 수 없다.
3. 그럼에도 불구하고 우리가 1의 명제를 정당한 명제로서 간주할 수 있는 이유는, 사실 1의 명제의 진짜 의미는 “나는 빨간색 시각, 새콤한 후각, 구형의 단단한 촉각 등을 느끼고 있다”이기 때문이다.

(크립키는 이런 식의 논증을 좋아하지 않는 티를 원 논문에서 팍팍 낸다. 필자 생각으로는 미국 기능주의 철학자들이 이러한 “회의주의적 해답”을 — 크립키가 보기에 — 부당할 정도로 몰아붙인 데서 온 반감이 아닐까 싶다.)

2.2. 흄의 회의주의

또다른 예시로, 흄의 인과에 대한 회의주의를 보자. 흄은 “사건 A가 사건 B의 원인이다”라는 명제에 대해, “사건 A와 사건 B가 잇달아 일어났다” 이상으로 제시할 수 있는 경험적 근거가 있는지를 질문한다. 그러한 근거는 자연에 실존하는 인과적 연결고리_nexus의 관측으로 구성될 것인데, 흄은 그러한 연결고리의 관측은 인간의 경험 영역을 벗어나 있음을 지적한다. 우리가 경험할 수 있는 것은 오직 사건들의 규칙성이다. 즉, 사건 유형_type A에 속하는 사건 사례_token가 일어날 때, 사건 유형 B에 속하는 사건 사례가 일어나는 것을 수 차례 관측한 것을 두고 우리는 유형 A와 B 사이에 인과가 성립한다고 말한다.

크립키는 흄의 인과 회의주의의 결론이 사적 인과의 불가능성임을 지적한다. 흄의 주장대로 인과가 두 사건 유형 간의 규칙성에 관한 진술이라면, 유형화도 불가능할 정도로 특이한 사건 사례에 대해서는 인과를 따지는 것이 무의미하다. 예를 들어 “중소수와 삼중소수의 충돌로 인해 헬륨이 발생했다”라는 명제는 “중소수”, “삼중소수”, “헬륨”이라는 유형에 해당하는 입자 사례가 여럿 있는데, 이들 입자를 수차례에 걸쳐 충돌시켜 보니 규칙성이 발견되었다는 진술로서 유의미하다. 그러나 우주에 딱 하나씩밖에 존재하지 않는 입자 X와 입자 Y가 있다면, 이들을 충돌시켜 입자 Z가 발생했다고 하더라도 “X와 Y의 충돌로 인해 Z가 발생했다”라고 말할 수 없다. 우리가 말할 수 있는 것은 “X와 Y의 충돌 직후 Z가 발생했다”뿐이다.

크립키는 흄의 이 논증을 염두에 두고 비트겐슈타인의 사적 언어 논증을 읽어볼 것을 제안한다. 크립키의 독해에 따르면 비트겐슈타인과 흄의 논증은 흐름이 매우 비슷하기 때문이다.

3. 사적 언어 논증

3.1. 전통적 해석

이제 본격적으로 사적 언어 논증을 살펴보자. 비트겐슈타인은 ⟪탐구⟫에서 다음과 같은 사례를 제시한다. 앨리스는 자신이 느끼는 어떤 특정한 감정을 언어로 표현하는 데 어려움을 느낀다. 그래서 그는 그 감정에 ’S’라는 이름을 붙이고는, 그 감정을 느낄 때마다 “S를 느낌”이라고 일기에 적는다. 그렇게 몇 년이 지나자 앨리스는 스스로 ’S’의 사용에 익숙해졌다고 느낀다. 여기서 비트겐슈타인은 질문을 던진다. 우리는 앨리스가 ’S’라는 기호에 자신만의 의미를 부여했다고, 즉 그가 사적 언어를 형성했다고 말할 수 있는가?

비트겐슈타인의 답은 부정적이다. 그러나 크립키 또한 지적하듯이, 비트겐슈타인이 사적 언어를 부정하는 이유는 해석자들에게 의문 투성이였다. 가장 표준적인 해석은 다음과 같다. 비트겐슈타인이 사적 언어가 불가능하다고 주장하는 이유는, 개인 혼자서는 자신이 이 기호를 올바르게 사용하고 있다는 확인을 받을 수 없기 때문이다. 가령 앨리스는 오늘 자신이 ’S’라고 부른 감정이 수년 전에 자신이 ’S’라고 부른 감정과 정말로 일치하는가에 대한 회의주의에서 벗어날 수 있다. 앨리스가 유아론적인 회의주의에서 벗어날 수 있는 유일한 길은, 통일된 기호들을 사용하는 언어 공동체에 속함으로써 그들로부터 자신의 기호 사용이 올바르다는 확인을 받는 것이다.

그러나 이 논증은, 일찍이 에이어를 비롯한 수많은 학자가 지적했듯이, 굉장히 허술하다. 가령 내가 지금 나의 감정을 ‘행복’이라고 불러도 되는지 확신할 수 없는 상황에서 다른 사람들에게 “너는 지금 행복한 게 맞아”라고 확인받는 것이 상황을 개선하는가? 그들의 판단이 올바른지는 어떻게 확신할 수 있는가? 오히려 “다른 사람들이 내가 지금 행복한 상태라고 알려주더라도 그들의 판단이 정말로 올바른지 확신할 수 없으니 나 스스로가 내면을 확인해야 한다”는 역방향의 논증이 더 그럴듯하다. 더구나 공동체의 확인 또한 결국에는 시청각을 비롯한 개인의 사적 감각을 통해 수용된다는 사실을 고려하면, 개인이 자신의 내면을 확인하는 것과 공동체의 확인을 받는 것 사이에는 애당초 본질적인 차이가 없다.

3.2. 크립키의 해석

그러나 크립키는 사적 언어 논증을 위와 같이 이해하는 것은 오해라고 주장한다. 비트겐슈타인의 의도는, 사적 언어를 불가능의 영역으로 내쫓는 것이 아니다. 오히려 회의주의 역설에 따르면 모든 언어 — 사적 언어이든 공적 언어이든 — 는 불가능하다. 비트겐슈타인은 이에 맞서 언어의 가능성을 구제하고자 한다. 그 구제의 전략이 언어의 공적성에 호소하는 것이기 때문에, 사적 언어는 불가능의 영역에 남는 것이다.

회의주의 역설에 대한 비트겐슈타인의 “해답”은 다음 세 가지 경우를 고려함으로써 이해할 수 있다. 첫째는 이 우주에서 ‘+’ 기호를 사용하는 사람이 앨리스뿐인 경우이다. 앨리스는 ‘+’에 대한 자신의 성향에 따라 ‘+’를 사용한다 (물론 이는 동어반복적인 진술이다). 이따금 앨리스는 ‘+’로 계산 실수를 할 것이고, 약물에 취해 있는 극단적인 경우에는 ‘+’를 컷셈과 같은 괴이한 방식으로 사용할 수도 있다. 그러나 모든 경우에 앨리스는 스스로 ‘+’를 정당한 규칙에 따라 사용한다고 믿을 것이다. 그리고 크립키-비트겐슈타인 역설에 따르면 앨리스의 믿음을 반증하는 사태는 존재하지 않으므로, 이것이 앨리스의 ‘+’ 사용에 대해 말할 수 있는 전부이다. 크립키의 말을 빌리자면,

화자가, 궁극적으로는 아무런 정당화 없이, 그 자신의 확신에 찬 성향에 따라, 이 방식으로 대답하는 것이 (가령 ‘125’라고 대답하는 것) 올바르고 다른 방식은 (가령 ‘5’라고 대답하는 것) 틀렸다고 말할 수 있다는 것은, ‘규칙에 관해 말하기’라는 우리의 언어게임을 구성하는 요소이다. […] 오직 한 명의 개인만을 고려했을 때 우리가 말할 수 있는 것은, 우리의 일상적 관습[‘규칙에 관해 말하기’라는 언어게임]이 그에게 그 자신에게 떠오르는 방식대로 규칙을 적용할 자격_license를 준다는 것이다.

It is part of our language game of speaking of rules that a speaker may, without ultimately giving any justification, follow his own confident inclination that this way (say, responding ‘125’) is the right way to respond, rather than another way (e.g. responding ‘5’). That is, the ‘assertability conditions’ that license an individual to say that, on a given occasion, he ought to follow his rule this way rather than that are, ultimately, that he does what he is inclided to do. […] All we can say, if we consider a single person in isolation, is that our ordinary practice licenses him to apply the rule in the way it strikes him.

(이탤릭체는 본문의 강조, 볼드체는 필자의 강조. “…라고 말할 수 있다는 것은 ‘규칙에 관해 말하기’라는 우리의 언어게임을 구성하는 요소이다”라는 진술을, 가령 “캐슬링을 할 수 있다는 것은 체스를 구성하는 요소이다”에 빗대어 이해하면 해당 진술이 ‘규칙에 대해 말하기’라는 언어게임의 정의의 일부와 다름없음을 알 수 있다. 즉, 그런 말하기가 가능하지 않은 언어게임은 ‘규칙에 대해 말하기’ 언어게임이라고 부를 수 없다.)

하지만 크립키가 지적하듯이 이것은 우리가 ‘규칙에 관해 말하기’라는 언어게임에서 기대하는 바가 아니다. 가령 혼자서 벽을 보고 체스를 두는 사람을 상상해 보자. 그는 1시간으로 체스 시계를 맞추고 백으로서 첫수를 두고는 “상대”, 즉 벽이 응수하기를 기다린다. 하지만 “상대”는 응수를 하지 않아 1시간 후에 시간패를 당하고 만다. 따라서 백은 언제나 승리한다. 이것을 사적 체스라고 부르자. 사적 체스는 체스의 모든 규칙을 만족하지만, 한편으로는 전혀 체스가 아니다. 적어도 우리가 기대하는 체스는 아니다. 통상적인 체스에서는 백이 질 수 있어야 하기 때문이다. 마찬가지로 사적 규칙은 설령 그것이 ‘규칙 말하기’ 언어게임의 규칙을 만족하더라도, 우리가 기대하는 ‘규칙 말하기’ 언어게임은 아니다. 통상적인 ‘규칙 말하기’ 언어게임에서는 화자가 규칙의 준수에 있어 실수를 할 수 있어야 하기 때문이다.

이제 다음 경우로 넘어가 보자. 둘째는 이 우주에서 ‘+’ 기호를 사용하는 사람이 앨리스와 스미스 두 명인 경우이다. ‘+’에 대한 둘의 성향은 일치할 수도, 어긋날 수도 있다. 만약 ‘68 + 57’에 대해 앨리스는 ‘125’라고 대답하고 스미스는 ‘5’라고 대답했다면, 앨리스는 스미스가 ‘+’를 올바른 규칙으로 사용하지 않는다고 지적할 것이다. 그러나 이 지적은 스미스 또한 앨리스에게 할 수 있는 것이다. 그리고 크립키-비트겐슈타인 역설에 따르면 둘 중 누구의 지적이 더 올바른지에 대응하는 사태는 존재하지 않으므로 이것이 둘의 ‘+’ 사용에 대해 말할 수 있는 전부이다.

마지막은 이 우주에서 ‘+’ 기호를 사용하는 사람이 앨리스뿐 아니라 충분히 큰 공동체를 이루는 경우이다. 이 경우, 초기에는 공동체와 상충하는 방식으로 ‘+’를 사용하는 화자들이 있을 수 있더라도, 이들 화자는 ‘+’ 기호가 공동체에서 수행하는 기능에 지장을 일으키기 때문에 공동체에서 점차 사라질 것이다 (여기서 비트겐슈타인이 실용주의적 고려를 중요시하는 이유가 드러난다). 예를 들어 ‘+’의 기능 중 하나는 장부를 관리하는 것이다. 그러나 ‘+’를 컷셈처럼 사용하는 사람들은 장부를 비표준으로 관리할 것이고, 이는 ‘+’를 덧셈처럼 사용하는 사람들이 그들에게 ‘+’의 사용을 더는 위임하지 않을 사유가 된다. 이렇듯 언어의 기능에 기반한 지속된 승인과 추방의 과정은 일관된 규칙을 따르는 화자들의 공동체로 수렴한다. 그리하여 “앨리스는 ‘+’로 덧셈을 의미한다”는, 앨리스의 ‘+’ 사용을 해당 공동체가 승인한다는 표현으로서 유용하며, 따라서 유의미하다.

여기서 크립키가 조건문의 반전_{inversion of a conditional}이라고 부르는 철학적 기술이 활용되었음에 유의하라. 조건문의 반전이란, “P라면 Q이다”라는 명제 대신에 “not Q라면 not P이다”를 주장하는 것이다. 물론 두 조건문은 대우 관계이므로 외연적으로 동치이지만, P와 Q의 우선순위를 설정하는 데 있어 차이가 있다. 전자의 경우에는 P의 성립이 Q의 성립을 결정하는 반면, 후자의 경우에는 Q의 성립이 P의 성립을 결정한다.

언어에 대한 전통적인 관점에 따르면, 화자들이 같은 기호를 같은 방식으로 사용하는 것은 그들이 그 기호에 같은 의미를 부여하고 있다는 사실로서 설명된다. 이 관점에 따르면 다음 조건문이 성립한다.

앨리스는 ‘+’로 덧셈을 의미한다 -> 앨리스는 ’68 + 57’에 대해 ‘125’라고 답한다

그러나 회의주의적 해답은 이 조건문을 다음과 같이 뒤집는다.

앨리스는 ’68 + 57’에 대해 ’125’라고 답하지 않는다 -> 앨리스는 ‘+’로 덧셈을 의미하지 않는다

회의주의적 해답은 진리조건이 아닌 주장조건을 기반으로 한다는 점을 고려하여 더 적확히 적자면 다음과 같다.

앨리스는 ’68 + 57’에 대해 ’125’라고 답하지 않는다 -> ‘규칙에 관해 말하기’ 언어게임이라는 맥락에서, 우리는 “앨리스는 ‘+’로 덧셈을 의미한다”라고 말할 수 없다.

물론 단순히 앨리스가 ’68 + 57’에 대해 ‘125’라고 대답하지 않았다고 해서 우리는 그가 ‘+’로 덧셈을 의미하지 않는다는 극단적인 결론을 바로 도출하지는 않을 것이다. 아마 우리는 앨리스가 계산 실수를 했다고 생각할 것이다. 그러나 앨리스가 ’68 + 57’에 대해 ‘5’라고 답하는 등, 매우 받아들이기 힘든 방식으로 ‘+’ 기호를 사용한다면, 우리는 그가 ‘+’으로 덧셈을 의미한다는 진술을 철회할 것이다.

요컨대 크립키-비트겐슈타인은 ‘규칙에 관해 말해기’라는 언어게임이 자명한 언어게임에서 유용한 언어게임으로 변이하는 과정을, 공동체를 통한 창발적 과정으로서 이해한다.

4. 회의주의적 해답의 특징

4.1. 삶의 형식_{form of life}

회의주의적 해답의 정당성은, 언어 사용자들이 ‘+’로 같은 연산, 즉 덧셈을 수행하는 것으로 수렴한다는 사실에 기반한다. 만약 ’68 + 57’에 대해 A는 125, B는 7, C는 58과 같이 개개인이 저마다 다른 답을 내놓았다면 회의주의적 해답은 성립할 수 없을 것이다.

크립키의 독해에 따르면, 비트겐슈타인은 우리가 기호 사용에서 보이는 동의_agreement와 (’68 + 57’에 대해 ‘125’라고 대답한다) 그로써 가능해지는 일련의 활동을 (따라서 가격이 125만 원인 컴퓨터를 68만 원과 57만 원으로 할부할 수 있다) “삶의 형식”이라고 부른다. 비트겐슈타인에 따르면, ’68 + 57’에 대해 우리가 ‘125’라는 일관된 답을 내놓을 수 있는 이유는 우리가 ‘+’로 동일한 연산, 즉 덧셈을 의미하기 때문이 아니다. 오히려, 우리가 ‘+’로 덧셈을 의미한다고 말할 수 있는 이유는, 우리가 공통된 삶의 형식을 기반으로 하는 언어게임에 참여하고 있기 때문이다. 비트겐슈타인의 분석에서 우리가 ’68 + 57’에 대해 ‘125’라는 일관된 답을 내놓는다는 사실은 그저 주어진 사실이지, 해명되어야 할 현상이 아니다.

(개인적 노트: 크립키의 주석 76과, 논리적 외계인 사고실험을 비교해 보자.)

76. Can we imagine forms of life other than our own, that is, can we imagine creatures who follow rules in bizarre quus-like ways? It seems to me that there may be a certain tension in Wittgenstein’s philosophy here. On the one hand, it would seem that Wittgenstein’s paradox argues that there is no a priori reason why a creature could not follow a quus-like rule, and thus in this sense we ought to regard such creatures as conceivable. On the other hand, it is supposed to be part of our very form of life that we find it natural and, indeed, inevitable that we follow the rule for addition in the particular way that we do. (See §231: ““But surely you can see . . . ?” That is just the characteristic expression of someone who is under the compulsion of a rule.”) But then it seems that we should be unable to understand ‘from the inside’ (cf. the notion of ‘Verstehen’ in various German writers) how any creature could follow a quus-like rule. We could describe such behavior extensionally and behavioristically, but we would be unable to find it intelligible how the creature finds it natural to behave in this way. This consequence does, indeed, seem to go with Wittgenstein’s conception of the matter.

Of course we can define the quus function, introduce a symbol for it, and follow the appropriate rule for computing its values. I have done so in this very essay. What it seems may be unintelligible to us is how an intelligent creature could get the very training we have for the addition function, and yet grasp the appropriate function in a quus-like way. If such a possibility were really completely intelligible to us, would we find it so inevitable to apply the plus function as we do? Yet this inevitability is an essential part ofWittgenstein’s own solution to his problem.

The point is even stronger with respect to a term like ‘green’. Can we grasp how someone could be presented with a number of green objects, and be told to apply the term ‘green’ just to ‘things like these’, and yet apply the term learnt as if it meant ‘grue’? It would seem that if we find our own continuation to be inevitable, in some sense we cannot.

4.2. 심리 현상의 외적 기준_criteria

기호 사용에 있어서의 동의야말로 화자가 해당 기호를 특정 의미로 사용한다는 진술의 내용이라는 회의주의적 해답은, 심리철학에 대한 비트겐슈타인의 다음 언명으로 이어진다.

“내적 현상은 외적 기준을 필요로 한다.” (§580)

어린아이가 ‘책상’과 ‘아프다’라는 두 단어를 배우는 경우를 생각해 보자. 전자의 경우, 어린아이가 책상을 가리키며 ‘책상’이라고 말하면 부모는 그 발화를 승인할 것이고, 의자를 가리키며 ‘책상’이라고 말하면 틀렸다고 알려줄 것이다. 이와 같은 과정을 통해 어린아이는 ‘책상’이라는 기호의 사용에 있어 언어 공동체와 동의를 이루게 된다. 그러나 ‘아프다’의 경우에는 이것이 불가능하다. 어린아이는 자신이 겪는 감정을 직접 내보임으로써 이것이 ‘아프다’에 해당하는지 확인을 받을 수 없기 때문이다. 대신 아이는 울음을 터뜨리거나, 얼굴을 찌푸리는 등의 외적 행동을 보일 것이고, 그 행동을 기준으로 부모는 ‘아프다’는 아이의 발화가 정당한지 결정할 것이다. 이것이 §580의 의미라면, §580은 — 전통적으로 간주되었던 것처럼 — 비트겐슈타인이 사적 언어 논증을 위해 마련하는 전제가 아니라, 사적 언어 논증과 마찬가지로 회의주의적 역설의 함의이다.

이와 관련해서 크립키는 §580의 유연한_liberal 해석과 엄격한 해석을 제시한다. §580을 엄격하게 해석하면, 심리 언어에 속하는 각각의 표현에는 해당 표현과 결부되는 자연적 행동_{natural expression}이 있어야 할 것이다. 예를 들어 아픔에 결부되는 자연적 행동은 얼굴을 찡그리는 것이다. 따라서 언어를 습득 중인 아이가 얼굴을 찡그리며 “아파!”라고 말한다면 우리는 그것을 승인한다. 이와 같은 식으로, 모든 심리적 표현에는 그와 결부되는 자연적 행동이 있으며 이 행동들의 관찰 가능성은 해당 표현들이 사적 언어로 퇴화되는 것을 방지한다.

그러나 크립키는 이보다 더 유연한 해석을 제시한다. 이에 따르면, 외적 기준을 필요로 하는 것은 개개의 심리 표현이 아닌, “심리 언어” 그 자체이다. 크립키는 이것이 심리 언어의 작동에 대한 더 정확한 고찰이라고 본다. 분명한 외적 기준을 가지는 심리 표현들 ‒ 가령, 아픔 ‒ 에 대해 충분한 숙지를 보이는 화자가 있으면, 우리는 그가 심리 언어 일반을 숙지했다고 판단하여, 그가 자신의 내면에서 특정한 감정 또는 퀄리아를 포착했다고 진술하면, 설령 그 감정 및 퀄리아가 어떠한 외적 기준을 가지지 않는다고 하더라도, 그 진술을 정당한 것으로 인정하기 때문이다. (필자가 보기에 “나는 의식을 가지고 있다”가 그러한 진술의 사례에 해당할 듯하다)

이에 관해서는 본문의 주석 81, 82, 83을 보라. (참고로 이 세 주석들은 독자적인 하나의 절을 구성할 만큼 분량이 많다…)

4.3. 회의주의적 해답은 자기순환적인가?

논문의 말미에서 크립키는 회의주의적 해답이 다음과 같이 오해될 수 있음을 경고한다.

언어 공동체가 ‘+’로 덧셈을 의미한다는 것은, 해당 공동체의 일원 대다수가 ‘+’를 덧셈으로 사용한다는 것이다.

또는, 더 엄밀하게 적자면,

언어 공동체가 ’+’로 의미하는 연산이 f라는 것은, 해당 공동체의 일원 대다수가 ‘x + y’에 대해 f(x, y)라고 답한다는 것이다.

크립키에 따르면 이는 잘못된 이해이다. 위와 같이 해석한 회의주의적 해답은 사실상 공동체 단위에서의 성향주의적 분석과 다름없으며, 따라서 성향주의적 분석이 직면하는 난점을 ‒ 전부 다가 아니라면 적어도 일부 ‒ 지니고 있다. 또한 위의 해석은 “언어 공동체가 …로 …을 의미한다”에 대한 진리조건을 제시하고 있다. 이는 진리조건론에서 주장조건론으로 이행하려는 비트겐슈타인의 기획을 근본적으로 잘못 짚은 것이다.

크립키는 비트겐슈타인의 회의주의적 해답이 “언어 공동체가 …로 …을 의미한다”에 대한 새로운 진리조건을 제시하려는 것이 아니라, 단지 그러한 진술을 가능하게 만드는 환경과, 그러한 진술을 사용함으로 인해 얻게 되는 이점에 주목함을 강조한다. 본문을 인용하자면,

이러한 주장조건들이 함의하는 것은, 특정한 덧셈 문제에 대해 모두가 내놓는 대답이, 정의에 의해, 올바른 대답이라는 것이 아니라, 모두가 특정한 대답에 동의한다면, 그 누구도 이 대답에 대한 이의 제기를 정당화하지 못할 것이라는 자명한 관찰이다.

What follows from these assertability conditions is not that the answer everyone gives to an addition problem is, by definition, the correct one, but rather the platitude that, if everyone agrees upon a certain answer, then no one will feel justified in calling the answer wrong.

아마 크립키는 이 대목이 많은 비판의 대상이 될 것임을 (정확히) 예측한 듯하다. 그래서 나중에 그는 긴 주석 87을 추가했다. 주석 87은 비트겐슈타인의 회의주의적 해답이 자기순환적이거나, 여전히 회의주의의 무한회귀에 빠진다는 비판에 대한 해명 스케치이다.

87. 만약 비트겐슈타인이 ‘5’가 아닌 ‘125’가 ‘68 + 57’에 대해 ‘올바른’ 대답임을 보이는 필요충분조건을 제시하려 했던 것이라면, 이는 자기순환의 오류라는 비판이 제기될 수 있었을 것이다. 누군가는 그의 입장을, 나의 대답이 올바른 대답일 필요충분조건은 그 대답이 다른 사람의 대답과 일치하는 것이라는 입장으로 받아들일 수 있다. 그러나 회의주의자와 내가 사전에 이 기준에 합의하더라도, 회의주의자는 내가 과거에 ‘+’로 무엇을 의미했는지에 관해 틀렸던 것처럼, 내가 ‘일치’라는 표현을 잘못된 의미로 사용한다고 말할 수 있지 않은가? 확실히, 덧셈에 대한 규칙을 다른 규칙으로 환원하는 것 — “덧셈 문제가 주어졌을 때, 다른 사람이 대답하는 대로 대답하라!” — 은 여타 환원의 시도만큼이나 비트겐슈타인의 ‘규칙을 해석하기 위한 규칙’이라는 혹독한 비판으로부터 자유롭지 못하다. 더구나 비트겐슈타인이라면 강조했겠듯이, 이 규칙은 언어 수행을 부정확하게 설명한다. 나는 덧셈을 할 때 다른 사람에게 도움을 구하지 않는다. (만약 모두가 이런 규칙을 따라야 했다면 우리는 모두가 서로의 대답을 기다리는 교착 상태에 빠졌을 것이다)

비트겐슈타인의 실제 목표는, 어떤 특정한 행위들이 우리의 삶에서 가지는 기능을 기술_describe하는 것이다. 필연적으로 그는 이 기술을 우리의 언어로 해야 한다. 이와 같은 언어 사용에서 항상 가능하듯이, 또다른 삶의 형식을 가지는 일원은 이 기술에 포함된 단어들을 (이를테면 “동의”) 컷셈과 같은 방식으로 해석할 수 있을 것이다. 따라서 우리가 공동체 안에서의 ‘동의’가 이루어졌다고 간주하는 상황에서, 상이한 삶의 형식을 가지는 혹자는 그들이 동의를 이루어내지 못했다고 판단할 수 있다. 이 사실은 비트겐슈타인의 회의주의적 해답에 대한 비판이 될 수 없다. 적어도, 그에게서 언어의 사용 일체를 박탈하려는 것이 아니라면 말이다.

87. If Wittgenstein had been attempting to give a necessary and sufficient condition to show that ‘125’, not ‘5’, is the ‘right’ response to ‘68+ 57’, he might be charged with circularity. For he might be taken to say that my response is correct if and only if it agrees with that of others. But even if the sceptic and I both accept this criterion in advance, might not the sceptic maintain that just as I was wrong about what ‘+’ meant in the past, so I was wrong about ‘agree’? Indeed, to attempt to reduce the rule for addition to another rule - “Respond to an addition problem exactly as others do!” - falls foul of Wittgenstein’s strictures on ‘a rule for interpreting a rule’ just as much as any other such attempted reduction. Such a rule, as Wittgenstein would emphasize, also describes what I do wrongly: I do not consult others when I add. (We wouldn’t manage very well, if everyone had to follow a rule of the proposed form - no one would respond without waiting for everyone else.)

What Wittgenstein is doing is describing the utility in our lives of a certain practice. Necessarily he must give this description in our own language. As in the case of any such use of our language, a participant in another form of life might apply various terms in the description (such as “agreement”) in a non-standard ‘quus-like’ way. Indeed, we may judge that those in a given community ‘agree’, while someone in another form of life would judge that they do not. This cannot be an objection to Wittgenstein’s solution unless he is to be prohibited from any use of language at all.

그러나 몇 가지 의문이 여전히 남는다. 첫째, “이 사실은 비트겐슈타인의 회의주의적 해답에 대한 비판이 될 수 없다”는 크립키의 변호가 타당한지에 대한 의문이 남는다. 둘째, 회의주의적 해답의 의도가 의미 진술의 진리조건을 제시하는 것이 아닌 (특정한 덧셈 문제에 대해 모두가 내놓는 대답이 올바른 대답이다), 의미 진술의 기능을 기술하는 것이라고 하더라도 (모두가 특정한 대답에 동의한다면 그 누구도 이 대답에 대한 이의 제기를 정당화하지 못할 것이다), 과연 후자의 기술이 올바른지에 관해 의문이 남을 수 있다. 즉, 정말로 모두가 특정한 대답에 동의한다면 그 누구도 이 대답에 대한 이의 제기를 정당화하지 못하는가? 이에 관해서, 이어지는 크립키의 주석을 보자.

[그렇다면] 우리 모두가 일치를 보이는 대답이 ‘올바른’ 대답이 아닐 수도 있다는 의문은 정당한가? 분명, 어떤 경우에 한 개인은, 자신의 언어 공동체가 한때 일치를 보였던 대답을 추후에 수정할 수도 있지 않을까, 하는 의문을 가질 수 있다. [필자 주: “간통은 범죄이다”에 대한 공동체의 입장 변경을 생각해 보라] 그러나 한 개인이, 자신의 공동체가 스스로 정정하지 않을지언정 사실은 언제나 틀린 것은 아닐까 하는 의문 또한 가질 수 있는가? 이와 같은 질문을 비트겐슈타인의 개념적 틀에서 정립하기란 어렵다는 것은 사실이다. 그것은, 어떤 ‘[객관적] 사실’로서, 우리가 항상 틀린 것은 아닌지에 대한 질문으로 보이는데, 그러한 사실은 존재하지 않기 때문이다.

Does it make any sense to doubt whether a response we all agree upon is ‘correct’? Clearly in some cases an individual may doubt whether the community may correct, later, a response it had agreed upon at a given time. But may the individual doubt whether the community may not in fact always be wrong, even though it never corrects its error? It is hard to formulate such a doubt within Wittgenstein’s framework, since it looks like a question, whether, as a matter of ‘fact’, we might always be wrong; and there is no such fact.

그렇다고 해서 크립키-비트겐슈타인이 의미의 규칙에 대한 전권을 오로지 공동체에 귀속하는 것은 아니다. 이어지는 주석에서 크립키는 의미와 규칙 따르기에 있어 개인이 가지는 자율성의 영역을 보장하는 단서를 남겨 놓는다.

다른 한편으로, 비트겐슈타인의 개념적 틀 안에서도 다음만큼은 여전히 사실이다. 공동체가 언제나 어떤 대답을 내놓았는지에 관한 정보는, 내가 덧셈 문제의 대답을 확정하는 데 있어 전혀 필요하지 않다. 설령 [덧셈의 사용에 관한 공동체의] 정보가 주어졌더라도, 나 혼자서 정당하게 계산을 수행할 수 있다는 사실 또한 우리의 ‘언어게임’의 일부이다. [필자 주: 이를 애쉬의 동조 실험과 비교해 보라.]

On the other hand, within Wittgenstein’s framework it is still true that, for me, no assertions about community responses for all time need establish the result of an arithmetical problem; that I can legitimately calculate the result for myself, even given this information, is part of our ‘language game’.

아마 독자 분은 그래서 도대체 크립키가 하고 싶은 말이 무엇인지 혼란스러울 것이다. 문제는, 필자도 매우 혼란스럽다는 것이다. 그리고 필자 생각에, 크립키 본인도 이 점에 관해서는 혼란을 느낀 듯하다. 크립키의 주석은 다음의 인정으로 맺는다.

나는 이러한 질문들에 대해 어떤 긴장감이 여전히 남아 있을 수 있다고 느낀다. 시간과 지면의 제약, 그리고 내가 변호자 및 해설자의 역할을 버리고 비판자의 입장을 취해야 할지도 모른다는 점 때문에, 나는 이 문제에 대해 더 깊이 논의하지 않기로 했다.

I feel some uneasiness may remain regarding these questions. Considerations of time and space, as well as the fact that I might have to abandon the role of advocate and expositor in favor of that of critic, have led me not to carry out a more extensive discussion.

요점을 정리해보자면 이렇다.

1. 회의주의적 해답을 다음과 같이 이해하는 것은 잘못되었다: “‘68 + 57’에 대해 ‘125’라고 대답하는 것은 옳다”가 참일 필요충분조건은, 공동체가 ‘68 + 57’에 대해 ‘125’라는 일치된 대답을 보인다는 것이다.

2. 회의주의적 해답은 다음과 같이 이해되어야 한다: “‘68 + 57’에 대해 ‘125’라고 대답하는 것은 옳다”가 공동체 안에서 받아들여질 필요충분조건은, 공동체가 ‘68 + 57’에 대해 ‘125’라는 일치된 대답을 보인다는 것이다.

   • 다르게 말해, 공동체가 ‘68 + 57’에 대해 ‘125’라는 일치된 대답을 보인다면, “‘68 + 57’에 대해 ‘125’라고 대답하는 것은 틀렸다”는 발화는 해당 공동체에서 정당하게 받아들여지지 않는다.

3. 2에 대해 다음의 의문이 제기될 수 있다.

   1. 1이 자기순환적이지만 2는 자기순환적이지 않은 이유가 불분명하다.
   2. 어떤 경우에는 공동체가 일치된 대답을 보이는 상황에서도 개인이 정당하게 그 대답이 정녕 올바른지에 관한 의문을 제기할 수 있는 것으로 보인다.

이 의문들은 크립키의 원 논문에서 다소 불명확하게 설명되었고, 실제로 이후 회의주의적 해답에 대해 제기된 비판들은 이들 의문에 초점을 맞춘다. 이에 관해서는 추후에 기회가 된다면 별도의 글로 정리해 보겠다.

---

Is Private Language Possible?

21 Jul 2025

This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.

In the previous post, I examined the Kripke-Wittgenstein paradox. To summarise, the Kripke-Wittgenstein paradox is based on the consideration that there are no normative facts encompassing the infinite cases in which a particular word can be used. From this, Kripke-Wittgenstein draws the following conclusion:

“Speaker A means M by symbol s” corresponds to no fact.

According to Kripke’s reading, Wittgenstein offers a “sceptical solution” to this conclusion. That is, he accepts the above conclusion as it stands—there is no fact corresponding to “Alice means addition by ‘+’“—while explaining how it can be used meaningfully, unlike “Alice’s thoughts are green”. The gist of the explanation is to emphasise the publicity of language: the meaning of language is inextricably linked to the function it has in the community, and therefore discussions of meaning are vacuous at the level of individual speakers but valid at the community level.

1. From the Tractus to the Investigations

Kripke belongs to the so-called “traditional interpretation” school, which sees a stark difference between early Wittgenstein, symbolised by the Tractatus Logico-Philosophicus, and later Wittgenstein, symbolised by the Philosophical Investigations. Kripke summarises the characteristics of the view of language presented in the Tractus as follows:

• Logical atomism. All meaningful propositions are analysed as logical compositions of atomic propositions.
• Picture theory. Atomic propositions and the states of affairs they represent correspond to each other like pictures. When the state of affairs represented by an atomic proposition obtains, the proposition is true.
• Truth-conditional theory. The meaning of a proposition lies in its truth conditions—that is, what state of affairs corresponds to that proposition.
• A priori approach. The characteristics of language outlined above can be inferred through a priori reasoning.

By contrast, Kripke analyses that the Investigations reveals two views of language that contrast with the Tractus.

• Assertability-conditional theory. The meaning of a proposition lies in its assertability conditions—that is, in what circumstances the proposition can be asserted or rejected.¹
• Pragmatism. Consideration of what role or function asserting or rejecting a particular proposition plays in our lives is central to a proper understanding of language.²

Here, assertability-conditional theory can be found in other philosophical positions even before Wittgenstein. Brouwer’s intuitionist mathematics and logical positivism’s verificationism are representative examples. Kripke sees Wittgenstein’s originality as lying in the second characteristic, namely pragmatism. Wittgenstein criticises the word-object correspondence demanded by Frege and others, urging instead that we consider the actual situations in which words are used. To take numbers as an example, Frege argues that there must be objects to which numbers refer.³ However, Wittgenstein mentions actual situations in which numbers are used—counting goods in the marketplace, teachers counting students—and emphasises that in these situations, if the alphabet had been recited instead of numbers, the purpose of the linguistic act would still have been achieved. In short, numbers are not, as Frege would have it, “language that refers to natural numbers” but “language that engages in the activity of counting things”.

2. The Sceptical Solution

From the perspective of Wittgenstein’s later view of language based on assertability-conditional theory, the sceptical argument does not immediately suggest that “Alice means addition by ‘+’” is meaningless. Even if there is no state of affairs corresponding to the proposition, the existence of a state of affairs is not—unlike the truth-conditional view of language—a necessary condition for a proposition to be meaningful.

On the other hand, pragmatism provides a separate necessary condition for “Alice means addition by ‘+’” to be regarded as a meaningful proposition. That is, the proposition must play a useful role in the language game. Kripke explains the role played by this proposition in connection with another thought experiment that appears in the Investigations, the “private language argument”. But before that, let us consider the characteristics of Wittgenstein’s sceptical solution in comparison with the scepticism of Berkeley and Hume.

2.1. Berkeley’s Scepticism

By the expression “sceptical solution”, Kripke collectively refers to arguments with the following characteristics:

1. Present a proposition P that we consider self-evident.
2. Present a “sceptical paradox” that claims that proposition P is in fact contradictory, incomprehensible, or unjustifiable.
3. Nevertheless, explain why we can regard P as a legitimate proposition in everyday life by reinterpreting the meaning of P, despite the sceptical paradox.
4. As a bonus, one can propagate that the meaning of P reinterpreted in 3 is the “real meaning”, the “meaning of ordinary people”, and that the meaning of P rejected in 2 is the “false meaning”, the “meaning misled by philosophers”.

Consider, for example, Berkeley’s idealism. Berkeley points out that what an individual can perceive is only the mental images that occur within him. Therefore, we can never prove the independent existence of ‘external objects’. This is because inferring the existence of external objects from a collection of internal mental images cannot be logically justified. To outline this in accordance with the three stages presented above:

1. We regard the proposition “There is an apple in my hand” as legitimate.
2. However, since what an individual can perceive is limited to internal mental images, the proposition in 1 cannot be justified.
3. Nevertheless, the reason we can regard the proposition in 1 as a legitimate proposition is that the real meaning of the proposition in 1 is actually “I am experiencing red visual sensations, sour olfactory sensations, spherical hard tactile sensations, etc.”

(Kripke clearly shows his distaste for this kind of argument in the original paper. In my view, this may stem from resentment at the way American functionalist philosophers have—in Kripke’s view—unjustifiably pushed such “sceptical solutions”.)

2.2. Hume’s Scepticism

As another example, consider Hume’s scepticism about causation. Hume asks whether there is empirical evidence for the proposition “Event A is the cause of event B” that can be presented beyond “Event A and event B occurred in succession”. Such evidence would consist of observations of causal nexuses that actually exist in nature, but Hume points out that observations of such nexuses are beyond the realm of human experience. What we can experience is only regularities of events. That is, when we observe several times that when an event token belonging to event type A occurs, an event token belonging to event type B occurs, we say that causation obtains between types A and B.

Kripke points out that the conclusion of Hume’s causal scepticism is the impossibility of private causation. If, as Hume argues, causation is a statement about regularities between two event types, then it is meaningless to discuss causation for event tokens that are so peculiar that they cannot even be typed. For example, the proposition “Helium was generated by the collision of a meson and a trion” is meaningful as a statement that there are several particle tokens corresponding to the types “meson”, “trion”, and “helium”, and that regularity was discovered by colliding these particles repeatedly. However, if there are particles X and Y that exist only once in the universe, then even if particle Z were generated by colliding them, we could not say “Z was generated because of the collision of X and Y”. All we can say is “Z was generated immediately after the collision of X and Y”.

Kripke suggests reading Wittgenstein’s private language argument with Hume’s argument in mind. According to Kripke’s reading, the flow of arguments between Wittgenstein and Hume is very similar.

3. The Private Language Argument

3.1. Traditional Interpretation

Now let us examine the private language argument proper. Wittgenstein presents the following case in the Investigations. Alice has difficulty expressing a particular emotion she feels in language. So she gives that emotion the name ‘S’ and writes “feeling S” in her diary whenever she feels that emotion. After several years, Alice feels that she has become familiar with the use of ‘S’. Here Wittgenstein poses a question. Can we say that Alice has given her own meaning to the symbol ‘S’, that is, that she has formed a private language?

Wittgenstein’s answer is negative. However, as Kripke also points out, Wittgenstein’s reasons for rejecting private language were puzzling to interpreters. The most standard interpretation is as follows. The reason Wittgenstein argues that private language is impossible is that an individual alone cannot receive confirmation that he is using this symbol correctly. For instance, Alice can escape from scepticism about whether the emotion she calls ‘S’ today really matches the emotion she called ‘S’ years ago. The only way Alice can escape from solipsistic scepticism is to belong to a linguistic community that uses unified symbols and receive confirmation from them that her use of symbols is correct.

However, this argument is, as numerous scholars including Ayer have long pointed out, extremely flimsy. For instance, when I am uncertain whether I may now call my emotion ‘happiness’, does receiving confirmation from others saying “You are indeed happy now” improve the situation? How can we be certain that their judgement is correct? Rather, the reverse argument that “Even if others tell me that I am now in a state of happiness, I cannot be certain that their judgement is really correct, so I myself must check my inner state” is more plausible. Moreover, considering that community confirmation is also ultimately received through an individual’s private senses, including sight and hearing, there is essentially no difference between an individual checking his own inner state and receiving confirmation from the community.

3.2. Kripke’s Interpretation

However, Kripke argues that understanding the private language argument in this way is a misunderstanding. Wittgenstein’s intention is not to banish private language to the realm of impossibility. Rather, according to the sceptical paradox, all language—whether private or public—is impossible. Wittgenstein seeks to rescue the possibility of language in response to this. Because the strategy of this rescue appeals to the publicity of language, private language remains in the realm of impossibility.

Wittgenstein’s “solution” to the sceptical paradox can be understood by considering the following three cases. The first is the case where Alice is the only person in this universe who uses the ‘+’ symbol. Alice uses ‘+’ according to her own inclination towards ‘+’ (of course, this is a tautological statement). From time to time Alice will make calculation errors with ‘+’, and in extreme cases when she is under the influence of drugs, she may use ‘+’ in bizarre ways like quaddition. But in all cases Alice will believe that she is using ‘+’ according to legitimate rules. And according to the Kripke-Wittgenstein paradox, there are no facts that refute Alice’s belief, so this is all that can be said about Alice’s use of ‘+’. To borrow Kripke’s words:

It is part of our language game of speaking of rules that a speaker may, without ultimately giving any justification, follow his own confident inclination that this way (say, responding ‘125’) is the right way to respond, rather than another way (e.g. responding ‘5’). That is, the ‘assertability conditions’ that license an individual to say that, on a given occasion, he ought to follow his rule this way rather than that are, ultimately, that he does what he is inclined to do. […] All we can say, if we consider a single person in isolation, is that our ordinary practice licenses him to apply the rule in the way it strikes him.

(Italics are the original emphasis, bold is my emphasis. The statement “It is part of our language game of speaking of rules that a speaker may say…” can be understood by analogy to “Castling is part of chess”, showing that such statements are no different from part of the definition of the language game of ‘speaking of rules’. That is, a language game in which such speech is not possible cannot be called the language game of ‘speaking of rules’.)

But as Kripke points out, this is not what we expect from the language game of ‘speaking of rules’. For instance, imagine someone playing chess alone against a wall. He sets a chess clock for one hour and makes the first move as white, then waits for his “opponent”, the wall, to respond. But the “opponent” does not respond and loses by timeout after an hour. Therefore white always wins. Let us call this private chess. Private chess satisfies all the rules of chess, but it is not chess at all. At least, it is not the chess we expect. In normal chess, white must be able to lose. Similarly, private rules, even if they satisfy the rules of the ‘rule-speaking’ language game, are not the ‘rule-speaking’ language game we expect. In the normal ‘rule-speaking’ language game, the speaker must be able to make mistakes in following rules.

Now let us move on to the next case. The second is the case where Alice and Smith are the two people in this universe who use the ‘+’ symbol. Their inclinations towards ‘+’ may match or diverge. If Alice answers ‘125’ and Smith answers ‘5’ to ‘68 + 57’, Alice will point out that Smith is not using ‘+’ according to the correct rule. However, this pointing out is something Smith can also do to Alice. And according to the Kripke-Wittgenstein paradox, there are no facts corresponding to which of their pointings out is more correct, so this is all that can be said about their use of ‘+’.

Finally, there is the case where those who use the ‘+’ symbol in this universe form a sufficiently large community, not just Alice. In this case, although there may initially be speakers who use ‘+’ in ways that conflict with the community, these speakers will gradually disappear from the community because they interfere with the function that the ‘+’ symbol performs in the community (here the reason why Wittgenstein values pragmatic considerations becomes apparent). For example, one of the functions of ‘+’ is to manage accounts. However, people who use ‘+’ like quaddition will manage accounts in a non-standard way, which gives those who use ‘+’ like addition reason not to delegate the use of ‘+’ to them any longer. In this way, the sustained process of approval and expulsion based on linguistic function converges to a community of speakers who follow consistent rules. Thus “Alice means addition by ‘+’” is useful as an expression that the community approves of Alice’s use of ‘+’, and therefore meaningful.

Note that what Kripke calls inversion of a conditional is employed here as a philosophical technique. Inversion of a conditional means asserting “if not Q then not P” instead of the proposition “if P then Q”. Of course, the two conditionals are contrapositives and therefore extensionally equivalent, but they differ in setting the priority between P and Q. In the former case, the obtaining of P determines the obtaining of Q, whereas in the latter case, the obtaining of Q determines the obtaining of P.

According to the traditional view of language, the fact that speakers use the same symbol in the same way is explained by the fact that they assign the same meaning to that symbol. According to this view, the following conditional obtains:

Alice means addition by ‘+’ -> Alice answers ‘125’ to ‘68 + 57’

However, the sceptical solution inverts this conditional as follows:

Alice does not answer ‘125’ to ‘68 + 57’ -> Alice does not mean addition by ‘+’

More precisely, considering that the sceptical solution is based on assertability conditions rather than truth conditions:

Alice does not answer ‘125’ to ‘68 + 57’ -> In the context of the language game of ‘speaking of rules’, we cannot say “Alice means addition by ‘+’”.

Of course, we would not immediately draw the extreme conclusion that Alice does not mean addition by ‘+’ simply because she did not answer ‘125’ to ‘68 + 57’. We would probably think that Alice made a calculation error. However, if Alice uses the ‘+’ symbol in a very unacceptable way, such as answering ‘5’ to ‘68 + 57’, we would withdraw the statement that she means addition by ‘+’.

In short, Kripke-Wittgenstein understands the process by which the language game of ‘speaking of rules’ transforms from a trivial language game to a useful language game as an emergent process through community.

4. Characteristics of the Sceptical Solution

4.1. Form of Life

The legitimacy of the sceptical solution is based on the fact that language users converge on performing the same operation, namely addition, with ‘+’. If individuals each gave different answers to ‘68 + 57’—A giving 125, B giving 7, C giving 58—the sceptical solution could not obtain.

According to Kripke’s reading, Wittgenstein calls the agreement we show in the use of symbols (answering ‘125’ to ‘68 + 57’) and the series of activities thereby made possible (thus being able to pay for a computer costing £125,000 in instalments of £68,000 and £57,000) a “form of life”. According to Wittgenstein, the reason we can give the consistent answer ‘125’ to ‘68 + 57’ is not because we mean the same operation, namely addition, by ‘+’. Rather, the reason we can say that we mean addition by ‘+’ is that we are participating in a language game based on a common form of life. In Wittgenstein’s analysis, the fact that we give the consistent answer ‘125’ to ‘68 + 57’ is simply a given fact, not a phenomenon to be explained.

(Personal note: Compare Kripke’s footnote 76 with the logical alien thought experiment.)

76. Can we imagine forms of life other than our own, that is, can we imagine creatures who follow rules in bizarre quus-like ways? It seems to me that there may be a certain tension in Wittgenstein’s philosophy here. On the one hand, it would seem that Wittgenstein’s paradox argues that there is no a priori reason why a creature could not follow a quus-like rule, and thus in this sense we ought to regard such creatures as conceivable. On the other hand, it is supposed to be part of our very form of life that we find it natural and, indeed, inevitable that we follow the rule for addition in the particular way that we do. (See §231: ““But surely you can see . . . ?” That is just the characteristic expression of someone who is under the compulsion of a rule.”) But then it seems that we should be unable to understand ‘from the inside’ (cf. the notion of ‘Verstehen’ in various German writers) how any creature could follow a quus-like rule. We could describe such behaviour extensionally and behaviouristically, but we would be unable to find it intelligible how the creature finds it natural to behave in this way. This consequence does, indeed, seem to go with Wittgenstein’s conception of the matter.

Of course we can define the quus function, introduce a symbol for it, and follow the appropriate rule for computing its values. I have done so in this very essay. What it seems may be unintelligible to us is how an intelligent creature could get the very training we have for the addition function, and yet grasp the appropriate function in a quus-like way. If such a possibility were really completely intelligible to us, would we find it so inevitable to apply the plus function as we do? Yet this inevitability is an essential part of Wittgenstein’s own solution to his problem.

The point is even stronger with respect to a term like ‘green’. Can we grasp how someone could be presented with a number of green objects, and be told to apply the term ‘green’ just to ‘things like these’, and yet apply the term learnt as if it meant ‘grue’? It would seem that if we find our own continuation to be inevitable, in some sense we cannot.

4.2. External Criteria for Psychological Phenomena

The sceptical solution that agreement in the use of symbols is the very content of the statement that a speaker uses that symbol with a particular meaning leads to the following statement by Wittgenstein about the philosophy of mind:

“An ‘inner process’ stands in need of outward criteria.” (§580)

Consider the case where a young child learns the two words ‘table’ and ‘hurt’. In the former case, if the child points to a table and says ‘table’, the parents will approve the utterance, and if they point to a chair and say ‘table’, they will tell them it is wrong. Through this process, the child comes to agree with the linguistic community in the use of the symbol ‘table’. However, in the case of ‘hurt’, this is impossible. The child cannot directly reveal the emotion they experience to receive confirmation that this corresponds to ‘hurt’. Instead, the child will show external behaviour such as bursting into tears or frowning, and based on that behaviour, the parents will decide whether the child’s utterance of ‘hurt’ is legitimate. If this is the meaning of §580, then §580 is not—as traditionally considered—a premise that Wittgenstein prepares for the private language argument, but rather an implication of the sceptical paradox, just like the private language argument.

In this regard, Kripke presents both liberal and strict interpretations of §580. If §580 is interpreted strictly, each expression belonging to psychological language must have a natural expression associated with that expression. For example, the natural expression associated with pain is grimacing. Therefore, if a child learning language grimaces and says “Ow!”, we approve it. In this way, all psychological expressions have natural behaviours associated with them, and the observability of these behaviours prevents these expressions from degenerating into private language.

However, Kripke presents a more liberal interpretation. According to this, what requires external criteria is not individual psychological expressions but “psychological language” itself. Kripke sees this as a more accurate consideration of how psychological language operates. If there is a speaker who shows sufficient mastery of psychological expressions that have clear external criteria—for instance, pain—we judge that they have mastered psychological language in general, and therefore, if they state that they have grasped a particular emotion or quale in their inner state, even if that emotion and quale have no external criteria, we acknowledge that statement as legitimate. (In my view, “I have consciousness” would seem to be an example of such a statement.)

For this, see footnotes 81, 82, and 83 in the main text. (Incidentally, these three footnotes are substantial enough to constitute a section on their own…)

4.3. Is the Sceptical Solution Circular?

At the end of the paper, Kripke warns that the sceptical solution can be misunderstood as follows:

That a linguistic community means addition by ‘+’ is that the majority of members of that community use ‘+’ as addition.

Or, more precisely:

That the operation a linguistic community means by ‘+’ is f means that the majority of members of that community answer f(x, y) to ‘x + y’.

According to Kripke, this is a mistaken understanding. The sceptical solution interpreted in this way is virtually no different from a dispositional analysis at the community level, and therefore has—if not all, then at least some of—the difficulties faced by dispositional analysis. Moreover, the above interpretation provides truth conditions for “a linguistic community means … by …”. This fundamentally misses Wittgenstein’s project of moving from truth-conditional theory to assertability-conditional theory.

Kripke emphasises that Wittgenstein’s sceptical solution does not seek to provide new truth conditions for “a linguistic community means … by …” but merely focuses on the environment that makes such statements possible and the advantages gained by using such statements. To quote from the text:

What follows from these assertability conditions is not that the answer everyone gives to an addition problem is, by definition, the correct one, but rather the platitude that, if everyone agrees upon a certain answer, then no one will feel justified in calling the answer wrong.

Kripke probably (accurately) predicted that this passage would be the subject of much criticism. So he later added a long footnote 87. Footnote 87 is a sketch of an explanation against the criticism that Wittgenstein’s sceptical solution is circular or still falls into the infinite regress of scepticism.

87. If Wittgenstein had been attempting to give a necessary and sufficient condition to show that ‘125’, not ‘5’, is the ‘right’ response to ‘68+ 57’, he might be charged with circularity. For he might be taken to say that my response is correct if and only if it agrees with that of others. But even if the sceptic and I both accept this criterion in advance, might not the sceptic maintain that just as I was wrong about what ‘+’ meant in the past, so I was wrong about ‘agree’? Indeed, to attempt to reduce the rule for addition to another rule - “Respond to an addition problem exactly as others do!” - falls foul of Wittgenstein’s strictures on ‘a rule for interpreting a rule’ just as much as any other such attempted reduction. Such a rule, as Wittgenstein would emphasise, also describes what I do wrongly: I do not consult others when I add. (We wouldn’t manage very well, if everyone had to follow a rule of the proposed form - no one would respond without waiting for everyone else.)

What Wittgenstein is doing is describing the utility in our lives of a certain practice. Necessarily he must give this description in our own language. As in the case of any such use of our language, a participant in another form of life might apply various terms in the description (such as “agreement”) in a non-standard ‘quus-like’ way. Indeed, we may judge that those in a given community ‘agree’, while someone in another form of life would judge that they do not. This cannot be an objection to Wittgenstein’s solution unless he is to be prohibited from any use of language at all.

However, several questions still remain. First, there remains a question about whether Kripke’s defence that “This cannot be an objection to Wittgenstein’s sceptical solution” is valid. Second, even if the intention of the sceptical solution is not to provide truth conditions for meaning statements (the answer everyone gives to a particular addition problem is the correct answer) but to describe the function of meaning statements (if everyone agrees upon a certain answer, then no one will feel justified in calling the answer wrong), questions may remain about whether the latter description is correct. That is, if everyone really agrees upon a certain answer, will no one feel justified in calling the answer wrong? Regarding this, let us look at Kripke’s following footnote:

Does it make any sense to doubt whether a response we all agree upon is ‘correct’? Clearly in some cases an individual may doubt whether the community may correct, later, a response it had agreed upon at a given time. [Author’s note: Think of the community’s change of position on “adultery is a crime”] But may the individual doubt whether the community may not in fact always be wrong, even though it never corrects its error? It is hard to formulate such a doubt within Wittgenstein’s framework, since it looks like a question, whether, as a matter of ‘fact’, we might always be wrong; and there is no such fact.

However, this does not mean that Kripke-Wittgenstein attributes full authority over the rules of meaning solely to the community. In the following footnote, Kripke leaves a clause guaranteeing the realm of autonomy that individuals have in meaning and rule-following:

On the other hand, within Wittgenstein’s framework it is still true that, for me, no assertions about community responses for all time need establish the result of an arithmetical problem; that I can legitimately calculate the result for myself, even given this information, is part of our ‘language game’. [Author’s note: Compare this with Asch’s conformity experiments.]

The reader will probably be confused about what exactly Kripke is trying to say. The problem is that I too am very confused. And in my view, Kripke himself seems to have felt confusion about this point. Kripke’s footnote concludes with the following admission:

I feel some uneasiness may remain regarding these questions. Considerations of time and space, as well as the fact that I might have to abandon the role of advocate and expositor in favour of that of critic, have led me not to carry out a more extensive discussion.

To summarise the key points:

1. It is wrong to understand the sceptical solution as follows: The necessary and sufficient condition for “‘125’ is the right answer to ‘68 + 57’” to be true is that the community shows a unanimous answer of ‘125’ to ‘68 + 57’.

2. The sceptical solution should be understood as follows: The necessary and sufficient condition for “‘125’ is the right answer to ‘68 + 57’” to be accepted within the community is that the community shows a unanimous answer of ‘125’ to ‘68 + 57’.

   • Put differently, if the community shows a unanimous answer of ‘125’ to ‘68 + 57’, then the utterance “‘125’ is the wrong answer to ‘68 + 57’” will not be legitimately accepted in that community.

3. The following questions can be raised about 2:

   1. It is unclear why 1 is circular but 2 is not circular.
   2. In some cases, it seems that an individual can legitimately raise questions about whether an answer is really correct even in situations where the community shows a unanimous answer.

These questions were explained somewhat unclearly in Kripke’s original paper, and indeed the criticisms subsequently raised against the sceptical solution focus on these questions. I shall try to organise these in a separate post if the opportunity arises in the future.

---

불 대수 구조의 아이디얼과 필터

18 Jul 2025

불 대수

불 대수_{boolean algebra}는 거짓을 의미하는 $0$과 참을 의미하는 $1$ 위에서 정의되는 $\lor, \land, \lnot$ 등의 논리 연산으로 이루어진 대수이다.

$a$	$b$	$a \lor b$	$a \land b$	$\lnot a$
$0$	$0$	$0$	$0$	$1$
$0$	$1$	$1$	$0$	$1$
$1$	$0$	$1$	$0$	$0$
$1$	$1$	$1$	$1$	$0$

여기서 $0$과 $1$을 거짓과 참을 나타내는 형식적 기호로서가 아닌, 대소 비교가 가능한 실제 수로서 간주하면, $\lor$는 $\max$에, $\land$은 $\min$에, $\lnot$은 켤레 연산 $\bar{(\cdot)}: 0 \mapsto 1, 1 \mapsto 0$에 대응됨을 확인할 수 있다.

$a$	$b$	$\max (a, b)$	$\min (a, b)$	$\bar{a}$
$0$	$0$	$0$	$0$	$1$
$0$	$1$	$1$	$0$	$1$
$1$	$0$	$1$	$0$	$0$
$1$	$1$	$1$	$1$	$0$

이에 착안하여, 우리는 불 대수의 정의역을 $\lbrace 0, 1 \rbrace$에서 $[0, 1]$로 자연스럽게 확장할 수 있다. 가령 $0.2 \lor 0.7 = 0.7, 0.3 \land \lnot(0.9) = 0.1$와 같이 말이다. 이 생각을 발전시켜 보면, 적절한 순서 관계가 주어진 집합 위에서는 불 대수와 구조적으로 비슷한 연산을 정의할 수 있으며, 반대로 불 대수와 구조적으로 비슷한 연산이 정의된 집합에는 적절한 순서 관계를 줄 수 있을 듯하다. 이것이 불 대수 구조의 발상이다.

정의. 어떤 두 원소 $0$과 $1$을 가지는 집합 $A$ 위에서 정의된 이항연산 $\lor, \land$과 단항연산 $\lnot$이 다음의 공리를 만족할 때, $(A, 0, 1, \lor, \land, \lnot)$을 불 대수 구조_{Boolean algebraic structure}라고 부른다.

공리	$\lor$	$\land$
결합	$a \lor (b \lor c) = (a \lor b) \lor c$	$a \land (b \land c) = (a \land b) \land c$
교환	$a \lor b = b \lor a$	$a \land b = b \land a$
분배	$a \lor (b \land c) = (a \lor b) \land (a \lor c)$	$a \land (b \lor c) = (a \land b) \lor (a \land c)$
항등원	$a \lor 0 = a$	$a \land 1 = a$
쌍역원	$a \lor \lnot a = 1$	$a \land \lnot a = 0$
흡수	$a \lor (a \land b) = a$	$a \land (a \lor b) = a$

Remark.

• 흡수법칙은 나머지 다섯 공리로부터 증명이 가능하다.

• “쌍역원”이라는 표현은, 원래 $x$에 곱의 역원 $x^{-1}$을 곱하면 곱의 항등원 $1$이 나오고, 합의 역원 $-x$를 더하면 합의 항등원 $0$이 나와야 하지만, 불 대수 구조의 경우 $x \lor \lnot x$의 결과가 $\lor$의 항등원 $0$이 아닌 $\land$의 항등원 $1$이고, $x \land \lnot x$의 결과가 $\land$의 항등원 $1$이 아닌 $\lor$의 항등원 $0$이기 때문에, 혼동의 여지를 줄이고자 도입했다.

서론의 두 예시는 불 대수 구조임을 확인하라. 또다른 예시로, 집합 $X = \lbrace p, q, r \rbrace $의 멱집합 $\mathcal{P}(X)$를 보자. 다음과 같이 두었을 때 $\mathcal{P}(X)$는 불 대수 구조가 됨을 확인하라.

• $a \lor b = a \cup b$
• $a \land b = a \cap b$
• $\lnot a = X \setminus a$
• $1 = X$
• $0 = \varnothing$

$X$가 임의의 집합일 때에도 일반적으로 $X$의 멱집합은 불 대수 구조를 이룬다.

불 대수 구조에는 자연스러운 방식으로 부분순서_{partial order}를 줄 수 있다.

정리. $A$가 불 대수 구조라고 하자. 다음의 이항관계를 정의한다.

\[a \leq b \iff a = a \land b\]

$\leq$는 $A$의 부분순서이다. $1$과 $0$은 각각 $\leq$의 최대 원소, 최소 원소이다. $\lor$와 $\land$는 각각 $\leq$에 대한 상한과 하한을 내놓는 연산이다.

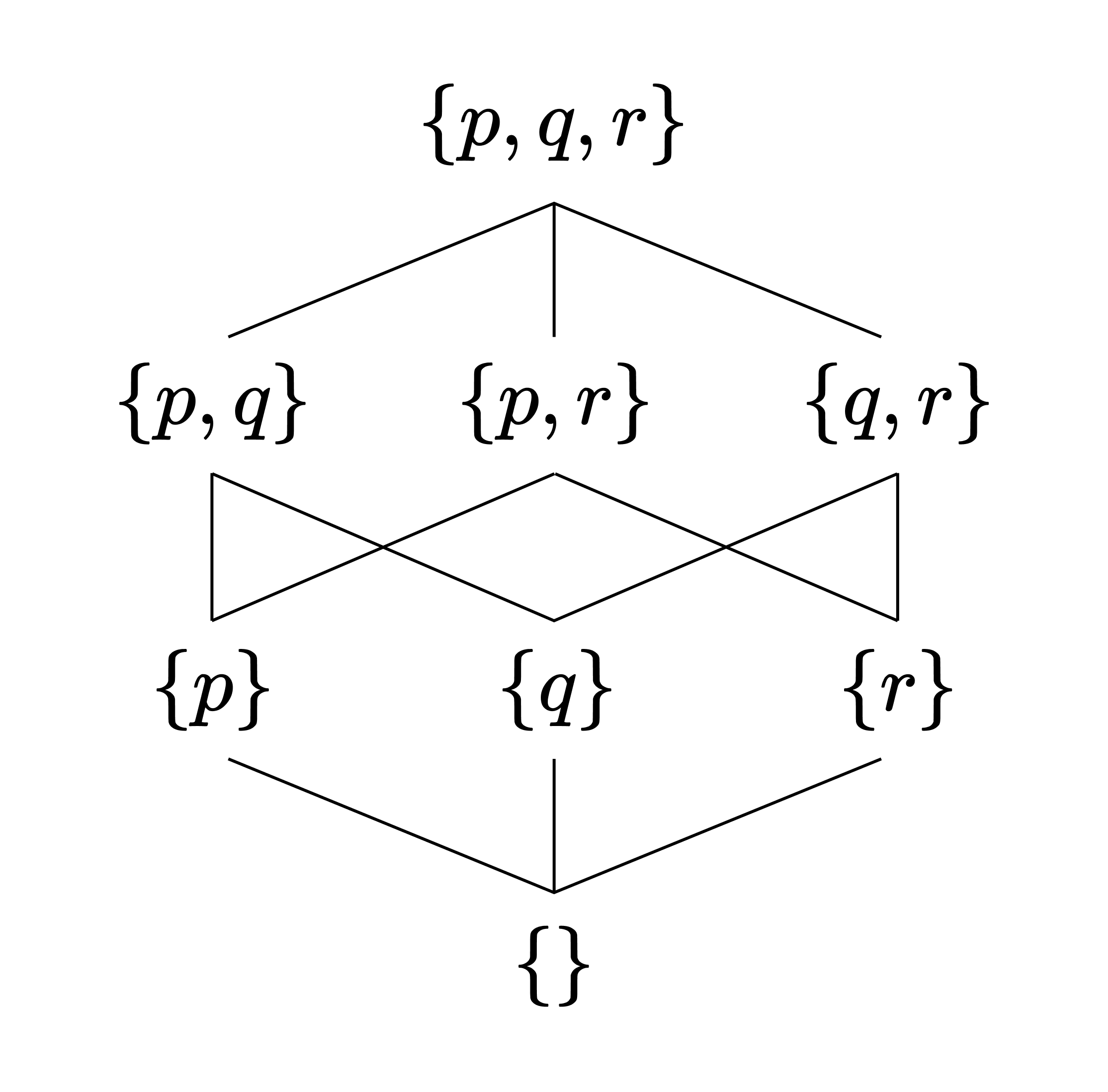
마찬가지로 증명은 생략한다. 이와 같이 불 대수 구조 $A$ 위에는 자연스러운 방식으로 부분순서 $\leq$를 줄 수 있으므로, $\leq$에 따라 $A$의 하세 다이어그램_{Hasse diagram}을 그릴 수 있다. 일례로 앞서 본 $X = \lbrace p, q, r\rbrace $에 대해 $\mathcal{P}(X)$가 이루는 불 대수 구조를 보자.

\[a \leq b \iff a = a \land b \iff a = a \cap b \iff a \subseteq b\]

이므로, 이 경우 불 대수 구조의 하세 다이어그램은 집합의 포함 다이어그램과 같다.

불 환

불 대수 구조는 두 개의 연산과, 각 연산에 해당되는 항등원을 요구한다는 점에서 환_ring과 정의가 비슷하다. 이는 단순한 우연이 아니다.

정의. 환 $R$이 불 환_{Boolean ring}이라는 것은, 임의의 $x \in R$에 대해 $x^2 = x$라는 것이다.

불 대수 구조와 불 환은 일대일 대응된다. 즉, 다음이 성립한다.

정리. $(R, 0, 1, +, \cdot)$가 불 환이라면, $(R, 0, 1, \lor, \cdot, (\cdot)^{-1})$은 불 대수 구조이다. 여기서 $\lor, \lnot$은 다음과 같이 정의된다.

\[\begin{gather} x \lor y = x + y + xy \\ \lnot x = 1 + x \end{gather}\]

역으로, $(A, 0, 1, \lor, \land, \lnot)$이 불 대수 구조라면 $(A, 0, 1, +, \land)$은 불 환이다. 여기서 $+$는 다음과 같이 정의된다.

\[x + y = (x \lor y) \land \lnot (x \land y)\]

증명은 공리를 따라 계산해 보면 되므로 생략한다.

아이디얼

대수학에서 다음의 정의를 상기하자.

정의. 환 $R$에 대해 공집합이 아닌 $I \subseteq R$이 아이디얼_ideal이라는 것은, $I$가 덧셈에 대해 군을 이루며, 임의의 $a \in R$과 $x \in I$에 대해 $ax \in I$라는 것이다. 즉, $aI \subseteq I$이다.

불 대수 구조와 불 환 대응에서 드러난 유사성에 착안하여, 다음과 같이 정의하자.

정의. 불 대수 구조 $A$에 대해 공집합이 아닌 $I \subseteq A$가 아이디얼이라는 것은, $I$가 $\lor$에 대해 닫혀 있고, 임의의 $a \in A$와 $x \in I$에 대해 $a \land x \in I$라는 것이다. 즉, $a \land I \subseteq I$이다.

예를 들어 다음의 색칠된 영역은 $\mathcal{P}(\lbrace p, q, r\rbrace )$의 아이디얼이다.

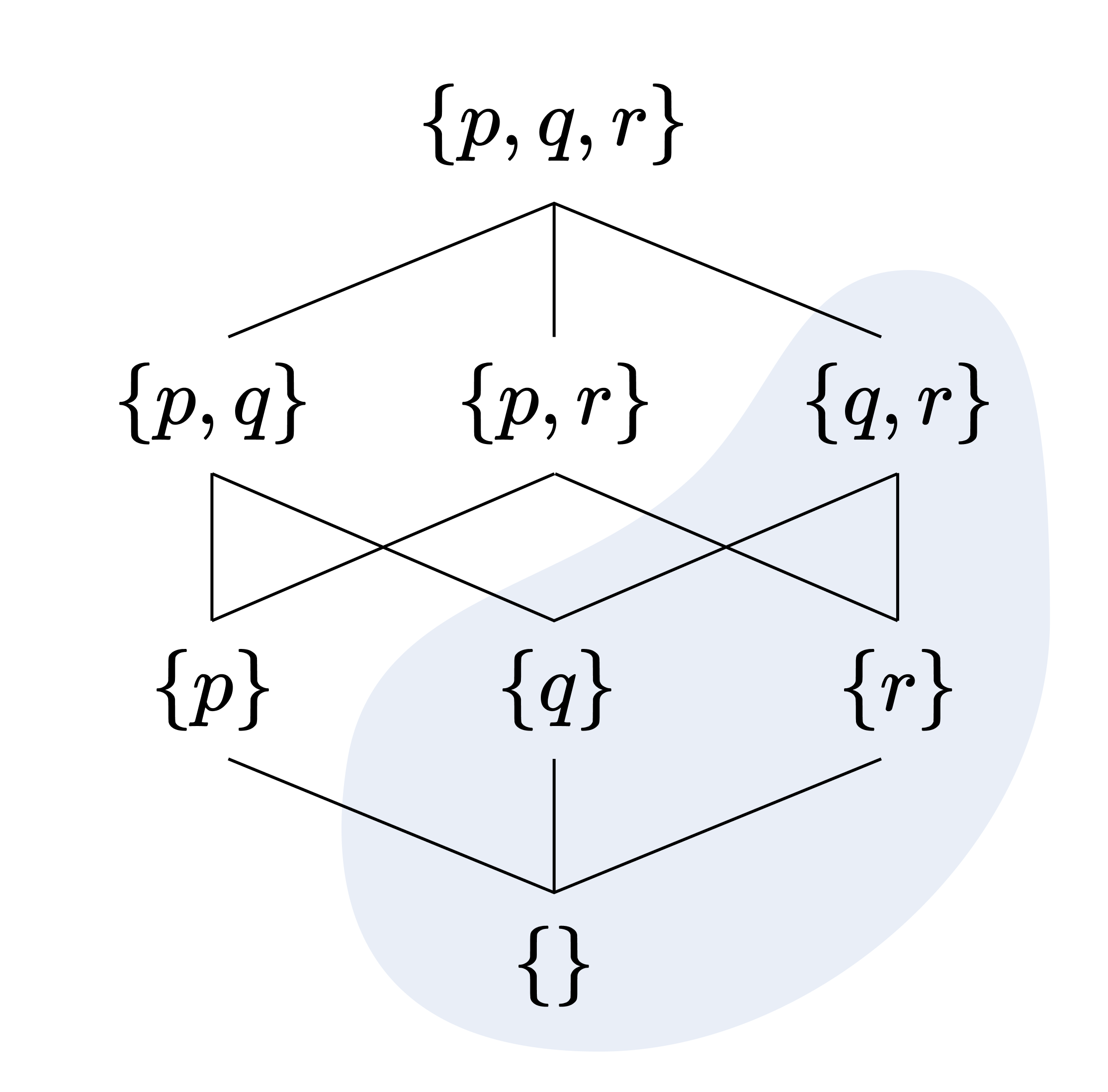
불 대수 구조를 불 환에 대응시키면, $I$가 전자에서 아이디얼이라는 것은 곧 후자에서 아이디얼이라는 것과 같다. 즉 다음이 성립한다.

정리. 불 대수 구조 $A$에 대해 $I \subseteq A$가 (불) 아이디얼일 필요충분조건은, 대응되는 불 환 $A$에서 $I$가 (환) 아이디얼인 것이다.

따라서 불 대수 구조에서도 소 아이디얼_{prime ideal}과 극대 아이디얼_{maximal ideal}을 정의할 수 있다.

정의. $I$가 불 대수 구조 $A$의 아이디얼이라고 하자. $I$가 소 아이디얼이라는 것은, 임의의 $a, b \in A$에 대해, $a \land b \in I$라면 $a \in I$이거나 $b \in I$라는 것이다. $I$가 극대 아이디얼이라는 것은, $J$가 $I$를 엄격히 포함하는 아이디얼일 때, $J = A$라는 것이다.

이들 개념 또한 불 환의 소 아이디얼과 극대 아이디얼에 정확히 상응한다. 앞서 본 아이디얼의 예시는 소 아이디얼인 동시에 극대 아이디얼임을 확인하라. 곧 드러나듯이, 이는 우연이 아니다.

몇 가지 사실을 관찰해 보자. $I \subset A$가 아이디얼이라고 하자.

• 임의의 $a \in I$에 대해, 아이디얼의 정의로부터 $a \land \lnot a = 0 \in I$임이 따라 나온다. 따라서 불 대수의 아이디얼은 항상 $0$을 원소로 가진다.

• 만약 $1 \in I$라면, 임의의 $a \in A$에 대해 $1 \land a = a \in I$임이 따라 나온다. 따라서 $1$을 원소로 가지는 아이디얼은 전체 구조가 유일하다.

• $I$가 소 아이디얼이라면, 임의의 $a \in A$에 대해 $a \land \lnot a = 0 \in I$이므로, $a \in I$ 또는 $\lnot a \in I$이다. 즉, 소 아이디얼은 언제나 임의의 원소 또는 그 부정을 포함한다.

• $I$가 극대 아이디얼이라고 하자. 만약 어떤 $a \in A$가 존재하여 $a \not\in I, \lnot a \not\in I$라면 $I \cup \lbrace x \land a : x \in A \rbrace$가 $I$를 엄격히 포함하며 $A$ 전체는 아닌 아이디얼이므로 $I$는 극대가 아니다. 따라서 극대 아이디얼 또한 언제나 임의의 원소 또는 그 부정을 포함한다.

위 사실로부터 조금의 추론을 거치면 다음을 알 수 있다.

정리. $A$가 불 대수 구조이고 $I$가 $A$의 아이디얼이라고 하자. 다음은 동치이다.

• $I$는 소 아이디얼이다.
• $I$는 극대 아이디얼이다.
• 임의의 $x \in A$에 대해, $x \in I$이거나 $\lnot x \in I$이다.

필터

필터_filter에 관해서는 이전 글에서 다룬 바가 있다. 정의를 상기해 보자.

정의. $X$가 집합이라고 하자. $X$의 부분집합들로 이루어진 집합 $\mathcal{F}$가 다음을 만족할 때, $X$의 필터라고 부른다.

1. $X \in \mathcal{F}$
2. $\varnothing \not\in \mathcal{F}$
3. 상위집합 닫힘: $A \in \mathcal{F}, A \subset B \implies B \in \mathcal{F}$
4. 유한 교집합 닫힘: $A, B \in \mathcal{F} \implies A \cap B \in \mathcal{F}$

이 정의를 불 대수 구조로 옮기면 다음과 같다.

정의. 불 대수 구조 $A$에 대해 $F \subseteq A$가 필터라는 것은, $F$가 $\land$에 대해 닫혀 있고, 임의의 $a \in A$와 $x \in I$에 대해 $a \lor x \in I$라는 것이다. 즉, $a \lor I \subseteq I$이다.

$\land$에 대해 닫혀 있음이 기존의 “유한 교집합 닫힘” 조건에 해당하고, $a \lor I \subseteq I$가 기존의 “상위집합 닫힘” 조건에 해당한다. 특히 $a \lor I \subseteq I$는, 불 대수 구조를 $\leq$ 방향으로 흐르는 일련의 물의 흐름으로 생각했을 때, $x \in I$에서 잉크를 떨어뜨리면 잉크가 퍼져나가는 영역이 모두 $I$에 포섭된다는 의미이다 (이를 이전 글에서 든 잉크의 예시와 비교해 보라). 예를 들어 다음의 색칠된 영역은 $\mathcal{P}(\lbrace p, q, r\rbrace )$의 필터이다.

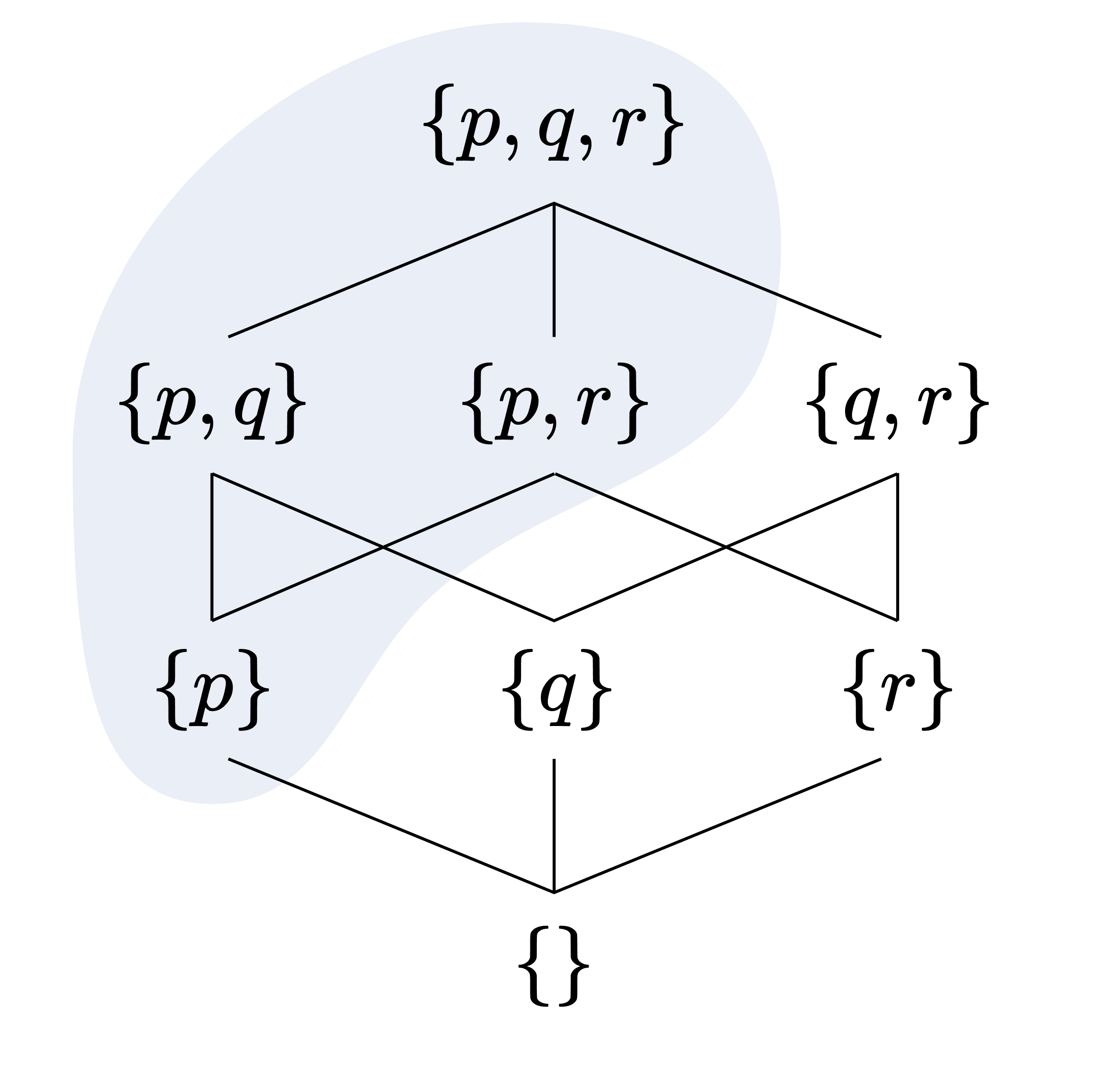
아이디얼과 필터의 쌍대성

아이디얼과 필터의 정의를 비교해 보면 흥미로운 사실을 발견할 수 있다. 한쪽 정의에서 $\land$과 $\lor$을 맞바꾸면 정확히 다른 쪽 정의가 된다. 이를 두고, 아이디얼과 필터는 서로 쌍대_dual라고 말한다.

쌍대성으로 인해, 한쪽 개념에 대해 증명된 사실은 자연스럽게 다른 쪽 개념에서도 성립한다. 일례로 다음이 성립한다.

정리. $A$가 불 대수 구조이고 $F$가 $A$의 필터라고 하자. 다음은 동치이다.

• $x \lor y \in F$라면 $x \in F$이거나 $y \in F$이다.
• $G$가 $F$를 엄격히 포함하는 필터라면 $G = A$이다.
• 임의의 $x \in A$에 대해, $x \in F$이거나 $\lnot x \in F$이다.

여기서 첫 번째 조건을 만족하는 필터를 소 필터, 두 번째 조건을 만족하는 필터를 극대 필터라고 부른다. 아이디얼의 경우와 달리 필터의 경우에는 세 번째 조건을 만족하는 필터에도 초필터_ultrafilter라는 이름이 붙어있다 (마찬가지로 이전 글 참조).

초필터를 사용한 불 대수 구조의 불 대수화

일반적인 불 대수 구조는, 우리에게 익숙한 불 대수와는 달리, 각각의 원소가 참 또는 거짓으로 이분화되지 않는다. $p$는 $p \land q$에 비해 $1$(참)로부터 같거나 더 가까운 “거리”만큼 떨어져 있지만, 그 자체로는 $0$도 아니고 $1$도 아니다.

그러나 불 대수 구조 $A$의 초필터, 또는 소 아이디얼이 주어졌을 때, 해당 필터(아이디얼)에 속하는 여부에 따라 $A$의 원소들을 “참” 또는 “거짓”으로 이분화할 수 있다. 앞서 본 아이디얼의 예시(왼쪽)와 필터의 예시(오른쪽)을 다시 보자. 왼쪽은 소 아이디얼이고, 오른쪽은 초필터이다.

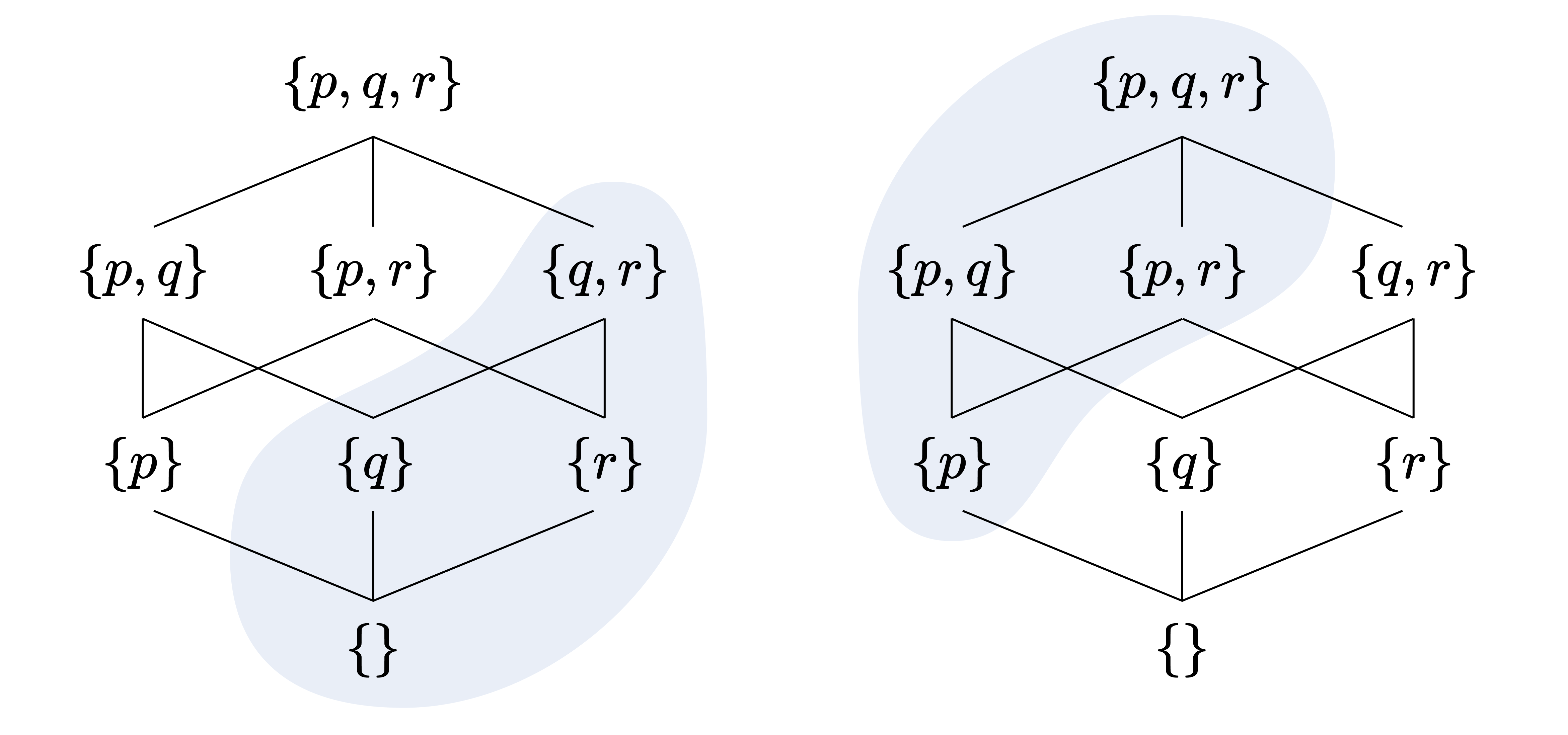
둘은 정확히 서로의 여집합임에 주목하라. 일반적으로 다음이 성립한다.

정리. 불 대수 구조 $A$의 부분집합 $I$에 대해, $I$가 소(극대) 아이디얼일 필요충분조건은 $A \setminus I$가 초(소, 극대) 필터인 것이다.

이에 착안하여, $A$의 원소 중 소 아이디얼 $I$에 속하는 원소는 $0$에, 속하지 않는 원소는 $1$에 대응하자. 또는 $A$의 원소 중 초필터 $F$에 속하는 원소는 $1$에, 속하지 않는 원소는 $0$에 대응하자. 방금의 예시를 사용하면 다음과 같다.

원소	값
$\lbrace \rbrace $	$0$
$\lbrace p\rbrace $	$1$
$\lbrace q\rbrace $	$0$
$\lbrace r\rbrace $	$0$
$\lbrace p, q\rbrace $	$1$
$\lbrace p, r\rbrace $	$1$
$\lbrace q, r\rbrace $	$0$
$\lbrace p, q, r\rbrace $	$1$

이때, 위 대응은 명제 논리의 모델을 이룬다. 특히, $P = \lbrace p \rbrace , Q = \lbrace q \rbrace , R = \lbrace r \rbrace $로 두고, $\cup \leftrightarrow \lor, \cap \leftrightarrow \land$ 대응에 따라 표를 다시 작성하면 다음과 같다.

원소	값
$\varnothing$	$0$
$P$	$1$
$Q$	$0$
$R$	$0$
$P \lor Q$	$1$
$P \lor R$	$1$
$Q \lor R$	$0$
$P \lor Q \lor R$	$1$

이는 $P$가 참이고 $Q, R$은 거짓인 명제 논리의 모델이다. 이와 같이 일반적으로 불 대수 구조에 소 아이디얼 또는 초필터가 주어지면, 해당 정보를 바탕으로 논리적 모델을 구성할 수 있다. 이는 추후 살펴 볼 스톤 표현 정리_{Stone representation theorem}으로 가는 길목이다.

Ideals and Filters in Boolean Algebraic Structures

18 Jul 2025

Boolean Algebra

Boolean algebra is an algebra consisting of logical operations such as $\lor, \land, \lnot$ defined over $0$ representing false and $1$ representing true.

$a$	$b$	$a \lor b$	$a \land b$	$\lnot a$
$0$	$0$	$0$	$0$	$1$
$0$	$1$	$1$	$0$	$1$
$1$	$0$	$1$	$0$	$0$
$1$	$1$	$1$	$1$	$0$

When we regard $0$ and $1$ not as formal symbols representing false and true, but as integers, we can check that $\lor$ corresponds to $\max$, $\land$ to $\min$, and $\lnot$ to the complement operation $\bar{(\cdot)}: 0 \mapsto 1, 1 \mapsto 0$.

$a$	$b$	$\max (a, b)$	$\min (a, b)$	$\bar{a}$
$0$	$0$	$0$	$0$	$1$
$0$	$1$	$1$	$0$	$1$
$1$	$0$	$1$	$0$	$0$
$1$	$1$	$1$	$1$	$0$

Building on this insight, we can naturally extend the domain of Boolean algebra from $\lbrace 0, 1 \rbrace$ to $[0, 1]$. For instance, $0.2 \lor 0.7 = 0.7$ and $0.3 \land \lnot(0.9) = 0.1$. Developing this idea further, we can define operations structurally similar to Boolean algebra on sets with appropriate order relations, and conversely, sets with operations structurally similar to Boolean algebra can be given appropriate order relations. This is the idea of Boolean algebraic structures.

Definition. When binary operations $\lor, \land$ and unary operation $\lnot$ defined on a set $A$ with two elements $0$ and $1$ satisfy the following axioms, we call $(A, 0, 1, \lor, \land, \lnot)$ a Boolean algebraic structure.

Axiom	$\lor$	$\land$
Associativity	$a \lor (b \lor c) = (a \lor b) \lor c$	$a \land (b \land c) = (a \land b) \land c$
Commutativity	$a \lor b = b \lor a$	$a \land b = b \land a$
Distributivity	$a \lor (b \land c) = (a \lor b) \land (a \lor c)$	$a \land (b \lor c) = (a \land b) \lor (a \land c)$
Identity	$a \lor 0 = a$	$a \land 1 = a$
Complement	$a \lor \lnot a = 1$	$a \land \lnot a = 0$
Absorption	$a \lor (a \land b) = a$	$a \land (a \lor b) = a$

Remark.

• The absorption law can be proved from the other five axioms.

• The term “complement” is used instead of “inverse”, because while multiplying $x$ by its multiplicative inverse $x^{-1}$ should yield the multiplicative identity $1$, and adding the additive inverse $-x$ should yield the additive identity $0$, in Boolean algebraic structures the result of $x \lor \lnot x$ is not the disjunctive identity $0$ but rather the conjuctive identity $1$, and the result of $x \land \lnot x$ is not $1$ but rather $0$.

Verify that the two examples in the introduction are Boolean algebraic structures. As another example, consider the power set $\mathcal{P}(X)$ of the set $X = \lbrace p, q, r \rbrace $. Verify that $\mathcal{P}(X)$ becomes a Boolean algebraic structure when we define:

• $a \lor b = a \cup b$
• $a \land b = a \cap b$
• $\lnot a = X \setminus a$
• $1 = X$
• $0 = \varnothing$

Generally, when $X$ is any set, the power set of $X$ forms a Boolean algebraic structure.

A Boolean algebraic structure can be given a partial order in a natural way.

Theorem. Let $A$ be a Boolean algebraic structure. Define the following binary relation:

\[a \leq b \iff a = a \land b\]

Then $\leq$ is a partial order on $A$. $1$ and $0$ are respectively the greatest and least elements of $\leq$. $\lor$ and $\land$ are respectively operations that yield the supremum and infimum with respect to $\leq$.

The proof is omitted. Since a Boolean algebraic structure $A$ can be given a partial order $\leq$ in this natural way, we can draw the Hasse diagram of $A$ according to $\leq$. For instance, consider the Boolean algebraic structure formed by $\mathcal{P}(X)$ for $X = \lbrace p, q, r\rbrace $ seen earlier.

\[a \leq b \iff a = a \land b \iff a = a \cap b \iff a \subseteq b\]

So in this case, the Hasse diagram of the Boolean algebraic structure is the same as the inclusion diagram of sets.

Boolean Rings

Boolean algebraic structures require two operations and the corresponding identity elements for each operation, which makes their definition similar to that of rings. This is not mere coincidence.

Definition. A ring $R$ is a Boolean ring if for any $x \in R$, we have $x^2 = x$.

Boolean algebraic structures and Boolean rings are in one-to-one correspondence. That is, the following holds:

Theorem. If $(R, 0, 1, +, \cdot)$ is a Boolean ring, then $(R, 0, 1, \lor, \cdot, (\cdot)^{-1})$ is a Boolean algebraic structure, where $\lor, \lnot$ are defined as follows:

\[\begin{gather} x \lor y = x + y + xy \\ \lnot x = 1 + x \end{gather}\]

Conversely, if $(A, 0, 1, \lor, \land, \lnot)$ is a Boolean algebraic structure, then $(A, 0, 1, +, \land)$ is a Boolean ring, where $+$ is defined as follows:

\[x + y = (x \lor y) \land \lnot (x \land y)\]

The proof is routine and is omitted. (Use the fact that in a boolean ring, $x + x = 0$.)

Ideals

Recall the following definition from algebra:

Definition. For a ring $R$, a non-empty subset $I \subseteq R$ is an ideal if $I$ forms a group under addition and for any $a \in R$ and $x \in I$, we have $ax \in I$. That is, $aI \subseteq I$.

Building on the correspondence between Boolean algebraic structures and Boolean rings, let us define:

Definition. For a Boolean algebraic structure $A$, a non-empty subset $I \subseteq A$ is an ideal if $I$ is closed under $\lor$ and for any $a \in A$ and $x \in I$, we have $a \land x \in I$. That is, $a \land I \subseteq I$.

For example, the following shaded region is an ideal of $\mathcal{P}(\lbrace p, q, r\rbrace )$:

When we correspond a Boolean algebraic structure to a Boolean ring, $I$ being an ideal in the former is equivalent to being an ideal in the latter. That is, the following holds:

Theorem. For a Boolean algebraic structure $A$, $I \subseteq A$ is a (Boolean) ideal if and only if $I$ is a (ring) ideal in the corresponding Boolean ring $A$.

We can also define prime ideals and maximal ideals in Boolean algebraic structures.

Definition. Let $I$ be an ideal of the Boolean algebraic structure $A$. $I$ is a prime ideal if for any $a, b \in A$, if $a \land b \in I$, then $a \in I$ or $b \in I$. $I$ is a maximal ideal if whenever $J$ is an ideal that strictly contains $I$, we have $J = A$.

These concepts also correspond exactly to prime ideals and maximal ideals of Boolean rings. Verify that the example ideal shown earlier is both a prime ideal and a maximal ideal. As will soon become apparent, this is not a coincidence.

Let us observe several facts. Let $I \subset A$ be an ideal.

• For any $a \in I$, by the definition of an ideal, it follows that $a \land \lnot a = 0 \in I$. Therefore, ideals of Boolean algebras always contain $0$ as an element.

• If $1 \in I$, then for any $a \in A$, it follows that $1 \land a = a \in I$. Therefore, the ideal containing $1$ as an element is uniquely the entire structure.

• If $I$ is a prime ideal, then for any $a \in A$, since $a \land \lnot a = 0 \in I$, we have $a \in I$ or $\lnot a \in I$. That is, prime ideals always contain either any element or its negation.

• Let $I$ be a maximal ideal. If there exists some $a \in A$ such that $a \not\in I, \lnot a \not\in I$, then $I \cup \lbrace x \land a : x \in A \rbrace$ is an ideal that strictly contains $I$ but is not the entire $A$, so $I$ is not maximal. Therefore, maximal ideals also always contain either any element or its negation.

From the above facts, with a little reasoning, we can deduce the following:

Theorem. Let $A$ be a Boolean algebraic structure and $I$ be an ideal of $A$. The following are equivalent:

• $I$ is a prime ideal.
• $I$ is a maximal ideal.
• For any $x \in A$, either $x \in I$ or $\lnot x \in I$.

Filters

Filters were discussed in a previous post. Let us recall the definition:

Definition. Let $X$ be a set. A collection $\mathcal{F}$ of subsets of $X$ is called a filter on $X$ if it satisfies the following:

1. $X \in \mathcal{F}$
2. $\varnothing \not\in \mathcal{F}$
3. Upward closure: $A \in \mathcal{F}, A \subset B \implies B \in \mathcal{F}$
4. Finite intersection closure: $A, B \in \mathcal{F} \implies A \cap B \in \mathcal{F}$

Translating this definition to Boolean algebraic structures gives us:

Definition. For a Boolean algebraic structure $A$, $F \subseteq A$ is a filter if $F$ is closed under $\land$ and for any $a \in A$ and $x \in I$, we have $a \lor x \in I$. That is, $a \lor I \subseteq I$.

Being closed under $\land$ corresponds to the original “finite intersection closure” condition, and $a \lor I \subseteq I$ corresponds to the original “upward closure” condition. In particular, $a \lor I \subseteq I$ means that if we think of the Boolean algebraic structure as a flow of water flowing in the direction of $\leq$, when ink is dropped at $x \in I$, all regions where the ink spreads are contained in $I$ (compare this with the ink example from the previous post). For example, the following shaded region is a filter of $\mathcal{P}(\lbrace p, q, r\rbrace )$:

Duality Between Ideals and Filters

Comparing the definitions of ideals and filters reveals an interesting fact. If we swap $\land$ and $\lor$ in one definition, we get exactly the other definition. We say that ideals and filters are dual to each other.

Due to this duality, facts proved for one concept naturally hold for the other concept as well. For instance, the following holds:

Theorem. Let $A$ be a Boolean algebraic structure and $F$ be a filter of $A$. The following are equivalent:

• If $x \lor y \in F$, then $x \in F$ or $y \in F$.
• If $G$ is a filter that strictly contains $F$, then $G = A$.
• For any $x \in A$, either $x \in F$ or $\lnot x \in F$.

Here, a filter satisfying the first condition is called a prime filter, one satisfying the second condition is called a maximal filter. Unlike the case of ideals, filters satisfying the third condition also have a name: ultrafilters (see also the previous post).

Booleanisation of Boolean Algebraic Structures Using Ultrafilters

General Boolean algebraic structures, unlike the Boolean algebra familiar to us, do not have each element dichotomised into true or false. $p$ is at the same or closer “distance” from $1$ (true) compared to $p \land q$, but it is neither $0$ nor $1$ in itself.

However, when an ultrafilter or prime ideal of a Boolean algebraic structure $A$ is given, we can dichotomise the elements of $A$ into “true” or “false” based on whether they belong to that filter (ideal). Consider again the ideal example (left) and filter example (right) seen earlier. The left is a prime ideal, and the right is an ultrafilter.

Note that they are exactly complements of each other. Generally, the following holds:

Theorem. For a subset $I$ of a Boolean algebraic structure $A$, $I$ is a prime (maximal) ideal if and only if $A \setminus I$ is an ultra-(prime, maximal) filter.

Building on this, let us map elements of $A$ that belong to the prime ideal $I$ to $0$, and those that do not belong to $1$. Or to put in other words, let us map elements of $A$ that belong to the ultrafilter $F$ to $1$, and those that do not belong to $0$. Using the example just given:

Element	Value
$\lbrace \rbrace $	$0$
$\lbrace p\rbrace $	$1$
$\lbrace q\rbrace $	$0$
$\lbrace r\rbrace $	$0$
$\lbrace p, q\rbrace $	$1$
$\lbrace p, r\rbrace $	$1$
$\lbrace q, r\rbrace $	$0$
$\lbrace p, q, r\rbrace $	$1$

The result is a model of propositional logic. In particular, setting $P = \lbrace p \rbrace , Q = \lbrace q \rbrace , R = \lbrace r \rbrace $ and rewriting the table according to the correspondence $\cup \leftrightarrow \lor, \cap \leftrightarrow \land$ gives:

Element	Value
$\varnothing$	$0$
$P$	$1$
$Q$	$0$
$R$	$0$
$P \lor Q$	$1$
$P \lor R$	$1$
$Q \lor R$	$0$
$P \lor Q \lor R$	$1$

This is a model of propositional logic where $P$ is true and $Q, R$ are false. In this way, generally when a Boolean algebraic structure is given a prime ideal or ultrafilter, we can construct a logical model based on that information. This is a stepping stone towards the Stone representation theorem.

스톤-체흐 콤팩트화

10 Jul 2025

정의. $\iota : X \to Y$가 임베딩이라고 하자. 즉, $\iota$는 단사이며 $X$와 $\iota [X]$의 위상동형사상이다. $Y$가 $X$의 콤팩트화_{compactification}라는 것은 $Y$가 콤팩트 공간이고, $\overline{\iota [X]} = Y$인 것이다.

고찰

• 일반적으로 $X$의 콤팩트화는 유일하지 않다. $\overline{X}$는 배경 위상에 따라 달라질 수 있기 때문이다.

• $X, Y$가 하우스도르프라면 $Y$는 콤팩트 하우스도르프 공간이므로 정규이고, 따라서 티호노프(완전 정칙)이다. 그리고 티호노프 공간의 부분공간은 티호노프임이 알려져 있기 때문에 $X$ 또한 티호노프이다. 즉, 하우스도르프 공간으로 콤팩트화 가능한 공간은 티호노프이다.

• 이의 역도 성립한다. 즉, 티호노프 공간은 하우스도르프 공간으로 콤팩트화 가능하다. 이것이 이 글에서 다루는 스톤-체흐 콤팩트화의 함의 중 하나이다.

국소적으로 콤팩트_{locally compact}한 하우스도르프 공간 $X$에 대해서는 $X$의 한점 콤팩트화_{one-point compactification} 공간 $X^\ast$가 존재한다. (이 사실과 위의 고찰로부터 국소적으로 콤팩트한 하우스도르프 공간은 티호노프임이 따라 나온다.) 특히 $X^\ast$는 $X$의 “가장 작은” 콤팩트화이다.

스톤-체흐 콤팩트화는 어떤 면에서 이의 반대 개념이다. $X$의 스톤-체흐 콤팩트화 공간 $\beta X$는 $X$의 “가장 큰” 콤팩트화이다. 여기서 “가장 큰”의 정확한 정의는 다음의 보편 성질_{universal property}이다.

정리 1. $X$가 티호노프일 때, 어떤 콤팩트 하우스도르프 공간 $\beta X$와 임베딩 $\iota: X \to \beta X$가 유일하게 존재하여, 다음을 만족한다: $K$가 임의의 콤팩트 하우스도르프 공간이고 $f: X \to K$가 연속사상일 때, $f = f^\ast \circ \iota$를 만족하는 연속사상 $f^\ast: \beta X \to K$가 유일하게 존재한다.

또한 $\beta X$는 $X$의 콤팩트화이다. 이를 스톤-체흐 콤팩트화_{Stone-Čech compactification}라고 한다.

여기서 $X$가 티호노프라는 조건을 빼도 꽤 강력한 결론을 유지할 수 있다.

정리 2. $X$가 일반 위상공간일 때, 어떤 콤팩트 하우스도르프 공간 $\beta X$와 연속함수 $e : X \to \beta X$가 유일하게 존재하여, 다음을 만족한다: $K$가 임의의 콤팩트 하우스도르프 공간이고 $f: X \to K$가 연속사상일 때, $f = f^\ast \circ \iota$를 만족하는 연속사상 $f^\ast: \beta X \to K$가 유일하게 존재한다.

차이점은 $e$가 임베딩이 아니라 연속함수라는 점이다. 실제로 $X$가 일반 위상공간일 때 $e$는 동형성은 고사하고 단사조차 아닐 수 있다. 이 경우 $\beta X$는 엄밀한 의미에서 $X$의 콤팩트화가 아니지만, 그럼에도 이 글에서는 편의를 위해 일반적으로 $\beta X$를 $X$의 스톤-체흐 콤팩트화라고 부를 것이다.

한점 콤팩트화가 국소적으로 콤팩트한 공간에서만 가능한 것과 달리, 정리 2에서 드러나듯이 스톤-체흐 콤팩트화는 모든 위상공간에서 가능하다. 덕분에 스톤-체흐 콤팩트화는 일반 위상공간의 범주 $\mathbf{Top}$를 콤팩트 하우스도르프 공간의 범주 $\mathbf{CHaus}$로 보내는 함자로서 간주될 수 있다. 실제로 다음이 성립한다.

정리 3. 망각함자_{forgetful functor} $U: \mathbf{CHaus} \to \mathbf{Top}$는 좌 어드조인트 $\beta: \mathbf{Top} \to \mathbf{CHaus}$를 가진다. 또한 $X \in \mathbf{Top}$에 대해 $\beta X$는 $X$의 스톤-체흐 콤팩트화에 해당한다.

예전 글에서 다룬 동치성으로 인해 이는 처음의 정의와 동치이다.

$\beta$의 존재성 증명은 크게 세 단계로 구성된다. 첫째, 임의의 위상공간 $X$에 대해 $\beta X$를 정의한다. 둘째, $\beta X$가 보편 성질을 만족함을 보인다. 셋째, $X$와 $\beta X$의 관계가 함수적_functorial임을, 즉 $\beta$가 함자임을 보인다. 위에서 정리 1, 정리 2, 정리 3을 구분하기는 했지만 아래의 증명에서는 세 정리를 함께 증명한다.

증명.

1. $\beta X$의 정의

집합 $C$를 다음과 같이 정의하자.

\[C = \{ f \mid f : X \to [0, 1] \text{ is continuous } \}\]

$[0, 1]^C$에 곱 위상을 주어 위상공간으로 만들자. $[0, 1]^C$는 $C \to [0, 1]$ 사상들의 공간으로 생각할 수 있다. 하우스도르프 공간의 곱은 언제나 하우스도르프이고, 콤팩트 공간의 곱 또한 언제나 콤팩트하므로 (티호노프 정리), $[0, 1]^C$는 콤팩트 하우스도르프 공간이다. 이제 $e: X \to [0, 1]^C$를 다음과 같이 정의한다.

\[e: x \mapsto \lambda_x \quad \text{where} \quad \lambda_x : f \mapsto f(x)\]

곱 위상의 성질(정의)에 의해 $e$는 연속함수이다. 특히 $X$가 티호노프 공간이라면 우리손 보조정리와 그 따름결과 (링크의 말단에 있는 정리) 에 의해 $e$는 임베딩이다.

$\beta X$를 $[0, 1]^C$에서 $e[X]$의 폐포로 정의하자. $\beta X$는 콤팩트 공간의 닫힌집합이므로 콤팩트이며, 하우스도르프 공간의 부분공간이므로 하우스도르프이다. 따라서 $\beta X$는 콤팩트 하우스도르프이다. 특히, 직전 문단의 고찰로 인해 $X$가 티호노프일 때 $\beta X$는 $X$의 콤팩트화이다.

2. $\beta X$의 보편 성질 확인

이제 $\beta X$가 보편 성질을 만족함을 보이자. 먼저 $K = [0, 1]$일 때를 보인다.

임의의 연속사상 $f: X \to [0, 1]$이 주어졌다고 하자. $f^\ast : \beta X \to [0, 1]$을 다음과 같이 정의한다.

\[f^\ast : \lambda \mapsto \lambda (f)\]

즉, $(x_g)_{g \in C}$를 $x_f$로 사상시키는 사영사상 $\pi_f: [0, 1]^C \to [0, 1]$에 대해, $f^\ast = \pi_f \rvert_{\beta X}$이다. $\pi_f$가 연속이므로 $f^\ast$는 연속이다. 또한 임의의 $x \in X$에 대해,

\[(f^\ast \circ e)(x) = f^\ast (\lambda_x) = \lambda_x(f) = f(x)\]

이므로 $f^\ast$는 보편 성질이 요구하는 사상이다.

이제 일반적인 콤팩트 하우스도르프 공간 $K$와 연속사상 $f: X \to K$을 고려하자. $K$는 티호노프 공간이므로 어떤 집합 $J$에 대해 $[0, 1]^J$에 임베딩될 수 있다. 그러므로 일반성을 잃지 않고 $K = [0, 1]^J$, $f: X \to [0, 1]^J$인 경우를 고려하면 충분하다. 이 경우 $f^\ast$를 다음과 같이 정의한다.

\[f^\ast : \lambda \mapsto (\lambda (\pi_\alpha f))_{\alpha \in J}\]

$K = [0, 1]$인 경우의 논증으로부터, $f^\ast$는 연속이며 보편 성질을 만족함이 따라 나온다. 따라서 $\beta X$는 $X$의 스톤-체흐 콤팩트화이다.

3. $\beta$의 함자 조건 확인

마지막으로 $\beta$가 함자임을 보이자. 임의의 위상공간 $X, Y$와 연속사상 $\psi : X \to Y$에 대해 다음 가환 도식이 성립하도록 $\beta \psi$를 정의할 수 있음을 보여야 한다.

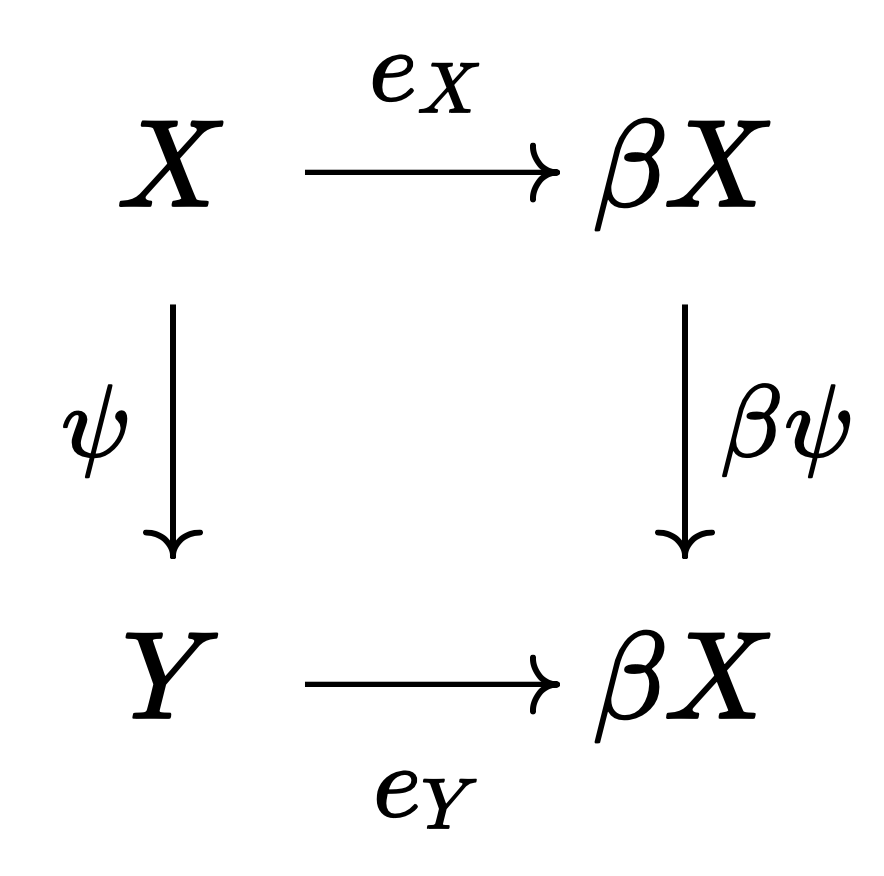
다음과 같이 $\beta \psi$를 정의하자. 임의의 $\lambda \in \beta X$에 대해,

\[\beta \psi : \lambda \mapsto (g \mapsto \lambda(g \circ \psi) )_{g \in C_Y}\]

여기서 $C_Y$는 연속인 $g : Y \to [0, 1]$의 모임이다. (연습문제: 위 식이 잘 정의되었음을 각 함수의 정의역과 공역을 따져 확인해 보라.) 가환 도식의 성립은 다음 식으로 환원된다.

\[\beta \psi(\lambda_x) = \lambda_{\psi(x)}\]

좌변을 정의에 따라 풀어쓰면 위 식이 성립함을 알 수 있다.

\[\begin{align*} \beta \psi(\lambda_x) &= (g \mapsto \lambda_x(g\circ \psi))_{g \in C_Y} \\ &= (g \mapsto (g \circ \psi)(x))_{g \in C_Y} \\ &= (g \mapsto g(\psi(x)))_{g \in C_Y} \\ &= \lambda_{\psi(x)} \end{align*}\]

따라서 $\beta : \mathbf{Top} \to \mathbf{CHaus}$는 함자이며, 특히 $U: \mathbf{CHaus} \to \mathbf{Top}$의 좌 어드조인트이다. 이로부터 임의의 $X$에 대해, 보편 조건을 만족하는 $(e, \beta X)$는 콤마 카테고리 $(A \Rightarrow U)$의 초기 대상이므로 동형성에 대해 유일함이 따라 나온다. (자세한 설명은 이 글을 참조) ■

Stone-Čech Compactification

10 Jul 2025

Definition. Let $\iota : X \to Y$ be an embedding. That is, $\iota$ is injective and a homeomorphism between $X$ and $\iota [X]$. $Y$ is said to be a compactification of $X$ if it is a compact space such that $\overline{\iota [X]} = Y$.

Remarks

• Generally, compactification of $X$ is not unique, as $\overline{X}$ may vary depending on the background topology.

• If $X$ and $Y$ are Hausdorff, then $Y$ is a compact Hausdorff space, hence normal, hence Tychonoff (completely regular). Since it is known that subspaces of Tychonoff spaces are Tychonoff, $X$ is also Tychonoff. Thus, spaces that can be compactified as Hausdorff spaces are Tychonoff.

• The converse also holds. That is, Tychonoff spaces can be compactified as Hausdorff spaces. This is one of the implications of the Stone-Čech compactification discussed in this post.

For a locally compact Hausdorff space $X$, there exists a one-point compactification space $X^\ast$. (From this fact and the above remark, it follows that locally compact Hausdorff spaces are Tychonoff.) In particular, $X^\ast$ is the “smallest” compactification of $X$.

The Stone-Čech compactification is, in some sense, the opposite concept. The Stone-Čech compactification space $\beta X$ of $X$ is the “largest” compactification of $X$. The precise definition of “largest” is given by the following universal property.

Theorem 1. If $X$ is Tychonoff, then there exists a unique compact Hausdorff space $\beta X$ and an embedding $\iota: X \to \beta X$ such that the following holds: for any compact Hausdorff space $K$ and any continuous map $f: X \to K$, there exists a unique continuous map $f^\ast: \beta X \to K$ such that $f = f^\ast \circ \iota$.

Furthermore, $\beta X = \overline{\iota[X]}$ and hence is a compactification of $X$. This is referred to as the Stone-Čech compactification.

Here, even without the condition that $X$ is Tychonoff, quite strong conclusions can still be maintained.

Theorem 2. If $X$ is a general topological space, then there exists a unique compact Hausdorff space $\beta X$ and a continuous function $e : X \to \beta X$ such that the following holds: for any compact Hausdorff space $K$ and any continuous map $f: X \to K$, there exists a unique continuous map $f^\ast: \beta X \to K$ such that $f = f^\ast \circ e$.

Furthermore, $\beta X = \overline{\iota[X]}$.

The difference is that $e$ is just a continuous function rather than an embedding. In fact, when $X$ is a general topological space, $e$ may not even be injective, let alone an homoemorphism. In this case, $\beta X$ is not a compactification of $X$ in the strict sense, but for convenience, this post will generally refer to $\beta X$ as the Stone-Čech compactification of $X$.

Unlike one-point compactifications, which are only possible for locally compact spaces, the Stone-Čech compactification is possible for all topological spaces. Consequently, the Stone-Čech compactification can be regarded as a functor that maps the category of general topological spaces $\mathbf{Top}$ to the category of compact Hausdorff spaces $\mathbf{CHaus}$. Indeed, the following holds.

Theorem 3. The forgetful functor $U: \mathbf{CHaus} \to \mathbf{Top}$ has a left adjoint $\beta: \mathbf{Top} \to \mathbf{CHaus}$.

Due to the equivalence discussed in a previous post, this may well be taken as the definition of Stone-Čech compactification.

The proof of Theorem 3 consists of three main steps. First, we define $\beta X$ for a topological space $X$. Second, we show that $\beta X$ satisfies the universal property. Third, we show that the relationship between $X$ and $\beta X$ is functorial, meaning that $\beta$ is a functor. Although Theorems 1, 2, and 3 are distinguished above, the proof below will demonstrate all three theorems together.

Proof.

1. Defining $\beta X$

Let us define the set $C$ as follows.

\[C = \{ f \mid f : X \to [0, 1] \text{ is continuous } \}\]

We shall give the product topology to $[0, 1]^C$ to form a topological space. $[0, 1]^C$ can be thought of as the space of maps from $C$ to $[0, 1]$. Note that the product of Hausdorff spaces is always Hausdorff, and the product of compact spaces is always compact (Tychonoff’s theorem), so $[0, 1]^C$ is a compact Hausdorff space. Now, let us define $e: X \to [0, 1]^C$ as follows.

\[e: x \mapsto \lambda_x \quad \text{where} \quad \lambda_x : f \mapsto f(x)\]

By the properties of the product topology (indeed, its definition), $e$ is a continuous function. In particular, if $X$ is a Tychonoff space, then by the Urysohn lemma and its corollary (the theorems in this post), $e$ is an embedding.

Let us define $\beta X$ as the closure of $e[X]$ in $[0, 1]^C$. Since $\beta X$ is a closed subset of a compact space, it is compact, and since it is a subspace of a Hausdorff space, it is Hausdorff. Therefore, $\beta X$ is compact Hausdorff. In particular, due to the remark in the previous paragraph, if $X$ is Tychonoff, then $\beta X$ is a compactification of $X$.

2. $\beta X$ satisfies the universal property

Now let us show that $\beta X$ satisfies the universal property. First, we consider the case when $K = [0, 1]$.

Let us assume we are given a continuous map $f: X \to [0, 1]$. We define $f^\ast : \beta X \to [0, 1]$ as follows.

\[f^\ast : \lambda \mapsto \lambda (f)\]

That is, for the projection map $\pi_f: [0, 1]^C \to [0, 1]$ that maps $(x_g)_{g \in C}$ to $x_f$, we have $f^\ast = \pi_f \rvert_{\beta X}$. Since $\pi_f$ is continuous, $f^\ast$ is continuous. Furthermore, for any $x \in X$,

\[(f^\ast \circ e)(x) = f^\ast (\lambda_x) = \lambda_x(f) = f(x)\]

Thus, $f^\ast$ is the map required by the universal property.

For general $K$ compact Hausdorff and $f: X \to K$ continuous, we observe that $K$ is Tychonoff, and hence can be embedded into $[0, 1]^J$ for some index set $J$. It then follows that without loss of generality we may only consider cases where $K = [0, 1]^J$ and $f: X \to [0, 1]^J$. In such cases, we let $f^\ast$ be:

\[f^\ast : \lambda \mapsto (\lambda (\pi_\alpha f))_{\alpha \in J}\]

It follows from the $K = [0, 1]$ case that $f^\ast$ is continuous, and satisfies the universal property. Therefore, $\beta X$ is the Stone-Čech compactification of $X$.

3. $\beta$ is a functor

Finally, we need to show that $\beta$ is a functor. That is, we need to show that for any topological spaces $X, Y$ and continuous map $\psi : X \to Y$, one can define $\beta \psi$ such that the following commutative diagram holds.

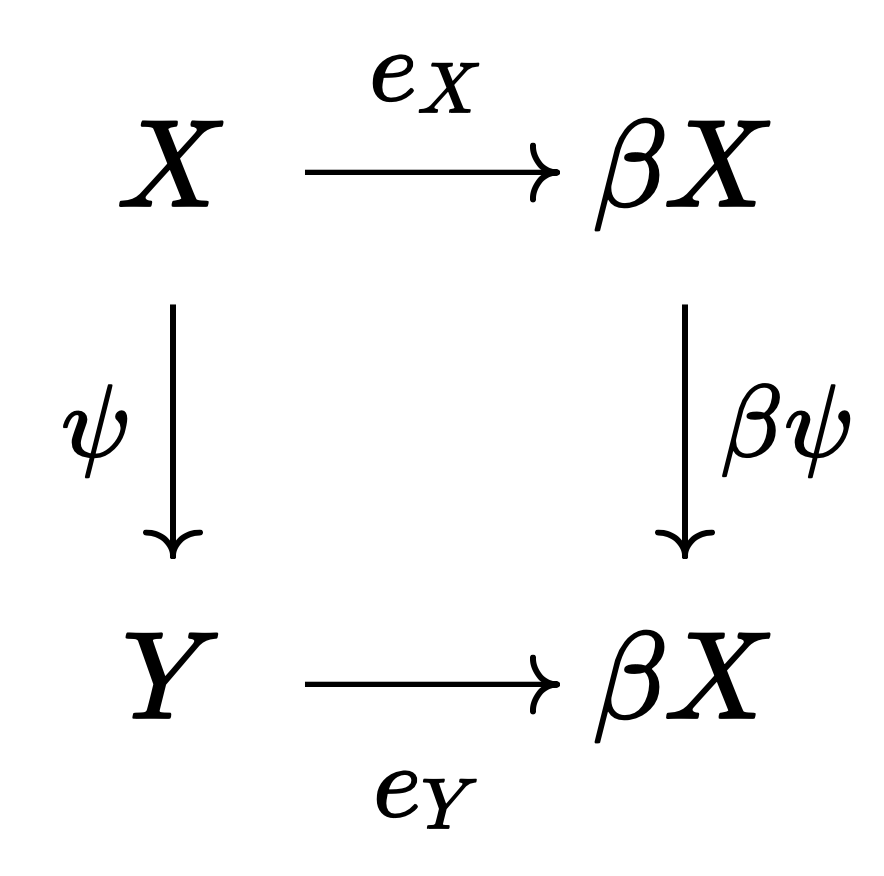
Let us define $\beta \psi$ as follows. For any $\lambda \in \beta X$,

\[\beta \psi : \lambda \mapsto (g \mapsto \lambda(g \circ \psi) )_{g \in C_Y}\]

where $C_Y$ is the collection of continuous functions $g : Y \to [0, 1]$. (Exercise: Verify that the above definition is well-defined by checking the domains and codomains of each function.) The commutativity of the diagram reduces to the following equation.

\[\beta \psi(\lambda_x) = \lambda_{\psi(x)}\]

Expanding the left-hand side according to the definition, we see that the equation indeed holds.

\[\begin{align*} \beta \psi(\lambda_x) &= (g \mapsto \lambda_x(g\circ \psi))_{g \in C_Y} \\ &= (g \mapsto (g \circ \psi)(x))_{g \in C_Y} \\ &= (g \mapsto g(\psi(x)))_{g \in C_Y} \\ &= \lambda_{\psi(x)} \end{align*}\]

Thus, $\beta : \mathbf{Top} \to \mathbf{CHaus}$ is a functor, and in particular, it is the left adjoint to $U: \mathbf{CHaus} \to \mathbf{Top}$. It follows that for any $X$, the pair $(e, \beta X)$ that satisfies the universal condition is the initial object in the comma category $(A \Rightarrow U)$, which implies uniqueness up to isomorphism. (For further details, refer to this post) ■

우리손 보조정리와 우리손 거리화 정리

09 Jul 2025

우리손 보조정리

우리손 보조정리_{Urysohn Lemma}. $X$가 정규_normal 공간이라고 하자. $A, B$가 서로소인 $X$의 닫힌집합일 때, 어떤 연속함수 $f: X \to [0, 1]$이 존재하여 $f[A] = \lbrace 0 \rbrace$, $f[B] = \lbrace 1 \rbrace$이다.

정규성을 비롯한 분리 공리는 해당 공간에서 점과 닫힌집합을 분리한다. 우리손 보조정리의 의의는, 정규성 분리 공리의 경우 두 닫힌집합은 좋은 공간에서도 분리 가능하다는 것이다. 구체적으로, 정규공간을 적절한 연속함수로 사상시켰을 때 두 닫힌집합은 $[0, 1]$에서 분리 가능하다. 그리고 $[0, 1]$의 여러 좋은 성질은 — 콤팩트 하우스도르프 거리 공간일 뿐 아니라 우리에게 굉장히 익숙한 공간이라 논증하기도 쉽다 — 우리손 보조정리의 굉장한 잠재력을 암시한다.

증명

$Q = [0, 1] \cap \mathbb{Q}$라고 하자 (사실 $[0, 1]$의 가산 조밀 집합이기만 하면 된다). $Q$가 가산이므로 $Q$의 원소를 열거_enumerate하는 방법이 존재한다. 일례로 분모-분자의 사전식 열거 $\prec$를 고려하자.

\[0 \prec 1 \prec 1/2 \prec 1/3 \prec 2/3 \prec 1/4 \prec 1/5 \prec 2/5 \prec \cdots\]

이제 다음과 같이 $\lbrace U_q \rbrace _{q \in Q}$를 정의하자. 먼저 $U_1 = X \setminus B$이다 ($B$가 닫힌집합이므로 $U_1$은 열린집합이다). 정규성에 의해 $A \subset U_0$이면서 $\overline{U_0} \subset U_1$인 $U_0$가 존재한다. 나머지 $U_q$는 열거 순서에 따라 다음과 같이 정의한다. $p \prec q$인 임의의 $p$에 대해,

• $p < q \implies \overline{U_p} \subset U_q$
• $q < p \implies \overline{U_q} \subset U_p$

정규성에 의해 위 조건을 만족하며 $\lbrace U_q \rbrace _{q \in Q}$를 완전히 정의할 수 있다.

이제 다음과 같이 함수 $f: X \to [0, 1]$을 정의하자.

\[f(x) = \begin{cases} \sup_{<}\{q \in Q : x \notin U_q \} & x \notin U_0 \\ 0 & x \in U_0 \end{cases}\]

$\sup_<$라는 표기는 $\prec$가 아닌 $<$에 대해 상한을 취함을 의미한다. 정의로부터 $f[A] = 0, f[B] = 1$가 따라 나온다.

이제 $f$가 연속임을 보이면 정리가 증명된다. $\lbrace B_\epsilon(q) \cap [0, 1] : q \in Q, \epsilon \in \mathbb{Q}_{>0} \rbrace $가 $[0, 1]$의 위상 기저이므로, 임의의 $q \in Q$와 특정 상한보다 작은 양의 유리수 $\epsilon$에 대해 $S_{q, \epsilon} = f^{-1}(B_\epsilon(q) \cap [0, 1])$가 열린집합임을 보이면 충분하다.

• $0 < q < 1$인 경우, $S_{q, \epsilon} = (X \setminus \overline{U_{q-\epsilon}}) \cap U_{q + \epsilon}$이므로 열린집합이다.
• $q = 0$인 경우, $S_{0, \epsilon} = U_\epsilon$이므로 열린집합이다.
• $q = 1$인 경우, $S_{1, \epsilon} = X \setminus \overline{U_{1 - \epsilon}}$이므로 열린집합이다.

따라서 $f$는 연속이다. ■

고찰

• 우리손 보조정리의 역은 자명히 성립한다. 즉, 임의의 닫힌집합 $A, B \subset X$에 대해 어떤 연속인 $f: X \to [0, 1]$가 $A, B$를 분리한다면, $U = f^{-1}[0, 1/2)$, $V = f^{-1}(1/2, 1]$는 $A, B$를 분리하는 서로소 열린집합이므로 $X$는 정규이다. 간단히 말해, 정규공간에서는 우리손 분리가능성과 분리 공리가 동치이다.

• 정칙_regular 공간에서는 이가 성립하지 않는다. 즉, 정칙 공간 $X$에서 임의의 닫힌집합 $F$와 점 $a$가 주어졌을 때, $f(a) = 0$, $f[F] = \lbrace 1 \rbrace$을 만족하는 연속인 $f: X \to [0, 1]$이 언제나 존재하는 것은 아니다. 우리손 분리가능한 정칙 공간을 티호노프_Tychonoff 공간 또는 완전 정칙_{completely regular} 공간이라고 하며, 정칙보다 엄격히 강한 조건이다.

• 우리손 보조정리의 증명이 정칙 공간에 대해 유효하지 않은 이유는 $p < q \implies \overline{U_p} \subset U_q$를 만족하는 $\lbrace U_q \rbrace $를 구성할 때 정규 공리가 필요하기 때문이다.

우리손 거리화 정리

우리손 보조정리의 응용으로서, 우리손 거리화 정리를 증명하자.

우리손 거리화 정리_{Urysohn metrisation theorem}. 2차 가산인 정규 공간은 거리화 가능하다.

그런데 2차 가산인 정칙 공간은 정규 공간임이 알려져 있으므로 위 정리의 진술은 “2차 가산인 정칙 공간은 거리화 가능하다”와 같이 자연스럽게 강화할 수 있다.

따라서 공간들 간의 시사 관계는 다음과 같다. 화살표의 길이가 길수록 요구되는 조건이 강해진다. $T_2 \to T_4$는 $T_3 \to T_4$보다 엄격히 어려운 시사 관계이며, 이것은 전자에서 요구되는 콤팩트성이 후자에서 요구되는 린델뢰프보다 엄격히 강한 조건인 데에서 드러난다. 마찬가지로 $T_3 \to \mathrm{Met}$는 $T_3 \to T_4$보다 엄격히 어려운 시사 관계이며, 전자에서 요구되는 2차 가산성은 후자에서 요구되는 린델뢰프보다 엄격히 강한 조건이다. 그러나 $T_2 \to T_4$와 $T_3 \to \mathrm{Met}$는 어느 한쪽이 엄격히 어려운 시사 관계가 아니다 (두 화살표의 길이는 엇비슷하다). 이것은 콤팩트성과 2차 가산성이 일반적으로 서로를 시사하지 않는다는 점에서 드러난다.

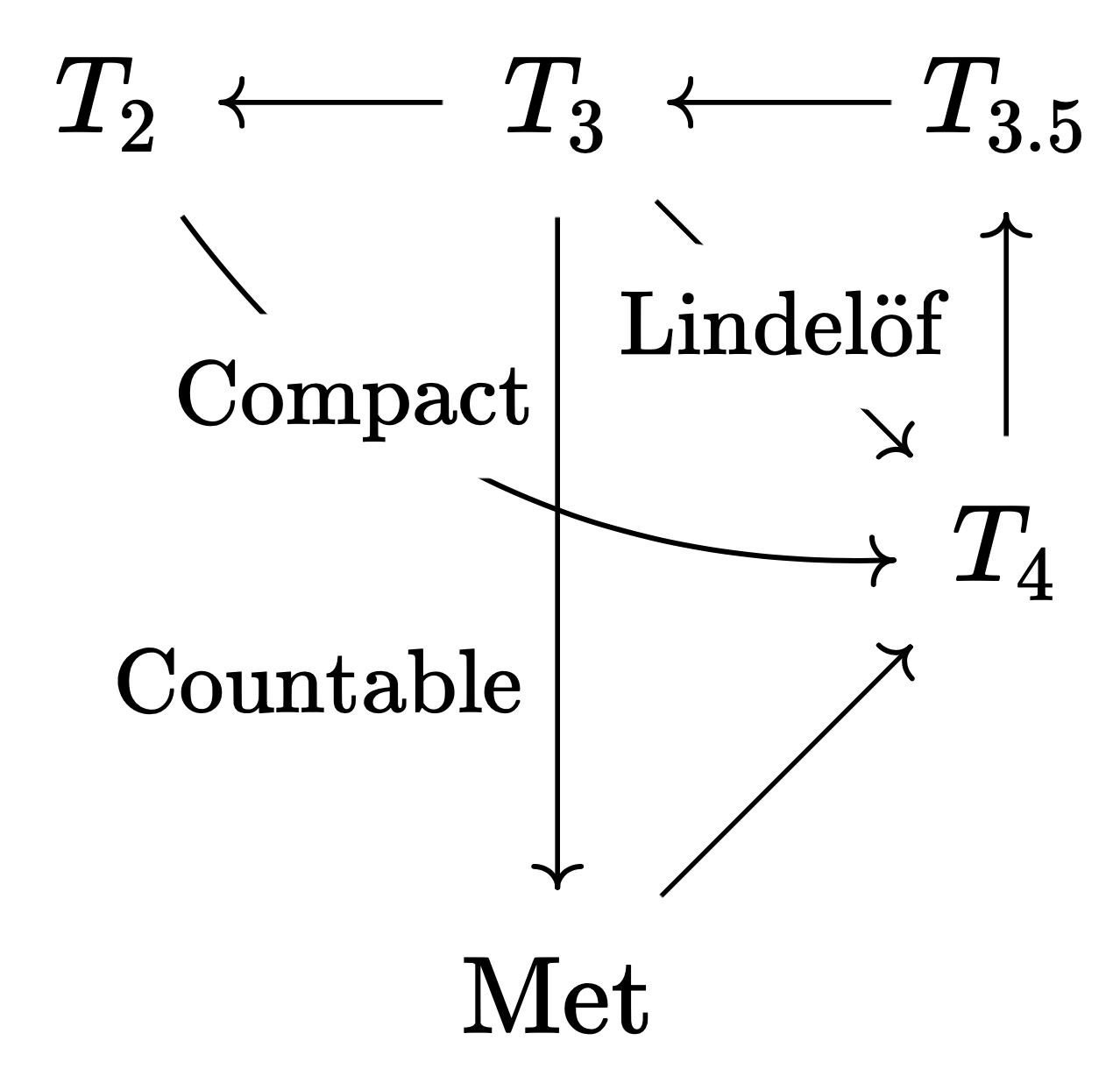
증명

$X$가 2차 가산인 정규 공간이라고 하자. 다음의 보조정리를 증명한다.

보조정리. $X$를 $[0, 1]$에 사상시키는 연속함수의 가산족 $\mathcal{F}$가 존재하여, 임의의 $x_0 \in X$와 그 근방 $U$에 대해, $f(x_0) > 0$이고 $f[X \setminus U] = \lbrace 0 \rbrace $인 $f \in \mathcal{F}$가 존재한다.

$x_0$와 $U$가 주어졌을 때 그러한 $f$가 존재함은 우리손 보조정리로부터 알 수 있다. 우리가 해야할 일은 이를 가산 함수족으로 줄이는 것이다. $\mathcal{B} = \lbrace B_n \rbrace $이 $X$의 가산인 위상기저라고 하자. $B_m \subset B_n$일 때, 우리손 보조정리로부터 $f_{nm}: X \to [0, 1]$을 다음을 만족하는 연속함수로 정의하자.

• $f_{nm}[\overline{B_m}] = 1$
• $f_{nm}[X \setminus B_n] = 0$

$\mathcal{F} = \lbrace f_{nm} \rbrace $으로 정의하자. 임의의 $x_0$와 그 근방 $U$가 주어졌을 때, 위상기저의 정의에 의해 $x_0 \in B_n \subset U$인 $B_n$이 존재한다. 또한 정규성에 의해 $x \in \overline{V} \subset B_n$인 열린집합 $V$가 존재한다. 다시 위상기저의 정의에 의해 $x \in B_m \subset V$인 $B_m$이 존재한다. 이때 $f_{nm} \in \mathcal{F}$가 보조정리의 조건을 만족하는 함수이다. □

이제 본 정리를 증명하자. 아이디어는 $X$를 $[0, 1]^\omega$에 임베딩하는 것이다. $[0, 1]^\omega$에 곱 위상이 주어지면 거리 공간임이 알려져 있으므로 $X$는 거리 공간의 부분공간과 동형인 공간으로서 거리화 가능함이 보여진다.

$\mathcal{F} = \lbrace f_n \mid n \in \omega \rbrace $가 보조정리로서 주어지는 가산 함수족이라고 하자. 다음과 같이 $F: X \to [0, 1]^\omega$를 정의한다.

\[F: x \mapsto (f_1(x), f_2(x), f_3(x), \dots)\]

$F$가 임베딩을 보이자. 즉, $F$가 연속이고, 단사이며, 정의역과 치역의 동형사상임을 보여야 한다.

각 $f_n$은 연속이므로 곱 위상의 성질(정의이기도 하다)에 의해 $F$는 연속이다. $F$가 단사임은 $X$가 하우스도르프라는 사실에서 따라 나온다. 따라서 다음을 보이면 충분하다.

$U \subset X$가 열린집합일 때, $F[U]$는 $\mathrm{im} F$에서 열린집합이다.

임의의 $y_0 \in F[U]$에 대해 $y_0 \in V \subset F[U]$이며 $\mathrm{im} F$에서 열린 $V$가 존재함을 보이자. $F[U]$의 정의에 의해 어떤 $x_0 \in X$가 존재하여 $F(x_0) = y_0$이다. $x_0$와 $U$에 대해 보조정리를 만족하는 함수가 $f_n \in \mathcal{F}$라고 하자. $f_n(x_0) = 1$이므로 $(y_0)_n = 1$이다. 따라서 $W = \pi_n^{-1}(0, 1] \subset [0, 1]^\omega$와 같이 정의하면 $W$는 $y_0$를 원소로 가지는 $[0, 1]^\omega$에서 열린집합이다.

$W \cap \mathrm{im} F \subset F[U]$임을 보이자. 임의의 $w \in W$는 $F(x_1) = w$와 같이 쓸 수 있다. 추가로 $w \in \mathrm{im} F$라면 $f_n(x_1) = 1$이다. 그런데 $f_n$은 $U$ 외부에서는 $0$이므로, $x_1 \in U$이다. 따라서 $w \in F[U]$이다. 따라서 $W \cap \mathrm{im} F$는 $F[U]$에 포함되며 $y_0$를 원소로 가지는 $\mathrm{im} F$의 열린집합이다. 따라서 $F[U]$는 $\mathrm{im} F$에서 열린집합이다. ■

고찰

• 우리손 거리화 정리는 나가타-스미로느프 거리화 정리_{Nagata-Smirnov metrisation theorem}로 강화할 수 있다. 진술은 다음과 같다.

  $X$가 거리화 가능할 필요충분조건은 $X$가 정칙이며 가산-국소적으로 유한한_{countably locally finite} 위상기저를 가지는 공간인 것이다.

  위상공간 $X$의 부분집합들로 이루어진 집합족 $\mathcal{A}$가 국소적으로 유한하다는 것은, 임의의 $x \in X$에 대해 어떤 근방 $U$가 존재하여 $U$가 $\mathcal{A}$의 오직 유한한 개수의 집합과만 교집합을 가진다는 것이다. 위상기저 $\mathcal{B}$가 가산-국소적으로 유한하다는 것은, 각각의 $\mathcal{B}_n$이 국소적으로 유한이도록 $\mathcal{B} = \bigcup_{n \in \omega}\mathcal{B}_n$와 같이 적을 수 있다는 것이다.

• 우리손 거리화 정리의 증명을 살짝 변형하면 다음 사실을 발견할 수 있다.

  정리. $T_1$ 공간인 $X$에 대해, $\lbrace f_{\alpha} \rbrace _{\alpha \in J} $가 다음 조건을 만족하는 연속함수 $f_\alpha : X \to [0, 1]$의 모임이라고 하자: 임의의 $x_0 \in X$와 근방 $U$에 대해, 어떤 $\alpha \in J$가 존재하여 $f_\alpha(x_0) = 1$이고 $f_\alpha[X \setminus U] = \lbrace 0 \rbrace $이다. 이때, $F(x) = (f_\alpha(x))_{\alpha \in J}$는 $X$를 $[0, 1]^J$로 임베딩하는 사상이다.

  $T_1$ 조건을 생략하면 $F$는 단사가 아닐 수 있음을 확인하라. 위 정리는 스톤-체흐 콤팩트화_{Stone-Čech compactification}를 증명하는 데 사용된다.

The Urysohn Lemma and Urysohn Metrisation Theorem

09 Jul 2025

Urysohn Lemma. Let $X$ be a normal space. If $A$ and $B$ are disjoint closed sets in $X$, then there exists a continuous function $f: X \to [0, 1]$ such that $f[A] = \lbrace 0 \rbrace$ and $f[B] = \lbrace 1 \rbrace$.

The separation axioms, e.g. normality, separate points from closed sets in the given space. The significance of the Urysohn Lemma lies in the fact that, in the case of the normal space, two closed sets can be further separated in a nice space. Specifically, with respect to an appropriate continuous map defined on the normal space to $[0, 1]$, two closed sets can be separated in $[0, 1]$. And the myriad “nice” properties of $[0, 1]$ — being a compact Hausdorff metric space, and a space which we are very familiar with and can visualise easily — suggest the remarkable potential of the Urysohn lemma.

Proof

Let us denote $Q = [0, 1] \cap \mathbb{Q}$ (actually it suffices for $Q$ to be a countable dense subset of $[0, 1]$). Since $Q$ is countable, there exists an enumeration of the elements of $Q$. For instance, consider the lexicographic enumeration of the numerators and denominators, $\prec$.

\[0 \prec 1 \prec 1/2 \prec 1/3 \prec 2/3 \prec 1/4 \prec 1/5 \prec 2/5 \prec \cdots\]

Let us now define the collection $\lbrace U_q \rbrace _{q \in Q}$. First, let $U_1 = X \setminus B$ (since $B$ is a closed set, $U_1$ is an open set). By normality, there exists an open set $U_0$ such that $A \subset U_0$ and $\overline{U_0} \subset U_1$. The remaining $U_q$ are recursively defined in the following manner. For any $p \prec q$,

• If $p < q$, then $\overline{U_p} \subset U_q$.
• If $q < p$, then $\overline{U_q} \subset U_p$.

By normality, these conditions can be satisfied, allowing us to fully define the collection $\lbrace U_q \rbrace _{q \in Q}$.

Now, let us define the function $f: X \to [0, 1]$ as follows.

\[f(x) = \begin{cases} \sup_{<}\{q \in Q : x \notin U_q \} & x \notin U_0 \\ 0 & x \in U_0 \end{cases}\]

The notation $\sup_<$ indicates that we are taking the supremum with respect to $<$ rather than $\prec$. From the definition, it follows that $f[A] = 0$ and $f[B] = 1$.

To complete the proof, we must show that $f$ is continuous. Since $\lbrace B_\epsilon(q) \cap [0, 1] : q \in Q, \epsilon \in \mathbb{Q}_{>0} \rbrace$ forms a basis for the topology on $[0, 1]$, it suffices to show that for any $q \in Q$ and postivie rational $\epsilon$ smaller than a certain supremum, the set $S_{q, \epsilon} = f^{-1}(B_\epsilon(q) \cap [0, 1])$ is an open set. Indeed,

• If $0 < q < 1$, then $S_{q, \epsilon} = (X \setminus \overline{U_{q-\epsilon}}) \cap U_{q + \epsilon}$, which is an open set.
• If $q = 0$, then $S_{0, \epsilon} = U_\epsilon$, which is an open set.
• If $q = 1$, then $S_{1, \epsilon} = X \setminus \overline{U_{1 - \epsilon}}$, which is an open set.

Thus, $f$ is continuous. ■

Remarks

• The converse of the Urysohn lemma trivially holds. That is, for any closed sets $A, B \subset X$, if there exists a continuous function $f: X \to [0, 1]$ that separates $A$ and $B$, then the sets $U = f^{-1}[0, 1/2)$ and $V = f^{-1}(1/2, 1]$ are disjoint open sets that separate $A$ and $B$, implying that $X$ is normal. In simple terms, in normal spaces, the Urysohn separation property and the separation axiom are equivalent.

• This does not hold in regular spaces. Specifically, given any closed set $F$ and point $a$ in a regular space $X$, it is not always the case that there exists a continuous function $f: X \to [0, 1]$ satisfying $f(a) = 0$ and $f[F] = \lbrace 1 \rbrace$. A regular space that is Urysohn separable is called a Tychonoff space or a completely regular space, which is a strictly stronger condition than regularity.

• The reason the proof of the Urysohn Lemma does not go through for regular spaces is that constructing the collection $\lbrace U_q \rbrace $ satisfying $p < q \implies \overline{U_p} \subset U_q$ requires the normality axiom.

Urysohn Metrisation Theorem

As an application of the Urysohn Lemma, let us prove the Urysohn Metrisation Theorem.

Urysohn Metrisation Theorem. A second countable normal space is metrizable.

Recall that a second countable regular space is a normal space. Hence the statement of the above theorem can be strengthened to “A second countable regular space is metrisable.”

Thus, the implications between spaces can be summarised as follows. Note that the longer the arrow, the stronger the required condition. The implication $T_2 \to T_4$ is strictly more difficult than $T_3 \to T_4$, and this is evidenced by the fact that the former requires a condition — compactness — strictly stronger than the latter — Lindelöf. Similarly, $T_3 \to \mathrm{Met}$ is strictly more difficult than $T_3 \to T_4$, as the second countability required in the former is strictly stronger than the Lindelöf property. However, neither $T_2 \to T_4$ nor $T_3 \to \mathrm{Met}$ is strictly more difficult than the other (the lengths of both arrows are similar). This is again evidenced by the fact that compactness and second countability do not generally imply each other.

Proof

Let $X$ be a second countable normal space. We will prove the following lemma.

Lemma. There exists a countable collection of continuous functions $\mathcal{F}$ mapping $X$ to $[0, 1]$ such that for any point $x_0 \in X$ and its neighbourhood $U$, there exists a function $f \in \mathcal{F}$ satisfying $f(x_0) > 0$ and $f[X \setminus U] = \lbrace 0 \rbrace$.

Given $x_0$ and $U$, the existence of such an $f$ follows from the Urysohn Lemma. Our task is to reduce this to a countable collection of functions. Let $\mathcal{B} = \lbrace B_n \rbrace $ be a countable basis for the topology on $X$. When $B_m \subset B_n$, we define a continuous function $f_{nm}: X \to [0, 1]$ satisfying the following conditions according to the Urysohn Lemma:

• $f_{nm}[\overline{B_m}] = 1$
• $f_{nm}[X \setminus B_n] = 0$

Let $\mathcal{F} = \lbrace f_{nm} \rbrace $. Given any point $x_0$ and its neighbourhood $U$, by the definition of a basis, there exists a basis element $B_n$ such that $x_0 \in B_n \subset U$. Furthermore, by normality, there exists an open set $V$ such that $x \in \overline{V} \subset B_n$. Again, by the definition of a basis, there exists a basis element $B_m$ such that $x \in B_m \subset V$. Hence $f_{nm} \in \mathcal{F}$ satisfies the conditions of the lemma. □

Now, let us prove the main theorem. The idea is to embed $X$ into $[0, 1]^\omega$, as $[0, 1]^\omega$ equipped with metric topology is known to be a metric space. It then follows that $X$ is metrisable, being a space homeomorphic to a subspace of a metric space.

Let $\mathcal{F} = \lbrace f_n \mid n \in \omega \rbrace $ be the countable collection of functions given by the lemma. We define the mapping $F: X \to [0, 1]^\omega$ as follows:

\[F: x \mapsto (f_1(x), f_2(x), f_3(x), \dots)\]

We will show that $F$ is an embedding. That is, we need to demonstrate that $F$ is continuous, injective, and a homeomorphism between the domain and the image.

Since each $f_n$ is continuous, by the properties of the product topology, $F$ is continuous (side note: one can regard this as the definition of the product toplogy). The injectivity of $F$ follows from the fact that $X$ is Hausdorff. Therefore, it suffices to show the following:

If $U \subset X$ is an open set, then $F[U]$ is open in $\mathrm{im} F$.

Let us show that for any $y_0 \in F[U]$, there exists a set $V \subset F[U]$ open in $\mathrm{im} F$ that contains $y_0$. By the definition of $F[U]$, there exists some $x_0 \in X$ such that $F(x_0) = y_0$. Let $f_n \in \mathcal{F}$ be a function satisfying the conditions of the lemma for $x_0$ and $U$. Since $f_n(x_0) = 1$, it follows that $(y_0)_n = 1$. Therefore, $W = \pi_n^{-1}(0, 1] \subset [0, 1]^\omega$ is a set containing $y_0$ that is open in $[0, 1]^\omega$.

Now, we need to show that $W \cap \mathrm{im} F \subset F[U]$. For any $w \in W$, we can write $F(x_1) = w$. Additionally, if $w \in \mathrm{im} F$, then $f_n(x_1) = 1$. However, since $f_n$ vanishes outside of $U$, it follows that $x_1 \in U$. Thus, $w \in F[U]$, i.e. $W \cap \mathrm{im} F$ is contained in $F[U]$ and is an open set in $\mathrm{im} F$ containing $y_0$. Hence, $F[U]$ is an open set in $\mathrm{im} F$. ■

Remarks

• The Urysohn Metrisation Theorem can be strengthened to the Nagata-Smirnov Metrisation Theorem. The statement is as follows:

  A space $X$ is metrizable if and only if $X$ is regular and has a countably locally finite topology basis.

  A collection of subsets $\mathcal{A}$ of a topological space $X$ is said to be locally finite if for any point $x \in X$, there exists a neighbourhood $U$ such that $U$ intersects only finitely many sets from $\mathcal{A}$. A topological basis $\mathcal{B}$ is said to be countably locally finite if it can be expressed as $\mathcal{B} = \bigcup_{n \in \omega}\mathcal{B}_n$ where each $\mathcal{B}_n$ is locally finite.

• A slight modification of the proof of the Urysohn Metrisation Theorem leads to the following result.

  Theorem. Let $X$ be a $T_1$ space, and let $\lbrace f_{\alpha} \rbrace_{\alpha \in J}$ be a collection of continuous functions $f_\alpha : X \to [0, 1]$ satisfying the following condition: for any point $x_0 \in X$ and its neighbourhood $U$, there exists $\alpha \in J$ such that $f_\alpha(x_0) = 1$ and $f_\alpha[X \setminus U] = \lbrace 0 \rbrace$. Then, the mapping $F(x) = (f_\alpha(x))_{\alpha \in J}$ embeds $X$ into $[0, 1]^J$.

  Omitting the $T_1$ condition may result in $F$ not being injective. This theorem is used to prove the Stone-Čech compactification.

크립키-비트겐슈타인 역설

03 Jul 2025

“2.2. 성향적 분석” 절에서 크립키의 원 논문과는 독자적인 필자의 보론이 많이 들어갔으니 유의 바랍니다.

개요

크립키는 비트겐슈타인의 ⟪철학적 탐구⟫의 핵심이 소위 규칙 따르기에 대한 회의주의_{Skepticism about rule following}에 있다고 주장한다.

크립키의 독해에 따르면 ⟪탐구⟫의 §1-137은 비트겐슈타인이 ⟪논리철학논고⟫의 언어관을 비판하고 극복하는 대목이다. §138-242에서는 규칙 따르기에 대한 회의주의가 제시된다. “앨리스는 ‘+’로 덧셈을 의미한다”와 같은 명제에 대응되는 사태가 있는지에 관해 의문을 제기하는 회의주의 논증은, ⟪논고⟫의 언어관이 올바를 수 없음을 보이는 최종적인 논증이라는 점에서 §1-137을 확정지을 뿐 아니라, 의미의 문제를 해명하는 이론은 어떠한 형태로든 가능하지 않다는 궤멸적인 결론을 시사하는 듯하다.

크립키에 따르면 비트겐슈타인은 이에 대해 “회의주의적 해답”을 제시한다. 즉, 회의주의자의 결론 — “앨리스는 ‘+’로 덧셈을 의미한다’“에 대응하는 사태는 없다 — 을 받아들이되, 그것이 어떻게 “초록색 생각이 잠을 잔다”와 같은 명제와는 달리 유의미하게 사용될 수 있는지를 해명하는 것이다. 그 해답이란, 언어의 의미는 그것이 공동체에서 가지는 기능과 불가결하며, 따라서 의미에 대한 논의는 개별 언어 사용자 단위에서는 공허하지만 언어 공동체 단위에서는 유효하다는 언어의 공적성을 강조하는 것이다.

§243 이후는 “회의주의적 해답”을 기타 철학적 문제에 적용하는 대목이다. 회의주의적 해답의 함의 중 하나는 사적 언어_{private language}의 불가능성이다. 그럼에도 사적인 방식으로 작동하는 듯한 영역의 언어가 대표적으로 두 가지 있는데, 바로 수학적 언어와 심리적 언어이다. 그러나 비트겐슈타인은 수학적 언어와 심리적 언어가 사적 언어에 해당한다는 생각이 착각이라고 역설한다. 이 대목에서 우리는 비트겐슈타인 특유의 수학철학적 · 심리철학적 입장을 엿볼 수 있다.

1. 크립키-비트겐슈타인 역설

크립키-비트겐슈타인 역설의 결론은 다음과 같다.

“화자 $A$는 기호 $s$로 의미 $m$을 의미한다” 꼴의 명제¹에는 대응되는 사태가 없다. 즉, 해당 명제는 진릿값을 결여한다.

따라서 가령 “앨리스는 ‘+’로 덧셈을 의미한다”라는 명제는 “앨리스의 생각은 초록색이다”라는 명제만큼이나 불가해한 명제이다.

1.1. 회의주의자의 등장

그렇다면 도대체 어째서 크립키-비트겐슈타인은 이토록 극단적인 주장을 하는 것일까? 논증의 핵심은, 언어 사용자가 단어의 의미를 파악하는 과정에 숨은, 간과하기 쉽지만 실로 모순적인 측면에 있다. 바로 과거의 유한한 학습 경험으로부터, 해당 단어가 사용될 수 있는 무한한 사례들에 대해 올바른 추론을 할 수 있어야 한다는 것이다.

예를 들어 앨리스는 지금까지 50이 넘는 두 수의 덧셈을 해본 적이 없다고 하자. 그렇다고 해도 누군가 앨리스에게 ’68 + 57’을 묻는다면 그는 어렵지 않게 ‘125’라고 답할 것이다. 그런데 이때 앨리스에게 한 회의주의자가 다가오더니, ‘125’라는 그의 답은 틀렸으며, 앨리스가 내놓았어야 하는 답은 ‘5’였다고 주장한다. 구체적으로, 회의주의자는 다음을 주장한다.

만약 앨리스가 과거에 ‘+’에 부여하던 의미와 현재 ‘+’에 부여하는 의미가 일치한다면, 앨리스는 ‘5’라고 답했어야 한다.

왜냐하면 — 적어도 회의주의자에 따르면 — 앨리스가 과거에 ‘+’에 부여했던 의미는 사실 덧셈(+)이 아니라 컷셈(⨁)이었기 때문이다. 컷셈의 정의는 다음과 같다.

\[x \oplus y = \begin{cases} x + y & x, y < 50 \\\ 5 & \text{otherwise} \end{cases}\]

이에 앨리스는 과거부터 자신은 ‘+’를 컷셈이 아닌 덧셈의 의미를 사용했다고 즉각 반박할 것이다. 그런데 여기부터 본격적인 문제가 시작된다. 과거에 앨리스가 ‘+’에 부여한 의미가 컷셈이 아닌 덧셈이었음을 어떻게 입증할 수 있는가? 문제의 가정으로 인해, 과거에 앨리스가 수행한 ‘+’의 계산 기록들로부터 이를 입증하는 것은 불가능하다.

방금 등장한 ‘입증’이라는 표현으로 인해 이 문제가 인식론에 속하는 것처럼 보일 수 있다 (“우리는 앨리스가 ‘+’로 덧셈을 의미한다는 사실을 어떻게 알 수 있을까?”). 그러나 크립키가 묻는 것은, 앨리스의 머리 속까지 들여다 볼 수 있는 전지전능한 관찰자라고 할지라도 앨리스가 ‘+’로 덧셈을 의미하는지, 혹은 덧셈과 충분히 많은 경우에 일치하는 비표준적인 연산을 의미하는지 알 수 있는가이다. 이런 점에서 크립키가 제시하는 회의주의는 존재론적인 것이다. 문제의 요점은 “앨리스가 컷셈이 아닌 덧셈을 의미한다”에 대응하는 사태_case가 있는가이다. 이는 후술하다시피 크립키가 반사실적 조건문 혹은 가능세계를 통해 회의주의를 해소하려는 시도까지 검토한다는 점에서 — 비록 그 시도 또한 실패한다고 결론 내리지만 — 드러난다.

1.2. 두 가지 조건

회의주의자의 주장에는 두 가지 주목할 점이 있다. 첫째, 회의주의자의 주장은 가정문이다. 회의주의자는 앨리스가 어떤 경우에서든 ’5’라고 답해야 함을 주장하는 것이 아니다. 그가 주장하는 바는, 만약 앨리스가 과거에 ‘+’에 부여하던 의미와 현재 ‘+’에 부여하는 의미가 일치한다면 ’5’라고 답해야 한다는 것이다. 둘째, 회의주의자의 주장은 규범적이다. 회의주의자의 주장은 — 앞서 말한 조건이 만족되었을 때 — 앨리스는 ‘5’라고 답할 것이라는 주장이 아니라 ‘5’라고 답해야 한다는 주장이다.² 달리 말해, 회의주의자는 만약 앨리스가 ’68 + 57’에 대해 ‘5’라고 대답했더라면 그 대답은 정당했을 것 임을 주장한다.

따라서 회의주의자의 주장에 대한 반박 또한 두 가지 특징을 갖춰야 한다. 첫째, 화자에 관한 어떠한 사실이, 해당 화자가 특정 기호를 특정 의미로 사용함을 구성하는지 설명해야 한다. 이 설명은 회의주의자의 주장에서 가정이 무엇을 의미하는지를 해명하기 위해 필요하다.³ 둘째, 해당 사실이 어떠한 방식으로 화자의 언어 사용을 정당화하는지 설명해야 한다. 이 설명은 회의주의자의 결론이 규범적이기 때문에 필요하다.

두 번째 조건의 의의가 안 와닿을 수도 있기 때문에 조금 더 설명을 해 보겠다. 가령 어떤 매드사이언티스트가 오더니 회의주의자에게 이렇게 말했다고 하자.

사실 나는 과거에 앨리스를 원자 단위로 스캔한 적이 있다. 그래서 나는 너의 말을 듣고 그 스캔본을 본따 만든 앨리스-2에게 ’68 + 57‘을 물어보았고, 앨리스-2는 ’125‘라고 대답했다. 따라서 과거의 앨리스는 ’+‘로 컷셈을 의미하지 않았다.

그러나 매드사이언티스트의 실험은 회의주의자의 주장을 반박하는 데 역부족이다. 매드사이언티스트의 실험은 두 번째 조건을 만족하지 않기 때문이다. 해당 실험의 결과는 앨리스가 언제나 ‘125’라고 답했을 것임을 보증할 뿐, 앨리스가 언제나 ‘125’라고 답해야만 했음은 보증하지 않는다.

이는 체계적 계산 오류의 사례를 통해 더 명확히 이해할 수 있다. 가령 덧셈을 처음 배우는 아이는 종종 받아올림을 까먹곤 한다. 그런 아이는 ’68 + 57’에 대해 ‘125’가 아니라 ‘115’라고 대답할 것이다. 그런데 모종의 문제로 인해 어른이 될 때까지 받아올림 실수를 교정하지 못한 존슨이라는 사람이 있다고 하자. 존슨은 덧셈이 무엇인지 이해하며, 구체적인 덧셈 문제가 아니라 덧셈에 대한 성질을 질문 받으면 — 가령, “결합법칙을 만족하는가?” — 올바르게 대답한다. 다만, 존슨은 그의 실수를 교정해 줄 지도자가 없는 상황에서 ’68 + 57’을 질문 받으면 언제나 ‘115’라고 대답했을 것이며, 앞으로도 그럴 것이다. 이를 두고 우리는 존슨이 ‘+’에 덧셈의 의미를 부여하고 있으나, 그 의미에 정당한 방식대로 ’68 + 57’에 대답하지 못하는 것이라 주장하고 싶다. 바로 이 주장을 성립시키기 위해 두 번째 조건이 필요한 것이다. 두 번째 조건을 만족하지 못하는 의미론을 채택한다면, 우리는 존슨이 ‘+’에 텃셈 — 두 수의 덧셈을 받아올림을 제하고 수행하는 연산 — 혹은 펏셈 — 곁에 지도자가 없는 상황에서는 텃셈을 수행하고, 있는 상황에서는 지도자의 교정을 받아 덧셈을 수행하는 연산 — 의 의미를 부여하고 있다고 수긍해야 하기 때문이다.⁴

2. 회의주의에 대한 반박 검토

2.1. 언어적 해명

회의주의자의 주장을 들은 앨리스가 내놓을 첫 번째 대답은 아마 이러할 것이다. “과거의 나는 ‘x + y’에 x개의 대상과 y개의 대상을 한데 모아 세는 연산의 의미를 부여해 왔다. 따라서 과거의 나는 ‘+’를 컷셈의 의미로 사용하지 않았다.”

그러나 회의주의자는 이에 대해 또 한번 회의주의를 펼칠 수 있다. 요컨대 그는 과거에 앨리스는 ‘모아 세다’라는 단어를 줄곧 셈_count이 아닌 켐_quont으로 이해하고 있었다고 주장할 수 있다. 묶음을 켄다는 것은 묶음의 크기가 50 미만일 때는 세는 것이고 50을 초과할 때는 5라고 대답하는 것이다.

요지는, ‘+’에 부여한 의미가 무엇인지를 다른 언어적 증거를 통해 입증하려는 시도는 해당 증거 또한 비표준적인 의미가 부여되었을 가능성을 제거하지 못하므로 무한 퇴행에 빠진다는 것이다.⁵

2.2. 성향적 분석_{dispositional analysis}

심리철학에서 성향적 분석은 행동주의_behaviourism가 심리 상태를 설명하는 방식으로, 핵심은 다음과 같다.

심리 상태의 성향적 분석. 주체 $A$가 과거, 현재, 또는 미래에 심리 상태 $\mathfrak{m}$에 있다는 것은, $A$에게 특정 자극 $s$이 주어졌더라면 / 주어진다면 / 주어지게 된다면, $A$는 반응 $b = f_\mathfrak{m}(s)$를 보였을 / 보일 / 보이게 될 것이라는 말이다. 즉, 심리 상태($\mathfrak{m}$)은 자극-반응 대응($f_\mathfrak{m}$)으로 환원된다.

예를 들어 금방 선잠에서 깬 앨리스가, 어둑어둑한 방과 창밖으로 들리는 물방울 소리를 듣고, “지금 비가 오고 있다”라는 믿음을 형성했다고 해보자. 성향적 분석에 따르면 “앨리스는 ‘지금 비가 오고 있다’고 믿는다”의 의미는 다음의 (무수히 많은) 자극-반응 대응과 다름이 없다.

• 친구에게서 같이 밥 먹으러 가자는 전화가 온다면, -> 우산을 챙길 것이다.
• 이웃에게서 밖에 당신의 빨래가 걸려 있다는 연락이 온다면, -> 빨래를 급히 거두러 갈 것이다.
• 내일 야외 일정이 잡힌다면, -> 내일의 날씨를 확인할 것이다, 등등…

만약 이러한 자극-반응 대응에서 크게 어긋나는 현상이 관측된다면 성향적 분석주의자는 앨리스의 믿음에 대한 견해를 수정할 것이다. 예를 들어 앨리스가 외출을 나서는데 우산을 챙기는 대신 선글라스를 챙긴다면, 그는 앨리스가 “비가 오고 있다”는 믿음이 아닌 “햇살이 쨍쨍하다”는 믿음을 가지고 있다고 판단할 것이다.

지금까지의 설명에서 주목할 성향적 분석의 특징은 두 가지이다.

1. 반사실적 조건문을 사용한다. 앨리스가 과거, 현재, 또는 미래에 외출을 나가지 않는다고 하더라도, “앨리스가 외출을 나갔더라면 / 나간다면 / 나가게 된다면 그는 우산을 챙겼을 / 챙길 / 챙기게 될 것이다”는 그가 가졌던 / 가지고 있는 / 가지게 될 믿음에 대한 성향적 분석의 일부를 이룬다.
2. 기술적이다. 성향적 분석은 행동주의를 기반으로 하기 때문에 “앨리스가 외출을 나간다면 그는 우산을 챙겨야 한다” 와 같은 규범적 명제가 아닌, “앨리스가 외출을 나간다면 그는 우산을 챙길 것이다” 와 같은 기술적 명제로 이루어진다. 성향적 분석에 따르면, 만약 앨리스가 외출을 나서는데 우산을 챙기는 대신 선글라스를 챙긴다면, 앨리스는 비가 오고 있다는 믿음을 가지고 있음에도 그에 정당하게 행동하지 않는 것이 아니라, 애초에 비가 오고 있다는 믿음을 가지고 있지 않은 것이다.

크립키는 자신과 사적인 자리에서 규칙 따르기 역설을 논의했던 일부 철학자들이, 성향적 분석의 1번 특징에 의존함으로써 성향적 분석을 통한 역설의 해결을 시도했다고 전한다. 이 접근법은 다음을 주장한다.

의미에 대한 성향적 분석. 화자 $A$가 과거, 현재, 또는 미래에 기호 $s$로 의미 $\mathfrak{m}$을 의미한다는 것은, $s$가 포함된 문장 $\phi$가 $A$에게 주어졌더라면 / 주어진다면 / 주어지게 된다면, $A$는 문장 $\psi = f_\mathfrak{m}(\phi)$로 대답했을 / 대답할 / 대답하게 될 것이라는 말이다. 즉, 의미($\mathfrak{m}$)는 문답 대응($f_\mathfrak{m}$)으로 환원된다.

이 분석에 따르면, 앨리스가 과거, 현재, 또는 미래에 ‘+’로 덧셈을 의미한다는 것은, 앨리스에게 x + y를 물어보았더라면 / 물어본다면 / 물어보게 될 때, $A$는 x와 y의 합으로 대답했을 / 대답할 / 대답하게 될 것이라는 말이다. 이러한 반사실적 조건문을 통해 회의주의를 극복하려는 철학자의 사고 흐름은 대략 다음과 같을 것이다.

1. 회의주의자는 과거의 앨리스가 ‘+’로 덧셈을 의미했는지, 덧셈이 아니지만 충분히 많은 경우에 덧셈과 일치하는 비표준적 연산을 의미했는지 구별하는 사태가 지금까지 없었고, 앞으로도 없을 것임을 지적한다.
2. 1이 주장 가능한 이유는, 앨리스가 지금까지 수행했고, 앞으로 수행할 ‘+’의 연산 횟수가 유한하기 때문이다.
3. 그러나 “과거의 앨리스에게 ’x + y’을 물어보았더라면 나는 x와 y의 합을 대답했을 것이다”, 또는 “미래의 앨리스에게 ‘x + y’를 물어본다면 나는 x와 y의 합을 대답할 것이다”라는 반사실적 조건문을 사용하면, 우리는 2의 유한성을 극복할 수 있다.
4. 이에 따라, 반사실적 조건문은 객관적인 진릿값을 가진다는 사실을 — 가능세계 존재론 등을 통해 — 인정한다면, ”앨리스가 ’+‘로 덧셈을 의미한다“에 대응되는 의미에 대한 성향적 분석은 앨리스가 ‘+’로서 의미하는 연산을 객관적으로 결정한다.

이 논증은 회의주의자에 대한 반박이 갖춰야 할 첫째 조건 — 화자에 관한 어떠한 사실이 해당 화자가 특정 기호를 특정 의미로 사용함을 구성하는지 설명해야 한다 — 을 만족한다. 그 사실이라 함은 반사실적 조건문인 것이다. 그러나 크립키는 둘째 조건 — 해당 사실이 어떠한 방식으로 화자의 언어 사용을 정당화하는지 설명해야 한다 — 을 갖추지 못하므로 성향적 분석은 역설을 해소하는 데 불충분하다고 지적한다. 이는 앞서 지적했듯이 성향적 분석이 본질적으로 기술적이기 때문이다. 크립키의 말을 인용하자면,

좋다. 나는 ‘125’가 내가 주어진 수식에 대해 내놓을 대답임을 알며, (실제로 그렇게 대답하고 있지 않은가!) 어쩌면 — 그저 하나의 주어진 사실로서 — 과거의 나에게 같은 수식이 주어졌다고 하더라도 똑같이 대답했으리라는 사실 또한 안다고 하자. 이 모든 사실들이 도대체 어떻게 — 현재 또는 과거에서 — ‘125’가, 내 내면의 어떤 규칙에 의거하여 도출된 정당화된 답이지, 그저 눈 가리고 아웅하며 내놓은 아무 근거 없는 답이 아니라는 사실을 보여주는가?

Well and good, I know that ‘125’ is the response I am disposed to give (I am actually giving it!), and maybe it is helpful to be told — as a matter of brute fact — that I would have given the same response in the past. How does any of this indicate that — now or in the past — ‘125’ was an answer justified in terms of instructions I gave myself, rather than a mere jack-in-the-box unjustified and arbitrary response?

(이탤릭체는 원문, 강조는 필자)

크립키가 지적하는 바는 다음과 같이 차근차근 이해할 수 있다. 기억을 되살려 보면, 회의주의자에게 대항하는 주장은 다음의 형식을 갖춰야 한다.

주장 1. 만약 앨리스가 과거에 ‘+’에 부여하던 의미와 현재 ‘+’에 부여하는 의미가 일치한다면,

1. 앨리스는 ‘5’라고 답해야 하는 것이 아니라,
2. 앨리스는 ‘125’라고 답해야 한다.

성향적 분석에 의하면 위 주장은 다음과 동의적이다.

주장 1.1. 만약 ‘+’에 대한 과거 앨리스의 문답 성향이 ‘+’에 대한 현재 앨리스의 문답 성향과 일치한다면,

1. 앨리스는 ‘5’라고 답해야 하는 것이 아니라,
2. 앨리스는 ‘125’라고 답해야 한다.

“그저 하나의 주어진 사실로서”, ‘+’에 대한 과거 앨리스의 문답 성향이 두 수가 주어졌을 때 그 합을 말하는 것이었다고 하자. 이 사실을 위에 대입하면,

주장 1.2. 만약 ‘+’에 대한 현재 앨리스의 문답 성향이 두 수가 주어졌을 때 그 합을 말하는 것이라면,

1. 앨리스는 ‘5’라고 답해야 하는 것이 아니라,
2. 앨리스는 ‘125’라고 답해야 한다.

그러나 주장 1을 주장 1.2.로 재진술하였다고 한들, 이를 성립시킬 근거는 여전히 전무하다. 만약 1, 2의 술어부가 “답할 것이다”였다면 주장이 성립하겠지만, 요구된 것은 “답해야 한다”이다. 이것은 문답 성향만 가지고서 알 수 있는 사실이 아니다.

그렇다면 처음부터 1, 2의 술어부를 ”답할 것이다“라고 둘 수는 없을까? 요컨대 회의주의자에게 다음을 주장하는 것이다.

주장 2. 만약 앨리스가 과거에 ‘+’에 부여하던 의미와 현재 ‘+’에 부여하는 의미가 일치한다면,

1. 앨리스는 ‘5’라고 답할 것이 아니라,
2. 앨리스는 ‘125’라고 답할 것이다.

그럴 수는 없다. 앞서 “체계적 계산 오류의 사례”에서 자세히 설명했듯이, 앨리스가 ‘68 + 57’에 대해 ‘125’라고 대답하지 않았다고 해서 그 사실이 즉시 앨리스가 ‘+’로 덧셈을 의미하지 않았음을 시사하지는 않기 때문이다. 우리는 덧셈을 수행함에 있어 때때로 실수를 하곤 하지만, 그런 실수가 저지를 때마다 ’+‘를 덧셈이 아닌 다른 의미로 사용했음을 뜻하지는 않는다. 오히려 내가 ‘+’ 연산을 수행함에 있어 실수를 저지를 수 있다는 사실 자체가, 내가 내놓는 계산 결과가 내가 ‘+’에 부여하는 의미를 결정하는 것이 아니라, 역으로 내가 ‘+’에 부여하는 의미가 선행하여 내가 내놓아야 할 결과를 결정함을 시사한다.

그럼에도 성향적 분석으로 의미의 규범성을 설명하기 위해서는 다음과 같이 회의주의자의 도전을 재해석해야만 할 듯하다.

주장 3. 만약 앨리스가 과거에 ‘+’에 부여하던 의미와 현재 ‘+’에 부여하는 의미를 일치시키고자 한다면,

1. 앨리스는 ‘5’라고 답해야 하는 것이 아니라,
2. 앨리스는 ‘125’라고 답해야 한다.

이는 다음 진술로 이어진다.

주장 3.1. 만약 ‘+’에 대한 현재 앨리스의 문답 성향이 두 수가 주어졌을 때 그 합을 말하는 것이 되고자 한다면,

1. 앨리스는 ‘5’라고 답해야 하는 것이 아니라,
2. 앨리스는 ‘125’라고 답해야 한다.

확실히 주장 3.1은 주장 1.1, 1.2보다는 그럴듯해 보인다. 그러나 필자가 보기에 주장 3.1에도 여전히 문제가 있다.

첫째 문제는, 설령 주장 3이 성립한다고 하더라도 그것이 주장 1을 시사하지는 않는다는 문제이다. $p, q$를 다음과 같이 두자.

• $p:$ 앨리스가 과거에 ‘+‘에 부여하던 의미와 현재 ’+‘에 부여하는 의미가 일치한다.
• $q:$ 앨리스는 ‘125’라고 답한다.

이 경우 주장 1과 주장 3은 각각 다음과 같다. ($W$는 ”하고자 한다“를, $\Box$는 “해야 한다”를 의미)

• 주장 1. $p \rightarrow \Box q$
• 주장 3. $Wp \rightarrow \Box q$

그러나 $p$는 $Wp$를 시사하지 않고 (내가 원하지 않는 일이 나에게 일어날 수 있다) $Wp$ 또한 $p$를 시사하지 않기 때문에 (내가 원하는 일이 나에게 일어나지 않을 수 있다) 주장 1과 주장 3에는 어떠한 논리적 관계도 없다. 구체적으로 전자의 경우로는, ‘+’를 곱셈의 의미로 사용하겠다고 다짐한 반항아 학생이 자신의 다짐이 무색하게 습관적으로 ‘68 + 57‘에 ’125‘라고 대답해버리는 상황이 있다. 후자의 경우로는 ‘+’ 기호를 덧셈의 의미로 사용하고자 하지만 아직 덧셈의 개념을 완전히 숙지하지 못한 학생의 경우가 있다.

둘째 문제는, 애초에 주장 3은 무한 회귀에 빠진다는 것이다. 잠시 설명의 편의를 위해 심리 상태의 사례로 돌아가 보자. 현재의 문제를 심리 상태에 관한 것으로 전환하면 다음과 같을 것이다. 앨리스는 지금 밖에 비가 오고 있다는 믿음을 가지고 있음에도 불구하고 우산이 아닌 다른 물건을 챙긴 채 밖으로 나갈 수 있다. 가령 앨리스가 허겁지겁 외출 준비를 하고는 우산꽂이에서 아무거나 뽑은 채 집을 나섰는데, 손에 잡힌 게 우산이 아니라 지팡이였던 상황을 고려해 보자. 기존의 성향적 분석에 따르면 이 경우 앨리스는 애초부터 비가 오고 있다는 믿음을 가지고 있지 않던 것인데 이는 반직관적인 결론이다. 이에 대해 성향적 분석주의자는 다음의 주장들을 대신 내세울지 모른다.

주장 4. 만약 앨리스가 과거에 ‘어두컴컴한 방과 창밖으로 떨어지는 물방울 소리’에 형성하던 믿음과 현재 동 상황에 형성하는 믿음을 일치시키고자 한다면,

1. 앨리스는 지팡이를 챙겨야 하는 것이 아니라,
2. 앨리스는 우산을 챙겨야 한다.

주장 4.1. 만약 ‘어두컴컴한 방과 창밖으로 떨어지는 물방울 소리’에 대해 앨리스가 보였을 자극-반응 대응과, 동 상황에 대한 현재 앨리스의 자극-반응 대응을 일치시키고자 한다면,

1. 앨리스는 지팡이를 챙기는 것이 아니라,
2. 앨리스는 우산을 챙겨야 한다.

주장 4.2. 만약 ‘어두컴컴한 방과 창밖으로 떨어지는 물방울 소리’에 대한 앨리스의 자극-반응 대응이 외출을 나가는 상황에 대하여 우산을 챙기는 것이 되고자 한다면,

1. 앨리스는 지팡이를 챙기는 것이 아니라,
2. 앨리스는 우산을 챙겨야 한다.

이미 앞서 말했듯이 주장 4는 $Wp \rightarrow \Box q$의 형태이므로 애초에 $p \rightarrow \Box q$와 논리적 관계가 없지만, 그 문제를 차치하더라도 일면 타당해 보이는 주장 4.2에는 본질적인 문제가 있다. 애당초 우리가 성향적 분석을 시도하는 이유는 심리 상태에 관한 진술을 행동주의적인 표현으로 옮기기 위해서이다. 그런데 주장 4.2는 한 특정 심리 상태 — 밖에 비가 오고 있다는 믿음 — 에 관한 진술을, 다른 심리 상태 — 외출을 나가는 상황에 대하여 우산을 챙기는 반응을 보이고자 하는 의도 — 에 관한 진술로 바꾼 것에 지나지 않는다. 이제 우리는 누군가가 ‘외출을 나가는 상황에 대하여 우산을 챙기는 반응을 보이고자 하는 상태’가 무엇인지를 성향적 분석으로 설명해야 하는데, 이는 결국 무한 회귀에 빠지는 것이다.

동일한 이유로 주장 3 또한 무한회귀에 빠진다. 앞선 논의를 되새겨 보면, 회의주의자의 주장에 대한 반박이 갖춰야 할 필요조건 중 하나는 “화자에 관한 어떠한 사실이, 해당 화자가 특정 기호를 특정 의미로 사용함을 구성하는지 설명할 것“이다. 그런데 주장 3.1은 이 문제에 대해 “문답 성향을 특정한 방식에 일치시키고자 하는 의도”라는 답을 제시한다. 그렇다면 회의주의자는 이에 대해, ”화자에 관한 어떠한 사실이, 해당 화자가 ‘+’ 기호에 대한 문답 성향을 특정한 방식 — 이를테면, 컷셈이 아닌 덧셈에 대응되는 문답 성향 — 에 일치시키고자 하는 의도를 가지고 있음을 구성하는가?“ 라고 반문할 수 있다.

결론적으로, 성향적 분석으로 의미의 문제를 해결하려는 시도는 의미의 규범성을 설명하지 못한다. 규범성을 설명할 수 있도록 성향적 분석을 억지로 끼워맞추려는 시도는 문제가 요구하는 바를 벗어날 뿐 아니라, 무한 회귀의 오류에까지 빠지게 된다.

2.3. 기계주의

그렇다면 언어적 해명이나 성향적 분석과 같은 추상적인 설명에 급급하는 대신, 아예 ‘+’가 의미하는 연산에 대응되는 구체적인 기계를 설계해 제시해 줌으로써 회의주의자에게 대응할 수는 없을까? 가령 기계식 계산기를 제작하거나, 논리 회로로 전가산기를 설계해 보이는 것이다. 그러나 크립키는 이 시도 또한 크게 세 가지 이유에서 부적절한다고 주장한다.

첫째, 기계의 사용법이 여전히 해명을 요하는 문제로 남는다. 튜링 기계로 예를 들면, 우리는 튜링 기계가 출력하는 이진 나열을 이진법으로 해석하여 결과를 읽을 것이다. 그러나 회의주의자는 이 기계를 해석하는 올바른 방식이 퀴진법 이며, 퀴진법에 따르면 튜링 기계는 덧셈이 아니라 컷셈을 출력하고 있다고 주장할 수 있다.

둘째, 실제 기계는 오직 유한한 입력만을 받을 수 있다. 그런 의미에서 실제 기계는 앨리스보다 더 ‘유능한’ 존재가 되지 못한다. 그렇다고 실제 기계를 구현하는 대신 기계의 알고리즘을 제시한다면, 이는 다시 “2.1. 언어적 해명”으로 돌아가는 것이다.

셋째, 기계는 오작동할 수 있다. 누군가 기계를 떨어뜨려서 기어가 빠지거나, 너무 오래 쓰다 보니 전선이 녹을 수도 있다. 따라서 우리는 기계에게 의미 해명의 책임을 전임하여 “이 기계는 언제나 내가 의미하는 연산을 계신한다”라고 주장할 수 없다. 그렇다고 우리는 “이 기계는 오작동하지 않는 한 언제나 내가 의미하는 연산을 계산한다”라고 주장할 수도 없다. 그렇게 주장하기 위해서는 기계가 정상적으로 작동하고 있는지 오작동하는지 판단하는 기준을 제시해야 하는데, 그 기준은 결국 우리가 이 기계를 어떤 의도로 사용하고자 하는지에 달려 있을 것이다 (어떤 괴이한 설계자는 기어의 빠짐과 전선의 녹아내림을 통해 덧셈을 계산하는 기계를 만들 수도 있지 않은가?). 따라서 오작동하지 않는 한 이라는 표현을 사용하는 순간 기계가 아닌 화자의 의도가 선행하게 된다.

2.4. 오컴의 면도날

크립키는 다음의 주장도 고려한다.

오캄 의미론. 두 가설 “화자 $A$는 기호 $s$로 의미 $\mathfrak{m}_1$을 의미한다”와 “화자 $A$는 기호 $s$로 의미 $\mathfrak{m}_2$를 의미한다”가 비결정 상태에 있을 때, $\mathfrak{m}_1$과 $\mathfrak{m}_2$ 중 더 단순한 쪽의 가설을 우선적으로 받아들여야 한다.

예를 들어 다음 두 가설을 보자.

    H1. 과거에 앨리스는 ‘+’로 덧셈을 의미했다.

    H2. 과거에 앨리스는 ‘+’로 컷셈을 의미했다.

과거에 앨리스가 수행한 ‘+’ 연산 기록의 양항은 모두 50 이하이므로, H1과 H2는 비결정 상태에 있다. 오캄 의미론이 주장하는 바는 이 경우 우리는 H1설을 우선적으로 받아들여야 한다는 것이다. 덧셈이 컷셈보다 더 단순한 연산이기 때문이다.

그러나 크립키는 이 주장을 짧게만 언급하고 넘어가는데, 회의주의를 논박하는 데 있어 부적절하다는 사실이 자명하기 때문이다. 이는 ‘단순하다’라는 술어가 주관적이라든가, 정의하기 어렵다든가, 화성인에게는 컷셈이 덧셈보다 더 단순할지도 모른다 등의 이유 — 물론 이 이유들도 매우 정당하다 — 때문만이 아니다. 더 본질적인 이유는, 회의주의 논증의 결론이 “H1과 H2 중 어느 하나가 참인지 미정이다”가 아니라, “H1과 H2 중 어느 하나가 참이라는 사실이 어떤 사태에 해당하는지가 미정이다”라는 것이다. 회의주의 논증에 따르면 우리는 H1과 H2가 서로 다른 사태를 나타내는지도 확실하지 않은 상황이다. 이토록 가설이 나타내는 사태가 명확하지 않다면 우리는 오컴의 면도날의 적용이 정당한지를 따지기도 전에 애초에 적용할 수 없다.

2.5. 심리주의

크립키가 더 중요하게 고려하는 반론은 심리주의이다.

심리주의 의미론. 화자 $A$가 기호 $s$로 $\mathfrak{m}$을 의미한다는 것은, 화자의 내면에 $\mathfrak{m}$에 대응되는 특유한_queer 심리적 경험 $p_\mathfrak{m}$이 형성되었다는 말이다.

여기서 “특유한 심리적 경험”은 퀄리아와 비슷한 것으로 생각할 수 있다. 요컨대 “빨간색을 보는 것”이 다른 술어나 경험으로 환원될 수 없는 특유 경험이듯이, “‘+’로 덧셈을 의미하는 것” 또한 그러한 특유 경험이라는 것이다.

크립키는 그러한 특유 경험이 존재할 가능성을 부정하지 않는다.⁶ 그러나 크립키는 심리주의 의미론 또한 회의주의 논증을 해결하지 못함을 지적한다. 문제는 어김없이 “1.2. 두 가지 조건” 중 2번 조건에 있다.

단적인 예시로, 앨리스는 ‘+’ 기호를 사용할 때마다 이마에서 통증을 느낀다고 해보자. 이 사실은 “1.2. 두 가지 조건” 중 1번 조건을 만족한다. 즉, 앨리스가 과거에 ‘+’에 부여한 의미와 현재 부여하는 의미가 같다는 것은 앨리스가 ‘+’ 기호를 사용할 때 느낀 과거의 통증과 현재의 통증이 질적으로 같다는 것이다. 그러나 그렇다고 해서, 그 통증이 도대체 어떤 방식으로 앨리스에게 ’68 + 57’에 대해 ‘125’라고 대답해야 한다는 사실을 알려줄 수 있다는 말인가?

크립키는 이 논의를 보다 일반적인 경험주의 반박과 연관짓는다. 경험주의에 따르면 내가 ‘삼각형’을 의미한다는 것은 내가 내면에서 삼각형의 인상을 떠올린다는 것이다. 그런데 이 삼각형의 인상이 어떻게 내가 ‘삼각형’이라는 단어를 사용하는 규칙을 알려준다는 말인가? 가령 나의 머리에 떠오른 인상이 예각삼각형이라고 하더라도 나는 둔각삼각형을 가리키며 정당하게 삼각형이라고 말할 수 있다. 반면 나의 머리에 떠오른 인상과 정확히 같은 모양의 밑변을 가지는 삼각뿔을 가리키며 삼각형이라고 말할 수는 없다. 요컨대 머리 속에서 어떤 인상이 제시된다고 한들, 그 인상을 어떻게 해석해 내야 할지는 미궁에 쌓여있다.

그럼에도 크립키는 우리가 반대 극단으로 치우쳐, 심리적 경험 내지 느낌이 의미의 문제와 완전히 무관하다고 결론내려서는 안 됨을 강조한다. 크립키는 ⟪철학적 탐구⟫의 논의에서 파생되는 다음의 사례들을 거론한다.

• 같은 단어를 수십 번 말하다 보면 마치 단어에서 의미가 빠져나가고 껍질만 남은 것처럼 ‘낯설게’ 느껴지는 현상
• ’배’를 운송수단을 떠올리며 말할 때와 과일을 떠올리며 말할 때의 차이 (이것을 네커 큐브 착시와 비교해 보라)
• 심리철학의 철학적 좀비와 유사한, 의미론적 좀비 — 발화 기록만으로는 일반적인 언어 사용자와 구별되지 않으나 내면에 어떠한 의미론도 가지고 있지 않은 화자

크립키는 위 사례들이 해명되어야 할 문제임을 인정하지만, 안타깝게도 지면의 문제로 인해 넘어간다.

2.6. 플라톤주의

마지막으로 크립키가 고려하는 반론은 플라톤주의다.

플라톤주의 의미론. 화자 $A$가 기호 $s$로 $\mathfrak{m}$을 의미한다는 것은, 화자가 의미 $\mathfrak{m}$에 대응되는 플라톤적 대상 $\pi_\mathfrak{m}$을 지향한다는 것이다.

따라서 앨리스가 ‘+’로 덧셈을 의미한다는 것은, 앨리스가 플라톤적 덧셈과 모종의 관계를 맺는 것이다.

이것은 프레게가 회의주의자에게 제시했을 대답이었을 걸로 짐작할 수 있다. 프레게에 따르면 기호는 화제에게 특정한 뜻_{sense, Sinn}으로서 나타나는데, 뜻은 지시체를 유일하게 결정한다. 여기서 뜻과 지시체는 플라톤적 대상이다.

프레게의 언어철학: 기호 -> 화자 -> 뜻 -> 지시체

그러나 크립키는 플라톤주의 또한 이전과 거의 같은 논리로 기각한다. 플라톤주의는 유한한 인간이 어떻게 덧셈과 같은 무한집합과 관계 맺을 수 있는지를 설명하지 못할 뿐더러, 이에 따라 앨리스가 지향하는 플라톤적 대상이 덧셈 집합인지 컷셈 집합인지를 어떻게 결정하냐는 문제를 낳는다.

이상으로 크립키-비트겐슈타인 역설과, 이에 대한 주요 반박 및 재반박을 살펴 보았다. 최종적으로 크립키는 회의주의 논증에 대한 직설적인 반박은 불가능하다고 결론 내린다. 따라서 이제 논의는, 정말로 회의주의 논증의 결론대로 “앨리스는 ‘+’로 덧셈을 의미한다”가 “앨리스의 생각은 초록색이다”와 다를 바 없이 대응되는 사태를 결여하는 명제라면, 어째서 전자는 후자와 달리 언어 생활에서 유의미하게 사용될 수 있는가를 해명하는 것으로 넘어간다. 이것은 비트겐슈타인의 사적 언어 논증에 대한 크립키의 독해와 밀접한 관련이 있으며, 다음 글에서 자세히 살펴보도록 한다.

---

The Kripke-Wittgenstein Paradox

03 Jul 2025

Disclaimer: Section “2.2. Dispositional Analysis” contains some commentary by myself indepedent from Kripke.

Overview

Kripke argues that the core of Wittgenstein’s Philosophical Investigations lies in a particular scepticism about rule following.

According to Kripke’s reading of Philosophical Investigations, Wittgenstein criticises the Tractarian conception on language in §1-137. In §138-242, scepticism about rule following is explicitly put forward. The sceptical argument, which questions whether there exists states of affairs corresponding to propositions such as “Alice means addition by ‘+’”, not only concludes §1-137 by driving the final nail on the coffin for Tractatus, but also seems to imply the devastating conclusion that all meaning propositions are ultimately unintelligile.

According to Kripke, Wittgenstein provides a “sceptical solution” to this. That is, while accepting the sceptic’s conclusion — that there is no state of affairs corresponding to “Alice means addition by ‘+’” — he explains how it can nonetheless be used meaningfully — unlike propositions such as “Alice’s thoughts are green”. This solution emphasises the publicity of language: that language is inseparable from its utility within a community, and therefore assertions about meaning are vacuous at the level of individuals, but are valid when situated with respect to a community of language users.

From §243 onwards is the application of the “sceptical solution” to other philosophical problems. One implication of the sceptical solution is the impossibility of private language. Nevertheless, there are two representative areas that appear to operate with a private language: mathematics and psychology. However, Wittgenstein argues that the idea that mathematics and psychology constitutes private language is a philosophical misconception. Here we can glimpse Wittgenstein’s distinctive philosophy of mathematics and psychology.

1. The Kripke-Wittgenstein Paradox

The conclusion of the Kripke-Wittgenstein paradox is as follows:

Propositions of the form “$A$ means $m$ by symbol $s$” have no corresponding state of affairs.¹ That is, such propositions lack truth values.

For instance, the proposition “Alice means addition by ‘+’” is as unintelligible as the proposition “Alice’s thoughts are green”.

1.1. The Appearance of the Sceptic

Why then do Kripke-Wittgenstein make such an extreme claim? The core of the argument lies in an easily overlooked but genuinely contradictory aspect hidden in the process by which language users grasp the meaning of words: from finite past learning experiences and cognitive ability, one must be able to make correct inferences for infinitely many cases in which that word could be used.

For example, suppose Alice has never performed addition of two numbers both exceeding 50. Even so, if someone asked Alice ‘68 + 57’, she would readily answer ‘125’. But at this point, a sceptic approaches Alice and claims that her answer is wrong, and that the answer she should have given was ‘5’. Specifically, the sceptic claims the following:

If what Alice means by ‘+’ presently is what she meant by ‘+’ in the past, then Alice should answer ‘5’.

Because, at least according to the sceptic, what Alice meant by ‘+’ in the past was actually not addition (+) but quaddition (⨁), defined as follows:

\[x \oplus y = \begin{cases} x + y & x, y < 50 \\ 5 & \text{otherwise} \end{cases}\]

Alice would immediately object that she has never used ‘+’ to mean quaddition. But here begins the real problem. How can Alice’s claim that she has meant addition rather than quaddition with ‘+’ be substantiated? Due to the assumption of the problem, it is impossible to substantiate her claim just from Alice’s previous records of ‘+’ calculations.

The expression ‘substantiate’ in the previous paragraph might make this problem appear epistemological (“How can we prove that Alice means addition by ‘+’?”). However, what Kripke asks is whether even an omniscient observer who could even see into Alice’s mind, past or future notwithstanding, could conclude whether Alice means addition by ‘+’, or whether she means some non-standard operation that agrees with addition in sufficiently many cases. In this respect, the scepticism Kripke presents is ontological. The point of the problem is whether there is a state of affairs corresponding to “Alice means addition rather than quaddition”. This is revealed by the fact that Kripke even examines attempts to resolve scepticism through counterfactual conditionals or possible worlds, though he concludes that these attempts also fail.

1.2. Two Conditions

There are two noteworthy points about the sceptic’s claim. First, the sceptic’s claim is conditional. The sceptic is not claiming that Alice should answer ‘5’ in any case. What he claims is that if the meaning Alice assigned to ‘+’ in the past matches the meaning she assigns to ‘+’ in the present, then she should answer ‘5’. Second, the sceptic’s claim is normative. The sceptic’s claim is not that — when the aforementioned condition is satisfied — Alice will answer ‘5’, but that she should answer ‘5’.² In other words, the sceptic claims that had Alice answered ‘5’ to ‘68 + 57’, that answer would have been justified.

Therefore, any refutation of the sceptic’s claim must also satisfy two conditions. First, it must explain what fact about a speaker constitutes that speaker’s use of a particular symbol with a particular meaning. This explanation is necessary to elucidate what the antecedent means in the sceptic’s claim.³ Second, it must explain how that fact justifies the speaker’s use of language. This explanation is necessary because the sceptic’s conclusion is normative.

The significance of the second condition may not be immediately apparent, so let me elaborate. Suppose some mad scientist approached the sceptic and said:

Actually, I once scanned Alice atom-by-atom in the past. So after hearing your claim, I copied out Alice-2 from that scan and asked her ‘68 + 57’, to which she answered ‘125’. Therefore, past Alice did not mean quaddition by ‘+’.

However, the mad scientist’s experiment is irrelevant in refuting the sceptic’s claim, as it does not satisfy the second condition. The experiment only reveals that Alice would have always answered ‘125’, and does not suggest in any way that Alice should have always answered ‘125’.

This point can be more clearly understood by examining cases of systematic errors. For instance, children learning addition often forget to “carry numbers”. Such a child would answer ‘115’ rather than ‘125’ to ‘68 + 57’. Now suppose there is someone called Johnson who, due to some problem, has failed to correct his tendency to forget carrying even as an adult. Johnson understands what addition is, and when asked about properties of addition rather than specific addition problems (e.g. “Is it associative?”), he answers correctly. However, in situations where Johnson has no instructor to point out his mistakes, he always would answer, and would have answered, ‘115’ to ‘68 + 57’. Here, the correct claim to make seems to be that although Johnson does mean addition by ‘+’, he is failing to answer ‘68 + 57’ in a way that would be justified by that meaning. It is precisely to make this claim possible that the second condition is needed. If we adopt a theory of meanings that fails to satisfy the second condition, we would have to concede that Johnson means by ‘+’ something like baddition — an operation that performs addition without carrying — or maddition — an operation that performs baddition when no instructor is present and performs addition when one is present to guide him.⁴

2. Proposed Refutations of the Paradox

2.1. Linguistic Regress

The first response Alice would give to the sceptic’s claim is probably be this: “In the past, I meant with ‘x + y’ the result of counting x objects and y objects together. Therefore, I did not use ‘+’ to mean quaddition in the past.”

However, the sceptic can simply deploy their scepticism once again. That is, they can claim that Alice has meant with the word ‘count’ not count, but quount. To quount a collection is to count it when the collection’s size is less than 50 and to answer 5 when it exceeds 50.

The point is that attempts to explain the meaning assigned to ‘+’ linguistically leads to infinite regress, as such explanation is equally prone to the possibility of non-standard interpretations.⁵

2.2. Dispositional Analysis

In the philosophy of mind, dispositional analysis is a behaviouristic explanation of psychological states.

Dispositional analysis of psychological states. A subject $A$ to be in psychological state $\mathfrak{m}$ in the past, present, or future if and only if, if stimulus $s$ was given / is given / should be given to $A$, then $A$ would have reacted / reacts / will react with response $b = f_\mathfrak{m}(s)$. That is, psychological state ($\mathfrak{m}$) is determined by its stimulus-response disposition ($f_\mathfrak{m}$).

For example, suppose Alice, having just awakened from a light sleep, formed the belief “it is raining now” upon seeing the dim room and hearing the sound of water drops from outside the window. According to dispositional analysis, Alice’s belief that it is raining now is amounts to the following disposition:

• If a friend calls to go eat together, she will bring an umbrella.
• If a neighbour calls her saying her laundry is hanging outside, she will rush to collect the laundry.
• If an outdoor schedule is planned for tomorrow, she will check tomorrow’s weather, etc…

If phenomena significantly deviating from these stimulus-response correspondences are observed, the dispositional analyst would revise their view of Alice’s belief. For instance, if Alice went out but brought sunglasses instead of an umbrella, they would judge that Alice has had the belief that it is sunny, rather than the belief that it is raining.

There are two characteristics of dispositional analysis to note.

1. It uses counterfactual conditionals. Even if Alice did not go out, “If Alice had gone out, she would have brought an umbrella” forms part of the analysis of the belief she had had.

2. It is descriptive. Because dispositional analysis is based on behaviourism, it consists of descriptive propositions such as “if Alice believes that it is raining, she will bring an umbrella” rather than normative propositions such as “if Alice believes that it is raining, she should bring an umbrella”. According to dispositional analysis, if Alice goes out but brings sunglasses instead of an umbrella, it is cannot be the case that she has the belief that it is raining but is failing to act justifiably according to it; rather, she simply does not have the belief that it is raining.

Kripke reports that some philosophers who discussed the rule-following paradox with him attempted to resolve the paradox through dispositional analysis. This approach claims the following:

Dispositional analysis of meaning. $A$ means $\mathfrak{m}$ by symbol $s$ in the past, present, or future if and only if, if sentence $\phi$ containing $s$ was given / is given / should be given to $A$, then $A$ would have answered / answers / will answer with sentence $\psi = f_\mathfrak{m}(\phi)$. That is, meaning ($\mathfrak{m}$) is determined by (counterfactual) question-answer disposition ($f_\mathfrak{m}$).

According to this analysis, for Alice to mean addition by ‘+’ in the past, present, or future means that when x + y had been asked / is asked / will be asked of Alice, she would have answered / answers / will answer with the sum of x and y. The strengths of such an analysis is that, aside from its counterfactual nature it is framed behaviouristically and hence directly observable, and due to its counterfactual nature it is able to cover the infinitely many cases in which Alice may use the symbol ‘+’. Hence, a dispositional analysist may rebut to the skeptic in the following manner.

1. The sceptic points out that there is no state of affairs that distinguishes whether Alice meant addition by ‘+’ or meant some non-standard operation that agrees with addition in sufficiently many cases.

2. The reason 1 can be claimed is that the number of ‘+’ operations Alice has performed and will perform is finite.

3. However, if we allow counterfactual conditionals such as “if ‘x + y’ had been asked of Alice, she would have answered the sum of x and y” or “if ‘x + y’ should be asked of Alice, she will answer the sum of x and y”, we can overcome the finitude of 2.

4. Accordingly, if we accept that counterfactuals have objective truth values (e.g. possible world semantics), the dispositional analysis of meaning objectively determines the operation that Alice means by ‘+’.

This argument satisfies the first condition: to explain what fact about a speaker constitutes that speaker’s use of a particular symbol with a particular meaning. That fact is the counterfactual conditional. However, Kripke points out that dispositional analysis is insufficient to resolve the paradox because it fails to satisfy the second condition: to explain how that fact justifies the speaker’s use of the symbol. This is because, as noted earlier, dispositional analysis is essentially descriptive. To quote Kripke:

Well and good, I know that ‘125’ is the response I am disposed to give (I am actually giving it!), and maybe it is helpful to be told — as a matter of brute fact — that I would have given the same response in the past. How does any of this indicate that — now or in the past — ‘125’ was an answer justified in terms of instructions I gave myself, rather than a mere jack-in-the-box unjustified and arbitrary response?

(Italics in original, emphasis mine)

What Kripke points out can be understood step by step as follows. Recall that any claim against the sceptic should result in the following:

Claim 1. If what Alice means by ‘+’ presently is what she meant by ‘+’ in the past, then

1. Alice should not answer ‘5’, but rather
2. Alice should answer ‘125’.

According to dispositional analysis, the Claim 1 is analysed as the following:

Claim 1.1. If Alice’s past disposition regarding ‘+’ matches Alice’s present disposition regarding ‘+’, then

1. Alice should not answer ‘5’, but rather
2. Alice should answer ‘125’.

“As a matter of brute fact”, suppose Alice’s past question-answer disposition regarding ‘+’ was to respond with the sum of given two numbers. Substituting this fact results in:

Claim 1.2. If Alice’s present disposition regarding ‘+’ is to respond with the sum of given two numbers, then

1. Alice should not answer ‘5’, but rather
2. Alice should answer ‘125’.

However, even after such analysis, there is still no basis for substantiating Claim 1.2. Had the predicates in Claim 1 been “Alice will answer”, Claim 1.2 would have held trivially. But the required predicate is “Alice should answer”, which does not follow from dispositional analysis.

Then what about simply setting the predicate in Claim 1 as “Alice will answer” from the beginning? That is, we claim the following to the sceptic instead:

Claim 2. If the meaning Alice assigned to ‘+’ in the past matches the meaning she assigns to ‘+’ in the present, then

1. Alice will not answer ‘5’, but rather
2. Alice will answer ‘125’.

This cannot be done. As explained earlier with the “case of systematic computational error”, the fact that Alice did not answer ‘125’ to ‘68 + 57’ does not immediately suggest that Alice did not mean addition by ‘+’. We sometimes make mistakes in performing addition, but such mistakes do not in themselves imply that ‘+’ was used to mean something other than addition. Indeed, the very fact that I can make mistakes in performing ‘+’ suggests that it is not the results I produce that determine what I mean by ‘+’, but conversely, what I mean by ‘+’ determines the result I should produce.

Nevertheless, to meet the challen of explaining the normativity of meaning through dispositional analysis, one seemingly has to interpret the sceptic’s challenge as follows:

Claim 3. If Alice intends to mean by ‘+’ what she meant by ‘+’ in the past,

1. Alice should not answer ‘5’, but rather
2. Alice should answer ‘125’.

This leads to the following statement:

Claim 3.1. If Alice intends her present disposition regarding ‘+’ to be that which responds with the sum of given two numbers,

1. Alice should not answer ‘5’, but rather
2. Alice should answer ‘125’.

Certainly, Claim 3.1 appears more plausible than Claims 1.1 and 1.2. However, I find Claim 3.1 to still be problematic.

The first problem is that Claim 3 is logically independent from Claim 1, and hence irrelevant to the skeptical paradox. Let $p$ and $q$ be as follows:

• $p:$ What Alice means by ‘+’ is what she meant by ‘+’ in the past.
• $q:$ Alice answers ‘125’.

Then Claim 1 and Claim 3 are as follows ($W$ means “intends to” and $\Box$ means “should”):

• Claim 1. $p \rightarrow \Box q$
• Claim 3. $Wp \rightarrow \Box q$

However, since $p$ does not suggest $Wp$ (something I do not want can be the case) and $Wp$ does not suggest $p$ either (something I want may not be the case), there is no logical relationship between Claim 1 and Claim 3. Specifically, for the former case, consider a rebellious student who intends to use ‘+’ to mean multiplication, yet answers ‘125’ to ‘68 + 57’ out of habit. For the latter case, consider a student who intends to mean addition by ‘+’ but has not yet fully mastered the practice of addition (e.g. they make carrying mistakes).

The second problem is that Claim 3 falls into infinite regress. For convenience of explanation, let me return to the case of psychological states. Converting the normative problem of meaning to one about psychological states would be as follows: Alice can go out carrying something other than an umbrella, despite having the belief that it is raining outside. For instance, consider a situation where Alice hurriedly prepared to go out and grabbed something from the umbrella stand right before leaving the house, but what she grabbed was not an umbrella but a walking stick. Dispositional analysis, as it stands, must conclude from such a case that Alice did not have the belief that it was raining, which is outlandish. In response, the dispositional analyst might instead put forward the following claims ($s$ stands for ‘a dim room and the sound of water drops falling outside the window’):

Claim 4. If Alice intends to have the belief that she had in the past regarding $s$,

1. Alice should not bring a walking stick, but rather
2. Alice should bring an umbrella.

Claim 4.1. If Alice intends to have the disposition that she had in the past regarding $s$,

1. Alice should not bring a walking stick, but rather
2. Alice should bring an umbrella.

Claim 4.2. If Alice intends her disposition regarding $s$ to be that of bringing an umbrella when going out,

1. Alice should not bring a walking stick, but rather
2. Alice should bring an umbrella.

As mentioned earlier, Claim 4 is of the form $Wp \rightarrow \Box q$, so it has no logical relationship with $p \rightarrow \Box q$ in the first place, but even setting aside that problem, the seemingly plausible Claim 4.2 is problematic. The motivation for dispositional analysis in the first place is to translate statements about psychological states into behaviourist expressions. However, Claim 4.2 has merely changed a statement about one specific psychological state — the belief that it is raining outside — into a statement about another psychological state — the intention to bring an umbrella when going out. Now we must analyse what ‘being in a state of intending to bring an umbrella when going out’ dispositionally, which falls into infinite regress.

For the same reason, Claim 3 also falls into infinite regress. Recalling the earlier discussion, a necessary condition that a refutation to the sceptic must satisfy is to “explain what fact about a speaker constitutes that speaker’s use of a particular symbol with a particular meaning”, to which Claim 3.1 purportedly answers “the intention to have certain question-answer disposition”. But then the sceptic can ask, “What fact about a speaker constitutes that speaker’s having the intention to have the disposition aligning with addition rather than the disposition aligning with quaddition?” It is not at all clear how dispositional analysis can provide such a distinction of intention.

In conclusion, attempts to resolve the paradox through dispositional analysis fail to explain the normativity of meaning. Attempts to force dispositional analysis to fit so as to explain normativity not only deviate from what the problem requires but also fall into infinite regress.

2.3. Mechanistic Approach

Then, instead of relying on abstract explanations like linguistic regress or dispositional analysis, could we not respond to the sceptic by designing and constructing a concrete machine that performs addition? For instance, one could construct a mechanical calculator or a full adder with logic circuits. However, Kripke argues that this attempt is also inappropriate for three main reasons.

First, the rules for using the machine remain susceptible to skeptical interpretations. Taking Turing machines as an example, users are expected to interpret the sequences of 0 and 1 output by the Turing machine in binary notation. However, the sceptic can claim that the correct way to interpret the sequence is with quinary notation, according to which the Turing machine is outputting quaddition, not addition.

Second, actual machines can only receive finite inputs. In that sense, actual machines are not in any way more ‘resilient’ to the skeptical argument than Alice. If instead of implementing a concrete machine we present the algorithm of the machine, this returns us to “2.1. Linguistic Regress”.

Third, machines can malfunction. Gears could fall out, and wires might melt from overuse. Therefore, to confer our way of meaning entirely to the machine and claim “this machine always calculates the operation I mean” is to bite the bullet. But nor can we claim “this machine always calculates the operation I mean unless it malfunctions”. To make such a claim, we would need to provide criteria for judging whether the machine is operating normally or malfunctioning. Yet those criteria would ultimately depend on the intention of the designer — could not some eccentric designer create a machine that calculates addition through the falling out of gears and the melting of wires? Therefore, relying on the expression “unless it malfunctions” puts the semantic intention, not the concrete working of the machine, into precedence — something which the skeptic claims to be non-existent in the first place.

2.4. Occam’s Razor

Kripke also considers the following claim:

Occamist semantics. When two hypotheses “$A$ means $\mathfrak{m}_1$ by $s$” and “$A$ means $\mathfrak{m}_2$ by $s$” are in an underdetermined state, we should accept the hypothesis of the simpler of $\mathfrak{m}_1$ and $\mathfrak{m}_2$.

For example, consider the following two hypotheses:

    H1. Past Alice meant addition by ‘+’.

    H2. Past Alice meant quaddition by ‘+’.

Since both terms in Alice’s past ‘+’ operation records are 50 or below, H1 and H2 are in an underdetermined state. What Occamist semantics claims is that in this case we should preferentially accept the H1 hypothesis. This is because addition is a simpler operation than quaddition.

However, Kripke only briefly mentions and passes over this claim, because it is self-evident that it is inappropriate for refuting scepticism. This is not only because the predicate ‘simple’ is subjective, difficult to define, or because quaddition might be simpler than addition for Martians—though these reasons are also very legitimate. The more essential reason is that the conclusion of the sceptical argument is not “it is undetermined which of H1 and H2 is true”, but “it is undetermined what state of affairs the truth of either H1 or H2 corresponds to”. According to the sceptical argument, we are in a situation where we are not even certain whether H1 and H2 represent different states of affairs. If the states of affairs that hypotheses represent are so unclear, we cannot even apply Occam’s razor before considering whether its application is justified.

2.5. Psychologism

A more important objection that Kripke considers is psychologism.

Psychologistic semantics. $A$ means $\mathfrak{m}$ by symbol $s$ if and only if, $A$ experiences a queer psychological experience $p_\mathfrak{m}$ corresponding to $\mathfrak{m}$.

Here, “quuer psychological experience” can be thought of as similar to qualia. In short, just as “seeing red” is a distinctive experience that cannot be reduced to other predicates or experiences, so too is “meaning addition by ‘+’” such a distinctive experience.

Kripke does not deny the possibility that such queer experiences may exist.⁶ However, Kripke points out that psychologism also fails to resolve the sceptical argument. The problem once again lies in normativity condition laid out in “1.2. Two Conditions”.

As a simple example, suppose Alice feels pain in her forehead every time she uses the ‘+’ symbol. This fact satisfies condition 1 of “1.2. Two Conditions”. That is, Alice means addition by ‘+’ if and only if her use of ‘+’ induces pain in her forehead. However, how could such pain possibly inform — let alone provide justification for — Alice that she should answer ‘125’ to ‘68 + 57’?

Kripke connects this discussion to a more general empiricist refutation. An empiricist may claim that to mean ‘triangle’ is to have an impression of a triangle in one’s mind when using that word. But how does an impression of a triangle inform of, or justify the rule for using the word ‘triangle’? For instance, even if the impression that comes to my mind is an acute triangle, I can legitimately point to an obtuse triangle and call it a triangle. On the other hand, I cannot point to a triangular prism and call it a triangle, even if it has a base the same shape as the impression in my mind. In short, even when some impression is presented in the mind, how that impression should be interpreted so as to justify rules for using a word remains obscure.

Nevertheless, Kripke emphasises that we should not sway to the opposite extreme and conclude that psychological experiences or feelings are completely irrelevant to problems of meaning. Kripke mentions the following cases derived from discussions in the Philosophical Investigations:

• The phenomenon where saying the same word dozens of times makes it feel ‘strange’, as if the meaning has drained out of the word
• The difference between saying ‘bat’ while thinking of the animal versus thinking of the sports equipment (compare this to Necker cube illusion)
• Semantic zombies: speakers — akin to philosophical zombies in philosophy of mind — who cannot be distinguished from ordinary language users by their utterances yet have no internal sense of meaning whatsoever

Kripke acknowledges that the above cases are problems that need further discussion, but passes over them, for otherwise he would stray away from the main point too much.

2.6. Platonism

The final objection Kripke considers is Platonism.

Platonistic semantics. $A$ means $\mathfrak{m}$ by symbol $s$ if and only if $A$ accesses the Platonic object $\pi_\mathfrak{m}$ corresponding to meaning $\mathfrak{m}$.

Therefore, for Alice to mean addition by ‘+’ is for Alice to establish some relationship with the specific set, residing in the Platonic realm, whose elements consist of triples $(a, b, c)$ where $c = a + b$.

This may be the answer Frege might have given to the sceptic. According to Frege, symbols appear to speakers with particular senses_Sinn, which uniquely determines reference_Bedeutung. Frege takes both sense and reference to be Platonic objects.

Frege’s philosophy of language: Symbol $\to$ Speaker $\to$ Sense $\to$ Reference

However, Kripke rejects Platonism with almost the same logic as before. Platonism not only fails to explain how finite humans can relate to infinite entities like the extension of addition, but also leaves the problem explaining what fact consists in Alice accessing the Platonic extension of addition, rather than the extension of quaddition.

We have thus examined the Kripke-Wittgenstein paradox and the main objections and counter-objections to it. Ultimately, Kripke concludes that a “direct” solution of the sceptical argument is impossible. Therefore, the discussion now moves to developing a “skeptical solution” — explaining how, despite the conclusion of the sceptical argument being correct, meaning-attributing sentences can be used legitimately in our language games. This is closely related to Kripke’s reading of Wittgenstein’s private language argument, which I hope to discuss in a future article.

---