로빈슨, 크레이그, 베스의 정리

08 May 2025

초등적 병합 성질_{Elementary amalgamation property}

정리. $\mathcal{L}$-구조 $\mathfrak{A}$와 $\mathcal{L}’$-구조 $\mathfrak{B}$에 대해, $\mathfrak{B}$의 $\mathcal{L}$-퇴화_{$\mathcal{L}$-reduct}가 $\mathfrak{A}$와 초등적으로 동등_{elementarily equivalent}하다고 하자. 이 때, $\mathcal{L}’$-구조 $\mathfrak{C}$가 존재하여, $f: \mathfrak{A} \to \mathfrak{C}$가 $\mathcal{L}$의 초등적 임베딩이고 $g: \mathfrak{B} \to \mathfrak{C}$가 $\mathcal{L}’$의 초등적 임베딩이다.

증명. 이 글의 표기법을 따라, 언어 $L_\mathfrak{A}$의 이론 $E(\mathfrak{A})$와 언어 $L’_\mathfrak{B}$의 이론 $E(\mathfrak{B})$를 생각하자. $T = E(\mathfrak{A}) \cup E(\mathfrak{B})$는 언어 $\mathcal{L}’_{\mathfrak{AB}} = \mathcal{L}_\mathfrak{A} \cup \mathcal{L}’_\mathfrak{B}$의 이론이다. $T$가 모델 $\mathfrak{C}$를 가짐을 보이자.

만약 $T$가 모델이 없다면 $T$는 모순적이다. 따라서 콤팩트성 정리에 의해 어떤 $\mathcal{L}$-논리식 $\phi$와 $\mathcal{L}’$-논리식 $\psi$가 존재하여, 적절한 $\lbrace a_i \rbrace \subset \mathcal{L}_\mathfrak{A}$, $\lbrace b_j \rbrace \subset \mathcal{L}_\mathfrak{B}$에 대해,

\[\lbrace \phi(a_1, \dots, a_n), \psi(b_1, \dots, b_m) \rbrace\]

이 모델을 가지지 않는다. $\mathfrak{B} \vDash \psi(b_1, \dots, b_m)$이므로, $\mathfrak{B} \vDash \phi(a_1, \dots, a_n)$를 만족하도록 상수 $a_1, \dots, a_n$을 $\mathfrak{B}$의 정의역에 대응시키는 방법이 존재하지 않아야 한다. 즉,

\[\mathfrak{B} \not\vDash \exists x_1, \dots x_n \; \phi(x_1, \dots, x_n)\]

그런데 $\mathfrak{B}$의 $\mathcal{L}$-퇴화가 $\mathfrak{A}$와 초등적으로 동등하며, 위 식의 우변이 $\mathcal{L}$-문장이고, $\mathfrak{A}$가 해당 문장을 만족하므로 이는 모순이다. 따라서 $T$는 모델 $\mathfrak{C}$를 가진다. 그리고 $\mathfrak{C}$는 $E(\mathfrak{A})$와 $E(\mathfrak{B})$의 모델이므로, $\mathfrak{A}$와 $\mathfrak{B}$는 $\mathfrak{C}$로 자연스럽게 초등적으로 임베딩된다. ■

로빈슨 건전성 정리_{Robinson consistency theorem}

정리. $\mathcal{L} = \mathcal{L}_1 \cap \mathcal{L}_2$라고 하자. $T$가 $\mathcal{L}$의 (의미론적으로) 완전한 이론이고, $T_1$과 $T_2$가 각각 $T$를 확장하는 건전한 $\mathcal{L}_1, \mathcal{L}_2$ 이론일 때, $T_1 \cup T_2$는 $\mathcal{L}_1 \cup \mathcal{L}_2$ 이론으로서 건전하다.

증명. $T_1 \cup T_2$의 모델을 구축하면 정리가 보여진다.

$T_1, T_2$가 각각 건전하므로, 모델 $\mathfrak{A}_0, \mathfrak{B}_0$를 가진다. $T = T_1 \cap T_2$가 완전하므로, $\mathcal{L}$-퇴화로서의 $\mathfrak{A}_0$와 $\mathfrak{B}_0$는 초등적으로 동등하다. 따라서 초등적 병합 성질에 의해, $\mathcal{L}$-초등적 임베딩 $f_0$와 $\mathcal{L}_2$-초등적 임베딩 $h_0$가 존재하여 다음이 성립한다.

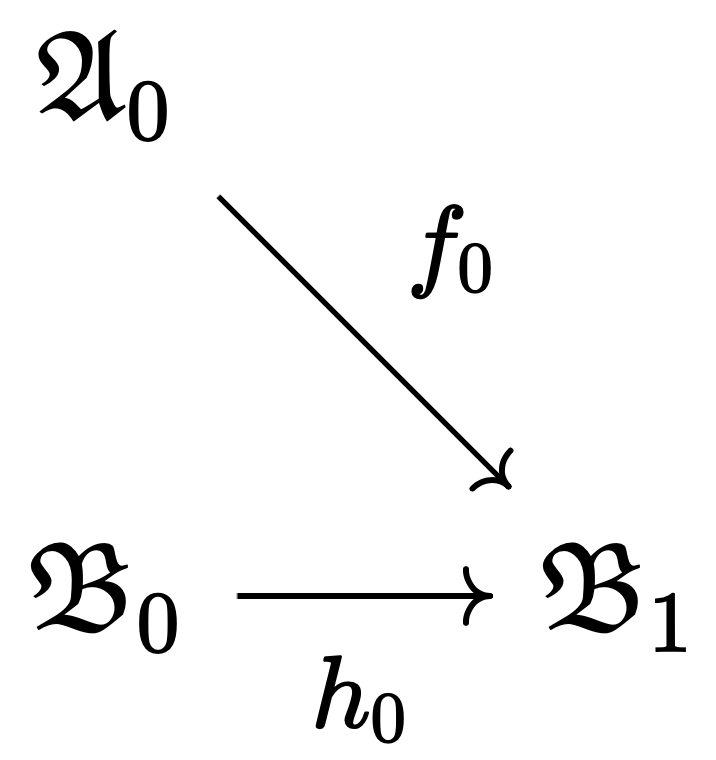
이제 $\mathfrak{B}_1$의 $\mathcal{L}$-퇴화를 생각해 보면, 이는 $\mathfrak{A}_0$와 초등적으로 동등하므로, 다시 초등적 병합 성질에 의해 $\mathcal{L}$-초등적 임베딩 $g_0$와 $\mathcal{L}_1$-초등적 임베딩 $k_0$가 존재하여 다음이 성립한다.

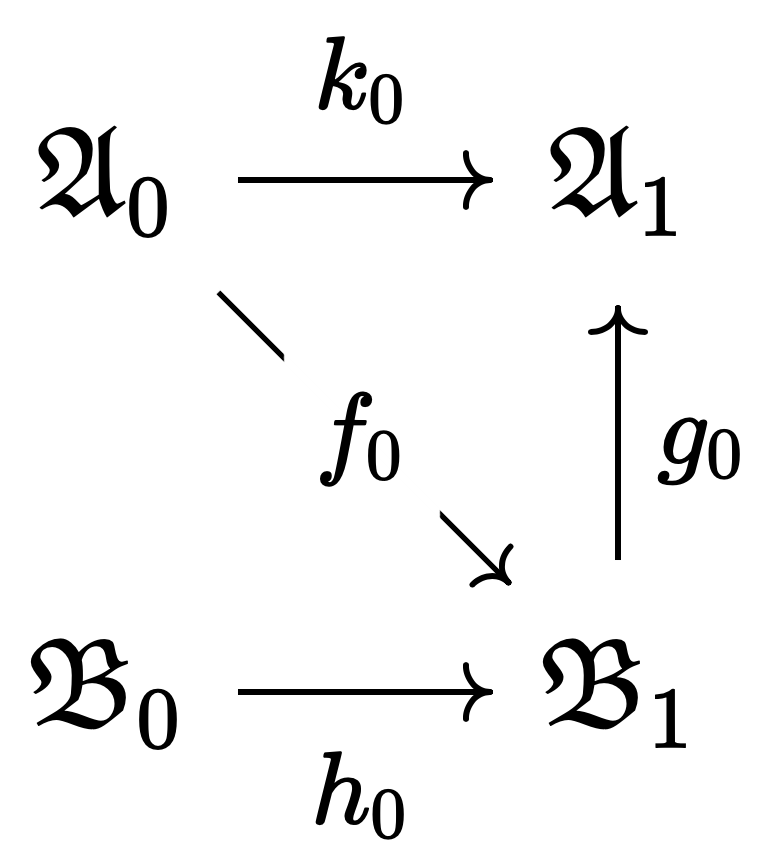
이 과정을 반복하여 다음의 구조 유도계_{directed system of structures}를 얻는다.

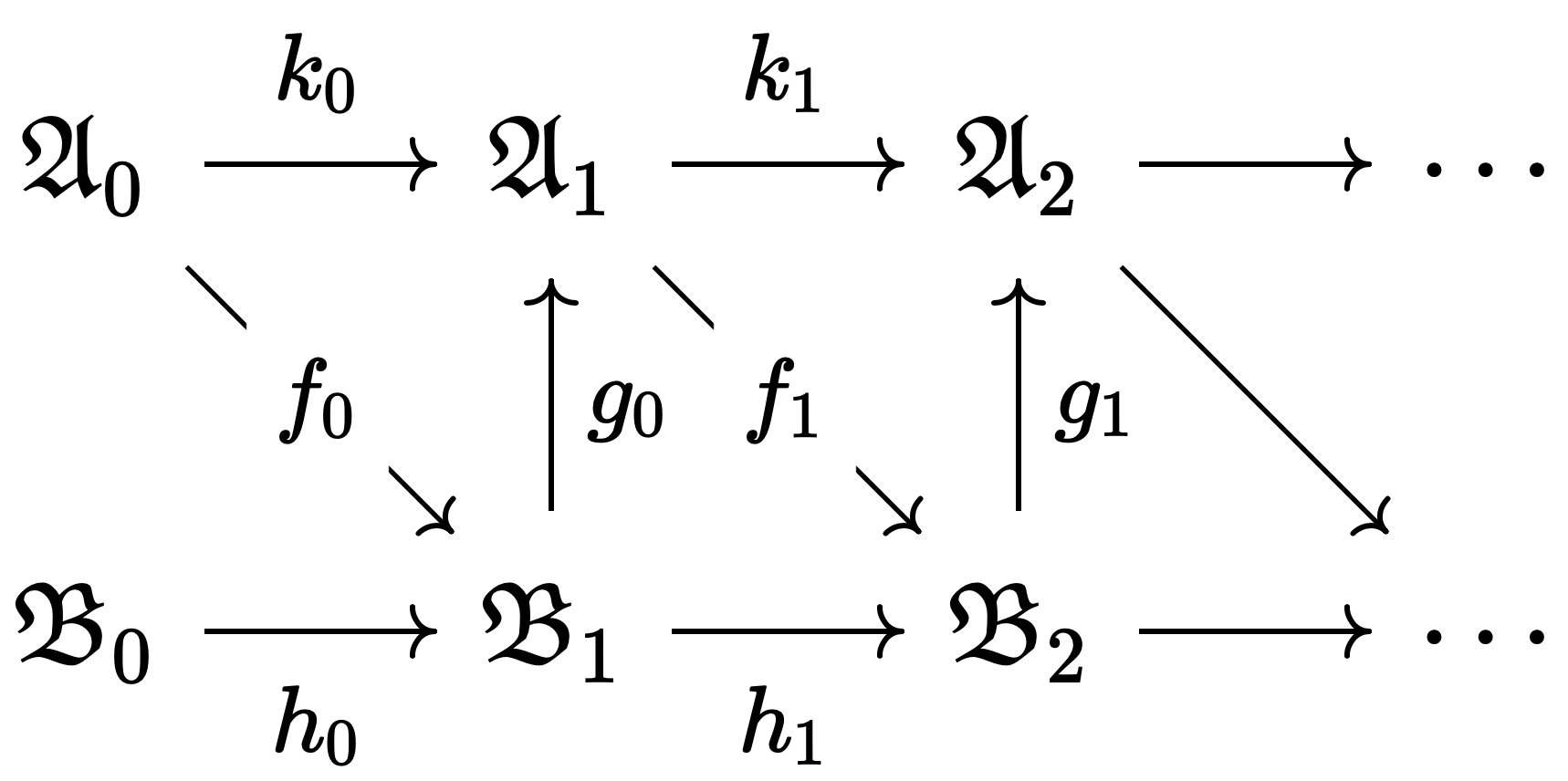
사상	성질
$f, g$	$\mathcal{L}$-초등적 임베딩
$k$	$\mathcal{L}_1$-초등적 임베딩
$h$	$\mathcal{L}_2$-초등적 임베딩

위 유도계의 모든 모델을 $\mathcal{L}$로 퇴화시키면 $\mathcal{L}$-구조 유도계를 얻는다. 해당 유도계의 쌍대극한_colimit을 $\mathfrak{C}$라고 하자. $\mathfrak{C}$는 다음의 $\lbrace \mathfrak{A}_i \rbrace $로 이루어진 유도계의 쌍대극한이기도 하다. 회색으로 표시된 원 유도계의 일부는 모두 $\lbrace \mathfrak{A}_i \rbrace $ 중 하나로 투사되기 때문이다. 따라서 $\mathfrak{C}$는 $\mathfrak{A}_0$를 초등적으로 임베딩하는 $\mathcal{L}_1$ 구조이다.

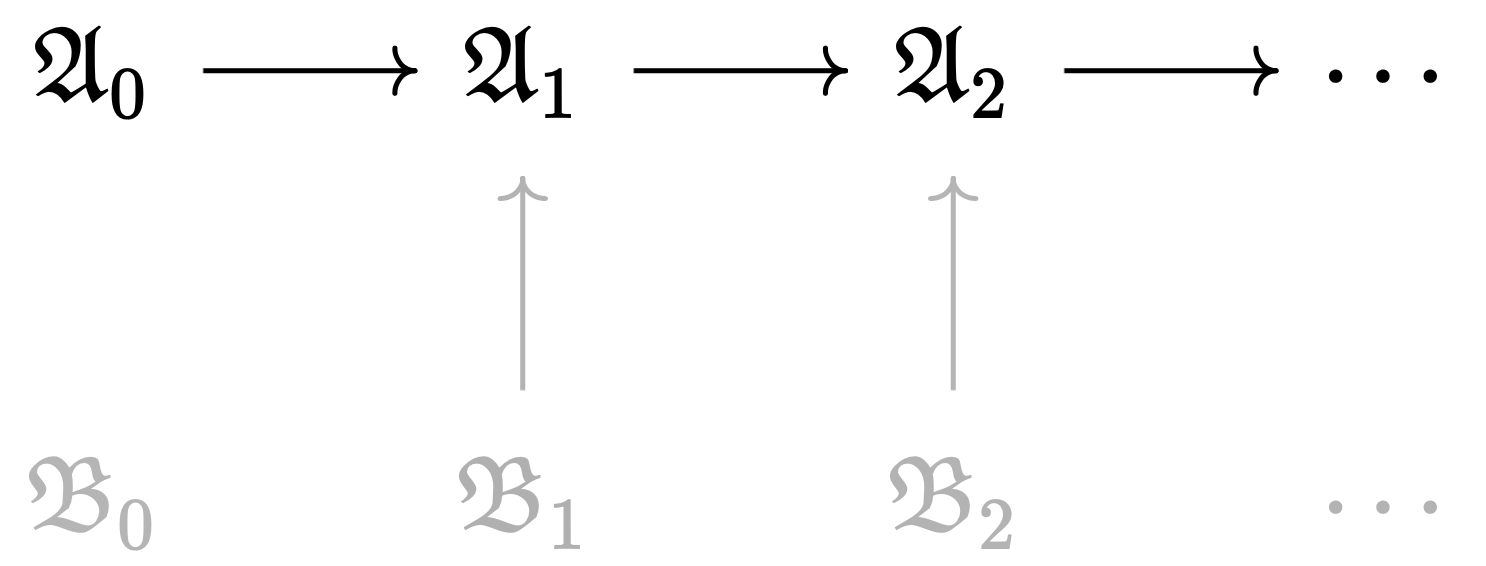
같은 이유로 $\mathfrak{C}$는 다음의 $\lbrace \mathfrak{B}_i \rbrace $로 이루어진 유도계의 쌍대극한이기도 하다. 따라서 $\mathfrak{C}$는 $\mathfrak{B}_0$를 초등적으로 임베딩하는 $\mathcal{L}_2$ 구조이다.

즉, $\mathfrak{C}$는 $\mathfrak{A}$와 $\mathfrak{B}$를 모두 임베딩하며, 이로부터 $T_1 \cup T_2$의 모델임이 보여졌다. ■

크레이그 보간 정리_{Craig interpolation theorem}

정리. $\mathcal{L}$-문장 $\phi, \psi$에 대해 $\phi \vDash \psi$라면, 어떤 $\mathcal{L}$-문장 $\theta$가 존재하여 $\phi \vDash \theta, \theta \vDash \psi$이다. 또한, $\theta$에 포함된 비논리 기호(상수, 술어, 함수)는 $\phi$와 $\psi$에 공통적으로 포함된다.

$\theta$를 $\phi$와 $\psi$의 크레이그 보간이라고 부른다.

증명. 귀류법으로 증명한다. 크레이그 보간이 존재하지 않는다고 가정하자. 그러면 $\phi$는 모델을 가진다. 만약 $\phi$가 모델을 가지지 않는다면 $\perp$가 $\phi, \psi$의 크레이그 보간이기 때문이다. 또한 $\lnot \psi$도 모델을 가진다. 그렇지 않다면 $\top$가 크레이그 보간이기 때문이다.

$\mathcal{L}’$을 $\phi$와 $\psi$에 공통적으로 포함되는 비논리 기호들로 이루어진 언어라고 하자. $\Gamma$를, $\phi \vDash \sigma$이거나 $\lnot \psi \vDash \sigma$인 $\mathcal{L}’$-문장 $\sigma$의 집합이라고 하자.

$\Gamma \cup \lbrace \phi \rbrace $는 무모순적임을 보이자. 만약 모순적이라면, 콤팩트성 정리에 의해 어떤 $\mathcal{L}’$-문장 $\sigma_1, \sigma_2$가 존재하여 $\phi \vDash \sigma_1, \lnot\psi \vDash \sigma_2$이고 $\lbrace \sigma_1, \sigma_2, \phi \rbrace $가 모순적이다. 그런데 $\phi \vDash \sigma_1$이므로 $\phi \vDash \lnot\sigma_2$이다. 대우법에 의해 $\lnot\psi\ \vDash \sigma_2$로부터 $\lnot\sigma_2 \vDash \psi$가 따라 나온다. 즉, $\sigma_2$는 $\phi, \psi$의 크레이그 보간이다. 이는 가정에 모순된다.

따라서 $\Gamma \cup \lbrace \phi \rbrace $는 무모순적이며, 같은 이유로 $\Gamma \cup \lbrace \lnot\psi \rbrace $ 또한 무모순적이다. 이제 초른의 보조정리를 적용하여, $\overline{\Gamma}$를 다음 $\mathcal{L}’$-이론들의 순서의 극대로 정의한다.

\[\{ \Gamma' : \Gamma \subseteq \Gamma', \Gamma' \cup \{\phi\} \text{ and } \Gamma' \cup \{\lnot \psi\} \text{ are consistent} \}\]

$\overline{\Gamma}$는 완전함을 보이자. 만약 $\overline{\Gamma}$가 완전하지 않다면, 어떤 $\mathcal{L}’$-문장 $\sigma$가 존재하여 $\sigma \notin \overline{\Gamma}$이고, $\overline{\Gamma} \cup \lbrace \sigma, \phi \rbrace $ 또는 $\overline{\Gamma} \cup \lbrace \sigma, \lnot \psi \rbrace $가 무모순적이다.

전자의 경우, 콤팩트성 정리에 의해 어떤 $\overline{\Gamma}$의 문장 $\theta$가 존재하여 $\phi \vDash \theta \rightarrow \lnot \sigma$이다. $\Gamma$의 정의에 의해 $\theta \rightarrow \lnot \sigma \in \Gamma \subseteq \overline{\Gamma}$이다. 따라서 $\overline{\Gamma} \cup \lbrace \sigma, \phi \rbrace $는 $\lnot\phi$를 증명한다. 이는 모순이다. 후자의 경우에도 마찬가지 모순이 발생한다. 따라서 $\overline{\Gamma}$는 완전하다.

$\overline{\Gamma}$가 완전하고, $\overline{\Gamma} \cup \lbrace \phi \rbrace , \overline{\Gamma} \cup \lbrace \lnot\psi \rbrace $가 건전하므로, 로빈슨 건전성 정리에 의해 $\overline{\Gamma} \cup \lbrace \phi, \lnot \psi \rbrace $가 건전하다. 그런데 이는 $\phi \vDash \psi$에 모순된다. 따라서 귀류법에 의해 $\phi, \psi$는 크레이그 보간을 가진다. ■

베스 정의 가능성 정리_{Beth definability theorem}

언어 $\mathcal{L}$과, $\mathcal{L}$에 포함되어 있지 않은 술어 $P$를 생각하자. $T$가 $\mathcal{L} \cup \lbrace P \rbrace $의 이론이라고 하자. $T$를 만족하는 $\mathcal{L}$의 구조 $\mathfrak{A}$를 $\mathcal{L} \cup \lbrace P \rbrace $로 확장하는 방법이 유일할 때, $T$가 $P$를 암시적으로 정의_{implicitly define}한다고 한다.

이는 다음과 같이 말할 수도 있다. $T(P’)$가 $T$에서 등장하는 모든 $P$를 $P’$으로 바꾼 $\mathcal{L} \cup \lbrace P’ \rbrace $ 이론이라고 하자. $T$가 $P$를 암시적으로 정의한다는 것은 다음이 성립한다는 것이다.

\[T \cup T(P') \vDash \forall x_1, \dots, x_n \; P(x_1, \dots, x_n) \leftrightarrow P'(x_1, \dots, x_n)\]

반면 $T$가 $P$를 명시적으로 정의_{explicitly define}한다는 것은 다음을 만족시키는 $\mathcal{L}$-논리식 $\phi$가 존재한다는 것이다.

\[T \vDash \forall x_1, \dots, x_n \; P(x_1, \dots, x_n) \leftrightarrow \phi(x_1, \dots, x_n)\]

예를 들어 보자. $\mathcal{L} = (0, S, +, \cdot)$의 이론 $\mathsf{PA}$에 술어 $P(x, y)$에 관한 공리를 추가한 다음의 이론을 $T$라고 하자.

\[T = \mathsf{PA} \cup \Big\{ \forall x, y \big[ P(x, y) \rightarrow x + y = S(0) \big] \Big\}\]

$T(P’)$은 다음과 같다.

\[T(P') = \mathsf{PA} \cup \Big\{ \forall x, y \big[ P'(x, y) \rightarrow x + y = S(0) \big] \Big\}\]

$T$가 $P$를 암묵적으로 정의한다는 것은 다음이 성립한다는 것이다.

\[T \cup T(P') \vDash \forall x, y \big[ P(x, y) \leftrightarrow P'(x, y) \big]\]

이는 귀납 공리꼴로부터 자연스럽게 따라 나온다. 그런데 $P$는 다음과 같이 $T$에서 명시적으로 정의될 수도 있다.

\[\begin{gather} T \vDash \forall x, y \big[ P(x, y) \leftrightarrow \phi(x, y) \big] \\\\ \text{where}\\\\ \phi(x, y) : \forall z \big[ x + z = S(0) \rightarrow z = y \big] \end{gather}\]

이는 우연이 아니다.

정리. 언어 $\mathcal{L}$에 대해, $\mathcal{L} \cup \lbrace P \rbrace $의 이론 $T$가 $P$를 암시적으로 정의하면, $T$는 $P$를 명시적으로 정의한다.

증명. $P$가 $n$항 술어라고 하자. $\mathcal{L}$에 새로운 상수 $c_1, \dots, c_n$을 추가한 언어를 $\mathcal{L}’$이라고 하자. $T$가 $P$를 암시적으로 정의하므로,

\[T \cup T(P') \vDash P(c_1, \dots, c_n) \rightarrow P'(c_1, \dots, c_n)\]

이다. 콤팩트성 정리에 의해 어떤 $\mathcal{L} \cup \lbrace P \rbrace $ 문장 $\psi$가 존재하여, $T \vdash \psi$이고 다음이 성립한다.

\[\psi \land \psi(P') \vDash P(c_1, \dots, c_n) \rightarrow P'(c_1, \dots, c_n)\]

함축 원리를 이용하여 이항하면 다음과 같다.

\[\psi \land P(c_1, \dots, c_n) \vDash \psi(P') \rightarrow P'(c_1, \dots, c_n)\]

좌변은 $\mathcal{L}’ \cup \lbrace P \rbrace $의 문장이고, 우변은 $\mathcal{L}’ \cup \lbrace P’ \rbrace $의 문장이다. 따라서 크레이그 보간 정리에 의해 $\mathcal{L}$-논리식 $\theta$가 존재하여 다음이 성립한다.

\[\begin{gather} \psi \land P(c_1, \dots, c_n) \vDash \theta(c_1, \dots, c_n), \\\\ \theta(c_1, \dots, c_n) \vDash \psi(P') \rightarrow P'(c_1, \dots, c_n) \end{gather}\]

다시 이항하고 $P’$을 $P$로 치환하면,

\[\begin{gather} \psi \vDash P(c_1, \dots, c_n) \rightarrow \theta(c_1, \dots, c_n), \\\\ \psi \vDash \theta(c_1, \dots, c_n) \rightarrow P(c_1, \dots, c_n) \end{gather}\]

따라서 $\theta$는 $P$를 명시적으로 정의한다. ■