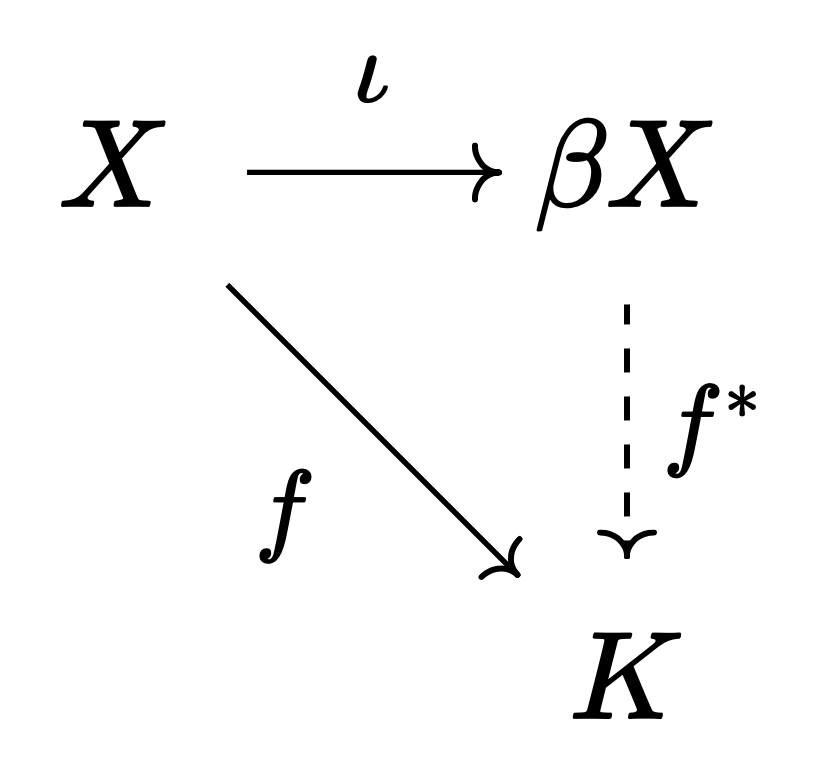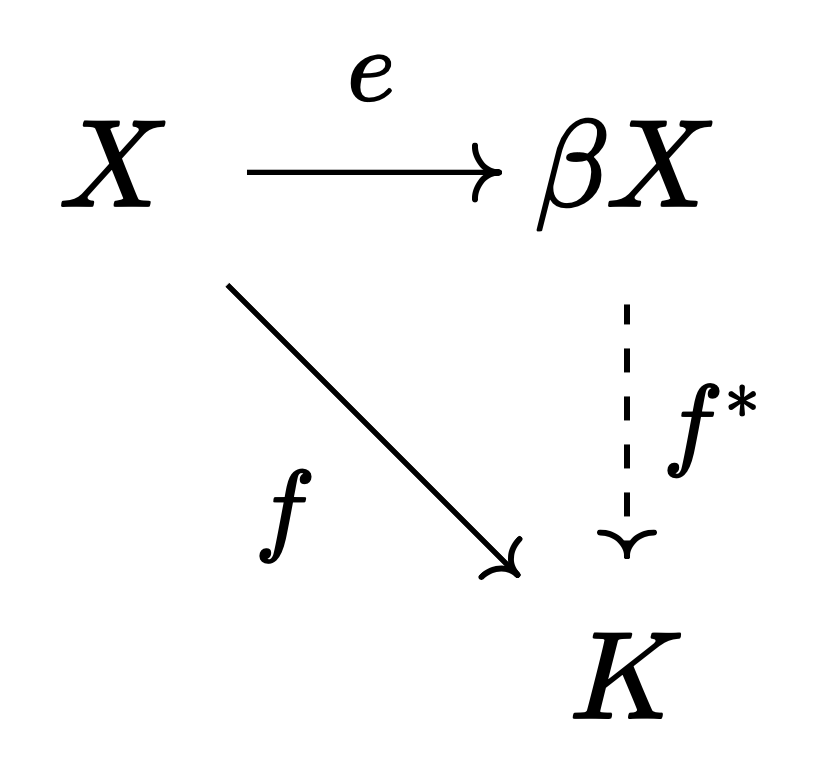스톤-체흐 콤팩트화

10 Jul 2025

정의. $\iota : X \to Y$가 임베딩이라고 하자. 즉, $\iota$는 단사이며 $X$와 $\iota [X]$의 위상동형사상이다. $Y$가 $X$의 콤팩트화_{compactification}라는 것은 $Y$가 콤팩트 공간이고, $\overline{\iota [X]} = Y$인 것이다.

고찰

• 일반적으로 $X$의 콤팩트화는 유일하지 않다. $\overline{X}$는 배경 위상에 따라 달라질 수 있기 때문이다.

• $X, Y$가 하우스도르프라면 $Y$는 콤팩트 하우스도르프 공간이므로 정규이고, 따라서 티호노프(완전 정칙)이다. 그리고 티호노프 공간의 부분공간은 티호노프임이 알려져 있기 때문에 $X$ 또한 티호노프이다. 즉, 하우스도르프 공간으로 콤팩트화 가능한 공간은 티호노프이다.

• 이의 역도 성립한다. 즉, 티호노프 공간은 하우스도르프 공간으로 콤팩트화 가능하다. 이것이 이 글에서 다루는 스톤-체흐 콤팩트화의 함의 중 하나이다.

국소적으로 콤팩트_{locally compact}한 하우스도르프 공간 $X$에 대해서는 $X$의 한점 콤팩트화_{one-point compactification} 공간 $X^\ast$가 존재한다. (이 사실과 위의 고찰로부터 국소적으로 콤팩트한 하우스도르프 공간은 티호노프임이 따라 나온다.) 특히 $X^\ast$는 $X$의 “가장 작은” 콤팩트화이다.

스톤-체흐 콤팩트화는 어떤 면에서 이의 반대 개념이다. $X$의 스톤-체흐 콤팩트화 공간 $\beta X$는 $X$의 “가장 큰” 콤팩트화이다. 여기서 “가장 큰”의 정확한 정의는 다음의 보편 성질_{universal property}이다.

정리 1. $X$가 티호노프일 때, 어떤 콤팩트 하우스도르프 공간 $\beta X$와 임베딩 $\iota: X \to \beta X$가 유일하게 존재하여, 다음을 만족한다: $K$가 임의의 콤팩트 하우스도르프 공간이고 $f: X \to K$가 연속사상일 때, $f = f^\ast \circ \iota$를 만족하는 연속사상 $f^\ast: \beta X \to K$가 유일하게 존재한다.

또한 $\beta X$는 $X$의 콤팩트화이다. 이를 스톤-체흐 콤팩트화_{Stone-Čech compactification}라고 한다.

여기서 $X$가 티호노프라는 조건을 빼도 꽤 강력한 결론을 유지할 수 있다.

정리 2. $X$가 일반 위상공간일 때, 어떤 콤팩트 하우스도르프 공간 $\beta X$와 연속함수 $e : X \to \beta X$가 유일하게 존재하여, 다음을 만족한다: $K$가 임의의 콤팩트 하우스도르프 공간이고 $f: X \to K$가 연속사상일 때, $f = f^\ast \circ \iota$를 만족하는 연속사상 $f^\ast: \beta X \to K$가 유일하게 존재한다.

차이점은 $e$가 임베딩이 아니라 연속함수라는 점이다. 실제로 $X$가 일반 위상공간일 때 $e$는 동형성은 고사하고 단사조차 아닐 수 있다. 이 경우 $\beta X$는 엄밀한 의미에서 $X$의 콤팩트화가 아니지만, 그럼에도 이 글에서는 편의를 위해 일반적으로 $\beta X$를 $X$의 스톤-체흐 콤팩트화라고 부를 것이다.

한점 콤팩트화가 국소적으로 콤팩트한 공간에서만 가능한 것과 달리, 정리 2에서 드러나듯이 스톤-체흐 콤팩트화는 모든 위상공간에서 가능하다. 덕분에 스톤-체흐 콤팩트화는 일반 위상공간의 범주 $\mathbf{Top}$를 콤팩트 하우스도르프 공간의 범주 $\mathbf{CHaus}$로 보내는 함자로서 간주될 수 있다. 실제로 다음이 성립한다.

정리 3. 망각함자_{forgetful functor} $U: \mathbf{CHaus} \to \mathbf{Top}$는 좌 어드조인트 $\beta: \mathbf{Top} \to \mathbf{CHaus}$를 가진다. 또한 $X \in \mathbf{Top}$에 대해 $\beta X$는 $X$의 스톤-체흐 콤팩트화에 해당한다.

예전 글에서 다룬 동치성으로 인해 이는 처음의 정의와 동치이다.

$\beta$의 존재성 증명은 크게 세 단계로 구성된다. 첫째, 임의의 위상공간 $X$에 대해 $\beta X$를 정의한다. 둘째, $\beta X$가 보편 성질을 만족함을 보인다. 셋째, $X$와 $\beta X$의 관계가 함수적_functorial임을, 즉 $\beta$가 함자임을 보인다. 위에서 정리 1, 정리 2, 정리 3을 구분하기는 했지만 아래의 증명에서는 세 정리를 함께 증명한다.

증명.

1. $\beta X$의 정의

집합 $C$를 다음과 같이 정의하자.

\[C = \{ f \mid f : X \to [0, 1] \text{ is continuous } \}\]

$[0, 1]^C$에 곱 위상을 주어 위상공간으로 만들자. $[0, 1]^C$는 $C \to [0, 1]$ 사상들의 공간으로 생각할 수 있다. 하우스도르프 공간의 곱은 언제나 하우스도르프이고, 콤팩트 공간의 곱 또한 언제나 콤팩트하므로 (티호노프 정리), $[0, 1]^C$는 콤팩트 하우스도르프 공간이다. 이제 $e: X \to [0, 1]^C$를 다음과 같이 정의한다.

\[e: x \mapsto \lambda_x \quad \text{where} \quad \lambda_x : f \mapsto f(x)\]

곱 위상의 성질(정의)에 의해 $e$는 연속함수이다. 특히 $X$가 티호노프 공간이라면 우리손 보조정리와 그 따름결과 (링크의 말단에 있는 정리) 에 의해 $e$는 임베딩이다.

$\beta X$를 $[0, 1]^C$에서 $e[X]$의 폐포로 정의하자. $\beta X$는 콤팩트 공간의 닫힌집합이므로 콤팩트이며, 하우스도르프 공간의 부분공간이므로 하우스도르프이다. 따라서 $\beta X$는 콤팩트 하우스도르프이다. 특히, 직전 문단의 고찰로 인해 $X$가 티호노프일 때 $\beta X$는 $X$의 콤팩트화이다.

2. $\beta X$의 보편 성질 확인

이제 $\beta X$가 보편 성질을 만족함을 보이자. 먼저 $K = [0, 1]$일 때를 보인다.

임의의 연속사상 $f: X \to [0, 1]$이 주어졌다고 하자. $f^\ast : \beta X \to [0, 1]$을 다음과 같이 정의한다.

\[f^\ast : \lambda \mapsto \lambda (f)\]

즉, $(x_g)_{g \in C}$를 $x_f$로 사상시키는 사영사상 $\pi_f: [0, 1]^C \to [0, 1]$에 대해, $f^\ast = \pi_f \rvert_{\beta X}$이다. $\pi_f$가 연속이므로 $f^\ast$는 연속이다. 또한 임의의 $x \in X$에 대해,

\[(f^\ast \circ e)(x) = f^\ast (\lambda_x) = \lambda_x(f) = f(x)\]

이므로 $f^\ast$는 보편 성질이 요구하는 사상이다.

이제 일반적인 콤팩트 하우스도르프 공간 $K$와 연속사상 $f: X \to K$을 고려하자. $K$는 티호노프 공간이므로 어떤 집합 $J$에 대해 $[0, 1]^J$에 임베딩될 수 있다. 그러므로 일반성을 잃지 않고 $K = [0, 1]^J$, $f: X \to [0, 1]^J$인 경우를 고려하면 충분하다. 이 경우 $f^\ast$를 다음과 같이 정의한다.

\[f^\ast : \lambda \mapsto (\lambda (\pi_\alpha f))_{\alpha \in J}\]

$K = [0, 1]$인 경우의 논증으로부터, $f^\ast$는 연속이며 보편 성질을 만족함이 따라 나온다. 따라서 $\beta X$는 $X$의 스톤-체흐 콤팩트화이다.

3. $\beta$의 함자 조건 확인

마지막으로 $\beta$가 함자임을 보이자. 임의의 위상공간 $X, Y$와 연속사상 $\psi : X \to Y$에 대해 다음 가환 도식이 성립하도록 $\beta \psi$를 정의할 수 있음을 보여야 한다.

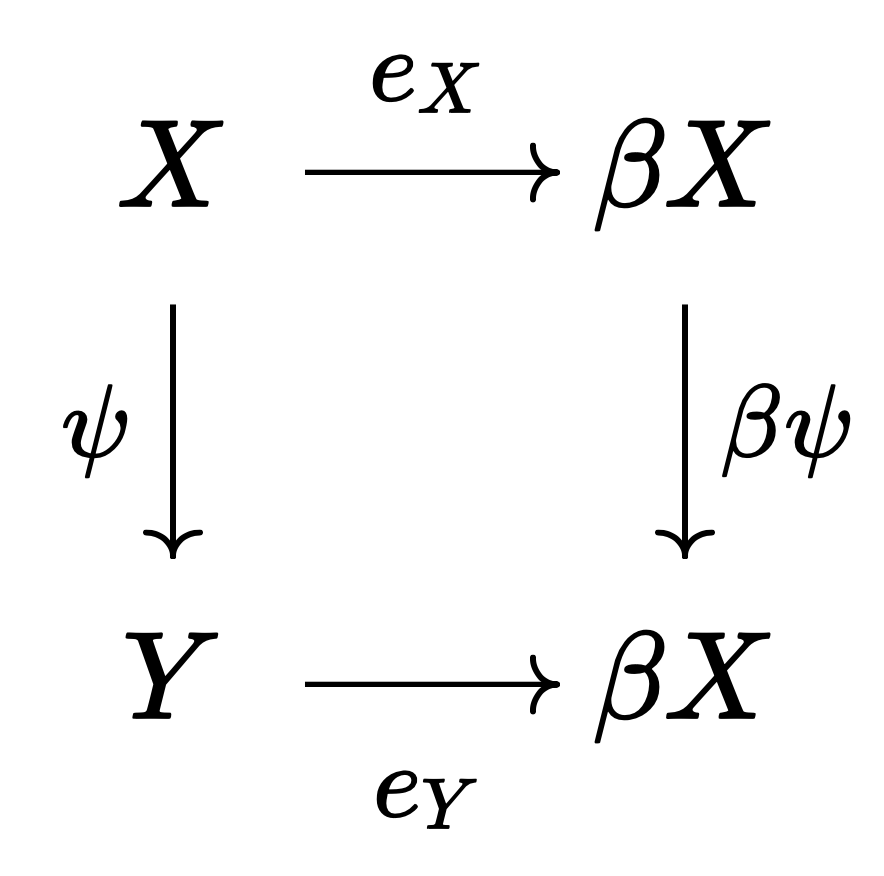
다음과 같이 $\beta \psi$를 정의하자. 임의의 $\lambda \in \beta X$에 대해,

\[\beta \psi : \lambda \mapsto (g \mapsto \lambda(g \circ \psi) )_{g \in C_Y}\]

여기서 $C_Y$는 연속인 $g : Y \to [0, 1]$의 모임이다. (연습문제: 위 식이 잘 정의되었음을 각 함수의 정의역과 공역을 따져 확인해 보라.) 가환 도식의 성립은 다음 식으로 환원된다.

\[\beta \psi(\lambda_x) = \lambda_{\psi(x)}\]

좌변을 정의에 따라 풀어쓰면 위 식이 성립함을 알 수 있다.

\[\begin{align*} \beta \psi(\lambda_x) &= (g \mapsto \lambda_x(g\circ \psi))_{g \in C_Y} \\ &= (g \mapsto (g \circ \psi)(x))_{g \in C_Y} \\ &= (g \mapsto g(\psi(x)))_{g \in C_Y} \\ &= \lambda_{\psi(x)} \end{align*}\]

따라서 $\beta : \mathbf{Top} \to \mathbf{CHaus}$는 함자이며, 특히 $U: \mathbf{CHaus} \to \mathbf{Top}$의 좌 어드조인트이다. 이로부터 임의의 $X$에 대해, 보편 조건을 만족하는 $(e, \beta X)$는 콤마 카테고리 $(A \Rightarrow U)$의 초기 대상이므로 동형성에 대해 유일함이 따라 나온다. (자세한 설명은 이 글을 참조) ■