우리손 보조정리와 우리손 거리화 정리
09 Jul 2025우리손 보조정리
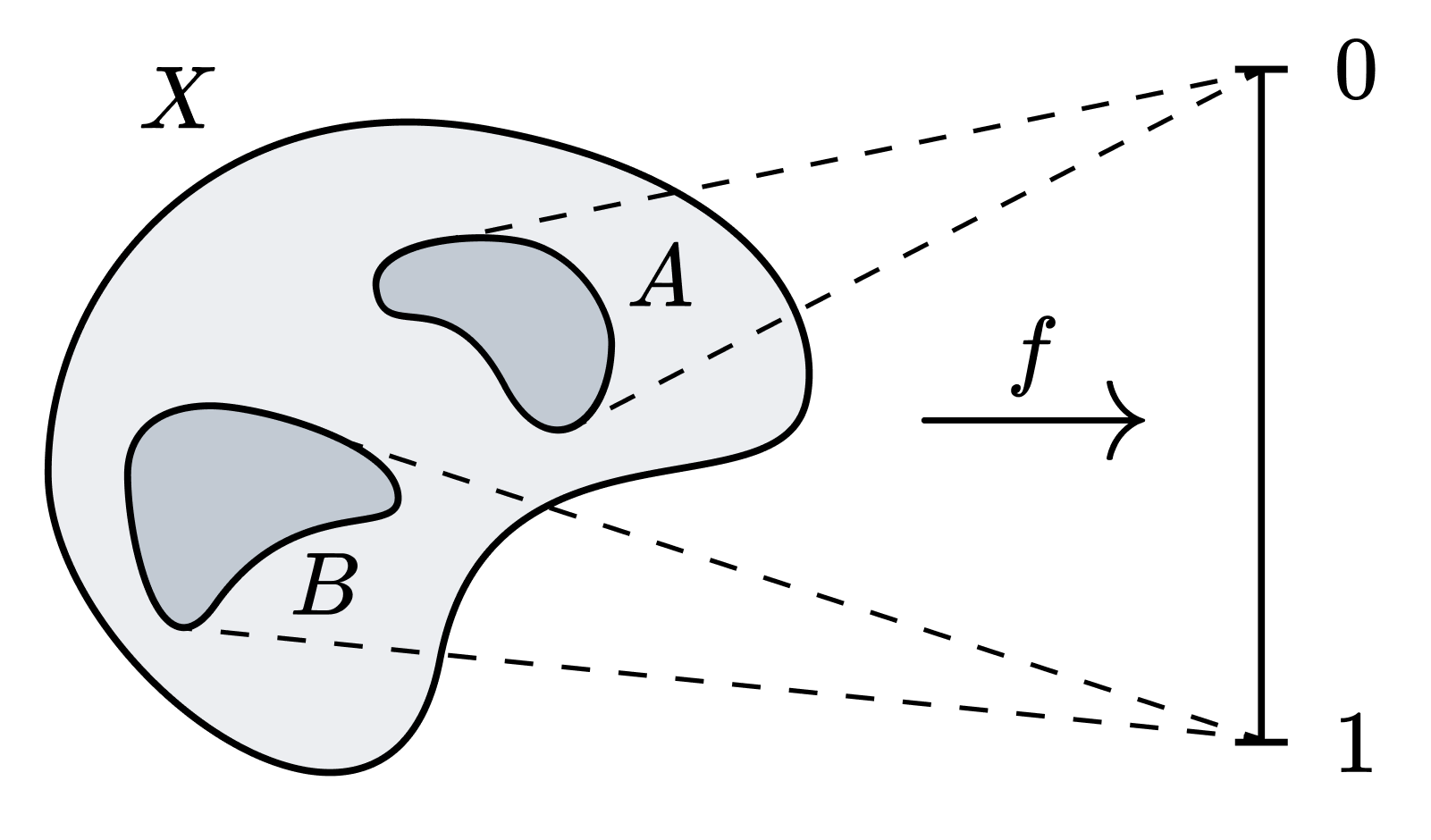
우리손 보조정리Urysohn Lemma. $X$가 정규normal 공간이라고 하자. $A, B$가 서로소인 $X$의 닫힌집합일 때, 어떤 연속함수 $f: X \to [0, 1]$이 존재하여 $f[A] = \lbrace 0 \rbrace$, $f[B] = \lbrace 1 \rbrace$이다.
정규성을 비롯한 분리 공리는 해당 공간에서 점과 닫힌집합을 분리한다. 우리손 보조정리의 의의는, 정규성 분리 공리의 경우 두 닫힌집합은 좋은 공간에서도 분리 가능하다는 것이다. 구체적으로, 정규공간을 적절한 연속함수로 사상시켰을 때 두 닫힌집합은 $[0, 1]$에서 분리 가능하다. 그리고 $[0, 1]$의 여러 좋은 성질은 — 콤팩트 하우스도르프 거리 공간일 뿐 아니라 우리에게 굉장히 익숙한 공간이라 논증하기도 쉽다 — 우리손 보조정리의 굉장한 잠재력을 암시한다.
증명
$Q = [0, 1] \cap \mathbb{Q}$라고 하자 (사실 $[0, 1]$의 가산 조밀 집합이기만 하면 된다). $Q$가 가산이므로 $Q$의 원소를 열거enumerate하는 방법이 존재한다. 일례로 분모-분자의 사전식 열거 $\prec$를 고려하자.
\[0 \prec 1 \prec 1/2 \prec 1/3 \prec 2/3 \prec 1/4 \prec 1/5 \prec 2/5 \prec \cdots\]이제 다음과 같이 $\lbrace U_q \rbrace _{q \in Q}$를 정의하자. 먼저 $U_1 = X \setminus B$이다 ($B$가 닫힌집합이므로 $U_1$은 열린집합이다). 정규성에 의해 $A \subset U_0$이면서 $\overline{U_0} \subset U_1$인 $U_0$가 존재한다. 나머지 $U_q$는 열거 순서에 따라 다음과 같이 정의한다. $p \prec q$인 임의의 $p$에 대해,
- $p < q \implies \overline{U_p} \subset U_q$
- $q < p \implies \overline{U_q} \subset U_p$
정규성에 의해 위 조건을 만족하며 $\lbrace U_q \rbrace _{q \in Q}$를 완전히 정의할 수 있다.
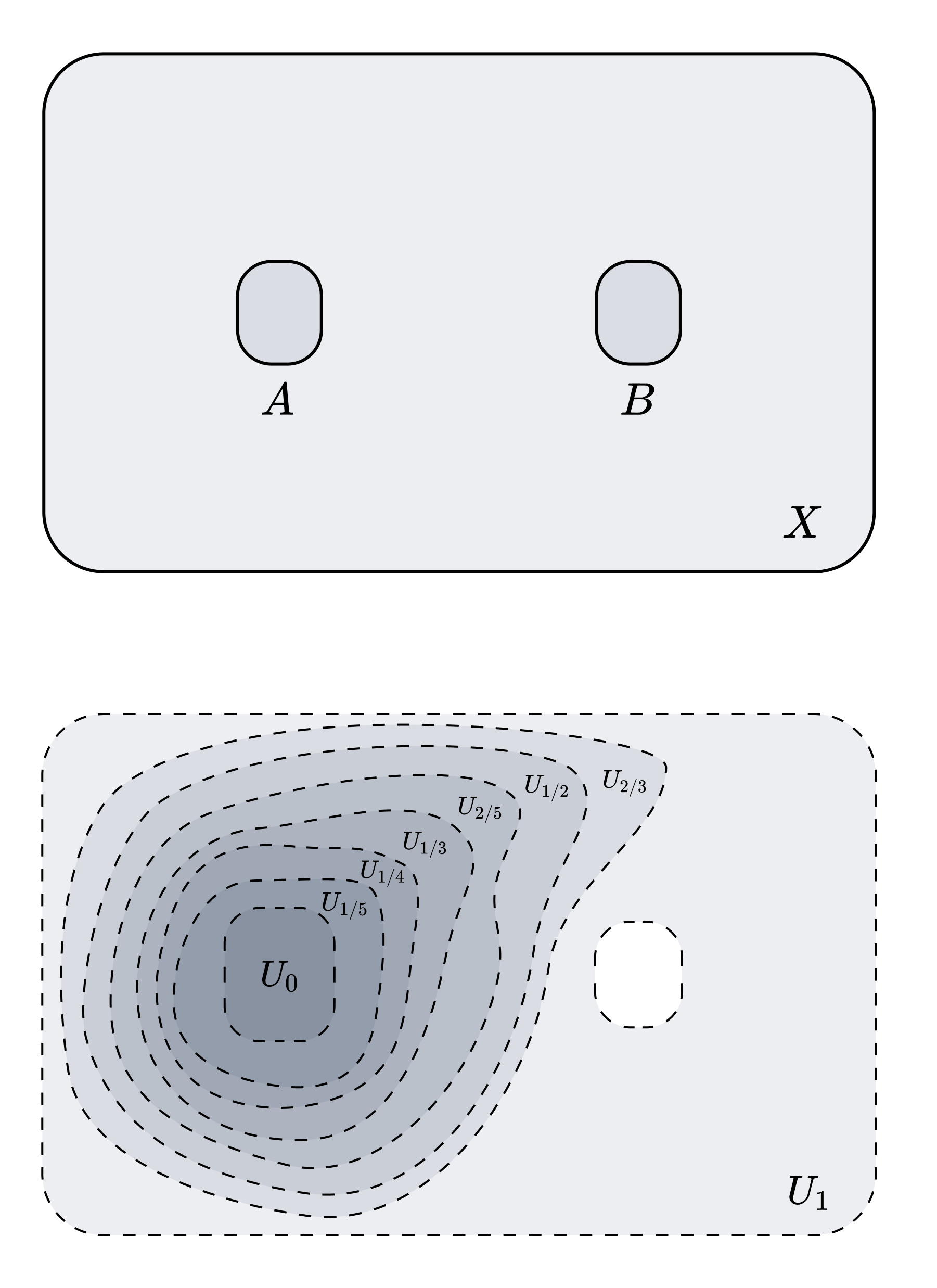
이제 다음과 같이 함수 $f: X \to [0, 1]$을 정의하자.
\[f(x) = \begin{cases} \sup_{<}\{q \in Q : x \notin U_q \} & x \notin U_0 \\ 0 & x \in U_0 \end{cases}\]$\sup_<$라는 표기는 $\prec$가 아닌 $<$에 대해 상한을 취함을 의미한다. 정의로부터 $f[A] = 0, f[B] = 1$가 따라 나온다.
이제 $f$가 연속임을 보이면 정리가 증명된다. $\lbrace B_\epsilon(q) \cap [0, 1] : q \in Q, \epsilon \in \mathbb{Q}_{>0} \rbrace $가 $[0, 1]$의 위상 기저이므로, 임의의 $q \in Q$와 특정 상한보다 작은 양의 유리수 $\epsilon$에 대해 $S_{q, \epsilon} = f^{-1}(B_\epsilon(q) \cap [0, 1])$가 열린집합임을 보이면 충분하다.
- $0 < q < 1$인 경우, $S_{q, \epsilon} = (X \setminus \overline{U_{q-\epsilon}}) \cap U_{q + \epsilon}$이므로 열린집합이다.
- $q = 0$인 경우, $S_{0, \epsilon} = U_\epsilon$이므로 열린집합이다.
- $q = 1$인 경우, $S_{1, \epsilon} = X \setminus \overline{U_{1 - \epsilon}}$이므로 열린집합이다.
따라서 $f$는 연속이다. ■
고찰
-
우리손 보조정리의 역은 자명히 성립한다. 즉, 임의의 닫힌집합 $A, B \subset X$에 대해 어떤 연속인 $f: X \to [0, 1]$가 $A, B$를 분리한다면, $U = f^{-1}[0, 1/2)$, $V = f^{-1}(1/2, 1]$는 $A, B$를 분리하는 서로소 열린집합이므로 $X$는 정규이다. 간단히 말해, 정규공간에서는 우리손 분리가능성과 분리 공리가 동치이다.
-
정칙regular 공간에서는 이가 성립하지 않는다. 즉, 정칙 공간 $X$에서 임의의 닫힌집합 $F$와 점 $a$가 주어졌을 때, $f(a) = 0$, $f[F] = \lbrace 1 \rbrace$을 만족하는 연속인 $f: X \to [0, 1]$이 언제나 존재하는 것은 아니다. 우리손 분리가능한 정칙 공간을 티호노프Tychonoff 공간 또는 완전 정칙completely regular 공간이라고 하며, 정칙보다 엄격히 강한 조건이다.
-
우리손 보조정리의 증명이 정칙 공간에 대해 유효하지 않은 이유는 $p < q \implies \overline{U_p} \subset U_q$를 만족하는 $\lbrace U_q \rbrace $를 구성할 때 정규 공리가 필요하기 때문이다.
우리손 거리화 정리
우리손 보조정리의 응용으로서, 우리손 거리화 정리를 증명하자.
우리손 거리화 정리Urysohn metrisation theorem. 2차 가산인 정규 공간은 거리화 가능하다.
그런데 2차 가산인 정칙 공간은 정규 공간임이 알려져 있으므로 위 정리의 진술은 “2차 가산인 정칙 공간은 거리화 가능하다”와 같이 자연스럽게 강화할 수 있다.
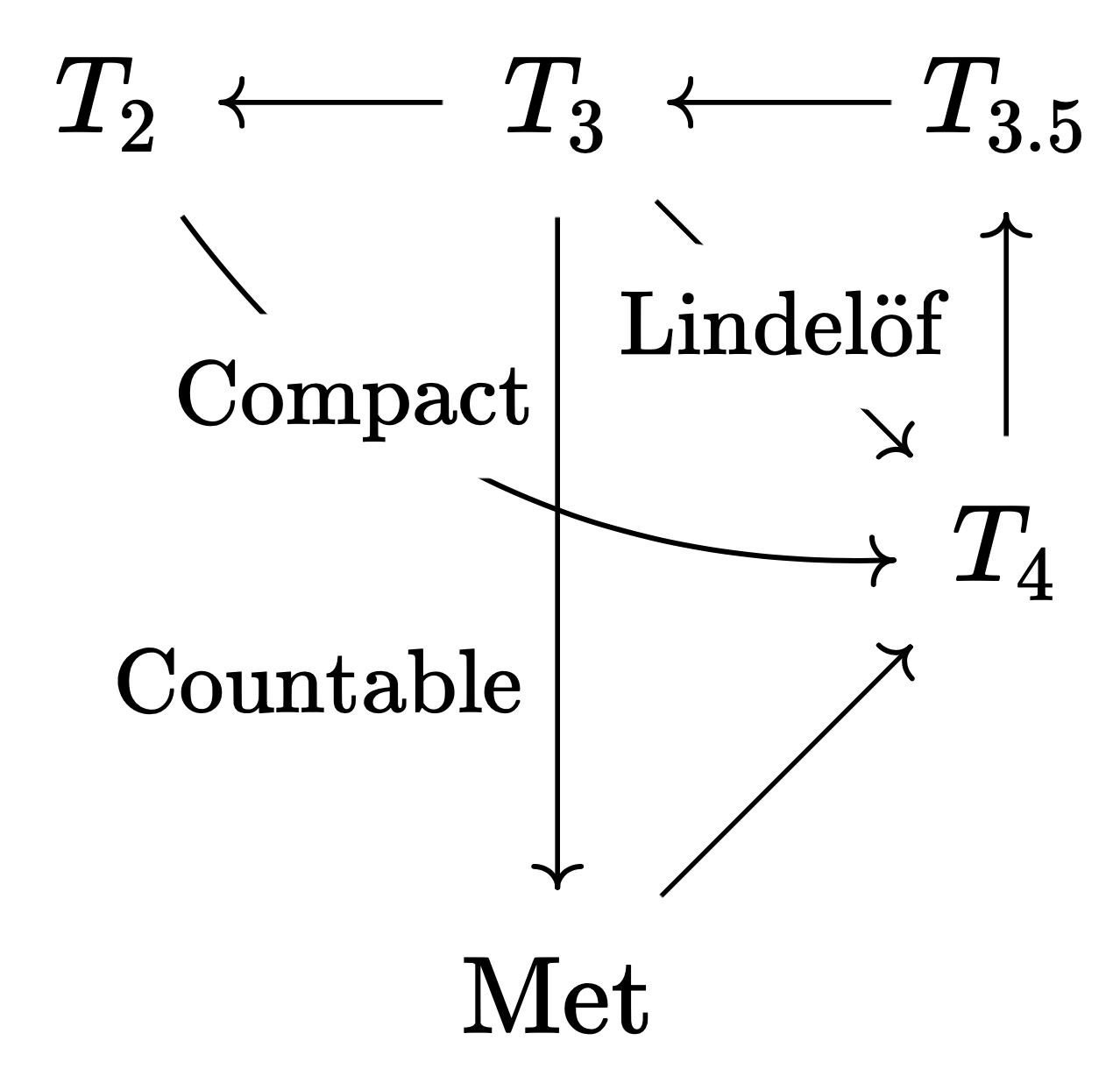
따라서 공간들 간의 시사 관계는 다음과 같다. 화살표의 길이가 길수록 요구되는 조건이 강해진다. $T_2 \to T_4$는 $T_3 \to T_4$보다 엄격히 어려운 시사 관계이며, 이것은 전자에서 요구되는 콤팩트성이 후자에서 요구되는 린델뢰프보다 엄격히 강한 조건인 데에서 드러난다. 마찬가지로 $T_3 \to \mathrm{Met}$는 $T_3 \to T_4$보다 엄격히 어려운 시사 관계이며, 전자에서 요구되는 2차 가산성은 후자에서 요구되는 린델뢰프보다 엄격히 강한 조건이다. 그러나 $T_2 \to T_4$와 $T_3 \to \mathrm{Met}$는 어느 한쪽이 엄격히 어려운 시사 관계가 아니다 (두 화살표의 길이는 엇비슷하다). 이것은 콤팩트성과 2차 가산성이 일반적으로 서로를 시사하지 않는다는 점에서 드러난다.
증명
$X$가 2차 가산인 정규 공간이라고 하자. 다음의 보조정리를 증명한다.
보조정리. $X$를 $[0, 1]$에 사상시키는 연속함수의 가산족 $\mathcal{F}$가 존재하여, 임의의 $x_0 \in X$와 그 근방 $U$에 대해, $f(x_0) > 0$이고 $f[X \setminus U] = \lbrace 0 \rbrace $인 $f \in \mathcal{F}$가 존재한다.
$x_0$와 $U$가 주어졌을 때 그러한 $f$가 존재함은 우리손 보조정리로부터 알 수 있다. 우리가 해야할 일은 이를 가산 함수족으로 줄이는 것이다. $\mathcal{B} = \lbrace B_n \rbrace $이 $X$의 가산인 위상기저라고 하자. $B_m \subset B_n$일 때, 우리손 보조정리로부터 $f_{nm}: X \to [0, 1]$을 다음을 만족하는 연속함수로 정의하자.
- $f_{nm}[\overline{B_m}] = 1$
- $f_{nm}[X \setminus B_n] = 0$
$\mathcal{F} = \lbrace f_{nm} \rbrace $으로 정의하자. 임의의 $x_0$와 그 근방 $U$가 주어졌을 때, 위상기저의 정의에 의해 $x_0 \in B_n \subset U$인 $B_n$이 존재한다. 또한 정규성에 의해 $x \in \overline{V} \subset B_n$인 열린집합 $V$가 존재한다. 다시 위상기저의 정의에 의해 $x \in B_m \subset V$인 $B_m$이 존재한다. 이때 $f_{nm} \in \mathcal{F}$가 보조정리의 조건을 만족하는 함수이다. □
이제 본 정리를 증명하자. 아이디어는 $X$를 $[0, 1]^\omega$에 임베딩하는 것이다. $[0, 1]^\omega$에 곱 위상이 주어지면 거리 공간임이 알려져 있으므로 $X$는 거리 공간의 부분공간과 동형인 공간으로서 거리화 가능함이 보여진다.
$\mathcal{F} = \lbrace f_n \mid n \in \omega \rbrace $가 보조정리로서 주어지는 가산 함수족이라고 하자. 다음과 같이 $F: X \to [0, 1]^\omega$를 정의한다.
\[F: x \mapsto (f_1(x), f_2(x), f_3(x), \dots)\]$F$가 임베딩을 보이자. 즉, $F$가 연속이고, 단사이며, 정의역과 치역의 동형사상임을 보여야 한다.
각 $f_n$은 연속이므로 곱 위상의 성질(정의이기도 하다)에 의해 $F$는 연속이다. $F$가 단사임은 $X$가 하우스도르프라는 사실에서 따라 나온다. 따라서 다음을 보이면 충분하다.
$U \subset X$가 열린집합일 때, $F[U]$는 $\mathrm{im} F$에서 열린집합이다.
임의의 $y_0 \in F[U]$에 대해 $y_0 \in V \subset F[U]$이며 $\mathrm{im} F$에서 열린 $V$가 존재함을 보이자. $F[U]$의 정의에 의해 어떤 $x_0 \in X$가 존재하여 $F(x_0) = y_0$이다. $x_0$와 $U$에 대해 보조정리를 만족하는 함수가 $f_n \in \mathcal{F}$라고 하자. $f_n(x_0) = 1$이므로 $(y_0)_n = 1$이다. 따라서 $W = \pi_n^{-1}(0, 1] \subset [0, 1]^\omega$와 같이 정의하면 $W$는 $y_0$를 원소로 가지는 $[0, 1]^\omega$에서 열린집합이다.
$W \cap \mathrm{im} F \subset F[U]$임을 보이자. 임의의 $w \in W$는 $F(x_1) = w$와 같이 쓸 수 있다. 추가로 $w \in \mathrm{im} F$라면 $f_n(x_1) = 1$이다. 그런데 $f_n$은 $U$ 외부에서는 $0$이므로, $x_1 \in U$이다. 따라서 $w \in F[U]$이다. 따라서 $W \cap \mathrm{im} F$는 $F[U]$에 포함되며 $y_0$를 원소로 가지는 $\mathrm{im} F$의 열린집합이다. 따라서 $F[U]$는 $\mathrm{im} F$에서 열린집합이다. ■
고찰
-
우리손 거리화 정리는 나가타-스미로느프 거리화 정리Nagata-Smirnov metrisation theorem로 강화할 수 있다. 진술은 다음과 같다.
$X$가 거리화 가능할 필요충분조건은 $X$가 정칙이며 가산-국소적으로 유한한countably locally finite 위상기저를 가지는 공간인 것이다.
위상공간 $X$의 부분집합들로 이루어진 집합족 $\mathcal{A}$가 국소적으로 유한하다는 것은, 임의의 $x \in X$에 대해 어떤 근방 $U$가 존재하여 $U$가 $\mathcal{A}$의 오직 유한한 개수의 집합과만 교집합을 가진다는 것이다. 위상기저 $\mathcal{B}$가 가산-국소적으로 유한하다는 것은, 각각의 $\mathcal{B}_n$이 국소적으로 유한이도록 $\mathcal{B} = \bigcup_{n \in \omega}\mathcal{B}_n$와 같이 적을 수 있다는 것이다.
-
우리손 거리화 정리의 증명을 살짝 변형하면 다음 사실을 발견할 수 있다.
정리. $T_1$ 공간인 $X$에 대해, $\lbrace f_{\alpha} \rbrace _{\alpha \in J} $가 다음 조건을 만족하는 연속함수 $f_\alpha : X \to [0, 1]$의 모임이라고 하자: 임의의 $x_0 \in X$와 근방 $U$에 대해, 어떤 $\alpha \in J$가 존재하여 $f_\alpha(x_0) = 1$이고 $f_\alpha[X \setminus U] = \lbrace 0 \rbrace $이다. 이때, $F(x) = (f_\alpha(x))_{\alpha \in J}$는 $X$를 $[0, 1]^J$로 임베딩하는 사상이다.
$T_1$ 조건을 생략하면 $F$는 단사가 아닐 수 있음을 확인하라. 위 정리는 스톤-체흐 콤팩트화Stone-Čech compactification를 증명하는 데 사용된다.