Suslin's Problem and the Diamond Principle
26 Dec 2025This post was originally written in Korean, and has been machine translated into English. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
In the previous post, the following theorem was introduced:
Definition of the set-theoretic real numbers. A totally ordered set $(R, <)$ satisfying the following properties is unique up to order isomorphism:
- It is a complete totally ordered set.
- It has no endpoints.
- It is separable, i.e., there exists a countable $Q \subset R$ such that $Q$ is dense in $R$.
From the third property, the following result follows:
Theorem. Let $\mathcal{C}$ be the collection of open intervals of $\mathbb{R}$. If the elements of $\mathcal{C}$ are pairwise disjoint, then $\mathcal{C}$ is countable.
Proof. Since the elements of $\mathcal{C}$ are pairwise disjoint, there exists an injective mapping $\mathcal{C} \to \mathbb{Q}$ that maps each $(x, y) \in \mathcal{C}$ to some $q \in (x, y) \cap \mathbb{Q}$. Hence, $\mathcal{C}$ is countable. ■
A totally ordered set in which any collection of pairwise disjoint open intervals is at most countable is said to have the countable chain condition. The peculiar name of this property will be explained later.
Suslin’s problem asks whether the separability condition in the definition of the set-theoretic real numbers can be weakened to the countable chain condition.
Definition. A complete totally ordered set without endpoints that satisfies the countable chain condition but is not order-isomorphic to the real numbers is called a Suslin line.
Thus, a Suslin line must not be separable.
Suslin’s problem. Does a Suslin line exist?
This problem, posed in 1920, was shown to be independent of ZFC by Solovay and Tennenbaum in 1971. Instead of examining the independence proof, this post will explore the combinatorial counterpart of Suslin lines, known as Suslin trees. Let us first consider the following well-known theorem:
König’s lemma. For a tree $T$, if $T$ has height $\omega$ and each node has finitely many children, then $T$ has a branch of length $\omega$.
Proof. Let $\alpha_0$ be the root node, and define a sequence of nodes inductively as follows. Given $\alpha_n$, since $\alpha_n$ has finitely many children, there exists a child node such that the subtree rooted at that node has infinite height. Choose one such child node (using the axiom of choice) and define it as $\alpha_{n+1}$. The sequence ${a_n}$ forms a branch of infinite length. ■
If the nodes of $T$ are allowed to have countably many children, it is possible for all branches of $T$ to have finite length while $T$ itself has height $\omega$, as illustrated below:
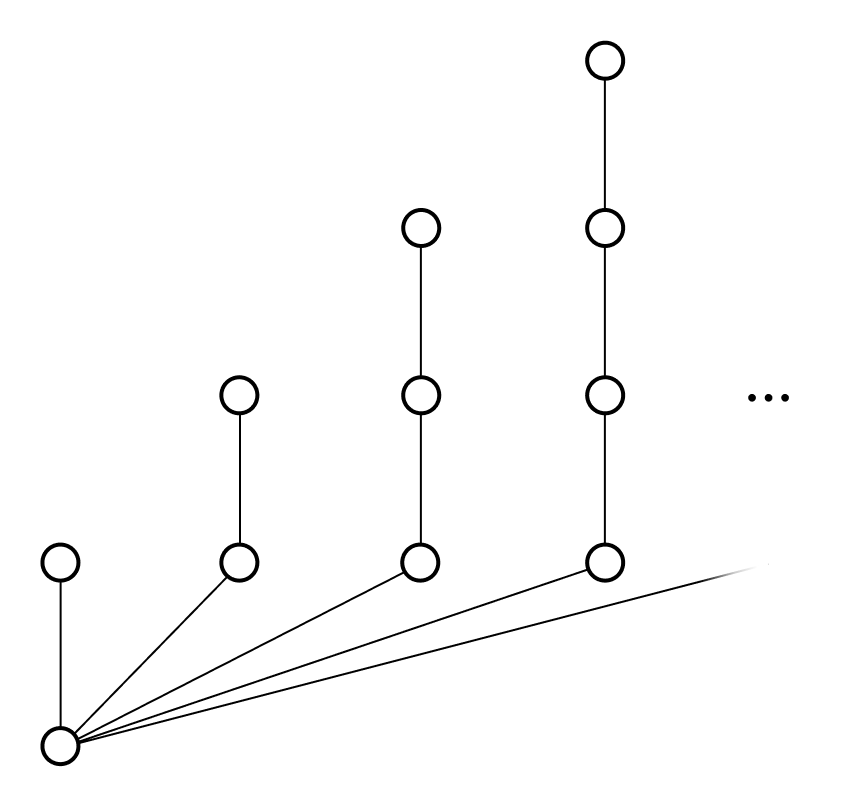
A natural question is whether König’s lemma can be extended to uncountable cardinals. However, the answer to this question is negative.
Aronszajn’s theorem. There exists a tree of height $\omega_1$ in which each node has countably many children, but no branch has length $\omega_1$. (Such a tree is called an Aronszajn tree of height $\omega_1$.)
Thus, to extend König’s lemma to uncountable cardinals, a stronger condition than “each node has countably many children” is required. To this end, the following definition is introduced:
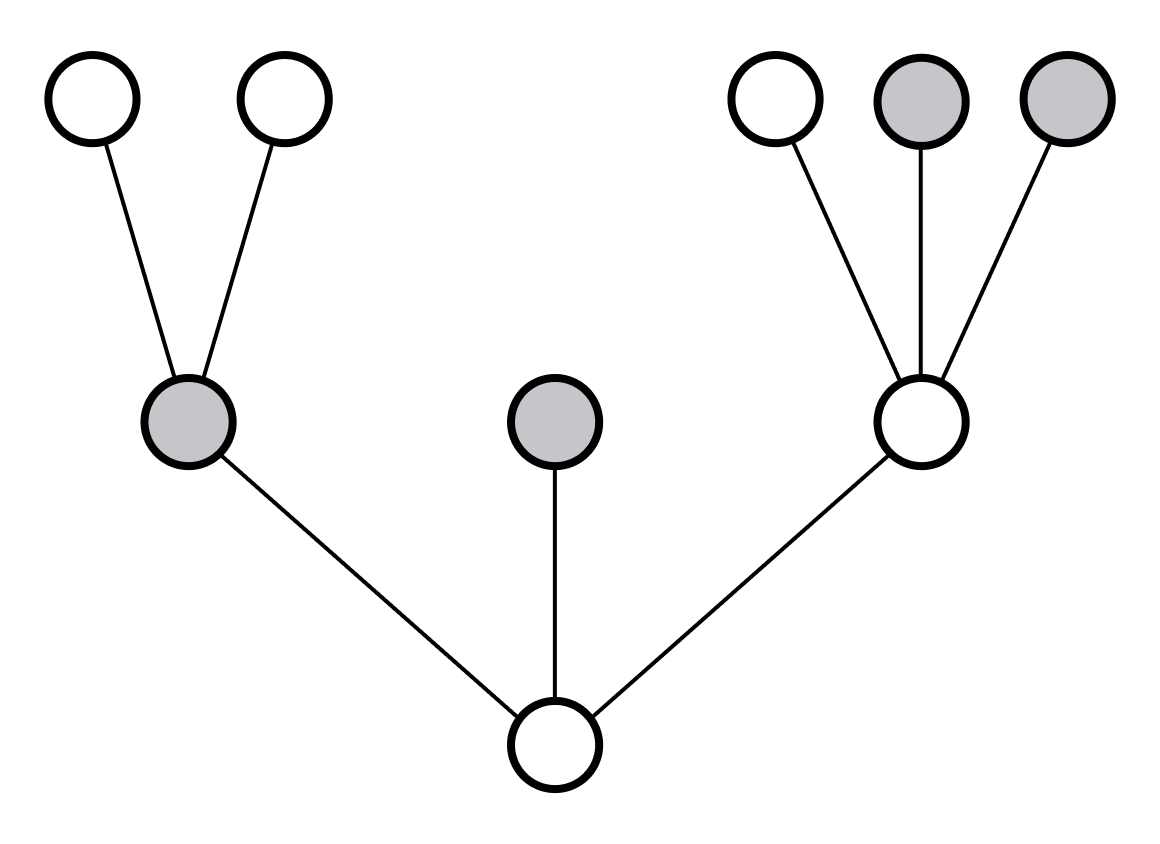
Definition. A subset $S$ of a tree $T$ is called an antichain if the elements of $S$ are mutually incomparable. A tree $T$ is said to have the countable chain condition if all antichains in $T$ are countable.
For example, in the tree below, the coloured nodes form an antichain:
While “each node has countably many children” is a local property, the countable chain condition is a global property of the entire tree. Intuitively, the countable chain condition implies that the “width” of the tree is less than $\omega_1$. Note that the term “countable chain condition” rather than “countable antichain condition” is used for historical reasons and need not be a cause for concern.
Earlier, it was mentioned that a collection of pairwise disjoint open intervals of the real numbers is at most countable, and this property is also referred to as the countable chain condition. The two usages are closely related. The general definition of an antichain is as follows:
Definition. Let $(P, \leq)$ be a partially ordered set. Two elements $x, y \in P$ are said to be incomparable if there does not exist $z \in P$ such that $z \leq x$ and $z \leq y$. A subset $S \subseteq P$ is called an antichain if its elements are mutually incomparable. $P$ is said to have the countable chain condition if all antichains in $P$ are countable.
In a tree $T$, let $x \leq y$ denote that the node $x$ is a descendant of the node $y$. Then, two nodes $x$ and $y$ are incomparable as tree nodes if and only if they are incomparable as elements of the partially ordered set $(T, \leq)$.
Definition. An Aronszajn tree with the countable chain condition is called a Suslin tree.
The existence of Suslin trees is equivalent to the existence of Suslin lines, and hence is independent of ZFC. The equivalence arises because each property corresponds as follows:
| Suslin line | Suslin tree |
|---|---|
| Non-separability | Height $\omega_1$ |
| Countable chain condition for open intervals | Countable chain condition for the tree |
The correspondence between non-separability and the height $\omega_1$ property can be understood as follows: the existence of a countable set $D$ such that $|D| \leq \aleph_0$ and every open interval $(a, b)$ intersects $D$ (non-separability) corresponds to the existence of an ordinal $\alpha$ such that $\alpha < \omega_1$ and every node $x \in T$ is the limit of a sequence of nodes in $T^{(\alpha)}$ (tree height being countable).
In connection with Suslin trees, consider the following non-standard axiom in set theory:
Diamond principle. There exists a sequence $\langle W_\alpha : \alpha < \omega_1 \rangle$ such that $W_\alpha \subseteq \mathcal{P}(\alpha)$, each $W_\alpha$ is countable, and for any $X \subseteq \omega_1$, the set ${\alpha : \alpha < \omega_1, X \cap \alpha \in W_\alpha}$ is stationary.
The diamond principle is often denoted by $\Diamond$, and the sequence $\langle W_\alpha \rangle$ is called a diamond sequence.
The set $X \cap \alpha$ can be thought of as the “reflection” of $X$ through the “mirror” $\alpha$. In this sense, the diamond principle implies that the reflection of $X$ at ordinals less than $\omega_1$ appears sufficiently often in $\langle W_\alpha \rangle$. (In this post, it was explained that stationary sets are the set-theoretic analogue of “measure > 0”.)
Thus, the diamond principle is a type of reflection principle and plays a role in regulating the set-theoretic universe, similar to the axiom $V = L$ (in fact, $V = L$ implies $\Diamond$). Like other axioms that regulate the set-theoretic universe, the diamond principle implies the continuum hypothesis.
Theorem. $\Diamond \implies \mathsf{CH}$
Proof. Let $X \subseteq \omega \subset \omega_1$. Since $X$ reflects stationarily at ordinals less than $\omega_1$, there exists some $\alpha > \omega$ such that $X \cap \alpha = X \in W_\alpha$. Hence, all subsets of $\omega$ are contained in $\bigcup_{\alpha < \omega_1} W_\alpha$, whose cardinality is $\aleph_1$. Therefore, $2^{\aleph_0} = \aleph_1$. ■
Theorem. If $\Diamond$ holds, then a Suslin line exists.
Proof. See Hrbacek & Jech (3rd ed), Chapter 12, Section 5. Note the following typographical error in the original text:
(Original) Lemma 5.3. $\Diamond$ implies that there exists a sequence $\langle Z_\alpha : \alpha < \omega_1 \rangle$ such that, for each $\alpha < \omega_1$, $Z_\alpha \subseteq \omega^{<\alpha}$, $Z_\alpha$ is at most countable, and for any $X \subseteq \omega^{<\omega_1}$ the set ${\alpha < \omega_1 : X \cap \omega^{<\alpha}}$ is stationary.
Proof. We note that […] Clearly, $Z_\alpha \subseteq \omega^{<\alpha}$ and is at most countable.
(Corrected) Lemma 5.3. $\Diamond$ implies that there exists a sequence $\langle Z_\alpha : \alpha < \omega_1 \rangle$ such that, for each $\alpha < \omega_1$, $Z_\alpha \subseteq \mathcal{P}(\omega^{<\alpha})$, $Z_\alpha$ is at most countable, and for any $X \subseteq \omega^{<\omega_1}$ the set ${\alpha < \omega_1 : X \cap \omega^{<\alpha}}$ is stationary.
Proof. We note that […] Clearly, $Z_\alpha \subseteq \mathcal{P}(\omega^{<\alpha})$ and is at most countable.
Additionally, the sentence “Let ${C_n : n \in \mathbb{N}}$ be the at most countable collection of those elements of $Z_\alpha$ which happen to be maximal antichains in $T^{(\alpha)}$.” just before Claim 5.5 means that for each $n$, $C_n \in Z_\alpha$, $C_n \subseteq \omega^\alpha$, and $C_n$ is an antichain when its elements are regarded as nodes of $T^{(\alpha)}$. ■
Corollary. If $V = L$, then a Suslin line exists.
Thus, the existence of Suslin lines is related to the regulation of the set-theoretic universe. While this may seem paradoxical, it is not so surprising when one considers that one of the conditions for Suslin lines is the “non-existence” of countable dense sets. Suslin lines are a feature of a “loose” set-theoretic universe that achieves the countable chain condition without generating countable dense sets.