서슬린의 문제와 다이아몬드 원리

26 Dec 2025

이전 글에서 다음 정리를 소개했다.

집합론적 실수의 정의. 다음을 만족하는 순서 집합 $(R, <)$은 순서 동형에 대해 유일하다.

1. 완비 전순서 집합이다.
2. 양끝점이 없다.
3. 분리 가능_separable하다. 즉, 어떤 가산인 $Q \subset R$이 존재하여 $Q$가 $R$에서 조밀_dense하다.

3번 성질로부터 다음이 따라 나온다.

정리. $\mathcal{C}$가 $\mathbb{R}$의 개구간들의 모임이라고 하자. $\mathcal{C}$의 원소들이 쌍으로 서로소_{pairwise disjoint}라면 $\mathcal{C}$는 가산이다.

증명. $\mathcal{C}$의 원소들이 쌍으로 서로소이므로, 각 $(x, y) \in \mathcal{C}$를 $q \in (x, y) \cap \mathbb{Q}$에 대응시키는 단사 사상 $\mathcal{C} \to \mathbb{Q}$가 존재한다. 따라서 $\mathcal{C}$는 가산이다. ■

쌍으로 서로소인 개구간들의 모임이 기껏 가산인 순서 집합은 가산 체인 성질_{countable chain condition}을 가진다고 한다. 이 특이한 이름의 이유는 뒤에서 설명할 것이다.

서슬린의 문제_{Suslin’s problem}는 집합론적 실수의 정의에서 분리 가능성을 가산 체인 성질로 약화시킬 수 있는지를 묻는다.

정의. 양끝점이 없고 가산 체인 성질을 가지는 완비 전순서 집합 중 실수와 순서 동형이 아닌 순서 집합을 서슬린 선_{Suslin line}이라고 한다.

따라서 서슬린 선은 분리 가능하지 않아야 한다.

서슬린의 문제. 서슬린 선이 존재하는가?

1920년에 제기된 이 문제는, 1971년 솔로베이_Solovay와 테넨바움_Tennenbaum에 의해 ZFC와 독립적임이 증명되었다. 이 글에서는 독립성 증명을 살펴보는 대신, 서슬린 선의 조합론적 버전인 서슬린 트리에 대해서 알아보고자 한다. 우선 다음의 유명한 정리를 보자.

쾨니히 보조정리_{König’s lemma}. 트리 $T$에 대해, $T$의 높이가 $\omega$이고, $T$의 각 노드가 유한한 수의 자식을 가진다면, $T$는 길이가 $\omega$인 가지를 가진다.

증명. $\alpha_0$를 루트 노드라고 하고, 다음과 같이 귀납적으로 노드열을 정의한다. $\alpha_n$이 주어졌을 때, $\alpha_n$의 자식 노드의 수는 유한하므로, 어떤 자식 노드에 대해 해당 노드를 루트로 하는 트리는 높이가 무한하다. 그러한 자식 노드 중 하나를 선택하여 (여기서 선택 공리가 필요하다) $\alpha_{n + 1}$로 정의한다. $\lbrace a_n \rbrace $은 길이가 무한한 가지이다. ■

$T$의 노드가 가산 수의 자식을 가질 수 있다면 다음과 같이 $T$의 모든 가지가 유한 길이임에도 $T$의 높이는 $\omega$일 수 있다.

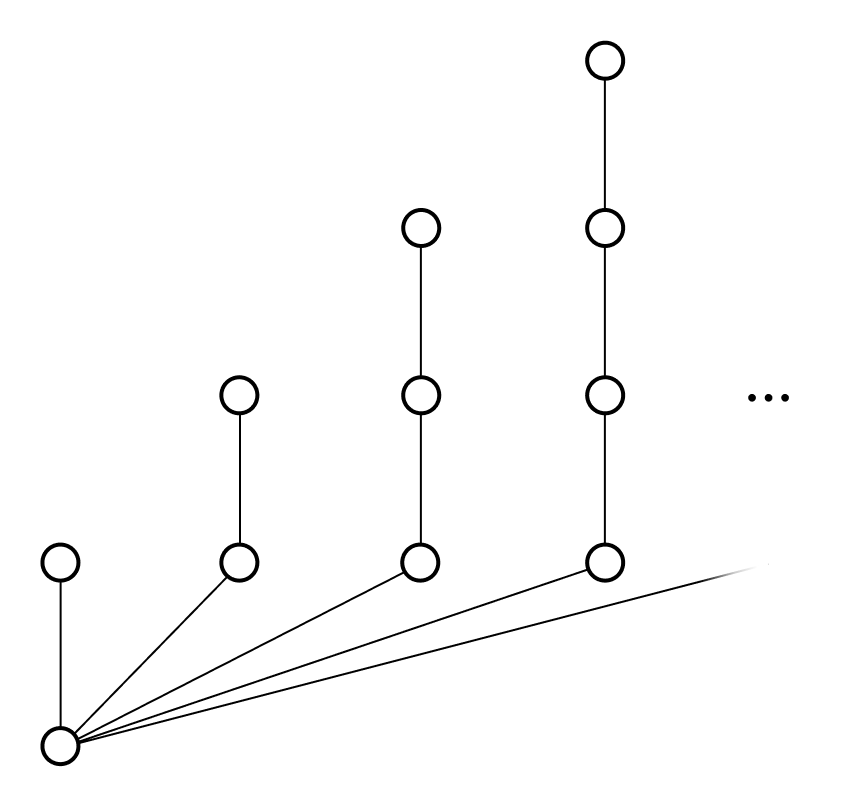
자연스러운 질문은, 쾨니히 보조정리를 비가산 기수에 대해 확장할 수 있는지이다. 그러나 이 질문에 대한 답은 부정적이다.

아론샤인 정리_{Aronszajn theorem}. 높이가 $\omega_1$이고, 각 노드가 가산 수의 자식을 가지지만, 길이가 $\omega_1$인 가지가 없는 트리가 존재한다. (그러한 트리를 높이 $\omega_1$의 아론샤인 트리라고 한다.)

따라서 쾨니히 보조정리를 비가산 기수로 확장하기 위해서는 “각 노드가 가산 수의 자식을 가진다”보다 더 강력한 조건이 필요하다. 이를 위해 다음의 정의를 도입한다.

정의. 트리 $T$의 부분집합 $S$에 대해, $S$의 원소들이 서로 비교 불가능_{mutually incomparable}할 때, $S$를 반체인_antichain이라고 한다. $T$의 모든 반체인이 가산일 때, $T$가 가산 체인 성질을 가진다고 한다.

예를 들어 다음 트리의 색칠된 노드들은 반체인을 이룬다.

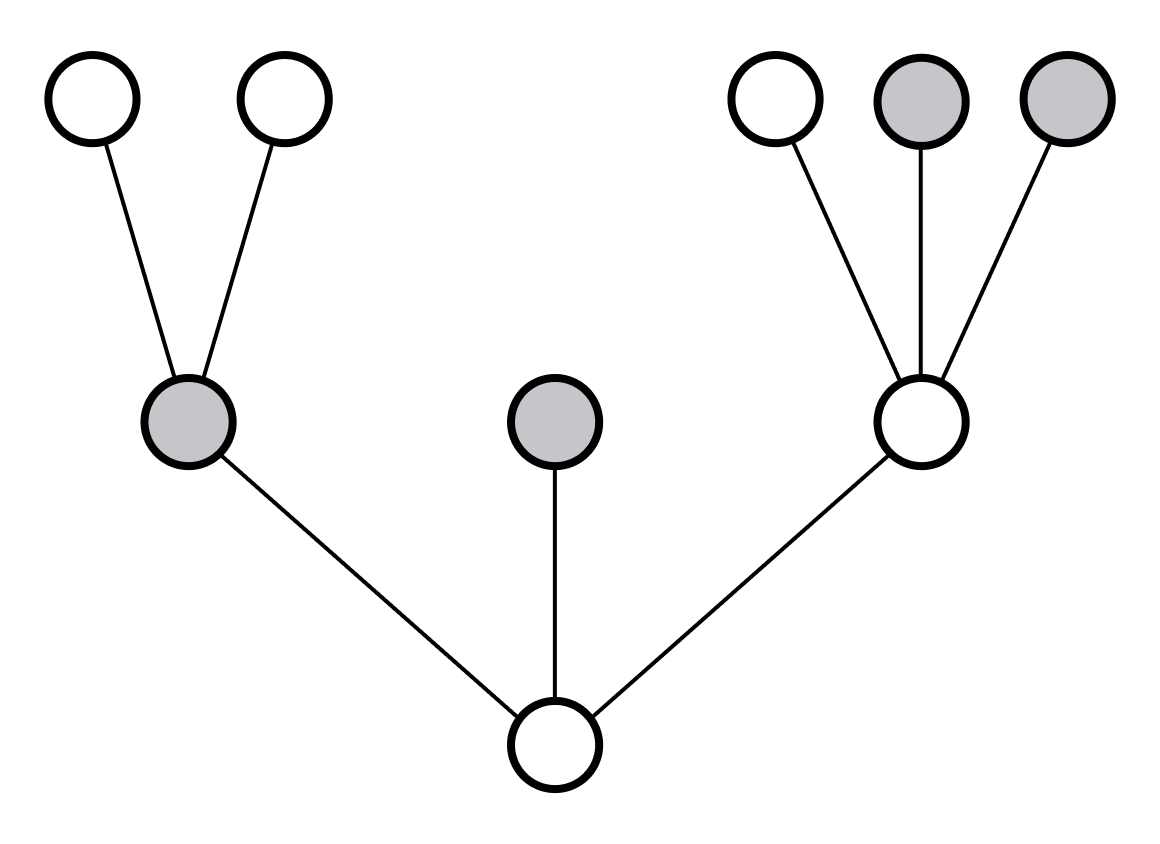
“각 노드가 가산 수의 자식을 가진다”가 국소적 성질이라면, 가산 체인 성질은 트리 전체에 관한 전역적 성질이다. 즉, 가산 체인 성질은 직관적으로 트리의 “너비”가 $\omega_1$보다 작다는 의미이다. 참고로 가산 반체인 성질이 아니라 가산 체인 성질이라고 부르는 것은 역사적 이유이기 때문에 크게 신경 쓸 필요는 없다.

앞서 쌍으로 서로소인 실수의 개구간들의 모임이 기껏 가산인 성질 또한 가산 체인 성질이라고 부른다고 했는데, 두 용법은 밀접한 관련이 있다. 반체인의 일반적인 정의는 다음과 같다.

정의. $(P, \leq)$가 부분순서라고 하자. $x, y \in P$가 비교 불가능하다는 것은, $z \leq x, z \leq y$인 $z \in P$가 존재하지 않는다는 것이다. $S \subseteq P$의 원소들이 서로 비교 불가능할 때 $S$를 반체인이라고 한다. $P$의 모든 반체인이 가산일 때, $P$가 가산 체인 성질을 가진다고 한다.

트리 $T$에서, 노드 $x$가 노드 $y$의 후손일 때 $x \leq y$라고 하자. 이때 트리의 노드로서 $x, y$가 비교 불가능한 것은 $(T, \leq)$의 원소로서 $x, y$가 비교 불가능한 것과 동치이다.

정의. 가산 체인 성질을 가지는 아론샤인 트리를 서슬린 트리라고 한다.

서슬린 트리의 존재성은 서슬린 선의 존재성과 동치이기 때문에 ZFC와 독립적이다. 동치가 되는 개략적인 이유는 각 성질이 다음 표와 같이 대응하기 때문이다.

서슬린 선	서슬린 트리
분리 불가능성	트리의 높이가 $\omega_1$
개구간의 가산 체인 성질	트리의 가산 체인 성질

분리 불가능성이 높이 $\omega_1$ 성질에 대응되는 개략적인 이유는, 어떤 집합 $D$가 존재하여 $|D| \leq \aleph_0$이고 임의의 개구간 $(a, b)$가 $D$와 교차한다는 사실이 (분리 가능성), 어떤 서수 $\alpha$가 존재하여 $\alpha < \omega_1$이고 임의의 노드 $x \in T$에 대해 $x$가 $T^{(\alpha)}$의 노드들로 이루어진 노드열의 극한이라는 사실과 (트리의 높이가 가산) 대응되기 때문이다.

서슬린 트리와 관련하여, 집합론의 다음 비표준 공리를 살펴보자.

다이아몬드 원리. 어떤 집합열 $\langle W_\alpha : \alpha < \omega_1 \rangle$가 존재하여 $W_\alpha \subseteq \mathcal{P}(\alpha)$이고, 각 $W_\alpha$가 가산집합이며, 임의의 $X \subseteq \omega_1$에 대해 $\lbrace \alpha : \alpha < \omega_1, X \cap \alpha \in W_\alpha \rbrace $가 정상 집합_{stationary set}이다.

다이아몬드 원리는 $\Diamond$로 자주 표기한다. 또한 다이아몬드 원리의 $\langle W_\alpha \rangle$을 다이아몬드 열이라고 부른다.

$X \cap \alpha$는 $\alpha$라는 “거울”을 통해 “비춰” 보인 $X$의 모습으로 생각될 수 있다. 이 경우, 다이아몬드 원리는 $\omega_1$보다 작은 서수들에서 $X$의 반사된 모습이 $\langle W_\alpha \rangle$에서 충분히 자주 나타난다는 의미로 이해될 수 있다 (이 글에서 정상 집합이 “측도 > 0”의 집합론적 버전임을 설명했다).

따라서 다이아몬드 원리는 반사 원리_{reflection principle}의 일종이며, $V = L$ 공리와 비슷하게 집합론적 우주를 규제하는 역할을 한다 (실제로 $V = L$은 $\Diamond$를 함의한다). 그리고 집합론적 우주를 규제하는 공리들이 그렇듯이, 다이아몬드 원리는 연속체 가설을 함의한다.

정리. $\Diamond \implies \mathsf{CH}$

증명. $X \subseteq \omega \subset \omega_1$이라고 하자. $X$가 $< \omega_1$에서 정상적으로 반사되므로, 어떤 $\alpha > \omega$에 대해 $X \cap \alpha = X \in W_\alpha$이다. 따라서 $\omega$의 부분집합들은 모두 $\bigcup_{\alpha < \omega_1} W_\alpha$에 속하는데, 후자의 기수가 $\aleph_1$이므로 $2^{\aleph_0} = \aleph_1$이다. ■

정리. $\Diamond$라면 서슬린 선이 존재한다.

증명. Hrbacek & Jech (3rd ed), Chapter 12, Section 5를 참고하라. 참고로 원문에는 다음의 오타가 있으니 주의하라.

(원문) Lemma 5.3. $\Diamond$ implies that there exists a sequence $\langle Z_\alpha : \alpha < \omega_1 \rangle$ such that, for each $\alpha < \omega_1$, $Z_\alpha \subseteq \omega^{<\alpha}$, $Z_\alpha$ is at most countable, and for any $X \subseteq \omega^{<\omega_1}$ the set $\lbrace \alpha < \omega_1 : X \cap \omega^{<\alpha} \rbrace $ is stationary.

Proof. We note that […] Clearly, $Z_\alpha \subseteq \omega^{<\alpha}$ and is at most countable.

(수정) Lemma 5.3. $\Diamond$ implies that there exists a sequence $\langle Z_\alpha : \alpha < \omega_1 \rangle$ such that, for each $\alpha < \omega_1$, $Z_\alpha \subseteq \mathcal{P}(\omega^{<\alpha})$, $Z_\alpha$ is at most countable, and for any $X \subseteq \omega^{<\omega_1}$ the set $\lbrace \alpha < \omega_1 : X \cap \omega^{<\alpha} \rbrace $ is stationary.

Proof. We note that […] Clearly, $Z_\alpha \subseteq \mathcal{P}(\omega^{<\alpha})$ and is at most countable.

또한 Claim 5.5 직전에 나오는 문장 “Let $\lbrace C_n : n \in \mathbb{N} \rbrace $ be the at most countable collection of those elements of $Z_\alpha$ which happen to be maximal antichains in $T^{(\alpha)}$.”의 의미는, 각 $n$에 대해 $C_n \in Z_\alpha$이고, $C_n \subseteq \omega^\alpha$이며, $C_n$의 원소들을 $T^{(\alpha)}$의 노드로 간주했을 때 $C_n$이 반체인이라는 것이다. ■

따름정리. $V = L$이라면 서슬린 선이 존재한다.

따라서 서슬린 선의 존재성은 집합론적 우주의 규제와 관련이 있다. 이 사실이 모순적으로 느껴질 수 있지만, 서슬린 선의 조건 중 하나가 가산 조밀 집합의 “비”존재라는 사실을 고려하면 그렇게 이상한 것은 아니다. 서슬린 선은 가산 체인 성질까지만 얻고 가산 조밀 집합은 발생시키지 않는 것이 가능한 “허술한” 집합론적 우주의 특징인 것이다.