수학과 윤리학은 같은 배를 탔는가? 진화론 논변을 중심으로

07 Nov 2025

이 글은 Justin Clarke-Doane, Morality and Mathematics: The Evolutionary Challenge (2012)를 정리한 것이다. “저자”는 논문의 저자를, “필자”는 이 글의 필자를 가리킨다. “도덕”과 “윤리”의 혼용을 방지하기 위해 “윤리”로 표현을 통일했다.

개요

윤리 실재론에 대한 반론 중 하나는 진화론 논변_{The Evolutionary Challenge}이다. 진화론 논변에 따르면, 오늘날의 인류가 가지는 윤리적 믿음들은 진화적 압력_{evolutionary forces}에 의해 형성되었다. 그러나 진화의 원리는 윤리적 사실들과 무관하므로, 윤리적 사실들이 완전히 다른 반사실적 세계에서도 인류는 동일한 윤리적 믿음들을 가지도록 진화했을 것이다. 그러므로 만약 우리의 윤리적 믿음들이 참이라면 이는 진화의 결과와 윤리의 명제들이 굉장한 우연으로 일치하게 된 것이다. 따라서 진화론 논변을 옹호하는 자들은 윤리 실재론이 굉장한 우연을 날것 그대로 받아들이거나, 혹은 우리의 윤리적 믿음들이 참이라고 생각할 근거가 없음을 인정해야 한다고 주장한다.

예를 들어 우리가 “타인을 배려해야 한다”라는 윤리적 믿음을 가지게 된 이유는, 아마 인류의 진화에 있어 상호 협력을 중시하는 집단이 이기주의를 중시하는 집단보다 생존 확률이 높았기 때문일 것이다. 그런데 상호 협력이 이기주의보다 생존 확률이 높다는 것은 윤리적 사실이 아니라, 두 전략의 기댓값에 대한 게임이론적 내지는 수학적 사실이다. 따라서 설령 상호 협력보다 이기주의가 윤리적이었다고 하더라도, 우리는 “타인을 배려해야 한다”라는 믿음을 가지도록 진화했을 것이다.

한편으로 진화론 논변은 수학 실재론을 위협하지는 않는 것으로 받아들여져 왔다. 왜냐하면 진화의 원리는 수학적 참에 의존적인 것으로 보이기 때문이다. 예를 들어 1 + 1 = 2임을 믿는 개체들은 그렇지 않은 개체보다 생존에 유리한데, 이는 1 + 1 = 2가 실제로 참이기 때문이다. 이를 조이스는 다음과 같이 설명한다.

수풀 A 뒤에 사자 한 마리가 있고 수풀 B 뒤에 사자 한 마리가 있다고 하자. 우리의 선조 P와 Q가 수풀 C 뒤에 숨어 있다. P는 사자 한 마리와 다른 사자 한 마리는 총 사자 두 마리가 된다고 믿고, Q는 사자 한 마리와 다른 사자 한 마리가 총 사자 0마리가 된다고 믿는다. 그렇다면 P가 Q보다 죽을 확률이 적으며, 자신의 유전자를 남길 확률이 크다. 왜냐하면 P는 Q보다 수풀 C에서 걸어나와 두 마리의 사자에게 잡아먹힐 확률이 적기 때문이다. 그러나 이 사실[이탤릭체로 표시된 사실]에 대한 설명은, 사자 한 마리와 다른 사자 한 마리가 정말로 0마리가 아니라 두 마리의 사자라는 사실을 전제한다.

그러나 논문에서 저자는 이것이 잘못된 생각이라고 주장한다. 저자는 진화론 논변이 윤리 실재론을 위협하는 것과 같은 정도로 수학 실재론을 위협한다고 주장한다. 결론적으로 저자는 윤리 실재론과 수학 실재론 중 하나만 받아들이는 입장은 비정합적이라고 피력한다.

1. 실재론은 정확히 무엇인가?

본 논증에 들어가기 앞서 저자는 윤리 실재론과 수학 실재론이 정확히 무엇을 의미하는지를 해명하고자 한다. 일반적으로, 저자는 어떤 논의 영역_{area of discourse} D에 대해, D-실재론을 다음 네 입장의 연언으로 정의한다.

1. D-참-적합성_{D-Truth-Aptness}. D의 문장들은 진릿값을 가진다.
2. D-참_D-Truth. 어떤 D의 원자명제 또는 존재 양화 명제는 참이다.
3. D-독립성_{D-Independence}. D의 문장들의 진릿값은 정신과 언어에 유의미한 의미에서 독립적이다.
4. D-액면성_{D-Literalness}. D의 문장들은 문자 그대로 받아들여져야 한다.

D를 윤리학으로 설정할 경우 1은 에이어의 감정주의_emotivism¹를 기각하고, 2는 매키의 오류 이론_{error theory}²을 기각하고, 3은 구성주의_{constructivism}³를 기각하고, 4는 하먼의 상대주의⁴를 기각한다. D를 수학으로 설정할 경우 1은 힐베르트의 형식주의_formalism⁵를 기각하고, 2는 필드의 허구주의_fictionalism⁶를 기각하고, 3은 브라우어르 구성주의⁷를 기각하고, 4는 만약주의_if-thenism⁸를 기각한다.

이 논문에서는 윤리 실재론과 수학 실재론을 기본적으로 전제한 뒤, 이들이 진화론 논변을 극복할 수 있는지 검토한다. 추가로 우리의 윤리적, 수학적 믿음들은 대부분 참이라고 전제한다.

2. 윤리 실재론에 대한 진화론 논변

실재론의 구성 요건을 밝혔으니, 진화론 논변이 어떻게 윤리 실재론을 공격하는지 살펴보자. 진화론 논변의 전제는 다음과 같다.

강한 전제. 우리의 윤리적 믿음은 참-독립적인 진화적 압력에 의해 형성되었다.

강한 전제는 다음 두 전제로 이루어져 있다.

NTT의 정확한 의미는 다음의 반사실적 조건문이다.

P. 나머지 사실은 모두 유지된 채 오직 윤리적 사실만이 현실과 아주 달랐다고 하자. 그럼에도 우리는 현실에서 참인 윤리적 믿음들을 가지도록 진화했을 것이다.

혹자는 P 대신 Q를 2의 의미로 해명할 수 있다고 지적할 수 있다.

Q. 우리는 틀린 윤리적 믿음들을 가지도록 진화할 수 있었다.

그러나 저자는 Q가 견지될 수 없는 입장이라고 주장한다. 물론, 다윈이 일찍이 지적했듯이 인류가 꿀벌과 같은 환경에서 발생했다면 인류는 결혼하지 않은 여성이 형제를 죽이는 것을 용인했을지 모른다. 그러나 이 사례 자체는 Q를 예증하지 않는다. 해당 사례가 Q를 예증하기 위해서는 “꿀벌과 같은 환경에서 결혼하지 않은 여성이 형제를 죽이는 것은 잘못되었다”가 윤리적 참이라는 추가적인 가정이 필요한데, 이는 자명한 가정이 아니기 때문이다. (기아가 빈번했던 전근대 사회에서의 영아 살해와 현대의 영아 살해가 가지는 윤리적 무게를 고려해 보라.) 따라서 저자는 Q를 예증하고자 할 경우 “고통은 좋다”, “쾌는 나쁘다”와 같이 기초적_{explanatorily basic}으로 틀린 윤리적 믿음들을 가지게 되는 경우를 제시해야 한다고 주장한다. 그러나 고통이 좋고 쾌가 나쁘다고 믿는 개체들은 진화론적으로 절멸했을 것이므로 Q는 견지될 수 없다. 따라서 P가 NPP의 올바른 해명이다.

그러나 P에도 문제가 있다. 많은 윤리 실재론자들은 윤리적 속성과 기술적_descriptive 속성의 동일시가 형이상학적으로 필연적_{metaphysically necessary}이라고 주장한다. 예를 들어 “쾌는 좋다”가 참이라면, 이 참은 형이상학적으로 필연적이다. 이 관점에 따르면 기술적 사실들이 고정된 채 윤리적 사실들만 달라지는 것은 형이상학적으로 불가능하다. 따라서 P에 대한 다음의 독해는 견지될 수 없다.

P₁. 형이상학적인 의미에서 나머지 사실은 모두 유지된 채 오직 윤리적 사실만이 현실과 아주 달랐다고 하자. 그럼에도 우리는 현실에서 참인 윤리적 믿음들을 가지도록 진화했을 것이다.

대신 저자는 P를 다음과 같이 이해해야 한다고 주장한다.

P₂. 나머지 사실은 모두 유지된 채 오직 윤리적 사실만이 현실과 아주 다른 상황을 정합적으로 상상해 보자_{intelligibly imagine}. 그럼에도 우리는 현실에서 참인 윤리적 믿음들을 가지도록 진화했을 것이다.

수학을 예시로 들어, $\zeta(-1)$을 구하는 문제의 답을 $-1/12$로 찍어서 맞힌 아이의 경우를 생각해 보자. $\zeta(-1) = -1/12$은 필연적이므로, “이 문제의 답이 달랐더라도 아이는 정답을 맞혔을 것이다 (아이의 대답은 참-의존적_{truth-tracking}이었다)”라는 반사실적 가정문은 형이상학적으로 공허참이다. 그럼에도 우리는 $\zeta(-1) = -1/12$이 아닌 경우를 상상할 수 있으며, 이 상상을 정합적으로_intelligibly 전개한다면 아이는 문제를 틀렸을 것이다. 이런 의미에서 아이의 대답은 참-독립적이었다.

E와 NTT의 의미가 해명되었으므로, 강한 전제로부터 어떻게 윤리 실재론에 대한 반박을 유도하는지 살펴보자. 스트리트 등은 다음의 논변을 제시한다.

1. 윤리적 사실이 아주 달라지는 것이 형이상학적으로는 불가능하더라도 그런 경우를 상상할 수는 있다.
2. 우리가 상상할 수 있는 한에서, 윤리적 사실이 아주 달랐더라도 우리가 진화론적으로 형성하게 된 윤리적 믿음들은 동일했을 것이다.
3. 따라서 현실의 우리가 윤리적으로 참인 믿음들을 가지게 되었다는 것은 설명될 수 없는 우연이다.

그러나 저자는 2로부터 3이 따라 나오지는 않는다고 주장한다. 2로부터 3을 도출하기 위해서는 다음의 일반적인 원리를 전제해야 한다.

D에 대한 기본적인 사실들이 달라지더라도 D에 대한 믿음들 중 달라지지 않는 믿음들의 참은 우연적이다.

저자는 위 원리에 대한 다음 반례를 든다. 철수는 자신을 향해 날아오는 농구공을 보며, “농구공이 내 눈앞으로 날라오고 있다”라고 믿는다. 여기서 농구공이 농구공처럼 배열된 원자들_{atoms arranged basketballwise}과 같다는 것은 형이상학적으로 필연적이다. 그러나 우리는 물질이 원자가 아닌 다른 요소로 구성된 세계를 상상할 수 있다. 그런 세계에 사는 철수 앞으로 농구공이 날라오더라도 철수는 동일한 믿음, 즉 “농구공이 내 눈앞으로 날라오고 있다”라고 믿을 것이다. 이처럼 농구공에 대한 기본적인 사실들이 달라지더라도 철수는 동일한 믿음을 견지하지만, 그럼에도 불구하고 현실의 철수가 “농구공이 내 앞으로 날라오고 있다”라고 믿는 것은 참이며, 이 참은 우연적이지 않다.

필자 주: 필자는 저자가 잘못된 유비를 들었다고 생각한다. 농구공이 원자로 구성된 세계의 철수가 “농구공이 내 앞으로 날라오고 있다”라고 믿는 것과, 농구공이 연속체로 구성된 세계의 철수가 “농구공이 내 앞으로 날라오고 있다”라고 믿는 것은 동일한 믿음이 아니다. 왜냐하면 두 철수에게 있어 “농구공”의 의미는 지시_ostension를 통해 결정되기 때문이다. 따라서 전자의 철수는 “농구공”으로 “농구공처럼 배열된 원자들”을 의미하고, 후자의 철수는 “농구공”으로 “농구공처럼 응축된 연속체”를 의미한다. 이렇듯 농구공에 대한 기본적인 사실이 달라지면 철수는 그에 상응하는 다른 믿음을 가지게 된다. 반면 윤리적 언어의 의미는 지시로 결정되지 않는 것으로 보인다.

그러나 저자는 비록 스트리트의 논증이 그 자체로는 우리가 참인 윤리적 믿음들을 가지는 것에 대한 설명이 완전히 불가능함을 보이지 않더라도, 적어도 다음의 두 설명은 잘못되었음을 입증한다고 지적한다.

1. 진화적 설명_{evolutionary explanation}. 우리가 참된 윤리적 믿음들을 가지는 이유는 우리가 참된 윤리적 믿음들을 가지도록 (자연)선택되었기 때문이다.
2. 자명한 설명_{trivial explanation}. 우리가 참된 윤리적 믿음들을 가지는 이유는 현재의 윤리적 사실들이 유일하게 가능한 윤리적 사실들이며, 그 사실들을 믿는 개체들이 진화에 더 유리하기 때문이다.

진화적 설명과 자명한 설명의 차이에 집중하라. 진화적 설명은 윤리적 사실이 “쾌는 좋다”에서 “고통은 좋다”로 — 형이상학적이지는 않을지언정 상상 속에서 — 바뀌었다면 우리 또한 “고통은 좋다”라는 믿음을 가지도록 진화했을 것이라고 주장한다. 반면 자명한 설명은 “쾌는 좋다”라는 윤리적 사실이 “고통은 좋다”로 바뀌는 것이 — 형이상학적인 의미에서나 상상 속에서나 — 불가능하다고 견지하며, 이에 따라 진화가 어떻게 현실의 윤리적 사실들을 믿는 개체를 탄생시키는지 설명한다면 그것으로 모든 문제는 해결된다고 주장한다.

필자 주: 자명한 설명은 개요에서 언급한 게임 이론적 설명을 전제하는 듯하다. 즉, 자명한 설명은 윤리 실재론에 대한 진화론 논변을 (i) 윤리적 사실들의 강한 필연성과, (ii) 해당 윤리적 사실들이 진화적으로 유리하다는 수학적 사실, 그리고 (iii) 수학적 사실들의 필연성이라는 세 전제를 통해 극복하고자 한다. 이는 (ii)라는 다리 원리를 통해 윤리적 믿음들의 참에 대한 설명을 수학적 믿음들의 참에 대한 설명에 정초하는 시도로 보인다.

그런데 진화적 설명과 자명한 설명이 잘못되었음을 주장하는 것이 진화론 논변의 목적이라면, 진화론 논변은 E ∧ NTT를 전제할 필요 없이 E → NTT만 전제해도 그 목적을 달성할 수 있다. 즉, 진화론 논변은 다음과 같다.

진화론 논변. E → NTT라면, 우리가 참된 윤리적 믿음들을 가진다는 사실을 진화적 설명 또는 자명한 설명으로 설명하는 것은 잘못되었다.

저자는 위와 같이 진화론 논변을 정리한 뒤, 해당 논변이 수학에서는 얼마나 유효한지를 검토한다.

3. 수학은 진화에 영향을 주는가?

통상적으로 수학은 진화론 논변의 대상이 되지 않는다고 생각된다. 윤리적 참이 진화와 무관한 것과 달리 (윤리적 참이 달라지더라도 진화에는 영향이 없다) 수학적 참은 진화에 영향을 준다고 생각되기 때문이다. 앞서 소개한 조이스는 사례를 다시 보자.

수풀 A 뒤에 사자 한 마리가 있고 수풀 B 뒤에 사자 한 마리가 있다고 하자. 우리의 선조 P와 Q가 수풀 C 뒤에 숨어 있다. P는 사자 한 마리와 다른 사자 한 마리는 총 사자 두 마리가 된다고 믿고, Q는 사자 한 마리와 다른 사자 한 마리가 총 사자 0마리가 된다고 믿는다. 그렇다면 P가 Q보다 죽을 확률이 적으며, 자신의 유전자를 남길 확률이 크다. 왜냐하면 P는 Q보다 수풀 C에서 걸어나와 두 마리의 사자에게 잡아먹힐 확률이 적기 때문이다. 그러나 이 사실[이탤릭체로 표시된 사실]에 대한 설명은, 사자 한 마리와 다른 사자 한 마리가 정말로 0마리가 아니라 두 마리의 사자라는 사실을 전제한다.

그러나 저자는 조이스의 논증에 두 가지 문제가 있다고 지적한다. 첫 번째 문제는, 조이스의 논증이 다음의 원리에 기반한다는 사실에 기인한다.

우리가 D에 관한 특정 믿음들을 가지는 것에 대한 진화적 설명이 해당 믿음들의 내용을 전제하면, 우리는 D에 관한 참인 믿음들을 가지도록 선택되었다.

그러나 저자는 우리가 참인 D-믿음들을 가지도록 선택되지 않았더라도 (즉 우리의 D-믿음들이 참이 아니거나, 참-독립적으로 형성되었다고 하더라도) 우리의 D-믿음들에 관한 진화적 설명이 우리의 D-믿음들의 내용을 전제할 수 있다고 주장한다. 가령 모든 유형의 설명은 우리의 논리적 믿음들에 대한 내용을 전제하지만, 그럼에도 불구하고 우리가 참인 논리적 믿음들을 가지도록 선택되었는지는 의문으로 남는 듯하다 (필자의 소논문 참고).

그럼에도 혹자는 콰인-퍼트넘 등의 전체론적 인식론을 채택함으로써, 수학적 사실이 우리의 수학적 믿음들을 설명하는 기반이 된다는 고찰을 해당 수학적 사실이 참인 잠정적 근거로 볼 수 있다고 반론할 수 있다. 이에 저자는 두 번째, 더 심각한 문제를 지적한다. 바로 우리의 수학적 믿음들에 관한 진화적 설명은 애당초 수학적 사실과는 관련이 없다는 것이다. 저자는 진화적 설명이 수학적 사실이 아닌 1차 논리적 사실과만 관련 있다고 주장한다. 앞선 사자의 사례를 보면, P가 Q보다 생존할 확률이 높았던 것은 M이 참이기 때문이 아니라 L이 참이기 때문이라는 것이다.

L은 다음과 같이 1차 논리식으로 풀어쓸 수 있다.

\[\begin{align} &\;\exists! x A(x) \land \exists! y B(y) \land \forall x, y (A(x) \land B(y) \rightarrow x \neq y) \\ &\rightarrow \exists x, y \big((x \neq y) \land (A(x) \lor B(x)) \land (A(y) \lor B(y)) \\ &\quad \quad \land\; \forall z ( (A(z) \lor B(z)) \rightarrow (z = x) \lor (z = y))\big) \end{align}\]

많은 수학자와 철학자가 수학이 논리로 환원될 수 있다는 입장을 견지하기는 하지만, 환원의 종착지가 1차 논리라고 주장하는 학자는 없다. 따라서 우리의 수학적 믿음들에 대한 진화적 설명이 수학적 사실이 아닌 1차 논리적 사실에만 의존한다면, 진화적 설명은 우리가 참인 수학적 믿음들을 가지도록 선택되었다는 결론을 확정적으로도, 잠정적으로도 도출해내지 못한다.

또한 수학 실재론자는 M과 L을 단순히 동일시할 수도 없다. 왜냐하면 실재론의 요건 중 D-액면성이 있기 때문이다. 1 + 1 = 2의 진술은 문자 그대로 받아들여져야 하며, 문자 그대로 받아들여졌을 때 이 진술은 1과 2라는 수가 존재하며, 해당 수들이 덧셈에 대해 특정 관계에 있다는 진술이다.

결론적으로, P가 Q보다 생존 확률이 높은 이유는 P가 가진 수학적 믿음 M의 내용이 참이기 때문이 아니라, 그 믿음에 대응되는 논리적 내용 L이 참이기 때문이다. 그리고 M이 L에 대응된다는 사실은 수학적 실재론을 전제하지 않더라도 충분히 해명될 수 있다. 전반부에서 언급된 여러 반실재론적 입장들 — 형식주의, 허구주의, 구성주의, 만약주의 — 은 각자 정도의 차이는 있지만 모두 M과 L의 대응을 수학적 대상을 가정하지 않으면서 설명해 낸다.

물론 우리는 1차 논리로 포착될 수 없는 수학적 믿음들 또한 가지고 있다. 귀납 공리에 대한 믿음이 한 예시이다. 그러나 저자는 귀납 공리가 직접적인 진화의 외압으로 인해 형성된 믿음이 아님을 지적한다. 귀납 공리는 17세기 전까지는 명시적으로 표현된 적조차 없었다. 귀납 공리에 대한 믿음은 기초적인 산술 믿음들을 형식화하여 정립하는 과정에서 발생한 것이다. 즉 우리가 귀납 공리를 믿는 이유는 기초적인 산술에 대한 믿음 때문이고, 그 믿음들은 수학적 사실이 아닌 1차 논리적 사실로 인해 형성된 것이다. 결론적으로, 논리를 초월하는 수학적 사실들은 정작 수학적 믿음의 진화적 형성에 아무런 영향을 미치지 않는다 (다음의 그림 참조: A → B는 “A로 인해 B를 믿는 개체가 진화한다”는 의미이다).

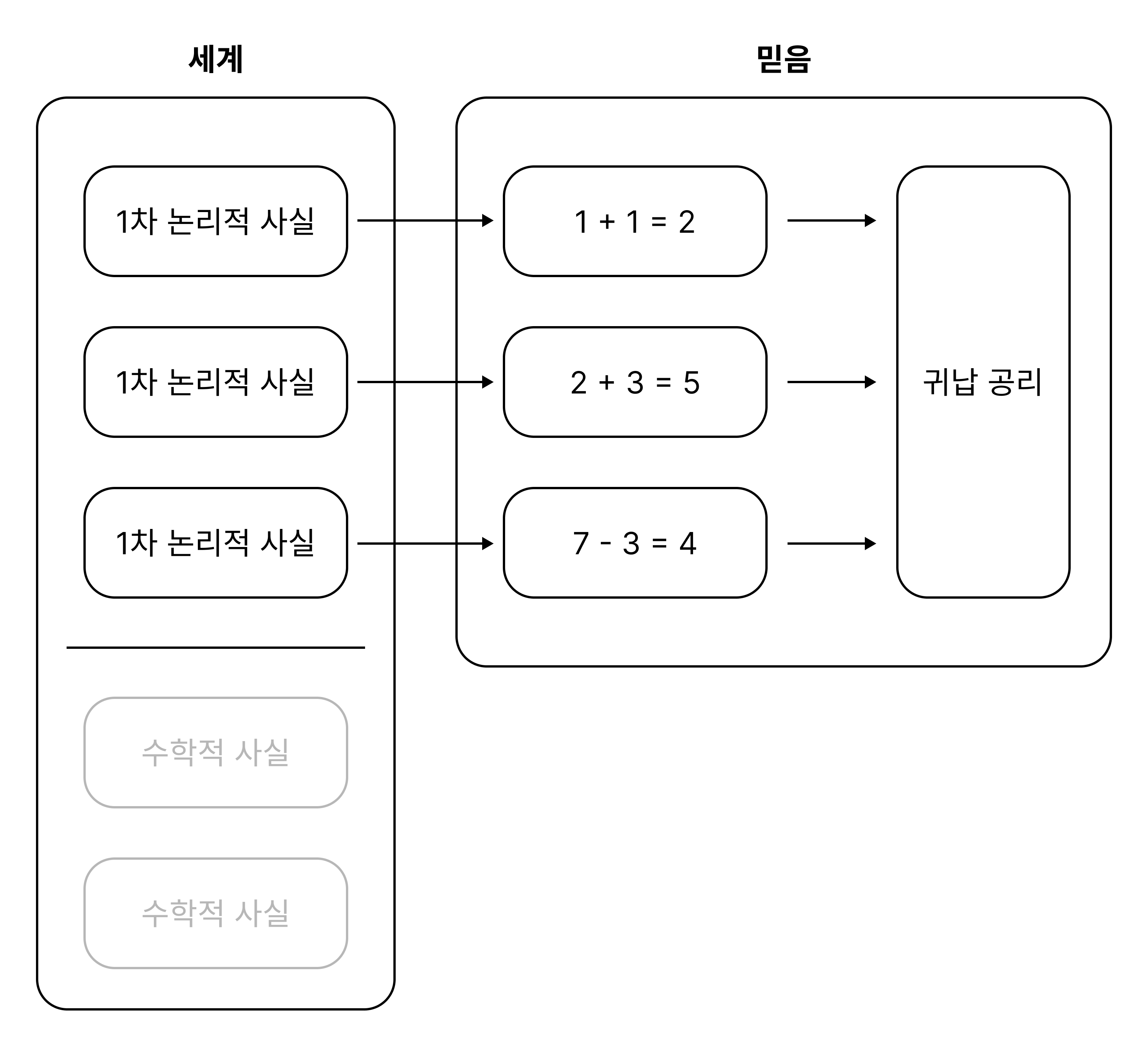
여기서 저자는 짧게 다음의 질문을 제시한다. 그렇다면 지금까지의 논의는 우리가 참인 1차 논리적 믿음들을 가지도록 진화했다는 것을 보여주는가? 저자는 이 질문의 답이 “아니오”일 것이라고 생각한다. 왜냐하면 논리적 사실들은 5 + 7 = 12와 같은 단순한 산술적 사실만 되어도 굉장히 복잡해지기 때문이다. 따라서 진화론적으로는 단순히 수학적 믿음을 가지는 개체가, 수학적 믿음, 논리적 믿음, 그리고 각각의 수학적 명제를 논리적 명제로 어떻게 번역할지에 관한 믿음을 가지는 개체보다 유리할 것으로 보인다. 즉, 논리적 사실들이 달랐더라면 우리의 수학적 믿음들 또한 달라졌을 것이지만 우리의 논리적 믿음들이 어떻게 되었을지는 불분명하다(— 라고 저자는 생각하는 듯한데, 사실 이 부분에 관한 저자의 코멘트가 너무 함축적이라서 잘 모르겠다. 논리적 믿음의 형성을 진화론적으로 설명할 수 없다는 별도의 논증으로 필자의 소논문을 참고하라.)

4. 또다른 수학은 상상 가능한가?

수학에 대한 진화적 설명을 기각한 저자는 자명한 설명으로 논의를 돌린다. 자명한 설명은, 현재의 수학적 사실들이 유일하게 가능한 수학적 사실들임을 주장한다.

통상적으로 윤리에 대한 자명한 설명은 설득력이 없는 것으로 간주되었다. 왜냐하면 윤리의 영역에서는 충분히 합리적인 개인들이 상충하는 입장을 가지는 경우가 자주 있기 때문이다. 서로 다른 윤리적 사실을 견지하는 합리적 개인들이 존재한다면, 현실과 다른 윤리적 사실을 가진 세계는 충분히 정합적으로 상상될 수 있다. 반면 수학의 경우에는 그런 상충이 거의 보이지 않는다. 트롤리 딜레마와 피타고라스 정리에 대한 사람들의 견해차를 비교해 보라.

그러나 저자는 이것이 윤리 실재론자에게 불리하도록 선별된 비교라고 주장한다. 우리는 윤리 실재론자들 사이에서 이견이 없는 명제들 — 이를테면 “아이를 재미로 고문하는 것은 정당하지 않다” — 을 찾을 수 있다. 반대로, 수학 실재론자들 사이에서 이견이 있는 수학의 공리들 또한 찾을 수 있다. 유한주의는 임의의 자연수보다 큰 자연수가 언제나 존재한다는 공리를 부정하고, 선택 공리는 전통적으로 굉장히 많은 논란을 야기했으며, 연속체 가설은 지금까지도 논란이 되고 있다. 따라서 저자는 현실과 다른 윤리적 참을 가지는 세계를 상상할 수 있는 것과 같은 정도로, 현실과 다른 수학적 참을 가지는 세계 — 이를테면 무한집합이 존재하지 않는 세계 — 를 상상할 수 있다고 주장한다.

5. 결론

저자는 진화론 논변이 윤리 실재론을 위협하는 것으로 여겨졌지만, 동일한 위협이 수학 실재론에도 가해짐을 논증했다. 저자는 수학 실재론 말고 오직 윤리 실재론만 위협하는 다른 논증이 있을 수도 있다는 사실을 인정한다. 일례로 하먼은 경험과학에서 수학의 필수불가결성_{indispensability}으로부터 수학적 참을 경험적으로 정당화하는 콰인-퍼트넘 논증이 윤리에서는 적용되지 않는다는 점을 지적했다. 하지만 저자는 경험과학-수학 불가결성에 대한 근래의 회의주의와 경험과학-윤리 불가결성에 대한 새로운 논증들, 그리고 베나세라프 등의 인식론적 고려들을 제시하며, 수학 실재론과 윤리 반실재론을 동시에 견지하는 것이 점점 어려워지고 있음을, 어쩌면 불가능해질지도 모른다고 결론 내린다.

---