체론 개괄

01 Dec 2025

학부 체론의 다음 주요 정리의 증명들을 개괄한다.

1. 크로네커 정리
2. 대수적 폐포_{algebraic closure}의 존재성
3. 켤레 동형 정리_{conjugation isomorphism theorem}
4. 분리 차수_{separable degree}의 well-definedness
5. 확장 차수_{extension degree}와 분리 차수의 곱법칙
6. 체의 유한부분곱군 정리
7. 원시 원소_{primitive element} 정리
8. 완벽체_{perfect field}의 분류
9. 갈루아-아틴_Galois-Artin 보조정리
10. 쿰머_Kummer 확장
11. 시클로토믹_cyclotomic 확장
12. 갈루아 정리

크로네커 정리. 체 $F$에 대해 $p \in F[x]$가 기약_irreducible이라고 하자. 어떤 $F$의 확장체 $E$가 존재하여, $p$는 $E$에서 근을 가진다.

증명. $E = F[x]/\langle p(x) \rangle$이라고 하자. $E$를 $F$의 확장체로 자연스럽게 간주할 수 있으며, $p$를 $E[y]$의 원소로 자연스럽게 간주할 수 있다. $x \in E$에 대해, $E[y]$에서 $p(y)\rvert^x_y = p(x) = 0$이다. 따라서 $p$는 $E$에서 근을 가진다. ■

대수적 폐포의 존재성. 체 $F$에 대해, $F$의 대수적 폐포 $\overline{F}$가 존재한다.

증명. $\Gamma$를 $ \lbrace \gamma_{f, i} : f \in F[x], 0 \leq i < \deg f \rbrace $보다 엄격히 크면서 $F$를 포함하는 집합이라고 하자. $E$가 $F$의 대수적 확장이라고 하자. $\alpha \in E \setminus F$에 대해 $f_\alpha$를 $F$에 대한 $\alpha$의 기약다항식이라고 하자 (이 글에서 계속 사용할 표기이다). $E$에서 $f_\alpha$의 근은 최대 $\deg f_\alpha$개이므로, 각각의 근을 서로 다른 $\lbrace \gamma_{f_\alpha, i} \rbrace$에 대응시킬 수 있다. 또한 체 $F$를 집합으로 간주했을 때 $|F^\omega| = |F|$이므로, 해당 근들이 $F$ 위에서 선형 생성하는 모든 원소들 또한 서로 다른 $\Gamma$의 원소들에 대응시킬 수 있다. 따라서 $E$와 동형이면서 $\Gamma$의 원소들로만 이루어진 체 $E_\Gamma$를 (선택 공리를 사용하여) 선택할 수 있다.

다음의 체 모임을 고려하자.

\[\mathcal{F} = \{ E_\Gamma : E/F \text{ is algebraic} \}\]

$\mathcal{F}$에 체 포함 관계 $\leq$로 순서를 주면 $\mathcal{F}$는 초른 보조정리의 조건을 만족하므로 극대 원소 $K$를 가지며, $K = \overline{F}$이다. ■

Remark. 대수적 폐포는 동형성에 대해 유일하다. 이에 따라 이후 나오는 모든 대수적 확장 $E/F$는 $\overline{F}$ 안에서 일어나는 것으로 생각한다.

켤레 동형 정리. $\alpha, \beta$가 체 $F$에 대해 대수적이라 하자. $\alpha \mapsto \beta$가 유도하는 사상 $\psi_{\alpha, \beta}: F(\alpha) \to F(\beta)$가 동형 사상일 필요충분조건은 $f_\alpha = f_\beta$인 것이다.

증명. $(\Rightarrow)$ $\psi = \psi_{\alpha, \beta}$가 동형 사상이라고 하자. $\psi$를 자연스러운 방식으로 $F(\alpha)[x] \to F(\beta)[x]$로 확장할 수 있다. $\psi$는 $F$에 대해 항등이므로 $f_\alpha(\beta) = \psi(f_\alpha(\beta)) = f_\alpha(\psi(\beta)) = f_\alpha(\alpha) = 0$이다. 따라서 $f_\beta | f_\alpha$이며, 역도 성립하므로 $f_\alpha = f_\beta$이다.

$(\Leftarrow)$ 크로네커 정리에 의해 $F(\alpha) \simeq F[x]/\langle f_\alpha = f_\beta \rangle = F(\beta)$이다. 크로네커 정리로부터 주어지는 동형 사상을 합성하면 $\psi$가 동형 사상임을 얻는다. ■

분리 차수의 well-definedness. $E/F$가 유한 대수적 확장이라고 하자. $\sigma: F \to F’$가 동형 사상일 때, 다음이 성립한다.

1. $\sigma$를 확장하는 사상 $\tau: E \to \overline{F’}$가 존재한다.
2. 그러한 $\tau$의 개수는 $E$와 $F$에 의해서 결정된다. 이 개수를 분리 차수라고 하며 $\lbrace E : F \rbrace $라고 표기한다.

증명. (1) 다음의 집합을 고려하자.

\[\mathcal{A} = \{ (L, \lambda): F \leq L \leq E, \lambda: L \to \overline{F'} \}\]

$\mathcal{A}$ 위에 다음과 같이 순서를 주자.

\[(L_1, \lambda_1) \preceq (L_2, \lambda_2) \iff L_1 \leq L_2,\; \lambda_1 = \lambda_2\rvert_{L_1}\]

$\mathcal{A}$는 초른 보조정리의 조건을 만족하므로 극대 원소 $(L, \lambda)$를 가진다. 이때 $L = E$임을 확인하라.

(2) 다음의 그림을 보고 잘 생각하자.

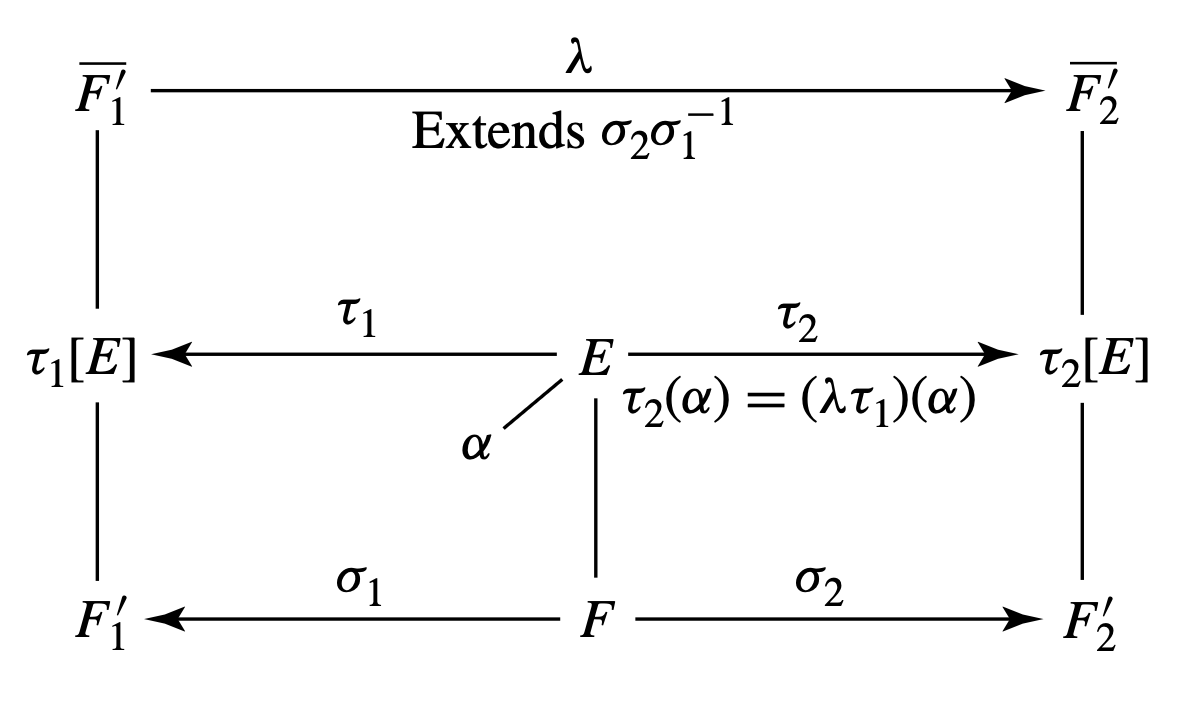
확장 차수와 분리 차수의 곱법칙. $K/E/F$가 유한 대수적 확장이라고 하자. 다음이 성립한다.

\[\begin{gather} \{ K : F \} = \{ K : E \}\{ E : F \} \\\\ [K:F] = [K:E][E:F] \end{gather}\]

증명. $\lbrace K : F \rbrace = \lbrace K : E \rbrace \lbrace E : F \rbrace $ 임은 “분리 차수의 well-definedness”의 증명으로부터 따라 나온다. $[ K : F ] = [ K : E ] [ E : F] $ 임은 벡터 차원의