오일러-푸앵카레 정리

23 Nov 2025

독자 분은 어렸을 때 다음의 정리를 배웠을 것이다.

오일러 공식. 볼록다면체의 꼭짓점, 모서리, 면의 개수를 $v, e, f$라고 할 때, $v - e + f= 2$이다.

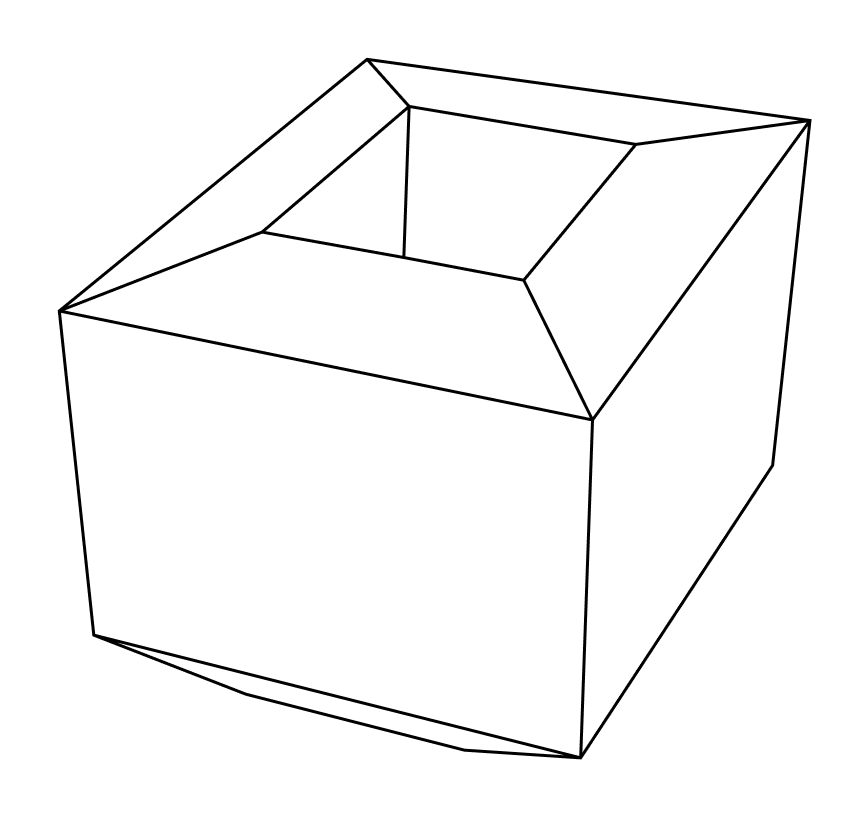
예를 들어 정육면체의 경우 $v = 8, e = 12, f = 6$이므로 $v - e + f = 2$가 성립한다. 볼록다면체라는 조건은 중요한데, 만약 다면체에 “구멍”이 있으면 공식이 성립하지 않기 때문이다. 예를 들어 아래의 구멍 난 프리즘의 경우 $v = 16, e = 32, f = 16$이므로 $v - e + f = 0$이다.

이로부터 우리는 $v - e + f$의 값이 도형의 위상에 의해 결정된다고 추측할 수 있다. 이것이 오일러-푸앵카레 정리의 내용이다. 정리를 진술하기 앞서, 먼저 다음의 개념을 정의하자.

정의. 위상공간 $X$에 대해, $X$의 호몰로지 군 $H_p(X)$의 자유 부분_{free part}의 랭크를 $X$의 $p$번째 베티 수_{Betti number}라고 하며 $R_p(X)$라고 적는다.

원래 $b_p(X)$라고 적는 것이 관행인데, 이 글에서는 $b_p$를 다른 의미로 사용할 것이기 때문에 다른 표기법을 채택했다. 호몰로지 군은 위상 불변이므로 베티 수 또한 위상 불변이다.

예를 들어 토러스의 호몰로지 군은 다음과 같다.

• $H_0(X) = \mathbb{Z}$
• $H_1(X) = \mathbb{Z} \oplus \mathbb{Z}$
• $H_2(X) = \mathbb{Z}$

따라서 토러스의 0차, 1차, 2차 베티 수는 각각 1, 2, 1이다. 베티 수는 직관적으로 구멍의 의미를 가진다 (이전 글 참조). 특히, 0차 베티 수는 $K$를 이루는 연결 요소들의 수이다. 즉, 두 개의 사면체를 하나의 단체 복합체로 간주한다면 이 복합체의 0차 베티 수는 2이다.

오일러-푸앵카레 정리. $n$-단체 복합체 $K$에 대해, $\alpha_p \; (p \leq n)$를 $K$의 $p$-단체들의 개수라고 하자. 다음이 성립한다.

\[\sum^n_{p = 0} (-1)^p\alpha_p = \sum^n_{p=0}(-1)^p R_p(K)\]

위 정리의 증명에서는 $p$-체인들을 자유군의 원소로 보는 것보다 선형 공간의 원소로 보는 것이 더 자연스럽기 때문에 이 접근을 취한다.

증명. $K$의 $p$-체인, 고리, 경계가 각각 유리수체에 대해 이루는 선형 공간을 $C_p, Z_p, B_p$라고 하자. $\lbrace d^i_p \rbrace $가 고리를 선형 생성하지 않는 $C_p$의 극대 부분집합이라고 하고, $\lbrace d^i_p \rbrace $가 생성하는 선형공간을 $D_p$라고 하자. 다음이 성립한다 ($\oplus$는 벡터 공간의 직합).

\[\begin{gather} C_p = D_p \oplus Z_p\\\\ \alpha_p = \dim C_p = \dim D_p + \dim Z_p \end{gather}\]

$p \leq n - 1$에 대해, $b^i_p = \partial d^i_{p + 1}$라고 하자. $\lbrace b^i_p \rbrace $가 생성하는 선형 공간을 $B_p$라고 하자. $\partial$은 선형 연산자이므로, $\lbrace d^i_{p +1} \rbrace $가 $D_{p + 1}$의 선형 기저라는 사실로부터 $\lbrace b^i_p \rbrace $가 $B_p$의 선형 기저라는 사실이 따라 나온다. 다음의 보조정리를 증명한다.

보조정리. $B_p$는 $K$의 모든 $p$-경계들을 포함한다.

증명. 만약 $b_p$가 $K$의 $p$-경계라면, 어떤 $c_{p + 1} \in C_{p + 1}$에 대해 $\partial c_{p + 1} = b_p$이다. $C_{p + 1} = D_{p + 1} \oplus Z_{p + 1}$ 관계에 의해 어떤 유일한 $d_{p + 1} \in D_{p + 1}, z_{p + 1} \in Z_{p + 1}$이 존재하여 $c_{p + 1 } = d_{p + 1} + z_{p + 1}$이다. 그런데 $\partial z_{p + 1} = 0$이므로 $\partial d_{p + 1} = b_p$이다. 따라서 $b_p \in B_p$이다. □

$\lbrace z^i_p \rbrace $가 $B_p$의 원소를 선형 생성하지 않는 $Z_p$의 극대 부분집합이라고 하고, $\lbrace z^i_p \rbrace $가 생성하는 선형공간을 $G_p$라고 하자. 보조정리에 의해 다음이 성립한다.

\[\dim G_p = R_p\]

따라서 다음이 성립한다.

\[\begin{gather} Z_p = B_p \oplus G_p\\\\ \dim Z_p = \dim B_p + \dim G_p = \dim D_{p + 1} + R_p \end{gather}\]

앞선 결과와 연립하면 다음을 얻는다 ($p \leq n - 1$).

\[\alpha_p = \dim D_{p + 1} + \dim D_p + R_p\]

$p = n$일 때 $\alpha_n = \dim D_n + R_n$이고, $p = 0$일 때 $\alpha_0 = \dim D_1 + R_0$이다. 따라서 다음을 얻는다 (wlog, $n$은 짝수).

\[\begin{alignat}{3} &\alpha_n &&= \;\cancel{\dim D_n} + R_p \\ &-\alpha_{n-1} &&= \;\cancel{-\dim D_{n}} \cancel{- \dim D_{n - 1}} - R_{n - 1} \\ &\alpha_{n-2} &&= \;\cancel{\dim D_{n - 1}} \cancel{ + \dim D_{n - 2}} + R_{n - 2} \\ &&\vdots \\ &-\alpha_{1} &&= \;\cancel{-\dim D_{2}} \cancel{-\dim D_{1}} - R_{1} \\ &\alpha_{0} &&= \;\cancel{\dim D_{1}} + R_{0} \\ \hline &\sum_{p = 0}^n (-1)^p \alpha_p &&= \;\sum_{p=0}^n (-1)^p R_p(K) \quad \blacksquare \end{alignat}\]

정의. 위상공간 X에 대해, 다음 값을 오일러 종수_{Euler characteristic}라고 한다.

\[\xi(X) = \sum (-1)^p R_p(X)\]

베티 수가 위상 불변이므로 오일러 종수 또한 위상 불변이다.

따름정리. 다면체 $P$의 꼭짓점, 모서리, 면의 개수를 $v, e, f$라고 하자. 2차원 위상공간으로서의 $P$의 표면을 $X$라고 하자. 다음이 성립한다.

\[v - e + f = \xi(X)\]

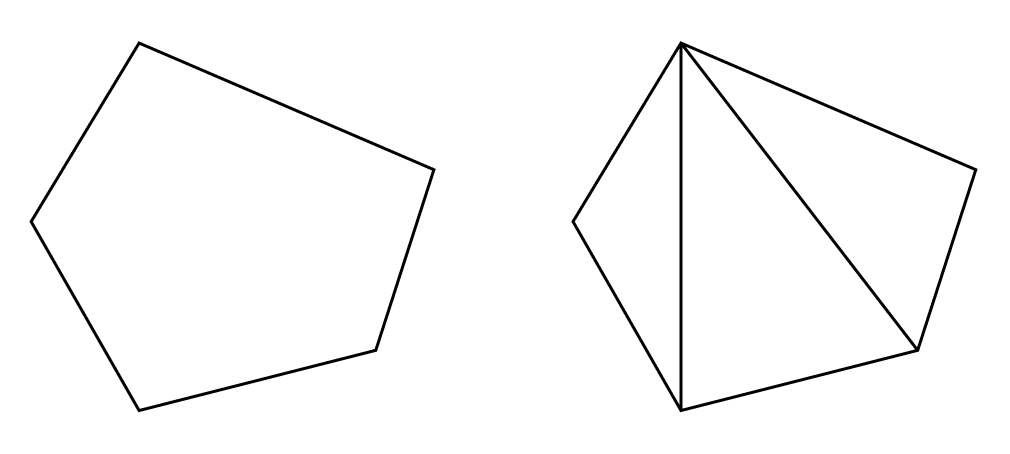
증명. $k$각형의 삼각화는 $k - 3$개의 모서리를 추가함으로써 얻을 수 있는데, 이 과정에서 $k - 3$개의 면이 생긴다. 따라서 $P$는 $P$의 삼각화와 $v - e + f$ 값이 같으며, 이는 오일러 종수와 같다. ■

앞서 우리는 구멍이 하나 있는 다면체의 경우 $v - e + f = 0$임을 보았다. 실제로 토러스의 0차, 1차, 2차 베티 수는 1, 2, 1이며, $1 - 2 + 1 = 0$이다. 한편 구의 호몰로지 군은 다음과 같다.

• $H_0(K) = \mathbb{Z}$
• $H_1(K) = 0$
• $H_2(K) = \mathbb{Z}$

따라서 구의 0차, 1차, 2차 베티 수는 1, 0, 1이며, $1 - 0 + 1 = 2$이다. 따라서 볼록다면체의 경우 $v - e + f = 2$이다.