Simplicial Homology

05 Nov 2025

This post was originally written in Korean, and has been machine translated into English. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.

Definition. Let $K$ be a pure $k$-simplicial complex, and for $p \leq k$, let $C_p(K)$ denote the set of $p$-chains of $K$.

• $z \in C_p(K)$ is called a $p$-cycle of $K$ if $z \in \ker \partial_p$.
• $b \in C_p(K)$ is called a $p$-boundary of $K$ if $b \in \operatorname{im} \partial_{p + 1}$.

The set of $p$-cycles is denoted by $Z_p(K)$, and the set of $p$-boundaries is denoted by $B_p(K)$.

When $C_p(K)$ is regarded as a free abelian group, $Z_p(K)$ and $B_p(K)$ are subgroups of $C_p(K)$. Since subgroups of free abelian groups are themselves free abelian, $Z_p(K)$ and $B_p(K)$ are free abelian groups. Moreover, as $\partial_p \partial_{p+1} = 0$, we have $B_p(K) \leq Z_p(K)$. Since subgroups of abelian groups are normal, the quotient group $Z_p(K)/B_p(K)$ can be formed. This quotient group is called the homology group and is denoted by $H_p(K)$.

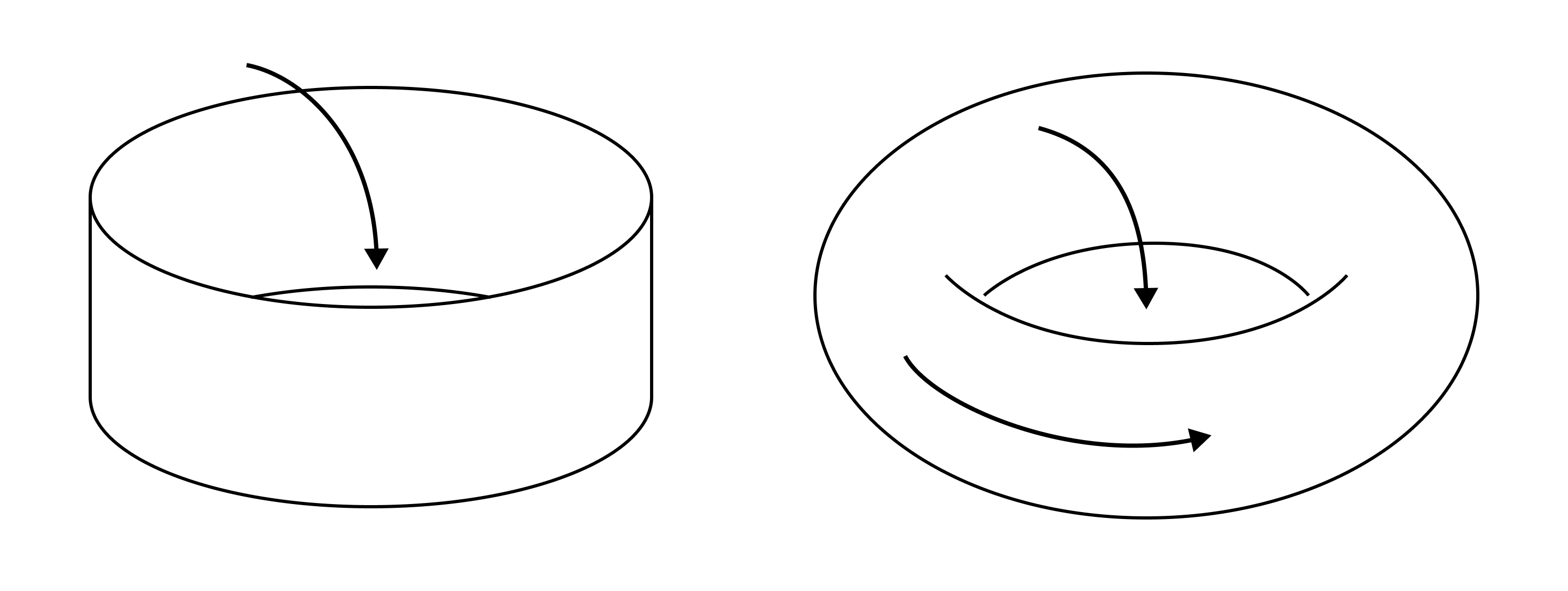
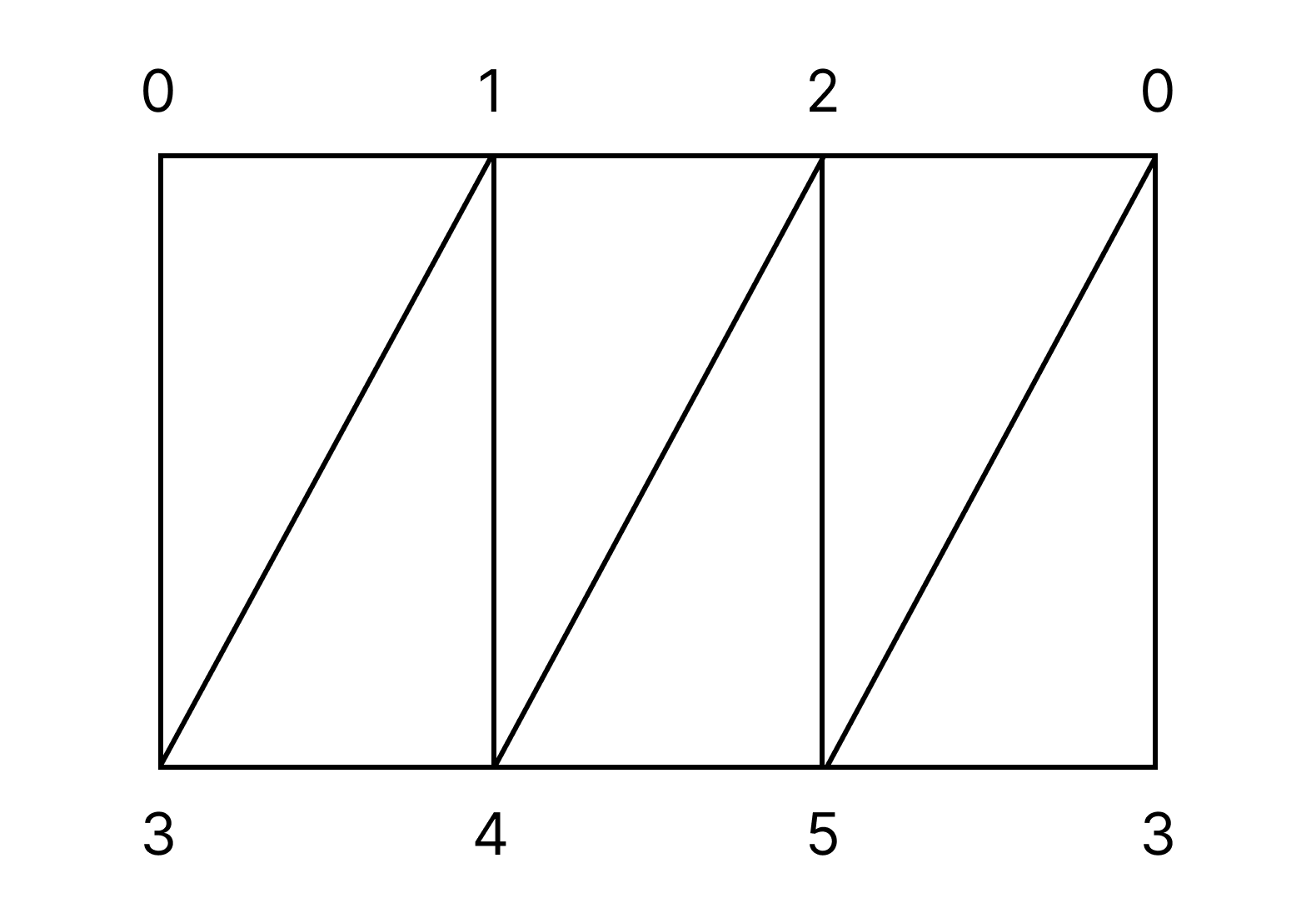
To explain in simpler terms, two 1-cycles $z_1$ and $z_2$ correspond to the same element in the homology group if $z_1 - z_2$ forms the boundary of some 2-chain. For example, consider the following simplicial complex $K$, which is a triangulation of a cylinder.

Let $z_1 = \langle 01 \rangle + \langle 12 \rangle + \langle 20 \rangle$ and $z_2 = \langle 34 \rangle + \langle 45 \rangle + \langle 53 \rangle$. Then $z_1 - z_2$ is as shown on the right.

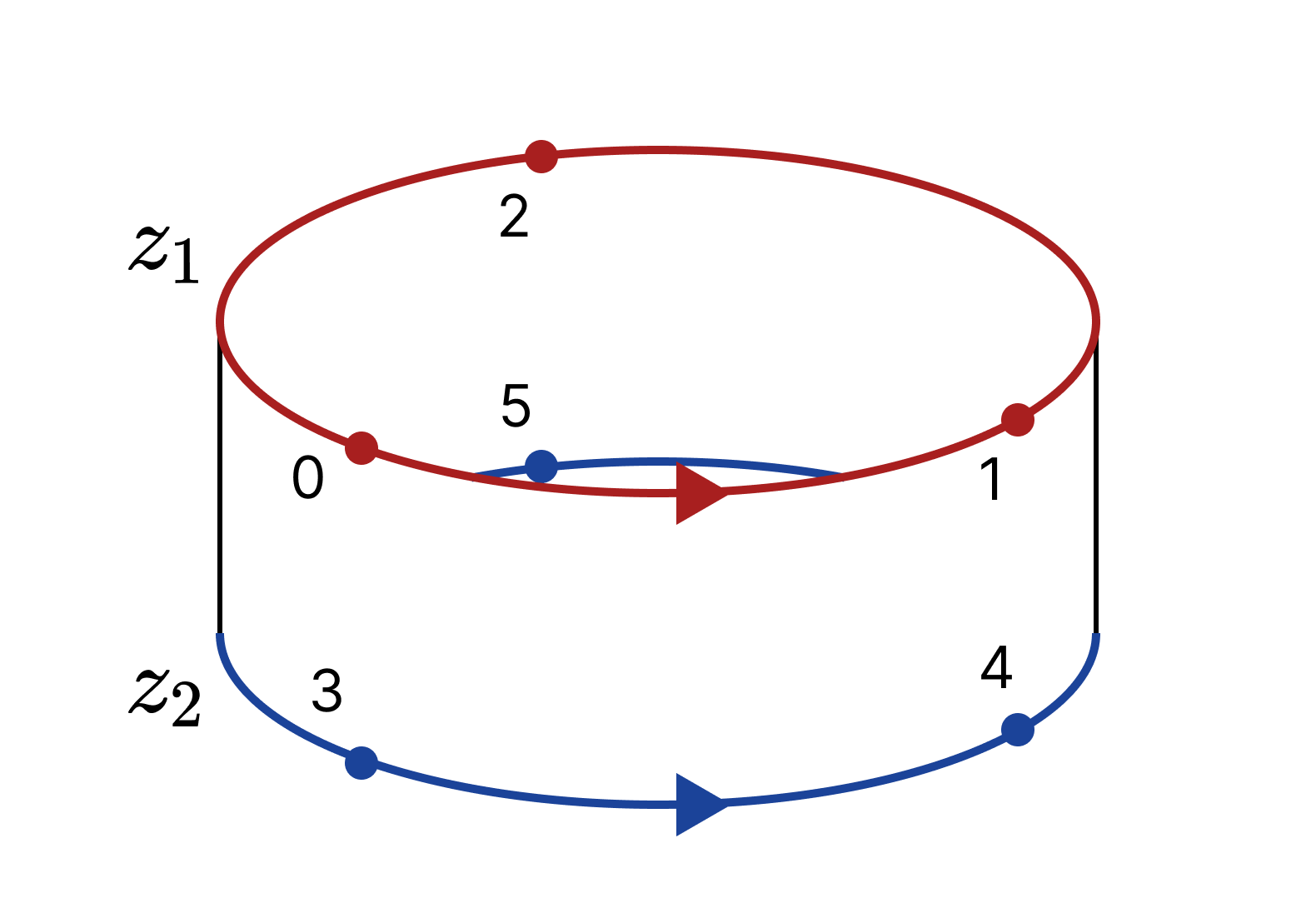
However, this is equal to the boundary of the entire cylinder. Specifically,

\[\begin{align*} &\partial (\langle 013 \rangle + \langle 143 \rangle + \langle 124 \rangle + \langle 254 \rangle + \langle 205 \rangle + \langle 035 \rangle) \\ &= (\langle 01 \rangle + \langle 12 \rangle + \langle 20 \rangle) - ( \langle 34 \rangle + \langle 45 \rangle + \langle 53 \rangle) \\ &= z_1 - z_2 \end{align*}\]

Thus, $z_1$ and $z_2$ correspond to the same element in the homology group. However, for $n, m \in \mathbb{Z}$ with $n \neq m$, $n \cdot z_1$ and $m \cdot z_1$ correspond to different elements in the homology group, as $(n - m) \cdot z_1$ does not belong to $B_1(K)$. From this, we can deduce that the 1-homology group of the cylinder is $\mathbb{Z}$, and this deduction is correct.

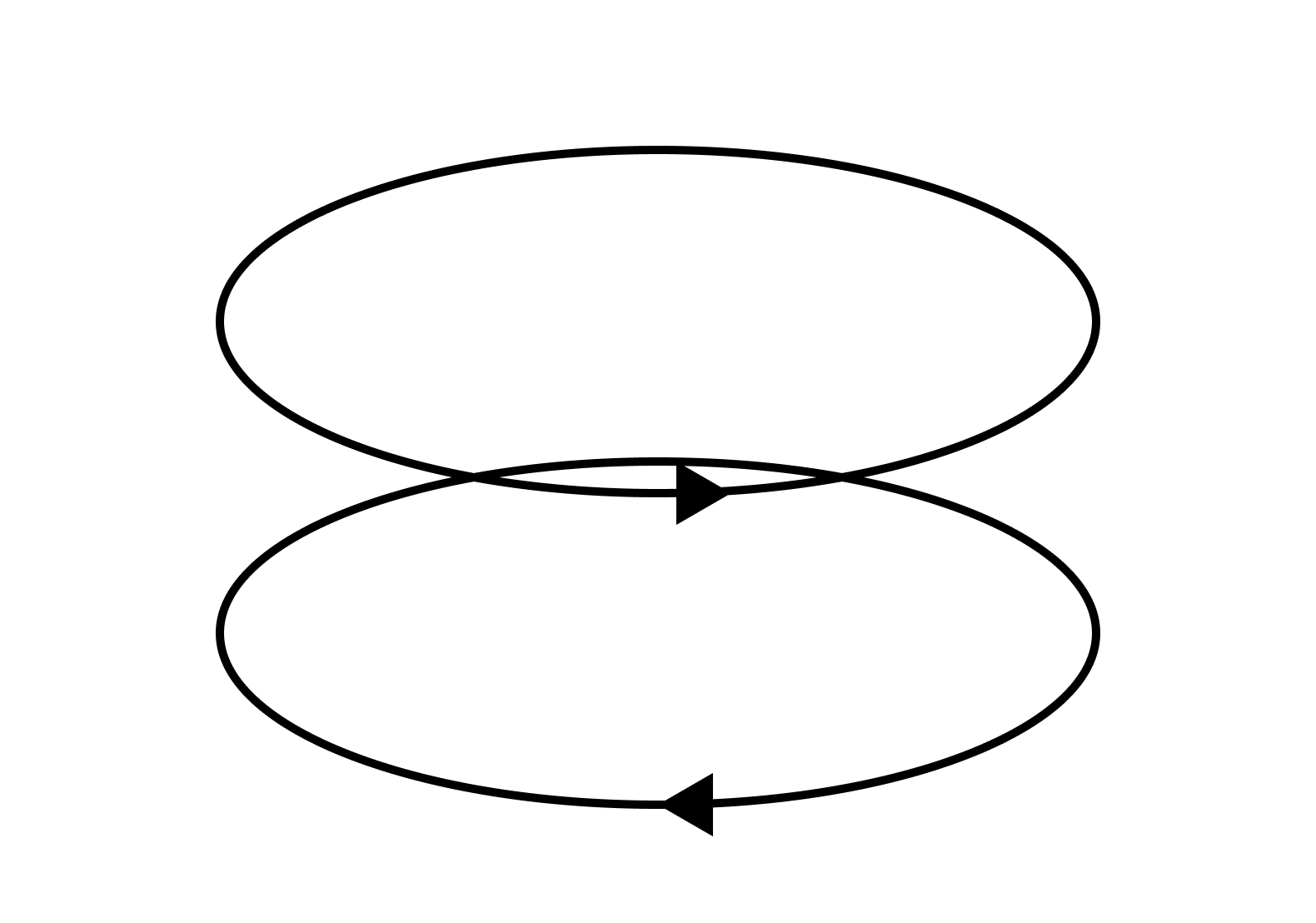
On the other hand, in the case of the torus, the following $w_1$ and $w_2$ correspond to different elements in the homology group. Intuitively, one can see that $w_1 - w_2$ is not the boundary of any 2-chain. Indeed, the 1-homology group of the torus is $\mathbb{Z} \oplus \mathbb{Z}$.

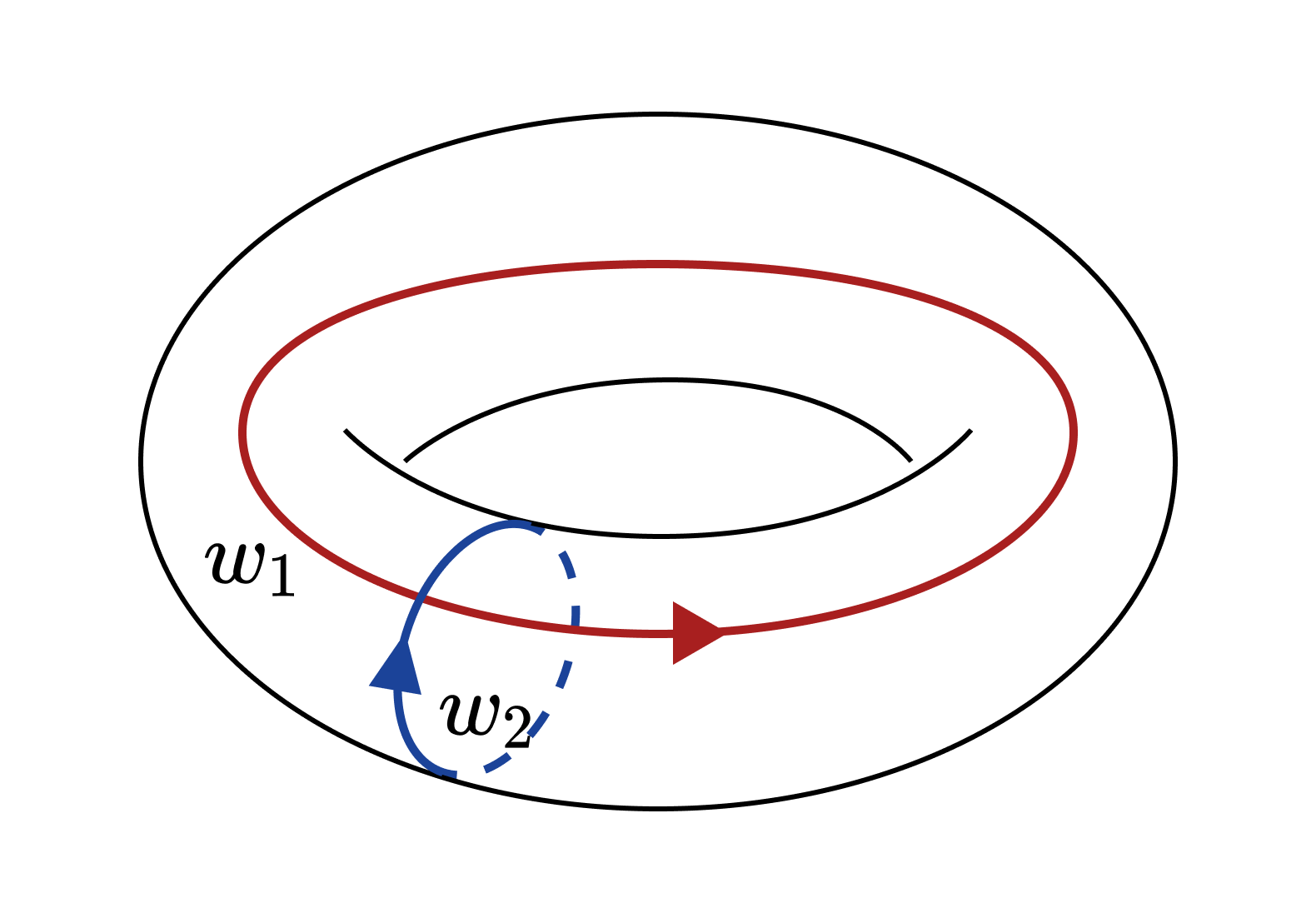
The rank of the homology group intuitively represents the number of holes. The fact that the rank of the 1-homology group of the cylinder is 1 indicates that the cylinder has one 1-dimensional hole, while the fact that the rank of the 1-homology group of the torus is 2 indicates that the torus has two 1-dimensional holes. (Here, an $n$-dimensional hole refers to a hole that can be enclosed by an $n$-dimensional path.)