단체 호몰로지

05 Nov 2025

정의. $K$가 순수 $k$-단체 복합체_{pure simplicial complex}이고, $p \leq k$에 대해 $C_p(K)$가 $K$의 $p$-체인_chain들의 집합이라고 하자.

• $z \in C_p(K)$가 $K$의 $p$-고리_cycle라는 것은 $z \in \ker \partial_p$라는 것이다.
• $b \in C_p(K)$가 $K$의 $p$-경계_boundary라는 것은 $b \in \operatorname{im} \partial_{p + 1}$이라는 것이다.

$p$-고리들의 집합을 $Z_p(K)$, $p$-경계들의 집합을 $B_p(K)$라고 적는다.

$C_p(K)$를 자유 아벨군으로 보았을 때 $Z_p(K)$와 $B_p(K)$는 $C_p(K)$의 부분군이다. 자유 아벨군의 부분군은 언제나 자유 아벨군이므로 $Z_p(K)$와 $B_p(K)$는 자유 아벨군이다. 또한 $\partial_p \partial_{p+1} = 0$이므로 $B_p(K) \leq Z_p(K)$이며, 아벨군의 부분군은 정규부분군이므로 몫군 $Z_p(K)/B_p(K)$를 취할 수 있다. 이 목군을 호몰로지 군_{homology group}이라고 하며 $H_p(K)$라고 적는다.

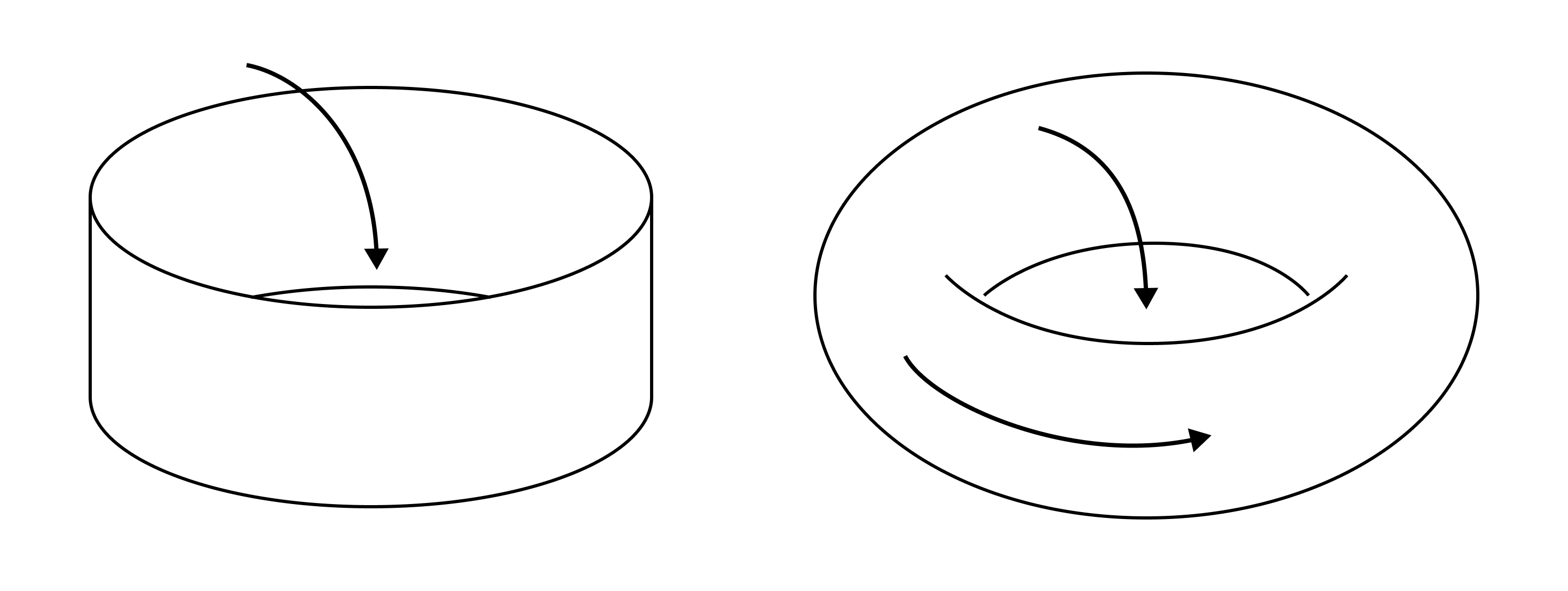
쉬운 언어로 설명하자면, 두 1-고리 $z_1, z_2$가 같은 호몰로지 군의 원소에 대응된다는 것은 $z_1 - z_2$가 어떤 2-체인의 경계를 이룬다는 것이다. 예를 들어 띠_cylinder의 삼각화인 다음 복합체 $K$를 보자.

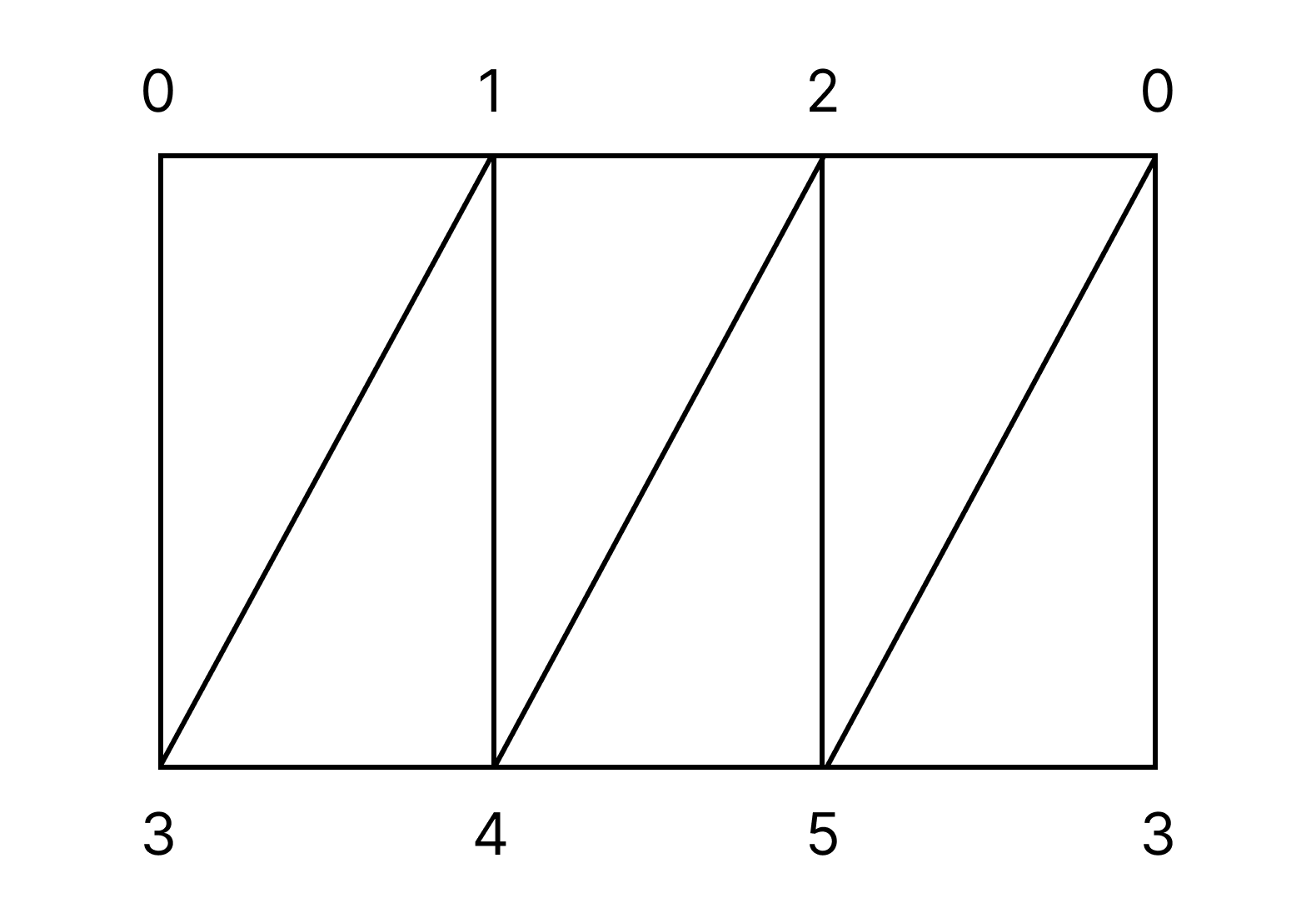
$z_1 = \langle 01 \rangle + \langle 12 \rangle + \langle 20 \rangle, z_2 = \langle 34 \rangle + \langle 45 \rangle + \langle 53 \rangle$이라고 하자. $z_1 - z_2$는 오른쪽과 같다.

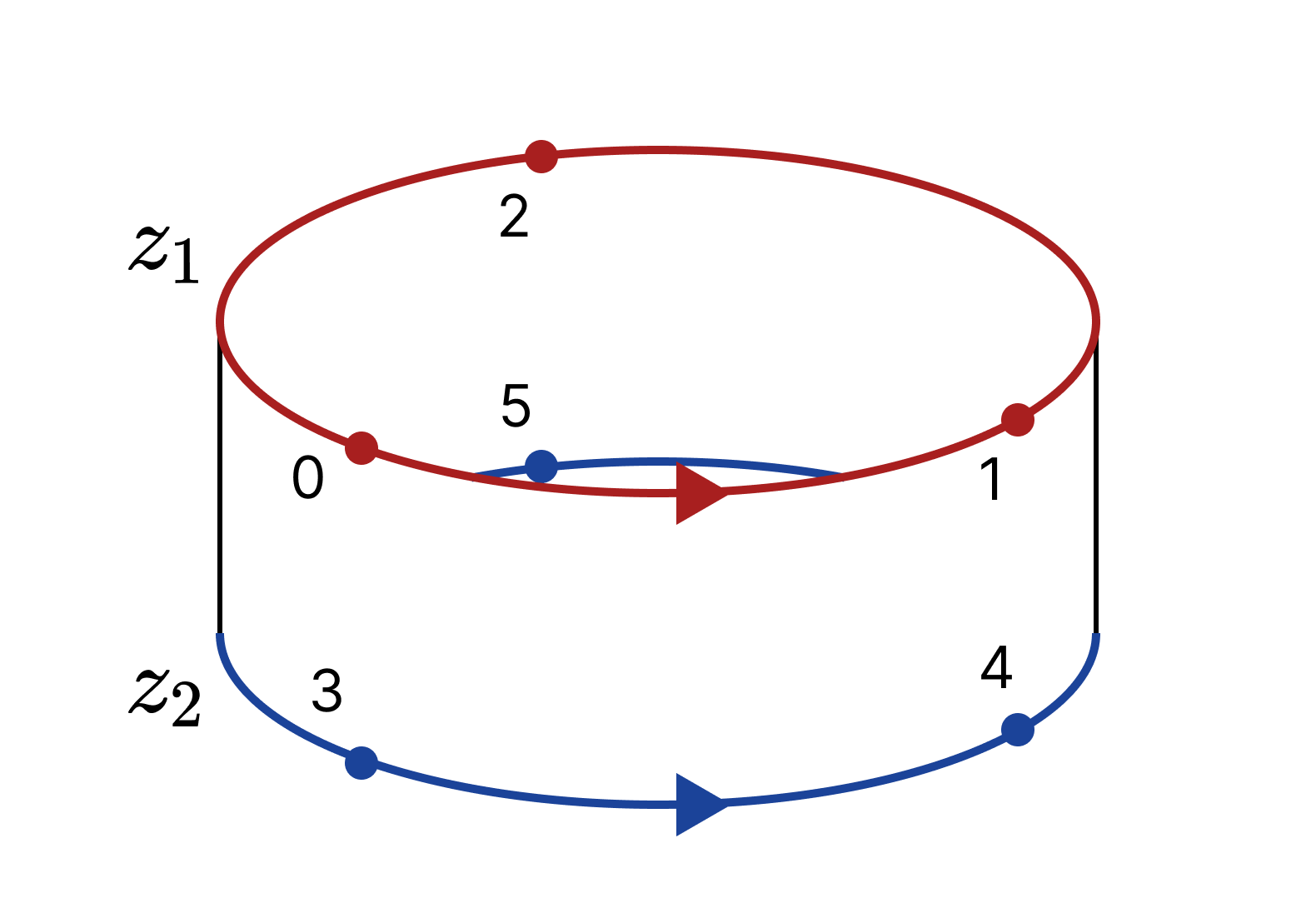
그런데 이는 띠 전체의 경계와 같다. 구체적으로,

\[\begin{align*} &\partial (\langle 013 \rangle + \langle 143 \rangle + \langle 124 \rangle + \langle 254 \rangle + \langle 205 \rangle + \langle 035 \rangle) \\ &= (\langle 01 \rangle + \langle 12 \rangle + \langle 20 \rangle) - ( \langle 34 \rangle + \langle 45 \rangle + \langle 53 \rangle) \\ &= z_1 - z_2 \end{align*}\]

따라서 $z_1$과 $z_2$는 같은 호몰로지 군의 원소에 대응된다. 그러나 $n, m \in \mathbb{Z}$에 대해 $n \neq m$이라면 $n \cdot z_1$과 $m \cdot z_1$은 서로 다른 호몰로지 군의 원소에 대응된다. $(n - m) \cdot z_1$이 $B_1(K)$에 속하지 않기 때문이다. 이로부터 띠의 1-호몰로지 군이 $\mathbb{Z}$임을 유추할 수 있으며, 이 유추는 올바르다.

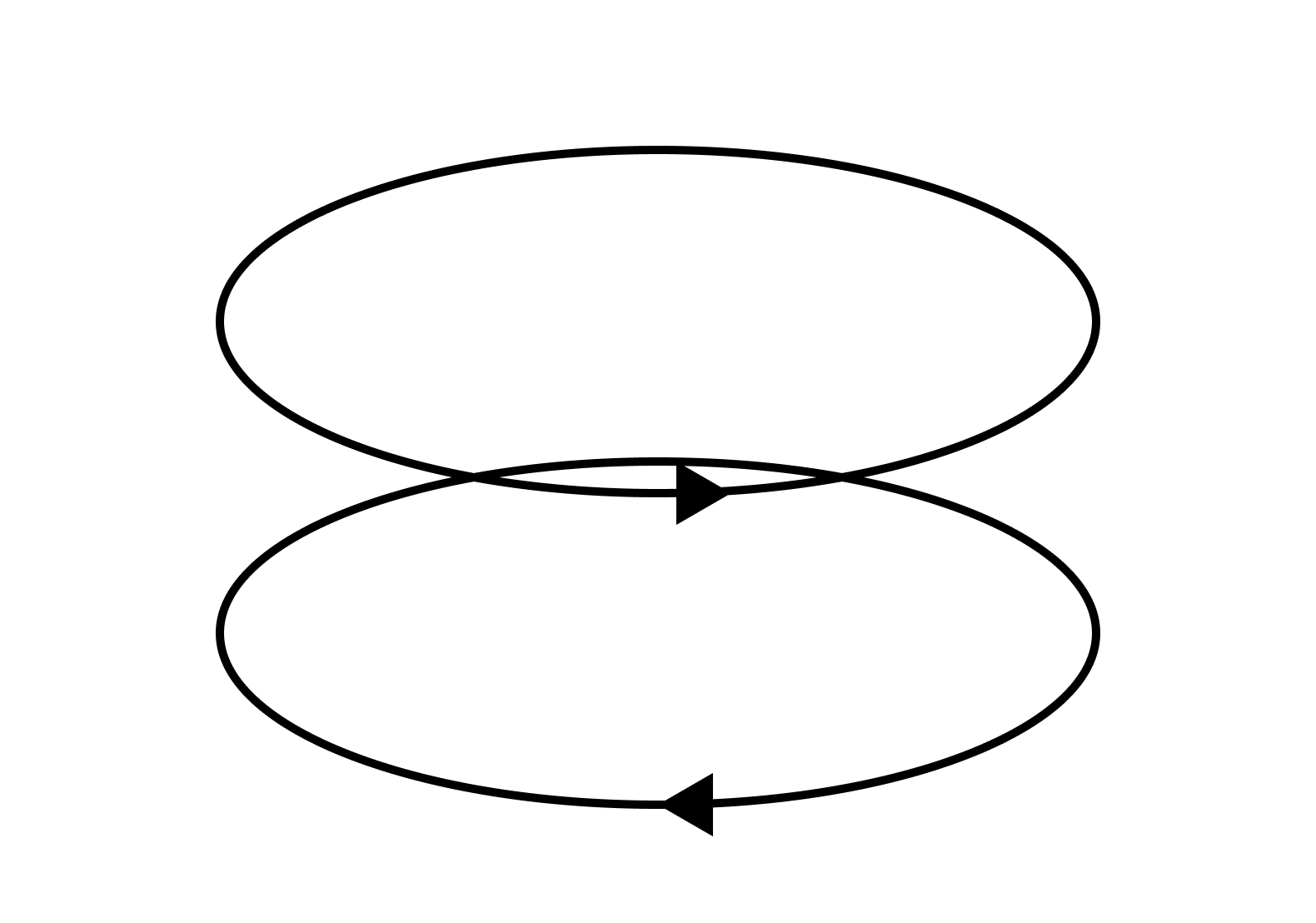
반면 토러스의 경우, 다음의 $w_1$과 $w_2$는 서로 다른 호몰로지 군의 원소에 대응된다. $w_1 - w_2$가 어떠한 2-체인의 경계도 아님을 직관적으로 파악할 수 있을 것이다. 실제로 토러스의 1-호몰로지 군은 $\mathbb{Z} \oplus \mathbb{Z}$이다.

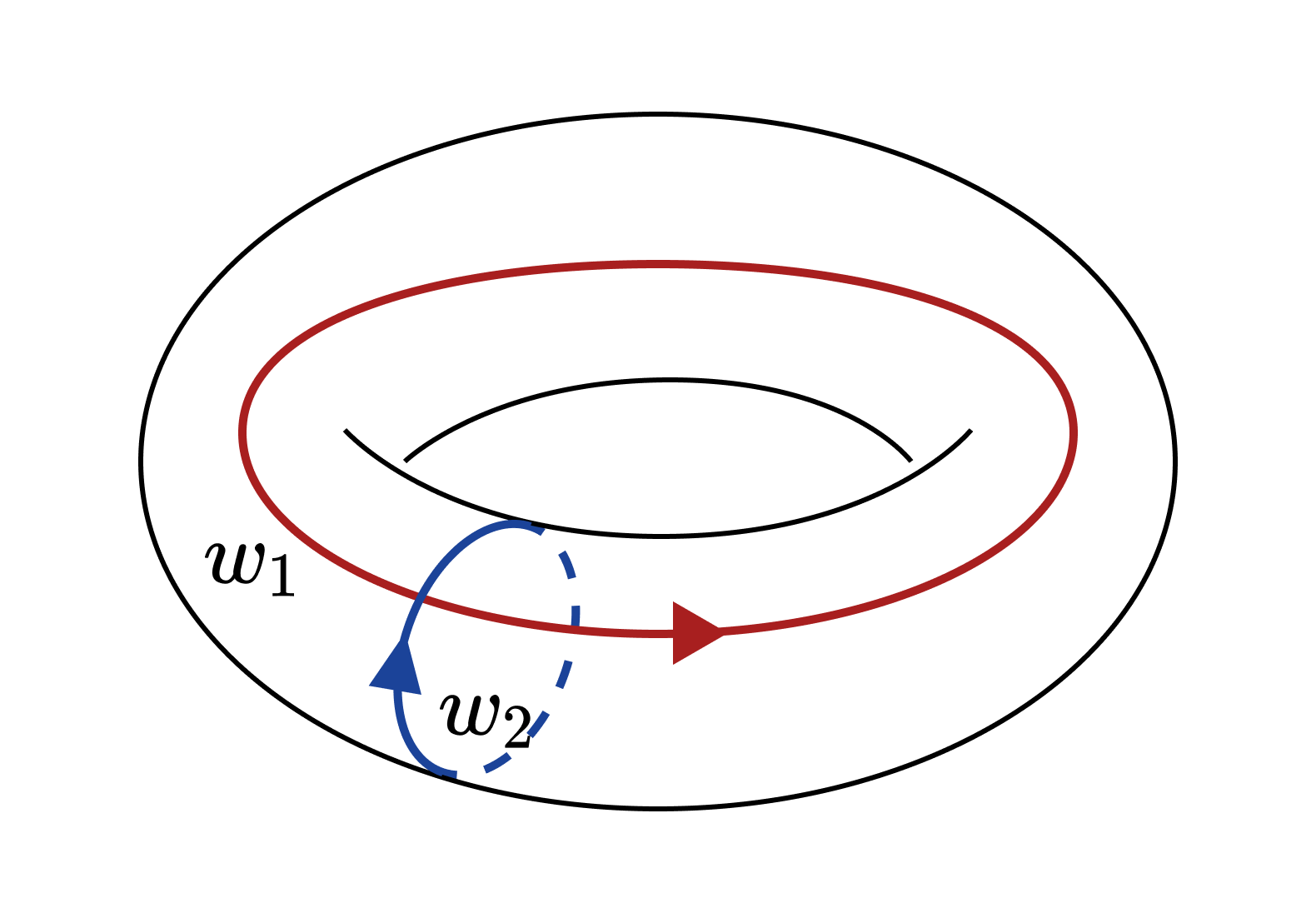
호몰로지 군의 랭크_rank는 직관적으로 구멍의 의미를 가진다. 띠의 1-호몰로지 군의 랭크가 1이라는 것은 띠의 1차원 구멍이 하나 있다는 것이고, 토러스의 1-호몰로지 군의 랭크가 2라는 것은 토러스의 1차원 구멍이 2개 있다는 것이다. (여기서 $n$차원 구멍이라 함은 $n$차원 경로에 의해 둘러질 수 있는 구멍을 말한다.)