Natural Numbers as a Mirage: A Short Story in Logic
14 Sep 2025This post was originally written in Korean, and has been machine translated into English. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.
One day, Dimen encountered an alien. The alien asked Dimen:
There's a concept that humans use which I don't understand. What exactly are natural numbers?

What do you mean? Natural numbers are a number system that starts from 1 and proceeds sequentially: 2, 3, … and so on.
AlienHmm... Then are these also natural numbers?
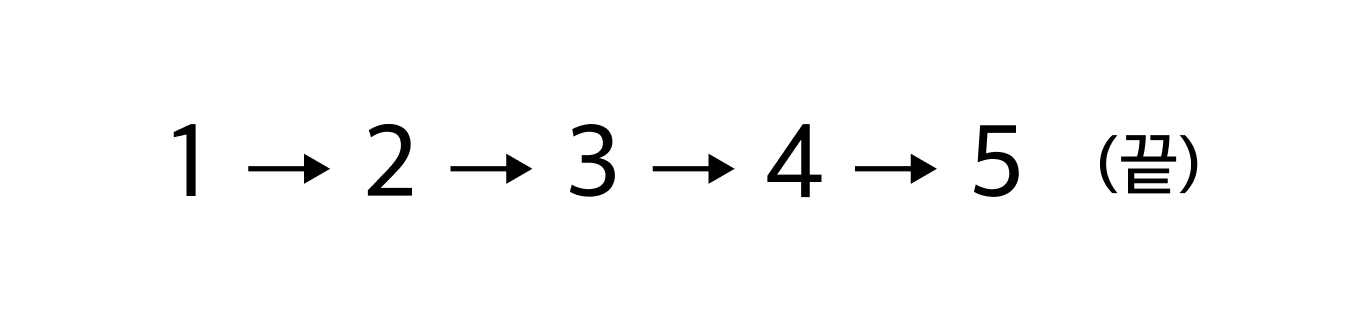
No way! Natural numbers continue indefinitely.
AlienContinue indefinitely? Do you mean they form a loop? Then they would continue indefinitely like this: 1, 2, 3, 4, 5, 3, 4, 5, 3, 4, 5, …
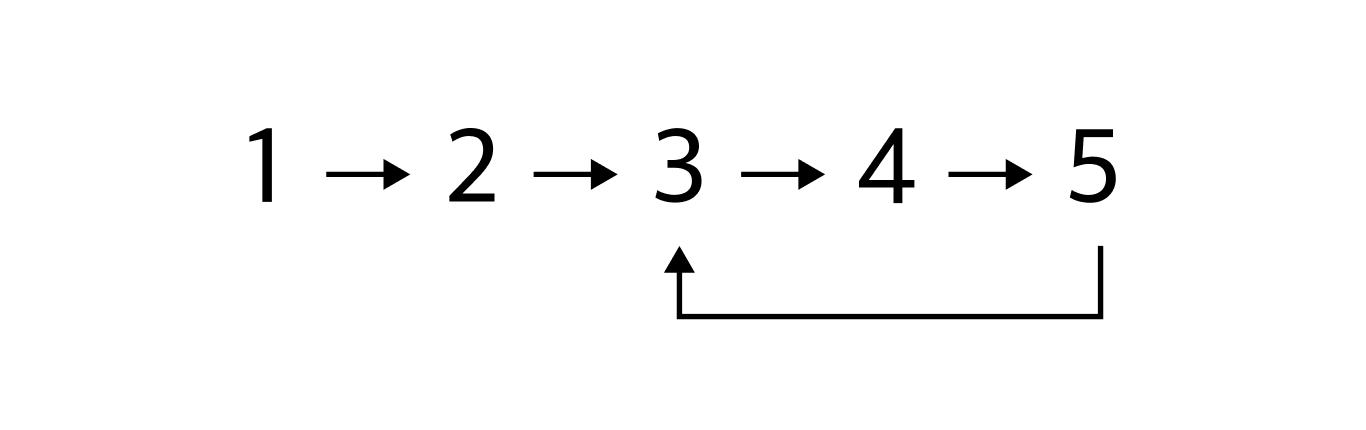
Good heavens, that's not what I meant. They continue indefinitely without any loops.
AlienHmm... Then do they branch somewhere?
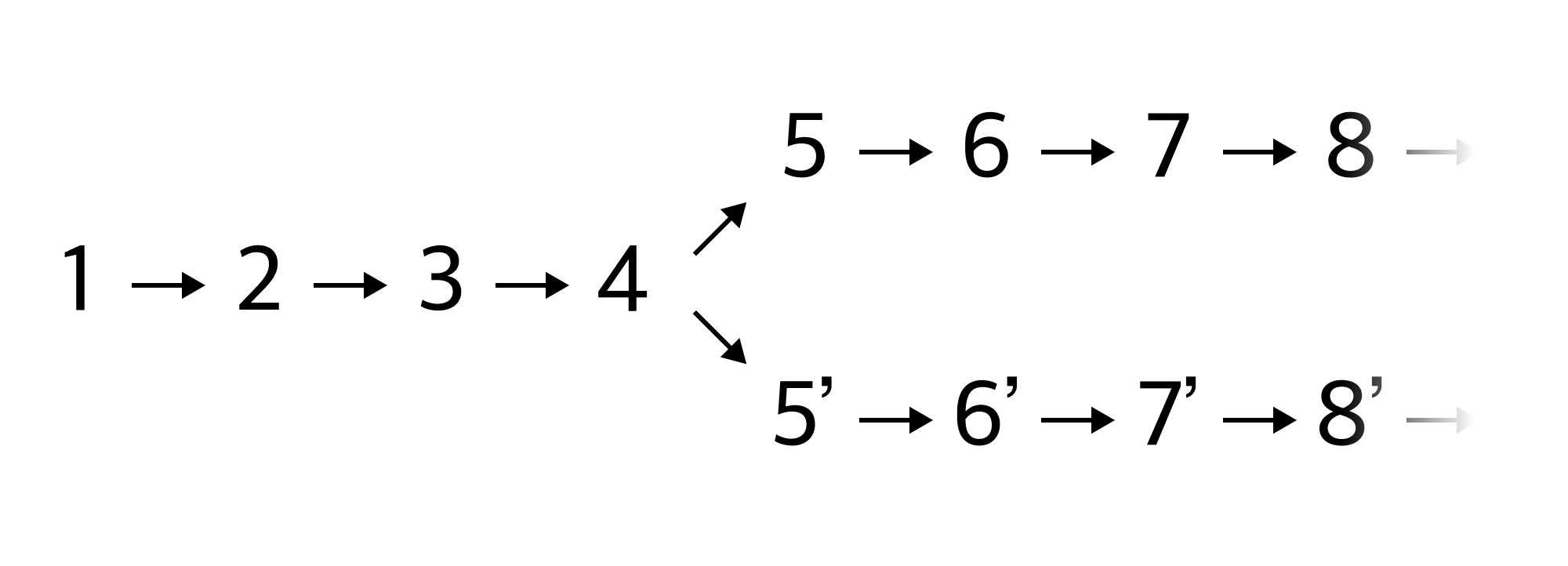
That's not it either! There are no branches!
AlienI see. Then is $c$ also a natural number by any chance?
Dimen$c$? What do you mean?
AlienAccording to the definition of natural numbers you've given me, there's no reason why $c$ shouldn't be a natural number. You said natural numbers continue indefinitely, but you didn't say that all natural numbers are included in such a chain.
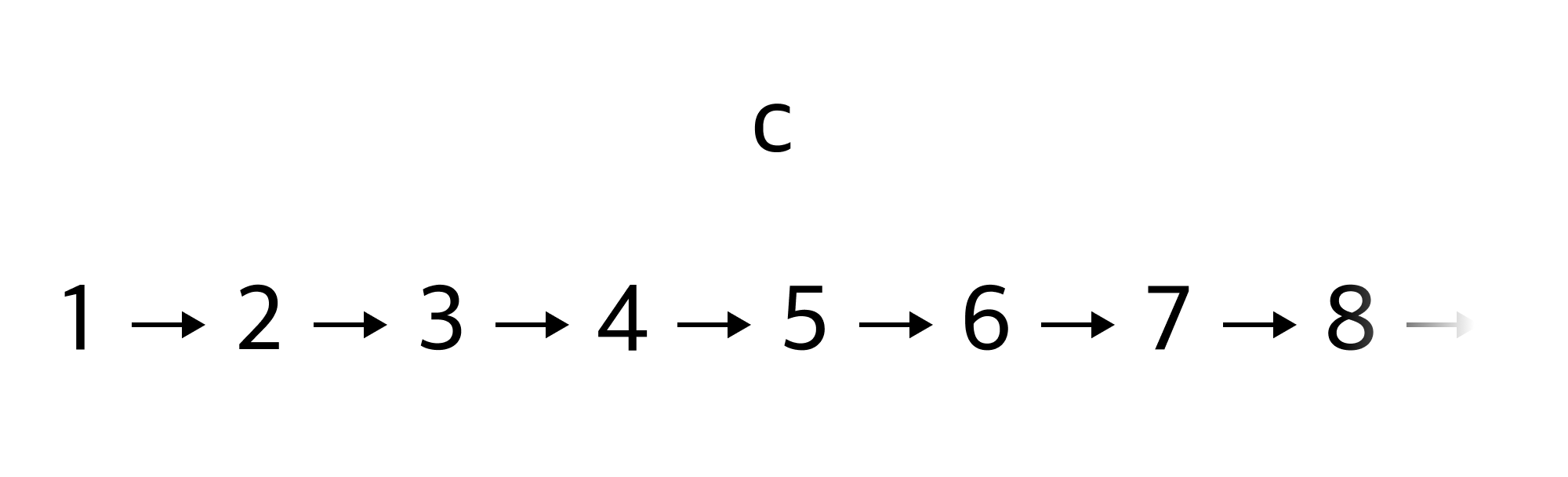
What is that supposed to be... Natural numbers contain only natural numbers!
AlienNatural numbers contain only natural numbers—that's nothing but circular reasoning.
DimenAre you making fun of me?
AlienWhat are you talking about? I genuinely don't understand what natural numbers are. You need to give me a proper definition of natural numbers for me to understand.
DimenNatural numbers are... well... that is... ugh, how do I explain this!

At that moment, a person named Dedekind appeared.
I shall resolve this problem definitively. Natural numbers are a set that satisfies the following three conditions. I have proven that a set satisfying these three conditions is unique, so there is no room for further misunderstanding.
Dedekind’s definition of natural numbers. If a set $A$, an element $e \in A$, and a function $S: A \to A$ satisfy the following three conditions, then $A$, $e$, and $S$ correspond to the set of natural numbers, $0$, and $x \mapsto x + 1$, respectively.
- There exists no $x$ such that $S(x) = e$.
- If $S(x) = S(y)$, then $x = y$.
- For any proposition $P(x)$ with domain $A$, if the following two conditions hold, then $P(x)$ is true for all elements of $A$:
- $P(e)$ is true.
- If $P(x)$ is true, then $P(S(x))$ is true.
The alien was satisfied with Dedekind’s answer, but soon looked puzzled again.
Does the expression "any proposition" in the third condition make sense? If $P(x)$ is any proposition, then $P(x)$ could be "$x$ is a natural number". But including a proposition about natural numbers in the definition of natural numbers would be circular reasoning, wouldn't it?
DedekindOh... is that so...?
AlienWhat exactly is a "proposition" anyway? Is "$x$ is a set that does not contain itself" a well-defined proposition?
Dimen(If $x$ is a set that does not contain itself, then $x$ satisfies the definition of $x$, so it contains itself; but if $x$ is a set that contains itself, then $x$ does not satisfy the definition of $x$, so it does not contain itself... huh?)
As Dedekind hesitated at this unexpected criticism, a person named Löwenheim interjected from the side.
Indeed, the expression "any proposition" seems problematic. We should restrict such expressions in mathematics. Let us call this restricted logic first-order logic.

Then we must now discover how to define natural numbers precisely using first-order logic.
At these words, a person named Skolem suddenly appeared.
Precisely. And I have discovered the answer to this question.
Everyone focused their attention on Skolem’s statement.
It's impossible. First-order logic cannot describe the necessary and sufficient conditions for natural numbers. Specifically, every first-order logical definition that attempts to define natural numbers has counterexamples that are not natural numbers. Therefore, natural numbers cannot be reduced to logic. Natural numbers cannot be defined without circular reasoning.
Löwenheim-Skolem theorem. Mathematical systems with infinitely many elements, including natural numbers, cannot be uniquely characterised by first-order logic.

A moment of silence followed.
Then how do humans know what natural numbers are? Don't humans actually understand natural numbers differently from one another?
No one could answer the alien’s question. They had nothing more to say about the mirage-like reality of natural numbers.
Note. For the natural flow of the narrative, there are distorted historical, mathematical, and philosophical contents. The birth of first-order logic was achieved through the gradual research of several mathematicians, including Löwenheim. Moreover, whether Dedekind’s definition of natural numbers using second-order logic is truly circular requires more detailed discussion. Finally, Skolem’s paradox concerns set theory rather than natural numbers, but it was included in the speech bubble because the two phenomena are similar as consequences of the Löwenheim-Skolem theorem.