Robinson, Craig, and Beth's Theorems

08 May 2025

This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.

Elementary Amalgamation Property

Theorem. Let $\mathfrak{A}$ be an $\mathcal{L}$-structure and $\mathfrak{B}$ be an $\mathcal{L}’$-structure such that the $\mathcal{L}$-reduct of $\mathfrak{B}$ is elementarily equivalent to $\mathfrak{A}$. Then there exists an $\mathcal{L}’$-structure $\mathfrak{C}$ such that $f: \mathfrak{A} \to \mathfrak{C}$ is an elementary embedding in $\mathcal{L}$ and $g: \mathfrak{B} \to \mathfrak{C}$ is an elementary embedding in $\mathcal{L}’$.

Proof. Following the notation of this post, consider the theory $E(\mathfrak{A})$ in language $L_\mathfrak{A}$ and the theory $E(\mathfrak{B})$ in language $L’\mathfrak{B}$. Let $T = E(\mathfrak{A}) \cup E(\mathfrak{B})$ be a theory in the language $\mathcal{L}’{\mathfrak{AB}} = \mathcal{L}\mathfrak{A} \cup \mathcal{L}’\mathfrak{B}$. We shall show that $T$ has a model $\mathfrak{C}$.

Suppose $T$ has no model. Then $T$ is inconsistent. By the compactness theorem, there exist some $\mathcal{L}$-formula $\phi$ and $\mathcal{L}’$-formula $\psi$ such that for appropriate ${a_i} \subset \mathcal{L}\mathfrak{A}$ and ${b_j} \subset \mathcal{L}\mathfrak{B}$,

\[\{\phi(a_1, \dots, a_n), \psi(b_1, \dots, b_m)\}\]

has no model. Since $\mathfrak{B} \vDash \psi(b_1, \dots, b_m)$, there must be no way to assign the constants $a_1, \dots, a_n$ to elements of the domain of $\mathfrak{B}$ such that $\mathfrak{B} \vDash \phi(a_1, \dots, a_n)$. That is,

\[\mathfrak{B} \not\vDash \exists x_1, \dots x_n \; \phi(x_1, \dots, x_n)\]

However, since the $\mathcal{L}$-reduct of $\mathfrak{B}$ is elementarily equivalent to $\mathfrak{A}$, and the right-hand side above is an $\mathcal{L}$-sentence that is satisfied by $\mathfrak{A}$, this yields a contradiction. Therefore, $T$ has a model $\mathfrak{C}$. Since $\mathfrak{C}$ is a model of both $E(\mathfrak{A})$ and $E(\mathfrak{B})$, both $\mathfrak{A}$ and $\mathfrak{B}$ are naturally elementarily embedded into $\mathfrak{C}$. ■

Robinson Consistency Theorem

Theorem. Let $\mathcal{L} = \mathcal{L}_1 \cap \mathcal{L}_2$. Suppose $T$ is a (semantically) complete theory in $\mathcal{L}$, and $T_1$ and $T_2$ are consistent theories in $\mathcal{L}_1$ and $\mathcal{L}_2$ respectively, each extending $T$. Then $T_1 \cup T_2$ is consistent as a theory in $\mathcal{L}_1 \cup \mathcal{L}_2$.

Proof. It suffices to construct a model of $T_1 \cup T_2$.

Since $T_1$ and $T_2$ are consistent, they have models $\mathfrak{A}_0$ and $\mathfrak{B}_0$ respectively. Since $T = T_1 \cap T_2$ is complete, the $\mathcal{L}$-reducts of $\mathfrak{A}_0$ and $\mathfrak{B}_0$ are elementarily equivalent. Therefore, by the elementary amalgamation property, there exist an $\mathcal{L}$-elementary embedding $f_0$ and an $\mathcal{L}_2$-elementary embedding $h_0$ such that the following holds:

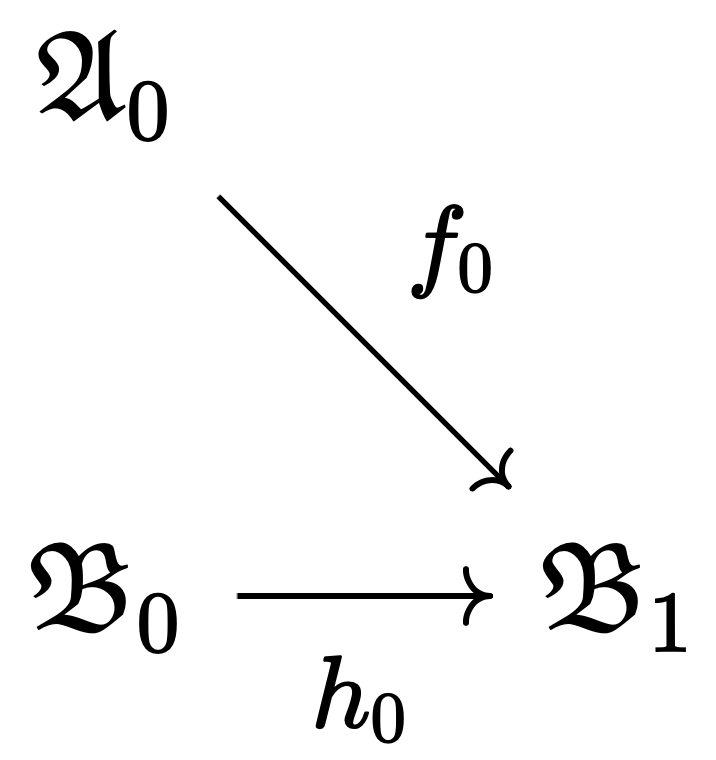
Now considering the $\mathcal{L}$-reduct of $\mathfrak{B}_1$, this is elementarily equivalent to $\mathfrak{A}_0$, so again by the elementary amalgamation property, there exist an $\mathcal{L}$-elementary embedding $g_0$ and an $\mathcal{L}_1$-elementary embedding $k_0$ such that the following holds:

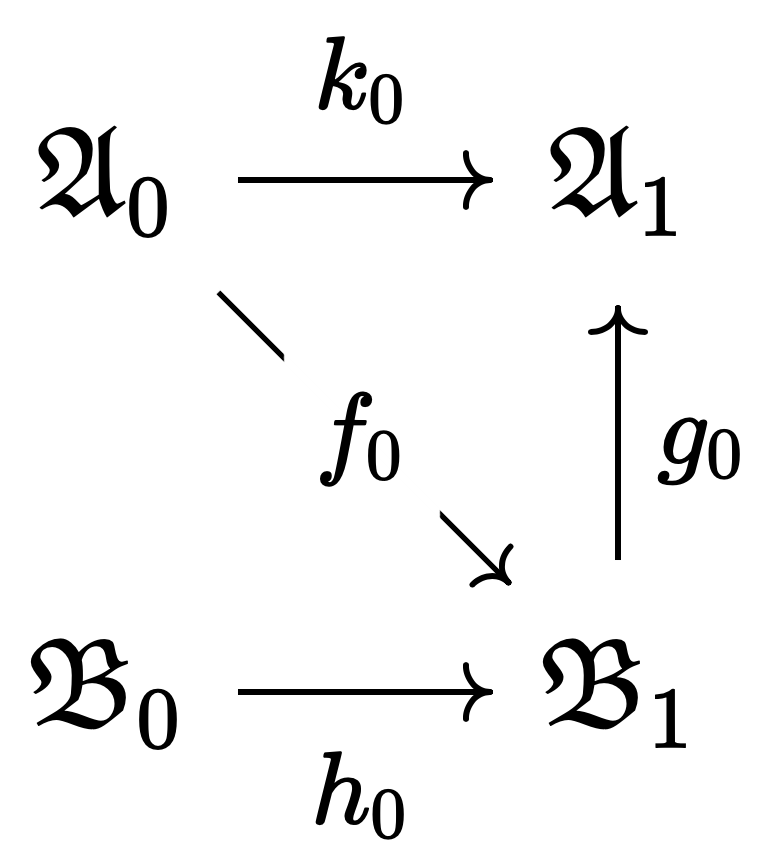
Repeating this process, we obtain the following directed system of structures:

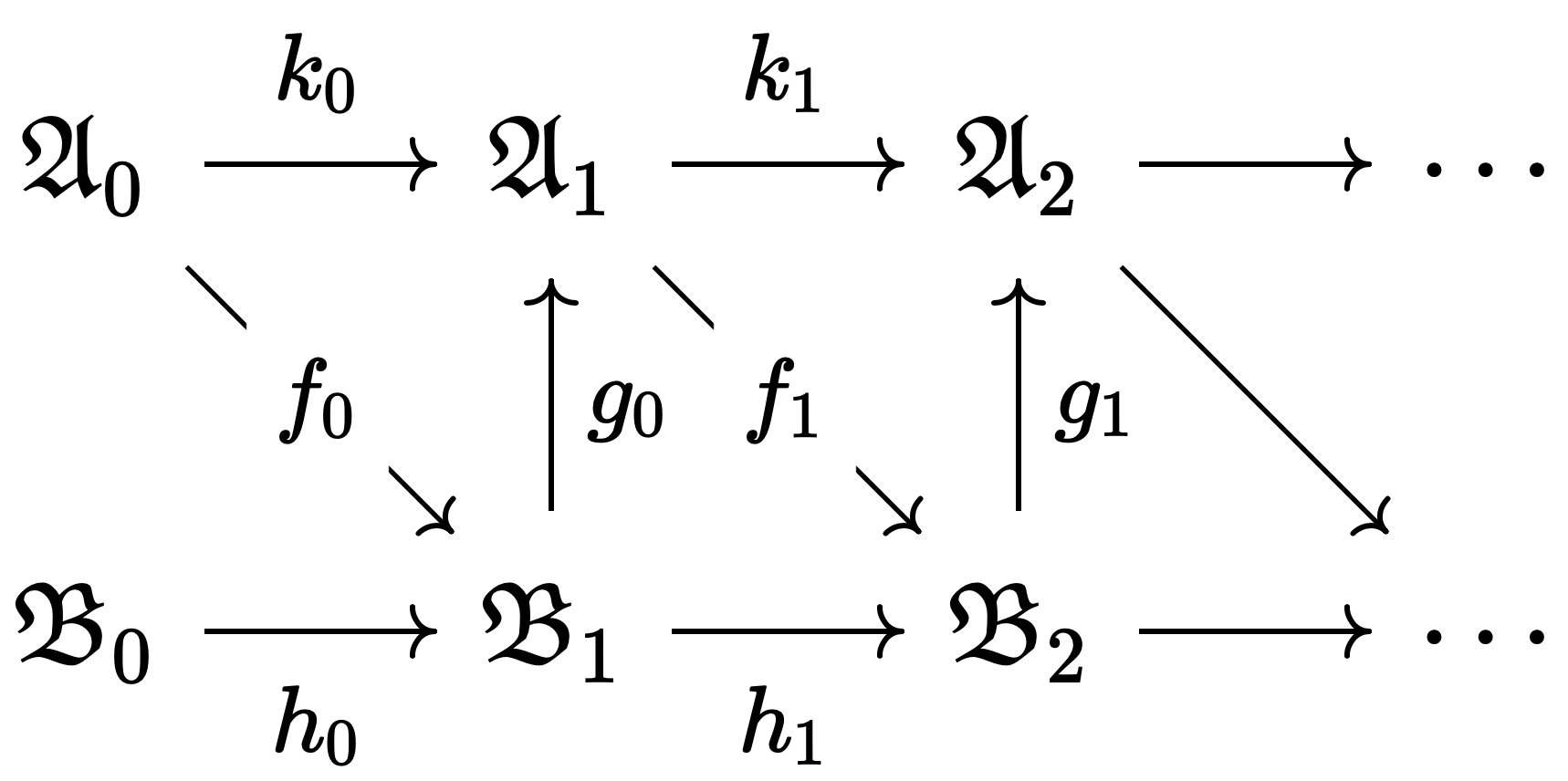
Map	Property
$f, g$	$\mathcal{L}$-elementary embedding
$k$	$\mathcal{L}_1$-elementary embedding
$h$	$\mathcal{L}_2$-elementary embedding

Reducing all models in the above directed system to $\mathcal{L}$ gives an $\mathcal{L}$-structure directed system. Let $\mathfrak{C}$ be the colimit of this directed system. $\mathfrak{C}$ is also the colimit of the directed system consisting of ${\mathfrak{A}_i}$, since the parts of the original directed system shown in grey all project to one of the ${\mathfrak{A}_i}$. Therefore, $\mathfrak{C}$ is an $\mathcal{L}_1$-structure that elementarily embeds $\mathfrak{A}_0$.

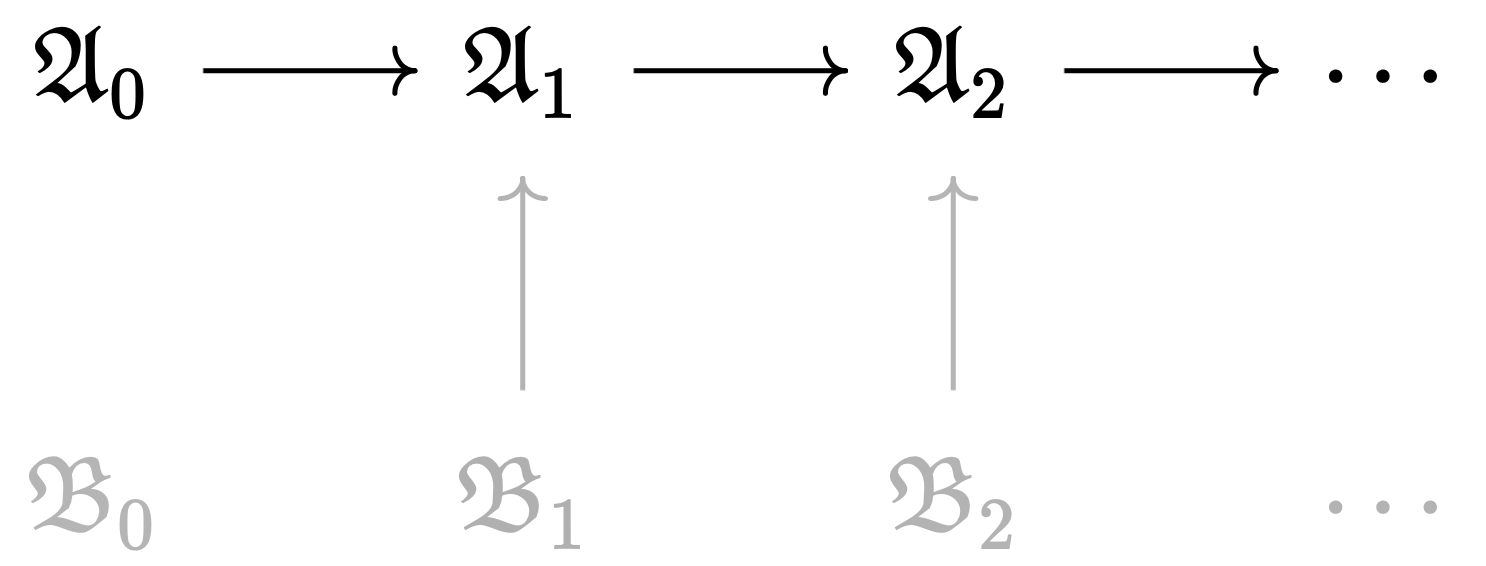
For the same reason, $\mathfrak{C}$ is also the colimit of the directed system consisting of ${\mathfrak{B}_i}$. Therefore, $\mathfrak{C}$ is an $\mathcal{L}_2$-structure that elementarily embeds $\mathfrak{B}_0$.

That is, $\mathfrak{C}$ embeds both $\mathfrak{A}$ and $\mathfrak{B}$, from which it follows that it is a model of $T_1 \cup T_2$. ■

Craig Interpolation Theorem

Theorem. For $\mathcal{L}$-sentences $\phi$ and $\psi$, if $\phi \vDash \psi$, then there exists an $\mathcal{L}$-sentence $\theta$ such that $\phi \vDash \theta$ and $\theta \vDash \psi$. Moreover, the non-logical symbols (constants, predicates, functions) contained in $\theta$ are those common to both $\phi$ and $\psi$.

$\theta$ is called a Craig interpolant of $\phi$ and $\psi$.

Proof. We prove by contradiction. Suppose no Craig interpolant exists. Then $\phi$ has a model, for if $\phi$ had no model, then $\perp$ would be a Craig interpolant of $\phi$ and $\psi$. Also, $\lnot \psi$ has a model, for otherwise $\top$ would be a Craig interpolant.

Let $\mathcal{L}’$ be the language consisting of the non-logical symbols common to both $\phi$ and $\psi$. Let $\Gamma$ be the set of $\mathcal{L}’$-sentences $\sigma$ such that either $\phi \vDash \sigma$ or $\lnot \psi \vDash \sigma$.

We show that $\Gamma \cup {\phi}$ is consistent. Suppose it is inconsistent. Then by the compactness theorem, there exist $\mathcal{L}’$-sentences $\sigma_1$ and $\sigma_2$ such that $\phi \vDash \sigma_1$, $\lnot\psi \vDash \sigma_2$, and ${\sigma_1, \sigma_2, \phi}$ is inconsistent. Since $\phi \vDash \sigma_1$, we have $\phi \vDash \lnot\sigma_2$. By contraposition, from $\lnot\psi \vDash \sigma_2$ we obtain $\lnot\sigma_2 \vDash \psi$. Thus $\lnot\sigma_2$ is a Craig interpolant of $\phi$ and $\psi$, contradicting our assumption.

Therefore, $\Gamma \cup {\phi}$ is consistent, and by the same reasoning, $\Gamma \cup {\lnot\psi}$ is also consistent. Now applying Zorn’s lemma, define $\overline{\Gamma}$ as the maximum of the following ordered set of $\mathcal{L}’$-theories:

\[\{ \Gamma' : \Gamma \subseteq \Gamma', \Gamma' \cup \{\phi\} \text{ and } \Gamma' \cup \{\lnot \psi\} \text{ are consistent} \}\]

We show that $\overline{\Gamma}$ is complete. Suppose $\overline{\Gamma}$ is not complete. Then there exists an $\mathcal{L}’$-sentence $\sigma$ such that $\sigma \notin \overline{\Gamma}$, and either $\overline{\Gamma} \cup {\sigma, \phi}$ or $\overline{\Gamma} \cup {\sigma, \lnot \psi}$ is consistent.

In the former case, by the compactness theorem, there exists a sentence $\theta$ in $\overline{\Gamma}$ such that $\phi \vDash \theta \rightarrow \lnot \sigma$. By the definition of $\Gamma$, we have $\theta \rightarrow \lnot \sigma \in \Gamma \subseteq \overline{\Gamma}$. Therefore, $\overline{\Gamma} \cup {\sigma, \phi}$ proves $\lnot\phi$, which is a contradiction. The latter case yields a similar contradiction. Therefore, $\overline{\Gamma}$ is complete.

Since $\overline{\Gamma}$ is complete and $\overline{\Gamma} \cup {\phi}$ and $\overline{\Gamma} \cup {\lnot\psi}$ are consistent, by Robinson’s consistency theorem, $\overline{\Gamma} \cup {\phi, \lnot \psi}$ is consistent. But this contradicts $\phi \vDash \psi$. Therefore, by contradiction, $\phi$ and $\psi$ have a Craig interpolant. ■

Beth Definability Theorem

Consider a language $\mathcal{L}$ and a predicate $P$ not contained in $\mathcal{L}$. Let $T$ be a theory in $\mathcal{L} \cup {P}$. We say that $T$ implicitly defines $P$ when there is a unique way to extend any $\mathcal{L}$-structure $\mathfrak{A}$ satisfying $T$ to $\mathcal{L} \cup {P}$.

This can also be stated as follows. Let $T(P’)$ be the theory in $\mathcal{L} \cup {P’}$ obtained by replacing every occurrence of $P$ in $T$ with $P’$. Then $T$ implicitly defines $P$ if and only if the following holds:

\[T \cup T(P') \vDash \forall x_1, \dots, x_n \; P(x_1, \dots, x_n) \leftrightarrow P'(x_1, \dots, x_n)\]

On the other hand, $T$ explicitly defines $P$ if there exists an $\mathcal{L}$-formula $\phi$ satisfying:

\[T \vDash \forall x_1, \dots, x_n \; P(x_1, \dots, x_n) \leftrightarrow \phi(x_1, \dots, x_n)\]

For example, consider the following theory $T$, which adds axioms concerning a predicate $P(x, y)$ to the theory $\mathsf{PA}$ in the language $\mathcal{L} = (0, S, +, \cdot)$:

\[T = \mathsf{PA} \cup \Big\{ \forall x, y \big[ P(x, y) \rightarrow x + y = S(0) \big] \Big\}\]

$T(P’)$ is as follows:

\[T(P') = \mathsf{PA} \cup \Big\{ \forall x, y \big[ P'(x, y) \rightarrow x + y = S(0) \big] \Big\}\]

That $T$ implicitly defines $P$ means the following holds:

\[T \cup T(P') \vDash \forall x, y \big[ P(x, y) \leftrightarrow P'(x, y) \big]\]

This follows naturally from the induction axiom schema. But $P$ can also be explicitly defined in $T$ as follows:

\[\begin{gather} T \vDash \forall x, y \big[ P(x, y) \leftrightarrow \phi(x, y) \big] \\\\ \text{where}\\\\ \phi(x, y) : \forall z \big[ x + z = S(0) \rightarrow z = y \big] \end{gather}\]

This is no coincidence.

Theorem. For a language $\mathcal{L}$, if a theory $T$ in $\mathcal{L} \cup {P}$ implicitly defines $P$, then $T$ explicitly defines $P$.

Proof. Suppose $P$ is an $n$-ary predicate. Let $\mathcal{L}’$ be the language obtained by adding new constants $c_1, \dots, c_n$ to $\mathcal{L}$. Since $T$ implicitly defines $P$, we have:

\[T \cup T(P') \vDash P(c_1, \dots, c_n) \rightarrow P'(c_1, \dots, c_n)\]

By the compactness theorem, there exists an $\mathcal{L} \cup {P}$-sentence $\psi$ such that $T \vdash \psi$ and the following holds:

\[\psi \land \psi(P') \vDash P(c_1, \dots, c_n) \rightarrow P'(c_1, \dots, c_n)\]

Using the deduction theorem and rearranging:

\[\psi \land P(c_1, \dots, c_n) \vDash \psi(P') \rightarrow P'(c_1, \dots, c_n)\]

The left-hand side is a sentence in $\mathcal{L}’ \cup {P}$, and the right-hand side is a sentence in $\mathcal{L}’ \cup {P’}$. Therefore, by Craig’s interpolation theorem, there exists an $\mathcal{L}’$-formula $\theta$ such that:

\[\begin{gather} \psi \land P(c_1, \dots, c_n) \vDash \theta(c_1, \dots, c_n), \\\\ \theta(c_1, \dots, c_n) \vDash \psi(P') \rightarrow P'(c_1, \dots, c_n) \end{gather}\]

Rearranging again and substituting $P$ for $P’$:

\[\begin{gather} \psi \vDash P(c_1, \dots, c_n) \rightarrow \theta(c_1, \dots, c_n), \\\\ \psi \vDash \theta(c_1, \dots, c_n) \rightarrow P(c_1, \dots, c_n) \end{gather}\]

Therefore, $\theta$ explicitly defines $P$. ■