준동형 사상, 임베딩, 초등적 임베딩

01 May 2025

이 글에서는 편의를 위해 술어와 함수를 별도의 대상으로 생각하는 대신, 함수식 $f(a) = c$를 이항 술어 $F(a, c)$로 환원하는 접근을 택한다.

정의. $\mathfrak{A}, \mathfrak{B}$가 언어 $\mathcal{L}$의 구조라고 하자. 다음을 만족하는 사상 $f: \mathfrak{A} \to \mathfrak{B}$을 준동형 사상_homomorphism이라고 부른다. $R$이 $\mathcal{L}$의 관계일 때, 임의의 $a_1, \dots, a_n \in \mathfrak{A}$에 대해,

\[R^\mathfrak{A}(a_1, \dots, a_n) \implies R^\mathfrak{B}(f(a_1), \dots, f(a_n))\]

이다.

추가로, 준동형사상 $f$가 단사이고 다음을 만족할 때 $f$를 임베딩_embedding이라고 부른다.

\[R^\mathfrak{A}(a_1, \dots, a_n) \iff R^\mathfrak{B}(f(a_1), \dots, f(a_n))\]

단사 준동형사상이라고 해서 임베딩인 것은 아니다. 일례로 하나의 이항 관계 $<$를 가지는 언어 $\mathcal{L}$의 다음의 두 구조를 보자. $<$를 만족시키는 대상은 화살표로 표시되었다. 즉, $b_1 <^\mathfrak{B} b_2$이다.

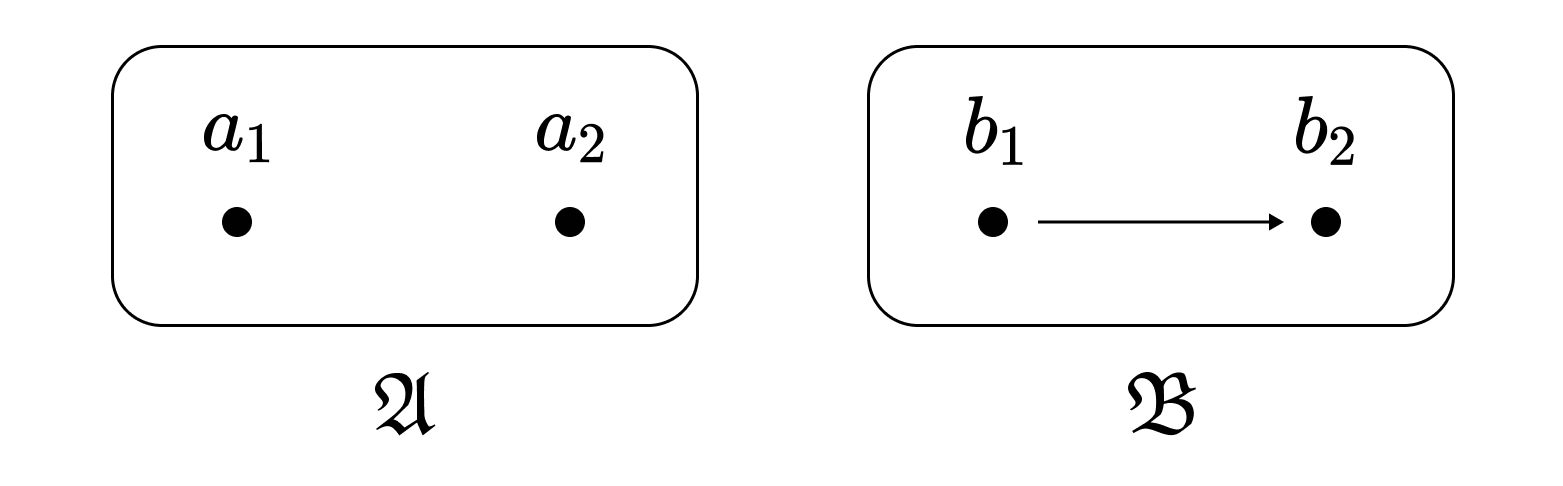
$\mathfrak{A}$의 원소들은 $<^\mathfrak{A}$를 만족시키는 경우가 없으므로 $f: a_1 \mapsto b_1, a_2 \mapsto b_2$는 자명하게 준동형사상이며, 단사이다. 그러나 $f$는 임베딩이 아니다. $f$가 임베딩이라면 $b_1 <^\mathfrak{B} b_2$으로부터 $a_1 <^\mathfrak{A} a_2$가 성립해야 하기 때문이다. 즉, 임베딩은 $\mathfrak{A}$의 원소들뿐 아니라 원소들 간의 관계까지 그대로 $\mathfrak{B}$에 대응시켜야 한다. 이런 면에서 임베딩은 범주론에서의 포화된 함자_{full functor}와 비슷하다.

정의. $\mathfrak{A}$가 언어 $\mathcal{L}$의 구조라고 하자. $\mathcal{L}_\mathfrak{A}$를 $\mathcal{L}$에 $\mathfrak{A}$의 정의역 크기만큼의 상수를 추가한 언어로 정의한다.

페아노 산술로 예를 들자면, $\mathcal{L} = (0, S, +)$이고 $\mathfrak{A}$가 산술의 표준 모형일 때, $\mathcal{L}_\mathfrak{A} = (0, 1, 2, 3, \dots, S, +)$이다.

정의. $\mathfrak{A}$가 만족시키는 모든 $\mathcal{L}_\mathfrak{A}$-원자명제들의 집합을 $\Delta_\mathfrak{A}^+$로 적는다. 즉,

\[\Delta_\mathfrak{A}^+ = \{ R(c_1, \dots, c_n) \mid R, c_i \in \mathcal{L}_\mathfrak{A}, \; \mathfrak{A} \vDash R^{\mathfrak{A}}(c_1^\mathfrak{A}, \dots, c_n^\mathfrak{A}) \}\]

추가로, $\Delta_\mathfrak{A}^+$에다 $\mathfrak{A}$가 만족시키지 않는 모든 $\mathcal{L}$-원자명제들의 부정까지 추가한 집합을 $\Delta_\mathfrak{A}$로 적는다. 즉,

\[\Delta_\mathfrak{A} = \Delta_\mathfrak{A}^+ \cup \{ \lnot R(c_1, \dots, c_n) \mid R, c_i \in \mathcal{L}_\mathfrak{A}, \; \mathfrak{A} \not\vDash R^{\mathfrak{A}}(c_1^\mathfrak{A}, \dots, c_n^\mathfrak{A}) \}\]

$\Delta$라는 표기법은 산술 위계와 관련이 있다.

$\Delta_\mathfrak{A}^+$에 빠진 원자명제들의 부정을 추가한 것이 곧 $\Delta_\mathfrak{A}$이기 때문에, 두 집합이 내포하는 정보량은 사실상 같다. 그럼에도 두 집합을 구분하여 정의하는 것은 다음의 정리 때문이다.

정리. $\mathfrak{A}, \mathfrak{B}$가 $\mathcal{L}$-구조라고 하자.

1. 단사 준동형사상 $f: \mathfrak{A} \to \mathfrak{B}$가 존재할 필요충분조건은 $\mathfrak{B}$가 $\Delta_\mathfrak{A}^+$의 $\mathcal{L}_\mathfrak{A}$-모델인 것이다.
2. 임베딩 $f: \mathfrak{A} \to \mathfrak{B}$가 존재할 필요충분조건은 $\mathfrak{B}$가 $\Delta_\mathfrak{A}$의 $\mathcal{L}_\mathfrak{A}$-모델인 것이다.

즉, $\mathfrak{B}$가 $\Delta_\mathfrak{A}^+$를 만족할 경우 $\mathfrak{B}$가 원자명제들을 ‘과도하게’ 만족시켜서, $\mathfrak{A}$가 $\mathfrak{B}$로 임베딩되지 못할 가능성이 있다. 그러나 $\mathfrak{B}$가 $\Delta_\mathfrak{A}$를 만족할 경우, $\mathfrak{B}$가 만족시킬 수 있는 원자명제에 한계가 걸리기 때문에 임베딩 가능성이 보장된다.

이전 글에서 초등적 부분모델이라는 개념을 소개한 바 있다. 이로부터 다음의 개념을 정의할 수 있다.

정의. $f: \mathfrak{A} \to \mathfrak{B}$가 임베딩이고, $f[\mathfrak{A}]$가 $\mathfrak{B}$의 초등적 부분모델일 때, $f$를 초등적 임베딩이라고 한다.

초등적 임베딩과 관련된 문장 집합은 다음과 같다.

정의. $\mathfrak{A}$가 만족시키는 모든 $\mathcal{L}_\mathfrak{A}$-명제들의 집합을 $E(\mathfrak{A})$로 적는다. 즉,

\[E(\mathfrak{A}) = \{ \phi : \mathfrak{A} \vDash \phi \}\]

$E(\mathfrak{A})$가 $\Delta_\mathfrak{A}$와 가장 구별되는 특징은 양화사가 있는 문장 또한 포함한다는 것이다.

정리. $\mathfrak{A}, \mathfrak{B}$가 $\mathcal{L}$-구조라고 하자. 초등적 임베딩 $f: \mathfrak{A} \to \mathfrak{B}$가 존재할 필요충분조건은 $\mathfrak{B}$가 $E(\mathfrak{A})$의 $\mathcal{L}_\mathfrak{A}$-모델인 것이다.

마지막으로 다음의 문장 집합을 언급할 만하다.

정의. $\mathfrak{A}$가 $\mathcal{L}$-구조라고 하자. $\mathfrak{A}$에서 참인 모든 $\mathcal{L}$-문장들의 집합을 $\mathrm{Th}(\mathfrak{A})$라고 한다.

정리. $\mathfrak{A}, \mathfrak{B}$가 $\mathcal{L}$-구조라고 하자. $\mathfrak{A}$와 $\mathfrak{B}$가 초등적으로 동등할 필요충분조건은 $\mathrm{Th}(\mathfrak{A}) = \mathrm{Th}(\mathfrak{B})$인 것이다.

사실 이는 초등적 동등성의 정의나 다름이 없어서 정리라고 부르기는 무색하지만, 이 글에서 소개한 나머지 정리들과 일관성을 유지하기 위해 소개하였다.

표로 정리하면 이렇다.

	정의	예시	사상
$\Delta_\mathfrak{A}^+$	$\mathfrak{A}$가 만족시키는 $\mathcal{L}_\mathfrak{A}$-원자명제	$0 < 1$	전사 준동형
$\Delta_\mathfrak{A}$	$\mathfrak{A}$가 만족시키는 $\Delta_0$ $\mathcal{L}_\mathfrak{A}$-명제	$\lnot(1 < 0)$	임베딩 (부분모델)
$\mathrm{Th}(\mathfrak{A})$	$\mathfrak{A}$가 만족시키는 $\mathcal{L}$-명제	$\forall x \exists y (x < y)$	초등적 동등성
$E(\mathfrak{A})$	$\mathfrak{A}$가 만족시키는 $\mathcal{L}_\mathfrak{A}$-명제	$\not \exists x (x < 0)$	초등적 임베딩 (초등적 부분모델)

예를 들어 $\mathfrak{A} = (\mathbb{N}, <)$은 $\mathfrak{B} = (\mathbb{Z}, <)$에 임베딩되지만, 초등적으로 임베딩되지는 않는다. $\mathfrak{B}$가 $E(\mathfrak{A})$의 문장인 $\not \exists x (x < 0)$을 만족하지 않기 때문이다.