연속체 가설과 동치인 색칠 문제

24 Apr 2025

문제. 좌표평면을 가산 개의 색깔을 사용하여 칠했을 때, 세 꼭짓점이 같은 색깔인 직각삼각형이 언제나 존재하는가?

예를 들어 다음의 색칠은 3개의 색깔을 사용하는데, 세 꼭짓점이 모두 같은 색인 직각삼각형을 쉽게 찾을 수 있다.

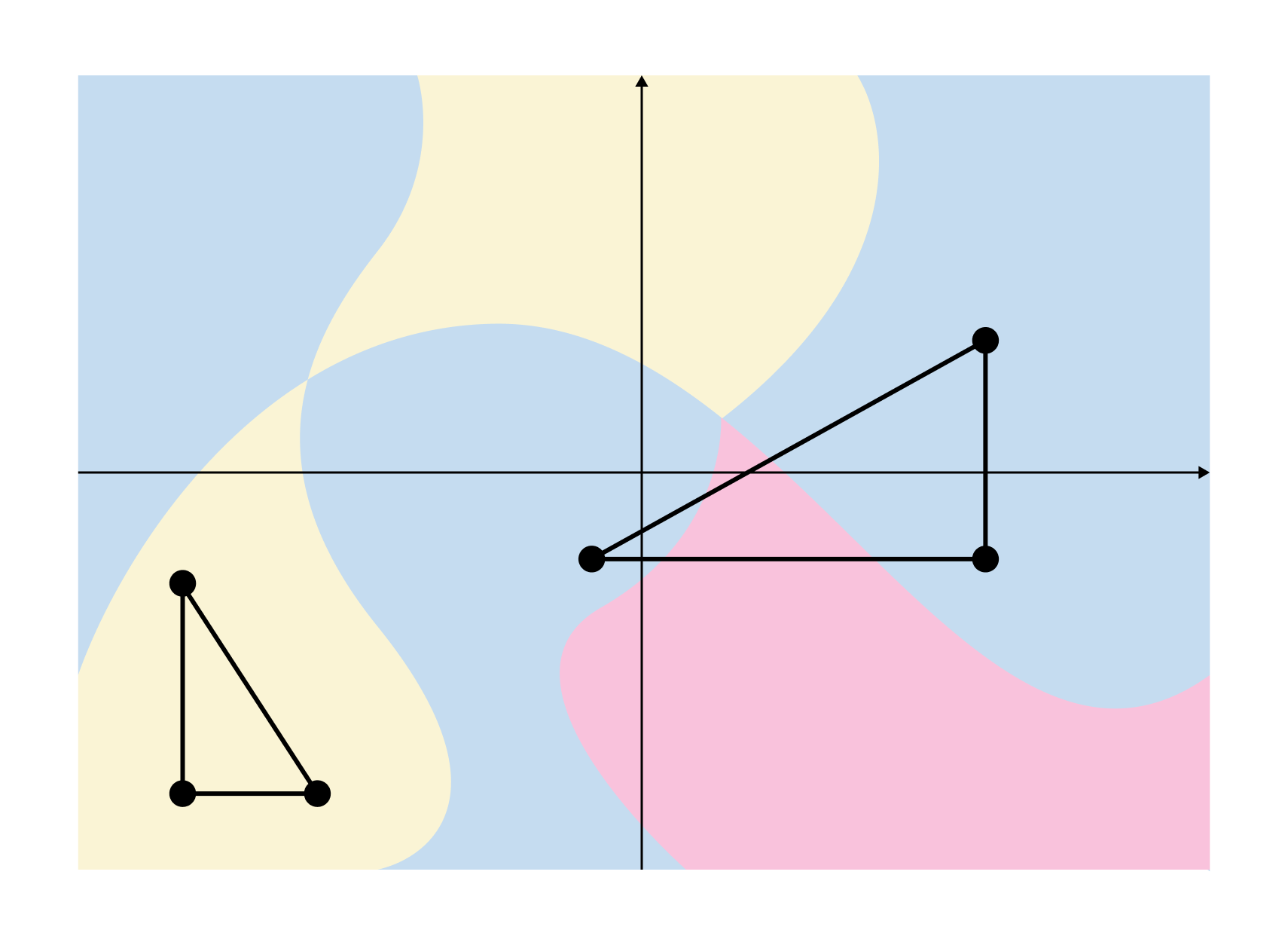
물론 위의 경우는 단순한 경우이고, 아래와 같이 무한히 많은 색깔들이 매우 불규칙적으로 칠해져 있는 경우에도 문제의 직각삼각형이 존재하는지를 따져야 한다.

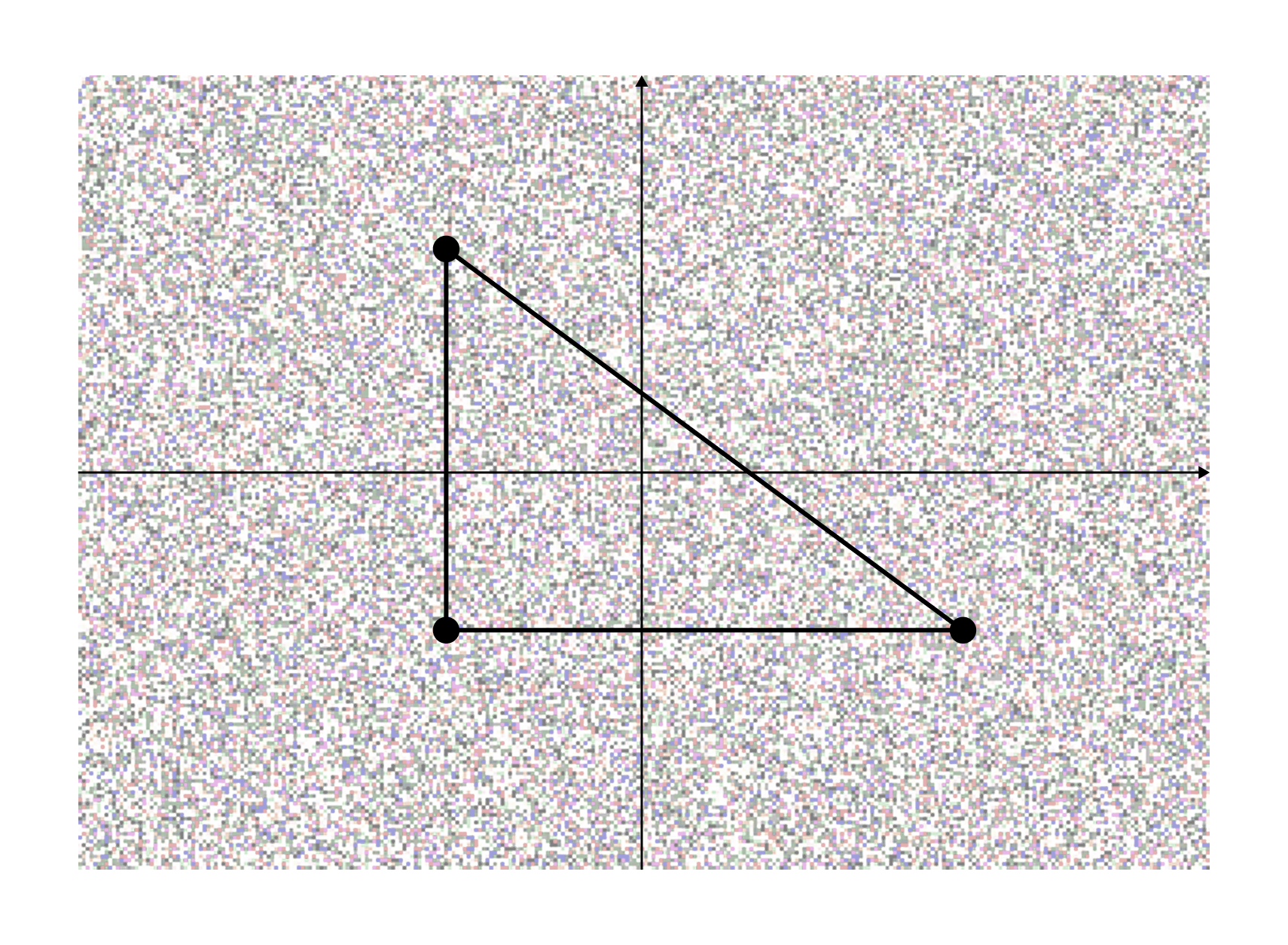
놀랍게도 언뜻 자명해 보이는 이 문제는 연속체 가설과 동치이다.

연속체 가설. 자연수보다 크고 실수보다 작은 무한집합은 존재하지 않는다.

가장 작은 무한집합인 자연수의 기수를 $\aleph_0$, 자연수보다 큰 무한집합 중 가장 작은 무한집합의 기수를 $\aleph_1$이라고 정의한다. 한편 실수는 자연수의 멱집합과 크기가 같음을 쉽게 보일 수 있으며 집합 $X$의 멱집합은 크기가 $2^{|X|}$이므로, 실수의 기수는 $2^{\aleph_0}$이다. 따라서 연속체 가설의 진술은 $\aleph_1 = 2^{\aleph_0}$와 같다.

정리. 문제의 반례가 존재할 필요충분조건은 $\aleph_1 = 2^{\aleph_0}$이다.

참고로 아래 증명은 필자가 구상한 것이기 때문에 오류가 있을 수도 있다.

증명. $\aleph_1 = 2^{\aleph_0}$라면 문제의 반례가 존재함과, 문제의 반례가 존재하면 $\aleph_1 = 2^{\aleph_0}$임을 각각 보인다.

$\aleph_1 = 2^{\aleph_0}$라면 문제의 반례가 존재한다.

가장 작은 비가산 서수 $\omega_1$에 대해, $\omega_1^2$은 세 꼭짓점이 같은 색인 직각삼각형이 존재하지 않도록 색칠하는 다음의 방법이 존재한다. 먼저 가산 개의 색을 정수와 일대일 대응시킨다. $\alpha < \omega_1$은 가산 서수이므로, 빨간색 선분 $\lbrace (\beta, \alpha) : 0 \leq \beta \leq \alpha \rbrace $의 모든 점을 서로 다른 가산 개의 색으로 칠할 수 있다. 이들 점을 양의 정수에 대응되는 색들로 칠한다. 한편 파란색 선분 $\lbrace (\alpha, \beta) : 0 \leq \beta < \alpha \rbrace $의 점들은 음의 정수에 대응되는 색들로 칠한다.

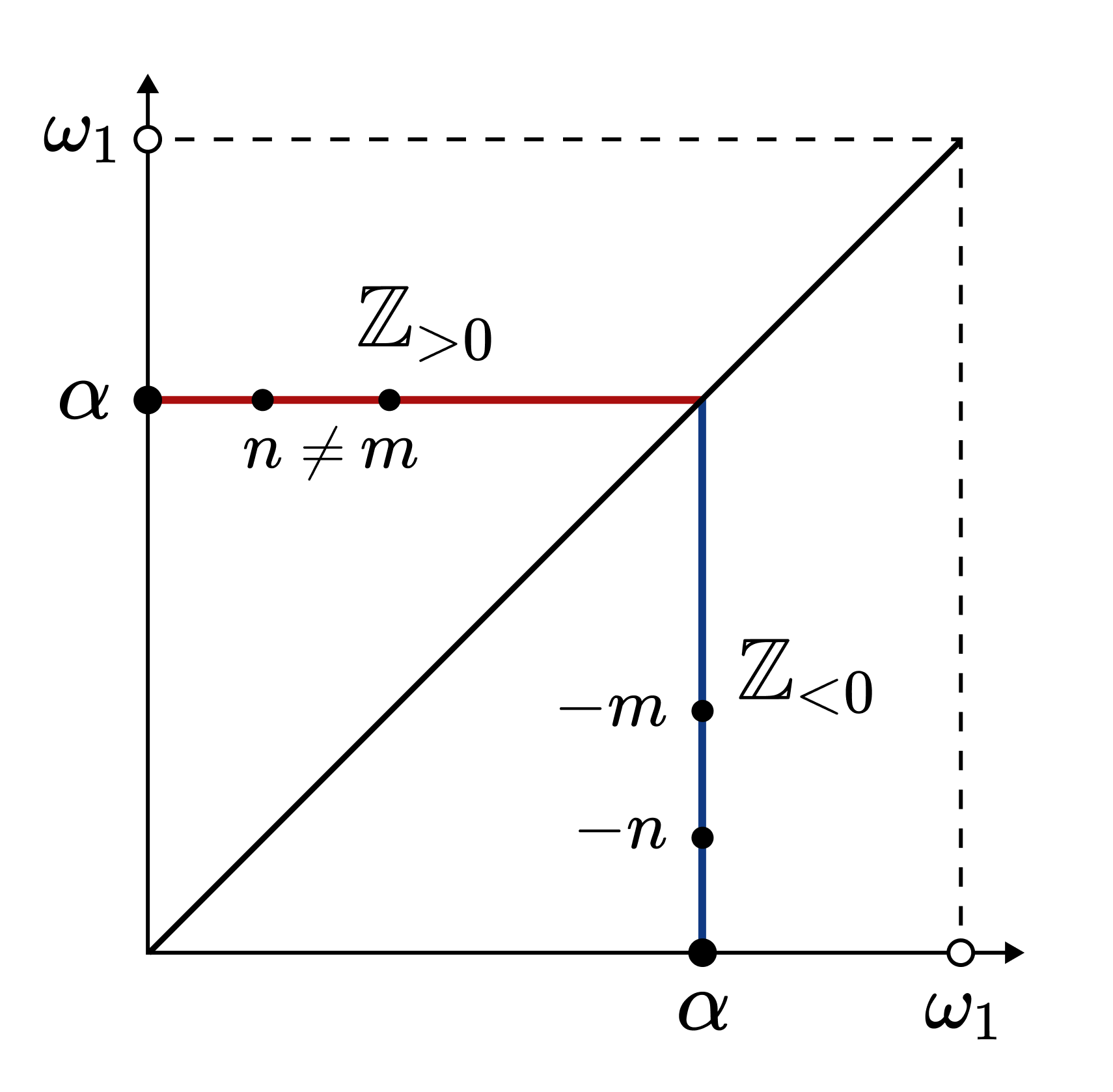
위와 같이 색칠했을 때 세 꼭짓점이 모두 같은 색인 직각삼각형이 없음을 쉽게 보일 수 있다.

만약 $\aleph_1 = 2^{\aleph_0}$라면, 어떤 일대일 대응 $f: \mathbb{R} \to \omega_1$이 존재한다. 이제 평면의 색칠을 다음과 같이 정의한다. 점 $p = (x, y) \in \mathbb{R}^2$을 점 $f(p) = (f(x), f(y)) \in \omega_1^2$와 같은 색으로 칠한다. $f$가 일대일 대응이기 때문에, 만약 해당 색칠해서 점 $p_1, p_2, p_3$가 색깔이 같은 직각삼각형의 세 꼭짓점이라면 $f(p_1), f(p_2), f(p_3)$ 또한 색깔이 같은 직각삼각형의 세 꼭짓점이다. 그런데 그러한 삼각형은 $\omega_1^2$에서 존재하지 않음을 보였으므로, 평면 또한 해당 색칠에서 요구되는 직각삼각형을 가지지 않는다.

문제의 반례가 존재한다면 $\aleph_1 = 2^{\aleph_0}$이다.

$2^{\aleph_0} > \aleph_1$이라고 가정하고 모순을 이끌어 내자. $I$가 크기 $\aleph_1$인 실수의 부분집합이라고 하자. 평면의 부분집합 $X = I \times \mathbb{R}$을 고려하자.

$x$축과 평행인 $X$의 직선들의 집합을 $L_0$라고 하자. $l \in L_0$에 대해, $l$을 이루는 점들 중 색깔 $c$로 칠해진 점의 개수가 $\aleph_1$ 이상일 때, $c \in \aleph_1(l)$이라고 적자. 임의의 $l \in L_0$에 대해, $|l| = \aleph_1$이므로 비둘기집의 원리에 의해 $c \in \aleph_1(l)$인 색깔 $c$가 직선마다 적어도 하나 존재함을 확인하라.

또한 $|L_0| = 2^{\aleph_0}$이므로 비둘기집의 원리에 의해 어떤 색깔 $c_0$가 존재하여, $c_0 \in \aleph_1(l)$을 만족하는 직선 $l$의 개수가 $2^{\aleph_0}$이다. 그러한 직선들의 집합 $L_0’$을 고려하자. $L_0’$의 직선들을 지나는 수직선을 그었을 때 어느 두 교점의 색이 $c_0$라면, 세 꼭짓점의 색이 모두 $c_0$인 직각삼각형이 존재하게 된다. 따라서 임의의 수직선과 $L_0’$의 직선들이 이루는 교점 중 $c_0$로 칠해진 점은 최대 1개이다. 수직선의 개수가 총 $|I| = \aleph_1$개이므로, $L_0’$에는 총 $\aleph_1$개의 $c_0$ 점들이 존재한다.

해당 점들을 모두 빼면 듬성듬성한 직선들의 집합이 된다. 이 집합을 $L_1$이라고 하자.

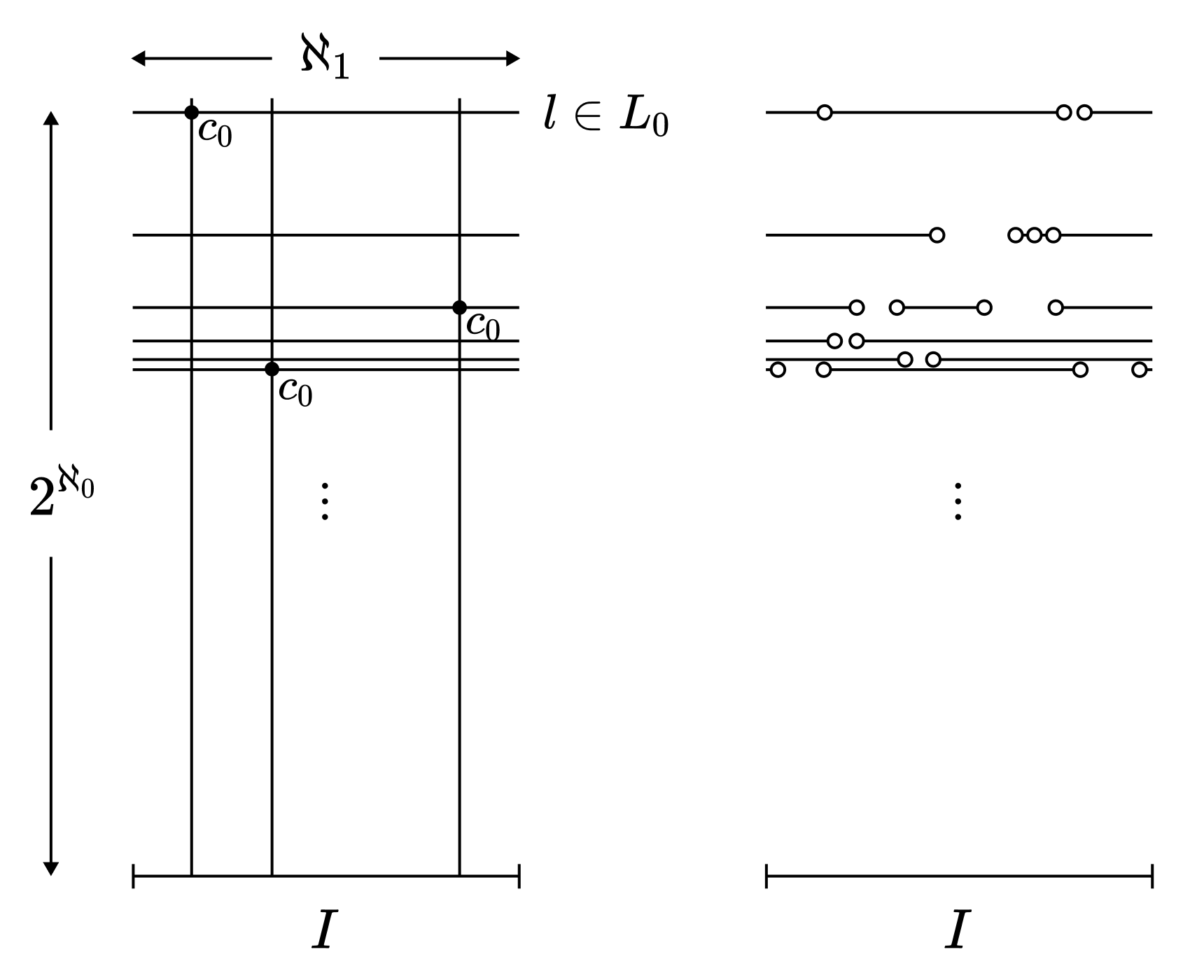
두 가지 경우가 가능하다. a) $L_1$의 직선들 중 $\aleph_1$개의 점들을 가지는 직선이 $2^{\aleph_0}$개이다. b) $L_1$의 직선들 중 $\aleph_1$개의 점들을 가지는 직선이 $\aleph_1$개 이하이다.

a의 경우, 다시 비둘기집의 원리에 의해 $c_1 \in \aleph_1(l)$을 만족하는 직선 $l \in L_1$의 개수가 $2^{\aleph_0}$인 색깔 $c_1$이 존재한다. 그러한 $L_1$의 직선들의 집합을 $L_1’$이라고 하자. 앞선 논의에 의해 $L_1’$에는 총 $\aleph_1$개의 $c_1$ 점들이 존재한다. 이 점들을 뺀 집합을 $L_2$라고 하자. 이같은 과정을 b가 될 때까지 반복한다. (색깔이 가산 개 있기 때문에 언젠가는 b에 도달함을 확인하라)

b가 되었을 때 $L_n$은 최대 $\aleph_1$개의 점들을 가진다. 그런데 $L$이 $L_n$이 되는 과정에서 빠진 점들의 개수는 $\aleph_1 \cdot \aleph_0 = \aleph_1$을 넘지 않는다. 한편 $L$은 $2^{\aleph_0}$개의 점들을 가지고 있었기 때문에, 이는 $\aleph_1 < 2^{\aleph_0}$에 모순된다. ■