Modal Logic

01 Apr 2025

This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.

Types

Name	Entailment	Axioms
K	Kripke model for possible worlds	$\Box(p \to q) \to (\Box p \to \Box q)$
T	Reflexivity	K + $\Box p \to p$
S4	Reflexivity + Transitivity	T + $\Box p \to \Box \Box p$
S4.2	Reflexivity + Transitivity + R-convergence	S4 + $\Diamond \Box p \to \Box \Diamond p$
S4.3	Reflexivity + Transitivity + R-linearity	S4 + $(\Diamond p \land \Diamond q) \to$ $(\Diamond (p \land \Diamond q) \lor \Diamond(\Diamond p \land q))$
S5	Reflexivity + Transitivity + Symmetry	S4 + $(p \to \Box \Diamond p)$

The logics become strictly stronger as one moves down the table.

Modal Reduction

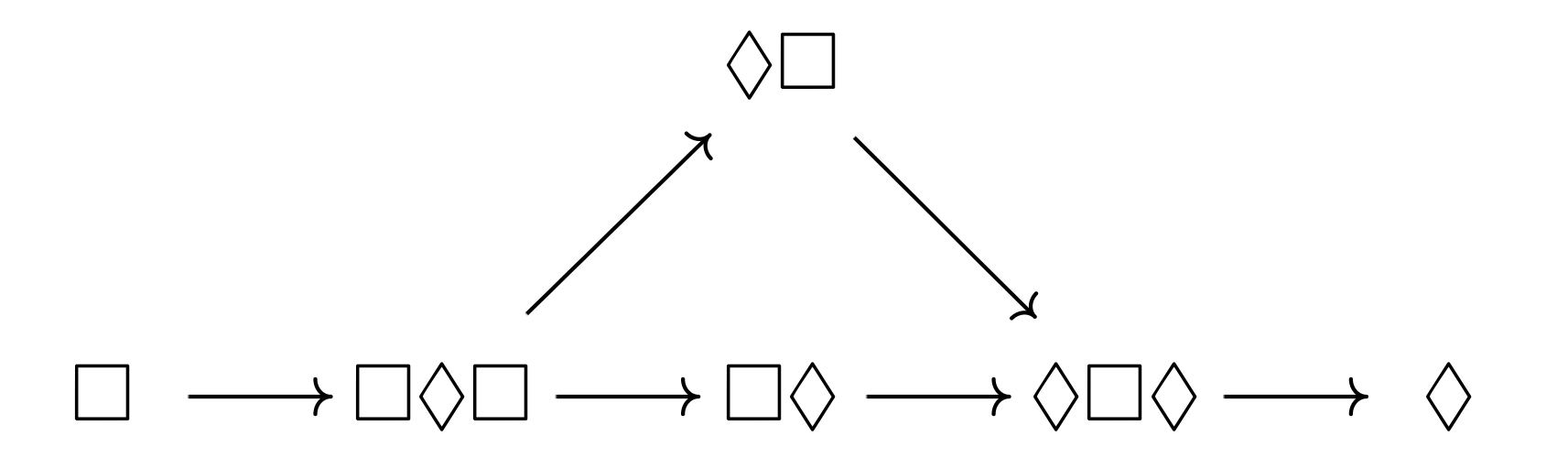
Theorem. In S4, any sequence of modal operators is equivalent to one of six combinations, and the entailment relations amongst these combinations are as follows:

Theorem. In S5, any sequence of modal operators is equivalent to either $\Box$ or $\Diamond$. Furthermore, every formula is equivalent to a flat formula—that is, a formula containing no modal operators within the scope of other modal operators.

Completeness Theorem

Theorem. K is complete.

Proof.

Lindenbaum’s Lemma. Any consistent theory can be extended to a maximally consistent theory.

The completeness statement is equivalent to “every consistent theory is satisfiable”, and applying Lindenbaum’s lemma, this is equivalent to “every maximally consistent theory is satisfiable”.

Let $u, v$ be maximally consistent theories. We write $u \lhd v$ when $\Box p \in u \implies p \in v$. The following can be shown without difficulty:

• When $u \lhd v$, we have $p \in v \implies \Diamond p \in u$
• For any maximally consistent theory $u$, if $p \in u$ and $\Box p \notin u$, then there exist maximally consistent theories $v, v’$ such that $p \in v, \lnot p \in v’$ and $u \lhd v, v’$.

From this, for a maximally consistent theory $u$, we can define the canonical Kripke model $\mathfrak{K} = (U, \prec, V)$ as follows:

• The collection of possible worlds $U$ is the collection of $v$ satisfying $u \lhd v$.
• The accessibility relation $\prec$ is $\lhd$.
• The valuation function $V(p, v)$ is true if and only if $p \in v$.

It can be shown without difficulty that $\mathfrak{K}$ satisfies $u$. ■