양상 논리
01 Apr 2025수학
논리학
종류
| 이름 | 함의 | 공리 |
|---|---|---|
| K | 가능세계에 대한 크립키 모델 | $\Box(p \to q) \to (\Box p \to \Box q)$ |
| T | 반사성 | K + $\Box p \to p$ |
| S4 | 반사성 + 추이성 | T + $\Box p \to \Box \Box p$ |
| S4.2 | 반사성 + 추이성 + R-수렴성 | S4 + $\Diamond \Box p \to \Box \Diamond p$ |
| S4.3 | 반사성 + 추이성 + R-선형성 | S4 + $(\Diamond p \land \Diamond q) \to$ $(\Diamond (p \land \Diamond q) \lor \Diamond(\Diamond p \land q))$ |
| S5 | 반사성 + 추이성 + 대칭성 | S4 + $(p \to \Box \Diamond p)$ |
표의 밑으로 갈수록 논리는 엄격히 강해진다.
양상의 축약
정리. S4에서 양상 연산자의 나열은 6개의 조합 중 하나와 동등하며, 각 조합의 함의 관계는 다음과 같다.
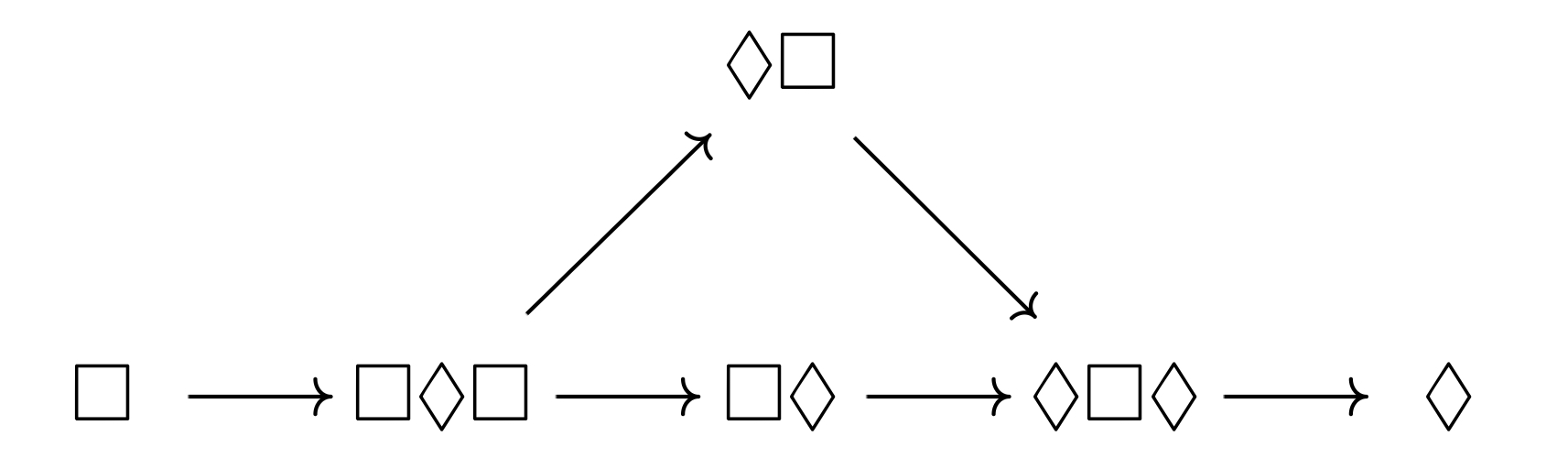
정리. S5에서 양상 연산자의 나열은 $\Box$ 또는 $\Diamond$와 동등하다. 나아가 모든 논리식은 평평한flat 논리식 — 즉, 양상 연산자 안에 양상 연산자가 있는 경우가 없는 논리식과 동치이다.
완전성 정리
정리. K는 완전하다.
증명.
린덴바움 보조정리. 임의의 무모순적인 이론은 극대적으로 무모순적인maximally consistent 이론으로 확장될 수 있다.
완전성 진술은 “무모순적인 이론은 만족 가능하다”와 동치이며, 여기에 린덴바움 보조정리를 적용하면 이는 “극대적으로 무모순적인 이론은 만족 가능하다”와 동치이다.
$u, v$가 극대적으로 무모순적인 이론이라고 하자. $\Box p \in u \implies p \in v$일 때 $u \lhd v$라고 적자. 다음을 어렵지 않게 보일 수 있다.
- $u \lhd v$일 때, $p \in v \implies \Diamond p \in u$
- 임의의 극대적으로 무모순적인 이론 $u$에 대해, $p \in u$이고 $\Box p \notin u$라면, 어떤 극대적으로 무모순적인 이론 $v, v’$가 존재하여 $p \in v, \lnot p \in v’$이고 $u \lhd v, v’$이다.
이로부터 극대적으로 무모순적인 이론 $u$에 대해, 표준적canonical 크립키 모델 $\mathfrak{K} = (U, \prec, V)$를 다음과 같이 정의할 수 있다.
- 가능세계들의 모임 $U$는 $u \lhd v$를 만족하는 $v$의 모임이다.
- 접근 관계 $\prec$은 $\lhd$이다.
- 평가 함수valuation function $V(p, v)$는 $p \in v$일 때, 그리고 오직 그 경우에만 참이다.
$\mathfrak{K}$가 $u$를 만족함을 어렵지 않게 보일 수 있다. ■