Yoneda Lemma

21 Mar 2025

This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.

Notation.

1. $-$ denotes a parameter placeholder. If two $-$ are used, it means there are two parameters. Which parameter corresponds to which position is determined by context.
2. $\bullet$ is a parameter that takes precedence over $-$. Therefore, $\hom(-, \bullet)$ is a functor that maps $A$ to the functor $\hom(-, A)$.
3. For functors $F, G$, we define $[F, G]$ as the collection of natural transformations from $F$ to $G$.
4. We assume all categories are locally small categories.

The Yoneda lemma is a theorem that tells us what a representable functor sees when it looks at another functor.

For example, for $A \in \mathcal{A}$, consider the representable functor $\hom_{\mathcal{A}}(-, A)$. This functor belongs to the category $[\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$. Therefore, what $\hom_{\mathcal{A}}(-, A)$ sees when it looks at a functor $F : \mathcal{A}^{\mathrm{op}} \to \mathbf{Set}$ is the following set of natural transformations:

\[[\hom_{\mathcal{A}}(-, A), F]\]

The above set is a set defined from $A \in \mathcal{A}$ and $F \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$. However, there is another natural way to define a set from $A, F$. Simply applying $F$ to $A$:

\[F(A)\]

According to the Yoneda lemma, the two sets are isomorphic. Moreover, they are not just isomorphic, but naturally isomorphic in $A \in \mathcal{A}$ and $F \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$. In short, the following two functors are isomorphic in $[\mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}], \mathbf{Set}]$:

\[\begin{aligned} \text{(i)} \quad \mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] &\xrightarrow{\hspace{0.15cm} \hom_{\mathcal{A}}(-, \cdot)^{\mathrm{op}} \times 1 \hspace{0.15cm}} [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] \\ &\xrightarrow{\hom_{[\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]}(-, -)} \mathbf{Set} \\\\ \text{(ii)} \quad \mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] &\xrightarrow{-(-)} \mathbf{Set} \end{aligned}\]

Remark. The $\mathrm{op}$ attached to $\hom_{\mathcal{A}}(-, \cdot)^{\mathrm{op}}$ is to adjust the domain of the functor to $\mathcal{A}^\mathrm{op}$, and is essentially the same as $\hom_{\mathcal{A}}(-, \cdot)$.

Proof. To outline the proof, we define $\hat{(\;\;)} : [\hom_\mathcal{A}(-, A), F] \to F(A)$ and $\tilde{(\;\;)}: F(A) \to [\hom_\mathcal{A}(-, A), F]$ as follows:

\[\hat{\alpha} = \alpha_A(1_A), \quad \tilde{x} = \theta\]

where $\theta$ is a natural transformation that maps $f : A’ \to A$ as follows:

\[\theta_{A'}: f \mapsto F(f^{\mathrm{op}})(x)\]

The reason for defining $\theta$ as above is to satisfy the following commutative diagram. (Verify by substituting $1_A$ for $(-)$.)

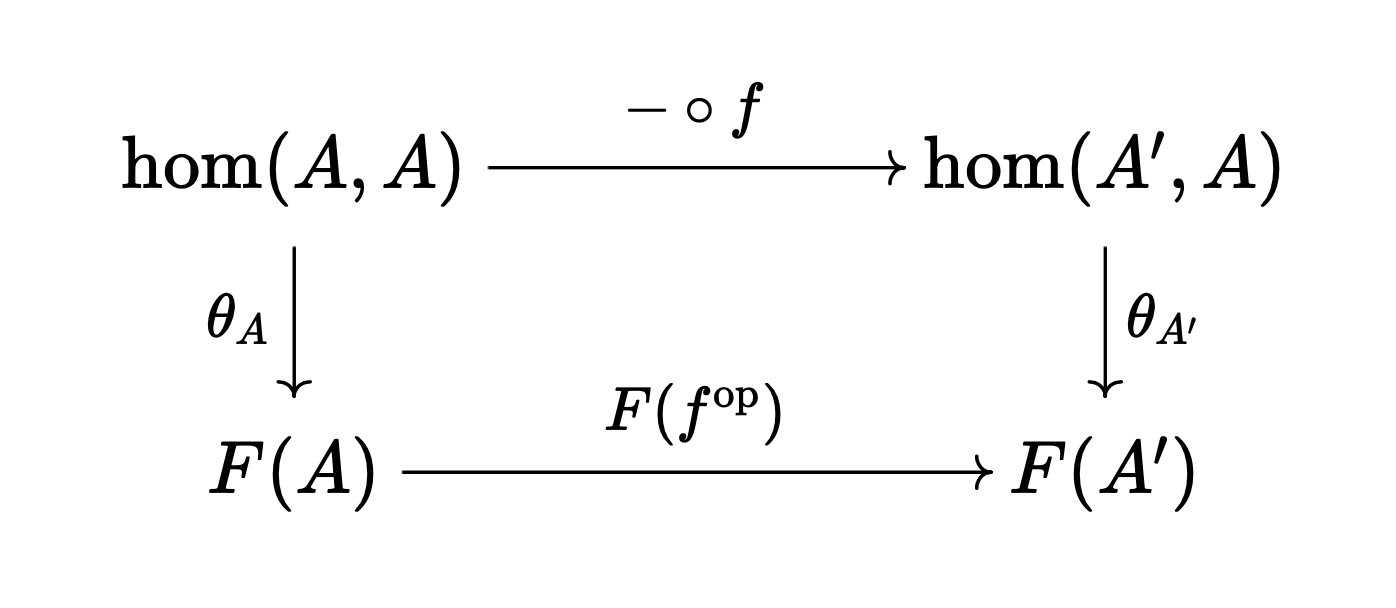
Now we must show that for any $A \in \mathcal{A}, F : \mathcal{A}^\mathrm{op} \to \mathbf{Set}$, the following holds:

• For any $\alpha \in [\hom_\mathcal{A}(-, A), F]$, we have $\tilde{\hat{\alpha}} = \alpha$.
• For any $x \in F(A)$, we have $\hat{\tilde{x}} = x$.

This shows that $[\hom_\mathcal{A}(-, A), F] \cong F(A)$. In addition, we must show that this isomorphism is natural. Upon careful consideration, this is equivalent to showing that for any $A, A’ \in \mathcal{A}$ and $F, G \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$ and $f: A’ \to A$ and $\alpha: F \Rightarrow G$, the following diagram commutes:

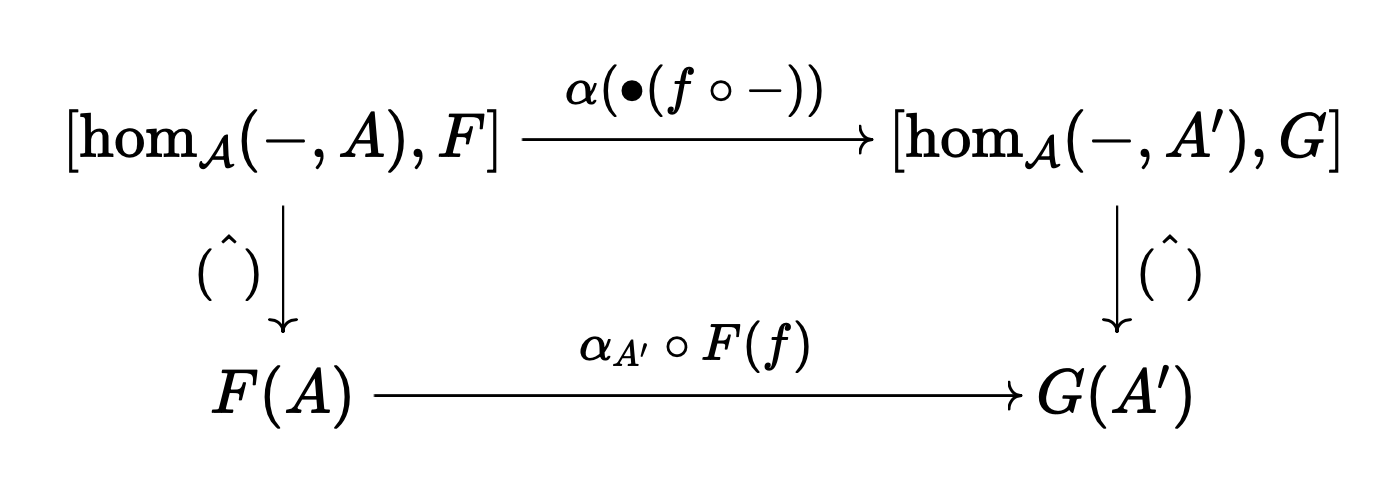
In terms of elements:

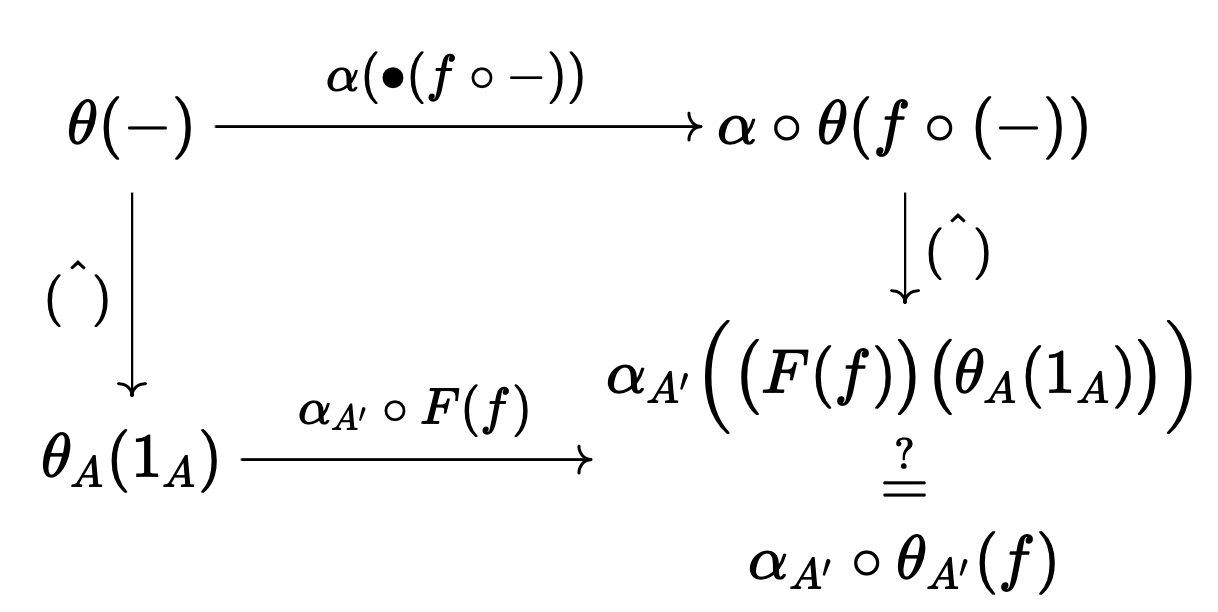
That the above holds follows from the naturality of $\theta$. ■

The Yoneda Corollary and Relational Ontology

Among the results implied by the Yoneda lemma, the following is particularly important. I shall simply call this the Yoneda corollary.

Yoneda Corollary. Let $X, Y \in \mathcal{A}$.

1. $[\hom(-, X), \hom(-, Y)] \cong \hom(X, Y)$
2. $X \cong Y \iff \hom(-, X) \cong \hom(-, Y)$

Proof. Let $F = \hom(-, Y)$. ■

In essence, in category theory, an object is nothing more than the collection of morphisms it receives. For instance, in the integer order category, $0$ can be defined as the initial object, and more generally, $n$ can be defined as the object that receives $n$ morphisms. The Yoneda corollary guarantees that this approach of defining objects through the morphisms they form with other objects is valid in all (strictly speaking, locally small) categories. I call this approach relational ontology.