요네다 보조정리

21 Mar 2025

Notation.

1. $-$는 매개변수의 자릿값이다. $-$가 두 개 쓰였으면 매개변수가 두 개라는 뜻이다. 어느 매개변수가 어느 자리에 해당하는지는 맥락으로 파악한다.
2. $\bullet$은 $-$를 우선하는 매개변수이다. 따라서 $\hom(-, \bullet)$은 $A$를 함자 $\hom(-, A)$에 대응시키는 함자이다.
3. 함자 $F, G$에 대해 $[F, G]$를 $F$에서 $G$로 가는 자연적 변환_{natural transformation}들의 모임으로 정의한다.
4. 모든 범주는 국소적으로 작은_{locally small} 범주라고 가정한다.

요네다 보조정리_{Yoneda lemma}는 표현가능함자_{representable}가 다른 함자를 바라볼 때 보이는 것이 무엇인지를 알려주는 정리이다.

예를 들어 $A \in \mathcal{A}$에 대해, 표현가능함자 $\hom_{\mathcal{A}}(-, A)$를 생각하자. 이 함자가 속하는 범주는 $[\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$이다. 따라서 $\hom_{\mathcal{A}}(-, A)$가 함자 $F : \mathcal{A}^{\mathrm{op}} \to \mathbf{Set}$를 바라볼 때 보이는 것은 다음 자연적 변환들의 집합이다.

\[[\hom_{\mathcal{A}}(-, A), F]\]

위 집합은 $A \in \mathcal{A}$와 $F \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$으로부터 정의된 집합이다. 그런데 $A, F$로부터 집합을 정의할 수 있는 또다른 자연스러운 방식이 있다. 단순히 $F$에 $A$를 취하는 것이다.

\[F(A)\]

요네다 보조정리에 따르면 두 집합은 동형_isomorphic이다. 게다가 그냥 동형인 것이 아니라, $A \in \mathcal{A}$와 $F \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$에서 자연스럽게 동형_{naturally isomorphic}이다. 요컨대 다음 두 함자가 $[\mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}], \mathbf{Set}]$에서 동형이다.

\[\begin{aligned} \text{(i)} \quad \mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] &\xrightarrow{\hspace{0.15cm} \hom_{\mathcal{A}}(-, \cdot)^{\mathrm{op}} \times 1 \hspace{0.15cm}} [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] \\ &\xrightarrow{\hom_{[\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]}(-, -)} \mathbf{Set} \\\\ \text{(ii)} \quad \mathcal{A}^{\mathrm{op}} \times [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}] &\xrightarrow{-(-)} \mathbf{Set} \end{aligned}\]

Remark. $\hom_{\mathcal{A}}(-, \cdot)^{\mathrm{op}}$에 붙은 $\mathrm{op}$는 함자의 정의역을 $\mathcal{A}^\mathrm{op}$로 맞춰주기 위함이고, 실질적으로는 $\hom_{\mathcal{A}}(-, \cdot)$와 같다.

증명. 증명의 개요만 적자면, $\hat{(\;\;)} : [\hom_\mathcal{A}(-, A), F] \to F(A)$와 $\tilde{(\;\;)}: F(A) \to [\hom_\mathcal{A}(-, A), F]$를 다음과 같이 정의한다.

\[\hat{\alpha} = \alpha_A(1_A), \quad \tilde{x} = \theta\]

여기서 $\theta$는 $f : A’ \to A$를 다음과 같이 사상하는 자연적 변환이다.

\[\theta_{A'}: f \mapsto F(f^{\mathrm{op}})(x)\]

$\theta$를 위와 같이 정의하는 이유는 다음 가환 도식을 만족하게끔 만들기 위함이다. ($(-)$에 $1_A$를 대입해 확인해 보라.)

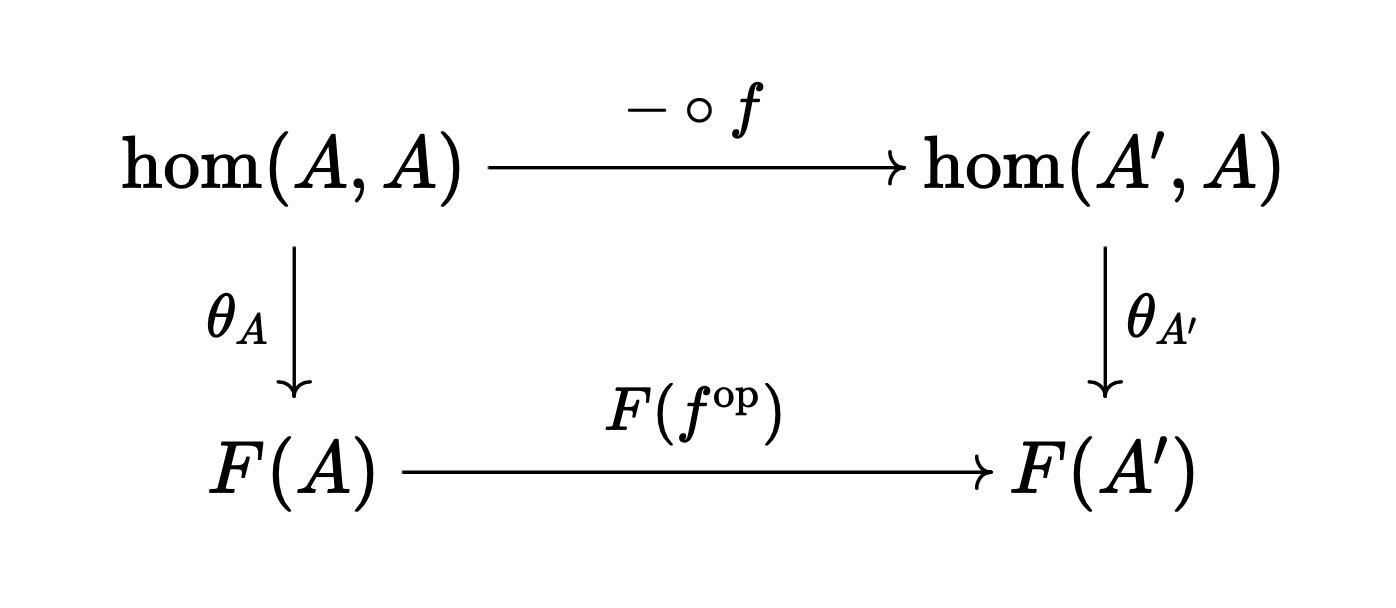
이제 임의의 $A \in \mathcal{A}, F : \mathcal{A}^\mathrm{op} \to \mathbf{Set}$에 대해 다음이 성립함을 보여아 한다.

• 임의의 $\alpha \in [\hom_\mathcal{A}(-, A), F]$에 대해 $\tilde{\hat{\alpha}} = \alpha$이다.
• 임의의 $x \in F(A)$에 대해 $\hat{\tilde{x}} = x$이다.

이것은 $[\hom_\mathcal{A}(-, A), F] \cong F(A)$임을 보인다. 여기에 더해, 해당 동형이 자연적임을 보여아 한다. 자아아알 생각해 보면 이것은 임의의 $A, A’ \in \mathcal{A}$와 $F, G \in [\mathcal{A}^{\mathrm{op}}, \mathbf{Set}]$와 $f: A’ \to A$와 $\alpha: F \Rightarrow G$에 대해 다음 도식이 가환임을 보이는 것과 같다.

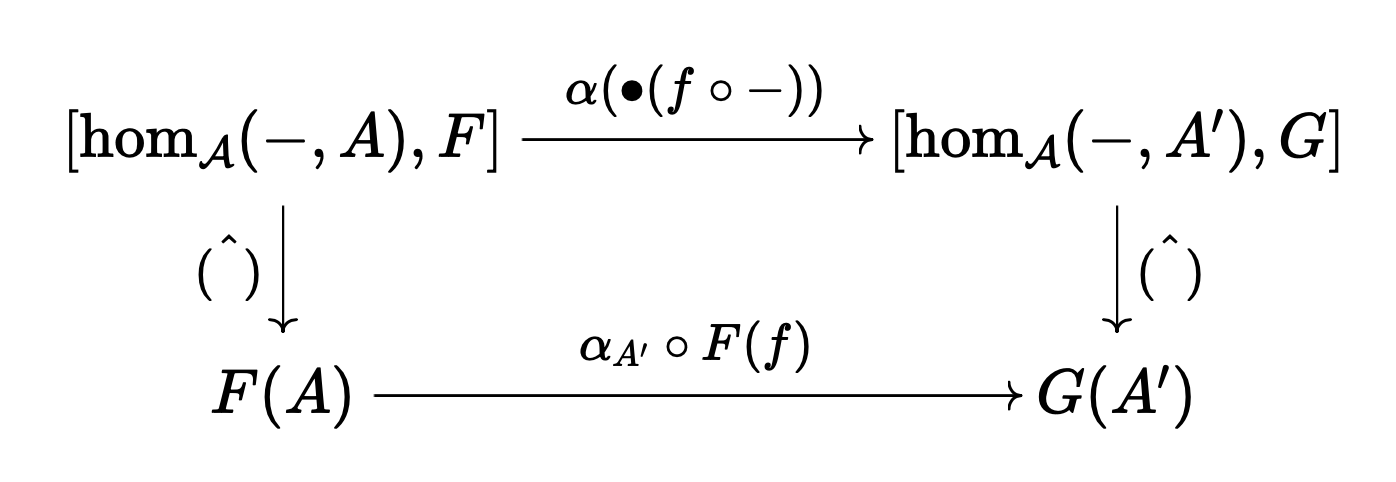
원소 단위로 적으면,

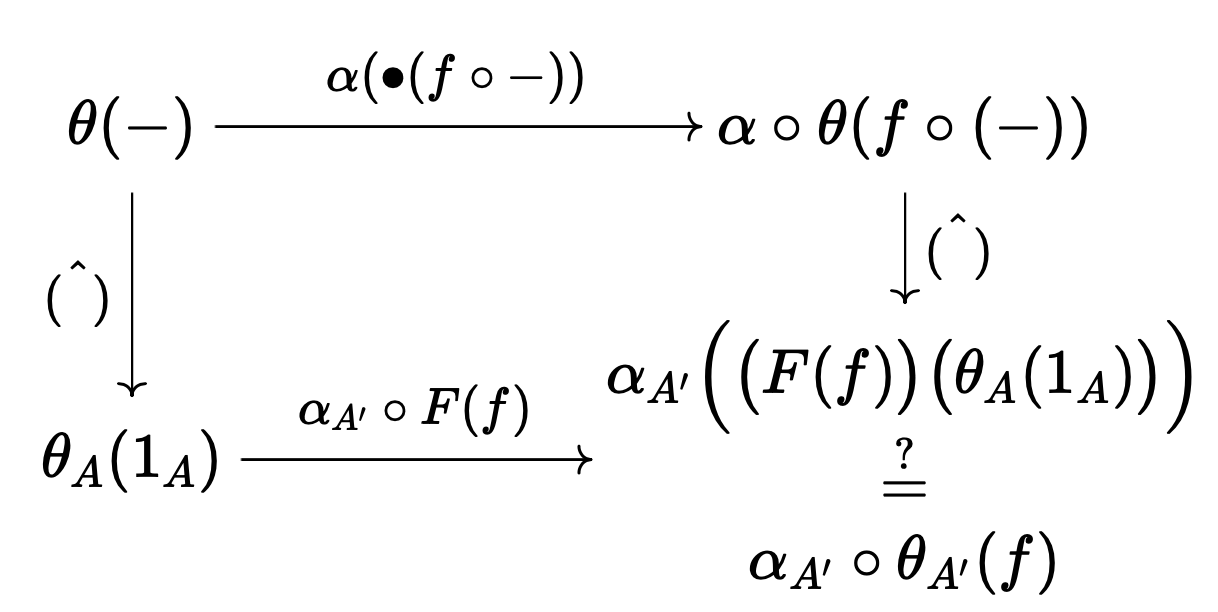
위가 성립함은 $\theta$의 자연성으로부터 따라 나온다. ■

요네다 따름정리와 관계론적 존재론

요네다 보조정리가 함의하는 결과 중 다음은 아주 중요하다. 필자는 이를 그냥 요네다 따름정리라고 부른다.

요네다 따름정리. $X, Y \in \mathcal{A}$라고 하자.

1. $[\hom(-, X), \hom(-, Y)] \cong \hom(X, Y)$
2. $X \cong Y \iff \hom(-, X) \cong \hom(-, Y)$

증명. $F = \hom(-, Y)$로 둔다. ■

요컨대 범주론에서 대상은, 그것이 받는 사상들의 집합과 다름없다. 일례로 정수 순서 범주에서 $0$은 초기 대상으로 정의할 수 있고, 더 일반적으로 $n$은 받는 사상들의 수가 $n$개인 대상으로 정의할 수 있다. 요네다 따름정리는 이처럼 대상을 그것이 다른 대상과 맺는 사상들로서 정의하는 접근이 모든(엄밀히는 국소적으로 작은) 범주에서 유효함을 보장한다. 필자는 이 접근을 관계론적 존재론이라고 부른다.