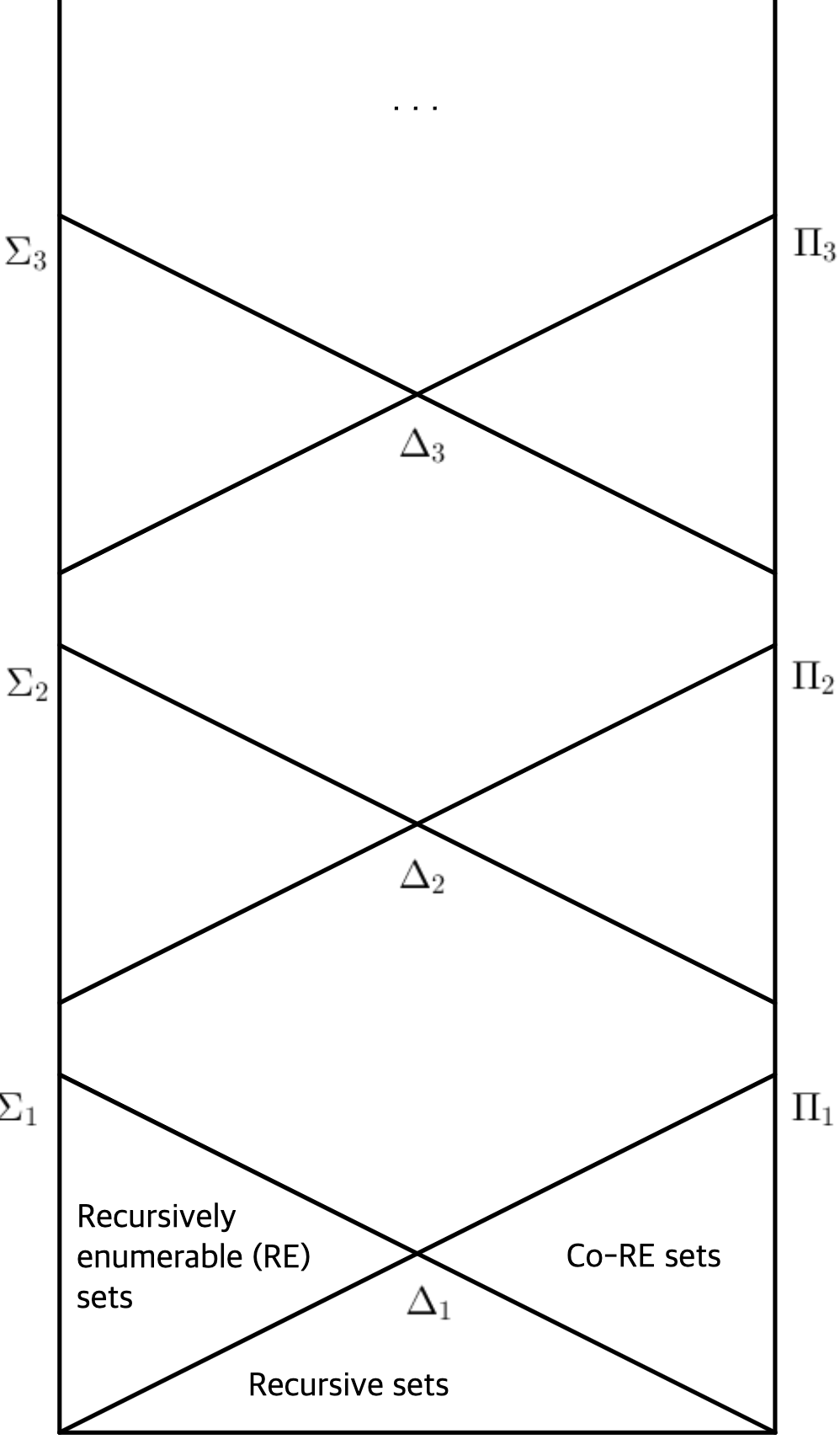
Arithmetic Hierarchy

This post was machine translated and has not yet been proofread. It may contain minor errors or unnatural expressions. Proofreading will be done in the near future.

Warning. This article was written informally and may therefore lack rigour or even contain incorrect content.

The arithmetic hierarchy is a classification of propositions in arithmetic — more precisely, first-order Peano arithmetic — according to the complexity of their quantifiers. The arithmetic hierarchy is a central concept in proof theory and computational complexity theory, and is also related to descriptive set theory.

1. $\Delta_0$ Propositions

1.1. Definition

Definition. $\Sigma_0 = \Pi_0 = \Delta_0$ is the set of propositions containing only bounded quantifiers.

Why the same class of propositions is referred to by three names will become clear shortly. In this article, unless there is a specific reason otherwise, we shall use $\Delta_0$ as the representative name among the three.

For example, the following four propositions are all $\Delta_0$.

$\phi_1$ is a false statement. $\phi_2$ is true when $x$ is even, and $\phi_3$ is true when $x$ is a divisor of $y$.

Since $\Delta_0$ propositions have bounded quantifiers, it is possible to determine whether an arbitrary $x$ satisfies the corresponding proposition using a Turing machine. For instance, a Turing machine that determines whether $x$ satisfies $\phi_2$ is as follows:

for y < x:
   if y + y == x:
      return true;

return false;

The above Turing machine halts within $x$ iterations. Therefore, $\Delta_0$ propositions are decidable, recursive, or computable (the three expressions are synonymous). However, as we shall explain in detail later, not all decidable propositions are $\Delta_0$.

According to Gödel’s representability theorem, decidable true propositions are provable. In this article, when we say that $\phi$ is ‘true’, we mean $\mathcal{N} \vDash \phi$ for the standard model of arithmetics $\mathcal{N}$, rather than $\mathsf{PA} \vDash \phi$.

The following holds:

Theorem. The set of true $\Delta_0$ sentences is complete. (That is, if $\phi$ is a true $\Delta_0$ sentence, then $\mathsf{PA} \vdash \phi$.)

1.2. $\Delta_0$ in Computational Theory

From a programming language perspective, $\Delta_0$ sentences correspond to the set of code that permits only the following:

• Conditional statements
• Bounded loops
• Addition and multiplication

It should be noted that unbounded loops and variable reassignment are not permitted. For example, the following code demonstrates that primality testing is $\Delta_0$:

for y < x:
  for z <= y:
    if yz == x:
      return false;

return true;

However, the following code that computes $x^y$ does not correspond to $\Delta_0$:

let a = 1
for 1<= z <= y:
   a = a * x

return a

So is exponentiation not $\Delta_0$? Not necessarily. Although complex, there are methods to express exponentiation with a $\Delta_0$ proposition. This case demonstrates that determining whether a given operation or predicate is $\Delta_0$ can be intricate. For instance, the following is known:

Theorem. Factorial is $\Delta_0$, but tetration is not $\Delta_0$.

However, tetration is decidable. Therefore, not all decidable propositions are $\Delta_0$.

2. Moving Up One Level

Definition.

\[\begin{gather} \Sigma_1 := \{ \exists x_1 \cdots \exists x_n \;\phi : \phi \in \Pi_0 \}\\ \Pi_1 := \{ \forall x_1 \cdots \forall x_n \;\phi : \phi \in \Sigma_0 \}\\ \Delta_1 := \Sigma_1 \cap \Pi_1 \end{gather}\]

2.1. $\Sigma_1$ Propositions

The following propositions are $\Sigma_1$:

$\phi_1$ is true in the set $\lbrace 1, 3, 7, 13, \ldots\rbrace $. $\phi_2$ is Goldbach’s conjecture; it is not known whether all $x$ satisfy this.

$\Sigma_1$ is the collection of recursively enumerable sets. That is, if $\phi \in \Sigma_1$, then there exists a Turing machine $M$ such that:

• If $\phi(c)$ is true, then $M$ is guaranteed to decide $\phi(c)$.
• If $\phi(c)$ is false, then $M$ is not guaranteed to decide $\phi(c)$.

For example, the following Turing machine shows that $\phi_2$ is recursively enumerable:

for y > 1:
   for z > 1:
      if isPrime(y) & isPrime(z) & x = y + z & isEven(x):
         return true;

return false;

Although there is a return false statement, since there is no break statement to exit the loop, return false is unreachable. That is, if $\phi_2(c)$ is true, the above Turing machine returns true, but if it is false, it falls into an infinite loop.

If $\phi \in \Sigma_1$ is a sentence that is true in the standard model of arithmetics, then $\mathsf{PA} \vdash \phi$. A proposition of the form $\phi : \exists x \; \psi(x)$ being true in the standard model of arithmetics means that $\psi(c)$ is true for some $c \in \mathbb{N}$, and since $\psi(c)$ is a true $\Pi_0$ sentence, it is provable. Therefore, the following holds:

Theorem. The set of true $\Sigma_1$ sentences is complete.

2.2. $\Sigma_1 \setminus \Delta_0$ Propositions

However, I have in fact been misleading the reader thus far. The propositions I listed earlier as examples of $\Sigma_1$ can actually be written as $\Delta_0$:

So what do propositions that strictly belong to $\Sigma_1$ look like? One answer can be found in the halting problem.

First, let $\mathrm{HaltsIn}(x, n)$ be a predicate that determines whether “the Turing machine with Gödel number $x$” produces an output within $n$ operations. This predicate can be easily defined from the Kleene predicate, and the Kleene predicate is known to be $\Sigma_0$. For example, if the Gödel number of a Turing machine that computes the square of 3 in 2 operations is $123$, then $\mathrm{HaltsIn}(123, 3)$ is true but $\mathrm{HaltsIn}(123, 1)$ is false.

Now consider the following proposition:

What this proposition states is that the Turing machine with Gödel number $x$ eventually halts. That is, the above proposition is equivalent to the halting problem. However, the halting problem is undecidable. Since we showed earlier that all $\Delta_0$ propositions are decidable, $\phi$ is a $\Sigma_1$ proposition that does not belong to $\Delta_0$.

As another example, consider the following proposition:

Here, $\mathrm{Proves}(x, y)$ is a predicate that is true when the Gödel number of “a proof of the sentence with Gödel number $x$” is $y$. That is, $\phi_2(x)$ is a predicate stating that the sentence with Gödel number $x$ is provable. However, this predicate is not decidable. If $\phi_2$ were decidable, then (under the assumption that PA is consistent) there would exist a proof in PA that $\phi_2(\ulcorner 0 = 1 \urcorner)$ is false, which would conflict with Gödel’s incompleteness theorem.

2.3. $\Pi_1$ Propositions

If $\Sigma_1$ propositions are the collection of recursively enumerable propositions, then $\Pi_1$ propositions are the collection of co-recursively enumerable propositions. That is, a $\Pi_1$ sentence is decidable if false, but not necessarily decidable if true. For example, the following two propositions are $\Pi_1$ sentences that are not $\Delta_0$:

Unlike the case of $\Sigma_1$, $\Pi_1$ is not complete. Since the negation of a $\Sigma_1$ sentence is $\Pi_1$, if $\Pi_1$ were also complete, then $\Sigma_1 = \Pi_1 =$ (collection of decidable propositions).

Theorem. The set of true $\Pi_1$ sentences is not complete.

2.4. $\Delta_1$ Propositions

$\Delta_1$ propositions belong to both $\Sigma_1$ and $\Pi_1$. Therefore, $\Delta_1$ is the collection of decidable propositions. The tetration we saw earlier is a $\Delta_1$ proposition that is not $\Delta_0$.

3. Moving Up Another Level

Definition.

\[\begin{gather} \Sigma_2 := \{ \exists x_1 \cdots \exists x_n \;\phi : \phi \in \Pi_1 \}\\ \Pi_2 := \{ \forall x_1 \cdots \forall x_n \;\phi : \phi \in \Sigma_1 \}\\ \Delta_2 := \Sigma_2 \cap \Pi_2 \end{gather}\]

I believe the pattern should now be clear. As an example of a $\Sigma_2$ proposition, consider the following:

Here, $\mathrm{DoesNotHaltOn}(x, y)$ is a predicate that is true if “the Turing machine with Gödel number $x$” does not halt when given input $y$. From the preceding discussion, it is not difficult to see that $\mathrm{DoesNotHaltOn}$ is $\Pi_1$.

Theorem. $\phi_5 \notin \Pi_1$

Proof. Suppose $\phi_5 \in \Pi_1$. Our goal is to show that this assumption implies “the set of true $\Pi_1$ sentences is complete”.

Let $\psi(x)$ be an arbitrary $\Delta_0$ proposition. Then $\theta : \forall x \;\psi(x)$ is a $\Pi_1$ sentence. Consider the following Turing machine $M$:

if ψ(x):
   return 1;

while True:

This Turing machine halts for value $x$ if $\psi(x)$ is true and does not halt if it is false. Therefore, $\theta$ being true is equivalent to $M$ halting for all $x$, which is equivalent to $\phi_5(\ulcorner M \urcorner)$ being false. By assumption, $\phi_5 \in \Pi_1$, so if $\phi_5(\ulcorner M \urcorner)$ is false, then $\mathsf{PA} \vdash \lnot \phi(\ulcorner M \urcorner)$. That is, $\mathsf{PA} \vdash \theta$, making all true $\Pi_1$ sentences provable. This is a contradiction. ■

Remark. Strictly speaking, one should show that the above proof is expressible within PA.

We said earlier that $\Sigma_1$ propositions are decidable when true, and $\Pi_1$ propositions are decidable when false. However, since $\Sigma_2$ sentences have mixed $\forall$ and $\exists$ quantifiers, there may be sentences that are undecidable both when true and when false.

3.1. Oracles

Definition. When $\mathcal{O}$ can obtain the result of problem $P$ in a single operation, we call $\mathcal{O}$ an oracle for $P$.

For example, an oracle for the halting problem is a truly divine entity that can determine whether a given Turing machine halts in a single operation.

Ascending the arithmetic hierarchy is equivalent to being given increasingly powerful oracles. We saw earlier the following as an example of a $\Sigma_1$ proposition:

However, if a halting problem oracle $\mathcal{O}$ were given, $\phi_1$ could be expressed simply as a $\Delta_0$ proposition:

Also, we saw earlier the following as an example of a $\Sigma_2$ proposition:

If a halting problem oracle $\mathcal{O}$ were given, $\phi_5$ could be expressed as a $\Sigma_1$ proposition:

Here, $x|_y$ is the Gödel number of the state where input $y$ is given to the Turing machine with Gödel number $x$. That is, $\Sigma_2$ propositions reduce to $\Sigma_1$ propositions when given an oracle for the halting problem. By similar principles, $\Pi_2$ and $\Delta_2$ propositions reduce to $\Pi_1$ and $\Delta_1$ propositions, respectively, when given an oracle for the halting problem.

Furthermore, we can define second-order oracles. A second-order halting problem oracle is a halting problem oracle for Turing machines that use halting problem oracles. For example, whilst $\mathcal{O}$ is limited to determining whether the following code halts:

for x > 0:
   for y > 0:
      for z > 0:
         for n > 2:
            if x^n + y^n == z^n:
               return True;
return False;

$\mathcal{O}^2$ can also determine whether the following code halts. The following code takes as input the Gödel number $x$ of an NP Turing machine, halts if there exists a P Turing machine whose output matches $x$, and does not halt if no such machine exists:

let x ∈ NP;
for y ∈ P:
   if !Halts(
      let z = 0
      while x(z) == y(z):
         z = z + 1
   ):
      return 1; // halts when x is an NP that belongs to P

In general, the following holds:

Theorem. Propositions in $\Pi_n$, $\Sigma_n$, $\Delta_n$ become propositions in $\Pi_{n-k}$, $\Sigma_{n-k}$, $\Delta_{n-k}$, respectively, when given a $k$-th order oracle.