산술 위계

07 Feb 2025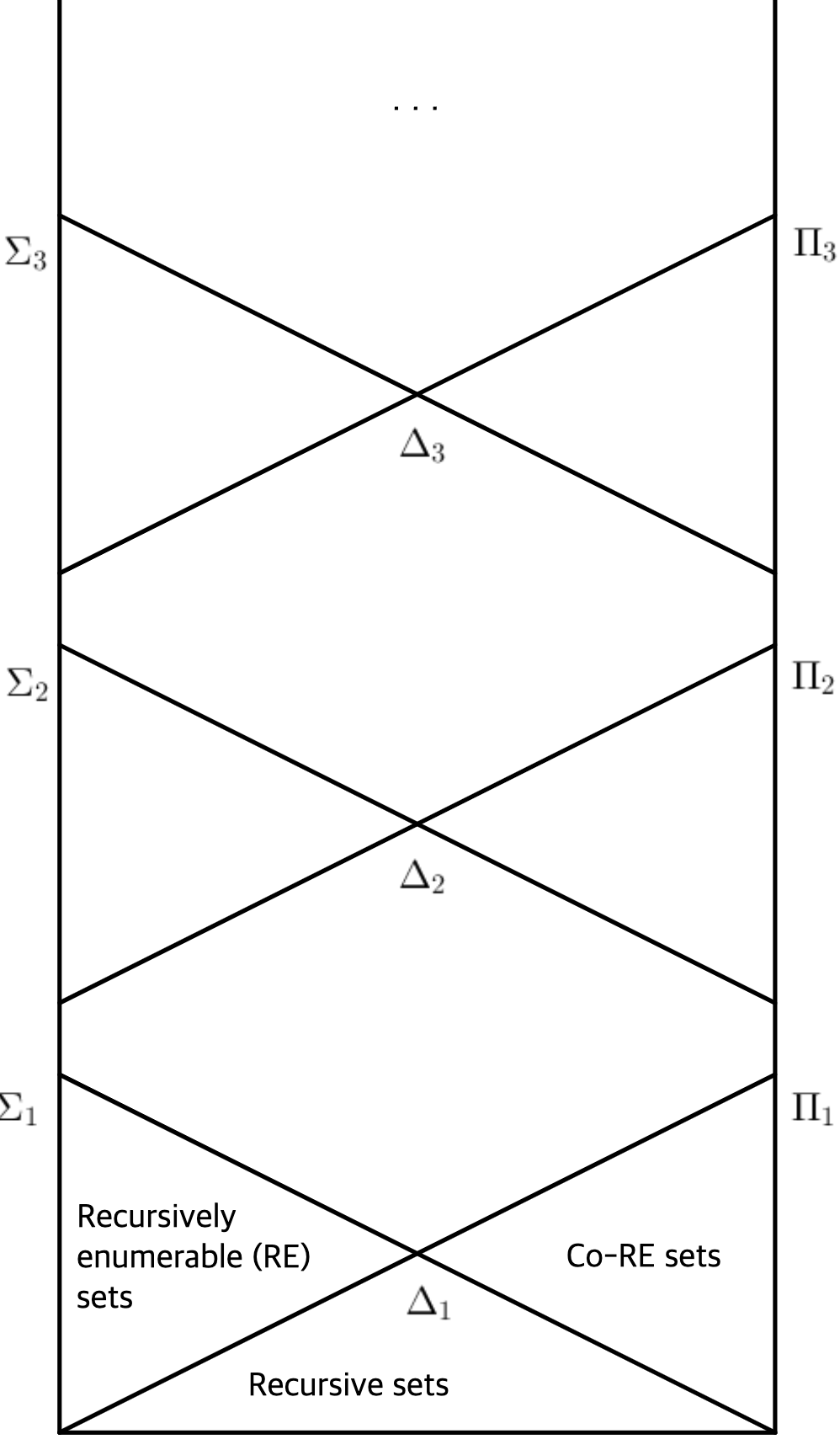

수학

논리학

주의. 이 글은 뇌피셜로 쓰였기 때문에 엄밀하지 않고, 심지어 틀린 내용이 있을 수 있습니다.

산술 위계(arithmetical hierarchy)는 산술 — 엄밀히는 1차 페아노 산술 — 의 명제들을 양화사의 복잡도에 따라 분류한 것이다. 산술 위계는 증명 이론 및 계산 복잡도 이론의 핵심 개념이며, 기술적 집합론과도 연관이 있다.

1. $\Delta_0$ 명제

1.1. 정의

정의. $\Sigma_0 = \Pi_0 = \Delta_0$는 상한이 있는 양화사만을 가지는 명제들의 집합이다.

왜 같은 부류의 명제를 세 개의 이름으로 부르는지는 곧 명확해질 것이다. 이 글에서는 특별한 이유가 없을 때에는 세 이름 중 $\Delta_0$라는 이름을 대표로 사용하겠다.

예를 들어 다음 네 명제들은 모두 $\Delta_0$ 명제들이다.

\[\begin{gather} \phi_1 : 0 = 1\\ \phi_2(x) : \exists y < x \; [y + y = x] \\ \phi_3(x, y) : \exists z \leq y \;[ xz = y ] \\ \end{gather}\]

$\phi_1$은 거짓인 문장이다. $\phi_2$는 $x$가 짝수일 때, $\phi_3$는 $x$가 $y$의 약수일 때 참인 명제이다.

$\Delta_0$ 명제들은 양화사에 상한이 걸려 있기 때문에, 임의의 $x$가 주어졌을 때 $x$가 해당 명제에 부합하는지를 튜링 기계로 판단할 수 있다. 예를 들어 $x$가 $\phi_2$를 만족하는지 판단하는 튜링 기계는 다음과 같다.

for y < x:
   if y + y == x:
      return true;

return false;

위 튜링 기계는 $x$번의 반복 이내에 정지한다. 따라서 $\Delta_0$는 또는 튜링 기계 등의 기계 장치로 결정 가능(decidable)한, 또는 재귀적인(recursive), 또는 계산 가능(computable)한 명제들이다(세 표현은 동의어이다). 그러나 뒤에서 자세히 설명하듯이, 모든 결정 가능한 명제들이 $\Delta_0$인 것은 아니다.

괴델의 표현가능성 정리에 따라 결정 가능한 참인 명제는 증명 가능하다. 그리고 이 글에서 $\phi$가 ‘참’이라 함은, $\mathsf{PA} \vDash \phi$가 아니라, 표준 자연수 모형 $\mathcal{N}$에 대해 $\mathcal{N} \vDash \phi$라는 의미이다. 다시 말해, 다음이 성립한다.

정리. 참인 $\Delta_0$ 문장들의 집합은 완전하다. (즉, $\phi$가 참인 $\Delta_0$ 문장이라면 $\mathsf{PA} \vdash \phi$이다.)

1.2. 계산 이론에서의 $\Delta_0$

프로그래밍 언어의 관점에서 보았을 때 $\Delta_0$ 문장들은 다음만을 허용하는 코드의 집합과 대응된다.

조건문
상한이 있는 반복문
덧셈과 곱셈

주의할 점은, 상한이 없는 반복문과 변수 재지정은 허용되지 않는다는 것이다. 예를 들어 다음의 코드는 소수 판별이 $\Delta_0$임을 입증한다.

for y < x:
  for z <= y:
    if yz == x:
      return false;

return true;

그러나 $x^y$를 계산하는 다음의 코드는 $\Delta_0$에 해당되지 않는다.

let a = 1
for 1<= z <= y:
   a = a * x

return a

그렇다면 지수 연산은 $\Delta_0$가 아닌 것일까? 그렇지는 않다. 복잡하긴 하지만, $\Delta_0$ 명제로 지수를 표현하는 방법이 있다. 이 사례는 주어진 연산 또는 술어가 $\Delta_0$인지 판단하는 일이 까다로울 수 있음을 방증한다. 일례로 다음이 알려져 있다.

정리. 팩토리얼은 $\Delta_0$이지만 테트레이션은 $\Delta_0$가 아니다.

그러나 테트레이션은 결정 가능하다. 따라서 모든 결정 가능한 명제들이 $\Delta_0$인 것은 아니다.

2. 한 단계 올라가기

정의.
\[\begin{gather} \Sigma_1 := \{ \exists x_1 \cdots \exists x_n \;\phi : \phi \in \Pi_0 \}\\ \Pi_1 := \{ \forall x_1 \cdots \forall x_n \;\phi : \phi \in \Sigma_0 \}\\ \Delta_1 := \Sigma_1 \cap \Pi_1 \end{gather}\]

2.1. $\Sigma_1$ 명제

다음 명제들은 $\Sigma_1$이다.

\[\begin{gather} \phi_1(x): \exists y \; \underbrace{[y^2 + y + 1 = x]}_{\Pi_0}\\ \phi_2(x): ∃y\; ∃z\; \underbrace{(y \text{ is prime} ∧ z \text{ is prime} ∧ x = y + z ∧ x \text{ is even})}_{\Pi_0} \end{gather}\]

$\phi_1$은 집합 $\lbrace 1, 3, 7, 13, \dots \rbrace$에서 참이다. $\phi_2$는 골드바흐의 추측으로, 모든 $x$가 이를 만족하는지는 알려져 있지 않다.

$\Sigma_1$은 재귀적으로 열거 가능(recursively enumerable)한 집합들의 모임이다. 즉, $\phi \in \Sigma_1$이라면 다음의 튜링 기계 $M$이 존재한다.

$\phi(c)$가 참이라면 $M$이 $\phi(c)$를 결정함이 보장된다.
$\phi(c)$가 거짓이라면 $M$이 $\phi(c)$를 결정함이 보장되지 않는다.

예를 들어 다음의 튜링 기계는 $\phi_2$가 재귀적으로 열거 가능함을 보여준다.

for y > 1:
   for z > 1:
      if isPrime(y) & isPrime(z) & x = y + z & isEven(x):
         return true;

return false;

return false 문이 있기는 하지만, 반복문에서 빠져나올 break 문이 없으므로 return false는 도달 불가능하다. 즉, $\phi_2(c)$가 참이라면 위의 튜링 기계는 참을 반환하지만 거짓이라면 무한 루프에 빠진다.

$\phi \in \Sigma_1$이 표준 자연수 모형에서 참인 문장이라면 $\mathsf{PA} \vdash \phi$이다. $\phi : \exists x \; \psi(x)$ 꼴의 명제가 표준 자연수 모형에서 참이라는 것은 어떤 $c \in \mathbb{N}$에 대해 $\psi(c)$가 참이라는 의미이며, $\psi(c)$는 참인 $\Pi_0$ 문장이므로 증명 가능하기 때문이다. 따라서 다음이 성립한다.

정리. 참인 $\Sigma_1$ 문장들의 집합은 완전하다.

2.2. $\Sigma_1 \setminus \Delta_0$ 명제

그런데 사실 지금까지 필자는 독자를 오도했다. 앞서 $\Sigma_1$의 예시로 나열한 명제들은 사실 $\Delta_0$로 쓸 수 있기 때문이다.

\[\begin{gather} \phi_1: \exists y<x \;{[y^2 + y + 1 = x]}\\ \phi_2(x): ∃y<x\; ∃z<x\; {(y \text{ is prime} ∧ z \text{ is prime} ∧ x = y + z ∧ x \text{ is even})} \end{gather}\]

그렇다면 $\Delta_0$에 속하지 않는 $\Sigma_1$ 명제는 어떻게 생겼을까? 한 가지 답은 정지 문제에서 찾을 수 있다.

먼저 $\mathrm{HaltsIn}(x, n)$를, “괴델 수가 $x$인 튜링 기계”가 $n$회의 연산 이내에 출력값을 내놓는지를 판별하는 술어라고 하자. 이 술어는 클레이니 술어로부터 쉽게 정의할 수 있으며, 클레이니 술어는 $\Sigma_0$임이 알려져 있다. 예를 들어 3의 제곱을 2회의 연산으로 계산하는 튜링 기계의 괴델 수가 $123$이라면 $\mathrm{HaltsIn}(123, 3)$은 참이지만 $\mathrm{HaltsIn}(123, 1)$는 거짓이다.

이제 다음 명제를 고려하자.

\[\phi_1(x): \exists y \;[ \mathrm{HaltsIn}(x, y) ]\]

위 명제가 말하는 바는, 괴델 수가 $x$인 튜링 기계가 언젠가 정지한다는 것이다. 즉, 위 명제는 정지 문제와 동치이다. 그런데 정지 문제는 결정 불가능하다. 앞서 $\Delta_0$ 명제는 모두 결정 가능함을 보았으므로, $\phi$는 $\Delta_0$에 속하지 않는 $\Sigma_1$ 명제이다.

다른 예시로, 다음 명제를 고려하자.

\[\phi_2(x): \exists y \; [ \mathrm{Proves}(x, y) ]\]

여기서 $\mathrm{Proves}(x, y)$는 “괴델 수가 $x$인 문장의 증명”의 괴델 수가 $y$일 때 참인 술어이다. 즉, $\phi_2(x)$는 괴델 수가 $x$인 문장이 증명 가능하다는 술어이다. 그런데 이 술어는 결정 가능하지 않다. 만약 $\phi_2$가 결정 가능하다면 (PA가 무모순적이라는 가정 하에) $\phi_2(\ulcorner 0 = 1 \urcorner)$이 거짓이라는 증명이 PA에 존재하게 되어 괴델의 불완전성 정리와 상충하기 때문이다.

2.3. $\Pi_1$ 명제

$\Sigma_1$ 명제가 재귀적으로 열거 가능한 명제들의 모임이라면, $\Pi_1$ 명제는 쌍대-재귀적으로 열거 가능한(co-recursively enumerable) 명제들의 모임이다. 즉 $\Pi_1$의 문장은 거짓이라면 결정 가능하지만 참이라면 결정 가능성이 보장되지 않는다. 예를 들어 다음 두 명제는 $\Delta_0$가 아닌 $\Pi_1$ 문장이다.

\[\begin{gather} \phi_3(x): \forall y \;[ \lnot \mathrm{HaltsIn}(x, y) ] \\ \phi_4(x): \forall y \; [ \lnot \mathrm{Proves}(x, y) ] \end{gather}\]

$\Sigma_1$의 경우와 달리, $\Pi_1$은 완전하지 않다. $\Sigma_1$ 문장의 부정이 $\Pi_1$이기 때문에, $\Pi_1$ 또한 완전하다면 $\Sigma_1 = \Pi_1=$ (결정 가능한 명제들의 모임)이 되기 때문이다.

정리. 참인 $\Pi_1$ 문장들의 집합은 완전하지 않다.

2.4. $\Delta_1$ 명제

$\Delta_1$ 명제는 $\Sigma_1$과 $\Pi_1$에 모두 속한다. 따라서 $\Delta_1$은 결정 가능한 명제들의 모임이다. 앞서 본 테트레이션은 $\Delta_0$가 아닌 $\Delta_1$ 명제이다.

3. 한 단계 더 올라가기

정의.
\[\begin{gather} \Sigma_2 := \{ \exists x_1 \cdots \exists x_n \;\phi : \phi \in \Pi_1 \}\\ \Pi_2 := \{ \forall x_1 \cdots \forall x_n \;\phi : \phi \in \Sigma_1 \}\\ \Delta_2 := \Sigma_2 \cap \Pi_2 \end{gather}\]

이제 패턴이 보일 거라 생각한다. $\Sigma_2$ 명제의 예시로, 다음을 보자.

\[\phi_5(x) : \exists y \; [ \mathrm{DoesNotHaltOn}(x, y)]\]

여기서 $\mathrm{DoesNotHaltOn}(x, y)$는, “괴델 수가 $x$인 튜링 기계”에 $y$를 입력했을 때 정지하지 않으면 참인 술어이다. 앞선 논의로부터 $\mathrm{DoesNotHaltOn}$이 $\Pi_1$임을 어렵지 않게 알 수 있다.

정리. $\phi_5 \notin \Pi_1$

증명. $\phi_5 \in \Pi_1$이라고 가정하자. 우리의 목표는 이 가정이 “참인 $\Pi_1$ 문장들의 집합은 완전하다”를 시사함을 보이는 것이다.

$\psi(x)$가 임의의 $\Delta_0$ 명제라고 하자. $\theta : \forall x \;\psi(x)$는 $\Pi_1$ 문장이다. 다음의 튜링 기계 $M$을 생각하자.

if ψ(x):
   return 1;

while True:

이 튜링 기계는 값 $x$에 대해 $\psi(x)$가 참이면 정지하고 거짓이면 정지하지 않는다. 따라서 $\theta$가 참이라는 것은 모든 $x$에 대해 $M$이 정지한다는 것과 동치이며, 이것은 $\phi_5(\ulcorner M \urcorner)$이 거짓임과 동치이다. 그리고 가정에 의해 $\phi_5 \in \Pi_1$이므로, $\phi_5(\ulcorner M \urcorner)$이 거짓이라면 $\mathsf{PA} \vdash \lnot \phi(\ulcorner M \urcorner)$이다. 즉, $\mathsf{PA} \vdash \theta$가 되어 모든 참인 $\Pi_1$ 문장은 증명 가능하게 된다. 이것은 모순이다. ■

Remark. 엄밀히는 위의 증명이 PA 내에서 표현 가능함을 보여야 한다.

앞서 $\Sigma_1$ 명제는 참일 때 결정 가능하고, $\Pi_1$ 명제는 거짓일 때 결정 가능하다고 했다. 그런데 $\Sigma_2$ 문장은 $\forall$과 $\exists$가 섞여 있기 때문에, 참일 때에도, 거짓일 때에도 결정이 불가능한 문장이 있을 수 있다.

3.1. 오라클

정의. $\mathcal{O}$가 단 한 번의 연산으로 문제 $P$의 결과를 구할 수 있을 때 $\mathcal{O}$을 $P$의 오라클이라고 한다.

예를 들어 정지 문제의 오라클은 주어진 튜링 기계의 정지 연부를 단 한 번의 연산으로 알아낼 수 있는, 그야말로 신적인 존재다.

산술 위계를 오르는 것은 점점 더 강한 오라클이 주어지는 것과 같다. 앞서 $\Sigma_1$ 명제의 예시로 다음을 보았다.

\[\phi_1(x): \exists y \;[ \mathrm{HaltsIn}(x, y) ]\]

그런데 만약 정지 문제 오라클 $\mathcal{O}$가 주어졌다면, $\phi_1$은 $\Delta_0$ 명제로 단순하게 표현 가능하다.

\[\phi_1(x) : \mathcal{O}(x)\]

또한 앞서 $\Sigma_2$ 명제의 예시로 다음을 보았다.

\[\phi_5(x) : \exists y \; [ \mathrm{DoesNotHaltOn}(x, y)]\]

정지 문제 오라클 $\mathcal{O}$가 주어졌다면, $\phi_5$는 $\Sigma_1$ 명제로 표현 가능하다.

\[\phi_5(x): \exists y \; \lnot \mathcal{O}(x|_y)\]

여기서 $x|_y$는 괴델 수가 $x$인 튜링 기계에 $y$를 입력한 상태의 괴델 수이다. 즉, $\Sigma_2$ 명제는 정지 문제의 오라클이 주어졌을 때 $\Sigma_1$ 명제로 환원된다. 비슷한 원리로, $\Pi_2$ 명제와 $\Delta_2$ 명제는 각각 정지 문제의 오라클이 주어졌을 때 $\Pi_1$ 명제와 $\Delta_1$ 명제로 환원된다.

나아가 2차 오라클을 정의할 수 있다. 2차 정지 문제 오라클은, 정지 문제 오라클을 사용하는 튜링 기계들에 대한 정지 문제 오라클이다. 예를 들어 $\mathcal{O}$가 다음 코드의 정지 여부를 판단하는 데 그치는 데 반해,

for x > 0:
   for y > 0:
      for z > 0:
         for n > 2:
            if x^n + y^n == z^n:
               return True;
return False;

$\mathcal{O}^2$은 다음 코드의 정지 여부를 판단할 수도 있다. 다음의 코드는 NP 튜링 기계의 괴델 수 $x$를 입력받았을 때, $x$와 출력이 일치하는 P 튜링 기계가 존재하면 정지하고 존재하지 않으면 정지하지 않는다.

let x ∈ NP;
for y ∈ P:
   if !Halts(
      let z = 0
      while x(z) == y(z):
         z = z + 1
   ):
      return 1; // x가 P에 속하는 NP일 때 정지

일반적으로 다음이 성립한다.

정리. $\Pi_n, \Sigma_n, \Delta_n$의 명제들은 $k$차 오라클이 주어졌을 때 각각 $\Pi_{n - k}, \Sigma_{n - k}, \Delta_{n - k}$의 명제들이 된다.

디멘의 블로그 이데아를 여행하는 히치하이커