벨의 우주선 사고실험: 수동적 로렌츠 수축과 능동적 로렌츠 수축

17 Nov 2024

우주선 A, B가 가느다란 실로 연결된 채 관성 상태에 있다가 동시에 같은 가속도로 광속에 가깝게 운동하기 시작한다. A와 B를 연결하는 실은 어떻게 되는가?

1. 끊어진다.
2. 느슨해진다.
3. 변화가 없다.

이 문제는 드원과 베란이 1959년에 처음 고안했으나 1976년에 벨¹이 CERN의 물리학자들과 나눈 토론을 통해 유명해졌다. 벨은 로렌츠 수축을 근거로 실이 끊어진다고 주장했으나 CERN의 물리학자들 대다수는 실에 변화가 없다고 반박했으며, 한 저명한 물리학자는 벨이 상대론을 오도하고 있다고까지 말했다. 그렇다면 정답은 과연 무엇일까?

정답은 1. 끊어진다 이다.

이 답은 일면 비직관적이다. 로렌츠 수축은 관성계에 의존적인 현상이기 때문이다. 일례로 철수에 대해 영희가 광속에 가깝게 움직인다면 영희는 수축한다. 하지만 동 상황에서 영희의 관성계를 기준으로는 철수가 광속에 가깝게 움직이므로 철수가 수축한다. 이같은 대칭성은 로렌츠 수축이 실재하는 물리적 현상이 아닌 관성계의 선택에 따른 수학적 현상임을 시사한다. 이같은 로렌츠 수축의 해석은 Rindler 1977의 글에서 볼 수 있듯이 물리학계에서 널리 퍼져있다.

로렌츠에 따르면 수축의 원인은 원자 구조를 밀집시키는 전기적 응집력이 [물체가 에테르를 통과함에 따라] 증가하는 데 있다… [하지만] 상대론에서 로렌츠 수축은 본질적으로 기하학적 투영 효과로서, 정지해 있는 막대기를 비스듬한 시선으로 보는 것과 유사하다.

In relativity the effect is essentially a geometric “projection” effect, quite analogous to looking at a stationary rod which is not parallel to the plane of the retina.²

그러나 Rindler의 설명은 반만 맞고 반은 틀렸다. 그 이유는 로렌츠 수축에 두 가지 유형이 있기 때문이다. 수동적 로렌츠 변환(passive Lorentz transformation)의 경우에는 Rindler의 주장대로 로렌츠 수축이 관성계의 선택에 따른 부수 현상에 불과하지만, 능동적 로렌츠 변환(active Lorentz transformation)의 경우에는 로렌츠 수축이 전기력의 증가와 같은 실질적 물리 현상을 야기한다. 본 글에서는 두 변환의 차이가 무엇인지, 그리고 어떻게 능동적 로렌츠 변환은 전기력과 연관되는지 살펴볼 것이다.

본론에 들어가기 앞서 해당 글의 내용은 Maudlin의 ⟪Philosophy of Physics: Space and Time⟫을 참고하여 작성되었음을 밝힌다.

1. 수동적 변환

점입자 A가 빈 공간에서 관성 운동한다. A에 대해 정지해 있는 관성좌표계 $(x, t)$를 기준으로 민코프스키 다이어그램을 그리면 해당 상황은 (가)와 같이 표현할 수 있다. 반면 $(x, t)$에 대해 $0.6c$의 속도를 가지는 관성좌표계 $(x’, t’)$을 기준으로 하는 민코프스키 다이어그램은 (나) 및 (나’)와 같다.³

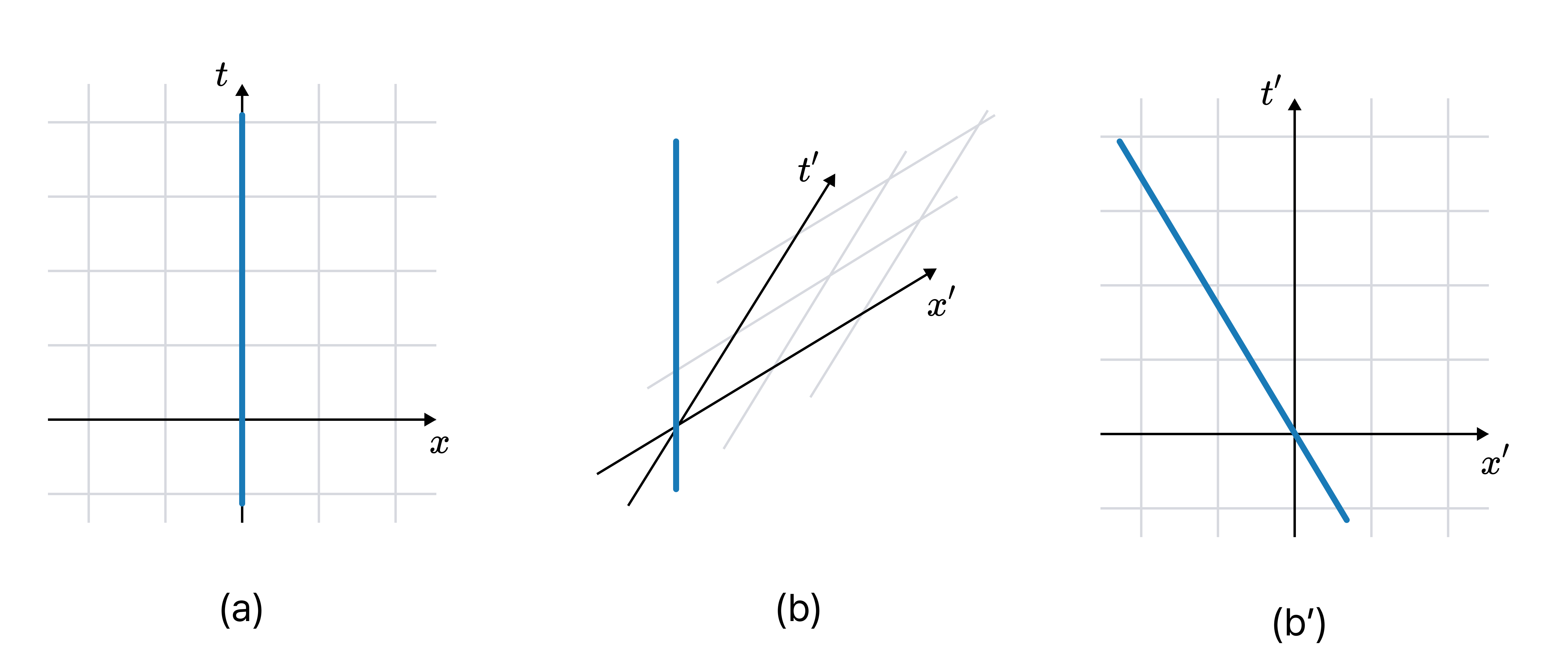
A의 운동에 좌표를 부여하는 방식은 다르지만 (가)와 (나)는 동일한 물리적 상황을 표현한다. 이와 같이 계의 물리적 속성을 보존하는 관성좌표계의 변환을 수동적 변환이라고 한다. 뉴턴 역학에서 시공간의 수동적 변환은 전단 변환shear transformation으로 주어지지만 잘 알려져 있듯이 상대론에서는 로렌츠 변환으로 주어진다.

2. 능동적 변환

이제 A의 속도에 순간적으로 $-0.6c$가 더해진 상황을 생각해 보자. $(x, t)$에 대해 속도가 더해진 후의 다이어그램은 (다)와 같다.

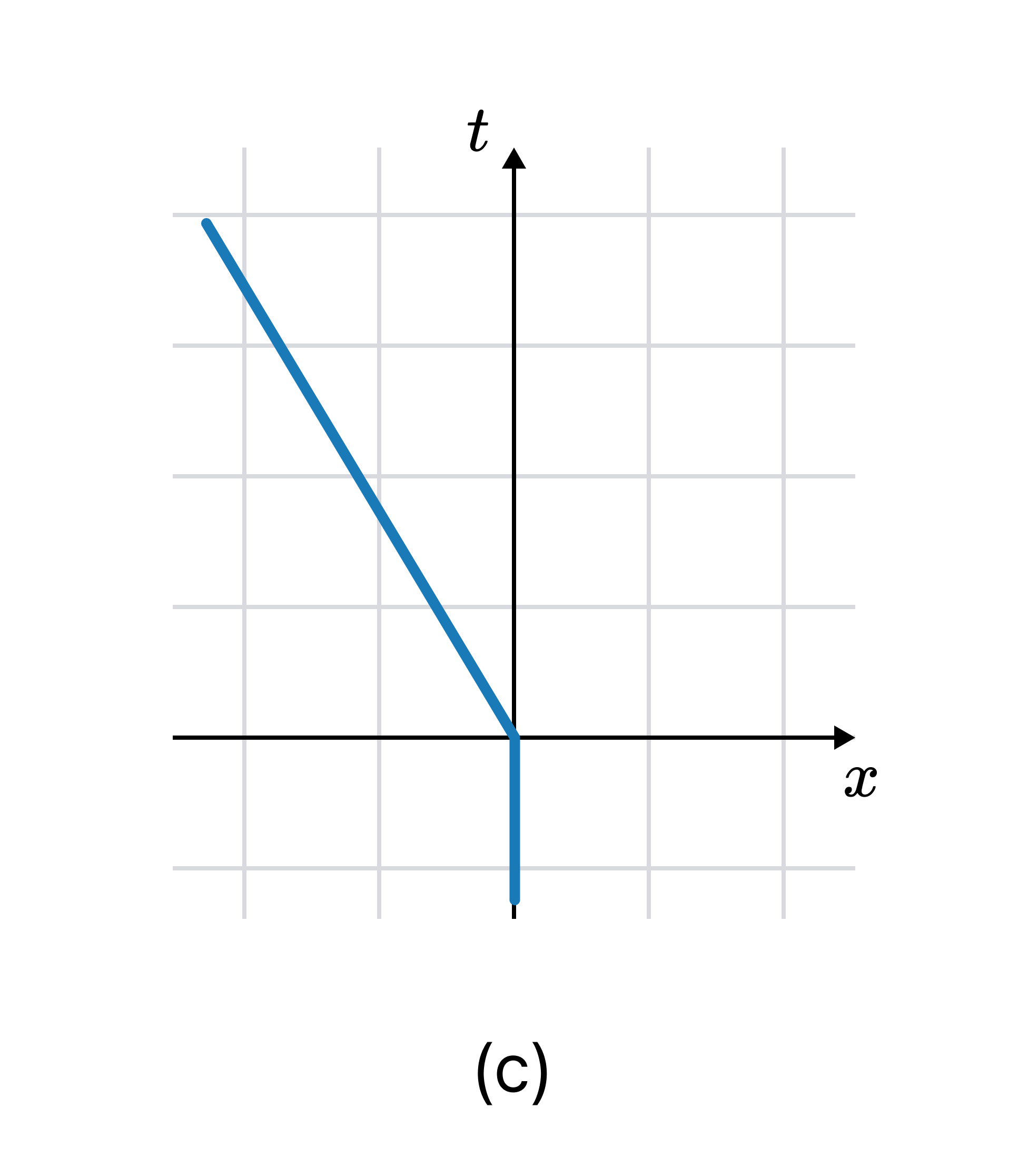
주목할 점은, (가)-(나)와는 달리 (가)-(다)는 같은 관성좌표계를 사용한다는 것이다. (가)-(다)의 변환은 관성좌표계의 변환이 아닌, A의 속도에 $-0.6c$가 더해졌다는 물리적 변화로 일어났다. 이처럼 물리적 변화로 인한 다이어그램의 변환을 능동적 변환이라고 한다.

일면 능동적 변환(나)와 수동적 변환(다)의 차이는 관점의 차이에 지나지 않는 것으로 보인다. 실제로 고전역학에서 능동적 변환과 수동적 변환은 동일시될 수 있으며, 이것은 고전역학에서 뇌터 정리를 적용할 수 있는 조건에 다름 아니다. 하지만 상대론에서 둘의 동일시는 매우 신중한 주의를 요구한다. 왜냐하면 상대론에서는 동시성의 상대성을 고려해야 하기 때문이다.

3. 동시성의 상대성

동시성의 상대성이 왜 중요한지 알아보기 위해 상황을 바꿔보자. 두 점입자 A, B가 빈 공간에서 서로 $c$의 거리를 유지하고 있다. 이 상황을 A에 대해 정지해 있는 관성좌표계 $(x, t)$와, A에 대해 $0.6c$로 움직이는 관성계 $(x’, t’)$으로 표현한 민코프스키 다이어그램은 각각 다음과 같다.

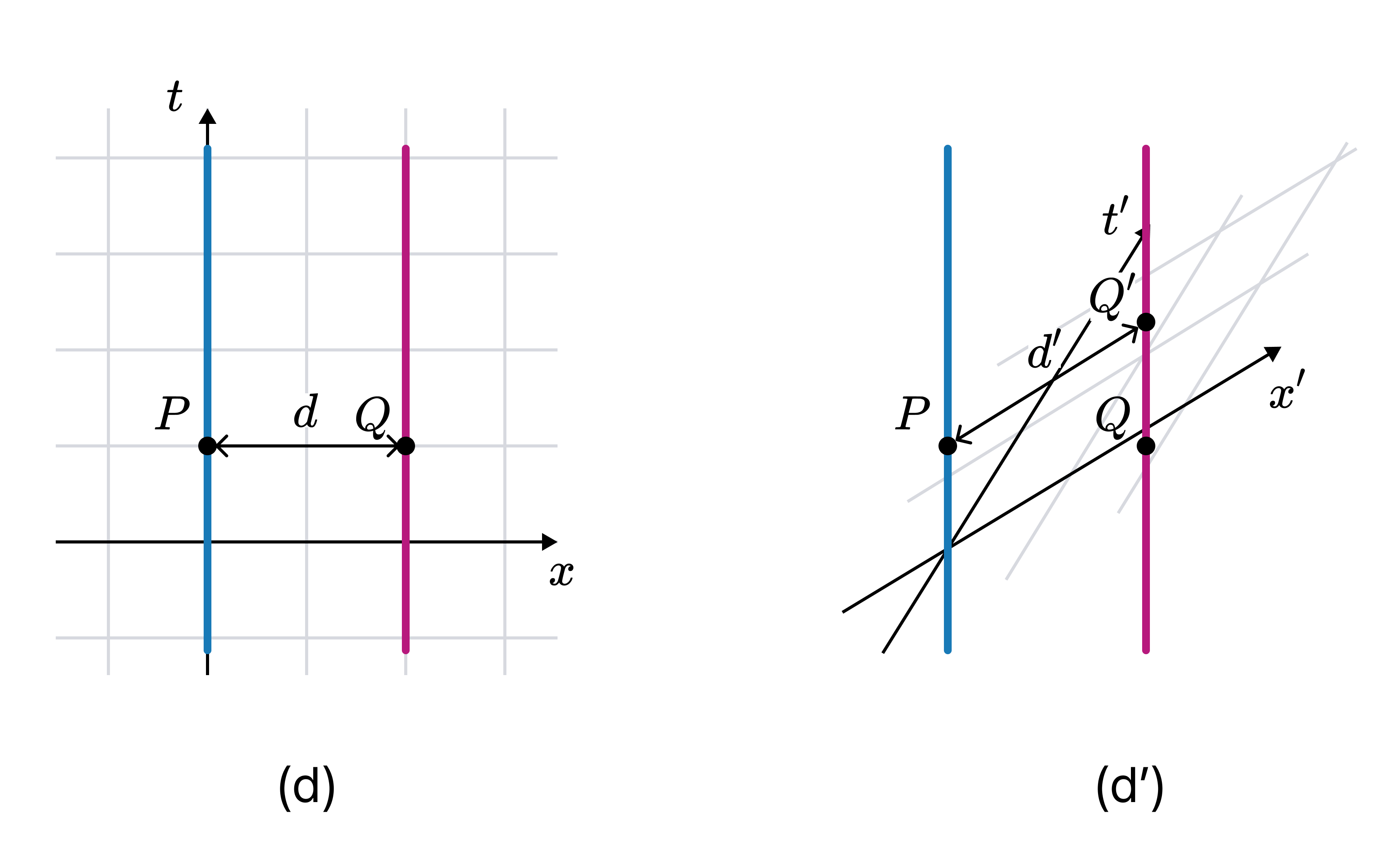
$(x, t)$에서 $P$와 $Q$가 동시적이므로 A, B의 거리는 $d$이다. 반면 $(x’, t’)$에서는 $P$와 $Q’$가 동시적이므로 A, B 거리는 $d’$이다. 민코프스키 기하학을 이용하여 계산하면 $d’ = 0.8c$ 이며 $d’ < d$이다.⁴

같은 현상을 능동적 변환으로 해석해 보자. A, B가 $c$의 거리를 유지하다가 $(x, t)$에 대해 동시에 $-0.6c$의 속도가 더해졌다고 하자. 민코프스키 다이어그램은 다음과 같다. $(x’’, t’’)$은 속도가 더해진 이후의 A를 기준으로 하는 관성좌표계이다.

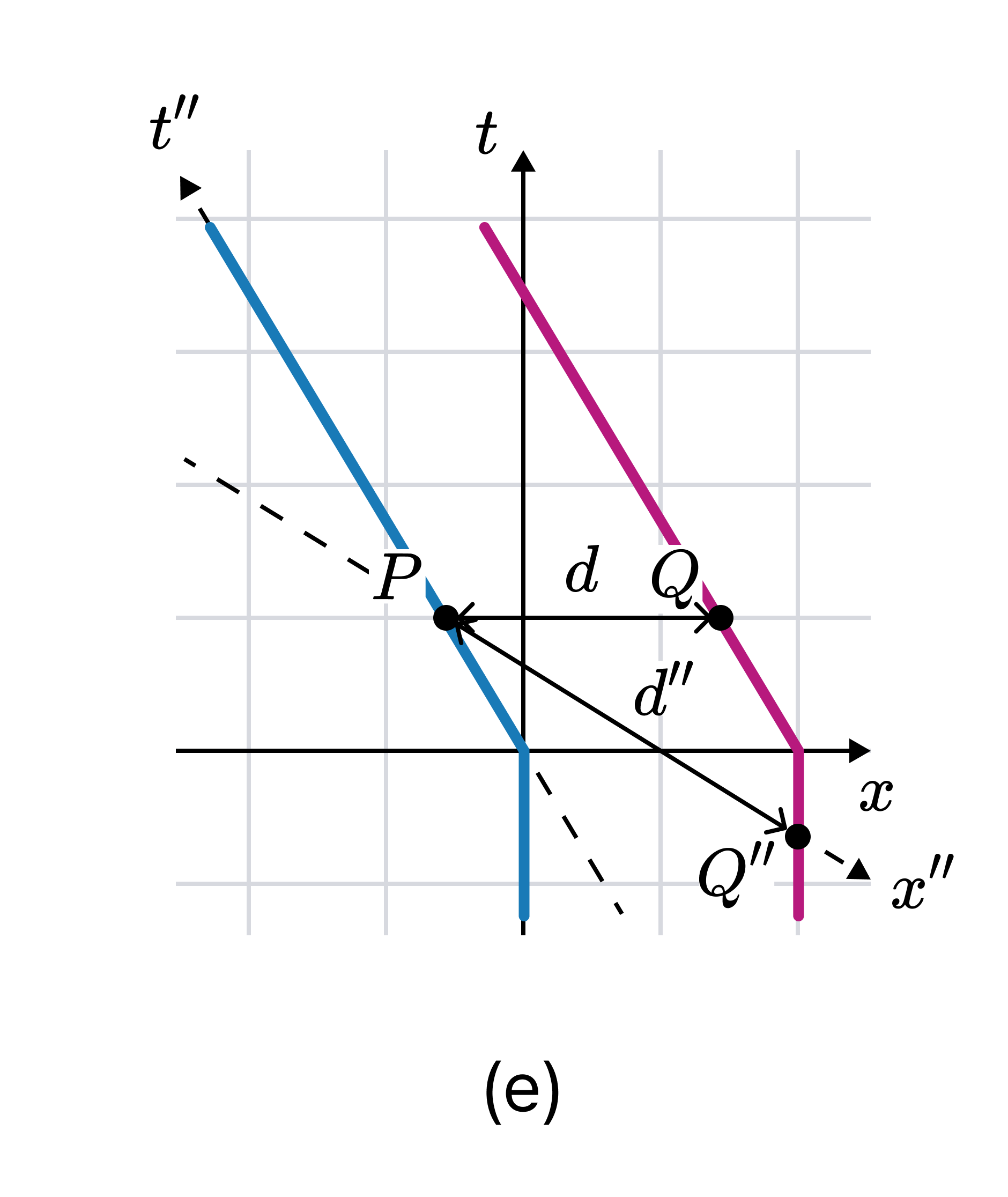
$(x, t)$에서 $(P, Q)$가 동시적이므로 A, B의 거리는 $d$이다. 반면 $(x’’, t’’)$에서는 $(P, Q’’)$가 동시적이므로 A, B의 거리는 $d’‘$이다. 마찬가지로 민코프스키 기하학을 이용하여 $d’‘$을 계산하면 $d’’ = 1.25c$ 이며 $d’’ > d$이다.

따라서 상대론에서는 수동적 변환과 능동적 변환 사이에 실질적인 차이가 있다. 수동적 변환은 A 관점의 거리를 유지시키고 새 관성좌표계 관점의 거리를 수축시키는 한편, 능동적 변환은 기존 관성좌표계 관점의 거리를 유지시키고 A 관점의 거리를 팽창시킨다.

A와 B의 거리	A 관점	A에 대해 움직이는 관성계 관점
수동적 변환	유지	수축
능동적 변환 (A와 B가 분리되어 있을 때)	팽창	유지

4. 강체의 능동적 변환

앞서 본 경우에는 A와 B가 분리되어 있었다. 이제 A와 B가 강체를 이루는 경우를 생각해 보자. 구체적으로 A, B가 길이가 $c$인 강철 막대기 M의 양끝점이라고 하자.

강체의 특징은 수용 가능한 변화에 대해 원 상태를 유지하는 성질을 가지고 있다는 것이다. 예를 들어 고무공은 강체가 아니기 때문에 힘을 가하면 부피가 줄어들거나 늘어나지만, 강철공은 부피가 변하지 않는다.

그렇다면 M이 능동적 변환에 가해졌을 때 무슨 일이 일어날 것인가? 예컨대 M이 관성좌표계 $(x, t)$에서 관성 운동하던 도중, M의 모든 부분이 “$(x, t)$에 대해 동시에” 가속하여 $0.6c$의 속도에 다다르면 M에는 무슨 일이 일어날 것인가?

M이 강체가 아니었다면 M의 길이는 A의 관점에서 $1.25c$로 팽창했을 것이다. 그러나 M은 강체이므로 자신의 원래 길이를 유지하려고 한다. 이에 따라 M이 가속하는 동안 M의 내부에서는 두 가지 효과가 대립하며 매우 복잡한 양상이 펼쳐진다.

• 효과 1: 동시성의 상대성으로 인해 B가 A보다 먼저 가속하여 M의 양끝이 잡아당겨진다.
• 효과 2: M의 강체적 특성으로 인해 M의 원자 구조가 효과 1에 저항하는 장력을 발생시킨다.

효과 2로 발생하는 내부 장력을 상대론적 장력(relativistic stress)이라고 부른다. 만약 M이 충분히 강한 강체라면 상대론적 장력을 버텨내어 M의 길이는 (A, B의 관점에서) $c$로 유지된다. 그러나 가속이 너무나 급격하여 상대론적 장력이 M의 수용 범위를 벗어나면 강체는 변형되거나 파괴된다. 일례로 쿠크다스를 광속에 가깝게 가속시키면 쿠크다스는 파괴된다.

5. 결론

A와 B의 거리	A 관점	A에 대해 움직이는 관성계 관점
수동적 변환	유지	수축
능동적 변환 (A와 B가 분리되어 있을 때)	팽창	유지
능동적 변환 (A와 B가 강체를 이룰 때)	유지	감소

이제 벨의 사고실험으로 돌아가자. 두 우주선 A, B가 가속할 때 “우주선-실-우주선” 계는 능동적 변환을 겪는다. A의 관점에서 두 효과가 관측된다.

• 효과 1: A와 B는 분리되어 있으므로 A와 B의 거리는 팽창한다.
• 효과 2: 팽팽히 당겨진 실의 강체적 특성에 의해 실의 길이는 유지된다.

이에 따라 가속이 일정 시간 이상 지속되면 효과 1이 효과 2를 압도하여 실은 끊어진다. 만약 A와 B가 실이 아니라 강철 케이블로 연결되어 있었다면 효과 2가 효과 1을 압도하여 A와 B는 (A 및 B의 관점에서) 일정한 거리를 유지하게 된다.

---

¹ 벨 부등식의 벨이 맞다.

² Rindler (1977), p. 41.

³ (나)와 (나’)은 같은 다이어그램이다. 이 부분이 이해가 안 된다면 이 글을 읽기에 앞서 로렌츠 변환과 민코프스키 다이어그램을 복습하자!

⁴ 그림에서는 $d’ > d$인 것으로 보이지만, 민코스프키 다이어그램의 기하학은 유클리드 기하학이 아닌 민코프스키 기하학임을 유념해야 한다. 평면지도에서는 알래스카가 아프리카와 거의 비슷한 크기이지만 실제로는 아프리카가 훨씬 더 크듯이, 민코프스키 다이어그램에서는 $d’ > d$인 것으로 보이지만 실제 로렌츠 변환을 계산하면 $d’ < d$이다.